Adaptive-Coefficient Finite Difference Frequency Domain Method for Solving Time-Fractional Cattaneo Equation with Absorbing Boundary Condition
Abstract
1. Introduction
2. Method
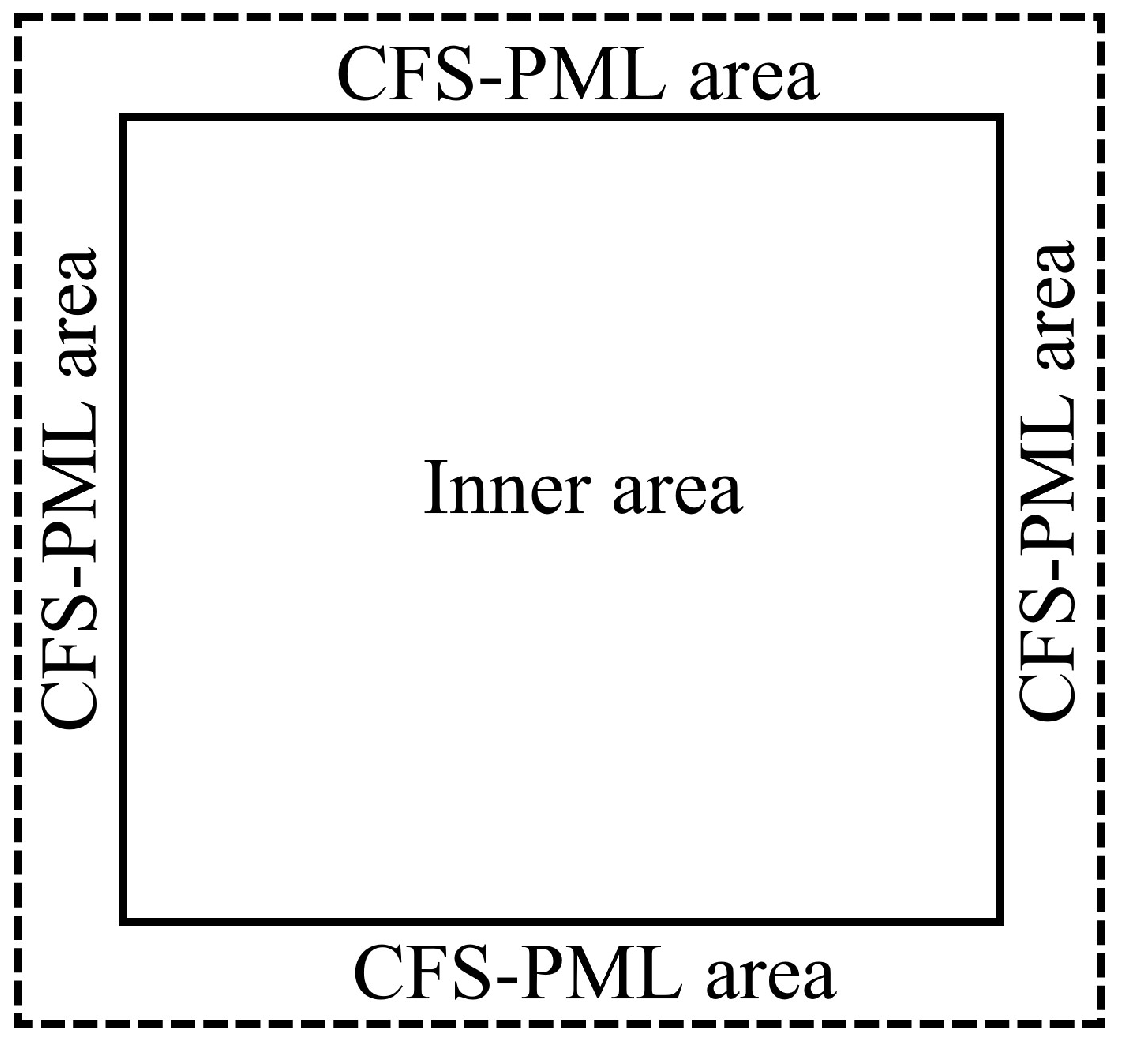
2.1. TFC Equation with CFS PML
2.2. AC FDFD Scheme
2.3. Adaptive FDFD Coefficients
2.4. Analytical Solution for 2D Homogeneous TFC Equation
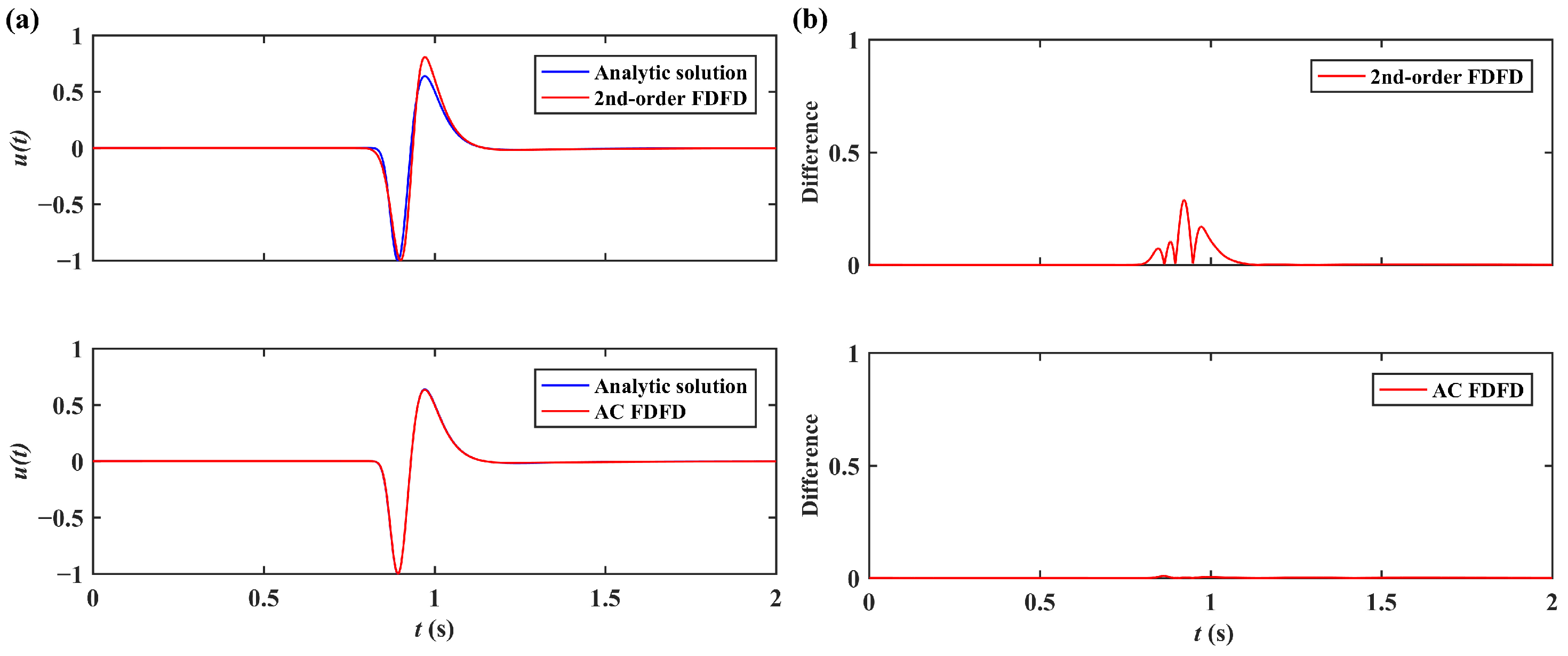
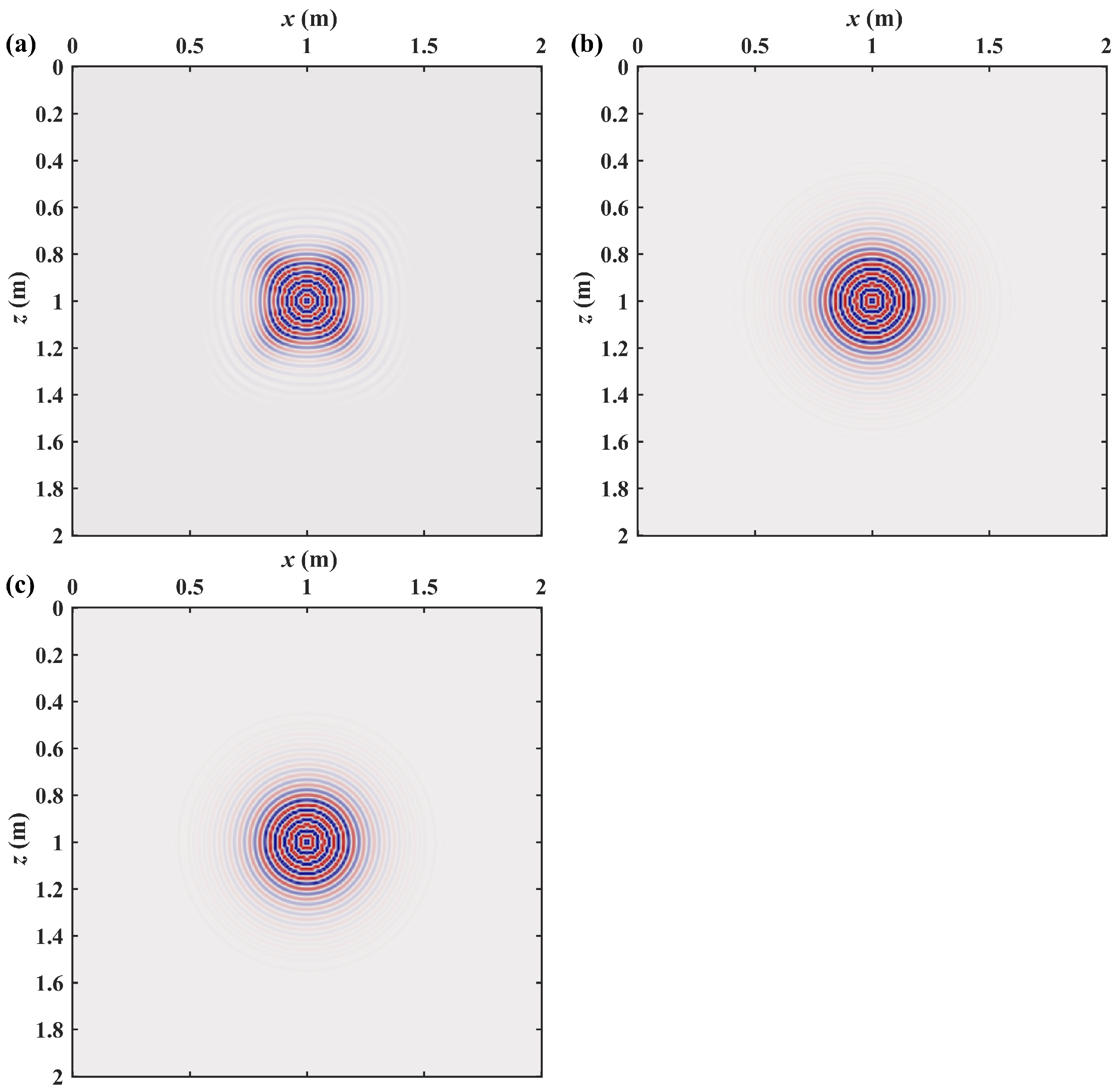
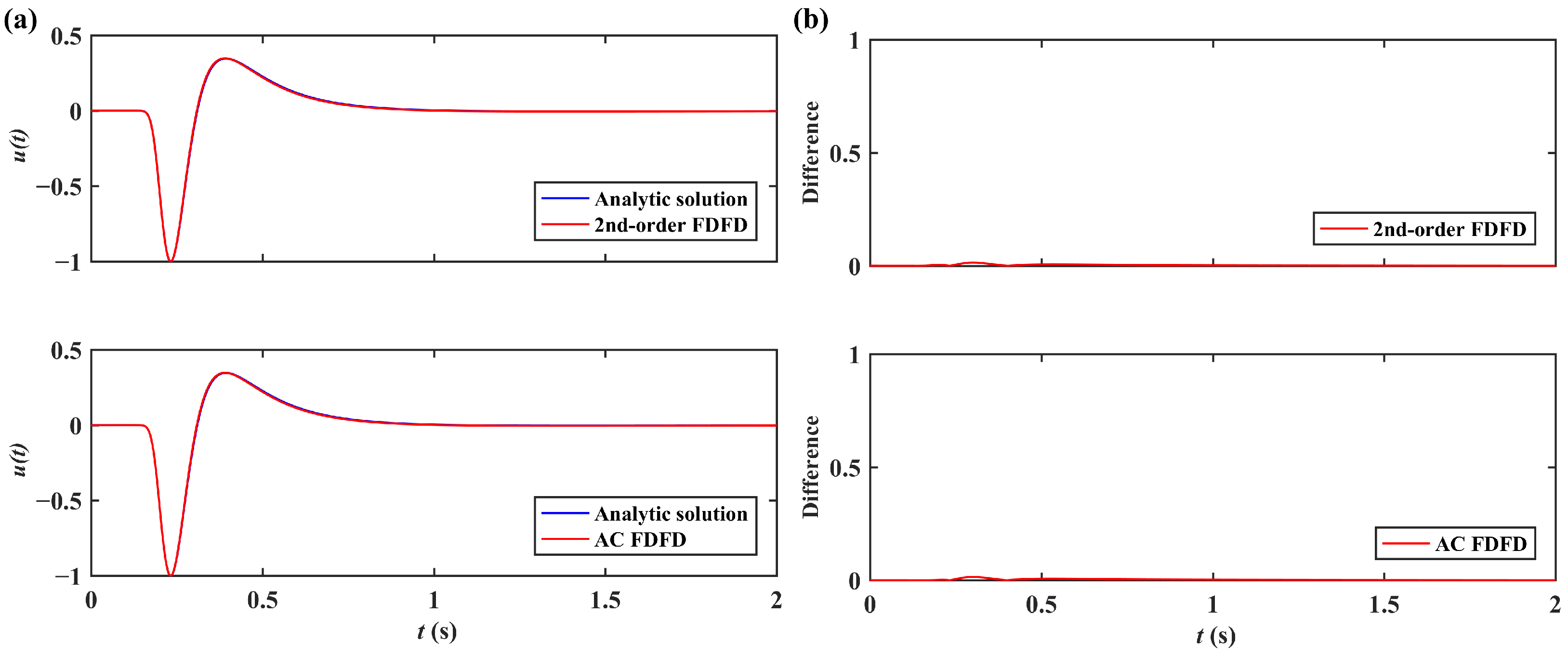
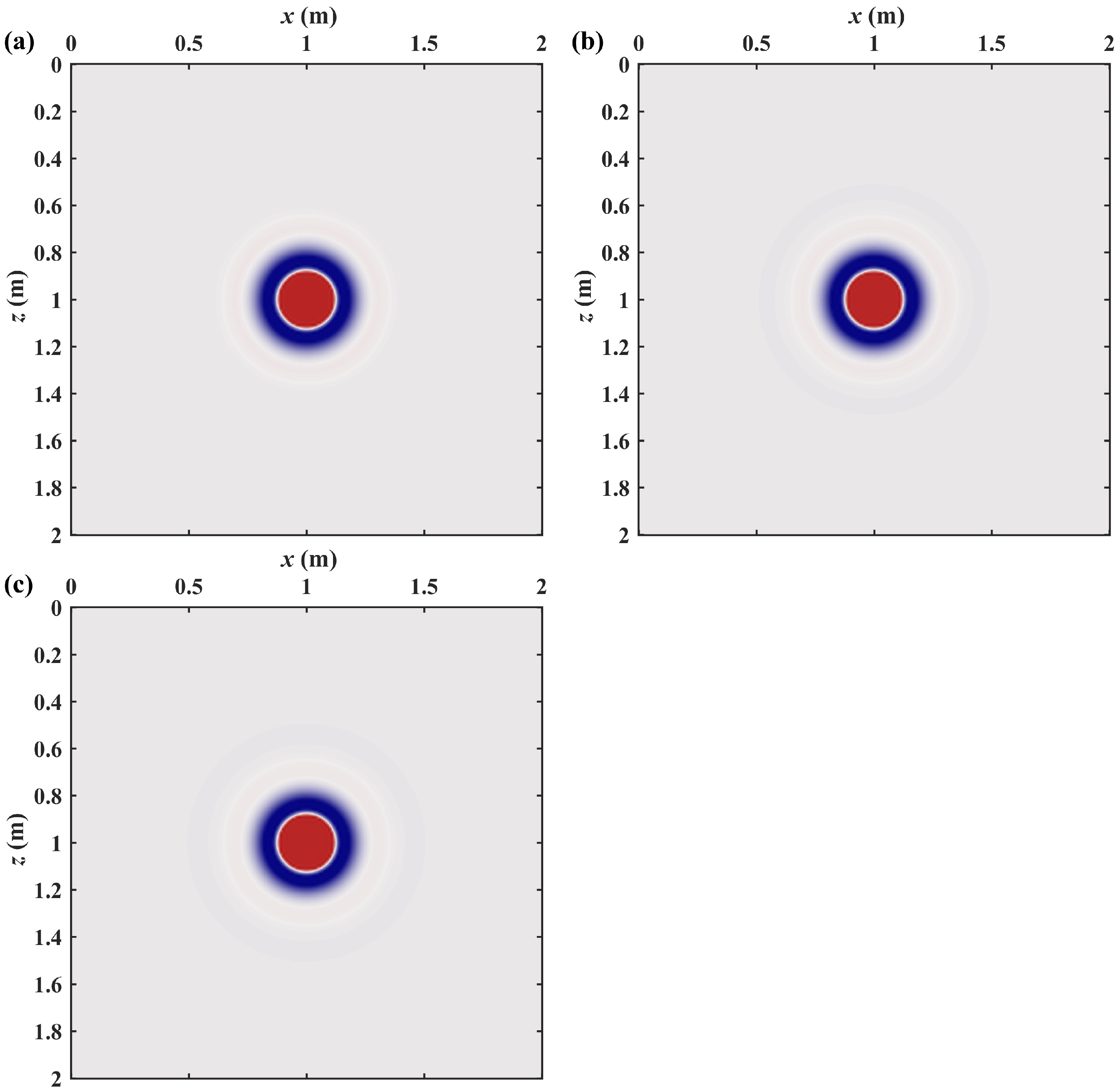
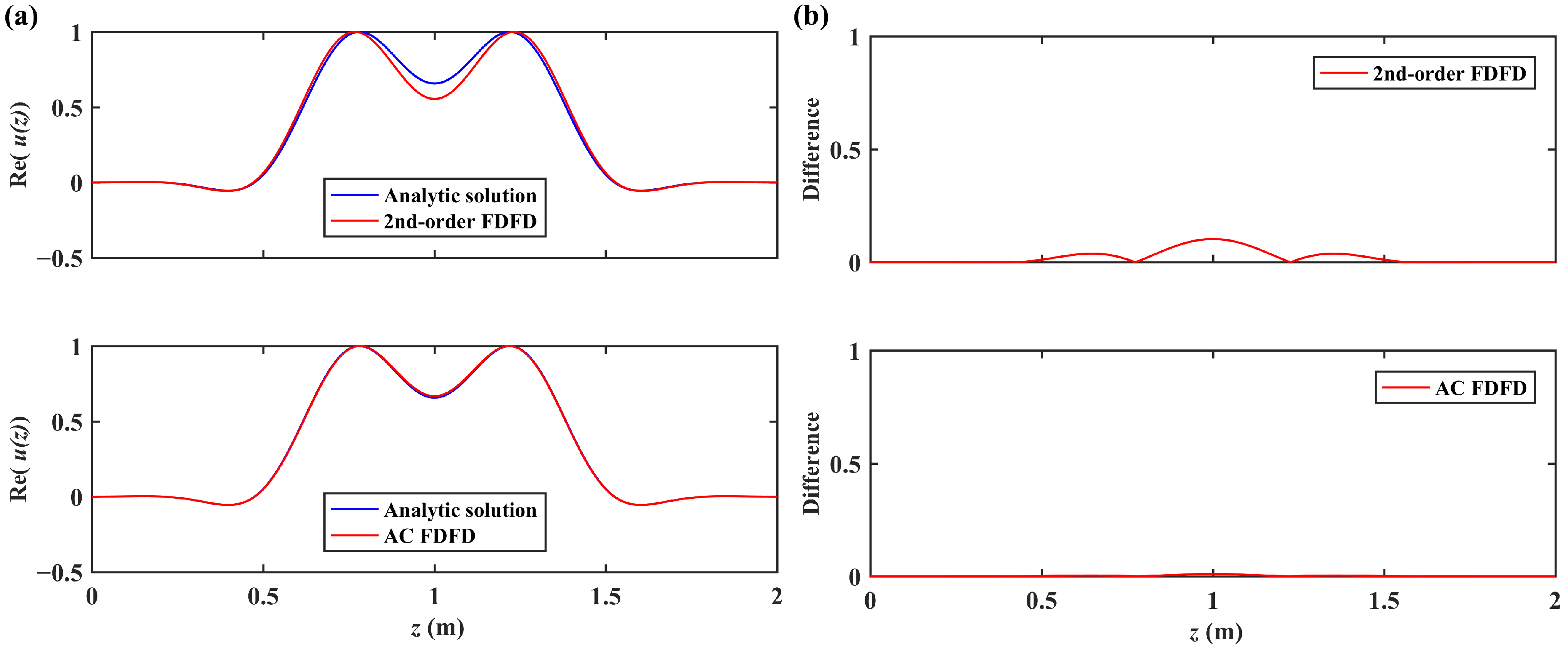
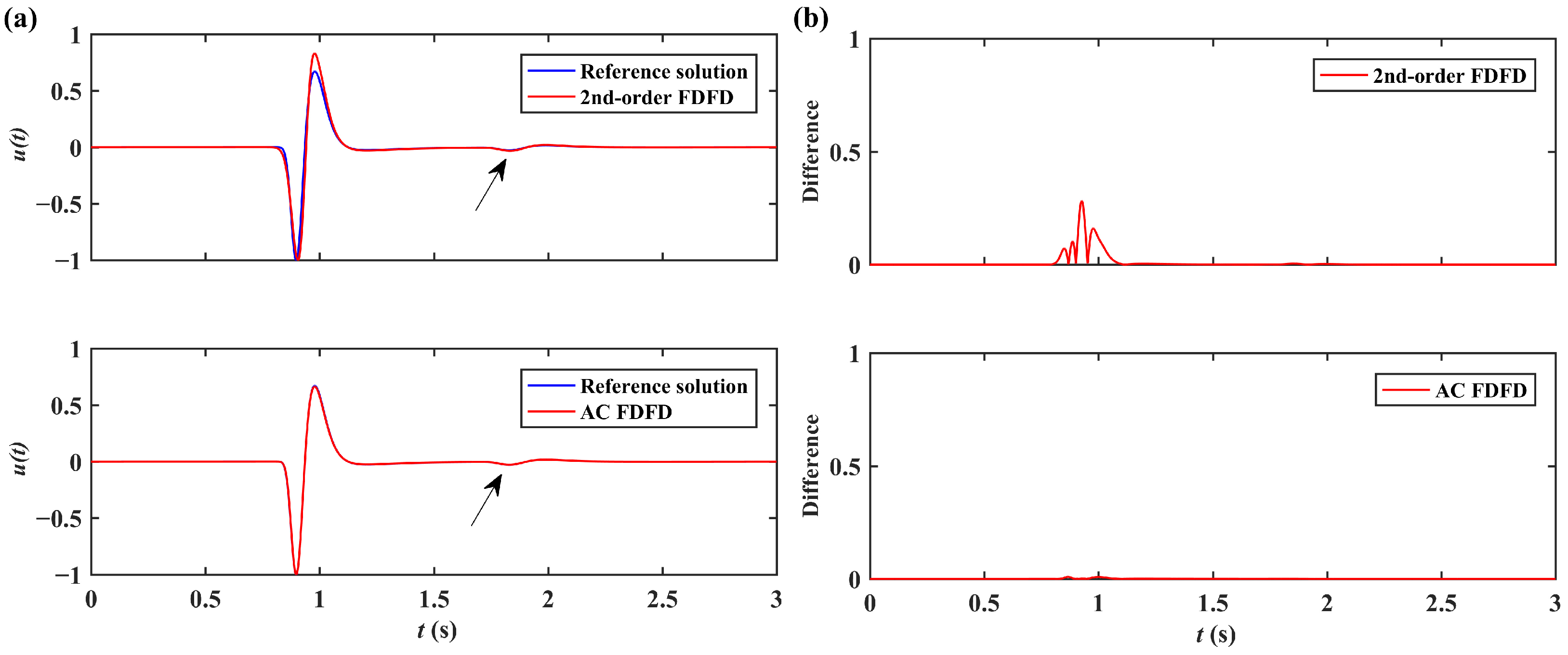
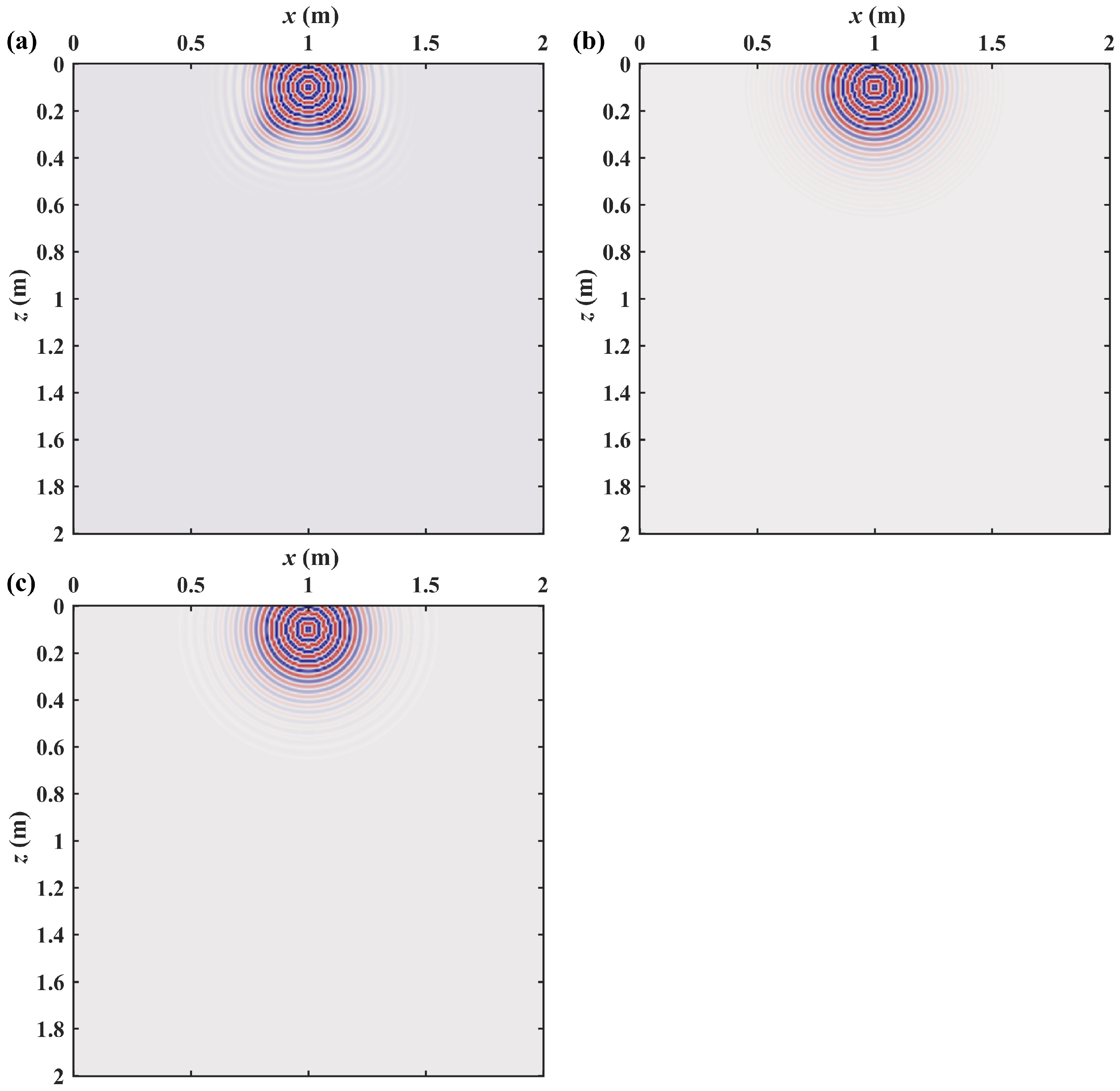
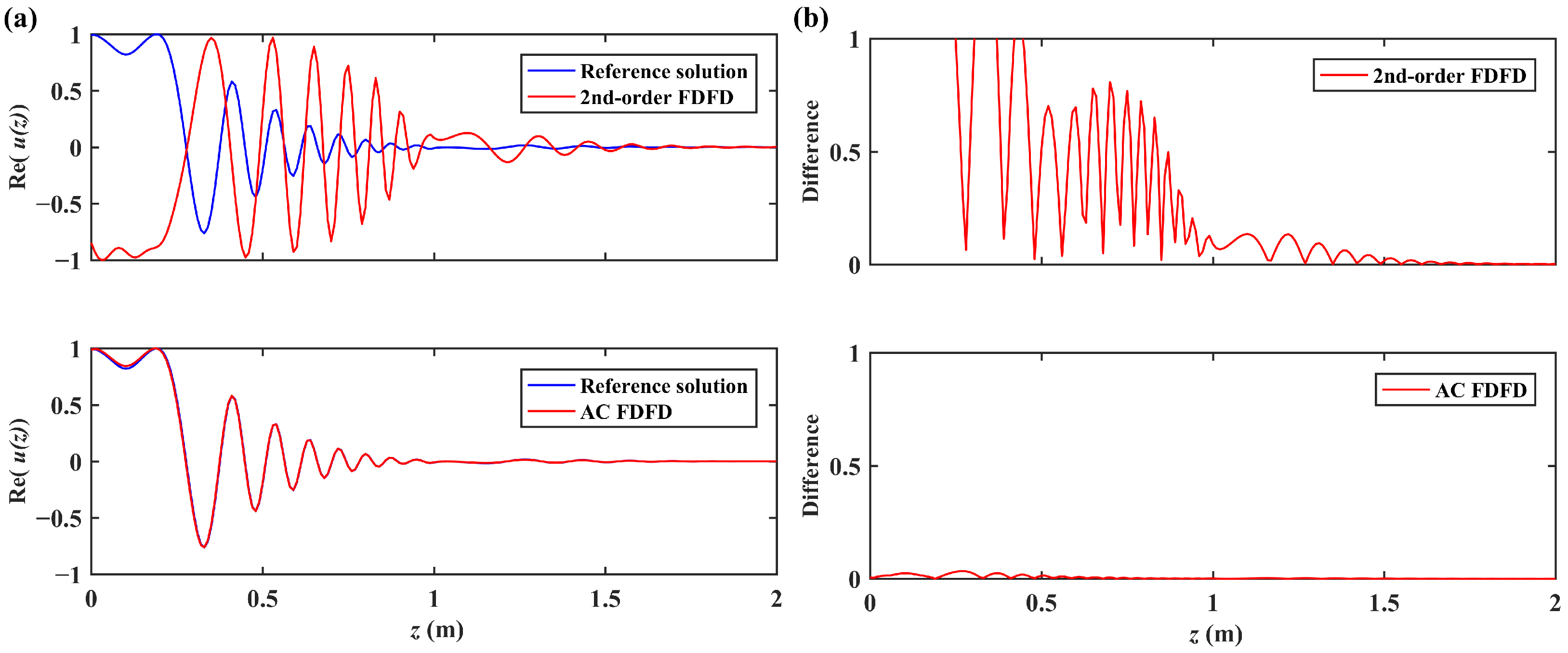
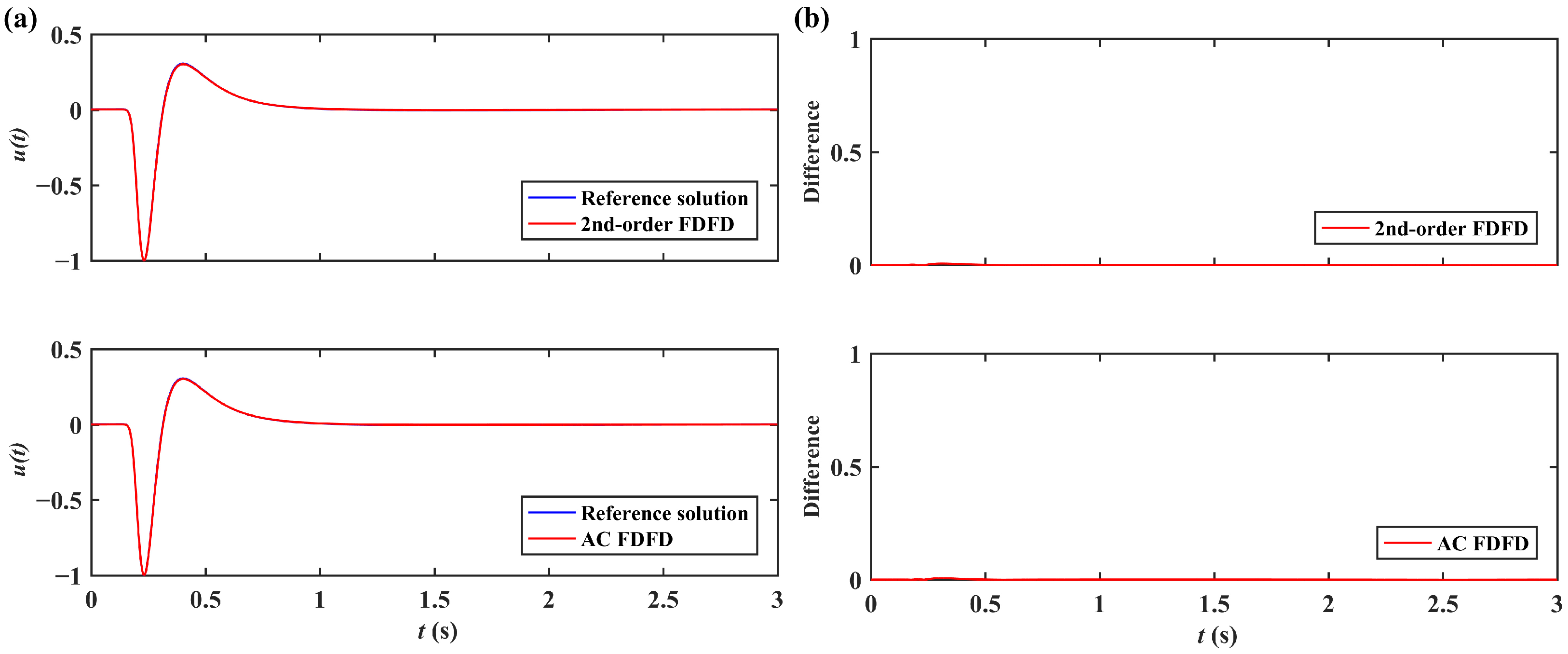
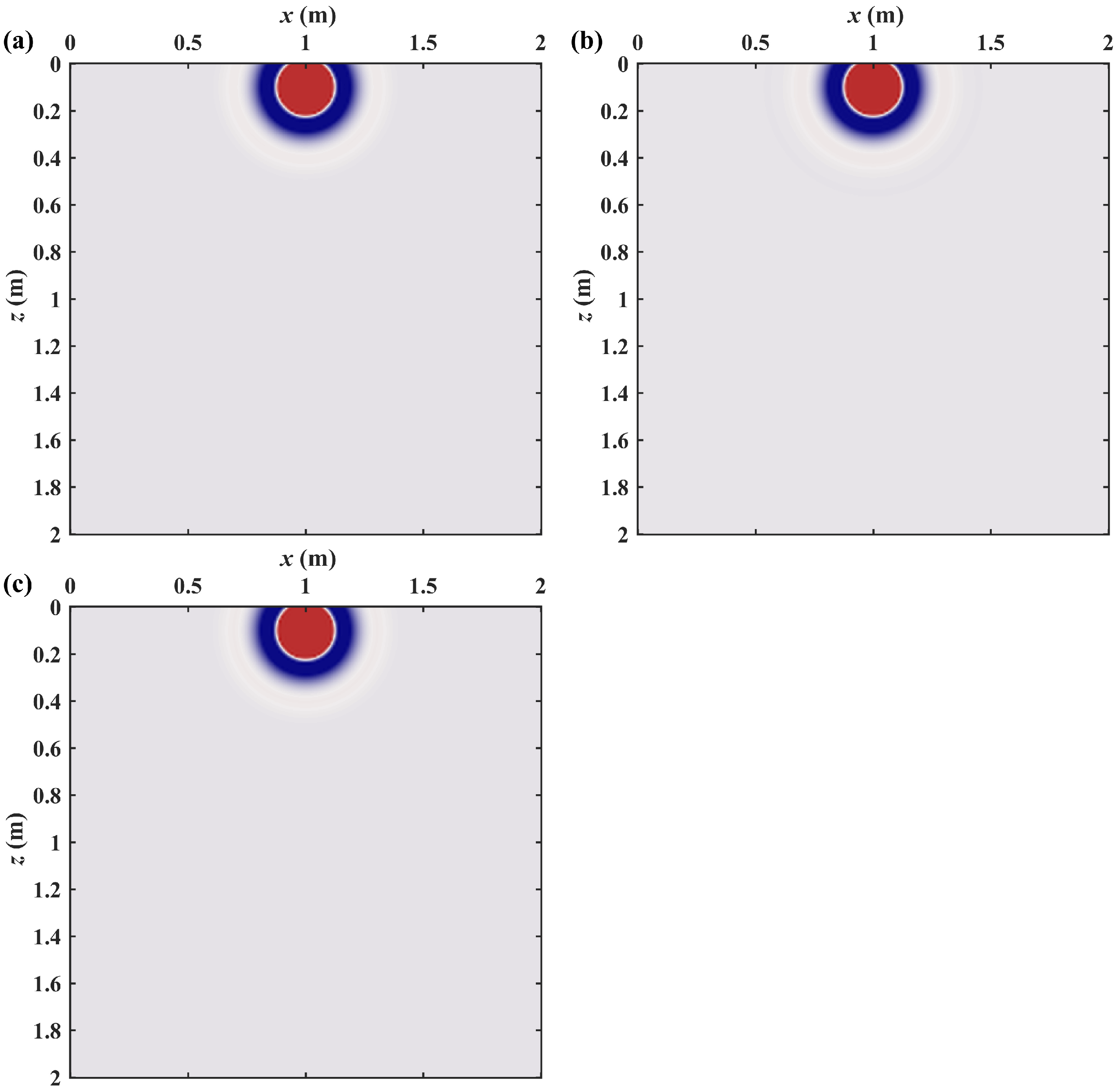
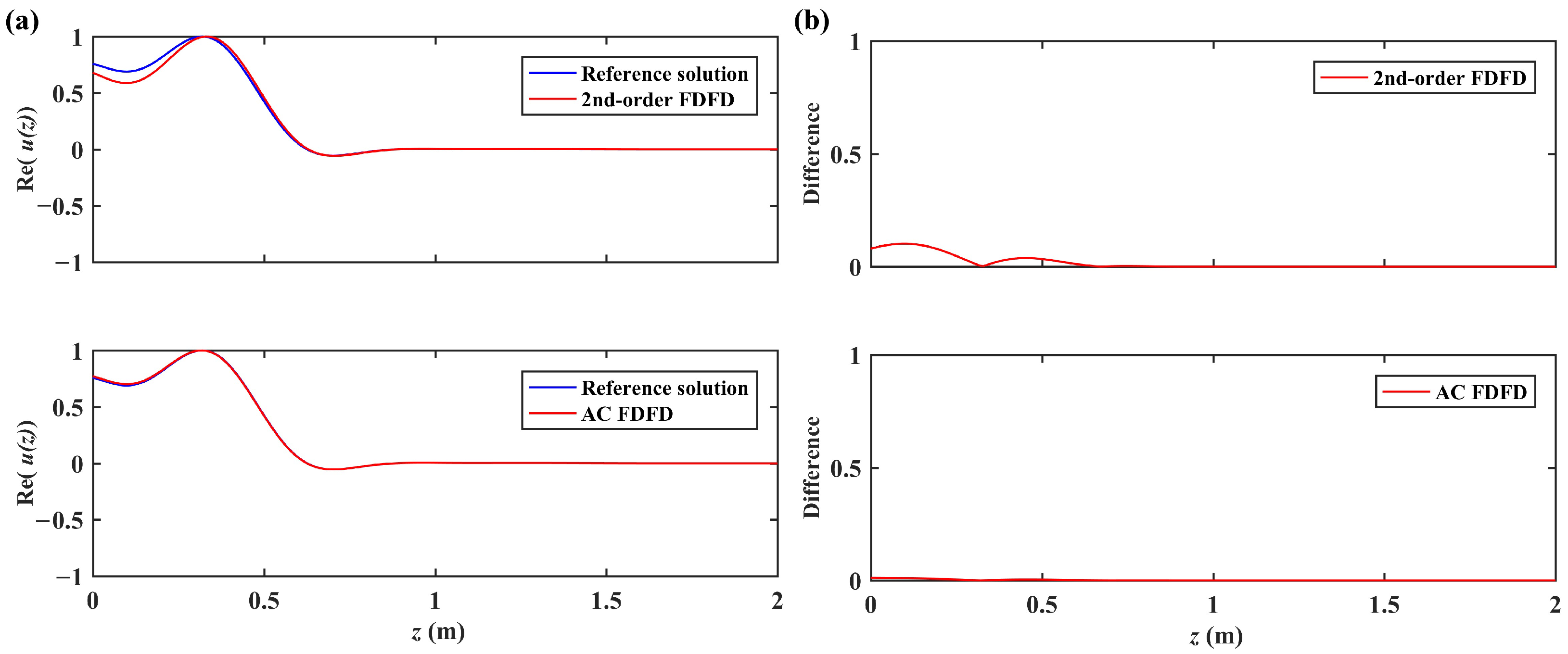
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Compte, A.; Metzler, R. The generalized Cattaneo equation for the description of anomalous transport processes. J. Phys. A Math. Gen. 1997, 30, 7277. [Google Scholar] [CrossRef]
- Awad, E.; Metzler, R. Crossover dynamics from superdiffusion to subdiffusion: Models and solutions. Fract. Calc. Appl. Anal. 2020, 23, 55–102. [Google Scholar] [CrossRef]
- Nong, L.; Yi, Q.; Cao, J.; Chen, A. Fast Compact Difference Scheme for Solving the Two-Dimensional Time-Fractional Cattaneo Equation. Fractal Fract. 2022, 6, 438. [Google Scholar] [CrossRef]
- Povstenko, Y. Fractional Cattaneo-type equations and generalized thermoelasticity. J. Therm. Stress. 2011, 34, 97–114. [Google Scholar] [CrossRef]
- Qi, H.; Jiang, X. Solutions of the space-time fractional Cattaneo diffusion equation. Phys. A Stat. Mech. Its Appl. 2011, 390, 1876–1883. [Google Scholar] [CrossRef]
- Qi, H.T.; Xu, H.Y.; Guo, X.W. The Cattaneo-type time fractional heat conduction equation for laser heating. Comput. Math. Appl. 2013, 66, 824–831. [Google Scholar] [CrossRef]
- Ghazizadeh, H.; Maerefat, M.; Azimi, A. Explicit and implicit finite difference schemes for fractional Cattaneo equation. J. Comput. Phys. 2010, 229, 7042–7057. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, Z.Z. Compact Crank–Nicolson schemes for a class of fractional Cattaneo equation in inhomogeneous medium. J. Sci. Comput. 2015, 62, 747–771. [Google Scholar] [CrossRef]
- Ren, J.; Gao, G.h. Efficient and stable numerical methods for the two-dimensional fractional Cattaneo equation. Numer. Algorithms 2015, 69, 795–818. [Google Scholar] [CrossRef]
- Wei, L. Analysis of a new finite difference/local discontinuous Galerkin method for the fractional Cattaneo equation. Numer. Algorithms 2018, 77, 675–690. [Google Scholar] [CrossRef]
- Li, H.; Jiang, W.; Li, W. Space-time spectral method for the Cattaneo equation with time fractional derivative. Appl. Math. Comput. 2019, 349, 325–336. [Google Scholar] [CrossRef]
- Chen, A.; Nong, L. Efficient Galerkin finite element methods for a time-fractional Cattaneo equation. Adv. Differ. Equ. 2020, 2020, 1–21. [Google Scholar] [CrossRef]
- Berenger, J.P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Fu, L.Y.; Wu, R.S. Infinite boundary element absorbing boundary for wave propagation simulations. Geophysics 2000, 65, 596–602. [Google Scholar] [CrossRef][Green Version]
- Xu, W.H.; Ba, J.; Carcione, J.M.; Yang, Z.F.; Yan, X.F. A simplified calculation for adaptive coefficients of finite-difference frequency-domain method. Appl. Geophys. 2023, 20, 1–16. [Google Scholar] [CrossRef]
- Zhang, L.X.; Fu, L.Y.; Pei, Z.L. Finite difference modeling of Biot’s poroelastic equations with unsplit convolutional PML and rotated staggered grid. Chin. J. Geophys. 2010, 53, 2470–2483. [Google Scholar]
- Fu, B.Y.; Fu, L.Y.; Wei, W.; Zhang, Y. Boundary-reflected waves and ultrasonic coda waves in rock physics experiments. Appl. Geophys. 2016, 13, 667–682. [Google Scholar] [CrossRef]
- Fu, L.Y.; Fu, B.Y.; Sun, W.; Han, T.; Liu, J. Elastic wave propagation and scattering in prestressed porous rocks. Sci. China Earth Sci. 2020, 63, 1309–1329. [Google Scholar] [CrossRef]
- Komatitsch, D.; Martin, R. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics 2007, 72, SM155–SM167. [Google Scholar] [CrossRef]
- Martin, R.; Komatitsch, D. An unsplit convolutional perfectly matched layer technique improved at grazing incidence for the viscoelastic wave equation. Geophys. J. Int. 2009, 179, 333–344. [Google Scholar] [CrossRef]
- Saenger, E.H.; Gold, N.; Shapiro, S.A. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion 2000, 31, 77–92. [Google Scholar] [CrossRef]
- Fu, L.Y.; Zhang, Y.; Pei, Z.; Wei, W.; Zhang, L. Poroelastic finite-difference modeling for ultrasonic waves in digital porous cores. Earthq. Sci. 2014, 27, 285–299. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, L.Y.; Zhang, L.; Wei, W.; Guan, X. Finite difference modeling of ultrasonic propagation (coda waves) in digital porous cores with un-split convolutional PML and rotated staggered grid. J. Appl. Geophys. 2014, 104, 75–89. [Google Scholar] [CrossRef]
- Yang, H.; Fu, L.Y.; Fu, B.Y.; Du, Q. Poro-acoustoelasticity finite-difference simulation of elastic wave propagation in prestressed porous media. Geophysics 2022, 87, T329–T345. [Google Scholar] [CrossRef]
- Yang, H.; Fu, L.Y.; Li, H.; Du, Q.; Zheng, H. 3D acoustoelastic FD modeling of elastic wave propagation in prestressed solid media. J. Geophys. Eng. 2023, 20, 297–311. [Google Scholar] [CrossRef]
- Hou, W.; Fu, L.Y.; Carcione, J.M.; Wang, Z.; Wei, J. Simulation of thermoelastic waves based on the Lord-Shulman theory. Geophysics 2021, 86, T155–T164. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, L.Y.; Deng, W.; Hou, W.; Carcione, J.M.; Wei, J. Simulation of wave propagation in thermoporoelastic media with dual-phase-lag heat conduction. J. Therm. Stress. 2023, 46, 1–19. [Google Scholar] [CrossRef]
- Bekri, Z.; ERTÜRK, V.S.; Kumar, P.; Govindaraj, V. Some novel analysis of two different Caputo-type fractional-order boundary value problems. Results Nonlinear Anal. 2022, 5, 299–311. [Google Scholar] [CrossRef]
- Prieur, F.; Holm, S. Nonlinear acoustic wave equations with fractional loss operators. J. Acoust. Soc. Am. 2011, 130, 1125–1132. [Google Scholar] [CrossRef]
- Pei, Z.; Fu, L.Y.; Sun, W.; Jiang, T.; Zhou, B. Anisotropic finite-difference algorithm for modeling elastic wave propagation in fractured coalbeds. Geophysics 2012, 77, C13–C26. [Google Scholar] [CrossRef]
- Chen, L.; Huang, J.; Fu, L.Y.; Peng, W.; Song, C.; Han, J. A Compact High-Order Finite-Difference Method with Optimized Coefficients for 2D Acoustic Wave Equation. Remote Sens. 2023, 15, 604. [Google Scholar] [CrossRef]
- Xu, W.; Zhong, Y.; Wu, B.; Gao, J.; Liu, Q.H. Adaptive complex frequency with V-cycle GMRES for preconditioning 3D Helmholtz equation. Geophysics 2021, 86, T349–T359. [Google Scholar] [CrossRef]
- Xu, W.; Wu, B.; Zhong, Y.; Gao, J.; Liu, Q.H. Adaptive 27-point finite-difference frequency-domain method for wave simulation of 3D acoustic wave equation. Geophysics 2021, 86, T439–T449. [Google Scholar] [CrossRef]
- Jo, C.H.; Shin, C.; Suh, J.H. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator. Geophysics 1996, 61, 529–537. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, S.; Xu, W.; Gao, J. Complex-valued adaptive-coefficient finite difference frequency domain method for wavefield modeling based on diffusive-viscous wave equation. Geophysics 2023, 89, 1–75. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Carcione, J.M.; Kosloff, D.; Kosloff, R. Wave propagation simulation in a linear viscoacoustic medium. Geophys. J. Int. 1988, 93, 393–401. [Google Scholar] [CrossRef]
- Petra, C.G.; Schenk, O.; Anitescu, M. Real-time stochastic optimization of complex energy systems on high-performance computers. Comput. Sci. Eng. 2014, 16, 32–42. [Google Scholar] [CrossRef]
- Ricker, N. Further developments in the wavelet theory of seismogram structure. Bull. Seismol. Soc. Am. 1943, 33, 197–228. [Google Scholar] [CrossRef]
- Dablain, M. The application of high-order differencing to the scalar wave equation. Geophysics 1986, 51, 54–66. [Google Scholar] [CrossRef]
- Liu, Y. Finite-difference numerical modeling of any even order accuracy. Oil Geophys. Prospect. 1998, 33, 1–10. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Ba, J.; Cao, J.; Luo, C. Adaptive-Coefficient Finite Difference Frequency Domain Method for Solving Time-Fractional Cattaneo Equation with Absorbing Boundary Condition. Fractal Fract. 2024, 8, 146. https://doi.org/10.3390/fractalfract8030146
Xu W, Ba J, Cao J, Luo C. Adaptive-Coefficient Finite Difference Frequency Domain Method for Solving Time-Fractional Cattaneo Equation with Absorbing Boundary Condition. Fractal and Fractional. 2024; 8(3):146. https://doi.org/10.3390/fractalfract8030146
Chicago/Turabian StyleXu, Wenhao, Jing Ba, Jianxiong Cao, and Cong Luo. 2024. "Adaptive-Coefficient Finite Difference Frequency Domain Method for Solving Time-Fractional Cattaneo Equation with Absorbing Boundary Condition" Fractal and Fractional 8, no. 3: 146. https://doi.org/10.3390/fractalfract8030146
APA StyleXu, W., Ba, J., Cao, J., & Luo, C. (2024). Adaptive-Coefficient Finite Difference Frequency Domain Method for Solving Time-Fractional Cattaneo Equation with Absorbing Boundary Condition. Fractal and Fractional, 8(3), 146. https://doi.org/10.3390/fractalfract8030146






