Abstract
In recent years, global attention to carbon emissions has increased, becoming one of the main drivers of global climate change. Accurate prediction of carbon emission trends in small and medium-sized countries and scientific regulation of carbon emissions can provide theoretical support and policy references for the effective and rational use of energy and the promotion of the coordinated development of energy, environment, and economy. This paper establishes a grey prediction model using the classical Logistic mathematical model in a determined environment to investigate the carbon emission system. At the same time, we use the basic principle of fractional-order accumulation to establish a grey prediction model with fractional-order Logistic and obtain the parameter estimation and time-response equation of the new model by solving the model through the theory related to fractional-order operators. The particle swarm optimization algorithm is used to complete the optimization process of the order of the fractional order grey prediction model and obtain the optimal model order. Then, the new model is applied to predict carbon emissions in five medium-emission countries: Ethiopia, Djibouti, Ghana, Belgium, and Austria. The new model shows better advantages in the validity analysis process, and the simulation results indicate that the new model proposed in this paper has stronger stability and better simulation and prediction accuracy than other comparative models, proving the model’s validity. Finally, the model is used to forecast the carbon emissions of these five countries for the five years of 2021–2025, and the results are analyzed, and relevant policy recommendations are made.
1. Introduction
Global carbon emissions are the main culprit of the greenhouse effect, which continues to affect the functioning of human society, with far-reaching impacts on the Earth’s climate and environment. In 2020, 25 scientists from the World Climate Research Program (WCRP) warned of a predicted increase in the Earth’s temperature of 2.6 °C to 3.9 °C if the amount of greenhouse gases in the atmosphere is doubled compared to the pre-industrial revolution level, triggering such disasters as glacier meltdowns and sea level rises. This global warming prediction has led to more urgent concerns about greenhouse gas emissions. One of the main components of greenhouse gases is carbon dioxide, and the sources of its emissions involve energy combustion, industrial manufacturing, transportation, and other aspects that are indispensable to the normal functioning of human society. Although these activities support social development, they are a major source of environmental threats. Against this background, addressing carbon emissions on a global scale has become an urgent task.
Concerning global climate change, there are common interests among countries that need to work together to face the challenges posed by climate change due to carbon emissions. The emission reduction efforts of large countries such as the United States, China, and Russia have attracted much attention. These countries are actively promoting the development of renewable energy, enhancing industrial upgrading, and promoting innovations in green transportation, among other things, to reduce carbon emissions. However, small and medium-sized countries are also indispensable in global emissions reduction goals. Although they do not emit as much as larger countries, their efforts to reduce emissions are equally important to realizing the global emissions reduction target. While these countries may face different challenges, their mitigation experiences and measures are also worthy of in-depth study to provide a more comprehensive perspective on global mitigation strategies.
Therefore, an in-depth study of the emission reduction actions of small and medium-sized countries is of great significance to realizing global emission reduction goals. Accurately predicting the trend of carbon emissions in small and medium-sized countries and scientifically regulating carbon emissions provide theoretical support and policy reference for the effective and rational use of energy and the promotion of the coordinated development of energy, the environment, and the economy, and by understanding the specific emission reduction initiatives, policy implementation and results achieved by these countries, we can gain a more comprehensive understanding of the actual situation of global emission reduction. This provides an opportunity for countries to draw on and learn from each other and helps form more effective and sustainable emission reduction strategies. Small and medium-sized countries may face unique challenges in terms of limited resources and relatively low levels of technology. However, it is through studying these challenges and responses that more comprehensive solutions can be provided for global emissions reduction. In jointly addressing the issue of carbon emissions, countries should work together to promote scientific and technological innovation and sustainable development to create a more sustainable and healthier environment for the planet’s future.
2. Literature Review
2.1. The Research on Carbon Emissions
The rapid growth of carbon emissions has people’s concerns simultaneously. However, it also spawned more related discussions and research on how to inhibit or reduce carbon emissions, how scientific and effective cooperation manage carbon emissions, and other issues that need to be resolved urgently. Many scholars on carbon emissions from various perspectives carry out a series of research, which has resulted in many valuable research results.
Among the studies on carbon quota allocation for individual countries or specific enterprises, Dong et al. [1] used a zero-sum game data envelopment model (ZSG-DEA) to discuss the initial allocation of regional quotas and the optimal carbon quota scheme based on the Chinese government’s expected carbon emission targets and economic and social development indicators. The study’s conclusions are important policy guidance for establishing a fair and effective carbon quota allocation mechanism, realizing the national total carbon emission control target, stimulating the vitality of the unified carbon market, and promoting regional coordinated emission reduction. Yuan et al. [2] proposed a two-tier collaborative demand-side management framework that allows users to participate in demand response for distributed energy systems. This ensures that the system’s carbon emissions do not exceed the quota while minimizing the impact on thermal comfort. This study is of great significance in promoting user participation in distributed energy systems for energy conservation and carbon reduction.
Regarding the carbon price prediction research in each carbon trading market, Ding et al. [3] proposed a new hybrid prediction model to predict the carbon price in China’s unified carbon market by combining the improved complete ensemble empirical mode decomposition with adaptive noise (iCEEMDAN), the variational mode decomposition (VMD), and the three-stage algorithm of fine-to-coarse (REC) data reconstruction. The proposed hybrid prediction model can more effectively help enterprises make decisions in the face of nonlinear, non-stationary, and irregular carbon prices, which is conducive to implementing the government’s energy-saving and emission-reduction policies. Wang et al. [4] developed a novel ensemble prediction system for point and interval carbon price forecasting based on data decomposition, feature selection, optimal sub-model determination, and improvement through multi-objective optimization. This system aims to provide a scientific and comprehensive reference for the carbon trading market. Considering the alignment between prediction models and carbon price markets, Cao et al. [5] designed a decomposed ensemble carbon price forecasting method incorporating a reinforcement learning model fusion. The model was validated in seven carbon trading markets, and experimental results demonstrated superior and stable predictive performance compared to other methods. The proposed model can serve as a feasible tool for the assessment and management of carbon price market prices.
Among the studies on energy saving and emission reduction in various industries, Zhang et al. [6] conducted a study using carbon emission rights trading pilot companies listed in the non-financial sector of the A-share market in China as samples. They employed a difference analysis method to examine the impact of carbon emission rights trading on the financial asset allocation of these companies. The analysis revealed a positive correlation between carbon emission rights trading and corporate financialization, which was more pronounced in non-state-owned enterprises, carbon-intensive enterprises, and companies operating in regions with developed financial markets or significant fluctuations in the carbon market. Ou et al. [7] used Guangdong Province, China, as an example to assess the land use carbon emissions (LUCE) at the city level in emerging economies through the extended STIRPAT model. The results of the study showed that the importance of construction land use planning and management in achieving emission reduction targets is increasing daily. Ma et al. [8] investigated the impact of the commercial building industry on carbon emissions, conducting case studies using various urban clusters. Their research made significant contributions to the analysis of carbon emission peaks in the Chinese commercial building industry.
2.2. The Research on Carbon Emissions Forecasting
Carbon emission is an important indicator to judge the overall trend, but also the focus of attention of countries. A timely and effective grasp of the changes in carbon emissions will help governments adjust the emission reduction measures promptly, so many scholars have researched the prediction of carbon emissions and have obtained some results. Generally, the prediction methods are divided into the following categories: statistical models, nonlinear intelligent prediction models, grey prediction models, and so on.
In terms of statistical modeling, Senatro et al. [9] used regression analysis to predict the energy demand in Italy and achieved better results. Son et al. [10] used statistical downscaling analysis to analyze the climate situation of the Korean Peninsula. Finally, they obtained the relationship between temperature increase and carbon dioxide emission, which can effectively predict Earth’s future climate. In terms of nonlinear intelligent modeling, Ahmadi et al. [11] used an artificial neural network (ANN) method, known as the grouping method of data processing (GMDH), to determine the emissions of the most important greenhouse gas, carbon dioxide, based on the proportion of various energy sources in the primary energy supply and gross domestic product (GDP), which is an indicator of economic activity, and the proposed method effectively improves the accuracy in predicting carbon dioxide emissions. Ye et al. [12] proposed a novel carbon emission prediction framework combining linear and machine learning models by integrating the autoregressive integrated moving average (ARIMA) and support vector regression (SVR) models, which take into account both temporal dynamics and external influences. Simulation results show that the proposed model has a stronger prediction performance than the benchmark model. Khajavi et al. [13] used a hybrid Random Forest, support vector regression, and response surface methodology to predict the CO2 emissions of 30 major cities in China. Jeong et al. [14] proposed a statistical forecasting model for predicting carbon emissions in the South Korean construction industry based on three models, including regression analysis. The model presented by them demonstrated high accuracy. Huang et al. [15] utilized principal component analysis to extract four major carbon emission influencing factors. They then employed Long Short-Term Memory (LSTM) to forecast carbon emissions in China, showcasing the effectiveness of principal component analysis and LSTM in carbon emission prediction. Ruiz et al. [16] introduced a time series clustering method for predicting energy consumption in public buildings, achieving favorable results.
Among the statistical models, a regression model can analyze the correlation between factors, which requires a large amount of valid data for simulation and verification. The time series model considers the impact of historical data on the current data, which requires the data to be sensitive to changes in time; nonlinear intelligent computing models such as neural networks, a research hotspot in recent years, which can learn the characteristics of the sample data by changing the network architecture and parameter settings. However, it also requires a large amount of data for determining the parameters. There may be a case of overfitting, which results in high accuracy of model simulation, but the actual predictive effect is not good.
To summarize, there are two main issues in the research of carbon emission prediction. On the one hand, the relevant data on carbon emission are only within the last 20 years, and the data samples are relatively small, so the model training results of the nonlinear intelligent model may not be satisfactory. On the other hand, carbon emission is primarily affected by external factors, such as socio-economic development, population growth, and others. Hence, the classical statistical model with a simpler structure makes it difficult to accurately describe the correlation. Therefore, there is a need for a model suitable for small-sample cases, which can consider the important influencing factors relatively completely and make more accurate predictions of carbon emissions. The grey prediction model happens to have such a nature.
2.3. The Research on Grey Prediction Model and Carbon Emission Forecasting
Deng proposed a “small sample, poor information” uncertain system as the object of study of the grey system theory in 1982 [17] and gave the theory based on the grey prediction model of the basic modeling steps and mechanisms, which has a high accuracy and stability. The grey theory includes the grey prediction model [18,19], the grey correlation model [20], and other theoretical parts. The grey prediction model can be relatively simple in structure, easy to calculate, and has good simulation and prediction performance [21]. Its results have been generally recognized by scholars at home and abroad and are widely used in many fields, such as energy [22,23,24], economy [25,26], transportation [27,28,29,30], and so on. Since carbon emissions are mainly based on small-sample data, in recent years, due to the excellent performance of the grey model in small-sample prediction, many scholars have considered using the grey prediction model for modeling and calculation and have achieved better results [31,32,33,34,35,36,37,38,39]. For example, Wu et al. [31] proposed a new grey prediction model and effectively applied it to predict carbon dioxide emissions in the BRIC countries. Javed et al. [32] improved the existing grey prediction model GM(1,1) by proposing an optimized model. They applied this model to forecast the consumption of biofuels in major CO2-emitting countries. Gao et al. [33] considered Gompertz’s law of slowing down the growth of carbon emissions to establish Gompertz’s differential equation, which was transformed into a fractional cumulative grey Gompertz model and effectively applied it to the prediction of carbon emissions in the US industry. Cheng et al. [34] established a combined Markov model applied to the prediction accuracy of carbon emissions from the transportation sector in China. They put forward some policy recommendations to the relevant departments to reduce the intensity of carbon emissions in the transportation sector. Zeng et al. [35] proposed an improved grey system model and applied it to predict the production of coalbed methane in China. Nie et al. [36] established a novel multivariate grey differential dynamic prediction model for analyzing and predicting China’s carbon emissions. Şahin et al. [37] combined the linear and nonlinear metabolic grey models with optimization techniques to propose an optimized nonlinear metabolic grey model to predict GHG emissions in Turkey. Zhao et al. [38] proposed a grey prediction model that effectively predicts the carbon emissions of 30 Chinese provinces by combining manta ray foraging optimization algorithms to find the optimal heterogeneity coefficients. Wang et al. [39] introduced a novel multivariate grey prediction model and applied it to forecast energy consumption in seven regions of China.
The accumulation technique is an important part of the modeling mechanism of the grey prediction model, and the above grey prediction model is built on the basis of first-order accumulation and gets better results. The fractional order theory has been applied to various fields in recent years. The grey system theory also introduces the fractional order theory, which is mainly put forward by Wu [40] under the influence of the “in-between” idea of the fractional order cumulant theory, which is to transform the original irregular fluctuation sequence into an exponential form through the cumulant operator to weaken the randomness of the data and show the regularity of the data, which is the most important component of the modeling mechanism. Many scholars are also studying the grey prediction model of fractional order [27,28,29,30,31,32,33]. For example, Wang et al. [41] proposed a reverse cumulative fractional order grey prediction model with a time power term. They applied it to the power generation of five clean energy sources in China: biomass, wind, nuclear, natural gas, and hydroelectricity to achieve better results. Wang et al. [42] proposed a new grey prediction model with a fractional-order grey Eulerian model with dynamic cumulative order and accurately predicted China’s hydroelectric power generation, China’s natural gas production, and China’s total primary energy production. Chen et al. [43] proposed a grey model with fractional Hausdorff derivatives, which has higher prediction accuracy than the traditional fractional and grey models. He et al. [44] introduced an enhanced fractional cumulative grey model with order optimization constraints through matrix decomposition, functional analysis, numerical simulation, and other perspectives. Zhang et al. [45] proposed a novel fractional discrete dynamic multivariate grey model to forecast food demand. The model is based on the discrete modeling idea, which considers the influence of the changing trend of the correlation factor series and improves the prediction accuracy and robustness. Yang et al. [46] proposed a novel structurally adaptive discrete fractional-order grey Bernoulli model, which uses a well-performing differential evolutionary algorithm to optimize the model in terms of the order, and better prediction performance can be obtained. Yan et al. [47] established a fractional-order multivariable time-lag discrete grey model to predict the trend of short-term online public opinion, and compared with the related grey model, the new grey model has higher prediction accuracy.
Accumulation and subtraction of information processing, as the main method of the grey system, occupies a very important position in the theory of the grey system. At the same time, the fractional-order cumulative generating operator is the basis for establishing the fractional-order grey prediction model. The above studies are some of the results of the fractional-order grey prediction model in recent years. The research methods of these results and the nature of the fractional-order grey cumulative operator help to enrich the theory of the fractional-order grey operator and lay the theoretical foundation for the fractional-order grey prediction model.
The fractional-order grey prediction model is currently a focal point in grey prediction model research, and our study also addresses this prominent issue. While there are existing studies on the application of grey prediction models to carbon emission forecasting, there are limited studies specifically focusing on small countries. The primary objective of our study is to apply the grey prediction model to carbon emissions in small and medium-sized countries and, subsequently, to summarize the experiences related to carbon emissions in these nations. Therefore, we introduce a novel approach by combining the classical Logistic model with fractional-order operator theory to create a fractional-order grey Logistic model for carbon emission prediction. The key contributions include:
- Integration of the classical Logistic model with the grey prediction mechanism to establish a grey Logistic prediction model. Introduction of the fractional-order cumulative operator theory to formulate a new fractional-order Logistic grey prediction model. Utilization of the particle swarm optimization algorithm to optimize the fractional-order grey prediction model, determining the optimal model order;
- In-depth examination of CO2 emissions in five medium-emission countries (Ethiopia, Djibouti, Ghana, Belgium, and Austria) using four grey models. Through thorough analysis and comparison of results, the proposed fractional grey model demonstrates superior stability, simulation, and prediction accuracy compared to the other three models, affirming its effectiveness;
- Effective application of the new fractional-order logistic grey prediction model in forecasting the five-year CO2 emissions for the mentioned countries from 2021 to 2025. We also conclude with policy recommendations based on the analysis of the prediction results.
The remainder of the paper is structured as follows: Section 3 develops a fractional order logistic grey prediction model, solves the model through the theory related to fractional order operators, and proves and discusses the nature of the model and the modeling mechanism. Section 4 applies the model to the CO2 emission examples of five medium-emission countries, namely, Ethiopia, Djibouti, Ghana, Belgium, and Austria; Section 5 describes the five-year CO2 emissions of the five countries for the period 2021–2025 for an effective forecast; and Section 6 concludes the paper.
3. Fractional Order Logistic Grey Prediction Model
This Section introduces the establishment of the logistic grey prediction model, the theory related to the fractional order operator, and the establishment of the fractional order logistic grey prediction model, as well as investigates the new model’s parameter estimation and time correspondence equation.
3.1. Logistic Grey Prediction Model
The logistic model is a classical mathematical model that studies a given population within a defined environment. Assuming that the individuals of the population do not discriminate between sizes, that they are uniformly distributed within the environment, that there is no out-migration or in-migration, and that the supply of resources within the environment always remains a constant and is equally distributed to each individual.
For ease of reference, we have organized the main notations into Table 1.

Table 1.
Main Notations.
The differential equations of the logistic model are as follows:
Assuming CO2 emissions at a given time, is the CO2 emission intensity at time t, and is the growth rate that can be achieved.
Define the sequence of carbon emissions as follows:
For an accumulative generating sequence,
where the logistic equation is deformed to the following:
Set ; thus, the differential equation of carbon emission versus time can be expressed as follows:
Replace the differential equation at the left end of Equation (4) with a first-order difference equation. Then, at , we have the following:
This leads to the definition of the following grey prediction model.
Definition 1.
Let the sequence , , as shown in Equations (2) and (3), then the sequence is said to be the mean generating sequence of :
where .
Definition 2.
Let the sequence , and , as shown in Equations (2), (3) and (5), then
Equation (6) is called the Logistic Grey model (abbreviated as (LGM(1,1) model), and differential equation Equation (4) is called the whitening equation of the model.
The parameters of LGM(1,1) can be estimated by the least squares method of the grey prediction model, and the following theorem can be obtained by using the method of solving differential equations in the literature [17]:
Theorem 1.
Let be carbon emission one time cumulative sequence of the neighboring mean generating sequence,
Then, the parameter estimates are obtained by least squares as follows:
Theorem 2.
Following Theorem 1, the time response sequence of the LGM(1,1) model is as follows:
where the initial value condition is as follows: when time , there is .
3.2. Fractional Order Operator Theory
Definition 3.
Let . By the definition of the first-order cumulative generator operator, where
therefore:
The definition and properties of the Gamma function are given below.
Definition 4.
Define to be the Gamma function for , and
There is when , then there are ,
Therefore:
In particular, when , the expansion factor of is
3.3. Fractional Order LGM(1,1) Model
This Section introduces the fractional order LGM(1,1) model, i.e., the FLGM(1,1) model, and analyzes its essential properties. The fractional order FLGM(1,1) model is first defined using the operator theory of Section 3.2.
Definition 5.
Let be the original sequence and be the r-order cumulative generated sequence of , given by Definition 3.
Equation (15) is referred to as the FLGM(1,1) model, where is given by Equation (10)
Specifically, when , Equation (10) becomes , which is the original form of the LGM(1,1) model.
According to the definition of the model FLGM(1,1) model, the following properties can be obtained:
Theorem 3.
Let be the parameter vector of the FLGM(1,1) model. After using the least squares method, we have the following:
where B, Y
Thus:
Definition 6.
Define Equation (18) as the differential whitening equation for the FLGM(1,1) model .
Theorem 4.
Define the time response function for the FLGM(1,1) model as
This leads to the cumulative reduction value , where .
3.4. Modeling Steps for the FLGM(1,1) Model
In this Section, the principle of the particle swarm optimization algorithm is given. Then, the optimization process of the fractional-order grey prediction model is completed, and the optimal model order is solved to establish the optimal fractional-order FLGM(1,1) model, which can be referred to in the literature [48].
The specific steps of the PONGM(1,N) model are described below as follows:
- (1)
- Collect the primary sequence of the original data ;
- (2)
- Calculate the sequence and the sequence of immediate neighboring means using Equation (5);
- (3)
- The resulting data are used to construct the matrix and substituted into Equation (17) of Theorem 3, and the coefficients are calculated using the least squares method;
- (4)
- Using Equation (19) of Theorem 4 to calculate the reduction value, the particle swarm algorithm is used to find the optimal fractional order , and to calculate the APEs and MAPEs, MAPEp, and CMRPE, which are defined as follows:
4. Applications and Analyzing
Global climate change is one of the most critical environmental issues today, with far-reaching implications for the future of the global economy and the natural environment, and carbon emissions are one of the main drivers of global climate change. Many countries are now making efforts to reduce CO2 emissions. Despite the increasingly urgent global need to reduce CO2 emissions, most researchers still focus on those countries with the largest emissions, such as the United States, China, and Russia. While the emission reduction efforts and achievements of these large countries are essential, the emission reduction actions of small and medium-sized countries should not be ignored, and their emission reduction trends and challenges are worthy of our in-depth discussion. Although small and medium-sized countries do not emit as much carbon dioxide as large countries, their efforts are equally crucial to realizing global emission reduction targets. By investigating the emission reduction actions of these medium-emitting countries, we can gain a more comprehensive understanding of the actual situation of global emission reduction and draw lessons from them to formulate more effective emission reduction strategies.
4.1. Simulation Setup
- (1)
- Dataset: Our study selected five medium-emitting countries, Ethiopia, Djibouti, Ghana, Belgium, and Austria, to provide insight into their efforts and challenges in reducing CO2 emissions. The raw data on CO2 emissions for these countries are derived from World Bank data https://data.worldbank.org.cn/ (accessed on 15 October 2023), where CO2 emissions are expressed in metric tons per capita. The raw data on CO2 emissions comprise the emission year and its corresponding carbon intensity;
- (2)
- Data preprocessing: The raw data on CO2 emissions from World Bank data adhere to standardization, exhibiting no instances of missing values or anomalies, thereby obviating the need for specialized processing. Since the CO2 emissions in the World Bank data are only updated until 2020, data from 2006 to 2020 were selected for the calculations in our manuscript. This is because the grey prediction model operates under the premise of “small sample, poor information,” hence the selection of these 15 data points from the years 2016 to 2020. These data were divided into two groups: the training and the testing group. The first 10 groups of data from 2006 to 2015, as the training set, were used to construct different types of models. The remaining data from 2016 to 2020, as the test set, were used to compare the performance of the models;
- (3)
- Simulation parameters: the APEs and MAPEs, MAPEp, and CMRPE are described at the end of Section 3;
- (4)
- Comparisons model: Comparisons were made with the existing grey prediction models LGM(1,1), WGM(1,1) [49], and CCRGM(1,1) [50] to validate the performance of the model in practical applications. The CO2 emissions of these five countries were predicted for 2021–2025 using each of the four models.
4.2. Carbon Emissions in Ethiopia
In this Section, CO2 emissions in Ethiopia are discussed through a grey prediction model. The PSO algorithm was first used to search for the MAPEtotal and the corresponding optimal value of r for the raw data for 2006–2015, which corresponded to 15.6520% and 0.1907, respectively, as shown in Table 2. Once the optimal fractional order has been determined, it is possible to establish a grey prediction model directly and predict the data for 2016–2020. Applying the grey system theory and actual data, we establish four prediction models: FLGM(1,1), LGM(1,1), WGM(1,1), and CCRGM(1,1), and the corresponding results are shown in Table 3. The comparison of APE (%) of Ethiopia’s CO2 emissions from four grey models is shown in Table 4. The results of the Mean Absolute Percentage Error (MAPE), the Composite Mean Relative Percentage Error (CMRPE), and the Root Mean Square Error (RMSPE) of four grey models for CO2 emissions in Ethiopia are presented in Table 5.

Table 2.
Minimum MAPEtotal and its corresponding optimal fractional order for FLGM(1,1) model based on the PSO algorithm.

Table 3.
Prediction results of four grey models for carbon emissions in Ethiopia.

Table 4.
Comparison of APE (%) of Ethiopia’s CO2 emissions from four grey models.

Table 5.
Error indicators (%) of four grey models for CO2 emissions in Ethiopia.
According to Table 5, it can be seen that the MAPEsim, MAPEpre, CMRPE, and RMSPE of the new model are 7.8859%, 7.7662%, 7.8260, and 9.7333%, respectively, which are much lower than those of the other three models. The new model almost achieves an unbiased simulation, with the best prediction accuracy among the four models predicting the data in 2011. The LGM(1,1) model has an error of more than 10% in both simulation and prediction, which is much larger than the FLGM(1,1) model. The WGM(1,1) model shows high prediction accuracy in the data prediction part. However, the MAPE value in the prediction part is significantly larger than that of the proposed model, with an error of up to 13.2714%. In addition, the CCRGM(1,1) model shows the worst results in both the simulation and prediction part, where the new model has the best values for the fitting and prediction error metrics. In summary, the FLGM(1,1) model proposed in this paper has high prediction accuracy, adaptability, and applicability. The result illustrates that the fractional-order grey model has higher accuracy than the integer-order grey model, which shows that the fractional-order accumulation improves the model’s accuracy and obtains satisfactory results. In order to further analyze the simulation and prediction effect of the model, Figure 1 is plotted.
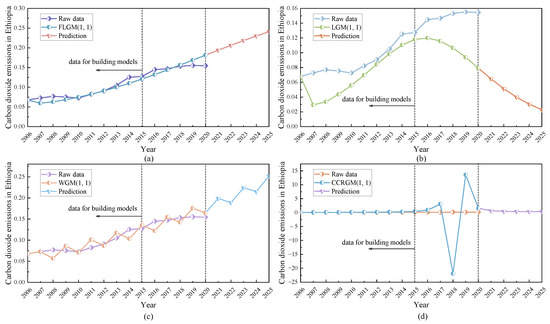
Figure 1.
Analysis of CO2 emissions in Ethiopia by four grey models. (a) by FLGM(1,1), (b) by LGM(1,1), (c) by WGM(1,1), (d) by CCRGM(1,1).
As shown in Figure 1, the LGM(1,1) model and CCRGM(1,1) model underestimated the trend of CO2 emissions in Ethiopia. In contrast, the FLGM(1,1) model and the WGM(1,1) model succeeded in identifying the trend. However, compared with the raw data, the WGM(1,1) model’s trend fluctuates too much and is not the same as the raw data. In contrast, the FLGM(1,1) model accurately captures the slow upward trend of the data set. This shows that the FLGM(1,1) model has the best prediction performance, the WGM(1,1) model is the second, and the CCRGM(1,1) model is the worst, which indicates that the new model successfully captures the trend of CO2 emissions in Ethiopia.
4.3. Carbon Emissions in Djibouti
This Section performs the validity analysis using Djibouti’s CO2 emissions by applying the PSO algorithm to determine the MAPEtotal and the corresponding optimal fractional order r. The corresponding results are 10.8330% and 0.3048, respectively, as shown in Table 2. Based on the modeling mechanism of the new model, the raw data from 2006–2015 were used to predict the data for the following five years. The simulation results are presented in Table 6, Table 7 and Table 8.

Table 6.
Prediction results of four grey models for carbon emissions in Djibouti.

Table 7.
Comparison of APE (%) of Djibouti’s CO2 emissions from four grey models.

Table 8.
Error indicators (%) of four grey models for CO2 emissions in Djibouti.
As shown in Table 6, Table 7 and Table 8, the LGM(1,1) and the CCRGM(1,1) models have negative values in their poor prediction performance, indicating that the two models do not accurately capture Djibouti’s CO2 emissions. Regarding simulation and prediction errors, the MAPEsim, MAPEpre, CMRPE, and RMSPE of these two models are well over 10%. Meanwhile, the FLGM(1,1) and WGM(1,1) models are better in the simulation part, with their performances of 5.6969% and 6.8833%, respectively. The simulation error of the new model is still smaller than that of the WGM(1,1) model by 1.1864%. It exhibits a MAPEpre of 5.1361% in the prediction part, which is much smaller than that of the WGM(1,1) model in the prediction part. The CMRPE and RMSPE of the new model are 5.4165% and 7.1232%, respectively, which are also the best among the four models. Then, we plot Figure 2 to compare these four models visually.
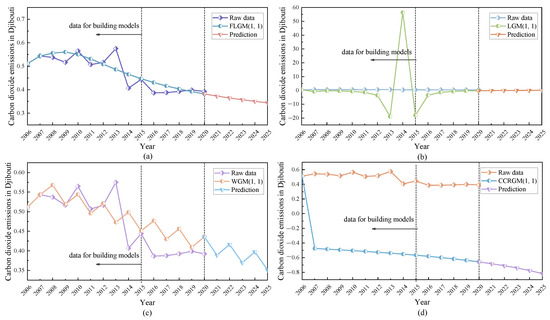
Figure 2.
Analysis of CO2 emissions in Djibouti by four grey models. (a) by FLGM (1,1), (b) by LGM(1,1), (c) by WGM(1,1), (d) by CCRGM(1,1).
The simulation and prediction fitting curves of the FLGM (1,1) model, LGM (1,1) model, WGM (1,1) model, and CCRGM (1,1) model are plotted in Figure 2, respectively. From Figure 2, it can be seen that the predicted trends of the LGM (1,1) model and the CCRGM (1,1) model are too far from the trends of the raw data, and the simulated trends are completely inconsistent with the trends of the actual CO2 emissions. Although the WGM(1,1) model fits the raw data trend relatively well before 2012, it performs poorly in the later part of the prediction. It does not recognize the trend of the data, which results in unsatisfactory predictions. The new model matches the trend of the raw data, fits the raw data better in the simulation stage, and gets the same reflection in the prediction stage. This indicates that the proposed model has good prediction performance and is suitable for calculating and predicting CO2 emission trends in Djibouti.
4.4. Carbon Emissions in Ghana
The data in this Section are the CO2 emissions of Ghana. Using the historical data from 2006–2015 for modeling. The optimal fractional order of the new model was derived as 0.1515 with the PSO algorithm, which corresponds to a MAPEtotal value of 11.5987%, as shown in Table 2. Based on the modeling mechanism of the new model, the simulation results are presented in Table 9, Table 10 and Table 11.

Table 9.
Prediction results of four grey models for carbon emissions in Ghana.

Table 10.
Comparison of APE (%) of Ghana’s CO2 emissions from four grey models.

Table 11.
Error indicators (%) of four grey models for CO2 emissions in Ghana.
Table 9, Table 10 and Table 11 show that the two models, the LGM(1,1) model and the CCRGM(1,1) model, have negative values in their predictions and are less effective, indicating that the two models do not accurately capture Ghana’s carbon emissions and their errors are much larger than those of the FLGM(1,1) and WGM(1,1) models. The MAPEsim, MAPEpre, CMRPE, and RMSPE of the new model performed 4.9712%, 6.6276%, 5.7994%, and 7.2655%, while the MAPEsim, MAPEpre, CMRPE, and RMSPE of the WGM(1,1) model performed 5.9366%, 12.5158%, 9.2274%, and 9.3382%. The four error evaluation metrics of the new model are all below 8%, and the simulation of the WGM(1,1) model, although second only to the new model, performs poorly in the prediction part with an error higher than 10%. It can be seen that the new model has the best performance in both modeling and prediction. Then, we plotted Figure 3 to compare these four models visually.
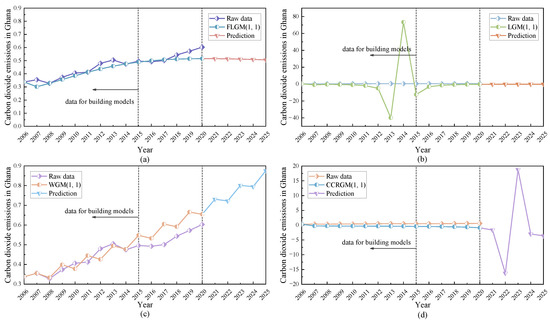
Figure 3.
Analysis of CO2 emissions in Ghana by four grey models. (a) by FLGM(1,1), (b) by LGM(1,1), (c) by WGM(1,1), (d) by CCRGM(1,1).
The modeling and prediction fitting curves for the FLGM (1,1) model, LGM (1,1) model, WGM (1,1) model, and CCRGM (1,1) model are plotted in Figure 3, respectively, from which it can be seen that the predicted trend of the LGM (1,1) model and the CCRGM (1,1) model is too far away from the trend of the raw data and that the LGM (1,1) model showed a steep downward and upward trend, and the CCRGM (1,1) model also shows the trend in the prediction stage, which is not consistent with the trend of CO2 emissions in Ghana. The WGM (1,1) model shows a slightly fluctuating trend, but it is not consistent with the fluctuating pattern of the raw data, and it gradually deviates from the prediction part in the later stage, which leads to a gradual increase in the prediction error. The new model can fit the trend of CO2 emissions in Ghana very well, indicating that the model has a good prediction performance. It can be seen that the new model has the best fitting performance among all the models and is suitable for simulating and predicting the trend of CO2 emissions in Ghana.
4.5. Carbon Emissions in Belgium
This Section investigates CO2 emissions in Belgium through different grey models. First, the optimal fractional order is derived using the PSO algorithm and the raw data for 2006–2015. The results are shown in Table 2. Four grey prediction models, FLGM(1,1), LGM(1,1), WGM(1,1), and CCRGM(1,1), were developed using the optimal value of r and the raw data of Belgium. The simulation results are presented in Table 12, Table 13 and Table 14.

Table 12.
Prediction results of four grey models for carbon emissions in Belgium.

Table 13.
Comparison of APE (%) of Belgium’s CO2 emissions from four grey models.

Table 14.
Error indicators (%) of four grey models for CO2 emissions in Belgium.
As can be seen from Table 12, there are negative values in the predicted values of the LGM(1,1) model, and its error is much larger than that of the FLGM(1,1) model, the WGM(1,1) model, and the CCRGM(1,1) model. Therefore, the LGM(1,1) model has the lowest prediction accuracy. Following Table 13 and Table 14, in terms of the prediction accuracy in the modeling part, the new model has a MAPEsim of 3.3520%, which indicates a higher prediction accuracy in the 10 years modeled. The WGM(1,1) model has a MAPEsim of 3.4497%, the second-highest simulation accuracy of the new model. However, the new model has a prediction error of only 2.0436% in the prediction part, and the WGM(1,1) model has a prediction error of 7.2447%, significantly larger than the proposed new model. The CMRPE and RMSPE of the new model perform 2.6978% and 3.4182%, which are much smaller than the other three models. It can be seen that the new model shows higher accuracy in both simulation and prediction parts. Then, we plotted Figure 4 to compare these four models visually.
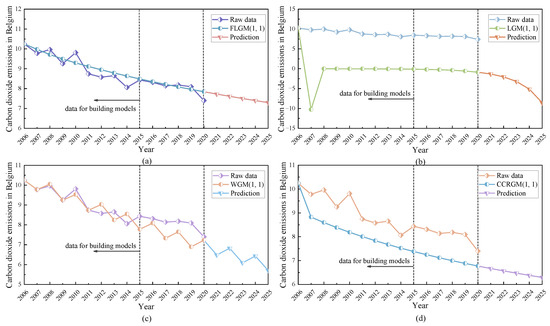
Figure 4.
Analysis of CO2 emissions in Belgium by four grey models. (a) by FLGM(1,1), (b) by LGM(1,1), (c) by WGM(1,1), (d) by CCRGM(1,1).
Figure 4 plots the degree of data fit of the FLGM(1,1) model, the LGM(1,1) model, the WGM(1,1) model, and the CCRGM(1,1) model to the raw CO2 emissions. It can be seen that both the LGM(1,1) and CCRGM(1,1) models underestimate the trend of CO2 emissions in Belgium to varying degrees, with the LGM(1,1) model having the most severe deviation from the trend. In contrast, the predicted values of the new model reflect the overall trend of CO2 emissions. Although the WGM(1,1) model performs better in the simulation phase, it does not match the actual values of CO2 emissions in the prediction part of the model. The direction of the trend of the model does not match the actual value, falling too fast and fluctuating too much. The new model almost matches the real-time CO2 emissions in the prediction part, closer to the observed values. Therefore, the model has the best fitting performance among all models.
4.6. Carbon Emissions in Austria
Based on similar arguments in the previous sections, CO2 emissions in Austria are also investigated through a grey prediction model. The PSO algorithm was utilized to search for MAPEtotal and the corresponding optimal fractional order r for the raw data from 2006–2015, and the optimal values of the parameters found are shown in Table 2. According to the modeling mechanism of the grey prediction model, four grey prediction models, FLGM(1,1), LGM(1,1), WGM(1,1), and CCRGM(1,1), were established, respectively. The simulation results are presented in Table 15, Table 16 and Table 17.

Table 15.
Prediction results of four grey models for carbon emissions in Austria.

Table 16.
Comparison of APE (%) of Austria’s CO2 emissions from four grey models.

Table 17.
Error indicators (%) of four grey models for CO2 emissions in Austria.
By observing Table 15, Table 16 and Table 17, the LGM(1,1) model has the lowest prediction accuracy in both the simulation and prediction parts. The FLGM(1,1) model has higher accuracy in the simulation part with its MAPEsim and RMSPE values of 3.5163% and 3.9267%, second only to the WGM(1,1) model. However, its MAPEpre and CMRPE are 2.4012% and 2.9588%, respectively. In comparison, the MAPEpre and CMRPE of the WGM(1,1) model are 3.7393% and 3.0676%, respectively, indicating that the accuracy of the new model in the prediction stage is higher than that of the WGM(1,1) model. The errors of both simulation and prediction of the CCRGM(1,1) model are above 10%, much larger than the new model. In summary, the FLGM(1,1) model proposed in this paper has high prediction accuracy and good applicability for predicting CO2 emissions in Austria. The trend comparison of the four models is plotted in Figure 5.
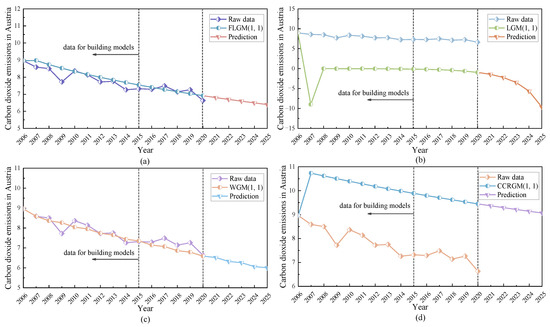
Figure 5.
Analysis of CO2 emissions in Austria by four grey models. (a) by FLGM(1,1), (b) by LGM(1,1), (c) by WGM(1,1), (d) by CCRGM(1,1).
Figure 5 shows the simulation and prediction fitting curves of the FLGM(1,1) model, LGM(1,1) model, WGM(1,1) model, and CCRGM(1,1) model. The whole-order LGM(1,1) model underestimates the trend of CO2 emissions in Austria and is poorly simulated and predicted, whereas the fractional-order grey model successfully identifies the trend of CO2 emissions. The CCRGM(1,1) model overestimates the trend of CO2 emissions in Austria with a large bias. The FLGM(1,1) model and the WGM(1,1) model in the simulation phase both better fit the trend of CO2 emissions in the region. However, in the prediction stage, the WGM(1,1) model does not perform as well as the new model, compared to the new model proposed in this paper, which has a higher prediction accuracy, higher flexibility, and better fitting accuracy.
5. Carbon Emission Predictions for the Next Five Years for Five Countries and Policy Recommendations
In Section 4.2, Section 4.3, Section 4.4, Section 4.5 and Section 4.6, we have conducted an in-depth study on the CO2 emissions of five countries through four different grey models: FLGM(1,1), LGM(1,1), WGM(1,1), and CCRGM(1,1). After detailed analysis and comparison, we can see from the simulation results that the two whole-order grey models, LGM(1,1) and CCRGM(1,1), have low-performance indexes in the five cases, which means they are ineffective in predicting carbon emissions. They cannot provide decision-makers with an accurate and reliable basis. On the other hand, although the WGM(1,1) model performs best in predicting the fifth country, the newly developed fractional grey model FLGM(1,1) exhibits the best performance index when predicting CO2 emissions in the first four countries. This demonstrates the significant advantage of fractional order accumulation in improving the accuracy of model prediction and verifies the applicability and reliability of the FLGM(1,1) model in making effective predictions of CO2 emissions for the next five years for the five countries. Figure 6 shows the predicted values of CO2 emissions for the next five years (2021–2025).
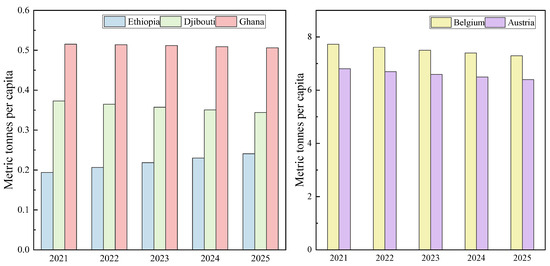
Figure 6.
FLGM(1,1) model predictions of CO2 emissions for 2021–2025 with five countries.
From Figure 6, it can be seen that Ethiopia’s CO2 emissions show an upward trend from 2021–2025. It is projected to increase from 0.1939 metric tons per capita in 2021 to 0.2409 metric tons per capita by 2025. This change is closely related to Ethiopia’s rapid economic growth in recent years. As a fundamental country in the Central African region, Ethiopia has experienced strong economic growth and is regarded as one of the fastest-growing economies in the world. However, this rapid growth has also brought about a sharp increase in energy demand, which has led to a rise in carbon emissions. The country’s transportation sector is the primary source of emissions from oil use, and other fossil energy sources are also proliferating under the development of infrastructure projects. At the same time, Ethiopia’s high economic growth, accompanied by a massive demand for energy, also implies the potential for high emissions.
Ghana’s CO2 emissions have shown a steady downward trend. Although the annual decline has not been significant, overall, it has remained relatively low, with per capita emissions stabilizing at around 0.5 metric tons. This phenomenon is closely related to the industrial model on which the Ghanaian region mainly relies. Ghana’s region mainly relies on industries such as agriculture, mining, and fisheries, with agriculture being one of the most important economic pillars of the Ghanaian region. While promoting economic development, the government also pays attention to environmental protection and social welfare, strives to realize the coordinated development of the economy, society, and the environment, and promotes the adoption of environmental protection measures by enterprises to maintain the stability of carbon emissions.
Djibouti’s carbon emissions are gradually decreasing over the next five years. Emissions per capita are expected to stabilize at 0.3442 metric tons by 2025, a slight decrease of 0.0287 metric tons compared to 2021. Behind this trend is a reflection of Djibouti’s efforts and commitment to sustainable development. It is well known that Djibouti is not rich in natural resources and has relatively little industrial activity. Despite this, its CO2 emissions are still lower than those of industry-dominated countries. In conclusion, the Government of Djibouti should take comprehensive measures to promote appropriate economic instruments, balance economic and environmental benefits, and promote sustainable regional development.
CO2 emissions in the Belgian region will gradually decrease by a small margin over the next five years, from 7.7250 metric tons per capita in 2021 to 7.2929 metric tons per capita in 2025, a decrease of about 0.4321 metric tons per capita. This shows that the Belgian government has achieved some success in its emission reduction efforts. However, Belgium still faces several challenges to achieve a more substantial reduction in emissions. The country is still highly dependent on fossil fuels, especially coal and natural gas, which leads to high carbon emissions. In order to meet these challenges, Belgium will need to continue to strengthen the implementation of its emission reduction measures and increase its international cooperation and assistance to meet the challenges posed by climate change in the future.
Austria’s carbon emissions show a decreasing trend from 2021 to 2025, from 6.8043 metric tons per capita in 2021 to 6.3964 metric tons per capita in 2025, a decrease of about 0.4079 metric tons per capita. Austria is a relatively industrially developed country, primarily known for its heavy steel and machine-building industries. In recent years, Austria has made many efforts to develop renewable energy and research new energy conservation and emission reduction technologies, especially in renewable energy, which has won the world’s praise. As a result, the country has increased its efforts in recent years in the research, development, and application of renewable energy and new technologies for energy conservation and emission reduction, and it has further increased its support for renewable energy and clean energy.
6. Conclusions
This paper proposes a logistic grey prediction model with fractional order using the characteristics of the carbon emission system. The model is solved by the theory related to the fractional order operator. The specific modeling and calculation steps are given, and then the parameter estimation and time response equation of the new model FGLM(1,1) are studied. The model combines with the principle of particle swarm optimization algorithm to complete the optimization process of the order of the fractional-order grey prediction model, solves the optimal model order, and finally establishes the optimal fractional-order FLGM(1,1) model.
The newly developed FLGM(1,1) model to predict carbon dioxide emissions in five medium-emission countries: Ethiopia, Djibouti, Ghana, Belgium, and Austria. In the analysis of the effectiveness of the FLGM(1,1) model, its performance is compared with three different grey models, namely LGM(1,1), WGM(1,1), and CCRGM(1,1). Historical data on carbon dioxide emissions from the years 2006 to 2015 for these five countries were selected. The first 10 sets of data from 2006 to 2015 were used for modeling, and the data from 2016 to 2020 were employed for prediction. The results consistently indicate that the new FLGM(1,1) model exhibits superior performance. The detailed comparative results for the five countries are presented below:
Through the analysis of Ethiopia, the results indicate that the LGM(1,1), CCRGM(1,1), and WGM(1,1) models underestimated the carbon dioxide emission trend of the country, while the FLGM(1,1) model successfully captured this trend. Specifically, the WGM(1,1) model exhibited significant fluctuations, deviating from the actual trend, while the FLGM(1,1) model accurately reflected the gradual upward trend, performing optimally. In the analysis of Djibouti, it was observed that the LGM(1,1) and CCRGM(1,1) models had significant prediction gaps, the WGM(1,1) model performed poorly in later stages, whereas the FLGM(1,1) model successfully simulated the actual trend, demonstrating excellent performance. The study on Ghana revealed that the LGM(1,1) and CCRGM(1,1) models were unable to accurately predict the trend, and the WGM(1,1) model exhibited significant fluctuations. In contrast, the FLGM(1,1) model successfully fitted Ghana’s CO2 emission trend, achieving the best results. The analysis for Belgium showed that the LGM(1,1) and CCRGM(1,1) models underestimated the emission trend, the WGM(1,1) model had inaccuracies in later predictions, while the FLGM(1,1) model accurately reflected the overall trend, possessing the best fitting performance. Finally, the study on Austria demonstrated that the LGM(1,1) model had poor simulation and prediction performance, the CCRGM(1,1) model overestimated the emission trend, the WGM(1,1) model had inaccuracies in the prediction phase, while the FLGM(1,1) model exhibited excellent performance in both simulation and prediction stages.
Through detailed analysis and comparison, it is evident from the simulation results that both the LGM(1,1) and CCRGM(1,1) whole-order grey models performed poorly in all five cases. This implies that these models are not ideal for predicting carbon dioxide emissions and cannot provide decision-makers with accurate and reliable guidance.
On the other hand, although the WGM(1,1) model performed optimally in predicting emissions for the fifth country, the new FLGM(1,1) demonstrated the best performance metrics when forecasting carbon dioxide emissions for the first four countries. This not only underscores the significant advantages of fractional-order accumulation in enhancing model prediction accuracy but also validates the applicability and reliability of the LFGM(1,1) model. Consequently, we employ the proposed FLGM(1,1) model in this study to effectively forecast the carbon dioxide emissions for the next five years (2021–2025) in these five countries, providing policy recommendations based on the predictions. For Ethiopia, the forecast for the period 2021–2025 indicates an upward trend in carbon dioxide emissions, rising from 0.1939 metric tons per capita to 0.2409 metric tons per capita. This is associated with its rapid economic growth but also signifies a sharp increase in energy demand and emissions from the transportation sector. Ghana’s emissions show a steady declining trend, maintaining at relatively low levels. This is primarily attributed to an agricultural-dominant industrial model, along with the government’s emphasis on environmental conservation and social welfare. Djibouti’s emissions are expected to gradually decrease, reflecting its efforts in sustainable development. Belgium is projected to experience a slight reduction in emissions, indicating governmental success in emission reduction efforts. However, the country still faces challenges related to fossil fuel dependence and high carbon emissions. Austria has achieved a reduction in emissions in recent years, acknowledging its efforts in developing renewable energy and researching new technologies. Nevertheless, there is a need to continue strengthening emission reduction measures, especially in reducing dependence on fossil fuels.
Carbon emissions are a complex system affected by various factors, so the prediction of carbon emissions also needs to consider various factors. This paper, from the optimization of the model structure, the establishment of a fractional-order Logistic grey prediction model, the model combined with the principle of particle swarm optimization algorithm, completed the optimization process of the order of fractional-order grey prediction model, and ultimately the establishment of the optimal fractional-order FLGM(1,1) model, and also proved the effectiveness and stability of the model in the actual case of carbon emissions, but there are still some problems that can be improved. On the one hand, considering the complexity of the carbon emission system itself, there is room for further optimization in the screening and cleaning of data, selecting relevant factors, etc. On the other hand, the model has a new structure, and it is also necessary to think about it from the perspective of the modeling mechanism and optimize and improve it in the calculation of the background value and the estimation of parameters. Moreover, carbon emissions are intricately linked to carbon trading prices, internal relationships within the energy structure, and economic growth. Therefore, predicting carbon emissions in such a scenario becomes more complex and challenging. How to establish grey prediction models that incorporate multiple factors and apply them to carbon emission forecasting in this context will be a further area of research. Consequently, in future work, due consideration will be given to the current challenges and limitations, paving the way for more in-depth research.
Author Contributions
Methodology, X.H. and H.D.; software, Y.S.; validation, X.H., Y.S. and H.D.; investigation, Y.S. and F.Y.; resources, X.H. and H.D.; data curation, X.H. and Y.S.; writing—original draft preparation, X.H., Y.S., F.Y. and H.D.; writing—review and editing, X.H., Y.S., F.Y. and H.D.; project administration, F.Y. and H.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (72171031) and the Humanities and Social Sciences Project of Chongqing Municipal Education Commission (No: 22SKGH144).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dong, H.; Yang, J. Study on regional carbon quota allocation at provincial level in China from the perspective of carbon peak. J. Environ. Manag. 2024, 351, 119720. [Google Scholar] [CrossRef]
- Yuan, J.; Gang, W.; Xiao, F.; Zhang, C.; Zhang, Y. Two-level collaborative demand-side management for regional distributed energy system considering carbon emission quotas. J. Clean. Prod. 2024, 434, 140095. [Google Scholar] [CrossRef]
- Ding, L.; Zhang, R.; Zhao, X. Forecasting carbon price in China unified carbon market using a novel hybrid method with three-stage algorithm and long short-term memory neural networks. Energy 2024, 288, 129761. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Li, H.; Yang, H.; Li, Z. Ensemble forecasting system based on decomposition-selection-optimization for point and interval carbon price prediction. Appl. Math. Model. 2023, 113, 262–286. [Google Scholar] [CrossRef]
- Cao, Z.; Liu, H. A novel carbon price forecasting method based on model matching, adaptive decomposition, and reinforcement learning ensemble strategy. Environ. Sci. Pollut. Res. 2023, 30, 36044–36067. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, X. Does carbon emission trading policy induce financialization of non-financial firms? Evidence from China. Energy Econ. 2024, 131, 107316. [Google Scholar] [CrossRef]
- Ou, Y.; Bao, Z.; Ng, S.T.; Song, W.; Chen, K. Land-use carbon emissions and built environment characteristics: A city-level quantitative analysis in emerging economies. Land Use Policy 2024, 137, 107019. [Google Scholar] [CrossRef]
- Ma, M.; Cai, W.; Dong, L. Whether carbon intensity in the commercial building sector decouples from economic development in the service industry? Empirical evidence from the top five urban agglomerations in China. J. Clean. Prod. 2019, 222, 193–205. [Google Scholar] [CrossRef]
- Di Leo, S.; Caramuta, P.; Curci, P.; Cosmi, C. Regression analysis for energy demand projection: An application to TIMES-Basilicata and TIMES-Italy energy models. Energy 2020, 196, 117058. [Google Scholar] [CrossRef]
- Son, S.; Lee, T. Prediction of Temperature in Korea Using Statistical Downscaling Model. Geogr. J. Korea 2017, 51, 323–334. [Google Scholar]
- Ahmadi, M.H.; Jashnani, H.; Chau, K.W.; Kumar, R.; Rosen, M.A. Carbon dioxide emissions prediction of five Middle Eastern countries using artificial neural networks. Energy Sources Part A Recovery Util. Environ. Eff. 2023, 45, 9513–9525. [Google Scholar] [CrossRef]
- Ye, L.; Du, P.; Wang, S. Industrial carbon emission forecasting considering external factors based on linear and machine learning models. J. Clean. Prod. 2024, 434, 140010. [Google Scholar] [CrossRef]
- Khajavi, H.; Rastgoo, A. Predicting the carbon dioxide emission caused by road transport using a Random Forest (RF) model combined by Meta-Heuristic Algorithms. Sustain. Cities Soc. 2023, 93, 104503. [Google Scholar] [CrossRef]
- Jeong, Y.S.; Cho, S. Post-2020 Greenhouse Gas Emission Projection in Building Sector. J. Archit. Inst. Korea 2020, 36, 117–125. [Google Scholar]
- Huang, Y.S.; Shen, L.; Liu, H. Grey relational analysis, principal component analysis and forecasting of carbon emissions based on long short-term memory in China. J. Clean. Prod. 2019, 209, 415–423. [Google Scholar] [CrossRef]
- Ruiz, L.G.B.; Pegalajar, M.C.; Arcucci, R.; Molina-Solana, M. A Time-Series Clustering Methodology for Knowledge Extraction in Energy Consumption Data. Expert Syst. Appl. 2020, 160, 113731. [Google Scholar] [CrossRef]
- Deng, J.L. Estimate and Decision of Grey System; Huazhong University of Science and Technology Press: Wuhan, China, 2002. [Google Scholar]
- Zeng, B.; Ma, X.; Zhou, M. A new-structure grey Verhulst model for China’s tight gas production forecasting. Appl. Soft Comput. 2020, 96, 106600. [Google Scholar] [CrossRef]
- Duan, H.; Luo, X. A novel multivariable grey prediction model and its application in forecasting coal consumption. ISA Trans. 2022, 120, 110–127. [Google Scholar] [CrossRef] [PubMed]
- Chu, J.; Xiao, X. Benefits evaluation of the Northeast Passage based on grey relational degree of discrete Z-numbers. Inf. Sci. 2023, 626, 607–625. [Google Scholar] [CrossRef]
- Zeng, B.; Tong, M.; Ma, X. A new-structure grey Verhulst model: Development and performance comparison. Appl. Math. Model. 2020, 81, 522–537. [Google Scholar] [CrossRef]
- Alptekin, O.; Alptekin, N.; Saraç, B. Evaluation of Low Carbon Development of European Union Countries and Turkey Using Grey Relational Analysis. Teh. Vjesn. 2018, 25, 1497–1505. [Google Scholar]
- Zeng, B.; Zhou, M.; Liu, X.; Zhang, Z. Application of a new grey prediction model and grey average weakening buffer operator to forecast China’s shale gas output. Energy Rep. 2020, 6, 1608–1618. [Google Scholar] [CrossRef]
- Xiao, Q.; Shan, M.; Gao, M.; Xiao, X.; Goh, M. Parameter optimization for nonlinear grey Bernoulli model on biomass energy consumption prediction. Appl. Soft Comput. 2020, 95, 106538. [Google Scholar] [CrossRef]
- Xiao, Q.; Gao, M.; Chen, L.; Jiang, J. Dynamic multi-attribute evaluation of digital economy development in China: A perspective from interaction effect. Technol. Econ. Dev. Econ. 2023, 29, 1728–1752. [Google Scholar] [CrossRef]
- Gao, M.; Yang, H.; Xiao, Q.; Goh, M. COVID-19 lockdowns and air quality: Evidence from grey spatiotemporal forecasts. Socio-Econ. Plan. Sci. 2022, 83, 101228. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.; Wang, G. Partial differential grey model based on control matrix and its application in short-term traffic flow prediction. Appl. Math. Model. 2023, 116, 763–785. [Google Scholar] [CrossRef]
- Kang, Y.; Mao, S.; Zhang, Y. Fractional time-varying grey traffic flow model based on viscoelastic fluid and its application. Transp. Res. Part B Methodol. 2022, 157, 149–174. [Google Scholar] [CrossRef]
- Xiao, X.; Yang, J. An improved seasonal rolling grey forecasting model using a cycle truncation accumulated generating operation for traffic flow. Appl. Math. Model. 2017, 51, 386–404. [Google Scholar] [CrossRef]
- Xiang, X.W.; Ma, X.; Ma, M.D. Research and application of novel Euler polynomial-driven grey model for short-term PM10 forecasting. Grey Syst. Theory Appl. 2021, 11, 498–517. [Google Scholar] [CrossRef]
- Wu, W.; Ma, X.; Zhang, Y.; Li, W.; Wang, Y. A novel conformable fractional non-homogeneous grey model for forecasting carbon dioxide emissions of BRICS countries. Sci. Total Environ. 2020, 707, 135447. [Google Scholar] [CrossRef]
- Javed, S.; Zhu, B.; Liu, S. Forecast of biofuel production and consumption in top CO2 emitting countries using a novel grey model. J. Clean. Prod. 2020, 276, 123997. [Google Scholar] [CrossRef]
- Gao, M.; Yang, H.; Xiao, Q.; Goh, M. A novel method for carbon emission forecasting based on Gompertz’s law and fractional grey model: Evidence from American industrial sector. Renew. Energy 2022, 181, 803–819. [Google Scholar] [CrossRef]
- Cheng, L.; Jian, X. A novel of fractional order predictive model on carbon emission intensity in China’s transportation sector. Environ. Eng. Manag. J. (EEMJ) 2021, 20, 1569–1581. [Google Scholar] [CrossRef]
- Zeng, B.; Li, H. Prediction of coalbed methane production in China based on an optimized grey system model. Energy Fuels 2021, 35, 4333–4344. [Google Scholar] [CrossRef]
- Nie, W.; Duan, H. A novel multivariable grey differential dynamic prediction model with new structures and its application to carbon emissions. Eng. Appl. Artif. Intell. 2023, 122, 106174. [Google Scholar] [CrossRef]
- Şahin, U. Forecasting of Turkey’s greenhouse gas emissions using linear and nonlinear rolling metabolic grey model based on optimization. J. Clean. Prod. 2019, 239, 118079. [Google Scholar] [CrossRef]
- Zhao, K.; Yu, S.; Wu, L.; Wu, X.; Wang, L. Carbon emissions prediction considering environment protection investment of 30 provinces in China. Environ. Res. 2024, 244, 117914. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Wang, W.; Wu, L. Application of a new grey multivariate forecasting model in the forecasting of energy consumption in 7 regions of China. Energy 2022, 243, 123024. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Yao, L.; Yan, S.; Liu, D. Grey system model with the fractional order accumulation. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1775–1785. [Google Scholar] [CrossRef]
- Wang, Y.; Chi, P.; Nie, R.; Ma, X.; Wu, W.; Guo, B. Self-adaptive discrete grey model based on a novel fractional order reverse accumulation sequence and its application in forecasting clean energy power generation in China. Energy 2022, 253, 124093. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Z.; Ye, L.; Wang, L.; Zhou, Y.; Luo, Y. A novel self-adaptive fractional grey Euler model with dynamic accumulation order and its application in energy production prediction of China. Energy 2023, 265, 126384. [Google Scholar] [CrossRef]
- Chen, Y.; Lifeng, W.; Lianyi, L.; Kai, Z. Fractional Hausdorff grey model and its properties. Chaos Solitons Fractals 2020, 138, 109915. [Google Scholar] [CrossRef]
- He, J.; Mao, S.; Kang, Y. Augmented fractional accumulation grey model and its application: Class ratio and restore error perspectives. Math. Comput. Simul. 2023, 209, 220–247. [Google Scholar] [CrossRef]
- Zhang, X.; Rao, C.; Xiao, X.; Hu, F.; Goh, M. Prediction of demand for staple food and feed grain by a novel hybrid fractional discrete multivariate grey model. Appl. Math. Model. 2024, 125, 85–107. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Y.; Zhou, Y.; Wang, L.; Ye, L.; Luo, Y. Forecasting China’s electricity generation using a novel structural adaptive discrete grey Bernoulli model. Energy 2023, 278, 127824. [Google Scholar] [CrossRef]
- Yan, S.; Su, Q.; Gong, Z.; Zeng, X. Fractional order time-delay multivariable discrete grey model for short-term online public opinion prediction. Expert Syst. Appl. 2022, 197, 116691. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. Proc. ICNN’95-Int. Conf. Neural Netw. 1995, 4, 1942–1948. [Google Scholar]
- Wu, L.; Liu, S.; Yang, Y. A grey model with a time varying weighted generating operator. IEEE Trans. Syst. Man Cybern. Syst. 2015, 46, 427–433. [Google Scholar] [CrossRef]
- Luo, X.; Duan, H.; He, L. A novel Riccati equation grey model and its application in forecasting clean energy. Energy 2020, 205, 118085. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).