Abstract
Over the past few years, the uncertain business environment has shaped the resilient development thinking of firms. Measuring and predicting innovation resilience plays a crucial role in fostering the sustainable development of enterprises. This paper used the entropy-weight TOPSIS model and FGM(1,1) model to measure the innovation resilience of companies based on an indicator system, covering aspects such as tolerance for factor scarcity, R&D safety, core technology self-sufficiency, and organizational change capacity. The results show that the MAPE of the FGM(1,1) model is 0.0136, which is lower than that of the GM(1,1) model, with the predicted annual growth rate of the resilience being −0.95% from 2020 to 2025. Consequently, the study investigated what policy configuration may improve innovation resilience using the fuzzy-set qualitative comparative analysis (fsQCA) model. It identified four policy configuration paths, of which the combination of a tax policy for an additional deduction of enterprise R&D expenses and an income tax reduction policy is an effective policy configuration. This research expands the application of the FGM(1,1) model and inspires managers to develop innovative policies to enhance corporate resilience.
1. Introduction
The emergence of the VUCA (volatility, uncertainty, complexity, and ambiguity) era is significantly influencing the mindset regarding the development of resilience in enterprises. Resilience generally pertains to the capacity of an entity to withstand and adapt in the face of challenging circumstances while effectively responding to them [1]. Innovation resilience denotes the intrinsic ability of innovation systems to endure external shocks, exhibit stability in the face of such shocks, adapt and recover from them, and potentially evolve into a more advanced and efficient state [2]. Firms with high resilience possess strong early warning signal detection capabilities and can initiate preventive measures. On the other hand, firms with low resilience often demonstrate weak risk perception and identification abilities, thus struggling to respond timely [3]. Therefore, given the ever-changing, complex, and unpredictable nature of uncertainty factors, firms can enhance their resilience to overcome the adverse effects of emergencies.
At present, most scholars measure firm resilience from three or four dimensions; for example, Lin Liang et al. [4] combined four perspectives—defense capability, resistance capability, recovery capability, and growth capability—to measure firm resilience. However, innovation resilience has not yet formed a unified system. Moreover, the existing measurements of innovation resilience only focus on the impact of the time point when a major emergency occurs, neglecting the hysteresis of the influence of an emergency on the firm. To deal with the impact of future uncertainty on firm innovation, it is crucial to use appropriate forecasting methods to predict innovation resilience.
The grey prediction model refers to a model that predicts systems with limited samples or weak data information. Due to the presence of uncertain factors in the data, the model incorporates the concept of grey. The grey system refers to a system that encompasses both known and unknown information, placing itself in an intermediate position between a white system characterized by complete knowledge and a black system characterized by absolute information uncertainty [5]. The grey model leverages the relationships between data, capturing relevant information from historical data to complement new data. By studying the relationship between information and additional data, the model establishes a predictive model to forecast future data through restoration. In this paper, we have selected the particle swarm optimization algorithm due to its succinct concepts, rapid convergence rate, and minimal parameter requirements for predicting innovation resilience.
The main contributions of this research can be summarized as follows: (1) This study describes innovation resilience from five dimensions: shortage tolerance, independent R&D security, core technology self-sufficiency rate, market discipline tolerance, and marketing innovation achievable rate. The chosen dimensions provide a comprehensive understanding of innovation resilience, reflecting its practical relevance in enterprise development more effectively than previous research. (2) The paper conducts exploratory research on predicting innovation resilience using the FGM(1,1) model, which demonstrates a higher level of prediction accuracy compared to the GM(1,1) model. (3) This article uses the fuzzy-set qualitative comparative analysis (fsQCA) model to study what policy configurations help improve innovation resilience and inspire managers to develop innovative policies to enhance corporate resilience.
2. Literature Review
Resilience was originally used in physics to describe a material’s ability to absorb energy during plastic deformation and fracture. Over time, resilience has gained attention in many fields, such as psychology, sociology, and management. However, there is currently no unified definition of the concept of resilience in the academic community. At present, relevant research on resilience in the field of management covers various aspects. For example, Hamidu et al. [6] found that supply chain technological innovation serves as a constructive mediator between supply chain resilience and supply chain performance. Previous studies have focused on the following areas. (1) Kyrdoda et al. [7] proposed that firm resilience plays a moderating role between learning from crises and firm survival. Conz and Magnani [8] propose a dynamic perspective on firm resilience, viewing it as an evolving process that unfolds over time. They contribute to this perspective by conceptualizing resilience as a dynamic process comprising absorption- and adaptation-related capabilities. This conceptualization enhances our understanding of the temporal nature of resilience in organizations. Firm resilience refers to a firm’s ability to respond to challenges, adapt to new scenarios, and actively learn to “survive well” [9]. (2) Organizational resilience is a framework for organizations to respond to crises, eliminate intervention factors, and adapt to new environments [10]. Organizational resilience reflects an organization’s ability to recover after facing difficulties and challenges [11]. Wang and Cai [12] regarded organizational resilience as a process, that is, in a challenging situation, firms try to avoid adverse reactions and construct and use all of their ability to interact with the environment, thus realizing positive adjustment and maintaining effective operation. Organizational resilience is influenced by various factors, such as digital corporate social responsibility, corporate resources, corporate social relationships, and so on [13,14]. (3) There is limited literature on the theory of innovation resilience. Hu and Yu [2] define innovation resilience as the ability of innovation systems to withstand external shocks, recover, and progress to a higher state. The innovation resilience of an ecosystem refers to the ability of innovation subjects to recover and adapt to the impact and disturbance of the external environment [4]. Wei and Ren [15] describe the resilience of cooperative innovation as the ability of regional innovation entities to recover and evolve through self-adaptation after external shocks.
The GM(1,1) model, as the fundamental model of grey prediction theory, is widely employed for short-term prediction of limited data quantities [16]. To enhance prediction accuracy, Lifeng Wu et al. [17] proposed a fractional order FGM(1,1) model. Zhang et al. and Zafar et al. [18,19] introduced this model that accumulates the original sequence by multiplying each sequence by a different fractional order and then accumulating it. This approach leads to more flexibility and accurate prediction results compared to the first-order accumulated sequence. When the fractional order value is 1, it represents the traditional grey GM(1,1) model. In the GM(1,1) model, all past data have the same value. FGM(1,1), grounded on the principle of prioritizing information, assigns higher weights to the new data when accumulating the original data. The specific weight allocation is calculated using fractional order, which can be determined using heuristic algorithms. Currently, the FGM(1,1) model has been widely utilized for various predictions, including energy consumption, environmental quality [20,21,22,23,24], express delivery business volume [25], the added value of high-tech industries [26], and the total output value of China’s construction industry [27].
Furthermore, innovation plays a crucial role in enhancing a firm’s competitiveness. Business model changes are recognized as key strategies for long-term innovation [6]. In the face of external impact, how to maintain a firm’s innovation system and ensure its development ability is the problem that a firm needs to solve. With the deepening of research, how to shape the innovation resilience of firms in a dynamic complex environment to resist the impact of future uncertainty or risk on firms has become an important topic for scholars.
3. The Index of a Firm’s Innovation Resilience
According to the implied meaning of resilience. Resilience involves the ability to withstand setbacks and recover from them [28]. And, based on this, it is believed that the connotation of innovation resilience is, when a firm’s innovation is faced with external shocks, the ability to resist shocks, maintain system stability, adapt to recovery, and even evolve into a better state [2]. Drawing on existing research, technological innovation can significantly enhance resilience and have a significantly higher impact on manufacturing resilience than other industries [29]. Factors such as R&D and market uncertainty can also influence innovation resilience [15]. Market uncertainty, for example, can affect the resilience of the manufacturing industry and regional economic resilience [30]. According to the above research, the paper describes innovation resilience from five dimensions. The five dimensions respectively are as follows: shortage tolerance, independent R&D security, core technology self-sufficiency rate, market discipline tolerance, and marketing innovation achievable rate. Among them, factor shortage tolerance includes the shortage of internal funds not being a major obstacle to innovation, the shortage of venture capital not being a major obstacle to innovation, etc. Independent R&D security includes independent R&D and cooperative R&D with firms in the group. The core technology self-sufficiency rate includes holding national or industry technical standards, holding secret technology, etc. Market discipline tolerance includes the shortage of market information not being a major obstacle to innovation, the market that has been occupied not being a major obstacle to innovation, etc. The marketing innovation achievable rate includes the number of firms that achieved organizational or marketing innovation, achieved organizational innovation, and achieved marketing innovation. The specific indicators are shown in Table 1.

Table 1.
Innovation resilience indicators.
4. Methodology
4.1. Entropy-Weight TOPSIS
This paper builds upon the works of Liu et al. [31] and Luo et al. [32] and utilizes the entropy-weight TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) model as a means to assess innovation resilience. Firstly, the indicators are objectively assigned weights based on standardized processing, which yields the entropy utility value of the indicator information. Subsequently, the development index is derived by assessing the gap between the evaluation unit and both the optimal solution and the worst solution, thereby minimizing redundancy and employing scholarly language. The specific steps for application are as follows.
Standardize the original data of various indicators and adopt extreme value standardization:
where is the standardized value of each index; is the evaluation index of item j of province i; is the minimum value of the index; and is the maximum value of the index; setting . Referring to Liu et al. [31], we take = 0.995 in this paper to circumvent the possible inability to compute the natural logarithm.
The following is used to calculate the value of entropy :
The following is used to calculate the index weight :
The following is used to establish a standardized decision matrix :
The following is used to determine the positive and negative ideal solutions:
where and are positive and negative ideal solutions, respectively.
The following is used to calculate the distance between the positive and negative ideal solutions for each province:
where and are the distances of the positive and negative ideal solutions, respectively.
The following is used to calculate the score of comprehensive evaluation:
where . The larger the value of , the stronger the indication of a firm’s innovation resilience; the smaller the value of , the weaker a firm’s innovation resilience is. The results of the firm’s innovation resilience are listed in Table 2.

Table 2.
The results of innovation resilience.
4.2. PSO Algorithm
The particle swarm optimization algorithm shares similarities with many other evolutionary optimization algorithms as it is based on a population that collaborates and competes to discover the optimal solution within a complex search space.
Suppose the target search space has a search dimension of D and the community consists of N particles. Within this D-dimensional space, the position and velocity of the i-th particle are represented as vectors and , respectively, and the individual and global extremum of the i-th particle and the entire particle swarm is denoted as and , respectively. The particle updates its velocity and position by using the formula below.
where c1 and c2 are the learning factors, w is the inertia weight, and and are uniform random numbers in the range of [0,1]. consists of the inertia or momentum part, the cognitive part, and the social part [33,34]. To avoid particles “oscillating” near the global optimal solution, the inertia weight w is linearly transformed between the maximum and minimum values [35].
where t is the number of current iterations.
4.3. PSO-FGM(1,1) Model
The accuracy of the model prediction is directly influenced by the data of r. To enhance the predictive capability of the model, heuristic algorithms can be employed to identify the optimal fractional order r. In this study, we propose the PSO-FGM(1,1) model and the specific process is outlined as follows.
The fitness value of the particle swarm optimization (PSO) algorithm is adopted as the criterion for determining the prediction result. In this case, the mean absolute percentage error (MAPE) is utilized:
The grey fractional order function for calculating the mean absolute percentage error is then established.
Construct the r-order accumulation sequence.
The original non-negative sequence of the original data was written as , and the cumulative sequence of order r was obtained by calculating , where
The whitening differential equation is established as follows:
where a and b are called the developmental grey number and endogenous control grey number, respectively. The solution of the above equation is as follows:
Using the least squares method, the numerical solutions of parameters and are , where
The time response function is as follows:
where is the value at time .
The reduction sequence of is as follows:
where
Thus, the prediction sequence is
Configure the parameters of the particle swarm optimization algorithm. Initially, the velocity and position of each particle are initialized with the fractional value r as the initial position. Subsequently, the fitness values are computed under the initial conditions. The velocity and position of the particles are then updated through iterations to identify the minimum fractional value r associated with the minimum fitness value.
The algorithm flowchart of the PSO is presented in Figure 1 below.
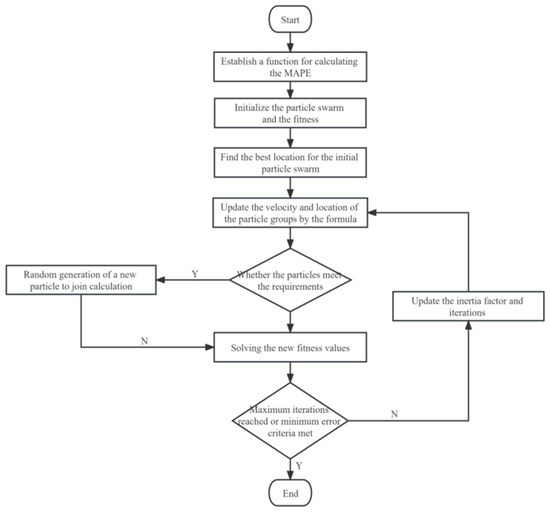
Figure 1.
Flow chart of the PSO-FGM(1,1) model.
4.4. The Fuzzy-Set Qualitative Comparative Analysis (fsQCA) Model
Qualitative comparative analysis (QCA) is a research method that surpasses both qualitative and quantitative approaches, adopting a holistic perspective to examine the configurational relationships among complex phenomena. It is highly applicable for analyzing the indispensability of an individual condition and the adequacy of multiple condition configurations while simultaneously reducing repetition and employing scholarly language [36]. In contrast to traditional quantitative analysis methods, QCA exhibits characteristics such as multiple concurrencies, equivalence, and causal asymmetry. It facilitates a comprehensive investigation of the influence of various combinations of conditions on outcomes, enabling researchers to delve deeper into the mechanisms underlying the relationships between conditional variables and results. Consequently, the QCA method has garnered notable attention and application in research domains such as entrepreneurship, innovation, marketing management, and strategic management in recent years. QCA can be further categorized into crisp set QCA (csQCA), fuzzy-set QCA (fsQCA), and multi-value QCA (mvQCA). Among these, fsQCA overcomes the limitations of traditional methods that solely analyze binary variables. It allows for the analysis of categorical variables and offers the flexibility to explore issues related to partial membership and degree changes that occur within a wide range of contexts, rendering it highly applicable and operative.
In this study, the fuzzy-set qualitative comparative analysis (fsQCA) method is utilized, employing fsQCA 3.0 software to conduct the analysis. The specific analysis comprises the following steps.
Calibration of conditions. Following the instructions provided by the fsQCA software, the variables specified in the article are transformed into fuzzy membership scores ranging from 0 to 1.
Construction of the truth table. In the QCA method, the analysis unit consists of combinations of conditions rather than individual cases. By assigning each conditional variable according to a predefined standard, we generate a truth table comprising all possible combinations of conditional variables and the outcome variable. It is important to identify and rectify any contradictory groups within the truth table.
Univariate necessity analysis. Univariate necessity analysis entails evaluating consistency and coverage indicators. Leveraging fsQCA 3.0 software, we conduct the univariate necessity analysis on the truth table. The consistency indicator helps determine whether a condition is essential for generating the observed outcomes, while coverage is utilized to assess the explanatory power of the outcome variable.
Conditional configuration analysis. By employing fsQCA 3.0 software, we obtain three types of solutions: parsimonious solutions, intermediate solutions, and complex solutions. Subsequently, we identify the core and edge conditions among numerous conditional variables and derive the conditional configuration path.
Robustness testing. For robustness testing, we employ two methods: altering the original consistency and modifying the PRI consistency.
Result analysis. To analyze the obtained configuration path, we regress it onto the case, identify various types of impact paths, and provide targeted policy recommendations.
The algorithm flowchart of the QCA method is illustrated in Figure 2 below.
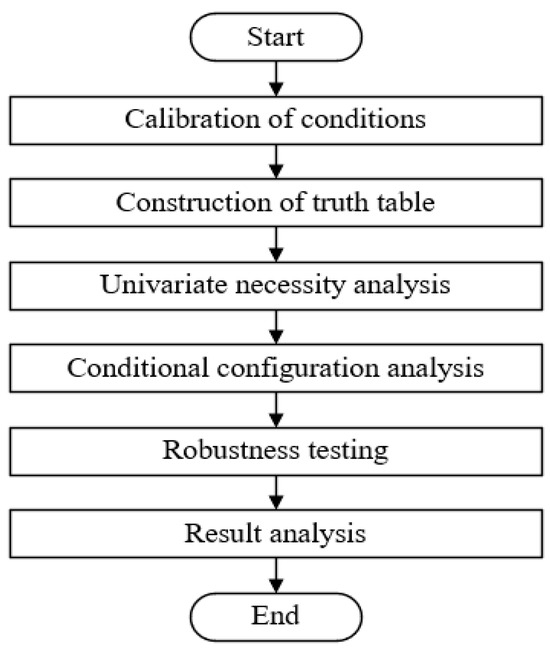
Figure 2.
Flow chart of the QCA algorithm.
5. Results
The data presented in this article are obtained from the National Survey of Enterprise Innovation Yearbooks conducted by the National Bureau of Statistics of China from 2017 to 2021. However, it should be noted that the study sample does not include certain regions of China, namely Xizang, Hong Kong, Macao, and Taiwan province, due to missing data. The findings, as depicted in Table 2, illustrate the results of innovation resilience of companies based on the entropy-weight TOPSIS method. On the whole, the overall trend of innovation resilience of firms appears to be stable. Taking a regional perspective, the top 10 regions with a five-year average ranking are Jiangsu (0.483), Guangdong (0.479), Zhejiang (0.448), Shandong (0.357), Anhui (0.300), Henan (0.272), Hunan (0.253), Chongqing (0.247), Hubei (0.246), and Fujian (0.239). Furthermore, the “peak areas” of enterprise innovation resilience are concentrated in Jiangsu, Zhejiang, and Guangdong, indicating that regions with higher economic levels tend to possess stronger innovation resilience. After the outbreak of COVID-19, some regions have experienced significant increases in their resilience levels. Jiangxi province has a 6% increase, followed by Shandong (4.5%), Henan (4%), and Anhui (3.7%).
5.1. Data Preprocessing
To analyze the variations in innovation resilience development across different regions, the sample was divided into four parts. Region 1 represents the eastern region of China, encompassing Beijing, Tianjin, Hebei, Shanghai, Jiangsu, Zhejiang, Fujian, Shandong, Guangdong, Hainan, Liaoning, Jilin, and Heilongjiang. Region 2 represents midwestern China, including Shanxi, Anhui, Jiangxi, Henan, Hubei, Hunan, Inner Mongolia, Guangxi, Chongqing, Sichuan, Guizhou, Yunnan, Shaanxi, Gansu, Qinghai, and Ningxia. Region 3 represents the Yangtze River economic belt of China, consisting of Shanghai, Jiangsu, Zhejiang, Anhui, Jiangxi, Hubei, Hunan, Chongqing, Sichuan, Guizhou, and Yunnan. Lastly, Region 4 represents the Yellow River basin of China, encompassing Shanxi, Inner Mongolia, Shandong, Henan, Sichuan, Shaanxi, Gansu, Qinghai, and Ningxia. The results of innovation resilience across the four regions are presented in Table 3. The eastern region of China and the Yangtze River economic belt exhibit a declining–growing–declining trend, while midwestern China, the Yellow River basin, and the overall trend for China show a growing–declining–growing–declining pattern. However, it should be emphasized that the future direction of these data changes is uncertain, and predicting these trends accurately is crucial.

Table 3.
Innovation resilience in different regions and the whole of China.
5.2. Data Prediction
To adapt the grey fractional order FGM(1,1) model for iterative optimization, the parameters of the particle swarm algorithm were set as follows. Initially, based on the characteristics of the particle swarm algorithm, the learning factor was set to c1 = c2 = 2. The number of particle swarms was chosen as N = 50, with a maximum iteration limit of 100. For the stopping criterion, eps was set to 10−6. Additionally, considering the concept of the FGM(1,1) model fractional order, the value range of r was set as [0,1]. The weight, w, was varied linearly within the range of 0.1 to 0.9. Using MATLAB, the national and regional data were predicted, employing both the GM(1,1) and FGM(1,1) models. The prediction results are presented in Table 4 and Table 5.

Table 4.
GM(1,1) prediction results.

Table 5.
FGM(1,1) prediction results.
- (1)
- Figure 3 depicts the convergence plot of the fractional order (r) and the mean absolute percentage error (MAPE) values for the data derived from eastern China, which underwent iterations through the IPSO algorithm. The convergence map plateaus at a number of iterations of about 20. At this stage, the fractional order (r) obtains a value of 0.0999, while the MAPE reaches its minimum value of 0.0099.
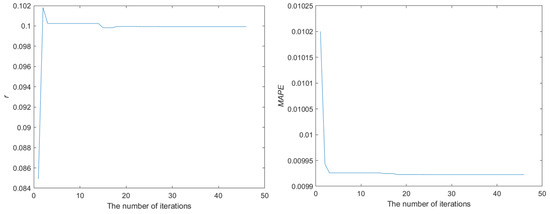 Figure 3. The convergence process of r and MAPE in Region 1.
Figure 3. The convergence process of r and MAPE in Region 1.
- (2)
- Figure 4 illustrates the convergence diagram of the fractional order (r) and the mean absolute percentage error (MAPE) values for the data in central and western China. The convergence map stabilizes at approximately 20 iterations. At this specific point, the fractional order (r) reaches a value of 0.9999, while the MAPE reaches its minimum with a value of 0.0155.
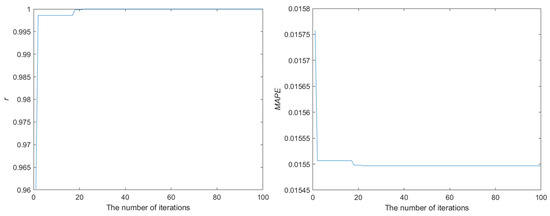 Figure 4. The convergence process of r and MAPE in Region 2.
Figure 4. The convergence process of r and MAPE in Region 2.
- (3)
- Figure 5 presents the convergence plot of the fractional order (r) and the MAPE values for the CHES data, which underwent iterations using the IPSO algorithm. The convergence map reaches a stable state after approximately 20 iterations. At this specific point, r takes on a value of 0.2004, while the MAPE reaches its minimum value of 0.0075.
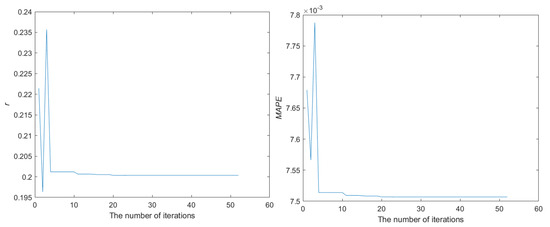 Figure 5. The convergence process of r and MAPE in Region 3.
Figure 5. The convergence process of r and MAPE in Region 3.
- (4)
- Figure 6 demonstrates the convergence diagram of the fractional order (r) and the MAPE values specifically for the Yellow River region in China. The convergence map reaches a stable state after approximately 20 iterations. At this specific point, r attains a value of 0.0922, while the MAPE achieves its minimum value, which is 0.0152.
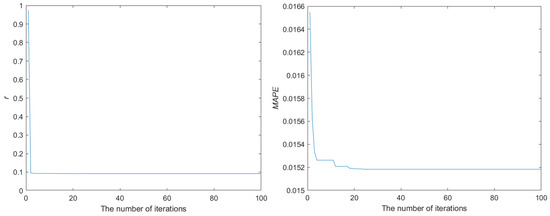 Figure 6. The convergence process of r and MAPE in Region 4.
Figure 6. The convergence process of r and MAPE in Region 4.
- (5)
- Figure 7 shows the convergence plot of the fractional and MAPE values of data covering the whole of China. The convergence map plateaus at a number of iterations of about 15. At this specific point, r is calculated as 0.0782, while the MAPE reaches its minimum value of 0.0136.
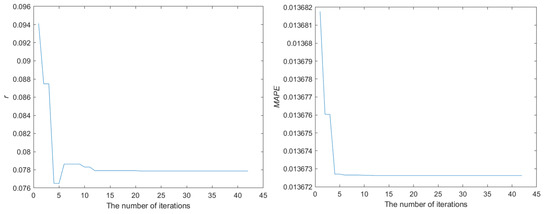 Figure 7. The convergence process of r and MAPE for the whole of China.
Figure 7. The convergence process of r and MAPE for the whole of China.
To investigate the benefits of the FGM(1,1) model, a comparison was made between the MAPE values of the FGM(1,1) and GM(1,1) models. The corresponding results are presented in Table 6. It can be observed that the mean absolute percentage error (MAPE) consistently demonstrates lower values for the FGM(1,1) model, indicating the superior performance of the FGM(1,1) model.

Table 6.
The comparison of MAPE between the FGM(1,1) model and GM(1,1) model.
5.3. Data Analysis
Table 4 indicates a high level of fitting between the forecasted data and the actual data. This suggests that the forecasted values can accurately reflect the fluctuations observed in the original data, particularly in cases where the volume of actual data is limited. Consequently, the growth rate and annual growth rate for the period of 2020–2025 are presented in Table 7.

Table 7.
The predicted growth rate and annual growth rate from 2020 to 2025.
The trend in innovation resilience of enterprises at the national level, in the central and western regions, and in the Yellow River basin is declining in the upcoming years. The annual decreases in these regions amount to 0.95%, 2.16%, and 1.42%, respectively. Conversely, the resilience index trends in the eastern region and the Yangtze River economic belt exhibit an upward trajectory, with annual increases of 0.34% and 0.44%, respectively. The data highlight a significant disparity between the decline and the increase in resilience. Several factors contribute to the downward trend. Firstly, unforeseen events such as the COVID-19 pandemic present substantial challenges and pressures for businesses. In response, companies must allocate limited resources to implement appropriate strategies and measures, albeit with the positive impacts of these events being overshadowed by their negative influences. Secondly, the central and western regions, along with the Yellow River basin, have a higher concentration of small and medium-sized enterprises or traditional industries. These entities often possess limited resources, low transformation efficiency, and inadequate capacity to withstand external shocks. Thirdly, due to the relatively lower economic level in these regions, inadequate policy support coupled with an unfavorable business environment has hindered their ability to sustain innovation.
Conversely, the Yangtze River economic belt and the eastern regions exhibit stronger innovation resilience due to several factors. Firstly, these regions benefit from various resource advantages, including abundant natural and human resources, strong financial capabilities, and technological accumulation. These advantages create a conducive environment for continuous technological innovation and market expansion, resulting in a leading position for enterprises in these regions. Secondly, enterprises in the eastern region, particularly in the Yangtze River economic belt, possess substantial technological strength and innovation capabilities. These companies prioritize technology research and development and are supported by robust government initiatives that foster technological innovation. Consequently, significant investments are made in technology research and development, enabling product and industrial upgrades that enhance their core competitiveness. Thirdly, the vast market demand in these regions provides ample application scenarios and development opportunities for enterprises. This market-driven demand stimulates corporate innovation vitality, thereby driving continuous product and business model innovation. Fourthly, substantial policy support, including financial subsidies, tax incentives, and talent recruitment, is provided by the government, especially in the Yangtze River economic belt and eastern regions. These policies reduce operating costs and enhance corporate innovation capabilities, further promoting innovation development. Lastly, the eastern region and the Yangtze River economic belt exhibit sound business environments, well-functioning market mechanisms, and high levels of information transparency. These conducive factors encourage companies to make informed decisions, adhere to standardized operations, and ultimately strengthen innovation resilience.
Overall, the innovation resilience of enterprises in the coming years is anticipated to experience a downward trajectory. To counteract this trend, appropriate policy measures must be implemented to drive and enhance the sustainability of innovation within enterprises.
6. Policy Configuration
In this section, we investigate the policy configuration that may enhance the resilience of enterprise innovation. Table 8 presents a compilation of macro- and micro-policies that have been found to have a significant impact on corporate innovation. In order to investigate the potential policy configurations that contribute to high innovation resilience, this research employs the fuzzy-set qualitative comparative analysis (fsQCA) model, as outlined in the framework presented by Witt et al. (2022). It is necessary to define the conditional variables and outcome variables to apply this model. For the conditional variables, we consider the effectiveness of each policy as measured by the proportion of entrepreneurs who believe that the policy listed in Table 6 has a significant effect on firm innovation. These effectiveness ratings serve as the condition variables in our analysis. In terms of the outcome variable, we utilize the corporate innovation resilience measure calculated earlier in the study. This outcome variable represents the level of resilience displayed by enterprises in terms of their innovation capabilities.

Table 8.
Calibration values and descriptive statistics.
6.1. Calibration of Conditions and Outcome
Based on prior research, we employ the direct calibration method [37] to transform the data into fuzzy-set affiliation scores, taking into account the available theoretical and empirical knowledge for each type of condition and outcome data. Given the lack of empirical knowledge as a calibration basis for the results and conditional variables under investigation, we draw upon prior studies [38,39] and utilize the 85th, 50th, and 15th percentiles as thresholds for full membership, crossover point, and full non-membership, respectively. These thresholds are applied to ten conditional variables and one outcome variable (innovation resilience). Table 8 offers a comprehensive overview of our calibrations along with the results of descriptive statistical analysis.
6.2. Analysis of the Necessity of a Single Policy
Before conducting the analysis of conditional configurations, it is crucial to individually assess the “necessity” of each policy. Following the mainstream QCA research approach, we examined whether each individual policy is a necessary condition for enterprise innovation resilience. Within qualitative comparative analysis methodologies, a condition is deemed necessary when its presence invariably coincides with the occurrence of the result [37]. To test the necessary conditions for high-level innovation resilience, we utilize fsQCA 3.0 software. The findings are illustrated in Table 9, which presents the results of the analysis. Based on the established criteria for determining significance, a policy is considered necessary for attaining innovation resilience if its consistency level surpasses 0.9 and demonstrates extensive coverage [40]. Nevertheless, the findings in Table 9 indicate that the consistency level of all conditions is less than 0.9. Thus, we can logically infer that the presence of a solitary policy is not a prerequisite for achieving a superior degree of innovation resilience in organizations. Consequently, it is crucial to further investigate the influence of policy configurations on innovation resilience.

Table 9.
Analysis of necessary conditions.
6.3. Sufficiency Analysis
In contrast to the examination of necessary conditions, the purpose of configuration analysis is to ascertain the adequacy of outcomes generated by various configurations that encompass multiple conditions. Configuration analysis aims to determine whether an outcome created by a composition of multiple conditions, represented by a configuration, is a subset of the result set from a set theory perspective. Consistency is utilized to evaluate the sufficiency of a configuration through the calculation methods and the acceptable minimum standards from those employed in the analysis of necessary conditions. Schneider and Wagemann (2012) advocate for a consistency level of no less than 0.75 for determining sufficiency, and the frequency threshold should be determined based on the sample size. In the case of small to medium-sized samples, it is advisable to set the frequency threshold at 1, whereas for larger samples, it is recommended to establish a frequency threshold exceeding 1.
Based on relevant studies, the initial consistency threshold was determined to be 0.8, while the PRI (parsimonious reduction index) consistency threshold was set at 0.6. Additionally, the case frequency threshold of 1 was applied to exclude non-representative combinations of conditions. The rationale behind these choices is to filter out inconsistent and unrepresentative configurations. Using fsQCA 3.0 software, we performed group analysis and determined the key groupings based on the comparison of results between the parsimonious solution and the intermediate solution. Table 10 showcases the results of our analysis. Specifically, core conditions are identified as conditional variables that manifest in both the intermediate and parsimonious solutions, which attests to their influential role in enhancing the innovation resilience of enterprises at a high level. In contrast, auxiliary conditions refer to conditional variables that appear in the intermediate solution but are not present in the parsimonious solution. This implies that their contribution to fostering high-level innovation resilience in enterprises is supplementary. Among the findings, there are three configurations (G1a, G1b, G2) of micro-policy conditions that generate high levels of innovation resilience in enterprises, and two configurations (G3, G4) of macro-policy conditions that yield the same outcome. To facilitate a more comprehensive analysis of the distinctions between these configurations, we further categorized the three configurations (G1a, G1b, G2) that generate high-level innovation resilience under micro-policy conditions into two groups, where G1a and G1b share the same core conditions and constitute an equivalent grouping [27]. The subsequent discussion provides a detailed analysis of each configuration’s impact on enterprise innovation resilience.

Table 10.
Configurations for high innovation resilience.
Within the context of micro-policy conditions, the consistency value of the single solution exceeds 0.8, suggesting that these configurations serve as sufficient conditions for attaining high-level innovation resilience. Moreover, the overall solution exhibits a consistency level of 0.841, indicating that among all cases satisfying these three condition configurations, 84.1% of policy configurations have achieved a high level of innovation resilience. Furthermore, the coverage of the overall solution is 0.801, indicating that these three configurations possess a strong explanatory power for enterprise innovation resilience.
Configuration G1a suggests that the core condition for generating high-level innovation resilience is the availability of tax incentives for additional deductions on enterprise R&D expenses, accompanied by the policy of income tax reduction and exemption for high-tech firms. The complementary marginal condition, in this case, entails the absence of an accelerated depreciation policy for specialized instruments and equipment used in R&D activities, as well as the absence of a technology introduction tax policy. The tested configuration demonstrates a consistency value of 0.814, a distinct coverage of 0.100, and a raw coverage of 0.277. As a result, this specific pathway can account for roughly 27.7% of cases exhibiting high-level innovation resilience, with only 10.0% of such cases having this pathway as their sole explanatory factor. Contrastingly, the G1b configuration emphasizes that optimal innovation resilience can be attained through core conditions that incorporate tax incentives for enterprise R&D expenses, along with income tax reduction and exemption policies tailored to high-tech firms. Additionally, the complementary conditions include an accelerated depreciation policy for specialized instruments and equipment used in R&D activities, as well as a technology introduction tax policy. The evaluated configuration exhibits a consistency value of 0.850, a distinct coverage of 0.350, and a raw coverage of 0.588. Therefore, this particular pathway can explain around 58.8% of cases characterized by high-level innovation resilience, with approximately 35.0% of these cases exclusively attributed to this pathway. To summarize, configurations G1a and G1b emphasize the positive impact of tax incentives for additional deductions on enterprise R&D expenses, as well as income tax reduction policies for high-tech enterprises, on the micro-policy conditions conducive to high-level innovation resilience in enterprises. When both of these conditions coexist, regardless of the favorable or unfavorable status of other relevant policy conditions, enterprises can engage in sustained and effective innovation activities even in the face of complex and dynamic environmental changes.
According to Configuration G2, optimal innovation resilience is achieved through a set of core conditions, which include the absence of the policy of income tax reduction and exemption for high-tech firms, the presence of an accelerated depreciation policy specifically for specialized instruments and equipment utilized in enterprise R&D activities, as well as the implementation of a technology introduction tax policy. Additionally, complementary conditions include the existence of policies on tax incentives for technology development and technology transfer. This configuration highlights the positive effects of accelerated depreciation policies for specialized instruments and equipment used in enterprise research and development activities, as well as import tax policies for technological innovation, on high-level innovation resilience in enterprises. Configuration G2 demonstrates a consistency value of 0.900, a distinctive coverage of 0.113, and a raw coverage of 0.316. As a result, this pathway can account for approximately 31.6% of cases exhibiting high-level innovation resilience, with approximately 11.3% of such cases being exclusively explained by this pathway.
The observed consistency value of the single solution surpasses 0.8 within the macro-policy conditions context, signifying that these configurations serve as adequate conditions for attaining a heightened degree of innovation resilience in enterprises. The comprehensive resolution exhibits a consistency level of 0.878, suggesting that among the policy conditional configurations that meet both conditional configurations, 87.8% have achieved a higher level of innovation resilience. Furthermore, the overall solution boasts a coverage value of 0.798, indicating that these two configurations possess a strong explanatory power for enterprise innovation resilience.
Configuration G3 highlights that high-level innovation resilience can be attained when there is a lack of policies related to enterprise talent recruitment and training, as well as policies concerning mass entrepreneurship and innovation. Moreover, the presence of policies on intellectual property protection, coupled with the absence of financial policies, serves as a marginal condition. This configuration underscores the positive influence of policies related to the creation and safeguarding of intellectual property rights on high-level innovation resilience in enterprises. The configuration’s consistency coefficient is calculated as 0.876. It exhibits a unique coverage value of 0.134 and an original coverage value of 0.335. Consequently, this specific pathway can explain around 33.5% of cases pertaining to high-level innovation resilience. Additionally, it solely accounts for an additional 13.4% of innovation resilience cases.
Configuration G4 posits that the core conditions for high-level innovation resilience include the presence of policies on enterprise recruitment and training, finance, intellectual property rights protection, mass entrepreneurship, and innovation, as well as the conversion of scientific and technological accomplishments. The consistency of this configuration is 0.878. The path also demonstrates a raw coverage value of 0.664 and a unique coverage value of 0.463. Consequently, this pathway can explain approximately 66.4% of high-level innovation resilience cases. Furthermore, about 46.3% of innovation resilience cases can only be attributed to this path. This configuration emphasizes that all policies within the macro-policy context serve as core conditions and asserts the significant impact of macro-policies on the innovation resilience of enterprises.
6.4. Robustness Testing
To ascertain the accuracy and dependability of the results, a robustness test was performed on the preliminary configuration of innovation resilience to examine the potential influences of extraneous factors. Firstly, the consistency threshold was elevated from 0.8 to 0.85 and presented the resulting outcomes in Table 11, which demonstrated a high degree of consistency with the original configuration. Secondly, we elevated the consistency threshold for policies related to the PRI from 0.6 to 0.65, and the results also exhibited a robust nature. Limitations relating to space necessitated the focus of this study being specifically on the robustness test aimed at improving the consistency threshold.

Table 11.
Robustness test for improving the consistency threshold.
6.5. Result Analysis
In the face of a complex and dynamic environment, improving innovation resilience is a key focus of government attention in facilitating sustainable development for enterprises. Both micro- and macro-policies play crucial roles in enhancing enterprise innovation capabilities. Hence, by utilizing a policy configuration framework alongside the fsQCA method, this research investigates the relationship between policy conditions and entrepreneurial resilience from a configurational standpoint.
From the viewpoint of horizontal individual conditions, it is evident that neither micro nor macro policy conditions can be isolated as sole determinants in augmenting the innovation resilience of enterprises. This indicates that the innovation resilience of enterprises is not driven by a single factor, but rather is the outcome of the collective effects of multiple factors. In other words, micro- and macro-policy conditions exhibit a “multiple concurrent” nature and effectively combine to influence the innovation resilience of enterprises in a manner characterized by “different paths leading to the same destination”.
Moreover, the results of the configuration analysis reveal five distinct pathways for enhancing the innovation resilience of enterprises under micro- and macro-policy conditions. Regarding the enhancement of enterprise innovation resilience, the configuration of micro-policy conditions reveals that tax incentives for an additional deduction of R&D expenses, the policy of income tax reduction and exemption for high-tech firms, and accelerated depreciation policies for specialized instruments and equipment utilized in R&D activities exert direct influence on the overall innovation resilience of enterprises. Even in the absence of favorable conditions in other relevant policy areas, enterprises can still engage in continuous and effective innovation activities under such circumstances. On the other hand, the two pathways of macro-policy configuration highlight the critical role of policies pertaining to intellectual property protection in enhancing innovation resilience as core conditions. As evident from the results, the enhancement of enterprise innovation resilience is a result of interconnectedness and synergy among multiple factors. This necessitates that managers strengthen the coordination and integration between micro- and macro-policy conditions when formulating policies. Taking a holistic perspective, it is vital to strive for the harmonization and alignment of multiple conditions while formulating targeted policies to improve enterprise innovation resilience. Additionally, attention should be given to the potential substitution effect amongst policy conditions. Even in situations where micro-policy support is insufficient, the government’s strong emphasis on policies related to intellectual property protection can still serve as an effective means to enhance innovation resilience.
7. Conclusions
7.1. Main Results
To examine the influence of future uncertainty on corporate innovation, this study employed entropy-weighted TOPSIS and FGM(1,1) models to assess and forecast corporate innovation resilience. The findings of the predictive analysis indicated a downward trend in innovation resilience in the future. Consequently, the fsQCA method was adopted to investigate which policy configurations could enhance the innovation resilience of enterprises, providing valuable insights for policymakers. The key findings can be summarized as follows.
Firstly, the indicator system encompassing factors such as tolerance for factor shortages, research and development security, and core technology supply manifested the innovation capabilities of enterprises within the context of uncertainty. The development trend of enterprise innovation resilience from 2016 to 2020, as identified through this indicator system, exhibited robustness from a national perspective, with variations observed across different regions. Enterprises in the eastern region demonstrated higher innovation resilience compared to those in the western region, and enterprises within the Yangtze River economic belt exhibited greater innovation resilience than those in the Yellow River basin, which is attributable to their resource endowments.
Secondly, according to the findings of the FGM(1,1) model, a general anticipation of decreasing innovation resilience in upcoming years was observed across enterprises, with particular emphasis on those located in central and western regions, as well as the Yellow River basin. Conversely, a noteworthy trend of enhanced innovation resilience was identified among the sampled enterprises situated in the eastern region and the Yangtze River economic belt. This trend could be linked to the economic level, policy enforcement, business environment, and enterprise scale prevalent in these regions.
Thirdly, the fsQCA findings revealed two distinct pathways for enhancing firm innovation resilience, as viewed from the perspective of micro-policy configurations. One path involved implementing tax incentives to enable additional deductions of enterprise R&D expenses alongside income tax reduction and exemption policies specifically targeted at high-tech enterprises. These measures were found to positively impact innovation resilience. The second path entailed the implementation of accelerated depreciation policies for R&D-related instruments and equipment alongside income tax incentives for technology development and transfer. These policies were identified as key drivers for improving the innovation resilience of firms. Interestingly, this configuration indicated that the policy of income tax reduction and exemption for high-tech firms demonstrated a substitution relationship with the aforementioned identified policies. This finding suggests that there is an interplay among policies in terms of corporate innovation resilience. In terms of macro-policy configuration, two distinct approaches were identified to strengthen resilience. One approach involved combining all macro-policies together, while the other approach focused on eliminating all policies except for those pertaining to intellectual property protection. Both approaches were found to enhance innovation resilience, and these conclusions were further validated through robustness testing.
7.2. Discussion
In terms of theoretical analysis, previous scholars have primarily focused on the impact of the timing of major emergencies on the measurement of innovation resilience, overlooking the delayed effects on enterprises. Hence, building upon prior research, we propose an index system for assessing enterprise innovation resilience from various perspectives, including factor shortage tolerance, R&D safety, core technology supply, and more. To measure and predict the future development trends of enterprise innovation resilience, we employ the entropy-weighted TOPSIS and FGM(1,1) models. This investigation enhances the research scope and approaches for evaluating corporate innovation resilience. It allows for the analysis of recent changes in the innovation resilience level of enterprises across different regions, along with informed projections of future trends in enterprise innovation resilience levels. Moreover, from a configurational standpoint, we explore the causal effects of policy conditions at both micro and macro levels on the innovation resilience of enterprises. The interplay between different policy conditions offers diverse pathways to enhance enterprise innovation resilience, thereby enhancing relevant research on enterprise innovation resilience from a policymaking perspective.
In terms of practical implications, the configuration results analyzed using the fsQCA method can inform governments and enterprises in formulating pertinent policies and systems to enhance enterprise innovation resilience. In the current uncertain environment, policymakers must prioritize enhancing the adaptability and adjustment capacity of innovation. From a micro-policy standpoint, the government should further promote tax incentives for additional deductions of enterprise R&D expenses, as well as income tax reductions and exemptions for high-tech enterprises. Additionally, implementing policies such as accelerated depreciation for specialized instruments and equipment in R&D activities, along with income tax incentives for technology development and transfer, will help improve the composition of innovation chain entities such as enterprises, customers, research institutions, and financial departments. These measures will optimize the regional innovation ecosystem. In terms of macro-policy configuration, a comprehensive assessment of macro-policies or a specific focus on enhancing intellectual property protection policies will create an environment conducive to enterprise innovation and consequently enhance innovation resilience.
7.3. Limitations and Steps for Further Research
This study is subject to several limitations that warrant consideration. Firstly, the sample size used in this research was relatively small, and it did not differentiate between the size and type of firms. The dataset included data from only 30 provinces in China spanning the period between 2016 and 2020, which served as the research sample for measuring enterprise innovation resilience. While this study has provided valuable insights and drawn meaningful conclusions, it is important to note that corporate resilience has multidimensional characteristics and that there may be differences in behavior among enterprises of different scales and types. Therefore, the findings of this research may have certain limitations in terms of generalizability. Additionally, this study did not consider the influence of time factors when analyzing the policy configuration that affects organizational resilience using the QCA method. In other words, the fsQCA method does not provide information about the chronological order in which policy conditions occur, nor does it indicate whether the sufficiency configuration obtained will remain stable over time. Future research should address these limitations and further explore the following two aspects. First, there is a need to construct more comprehensive measurement indicators for corporate innovation resilience to improve the applicability of the conclusions. Second, conducting a time series configuration analysis using the T-QCA method would allow for an exploration of how the sequence of policy condition implementation affects the level of innovation resilience in enterprises. By addressing these limitations, future research can provide a more nuanced understanding of enterprise innovation resilience and its determinants.
Author Contributions
Conceptualization, H.X. and L.W.; methodology, C.X. and X.T.; validation, P.W.; investigation, L.W.; writing—original draft preparation, J.J.; writing—review and editing, H.X.; supervision, L.W.; funding acquisition, H.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Social Science Foundation of China (granted number: 21CJY055) and the Project of Philosophy and Social Science Research in Colleges and Universities of Jiangsu Province (granted number: 2020SJA0209).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rao, H.; Greve, H.R. Disasters and Community Resilience: Spanish Flu and the Formation of Retail Cooperatives in Norway. Acad. Manag. J. 2017, 61, 5–25. [Google Scholar] [CrossRef]
- Hu, J.; Yu, L. Research on the Influence Mechanism and Characteristics of Innovation Resilience on High-tech Industry Innovation. Sci. Technol. Prog. Policy 2022, 39, 49–59. [Google Scholar]
- Li, E.; Zhang, C.; Wan, X. The Innovation Decision-Making under Economic Policy Uncertainty: From the Perspective of Enterprise Tenacity. Contemp. Financ. Econ. 2022, 10, 102–114. [Google Scholar]
- Liang, L.; Zhao, Y.; Liu, B. Research on Monitoring and Early Warning of the Resilience of the Innovation Ecosystem in the China’s National New Districts. China Soft Sci. 2020, 7, 92–111. [Google Scholar]
- Deng, J. Control problems of grey systems. Syst. Control. Lett. 1982, 1, 288–294. [Google Scholar]
- Hamidu, Z.; Mensah, B.D.; Issau, K.; Asafo-Adjei, E. Does technological innovation matter in the nexus between supply chain resilience and performance of manufacturing firms in a developing economy? J. Manuf. Technol. Manag. 2023, 34, 981–1003. [Google Scholar] [CrossRef]
- Kyrdoda, Y.; Balzano, M.; Marzi, G. Learn to survive crises: The role of firm resilience, innovation capabilities and environmental dynamism. Technol. Soc. 2023, 74, 102285. [Google Scholar] [CrossRef]
- Conz, E.; Magnani, G. A dynamic perspective on the resilience of firms: A systematic literature review and a framework for future research. Eur. Manag. J. 2020, 38, 400–412. [Google Scholar] [CrossRef]
- Wei, L.; Geng, Y. Construction of firm resilience evaluation index system in the context of COVID-19 epidemic. Contemp. Econ. 2021, 8, 108–113. [Google Scholar]
- Burnard, K.; Bhamra, R. Organisational resilience: Development of a conceptual framework for organisational responses. Int. J. Prod. Res. 2011, 49, 5581–5599. [Google Scholar] [CrossRef]
- Zhang, X.; Ten, X. The Essence, Dimensions, and Measurement of Organizational Resilience. Sci. Technol. Prog. Policy 2021, 38, 9–17. [Google Scholar]
- Wang, Y.; Cai, J. Organizational Resilience Scale Development and Its Reliability and validity verification. Stat. Decis. 2019, 35, 178–181. [Google Scholar]
- Al-Omoush, K.; Ribeiro-Navarrete, B.; Mcdowell, W.C. The impact of digital corporate social responsibility on social entrepreneurship and organizational resilience. Manag. Decis. 2023. ahead of print. [Google Scholar] [CrossRef]
- Li Peter Ping, Z.J. A Literature Review of Organizational Resilience. Foreign Econ. Manag. 2021, 43, 25–41. [Google Scholar]
- Wei, J.; Ren, T. Innovation Diversification, Economic Structure and Innovation Resilience. Sci. Technol. Manag. Res. 2022, 42, 39–48. [Google Scholar]
- Julong, D. Properties of Gray Forecasting Models GM(1,1). J. Huazhong Univ. Sci. Tech. 1987, 5, 3–8. [Google Scholar]
- Wu, L.F.; Liu, S.F.; Yao, L.G. Discrete grey model based on fractional order accumulate. Syst. Eng. Theory Pract. 2014, 34, 1822–1827. [Google Scholar]
- Zhang, K.; Alshehry, A.S.; Aljahdaly, N.H.; Shah, R.; Shah, N.A.; Ali, M.R. Efficient computational approaches for fractional-order Degasperis-Procesi and Camassa–Holm equations. Results Phys. 2023, 50, 106549. [Google Scholar] [CrossRef]
- Zafar, A.; Raheel, M.; Mahnashi, A.M.; Bekir, A.; Ali, M.R.; Hendy, A.S. Exploring the new soliton solutions to the nonlinear M-fractional evolution equations in shallow water by three analytical techniques. Results Phys. 2023, 54, 107092. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Liu, J. GM(1,1) model based on fractional order accumulating method and its stability. Control. Decis. 2014, 29, 6. [Google Scholar]
- Zhang, Y.; Wang, Z.; Yu, N.; Zhang, M.; Tang, S. Research on airport air quality forecast based on wavelet period and FGM(1,1) model. Math. Pract. Theory 2021, 51, 82–92. [Google Scholar]
- Tong, Y.; Chen, H.; Zhang, X.; Wu, L. Forecast of Beijing natural gas consumption based on FGM(1,1) model. Math. Pract. Theory 2020, 50, 79–83. [Google Scholar]
- Zhang, S.; Wu, L.; Cheng, M.; Zhang, D. Prediction of whole social electricity consumption in Jiangsu province based on metabolic FGM(1,1) model. Mathematics 2022, 10, 1791. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Dai, W.; Wu, L. Prediction of the Share of Solar Power in China Based on FGM(1,1) Model. Axioms 2022, 11, 581. [Google Scholar] [CrossRef]
- Xiong, C.; Wu, L. Prediction of China’s express business volume based on FGM(1,1) model. J. Math. 2021, 2021, 8585238. [Google Scholar] [CrossRef]
- Zhao, G. Prediction of the added value of high-tech industry in Hebei province based on FGM(1,1) model. Math. Pract. Theory 2021, 51, 313–317. [Google Scholar]
- Zhang, X.; Wang, J.; Wu, L.; Cheng, M.; Zhang, D. Prediction of the total output value of China’s construction industry based on FGM(1,1) model. Axioms 2022, 11, 450. [Google Scholar] [CrossRef]
- Walker, B.; Hollin, C.S.; Carpenter, S.R.; Kinzig, A. Resilience, Adaptability and Transformability in Social-ecological Systems. Ecol. Soc. 2004, 9, 5. [Google Scholar] [CrossRef]
- Zhu, L.; Dong, P. The Spatial Effect of Innovation Factors and Economic Resilience. Sci. Technol. Prog. Policy 2023, 2023, 1–11. [Google Scholar]
- Zhu, L.; Ge, Y. Empirical Testing of the Relationship between Market Segmentation and Regional Economic Resilience. Stat. Decis. 2023, 39, 121–125. [Google Scholar]
- Liu, Z.; Jiang, Z.; Xu, C.; Cai, G.; Zhan, J. Assessment of provincial waterlogging risk based on entropy weight TOPSIS–PCA method. Nat. Hazards 2021, 108, 1545–1567. [Google Scholar] [CrossRef]
- Luo, J.; Chen, S.; Sun, X.; Zhu, Y.; Zeng, J.; Chen, G. Analysis of city centrality based on entropy weight TOPSIS and population mobility: A case study of cities in the Yangtze River Economic Belt. J. Geogr. Sci. 2020, 30, 515–534. [Google Scholar] [CrossRef]
- Kennedy, J. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Eberhart, R.C.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the 6th International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Zhi-Rong, H.; Zhen-Su, L.U. Particle Swarm Optimization with Application Based on MATLAB. Comput. Simul. 2003, 20, 68–70. [Google Scholar]
- Fiss, P.C. A Set-Theoretic Approach to Organizational Configurations. Acad. Manag. Rev. 2007, 32, 1180–1198. [Google Scholar] [CrossRef]
- Ragin, C.C.; Fiss, P.C. Net effects analysis versus configurational analysis: An empirical demonstration. Redesigning Soc. Inq. Fuzzy Sets Beyond 2008, 240, 190–212. [Google Scholar]
- Fiss, P.C. Building Better Causal Theories: A Fuzzy Set Approach to Typologies in Organization Research. Acad. Manag. J. 2011, 54, 393–420. [Google Scholar] [CrossRef]
- Greckhamer, T. CEO compensation in relation to worker compensation across countries: The configurational impact of country-level institutions. Strateg. Manag. J. 2016, 37, 793–815. [Google Scholar] [CrossRef]
- Thomas, G.; Santi, F.; Fiss, P.C.; Aguilera, R.V. Studying configurations with qualitative comparative analysis: Best practices in strategy and organization research. Strateg. Organ. 2018, 16, 1029117576. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).