Abstract
In this paper, we propose a secure image encryption method using compressive sensing (CS) and a two-dimensional linear canonical transform (2D LCT). First, the SHA256 of the source image is used to generate encryption security keys. As a result, the suggested technique is able to resist selected plaintext attacks and is highly sensitive to plain images. CS simultaneously encrypts and compresses a plain image. Using a starting value correlated with the sum of the image pixels, the Mersenne Twister (MT) is used to control a measurement matrix in compressive sensing. Then, the scrambled image is permuted by Lorenz’s hyper-chaotic systems and encoded by chaotic and random phase masks in the 2D LCT domain. In this case, chaotic systems increase the output complexity, and the independent parameters of the 2D LCT expand the key space of the suggested technique. Ultimately, diffusion based on addition and modulus operations yields a cipher-text image. Simulations showed that this cryptosystem was able to withstand common attacks and had adequate cryptographic features.
1. Introduction
The rapid development of the internet has brought convenience to daily life, but privacy leakage incidents occur frequently. The issue of security has garnered extensive attention. Optical encryption, compressed sensing (CS), and network learning are effective means of protecting image security [1,2,3]. In 1995, Refregier and Javidi introduced the double random algorithm [4], which utilizes four optical processors and has garnered significant attention. To enhance security and increase the range of possible keys, the DRPE technique has been expanded into additional domains. However, it needs to be pointed out that these double-random phase-encoding (DRPE)-based encryption systems are linear systems [4,5,6,7], and these encryption methods are all types of symmetrical encryption systems. Due to the inherently linear nature of mathematics and optical transformation, the vulnerability of various encryption schemes to plaintext assaults is rather high [8].
Consequently, many nonlinear optical image encryption systems that can enhance security and resist plaintext attacks have been recently put forward [9,10,11,12]. An image encryption technique based on a chaotic system and transform was presented by Zhou et al. [9]. FRMTs of varying orders alter distinct annular areas of the original image, and this can be used to overcome the disadvantage of using linear transforms and having large key space. Since then, both signal processing and encryption have involved the more flexible linear canonical transform (LCT), which has three free parameters [13,14]. On the basis of the LCT, Wei et al. proposed the random discrete linear regular transform (RDLCT) [13]. The randomness of the RDLCT’s output phase and magnitude can strengthen an encryption system’s security. Recent designs have included further techniques based on the 2D LCT [14,15]. The 2D LCT has the natural advantage of multiple parameters, which can expand the key space and improve the security of an algorithm.
Chaos-based encryption schemes have frequently been utilized to further increase security [16,17,18,19,20]. This is because of their significant sensitivity to beginning circumstances, good pseudo-randomness, and ergodicity. In 1998, Fridrich proposed the classic framework of image encryption [16]. An image encryption technique based on spatiotemporal chaos was created using the framework mentioned above [17]. However, both of them were proven to be unable to resist chosen plaintext attacks [19,21]. Image encryption systems use an increasing amount of high-dimensional chaos due to their increasingly complicated dynamic nature, and they are more sensitive to initial values and higher security than to low-dimensional chaos [22]. Saljoughi presented an encryption algorithm using three-dimensional logistic maps [23]. A scale-invariant digital image encryption technique based on chaotic 3D maps was introduced by Hamed et al. [24], and it had excellent security capacity and high efficiency. Additionally, a number of hyper-chaotic systems were incorporated to enhance security [25,26,27]. To sum up, hyper-chaotic systems provide sequences with high pseudo-randomness that are ideal for encryption.
Meanwhile, CS is widely used because it allows data to be compressed directly at the time of collection, rather than being transmitted or stored after collection [28,29,30]. This can reduce the amount of data transferred and stored, increasing efficiency. At the same time, the nature of random measurements makes it more difficult to reconstruct information from raw data, which can increase the strength of encryption. Measurement matrices are typically thought of as the key in compressive-sensing-based algorithms [31,32,33]. However, the most popular approach generates an image-encrypted measurement matrix using a chaotic system [31,32,34,35,36]. Zhou developed an approach that employed two measurement matrices under the control of a logistic map to compress and encrypt pictures [31]. Nevertheless, the aforementioned techniques’ secret keys were unrelated to plaintext pictures, making them susceptible to specific plaintext assaults. Some recent methods can reduce these problems. The work in [37] introduced parallel compressive sensing (PCS), which was resistant to specific plaintext assaults. Above all, we created a unique image encryption technique based on CS and 2D LCT that could withstand typical assaults and had a huge key space.
In this study, we introduced a unique image encryption technique based on CS and the 2D LCT to further increase security. First, CS offers trustworthy and effective encryption and compression services, and a plaintext image controls the CS measurement matrix’s construction parameters. Second, to prevent certain plaintext assaults, the hyper-chaotic system’s initial values were generated by using the SHA 256 value of the original image. Third, the 2D LCT had six free parameters, which greatly enhanced the key space. The suggested scheme’s security against various assaults was demonstrated by the findings in security analysis and testing.
The following is the format for the remainder of this paper: Section 2 presents a few foundational theories. Section 3 provides a detailed explanation of the recommended image encryption method. A number of presentations and simulations are presented in Section 4. In Section 5, a succinct summary of the findings is provided.
2. Preliminaries
We first give a few related definitions before going into detail about the suggested algorithm.
2.1. Linear Canonical Transform
The linear canonical transform (LCT) is a class of linear integral transformations with three parameters, which is the general case of FrFT and Fresnel transformations (FSTs) [38]. The LCT is also useful in optical signal processing and encryption in a number of ways due to its multi-parameter advantages. The LCT of a transformable signal can be defined as [39]
where , , and constants are related by a parameter matrix A, which is also called unit-modular matrix and is represented as
where . Consequently, the LCT has three independent parameters.
A function’s continuous 2D LCT can be expressed as
where , , , and are real matrices. , . The constraint condition of the matrix C and D is .
2.2. Compressive Sensing
A unique method that can accomplish compression during the sampling process is called compressive sensing (CS) [28]. One might refer to a plain picture, secret key, or cipher image for the original image, the measurement matrix, and the image measured in CS, in that order. In accordance with the CS theory, sparse signals can yield a small quantity of observation data, and by resolving an optimization issue, we can roughly reconstruct these signals.
Suppose that x is a signal and can be measured by
where is the sparse coefficient vector and is an orthonormal sparse basis. The measured values can be obtained through the projection of a coefficient series on . After that, the following signal CS procedure can be stated:
where , , . Similarly, 2D or high dimension (HD) signals can be reduced to the 1D format by superimposing column vectors.
Reconstructing the original signal x from the measurements requires figuring out how to solve the following issue:
where the -norm of a vector is indicated by . Several popular reconstruction techniques have been introduced [40,41,42].
In this work, we implement the discrete wavelet transform (DWT) to achieve sparsity in the signals. A technique for signal processing called DWT breaks a signal down into many signals with varying scales, temporal resolutions, and frequency resolutions. The next part will provide a detailed description of how the measurement matrix was constructed. Eventually, x is restored by utilizing the orthogonal matching pursuit (OMP) method.
2.3. Lorenz’s Hyper-Chaotic System
Mathematically, Lorenz’s hyper-chaotic system is defined as
where the hyper-chaotic system’s control parameters are d, e, f, and r, and , , , . Figure 1 displays the system’s attractors. The average exponential divergence of neighboring trajectories in phase space is numerically represented by the Lyapunov exponent. This is one of the characteristics that helps distinguish chaotic motion. A chaotic system is often characterized by a positive maximum Lyapunov exponent. As a result, this hyper-chaotic system predicts events more quickly than a typical chaotic system does. Simultaneously, this feature makes the encryption system more secure.
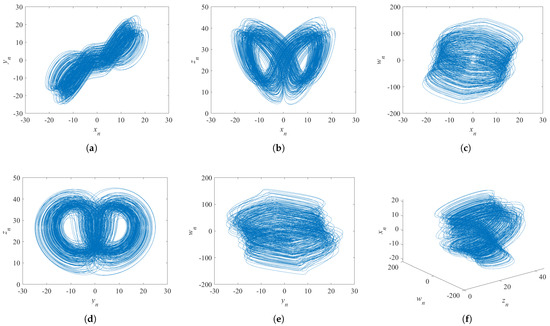
Figure 1.
Lorenz’s hyper-chaotic attractor: (a) x-y plane; (b) x-z plane; (c) x-w plane; (d) y-z plane; (e) y-w plane; (f) x-w-z plane.
3. The Proposed Image Encryption and Decryption Algorithm
3.1. Encryption Process
Four steps make up the majority of the suggested encryption method. The image must first be compressed and encrypted. Next, a prior image is jumbled using Lorenz’s hyper-chaotic system. The encrypted image is then encrypted using a 2D LCT. The image that was processed above is diffused the final stage. The suggested algorithm’s encryption procedure is depicted in Figure 2. Here, we take an image of size as an example to discuss the four parts in detail.

Figure 2.
A flowchart of the procedure for encryption and decoding.
3.1.1. Key Generation
The cryptosystem’s secret key structure has two parts. The first part is given by the encryption system user. Another part is obtained by SHA-256. Because SHA-256 is so dependent on the initial values of the original picture, even a small change might provide completely different secret keys. Therefore, we might use it to generate the keys for the suggested encryption technique, which can withstand attacks with carefully selected and well-known plaintext.
SHA-256 generates a 256-bit secret key as the hash value. This may be represented as and split up into 8-bit chunks: (). It is simultaneously converted into 32 decimal numbers for easier application. The following can be used to obtain the starting values.
Step 1: The parameters of Lorenz’s hyper-chaotic system are follows:
where denotes the sum of , , , and ; , , , are the starting points of permutation, and are the starting points of diffusion.
Step 2: The following are the starting values that are applied to chaotic random phase masks (CRPMs):
where ⊕ is the bitxor operation. and are the starting values of the two CRPMs.
The starting numbers are , , , , which fluctuate in tandem with the original image. ,, and are supplied by the encryption system’s user to increase security even more.
3.1.2. The Compression–Encryption Steps
First, the original picture was made sparser by applying a discrete wavelet transform. Then, to balance the sparsity of each row and improve the encryption performance, the resultant image was permuted using the Arnold transform, and this was repeated 25 times with starting values of and . Lastly, the encrypted image was obtained by using CS, which had the ability to both compress and encrypt images.
In CS, the measurement matrix was managed by the Mersenne Twister (MT) algorithm, which is based on a twisted generalized feedback shift register and can produce high-quality pseudo-random numbers. The random sequence was reshaped to generate a measurement matrix. This was efficient and made up for the shortcomings of traditional pseudo-random number generators. The initial conditions of MT were as follows:
where the closest integer to x is indicated by , and represents the sum of the pixel values of image I.
3.1.3. Permutation and Diffusion
To confuse and disperse pictures, Lorenz’s hyper-chaotic system generated pseudo-random sequences using the starting values generated in Equation (8). The process of permutation is given in detail:
Step 1: To create a one-dimensional vector in rows or columns, the original two-dimensional image matrix P (in this paper, expanded by row), denoted as A, is expanded.
Step 2: A pseudo-random sequence () of length is generated with the aid of the Lorenz system.
Step 3: Only the first pseudo-random number that appears repeatedly in X is retained, and, in order of smallest to greatest, the values in the set that are absent from X are appended to the end of X.
Step 4: The positions of and are swapped.
The diffusion algorithm in our proposed encryption based on addition and modulus operations is represented by the following equation.
where is the pseudo-random sequence produced by Lorenz’s system, represents the cypher vectors, and is a vector that expands from the plaintext image. Equation (13) is expanded:
It can be found in the Equation (14) that the information of the plaintext pixel can only be hidden in . In order to achieve the dispersion of each plaintext pixel over the whole cipher-text picture, this approach must be run twice. The following is the diffusion process.
Step 1: Using rows or columns, a one-dimensional vector is created by expanding the two-dimensional original image matrix P, denoted as A.
Step 2: With the initial values of Lorenz’s hyper-chaotic system from Equation (9) in the first part, we generate two pseudo-random sequences and , which are used for forward diffusion and reverse diffusion, respectively.
Step 3: is used to perform forward diffusion for the image to be encrypted using Equation (13).
Step 4: is used to perform reverse diffusion for the image to be encrypted. Reverse diffusion is expressed as follows: .
3.1.4. CRPMs and 2D LCT Encryption
The four phases involved in the encryption process utilizing the 2D LCT and CRPMs are as follows:
Step 1: is the first chaotic random phase mask generated with Equation (10) using the logistic map with the starting value .
Step 2: To obtain the image , the previously encrypted complex image is modulated with the first random phase mask and encrypted using the 2D LCT.
Step 3: The logistic map with an initial value of produced with Equation (11) is used to generate the second chaotic random phase mask .
Step 4: After modulating , the inverse 2D LCT (I–LCT) operation on yields a white-noise-like image .
The encryption process using the 2D LCT and CRPMs can be simplified as follows:
Figure 2 provides an illustration of the decryption procedure. It is evident that the decryption process is the opposite of the encryption technique described above.
4. Simulation Results and Security Analysis
4.1. Results of Encryption and Decryption
To test the suggested encryption scheme, four grayscale pictures of pixels each—“Boat,” “Zelda,” “Gold hill,” and “Einstein”—were chosen. The following are the parameters that we utilized in the simulation: , , , , , , , , , , , , , , , , , , and . Figure 3 presents the validation results for the encryption and decryption algorithms at CR = 0.5. The encrypted images are, as we can see, smaller than those with plaintext. This denotes a compression of the original image. In this case, the encrypted images were half the size of the original images, which allowed the encryption effect to be accomplished, in addition to lowering the quantity of data transmitted throughout the process. Furthermore, the encrypted images had a noise-like quality, indicating that the encryption technique effectively concealed the original images’ content. The decoded images were about the same as the plaintext images. In order to conduct a quantitative assessment of the quality of the reconstructed picture, the peak signal-to-noise ratio (PSNR) was introduced:
where the pixel values of the restored picture and the original image I are denoted by and , respectively. The four reconstructed pictures had PSNRs of 32.1021 dB, 34.0968 dB, 31.8867 dB, and 33.5572 dB. This demonstrated the algorithm’s strong decryption performance and great accuracy in image reconstruction.

Figure 3.
The results of encryption and decryption: (a,d,g,j) Unencrypted images; (b,e,h,k) the corresponding encrypted images at CR ; (c,f,i,l) the decrypted images.
The compression ratio (CR) is defined by
where , and , indicate the height and width of the image, respectively. The encrypted and decrypted results for Zelda with various CRs are listed in Figure 4. Figure 4 illustrates that, despite the modest CR, the reconstructed images exhibited remarkable similarity to the original images. When CR = 0.2, the cypher image’s PSNR was 30.9034 dB. Table 1 displays the PSNRs for Lena for comparison with those of other techniques [26,32,43]. It is evident that the suggested method’s reconstruction outperformed that of other approaches when the CR was higher than 0.5. Moreover, at CR = 0.4, the decrypted image’s PSNR might have been higher than 30 dB. Optimizing sparsity prior to compression could enhance the effect of reconstruction. In summary, our method was able to produce better results with a smaller sample size of data.

Figure 4.
Results of encryption and decryption for Zelda with various CRs: (a–d) the cypher pictures for CR values of , and , respectively; (e–h) the corresponding decrypted images.

Table 1.
PSNRs () for Lena with various CRs.
We tested the complexity of encryption and decryption algorithms when CR = 0.5, and the results are shown in Table 2. As can be seen from the results, the encryption time is very short, and the decryption time takes a few seconds. This is because the measurement matrix is easily generated during the encryption process, and during the decryption process, we used the OMP algorithm to iteratively solve it.

Table 2.
The encryption and decryption times for different images at CR (unit: seconds).
The mean square error (MSE) below the division sign of Equation (16) can be used to reflect the difference between the two images before and after encryption. The greater the MSE, the greater the difference between the two images. We calculated the MSE of the four images before and after encryption and summarized them in Table 3. In combination with Figure 3, the difference between the images before and after encryption is huge, indicating that our algorithm can hide image information well.

Table 3.
MSE between plaintext images and cipher-text images at CR .
4.2. Security Evaluation
We assessed the encryption system’s effectiveness from many angles based on the image properties in order to confirm the security of the suggested encryption system.
4.2.1. Analysis of Key Spaces
The key space is a crucial metric for assessing a cryptosystem’s quality. Furthermore, it needs to be large enough to withstand brute-force attacks [44]. The suggested algorithm’s secret key, which was mostly generated via SHA-265 of the plaintext image, is explained in Section 3.1.1. The encryption method involved 19 parameters and initial keys, which were for the measurement matrix and for the Arnold map in CS, and for Lorenz’s hyper-chaotic system in confusion and diffusion, for the 2D LCT, and for CRPM. We used the 2D LCT and Arnold map parameters as the public key. Presuming that the precision of the computer was , the key space was large compared to , as it was about . As a result, the suggested method was immune to all types of brute-force assaults. Furthermore, a comparison is made between the key spaces of four encryption techniques [26,32,45]. Table 4 illustrates that our scheme had the greatest key space.

Table 4.
Comparison of several approaches’ key spaces.
4.2.2. Histogram Analysis
A histogram provides statistical information in addition to displaying the distribution of pixels in an image. The even and smooth distribution of a cipher-text histogram can prevent attackers from breaking the image with statistical pixel value analysis. The histograms of the four images—“Boat”, “Zelda”, “Gold hill”, and “Einstein”—at CR = 0.75, each with pixels, are provided in Figure 5. As can be seen in Figure 5a–d, the histograms were often unevenly distributed and carried certain features of plaintext images. Figure 5e–h shows that the probability of pixels in the cipher-text image appearing in any value in the range of 0–255 was basically the same, and the height was approximately a straight line. After decrypting the cipher-text image with a decryption algorithm, the calculated histogram was similar to that of the plaintext image, indicating that our image decryption method recoverde the image information well.
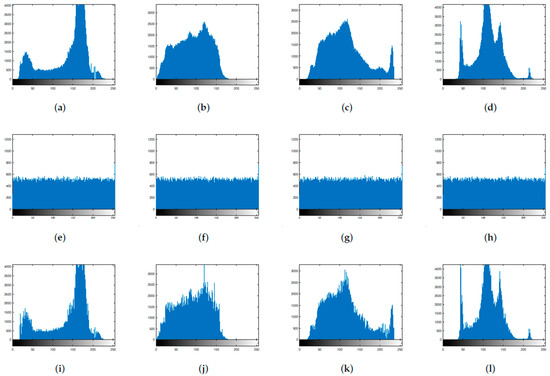
Figure 5.
Histogram analysis: The histograms of the plaintext images are shown in (a–d); the ground histograms of the cipher-text images are shown in (e–h); the histograms of the decrypted images are shown in (i–l).
More precisely, the distance of the histogram represents the similarity between a plaintext image and an encrypted image. For grayscale images, this is defined as the sum of the minimum heights of any pixel of the two histograms from 0 to 255, divided by the sum of the heights of all pixels of one of the histograms. The distance of the histogram is between 0 and 1, and the closer to 1, the more similar the two are. We calculated the histogram distance in the four selected graphs, and the results are shown in Table 5 and compared with those in the relevant literature. Although our algorithm was slightly worse than that in Ref. [26], the distance value was able to reach more than 0.9, indicating that our algorithm could also recover the original image well. In addition, according to Figure 5, our algorithm was able to resist statistical attacks well.

Table 5.
The histogram distance between a plaintext image and a decrypted image.
4.2.3. Analysis of Correlation Coefficients
Plaintext images can be attacked because of the significant correlations between their neighboring pixels. A strong method for image encryption can completely destroy the correlations. The measurement of correlation coefficients between plaintext and cipher-text images is a commonly used method for the qualitative assessment of encryption algorithms. This can be defined as [34]
where the standard variances of the values are represented by , and the average values of the image pixels are indicated by . There are 0 to 1 correlation coefficients. The link is greater the closer it gets to 1.
In this study, we computed the correlations from three directions at random locations. Table 6 and Figure 6 present the correlation coefficient performance on several images that were encrypted using the suggested approach. The plaintext images’ pixel coordinates were clearly clustered close to the diagonal, indicating a strong correlation coefficient. Nevertheless, the cipher-text images’ pixel locations filled the whole coordinate space, and the correlation coefficient dropped to almost zero. Additionally, using various encryption techniques, Table 7 contrasts Lena’s correlation coefficients with pixels [31,34,43]. In the cipher-text images, there was essentially no connection between neighboring pixels, suggesting that the suggested approach may entirely eliminate pixel correlation and fend off statistical assaults.

Table 6.
Correlation between neighboring pixels in various images.
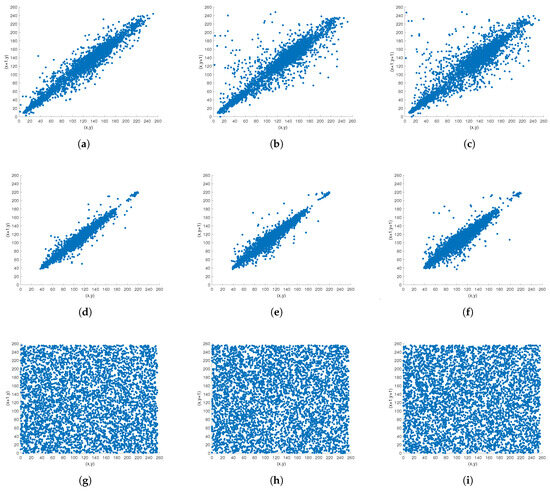
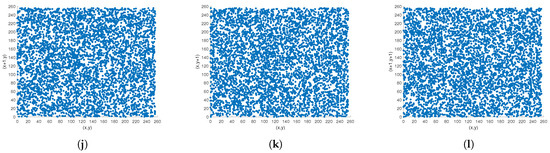
Figure 6.
Correlation coefficient analysis: (a–c) Einstein’s correlations from three directions; (g–i) the corresponding encrypted image correlations; (d–f) Boat’s correlations from three directions; (j–l) the corresponding encrypted image correlations.

Table 7.
Correlation between neighboring Lena pixels using several techniques.
4.2.4. Analysis of Information Entropy
An image I’s information entropy is described as [46]
where represents an element’s chance of occurring. The information entropies of several images are shown in Table 8. The entropy in the encrypted Lena image was compared with those in Refs. [25,26,47], as displayed in Table 9. It appears that the entropy values for several hidden images were around 8. From this, we may infer that the encrypted image data had a high degree of unpredictability and that the suggested approach could fend off statistical assaults.

Table 8.
Entropy of information for several images.

Table 9.
Comparison the information entropy.
4.2.5. Analysis of Cropping Attacks
During the image transfer procedure, data loss frequently occurs. A restored image can be significantly impacted by the loss of encrypted image data. Cropping attacks should be thwarted by a strong cryptosystem. Figure 7 displays a cypher image cropped at various sizes and places, whereas Figure 7 illustrates the matching reconstructed images. We conclude that while cropping affects the restoration of an image, the original image may still be recognized. Additionally, the quality of the recovered image deteriorates as the cropping area increases. As a result, our technique is resistant to a variety of cropping assaults.

Figure 7.
Cropping attack analysis: (a–d) are encrypted images with data loss in different size and position; (e–h) are corresponding decrypted images.
4.2.6. Crucial Sensitivity Testing
A safe cryptosystem is extremely sensitive to private keys. Changes in the cypher image and recovered image can be significant even with a small modification in the secret key. To subjectively assess the decryption process’s key sensitivity, we changed each of for permutation, for diffusion, for CRPM, and for the 2D LCT by adding . Figure 8 displays the findings on key sensitivity during the decryption procedure. As Figure 8 illustrates, minor changes in the keys would not allow the original image to be accurately reconstructed, and we did not get any original information from the plaintext images.

Figure 8.
Key sensitivity analysis. A decrypted image was obtained by slightly changing the keys: for permutation, for diffusion, and , for CRPM and the 2D LCT.
Furthermore, the difference between two images is frequently measured by using the unified average change intensity (UACI) and number of pixels changed (NPCR). The following are the definitions of the NPCR and UACI between two distinct images [48]:
One pixel each of the two images is represented by and . We used the key change method proposed above to calculate NPCR and UACI in the encryption process. For the encryption process, two cipher images were obtained by changing , , and by adding . The NPCR and UACI of the images during the encryption process are displayed in Table 10. The ideal values of the NPCR and UACI were NPCR = 99.6094% and UACI = 33.4635%. It was evident that the NPCR and UACI values closely resembled their theoretical counterparts. In conclusion, Table 10 and Figure 8 demonstrate that the suggested method had significant key sensitivity and can resist known cipher-text attacks.

Table 10.
The NPCRs and UACIs between cipher images created with slightly different keys.
4.2.7. Analysis of Differential Attacks
Creating a connection between a plaintext picture and its matching cipher-text image is the fundamental idea behind a differential attack. The sensitivity of a plaintext images determines whether or not the method can withstand differential assaults. Similarly, we encrypted a plaintext image by slightly changing the value of one of the pixels and using the same encryption process. The values of NRCR and UACI of the images before and after the change were calculated, and the results are shown in Table 11. It can be seen that the NRCR and UACI values of the proposed algorithm were still close to the theoretical values with different images. This was because in this work, we used highly sensitive SHA-256 and hyper-chaotic systems to generate a series of parameters. The data compression capabilities in CS and the multi-parameter properties of the 2D LCT were able to improve the effectiveness of the algorithm against differential attacks.

Table 11.
The UACIs and NPCRs of various encrypted images.
5. Conclusions
In this study, we illustrated a novel approach to image encryption in 2D LCT domains by utilizing CS, Lorenz’s hyper-chaotic system, and chaotic random phase encoding. SHA-256 helps strengthen defenses against specific plaintext attacks. The measurement matrix in CS is connected to the total of an image’s pixels, which may further increase the sensitivity to plaintext. CS can also efficiently minimize the size of encrypted images. Two positive Lyapunov exponents and a vast parameter space characterize Lorenz’s hyper-chaotic system. It is, therefore, ideal for applications involving image encryption. Additionally, the image is re-encrypted using the 2D LCT based on chaotic random phase masks. The suggested approach has a wide key space and high key sensitivity, and it is especially sensitive to plaintext, according to the simulation findings and security assessments. As such, it is resistant to well-known attacks, such as chosen-plaintext, known-plaintext, and brute-force attacks.
Author Contributions
Conceptualization, Y.-M.L. and D.W.; methodology, Y.-M.L. and D.W.; software, M.J.; validation, D.W.; formal analysis, Y.-M.L. and D.W.; investigation, M.J. and Y.D.; resources, M.J. and Y.D.; data curation, M.J. and Y.D.; writing—original draft preparation, M.J.; writing—review and editing, Y.-M.L. and D.W.; supervision, Y.-M.L. and D.W.; project administration, Y.-M.L. and D.W.; funding acquisition, Y.-M.L. and D.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 62371364 and in part by the Natural Science Basic Research Program of Shaanxi (Program No. 2023-JC-YB-048).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Matoba, O.; Nomura, T.; Perez-Cabre, E.; Millan, M.S.; Javidi, B. Optical techniques for information security. Proc. IEEE 2009, 97, 1128–1148. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Xu, J.; Yan, W. Heterogeneous network representation learning approach for ethereum identity identification. IEEE Trans. Comput. Soc. Syst. 2022, 10, 890–899. [Google Scholar] [CrossRef]
- Zhao, J.; Lv, Y. Output-feedback Robust Tracking Control of Uncertain Systems via Adaptive Learning. Int. J. Control Autom. Syst. 2023, 21, 1108–1118. [Google Scholar] [CrossRef]
- Refregier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 1995, 20, 767–769. [Google Scholar] [CrossRef]
- Situ, G.; Zhang, J. Double random-phase encoding in the Fresnel domain. Opt. Lett. 2004, 29, 1584–1586. [Google Scholar] [CrossRef]
- Chen, J.X.; Zhu, Z.L.; Fu, C.; Yu, H. Optical image encryption scheme using 3-D chaotic map based joint image scrambling and random encoding in gyrator domains. Opt. Commun. 2015, 341, 263–270. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, D. Simultaneous nonlinear encryption of grayscale and color images based on phase-truncated fractional Fourier transform and optical superposition principle. Appl. Opt. 2013, 52, 6170–6178. [Google Scholar] [CrossRef]
- Javidi, B.; Artur Carnicer, E.A. Roadmap on optical security. J. Opt. 2016, 18, 83001. [Google Scholar] [CrossRef]
- Zhou, N.; Wang, Y.; Gong, L. Novel optical image encryption scheme based on fractional Mellin transform. Opt. Commun. 2011, 284, 3234–3242. [Google Scholar] [CrossRef]
- Qin, W.; Peng, X. Asymmetric cryptosystem based on phase-truncated Fourier transforms. Opt. Lett. 2010, 35, 118–120. [Google Scholar] [CrossRef]
- Zhou, N.; Wang, Y.; Wu, J. Image encryption algorithm based on the multi-order discrete fractional Mellin transform. Opt. Commun. 2011, 284, 5588–5597. [Google Scholar] [CrossRef]
- Patra, A.; Saha, A.; Bhattacharya, K. Multiplexing and encryption of images using phase grating and random phase mask. Opt. Eng. 2020, 59, 33105. [Google Scholar] [CrossRef]
- Wei, D.; Wang, R.; Li, Y.M. Random discrete linear canonical transform. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2016, 33, 2470–2476. [Google Scholar] [CrossRef]
- Huang, Z.J.; Cheng, S.; Gong, L.H.; Zhou, N.R. Nonlinear optical multi-image encryption scheme with two-dimensional linear canonical transform. Opt. Lasers Eng. 2020, 124, 105821. [Google Scholar] [CrossRef]
- Rakheja, P.; Vig, R.; Singh, P. Double image encryption using 3D Lorenz chaotic system, 2D non-separable linear canonical transform and QR decomposition. Opt. Quantum Electron. 2020, 52, 103. [Google Scholar] [CrossRef]
- Fridrich, J. Symmetric ciphers based on two-dimensional chaotic maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Song, C.Y.; Qiao, Y.L.; Zhang, X.Z. An image encryption scheme based on new spatiotemporal chaos. Optik 2013, 124, 3329–3334. [Google Scholar] [CrossRef]
- Wang, X.; Xu, D. A novel image encryption scheme based on Brownian motion and PWLCM chaotic system. Nonlinear Dyn. 2014, 75, 345–353. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Xie, T.; Chen, M.Z.Q. Breaking a novel image encryption scheme based on improved hyperchaotic sequences. Nonlinear Dyn. 2013, 73, 2083–2089. [Google Scholar] [CrossRef]
- Quadri, S.Z.A. Multiple-information security system using spherical wave and chaotic random phase mask encoding. Opt. Eng. 2018, 57, 93103. [Google Scholar] [CrossRef]
- Bechikh, R.; Hermassi, H.; El-Latif, A.A.A.; Rhouma, R.; Belghith, S. Breaking an image encryption scheme based on a spatiotemporal chaotic system. Signal Process. Image Commun. 2015, 39, 151–158. [Google Scholar] [CrossRef]
- Arroyo, D.; Rhouma, R.; Alvarez, G.; Li, S.; Fernandez, V. On the security of a new image encryption scheme based on chaotic map lattices. Chaos 2008, 18, 33112. [Google Scholar] [CrossRef]
- Saljoughi, A.S.; Mirvaziri, H. A new method for image encryption by 3D chaotic map. Pattern Anal. Appl. 2019, 22, 243–257. [Google Scholar] [CrossRef]
- Ghazanfaripour, H.; Broumandnia, A. Designing a digital image encryption scheme using chaotic maps with prime modular. Opt. Laser Technol. 2020, 131, 106339. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Chen, H. A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation. Opt. Lasers Eng. 2017, 90, 238–246. [Google Scholar] [CrossRef]
- Xu, Q.; Sun, K.; Cao, C.; Zhu, C. A fast image encryption algorithm based on compressive sensing and hyperchaotic map. Opt. Lasers Eng. 2019, 121, 203–214. [Google Scholar] [CrossRef]
- Luo, Y.; Lin, J.; Liu, J.; Wei, D.; Cao, L.; Zhou, R.; Cao, Y.; Ding, X. A robust image encryption algorithm based on Chua’s circuit and compressive sensing. Signal Process. 2019, 161, 227–247. [Google Scholar] [CrossRef]
- Candes, E.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Candes, E.; Wakin, M. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Huang, X.; Dong, Y.; Ye, G.; Shi, Y. Meaningful image encryption algorithm based on compressive sensing and integer wavelet transform. Front. Comput. Sci. 2023, 17, 173804. [Google Scholar] [CrossRef]
- Zhou, N.; Li, H.; Wang, D.; Pan, S.; Zhou, Z. Image compression and encryption scheme based on 2D compressive sensing and fractional Mellin transform. Opt. Commun. 2015, 343, 10–21. [Google Scholar] [CrossRef]
- Chai, X.; Zheng, X.; Gan, Z.; Han, D.; Chen, Y. An image encryption algorithm based on chaotic system and compressive sensing. Signal Process. 2018, 148, 124–144. [Google Scholar] [CrossRef]
- Huang, R.; Rhee, K.H.; Uchida, S. A parallel image encryption method based on compressive sensing. Multimed. Tools Appl. 2014, 72, 71–93. [Google Scholar] [CrossRef]
- Zhou, N.; Zhang, A.; Zheng, F.; Gong, L. Novel image compression–encryption hybrid algorithm based on key-controlled measurement matrix in compressive sensing. Opt. Laser Technol. 2014, 62, 152–160. [Google Scholar] [CrossRef]
- Chai, X.; Gan, Z.; Chen, Y.; Zhang, Y. A visually secure image encryption scheme based on compressive sensing. Signal Process. 2017, 134, 35–51. [Google Scholar] [CrossRef]
- Zhang, L.Z.; Zhou, X.; Wang, D.; Li, N.N.; Bai, X.; Wang, Q.H. Multiple-image encryption based on optical scanning holography using orthogonal compressive sensing and random phase mask. Opt. Eng. 2020, 59, 1. [Google Scholar] [CrossRef]
- Hu, G.; Xiao, D.; Wang, Y.; Xiang, T.; Zhou, Q. Securing image information using double random phase encoding and parallel compressive sensing with updated sampling processes. Opt. Lasers Eng. 2017, 98, 123–133. [Google Scholar] [CrossRef]
- Wei, D.; Li, Y. Convolution and Multichannel Sampling for the Offset Linear Canonical Transform and Their Applications. IEEE Trans. Signal Process. 2019, 67, 6009–6024. [Google Scholar] [CrossRef]
- Wolf, K.B. Construction and Properties of Canonical Transforms; Springer: Berlin/Heidelberg, Germany, 1979; pp. 381–416. [Google Scholar]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. Siam Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Pati, Y.; Rezaiifar, R.; Krishnaprasad, P. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; pp. 40–44. [Google Scholar]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Commun. ACM 2010, 53, 93–100. [Google Scholar] [CrossRef]
- Zhou, N.; Zhang, A.; Wu, J.; Pei, D.; Yang, Y. Novel hybrid image compression–encryption algorithm based on compressive sensing. Optik 2014, 125, 5075–5080. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based crytosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Xingyuan, W.; Junjian, Z.; Guanghui, C. An image encryption algorithm based on ZigZag transform and LL compound chaotic system. Opt. Laser Technol. 2019, 119, 105581. [Google Scholar] [CrossRef]
- Awad, A.; Awad, D. Efficient image chaotic encryption algorithm with no propagation error. Etri J. 2010, 32, 774–783. [Google Scholar] [CrossRef]
- Zhou, K.; Fan, J.; Fan, H.; Li, M. Secure image encryption scheme using double random-phase encoding and compressed sensing. Opt. Laser Technol. 2020, 121, 105769. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI Randomness Tests for Image Encryption. J. Sel. Areas Telecommun. 2011, 1, 31–37. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).