An Efficient Cubic B-Spline Technique for Solving the Time Fractional Coupled Viscous Burgers Equation

Abstract

The second order Burger’s equation model is used to study the turbulent fluids, suspensions, shock waves, and the propagation of shallow water waves. In the present research, we investigate a numerical solution to the time fractional coupled-Burgers equation (TFCBE) using Crank–Nicolson and the cubic B-spline (CBS) approaches. The time derivative is addressed using Caputo’s formula, while the CBS technique with the help of a $\theta$-weighted scheme is utilized to discretize the first- and second-order spatial derivatives. The quasi-linearization technique is used to linearize the non-linear terms. The suggested scheme demonstrates unconditionally stable. Some numerical tests are utilized to evaluate the accuracy and feasibility of the current technique.

1. Introduction

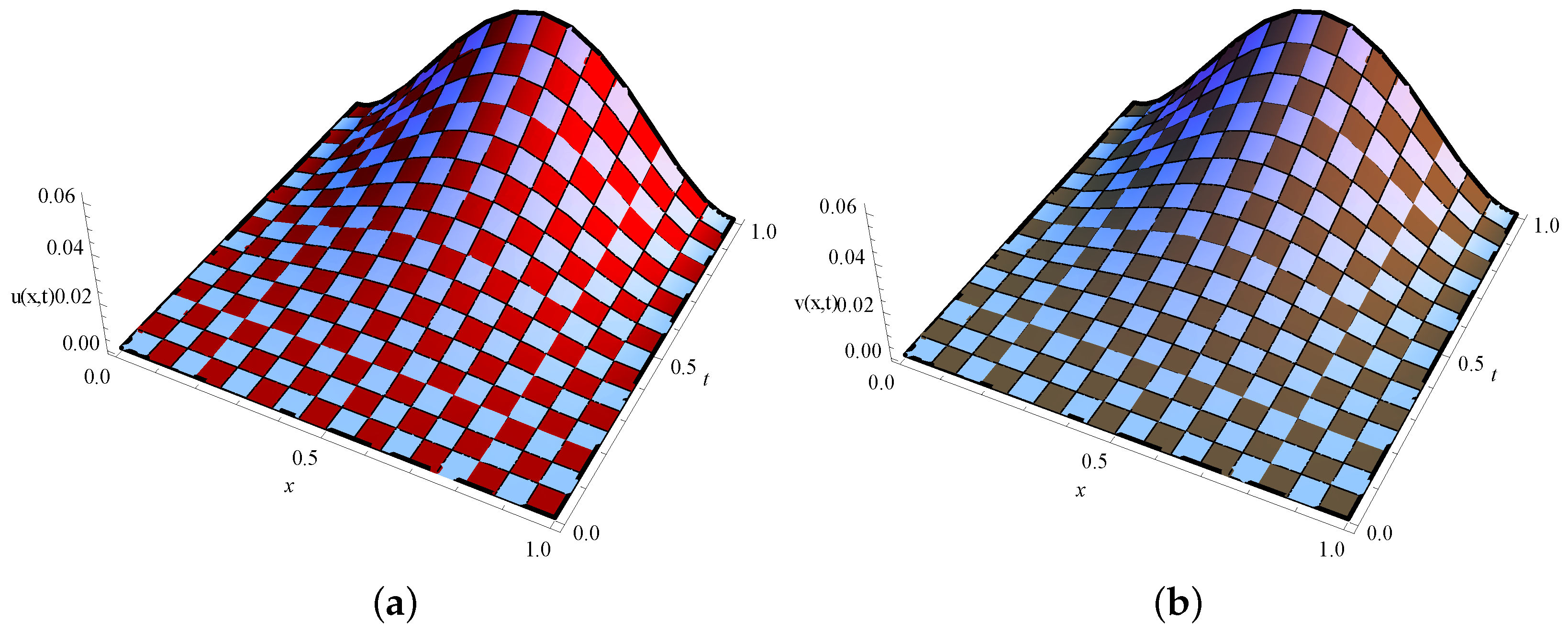
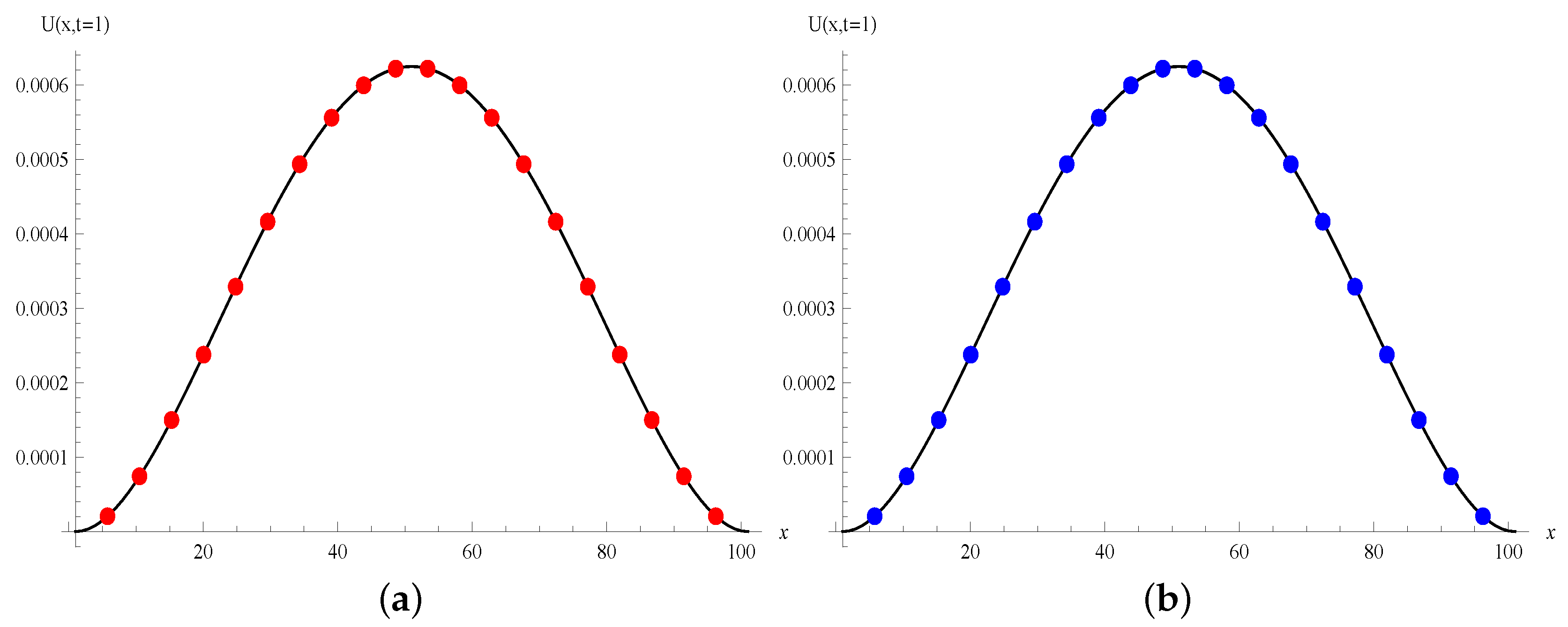
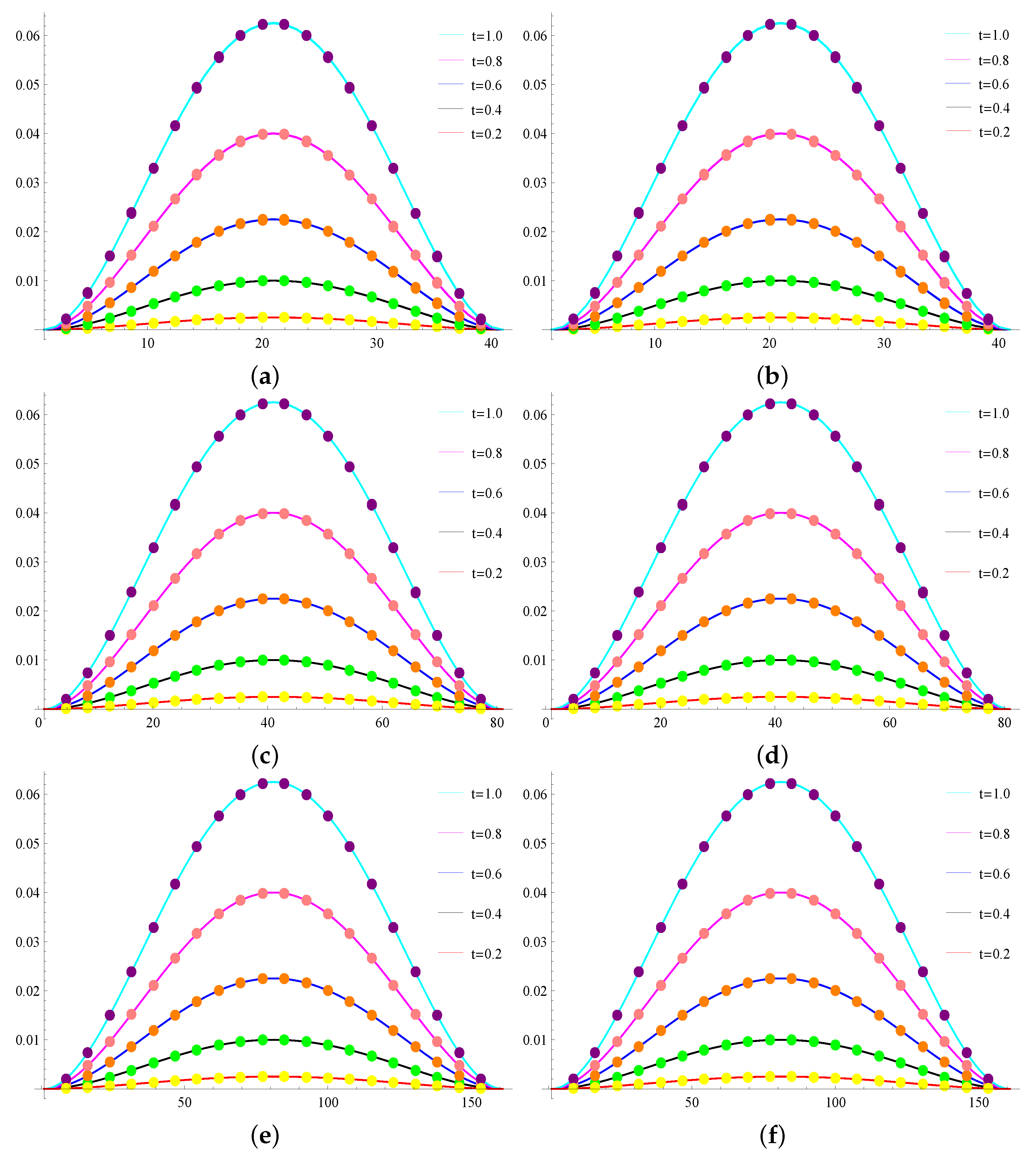
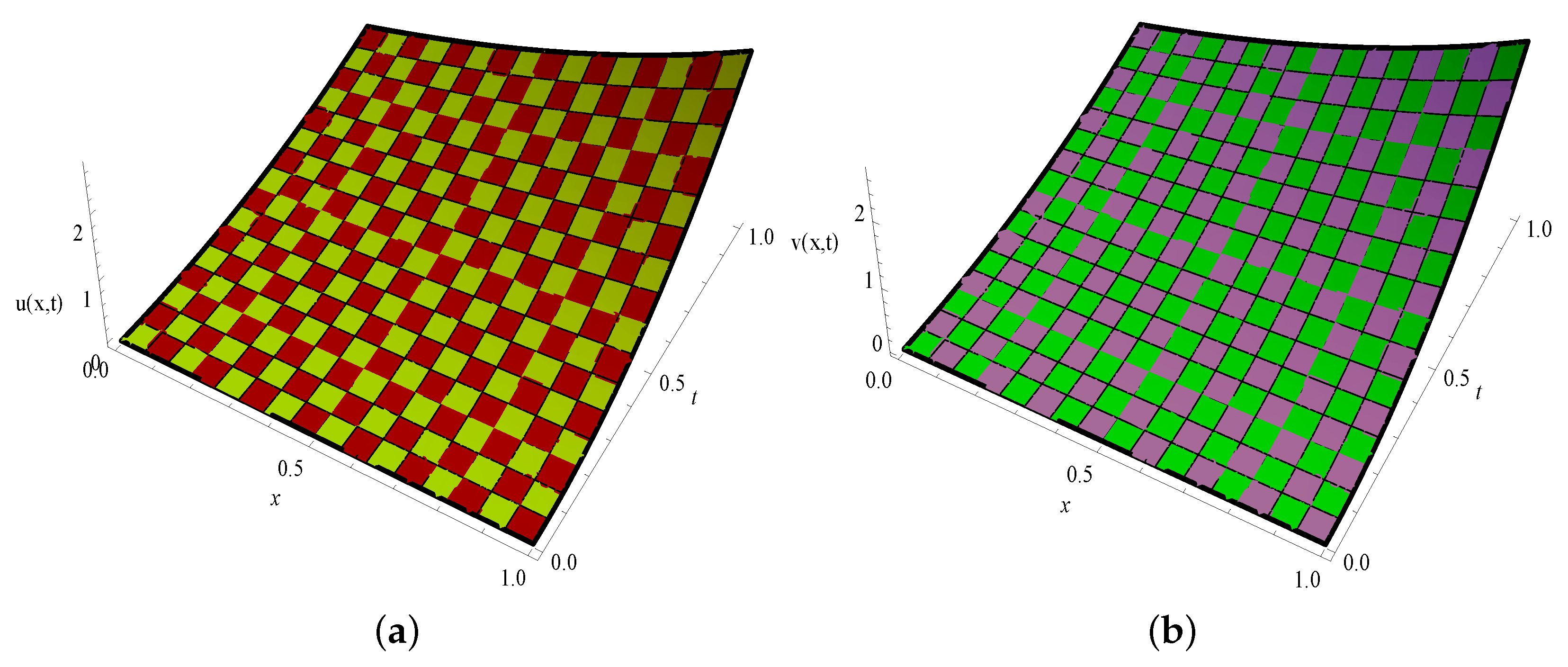
The second order viscous Coupled Burgers equations (VCBEs) are considered for numerical solution in this article. This model is used to study physical phenomena such as turbulent fluids, fluid suspensions, shock waves, arising in gas dynamics, the propagation of shallow water waves, continuous stochastic processes, flow theory, and chromatography [1,2,3,4,5]. The non-linear VCBEs are defined as follows:

$$\left\{\begin{array}{c}{U}_t(x,t)-U_{xx}(x,t)+{\alpha }_1{\left(U(x,t)V(x,t)\right)}_x+\gamma U(x,t)U_x(x,t)=0,a\le x\le b,t\in [0,T],\hfill \\ V_t(x,t)-V_{xx}(x,t)+{\alpha }_2{\left(V(x,t)U(x,t)\right)}_x+\gamma V(x,t)V_x(x,t)=0,a\le x\le b,t\in [0,T],\hfill \end{array}\right.$$

(1)

with initial conditions (ICs)

$$U(x,0)={\varphi }_1\left(x\right),V(x,0)={\varphi }_2\left(x\right),a\le x\le b$$

(2)

and boundary conditions (BCs)

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}U(a,t)\hfill & ={\phi }_1\left(t\right),V(a,t)={\psi }_1\left(t\right),\hfill \\ U(b,t)\hfill & ={\phi }_2\left(t\right),V(b,t)={\psi }_2\left(t\right),\hfill \end{array}\right.t\in [0,T]\end{array}$$

(3)

where ${\alpha }_1$ and ${\alpha }_2$ are system parameters, which represent the diffusion and interaction of two fluids, respectively, and $\gamma$ is a constant.

Fractional calculus involves the study of non-integer order derivatives and integrals [6,7,8]. The nonlinear TFCBE with different parameters is defined as follows:

$$\left\{\begin{array}{c}\frac{{\partial }^{\lambda }U(x,t)}{\partial t^{\lambda }}-\frac{{\partial }^{2}U(x,t)}{\partial x^2}+{\alpha }_1\frac{\partial \left(U\right(x,t\left)V\right(x,t\left)\right)}{\partial x}+\gamma U(x,t)\frac{\partial U(x,t)}{\partial x}=Q_1,\hfill \\ \frac{{\partial }^{\lambda }V(x,t)}{\partial t^{\lambda }}-\frac{{\partial }^{2}V(x,t)}{\partial x^2}+{\alpha }_2\frac{\partial \left(U\right(x,t\left)V\right(x,t\left)\right)}{\partial x}+\gamma V(x,t)\frac{\partial V(x,t)}{\partial x}=Q_2,\hfill \end{array}\right.x\in [a,b],t\in [0,T],\lambda \in (0,1),$$

(4)

with ICs:

$$U(x,0)={\varphi }_1\left(x\right),V(x,0)={\varphi }_2\left(x\right),$$

(5)

the BCs:

$$\left\{\begin{array}{c}U(a,t)={\phi }_1\left(t\right),U(b,t)={\phi }_2\left(t\right),\hfill \\ V(a,t)={\psi }_1\left(t\right),V(b,t)={\psi }_2\left(t\right),\hfill \end{array}\right.$$

(6)

where $\lambda$ is the fractional parameter, $\frac{{\partial }^{\lambda }U(x,t)}{\partial t^{\lambda }}$ is the time fractional derivative (FD) in the Caputo sense, and $\frac{\partial U(x,t)}{\partial x}=U_x(x,t)$ and $\frac{{\partial }^{2}U(x,t)}{\partial t^2}=U_{xx}(x,t)$ are first- and second-order spatial derivatives, respectively. This model represents the time fractional coupled-Burgers equation (TFCBE) in Caputo’s sense that satisfies the mathematical model accurately and represents the real-world system. These equations are well defined and capture the memory in time direction. The velocity profiles of two distinct fluids are denoted as $U(x,t)$ and $V(x,t)$. There are numerous methods to deal with the FD. Usually, the Caputo FD is used to acquire the appropriate real world physical models. In this paper, Caputo’s FD of the function is employed to discretize the temporal derivative. The Caputo FD of the function $U(x,t)$ with order $\lambda \in (0,1)$ is given as follows:

$$\frac{{\partial }^{\lambda }U(x,t)}{\partial t^{\lambda }}=\left\{\begin{array}{cc}\frac{1}{\Gamma (1-\lambda )}{\int }_0^t\frac{\partial U(x,\kappa )}{\partial \kappa }\frac{d\kappa }{{(t-\kappa )}^{\lambda }},\hfill & 0<\lambda <1,\hfill \\ \frac{\partial U(x,t)}{\partial t},\hfill & \lambda =1,\hfill \end{array}\right.$$

(7)

where the Euler’s Gamma function is represented by $\Gamma$.

Numerous approaches have been developed to deal with the initial and boundary value problems. Chen et al. [9] represented an approximate solution to coupled Burgers equations (CBEs) with FD using the Adomian decomposition method (ADM). Khan et al. [10] studied the Burgers and a system of Burgers equations using the homotopy perturbation method (HPM). They also solved these problems using a generalized differential transform method (GDTM) involving the Caputo time FD. CBEs have been solved by Prakash et al. [11] via a time fractional variational iteration approach. They compared their results with other methods, namely the HPM, the ADM, and the generalized differential transformation method (GDTM). The CBEs have also been solved using the q-homotopy analysis transform method by Singh et al. [12]. Aminikhah and Malekzadeh [13] developed a new HPM, in order to calculate the system of the CBEs and temporal FD that is used with the Caputo formula. In [14], a reduced differential transform method, the Laplace ADM, and the Laplace-variational iteration scheme have been utilized to investigate a solution to the CBEs. Albuohimad and Adibi proposed a solution to the CBEs using the hybrid spectral exponential Chebyshev method (HSECM), and the FD derivative was discretized utilizing the finite difference method (FDM) [15]. Sulaiman investigated the system of viscous Burgers equations using the Atangana–Baleanu FD to obtain a numerical simulation in [16]. A system Burgers equation was estimated using the generalized differential transform method (DTM) and the Caputo derivative (CD), employed to solve the temporal FD in [17]. Ozdemir et al. [18] calculated approximate solutions to Burgers equations by proposing Gegenbauer wavelets-based computational methods with TFD. Abazari and Borhanifar [19] developed an approximate solution to the CBEs through a differential transformation method. They also compared their approximate results with three different methods, namely the variational iteration, HPM, and analysis techniques. Mittal and Arora [20] investigated a system of viscous Burgers equations, discretized the scheme using the CBS collocation, and investigated the stability of the scheme. Shukla et al. [21] used a modified CBS to study the two-dimensional nonlinear VCBEs and found approximate solutions using the differential quadrature method. Kumar and Arora [22] employed approximate solutions to the coupled Klein Gordon equation and a system of Burgers equations through a reduced differential transformation scheme. Srivastava et al. [23] used the implication logarithmic FDM to present an approximation of a solution to the nonlinear CBEs. Mittal and Tripathi [24] investigated an approximate solution to a system of Burgers equation with the help of a modified spline. Sarboland and Aminataei [25] solved the nonlinear CBEs through a multiquadric quasi-interpolation scheme. Salih et al. [26] proposed a numerical solution to CBEs with Dirichlet’s boundary conditions by using trigonometric spline functions. He and Tang [27] developed a lattice Boltzmann to find a numerical solution to CBEs. Chuathong and Kaennakham [28] suggested a collocation method to determine approximate solutions to CBEs. Jima et al. [29] presented an approximated solution using a differential quadrature method. In [30], the authors presented a Chebyshev wavelets method to investigate a CBE. Guo-Cheng et al. [31] discussed the concept of short memory fractional differential equations with impulses and provided exact solutions for linear cases. Dubey et al. [32] presented a computational algorithm called a local fractional natural homotopy analysis method to solve local fractional coupled Helmholtz and CBEs in fractal media. They also discussed the uniqueness, convergence, and error analysis of the solutions obtained using the method. Numerical simulations on the Cantor set validate the effectiveness of the proposed method. WANG [33] proposed a new fractal modified equal width-Burgers equation (MEWBE) with the local fractional derivative using a Mittag–Leffler function.

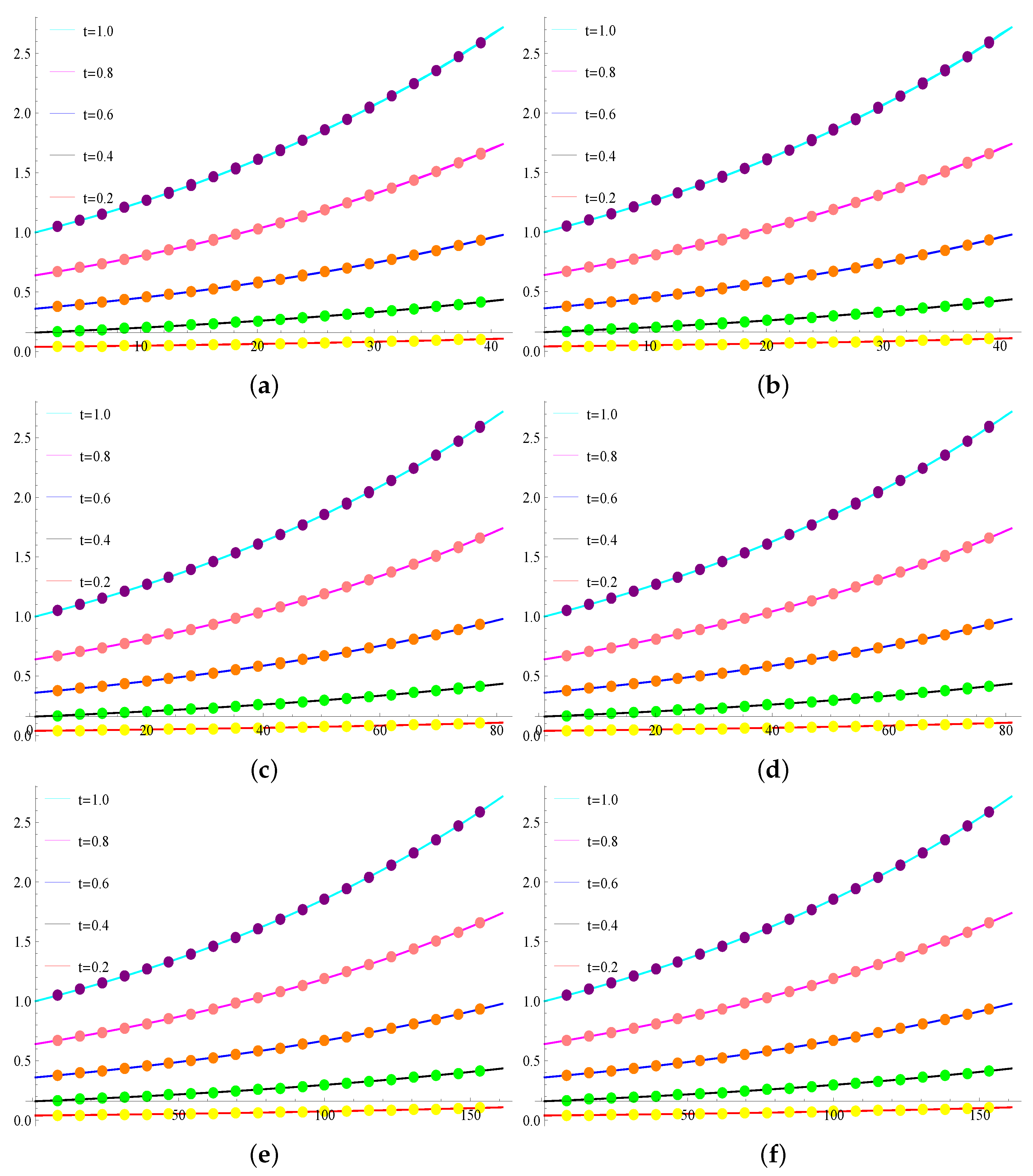
Spline interpolation is a valuable method for approximating mathematical functions with a piecewise smooth curve. Specifically, B-spline interpolation utilizes a type of piecewise polynomial that exhibits high localization. There is no study on the implementation of cubic B-spline for the TFCBEs. Inspired by the success of the spline in the numerical solution to integer-order differential equations and fractional order differential equations, the main aim of this study is to investigate the numerical solution to TFCBEs by using cubic B-spline functions. They have been employed by several researchers for solving fractional partial differential equations. The novelty of the proposed work is to discretize the first-order time fractional derivative in the Caputo sense with a first-order Crank–Nicholson finite difference scheme, while the CBS functions are used to discretize the spatial derivatives for coupled equations. It can be easily seen that the work done in this paper provides a more accurate numerical solution to the proposed problem because we use a combination of a Crank–Nicholson finite difference scheme and CBS functions with the help of a $\theta$-weighted scheme. This first-order time fractional derivative discretization in the Caputo sense for coupled equations has never been used, as far as we are aware, for the case of first-order TFCBEs. The superiority of the proposed method is to provide a numerical solution in a piecewise cubic function with the smoothness of $C^2$ continuity at each joint point of solution.

The paper is structured as follows: Section 2 describes the CBS functions at different knots. Section 3 and Section 4 present the discretization of the fractional derivative and the procedure of the proposed numerical technique, respectively. Section 5 discusses the stability of the suggested technique. The conclusion of the study is presented in Section 6.

2. B-Spline Approximation

Let $a=x_0<x_1...x_{N-1}<x_N=b$ be the spatial domain on the interval $[a,b]$. In the present section, cubic B-spline approximation for $U(x,t)$ and $V(x,t)$ is constructed. We define the partition into equivalent sub-intervals of length $h=\frac{b-a}{N}$, where $x_i=a+ih$, where $i=0,1,2,3,...,N$. The cubic B-spline can be defined as follows:

$$B_i\left(x\right)=\frac{1}{6h^3}\left\{\begin{array}{cc}{(x-x_{i-2})}^3,\hfill & x\in [x_{i-2},x_{i-1}],\hfill \\ h^3-3{(x-x_{i-1})}^3+3h{(x-x_{i-1})}^2+3h^2(x-x_{i-1}),\hfill & x\in [x_{i-1},x_i],\hfill \\ h^3-3{(x_{i+1}-x)}^3+3h{(x_{i+1}-x)}^2+3h^2(x_{i+1}-x),\hfill & x\in [x_i,x_{i+1}],\hfill \\ {(x_{i+2}-x)}^3,\hfill & x\in [x_{i+1},x_{i+2}],\hfill \\ 0,\hfill & \mathrm{Otherwise}.\hfill \end{array}\right.$$

(8)

The B-spline $\{B_{-1},B_0,...,B_N,B_{N+1}\}$ establishes a basis over the assumed domain. The values of $B_i\left(x\right)$ at the different knots are given in

Table 1. $B_i\left(x\right)$, ${B_i}^{\prime }\left(x\right)$, and ${B_i}^{″}\left(x\right)$ at the knots.

	${\mathit{x}}_{\mathit{i}+1}$	${\mathit{x}}_{\mathit{i}}$	${\mathit{x}}_{\mathit{i}-1}$	Else
$B_i\left(x\right)$	$1/6$	$2/3$	$1/6$	0
${B_i}^{\prime }\left(x\right)$	$-1/2h$	0	$1/2h$	0
${B_i}^{″}\left(x\right)$	$1/h^2$	$-2/h^2$	$1/h^2$	0

.

The solution to Equation (4) is considered a linear combination of the CBS by joining the $N+1$ number of control points with lines from ${\mu }_{-1}\left(t\right)$ to ${\mu }_{N+1}\left(t\right)$ and ${\nu }_{-1}\left(t\right)$ to ${\nu }_{N+1}\left(t\right)$ [34]. Our approach for the TFCBE with CBS is to seek as approximate solutions $U(x,t)$ and $V(x,t)$ in the following form [35]:

$$\left\{\begin{array}{c}U(x,t)={\displaystyle {\sum }_{i=-1}^{N+1}}{\mu }_i\left(t\right)B_i\left(x\right),\hfill \\ V(x,t)={\displaystyle {\sum }_{i=-1}^{N+1}}{\nu }_i\left(t\right)B_i\left(x\right),\hfill \end{array}\right.$$

(9)

where ${\mu }_i\left(t\right)$ and ${\nu }_i\left(t\right)$ are control points (or de Boor points), which depend on time and are to be computed at each time level for the approximate solution. $B_i\left(x\right)$ represents the CBS basis functions defined in (8). They are piecewise CBS functions with geometric properties like $C^2$ continuity, non-negativity, and partition of unity [36]. The approximations at each sub-interval $[x_i,x_{i-1}]$ contain $B_{i-1}\left(x\right),B_i\left(x\right),B_{i+1}\left(x\right)$ non-zero basis functions.

3. Discretization

The forward FDM is applied to discretize the Caputo time FD. Consider $t_k=k\tau$, where $k=0,1,...,m$ and the step size is $\tau =\frac{T}{m}$. The Caputo time FD can be described as follows at point $t=t_k$:

$$\begin{array}{cc}\hfill \frac{{\partial }^{\lambda }U(x,t_{k+1})}{\partial t^{\lambda }}& =\frac{1}{\Gamma (1-\lambda )}{\int }_0^t\frac{\partial U(x,\sigma )}{\partial \sigma }\frac{d\kappa }{{(t_{k+1}-\sigma )}^{\lambda }}\hfill \\ \hfill & =\frac{1}{\Gamma (1-\lambda )}{\displaystyle \sum _{p=0}^k}{\int }_{t_p}^{t_{p+1}}\frac{\partial U(x,\sigma )}{\partial \sigma }\frac{d\kappa }{{(t_{k+1}-\sigma )}^{\lambda }}\hfill \\ \hfill & =\frac{1}{\Gamma (1-\lambda )}{\displaystyle \sum _{p=0}^k}\frac{U(x,t_{p+1})-U(x,t_p)}{\tau }{\int }_{p\tau }^{(p+1)\tau }\frac{d\kappa }{{(t_{k+1}-\kappa )}^{\lambda }}+Z_{\tau }^{k+1}\hfill \\ \hfill & =\frac{1}{\Gamma (1-\lambda )}{\displaystyle \sum _{p=0}^k}\frac{U(x,t_{1-p+k})-U(x,t_{k-p})}{\tau }{\int }_{p\tau }^{(p+1)\tau }\frac{d\varpi }{{\varpi }^{\lambda }}+Z_{\tau }^{k+1}\hfill \\ \hfill & =\frac{1}{\Gamma (1-\lambda )}{\displaystyle \sum _{p=0}^k}\frac{U(x,t_{1-p+k})-U(x,t_{k-p})}{{\tau }^{\lambda }}[{(p+1)}^{-\lambda +1}-p^{-\lambda +1}]+Z_{\tau }^{k+1}.\hfill \end{array}$$

(10)

Equation (10) becomes

$$\begin{array}{c}\hfill \frac{{\partial }^{\lambda }U(x,t_{\sigma +1})}{\partial t^{\lambda }}=\frac{1}{\Gamma (2-\lambda )}{\displaystyle \sum _{p=0}^k}{Y}_p\frac{U(x,t_{1-p+k})-U(x,t_{k-p})}{{\tau }^{\lambda }}+Z_{\tau }^{k+1},\end{array}$$

(11)

where $Y_p={(p+1)}^{-\lambda +1}-p^{-\lambda +1}$, and the truncation error is $Z_{\tau }^{k+1}$, which is bounded, i.e., $|Z_{\tau }^{k+1}|\le \theta {\tau }^{2-\lambda }$ [37]. The coefficients $Y_p$ preserve the following properties [38]:

• $Y_0=1$,
• $Y_0>Y_1>Y_2>...>Y_p,Y_p\to 0asp\to \infty ,$
• $Y_p>0forp=0,1,...k,$ and
• ${\sum }_{p=0}^k(Y_p-Y_{p+1})+Y_{k+1}=(1-Y_1)+{\sum }_{p=1}^{k-1}(Y_p-Y_{p+1})+Y_k=1.$

4. Numerical Technique

The $\theta$-weighted scheme [39,40] for the system (4) at the $t_{k+1}^{th}$ time level is defined as

$$\left\{\begin{array}{c}{\left(U_t\right)}_j^k-\theta p_j^{k+1}=(1-\theta )p_j^k,\hfill \\ {\left(V_t\right)}_j^k-\theta q_j^{k+1}=(1-\theta )q_j^k,\hfill \end{array}\right.$$

(12)

where

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}_j^k={\left(U_{xx}\right)}_j^k-\gamma {\left(U{U}_x\right)}_j^k-{\alpha }_1[{\left(U{V}_x\right)}_j^k+{\left(U_{x}V\right)}_j^k],\hfill \\ q_j^k={\left(V_{xx}\right)}_j^k-\gamma {\left(V{V}_x\right)}_j^k-{\alpha }_1[{\left(V{U}_x\right)}_j^k+{\left(V_{x}U\right)}_j^k].\hfill \end{array}\right.\end{array}$$

It is noted that, when $\theta =0$, the above scheme becomes explicit; when $\theta =1$, it reduces to an implicit scheme; when $\theta =1/2$, it reduces to a Crank–Nicolson scheme. Using (11) and the $\theta$-weighted scheme (12) on the spatial derivative, Equation (4) then becomes

$$\begin{array}{c}\frac{1}{\Gamma (2-\lambda )}{\displaystyle \sum _{p=0}^k}{Y}_p\frac{U_j^{k-p+1}-U_j^{k-p}}{{\tau }^{\lambda }}-\theta [{\left(U_{xx}\right)}_j^{k+1}-\gamma {\left(U{U}_x\right)}_j^{k+1}-{\alpha }_1[{\left(U{V}_x\right)}_j^{k+1}+{\left(U_{x}V\right)}_j^{k+1}]]\hfill \\ \hfill =(1-\theta )[{\left(U_{xx}\right)}_j^k-\gamma {\left(U{U}_x\right)}_j^k-{\alpha }_1[{\left(U{V}_x\right)}_j^k+{\left(U_{x}V\right)}_j^k]]+Q_1,\end{array}$$

(13)

$$\begin{array}{c}\frac{1}{\Gamma (2-\lambda )}{\displaystyle \sum _{p=0}^k}{Y}_p\frac{V_j^{k-p+1}-V_j^{k-p}}{{\tau }^{\lambda }}-\theta [{\left(V_{xx}\right)}_j^{k+1}-\gamma {\left(V{V}_x\right)}_j^{k+1}-{\alpha }_2[{\left(V{U}_x\right)}_j^{k+1}+{\left(V_{x}U\right)}_j^{k+1}]]\hfill \\ \hfill =(1-\theta )[{\left(V_{xx}\right)}_j^k-\gamma {\left(V{V}_x\right)}_j^k-{\alpha }_2[{\left(V{U}_x\right)}_j^k+{\left(V_{x}U\right)}_j^k]]+Q_2,\end{array}$$

(14)

The quasi-linearization technique [41] at the ${(k+1)}^{th}$ stage is defined as

$$\left\{\begin{array}{c}{\left(U{U}_x\right)}_j^{k+1}=U_j^k{\left(U_x\right)}_j^{k+1}-{\left(U{U}_x\right)}_j^k+U_j^{k+1}{\left(U_x\right)}_j^k,\hfill \\ {\left(V{V}_x\right)}_j^{k+1}=V_j^k{\left(V_x\right)}_j^{k+1}-{\left(V{V}_x\right)}_j^k+V_j^{k+1}{\left(V_x\right)}_j^k,\hfill \\ {\left(U{V}_x\right)}_j^{k+1}=U_j^k{\left(V_x\right)}_j^{k+1}-{\left(U{V}_x\right)}_j^k+U_j^{k+1}{\left(V_x\right)}_j^k,\hfill \\ {\left(V{U}_x\right)}_j^{k+1}=V_j^k{\left(U_x\right)}_j^{k+1}-{\left(V{U}_x\right)}_j^k+V_j^{k+1}{\left(U_x\right)}_j^k.\hfill \end{array}\right.$$

(15)

Using the quasi-linearization technique (15), the non-linear terms in Equations (13) and (14) are linearized as

$$\begin{array}{c}\frac{1}{\Gamma (2-\lambda )}{\displaystyle \sum _{p=0}^k}{Y}_p\frac{U_j^{k-p+1}-U_j^{k-p}}{{\tau }^{\lambda }}-\theta [{\left(U_{xx}\right)}_j^{k+1}-\gamma [U_j^k{\left(U_x\right)}_j^{k+1}-{\left(U{U}_x\right)}_j^k+U_j^{k+1}{\left(U_x\right)}_j^k]\hfill \\ \hfill -{\alpha }_1[U_j^k{\left(V_x\right)}_j^{k+1}-{\left(U{V}_x\right)}_j^k+U_j^{k+1}{\left(V_x\right)}_j^k+{\left(U_{x}V\right)}_j^{k+1}]]=(1-\theta )[{\left(U_{xx}\right)}_j^k-\gamma {\left(U{U}_x\right)}_j^k-{\alpha }_1({\left(U{V}_x\right)}_j^k+{\left(U_{x}V\right)}_j^k)]+Q_1,\end{array}$$

(16)

$$\begin{array}{c}\frac{1}{\Gamma (2-\lambda )}{\displaystyle \sum _{p=0}^k}{Y}_p\frac{V_j^{k-p+1}-V_j^{k-p}}{{\tau }^{\lambda }}-\theta [{\left(V_{xx}\right)}_j^{k+1}-\gamma [U_j^k{\left(V_x\right)}_j^{k+1}-{\left(U{V}_x\right)}_j^k+U_j^{k+1}{\left(V_x\right)}_j^k]\hfill \\ \hfill -{\alpha }_2[V_j^k{\left(U_x\right)}_j^{k+1}-{\left(V{U}_x\right)}_j^k+V_j^{k+1}{\left(U_x\right)}_j^k+{\left(V_{x}U\right)}_j^{k+1}]]=(1-\theta )[{\left(V_{xx}\right)}_j^k-\gamma {\left(V{V}_x\right)}_j^k-{\alpha }_2({\left(V{U}_x\right)}_j^k+{\left(V_{x}U\right)}_j^k)]+Q_2,\end{array}$$

(17)

After some simplification of Equations (16) and (17), we obtain

$$\begin{array}{c}\frac{1}{\Gamma (2-\lambda )}{\displaystyle \sum _{p=0}^k}{Y}_p\frac{U_j^{k-p+1}-U_j^{k-p}}{{\tau }^{\lambda }}-\theta {\left(U_{xx}\right)}_j^{k+1}+\theta [\gamma {\left(U_x\right)}_j^k+{\alpha }_1{\left(V_x\right)}_j^k]U_j^{k+1}+\theta [\gamma U_j^k+{\alpha }_1{V}_j^k]{\left(U_x\right)}_j^{k+1}\hfill \\ \hfill +{\alpha }_1\theta [U_j^k{\left(V_x\right)}_j^{k+1}+{\left(U_x\right)}_j^k{V}_j^{k+1}]=(1-\theta ){\left(U_{xx}\right)}_j^k-\gamma (1-2\theta ){\left(U{U}_x\right)}_j^k-{\alpha }_1(1-2\theta ){\left(U{V}_x\right)}_j^k-{\alpha }_1(1-2\theta ){\left(U_{x}V\right)}_j^k+Q_1,\end{array}$$

(18)

$$\begin{array}{c}\frac{1}{\Gamma (2-\lambda )}{\displaystyle \sum _{p=0}^k}{Y}_p\frac{V_j^{k-p+1}-V_j^{k-p}}{{\tau }^{\lambda }}-\theta {\left(V_{xx}\right)}_j^{k+1}+\theta [\gamma {\left(V_x\right)}_j^k+{\alpha }_2{\left(U_x\right)}_j^k]V_j^{k+1}+\theta [\gamma V_j^k+{\alpha }_2{U}_j^k]{\left(V_x\right)}_j^{k+1}\hfill \\ \hfill +{\alpha }_2\theta [V_j^k{\left(U_x\right)}_j^{k+1}+{\left(V_x\right)}_j^k{U}_j^{k+1}]=(1-\theta ){\left(V_{xx}\right)}_j^k-\gamma (1-2\theta ){\left(V{V}_x\right)}_j^k-{\alpha }_2(1-2\theta ){\left(V{U}_x\right)}_j^k-{\alpha }_2(1-2\theta ){\left(V_{x}U\right)}_j^k+Q_2,\end{array}$$

(19)

The Crank–Nicolson approach is used because it is an unconditionally stable scheme and provides a more reasonable accuracy [42] than other finite difference schemes. Equations (18) and (19) provide the following relations:

$$\begin{array}{c}{\eta }_1{Y}_0{U}_j^{k+1}-\frac{1}{2}{\left(U_{xx}\right)}_j^{k+1}+\frac{{\gamma }_1}{2}{U}_j^{k+1}+\frac{{\gamma }_2}{2}{\left(U_x\right)}_j^{k+1}+\frac{{\alpha }_1}{2}[{\gamma }_3{\left(V_x\right)}_j^{k+1}+{\gamma }_4{V}_j^{k+1}]=\hfill \\ \hfill \frac{1}{2}{\left(U_{xx}\right)}_j^k-{\eta }_1{\displaystyle \sum _{p=1}^k}{Y}_p(U_j^{k-p+1}-U_j^{k-p})+{\left(Q_1\right)}_j^{k+1},\end{array}$$

(20)

$$\begin{array}{c}{\eta }_1{Y}_0{V}_j^{k+1}-\frac{1}{2}{\left(V_{xx}\right)}_j^{k+1}+\frac{{\gamma }_1}{2}{V}_j^{k+1}+\frac{{\gamma }_2}{2}{\left(V_x\right)}_j^{k+1}+\frac{{\alpha }_2}{2}[{\gamma }_3{\left(U_x\right)}_j^{k+1}+{\gamma }_4{U}_j^{k+1}]=\hfill \\ \hfill \frac{1}{2}{\left(V_{xx}\right)}_j^k-{\eta }_1{\displaystyle \sum _{p=1}^k}{Y}_p(V_j^{k-p+1}-V_j^{k-p})+{\left(Q_2\right)}_j^{k+1},\end{array}$$

(21)

where

• ${\eta }_1=\frac{1}{{\tau }^{\lambda }\Gamma (2-\lambda )}$,
• ${\gamma }_1=\gamma {\left(U_x\right)}_j^k+{\alpha }_1{\left(V_x\right)}_j^k=\gamma {\left(V_x\right)}_j^k+{\alpha }_2{\left(U_x\right)}_j^k$,
• ${\gamma }_2=\gamma U_j^k+{\alpha }_1{V}_j^k=\gamma V_j^k+{\alpha }_2{U}_j^k$, and
• ${\gamma }_3=U_j^k=V_j^k$ and ${\gamma }_3={\left(U_x\right)}_j^k={\left(V_x\right)}_j^k$.
• The boundary conditions are utilized to obtain a numerical solution to the proposed problem. Four extra linear equations are designed, as follows:

$$\left\{\begin{array}{c}{\left(U\right)}_0^{k+1}={\phi }_1\left(t_{k+1}\right),\hfill \\ {\left(U\right)}_n^{k+1}={\phi }_1\left(t_{k+1}\right),\hfill \\ {\left(V\right)}_0^{k+1}={\psi }_1\left(t_{k+1}\right),and\hfill \\ {\left(V\right)}_n^{k+1}={\psi }_1\left(t_{k+1}\right).\hfill \end{array}\right.$$

The initial conditions are listed below:

$$\left\{\begin{array}{c}{\left(U_x\right)}_m^{k+1}={\varphi }_1^{\prime }\left(t_m\right),m=0,M\hfill \\ {\left(U\right)}_m^{k+1}={\varphi }_1\left(t_m\right),m=0,1,2,...,M\hfill \\ {\left(V_x\right)}_m^{k+1}={\varphi }_2^{\prime }\left(t_m\right),m=0,M\hfill \\ {\left(V\right)}_m^{k+1}={\varphi }_2\left(t_m\right),m=0,1,2,...,M.\hfill \end{array}\right.$$

Equations (20) and (21) can be written in matrix form as follows:

$$A{C}^{k+1}=C^{k}B+D[{\eta }_1{Y}_k{\mu }^0+{\displaystyle \sum _{p=0}^{k-1}}(Y_p-Y_{p+1}){\mu }^{p-s}+{\eta }_1{Y}_k{\nu }^0+{\displaystyle \sum _{p=0}^{k-1}}(Y_p-Y_{p+1}){\nu }^{p-s}]+q^{k+1}.$$

(22)

where $C^{k+1}={[{\mu }_{-1}^{k+1},{\mu }_0^{k+1},...{\mu }_{M+1}^{k+1},{\nu }_{-1}^{k+1},{\nu }_0^{k+1},...{\nu }_{M+1}^{k+1}]}^T$ and $C^k={[{\mu }_{-1}^k,{\mu }_0^k,...{\mu }_{M+1}^k,{\nu }_{-1}^k,{\nu }_0^k,...{\nu }_{M+1}^k]}^T.$

After some simplification, we obtain

$$A{C}^{k+1}=F.$$

(23)

where A represents the square matrix of order $(2M+6)\times (2M+6)$, and F is the column vector of order $(2M+6)$.

$$A=\left(\begin{array}{ccc}{A}_1& ⋮& B_1\\ \cdots & \cdots & \cdots \\ B_1& ⋮& A_1\end{array}\right),B=\left(\begin{array}{ccc}{A}_2& ⋮& B_2\\ \cdots & \cdots & \cdots \\ B_2& ⋮& A_2\end{array}\right),$$

$$D=\left(\begin{array}{ccc}{A}_3& ⋮& B_2\\ \cdots & \cdots & \cdots \\ B_2& ⋮& A_3\end{array}\right),q^{k+1}=\left(\begin{array}{cc}{q}_1& \\ \cdots & \\ q_2\end{array}\right).$$

where

$$A_1=\left(\begin{array}{ccccccc}\frac{1}{6}& \frac{4}{6}& \frac{1}{6}& & & & \\ p_1& p_2& p_1& & & & \\ & p_1& p_2& p_1& & & \\ & & \ddots & \ddots & \ddots & & \\ & & & p_1& p_2& p_1& \\ & & & & p_1& p_2& p_1\\ & & & & \frac{1}{6}& \frac{4}{6}& \frac{1}{6}\end{array}\right),B_1=\left(\begin{array}{ccccccc}0& 0& 0& & & & \\ p_3& p_4& p_3& & & & \\ & p_3& p_4& p_3& & & \\ & & \ddots & \ddots & \ddots & & \\ & & & p_3& p_4& p_3& \\ & & & & p_3& p_4& p_3\\ & & & & 0& 0& 0\end{array}\right),$$

$$A_2=\left(\begin{array}{ccccccc}0& 0& 0& & & & \\ p_5& p_6& p_5& & & & \\ & p_5& p_6& p_5& & & \\ & & \ddots & \ddots & \ddots & & \\ & & & p_5& p_6& p_5& \\ & & & & p_5& p_6& p_5\\ & & & & 0& 0& 0\end{array}\right),B_2=\left(\begin{array}{ccccccc}0& 0& 0& & & & \\ 0& 0& 0& & & & \\ & 0& 0& 0& & & \\ & & \ddots & \ddots & \ddots & & \\ & & & 0& 0& 0& \\ & & & & 0& 0& 0\\ & & & & 0& 0& 0\end{array}\right),$$

$$A_3=\left(\begin{array}{ccccccc}0& 0& 0& & & & \\ \frac{1}{6}& \frac{4}{6}& \frac{1}{6}& & & & \\ & \frac{1}{6}& \frac{4}{6}& \frac{1}{6}& & & \\ & & \ddots & \ddots & \ddots & & \\ & & & \frac{1}{6}& \frac{4}{6}& \frac{1}{6}& \\ & & & & \frac{1}{6}& \frac{4}{6}& \frac{1}{6}\\ & & & & 0& 0& 0\end{array}\right),q_1=\left(\begin{array}{c}{\phi }_1^{k+1}\\ {\left(Q_1\right)}_0^{k+1}\\ {\left(Q_1\right)}_1^{k+1}\\ ⋮\\ {\left(Q_1\right)}_{N-1}^{k+1}\\ {\left(Q_1\right)}_N^{k+1}\\ {\phi }_2^{k+1}\end{array}\right),q_2=\left(\begin{array}{c}{\varphi }_1^{k+1}\\ {\left(Q_2\right)}_0^{k+1}\\ {\left(Q_2\right)}_1^{k+1}\\ ⋮\\ {\left(Q_2\right)}_{N-1}^{k+1}\\ {\left(Q_2\right)}_N^{k+1}\\ {\varphi }_2^{k+1}\end{array}\right),$$

where

• $p_1=\frac{{\eta }_1{Y}_0}{6}-\frac{1}{2h^2}+\frac{1}{12}{\gamma }_1-\frac{1}{4h}{\gamma }_2,$
• $p_1=\frac{2{\eta }_1{Y}_0}{3}-\frac{1}{h^2}+\frac{1}{3}{\gamma }_1,$
• $p_3=\frac{\alpha }{2}(-\frac{{\gamma }_3}{2h}+\frac{{\gamma }_4}{6}),$
• $p_4=\frac{\alpha }{2}(\frac{{\gamma }_3}{2h}+\frac{2{\gamma }_4}{3}),$
• $p_5=\frac{1}{2h^2}+\frac{{\eta }_1{Y}_0}{6},$ and
• $p_6=-\frac{1}{h^2}+\frac{2{\eta }_1{Y}_0}{3}.$

Algorithm

•

Describe the model of TFCBEs.

•

Use quasi-linearization technique to linearize the problem.

•

Use the Caputo FD and the CBS functions to discretize the presented problem.

•

Obtain the system of order $(2M+6)\times (2M+6)$.

•

For each time step, solve the above system using Wolfram Mathematica 11.

5. Stability Analysis

A stability analysis is introduced to affirm that the scheme does not amplify errors. The numerical error and stability of the numerical scheme are strongly related. If problems committed during one computing time step do not result in additional errors as the computations proceed, then the finite difference scheme is stable. When errors in a scheme do not change as calculations are performed, it is said to be unconditionally stable [42]. The principle of stability is connected to computation technique errors that do not rise as the method progresses [43]. In this section, we will utilize the Fourier series scheme to assess the stability of the suggested methodology [44,45]. In order to perform Fourier stability analysis, a temporary freeze is applied to the non-linear terms. As a result, we have frozen U and V as constants ${\omega }_1$ and ${\omega }_2$, respectively [46]. Only linear equations are appropriate for stability analysis. The following equation is constructed by substituting an approximation of Equation (18):

$$\begin{array}{c}{\eta }_1{Y}_0{U}_j^{k+1}-\frac{1}{2}{\displaystyle \sum _{\iota =0}^M}{D}_{j\iota }^2{U}_{\iota }^{k+1}+\frac{1}{2}(\eta {\omega }_1+{\alpha }_1{\omega }_2){\displaystyle \sum _{\iota =0}^M}{D}_{j\iota }^1{U}_{\iota }^{k+1}+\frac{{\alpha }_1{\omega }_1}{2}{\displaystyle \sum _{\iota =0}^M}{D}_{j\iota }^1{V}_{\iota }^{k+1}=-\frac{1}{2}(\eta {\omega }_1+{\alpha }_1{\omega }_2){\displaystyle \sum _{\iota =0}^M}{D}_{j\iota }^1{U}_{\iota }^k\hfill \\ \hfill -\frac{{\alpha }_1{\omega }_1}{2}{\displaystyle \sum _{\iota =0}^M}{D}_{j\iota }^1{V}_{\iota }^k+\frac{1}{2}{\displaystyle \sum _{\iota =0}^M}{D}_{j\iota }^2{U}_{\iota }^k+{\eta }_1{Y}_0{U}_j^k-{\eta }_1{\displaystyle \sum _{p=1}^k}{Y}_p[U_j^{k-s+1}-U_j^{k-s}]+Q_1.\end{array}$$

(24)

Let ${\tilde{U}}_j^k$ and ${\tilde{V}}_j^k$ be the estimated solution to (24), and errors ${\mu }_j^k$ and ${\nu }_j^k$ can be presented as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mu }_j^k=U_j^k-{\tilde{U}}_j^k,\hfill \\ {\nu }_j^k=V_j^k-{\tilde{V}}_j^k,\hfill \end{array}\right.k=0,1,...M,j=0,1,...N-1\end{array}$$

(25)

Corresponding vectors are as follows:

$$\left\{\begin{array}{c}{\mu }^k={[{\mu }_1^k,{\mu }_2^k,...{\mu }_{N-1}^k]}^T,\hfill \\ {\nu }^k={[{\nu }_1^k,{\nu }_2^k,...{\nu }_{N-1}^k]}^T.\hfill \end{array}\right.$$

(26)

We analyze the stability of the scheme given in (24), and the source term is considered to be zero. We obtain the round-off error equation as follows:

$$\begin{array}{c}\left[-\frac{1}{2h^2}-\frac{\zeta }{4h}+\frac{{\eta }_1{Y}_0}{6}\right]{\mu }_{j-1}^{k+1}+\left[\frac{2{\eta }_1{Y}_0}{3}+\frac{1}{h^2}\right]{\mu }_j^{k+1}+\left[-\frac{1}{2h^2}+\frac{\zeta }{4h}+\frac{{\eta }_1{Y}_0}{6}\right]{\mu }_{j-1}^{k+1}-\frac{{\alpha }_1{\omega }_1}{4h}{\nu }_{j-1}^{k+1}\hfill \\ +\frac{{\alpha }_1{\omega }_1}{4h}{\nu }_{j+1}^{k+1}=\left[\frac{1}{2h^2}+\frac{\zeta }{4h}+\frac{{\eta }_1{Y}_0}{6}\right]{\mu }_{j-1}^k+\left[\frac{2{\eta }_1{Y}_0}{3}-\frac{1}{h^2}\right]{\mu }_j^{k+1}+\left[\frac{1}{2h^2}-\frac{\zeta }{4h}+\frac{{\eta }_1{Y}_0}{6}\right]{\mu }_{j+1}^{k+1}\\ \hfill +\frac{{\alpha }_1{\omega }_1}{4h}{\nu }_{j-1}^k-\frac{{\alpha }_1{\omega }_1}{4h}{\nu }_{j+1}^k+{\eta }_1{\displaystyle \sum _{p=1}^k}{Y}_p\left[\frac{1}{6}\left({\mu }_{j-1}^{k-p+1}-{\mu }_{j-1}^{k-p}\right)+\frac{2}{3}\left({\mu }_j^{k-p+1}-{\mu }_j^{k-p}\right)+\frac{1}{6}\left({\mu }_{j+1}^{k-p+1}-{\mu }_{j+1}^{k-p}\right)\right],\end{array}$$

(27)

where $\zeta =(\eta {\omega }_1+{\alpha }_1{\omega }_2)$.

Grid functions are defined as follows:

$${\mu }^k\left(x\right)=\left\{\begin{array}{cc}{\mu }_j^k,\hfill & x_j-\frac{h}{2}<x\le x_j+\frac{h}{2},\hfill \\ \\ 0,\hfill & 0<x\le \frac{h}{2} or L-\frac{h}{2}<x\le L,\hfill \end{array}\right.,{\nu }^k\left(x\right)=\left\{\begin{array}{cc}{\nu }_j^k,\hfill & x_j-\frac{h}{2}<x\le x_j+\frac{h}{2},\hfill \\ \\ 0,\hfill & 0<x\le \frac{h}{2} or L-\frac{h}{2}<x\le L,\hfill \end{array}\right.$$

Fourier expansion for ${\mu }^k\left(x\right)$ and ${\nu }^k\left(x\right)$ can be represented as

$$\left\{\begin{array}{c}{\mu }^k\left(x\right)={\displaystyle {\sum }_{p=-\infty }^{\infty }}{X}_k\left(p\right)e^{i2\pi px/L},\hfill \\ {\nu }^k\left(x\right)={\displaystyle {\sum }_{p=-\infty }^{\infty }}{Y}_k\left(p\right)e^{i2\pi px/L},\hfill \end{array}\right.$$

(28)

where $X_k\left(p\right)=\frac{1}{L}{\int }_0^L{\mu }^k\left(x\right)e^{i2\pi px/L}dx$ and $Y_k\left(p\right)=\frac{1}{L}{\int }_0^L{\nu }^k\left(x\right)e^{i2\pi px/L}dx$.

The Parseval equation is given as [47]:

$$\left\{\begin{array}{c}{\int }_0^L\parallel {\mu }^k{\left(x\right)\parallel }^{2}dx={\displaystyle {\sum }_{p=-\infty }^{\infty }}\parallel X_k{\left(p\right)\parallel }^2,{\int }_0^L\parallel {\nu }^k{\left(x\right)\parallel }^{2}dx={\displaystyle {\sum }_{p=-\infty }^{\infty }}{\parallel Y_k\left(p\right)\parallel }^2,\hfill \end{array}\right.$$

(29)

Applying the Parseval equality [48], which is

$$\left\{\begin{array}{cc}{\int }_0^L{\parallel {\mu }^k\left(x\right)\parallel }^{2}dx\hfill & ={\displaystyle {\sum }_{j=1}^{M-1}}h{\parallel {\mu }_j^k\parallel }^2,\hfill \\ {\int }_0^L{\parallel {\nu }^k\left(x\right)\parallel }^{2}dx\hfill & ={\displaystyle {\sum }_{j=1}^{M-1}}h{\parallel {\nu }_j^k\parallel }^2,\hfill \end{array}\right.$$

we have

$$\left\{\begin{array}{cc}\parallel {\mu }^k{\parallel }_2^2\hfill & ={\displaystyle {\sum }_{\ell =-\infty }^{\infty }}{\parallel X_k(\ell )\parallel }^2,\hfill \\ \parallel {\nu }^k{\parallel }_2^2\hfill & ={\displaystyle {\sum }_{\ell =-\infty }^{\infty }}{\parallel Y_k(\ell )\parallel }^2.\hfill \end{array}\right.$$

Now we suppose the solution in the form of Fourier series analysis, described as follows:

$$\left\{\begin{array}{c}{\mu }_j^k=X_k{e}^{i{\psi }_{x}jh},\hfill \\ {\nu }_j^k=Y_k{e}^{i{\psi }_{x}jh},\hfill \end{array}\right.$$

(30)

where ${\psi }_x=(2\pi \ell /L)$. Substituting the above relations into (24), we obtain

$$\begin{array}{c}\left[\frac{{\eta }_1{Y}_0}{3}cos\left({\psi }_{x}h\right)-\frac{1}{h^2}cos\left({\psi }_{x}h\right)+\frac{2{\eta }_1{Y}_0}{3}+\frac{1}{h^2}\right]X_{k+1}+\dot{\iota }\left[\frac{\zeta }{2h}sin\left({\psi }_{x}h\right)\right]X_{k+1}+\dot{\iota }\left[\frac{{\alpha }_1{\omega }_1}{2h}sin\left({\psi }_{x}h\right)\right]Y_{k+1}\hfill \\ =\left[\frac{{\eta }_1{Y}_0}{3}cos\left({\psi }_{x}h\right)+\frac{1}{h^2}cos\left({\psi }_{x}h\right)+\frac{2{\eta }_1{Y}_0}{3}-\frac{1}{h^2}\right]X_k-\dot{\iota }\left[\frac{\zeta }{2h}sin\left({\psi }_{x}h\right)\right]X_k-\dot{\iota }\left[\frac{{\alpha }_1{\omega }_1}{2h}sin\left({\psi }_{x}h\right)\right]Y_k\\ \hfill +{\eta }_1{\displaystyle \sum _{p=1}^k}\left[(X_{k-p+1}-X_{k-p})\frac{1}{3}cos\left({\psi }_{x}h\right)+\frac{2}{3}\right].\end{array}$$

(31)

Set

$$\begin{array}{cc}\hfill A& =\frac{{\eta }_1{Y}_0}{3}cos\left({\psi }_{x}h\right)-\frac{1}{h^2}cos\left({\psi }_{x}h\right)+\frac{2{\eta }_1{Y}_0}{3}+\frac{1}{h^2},\hfill \\ \hfill B& =\frac{\zeta }{2h}sin\left({\psi }_{x}h\right),\hfill \\ \hfill C& =\frac{{\alpha }_1{\omega }_1}{2h}sin\left({\psi }_{x}h\right),\hfill \\ \hfill D& =cos\left({\psi }_{x}h\right).\hfill \end{array}$$

We have

$$A{X}_{k+1}+\dot{\iota }(B{X}_{k+1}+C{Y}_{k+1})=-(A+\dot{\iota }B)X_k-\dot{\iota }C{Y}_k+\frac{{\eta }_1}{3}{\displaystyle \sum _{p=1}^k}\left[(X_{k-p+1}-X_{k-p})D+2\right]$$

$$(A+\dot{\iota }B)X_{k+1}+\dot{\iota }C{Y}_{k+1}=-(A+\dot{\iota }B)X_k-\dot{\iota }C{Y}_k+\frac{{\eta }_1}{3}{\displaystyle \sum _{p=1}^k}\left[(X_{k-p+1}-X_{k-p})D+2\right]$$

$$(A+\dot{\iota }B)X_{k+1}=-(A+\dot{\iota }B)X_k-\dot{\iota }C(Y_{k+1}+Y_k)+\frac{{\eta }_1}{3}{\displaystyle \sum _{p=1}^k}\left[(X_{k-p+1}-X_{k-p})D+2\right]$$

(32)

Then

$$|X_{k+1}|\le \mid X_k\mid +\frac{\mid \dot{\iota }C\mid }{\mid A+\dot{\iota }B\mid }(\mid Y_{k+1}\mid +\mid Y_k\mid )+\frac{1}{\mid A+\dot{\iota }B\mid }\frac{{\eta }_1}{3}{\displaystyle \sum _{p=1}^k}\left[(X_{k-p+1}-X_{k-p})D+2\right].$$

(33)

Theorem 1.

Let $X_k$ be the solution to (32). Then $E_k$ is the positive constant, and we have

$$\mid X_k\mid \le E_k\mid X_0\mid ,k=1,2,3,...,N-1.$$

(34)

Proof. 

Using mathematical induction, let $k=1$ in Equation (33) yield

$$|X_1|\le \mid X_0\mid +\frac{\mid \dot{\iota }C\mid }{\mid A+\dot{\iota }B\mid }(\mid Y_1\mid +\mid Y_0\mid ).$$

(35)

Using the convergence of the series on the right-hand side of Equation (33),

$$\mid Y_k\mid \le P_1\mid X_0\mid ,k=0,1,2,...,N-1,$$

where $P_1$ is a positive constant. Equation (35) becomes

$$\mid X_1\mid \le \mid X_0\mid +P_1(\mid X_0\mid )\le (1+P_1)\mid X_0\mid \le E_1\mid X_0\mid ,$$

where $E_1=1+P_1$. Now, suppose that

$$\mid X_k\mid \le E_k\mid X_0\mid ,k=1,2,...,N-2.$$

(36)

Using Equation (36), Equation (33) yields

$$\mid X_{k+1}\mid \le E_k\mid X_0\mid +G{E}_1\mid X_0\mid +H{\displaystyle \sum _{p=1}^k}\left[(X_0-X_0)D+2\right]\le E_{k+1}\mid X_0\mid ,$$

(37)

where $G=\frac{\mid \dot{\iota }C\mid }{\mid A+\dot{\iota }B\mid },$ and $H\frac{\mid 1\mid }{\mid A+\dot{\iota }B\mid }.$ □

Remark 1.

Similar to the above, positive constants $I_k$ are such that

$$\mid Y_k\mid \le I_k\mid Y_0\mid ,k=1,2,...,N-1.$$

(38)

Theorem 2.

The FD scheme (20) and (21) are unconditionally stable for $\lambda ϵ(0,1)$.

Proof. 

According to Theorem 1 and Remark 1, we obtain

$$\left\{\begin{array}{cc}\parallel {\mu }^k{\parallel }_2^2\hfill & ={\displaystyle {\sum }_{\ell =-\infty }^{\infty }}\parallel X_k{(\ell )\parallel }^2\le {\displaystyle {\sum }_{\ell =-\infty }^{\infty }}{E}_k^2\parallel X_0{(\ell )\parallel }^2=E_k^2{\parallel {\mu }^0\parallel }_2^2,\hfill \\ \parallel {\nu }^k{\parallel }_2^2\hfill & ={\displaystyle {\sum }_{\ell =-\infty }^{\infty }}\parallel Y_k{(\ell )\parallel }^2\le {\displaystyle {\sum }_{\ell =-\infty }^{\infty }}{I}_k^2\parallel Y_0{(\ell )\parallel }^2=I_k^2{\parallel {\nu }^0\parallel }_2^2,\hfill \end{array}\right.$$

(39)

$$\begin{array}{cc}\hfill \parallel U^k-\widetilde{u^k}{\parallel }_2^2& \le E_k{\parallel U^0-\widetilde{u^0}\parallel }_2^2,\hfill \\ \hfill \parallel V^k-\widetilde{v^k}{\parallel }_2^2& \le I_k{\parallel V^0-\widetilde{v^0}\parallel }_2^2,\hfill \end{array}$$

(40)

Hence, the proposed scheme is unconditionally stable. □

6. Numerical Results

In this segment, we describe two examples to illustrate the performance of the scheme (18) and (19). Results are obtained by using the cubic B-spline. Absolute errors are calculated using the ${\Vert L\Vert }_{\infty }$ and ${\Vert L\Vert }_2$ errors, i.e.,

$${\Vert L\Vert }_{\infty }={\Vert U(x_r,t)-\tilde{u}(x_r,t)\Vert }_{\infty }=\underset{0\le r\le N}{max}\mid U(x_r,t)-\tilde{u}(x_r,t)\mid ,$$

and

$${\Vert L\Vert }_2={\Vert U(x_r,t)-\tilde{u}(x_r,t)\Vert }_2={(h{\displaystyle \sum _{i=0}^N}\mid U(x_r,t)-\tilde{u}(x_r,t){\mid }^2)}^{\frac{1}{2}}.$$

where $\tilde{u}(x_r,t)$ is an approximate solution.

Example 1.

Consider the TFCBE in the Caputo sense, when $\gamma =1000$ and ${\alpha }_1={\alpha }_2=0.001$,

$$\left\{\begin{array}{c}\frac{{\partial }^{\lambda }U}{\partial t^{\lambda }}-\frac{{\partial }^{2}U}{\partial x^2}+\gamma U\frac{\partial U}{\partial x}+{\alpha }_1\frac{\partial \left(UV\right)}{\partial x}=Q_1\hfill \\ \frac{{\partial }^{\lambda }V}{\partial t^{\lambda }}-\frac{{\partial }^{2}V}{\partial x^2}+\gamma V\frac{\partial V}{\partial x}+{\alpha }_2\frac{\partial \left(UV\right)}{\partial x}=Q_2\hfill \end{array}\right.a\le x\le b,0\le t\le T,0<\lambda <1$$

(41)

where BCs and ICs are $\left\{\begin{array}{c}u(0,t)=u(1,t)=0\hfill \\ v(0,t)=v(1,t)=0\hfill \end{array}\right.$ and $\left\{\begin{array}{c}u(x,0)=0\hfill \\ v(x,0)=0\hfill \end{array}\right.$, respectively.

The exact solutions are $U(x,t)=V(x,t)=x^2{(x-1)}^2{t}^2$ [48]. In

Table 2. Absolute error of $U(x,t)$ and $V(x,t)$ at $\lambda =0.3$ for Example 1, when $\Delta t=\frac{1}{1000}$, and N = 100.

		For $\mathit{U}(\mathit{x},\mathit{t})$		For $\mathit{V}(\mathit{x},\mathit{t})$
$\mathit{x}$	Exact	Approximated	Error	Approximated	Error
	Solution	Solution		Solution
$0.1$	0.0081	0.0080992	7.95989 × 10${ }^{-7}$	0.0080992	7.95986 × 10${ }^{-7}$
$0.2$	0.0256	0.0255991	8.90499 × 10${ }^{-7}$	0.0255991	8.90497 × 10${ }^{-7}$
$0.3$	0.0441	0.0440991	9.17458 × 10${ }^{-7}$	0.0440991	9.17457 × 10${ }^{-7}$
$0.4$	0.0576	0.0575990	1.01942 × 10${ }^{-6}$	0.0575990	1.01942 × 10${ }^{-6}$
$0.5$	0.0625	0.0624987	1.27097 × 10${ }^{-6}$	0.0624987	1.27097 × 10${ }^{-6}$
$0.6$	0.0576	0.0575982	1.82313 × 10${ }^{-6}$	0.0575982	1.82313 × 10${ }^{-6}$
$0.7$	0.0441	0.0440967	3.31485 × 10${ }^{-6}$	0.0440967	3.31485 × 10${ }^{-6}$
$0.8$	0.0256	0.0255910	9.02991 × 10${ }^{-6}$	0.0255910	9.02991 × 10${ }^{-6}$
$0.9$	0.0081	0.0080862	1.38116 × 10${ }^{-5}$	0.0080862	1.38116 × 10${ }^{-5}$

, the computational results exhibit the value of $U(x,t)$ and $V(x,t)$ at different stages of x, for Example 1. In

Table 3. Absolute error and order of convergence of $U(x,t)$ when $\lambda =0.1,0.3,0.5$ and $\Delta t=0.001$ for Example 1.

h	${\Vert \mathit{L}\Vert }_{\mathit{\infty }}$	Order	${\Vert \mathit{L}\Vert }_{\mathit{\infty }}$	Order	${\Vert \mathit{L}\Vert }_{\mathit{\infty }}$	Order
	$\mathbf{\lambda }=\mathbf{0}.\mathbf{1}$		$\mathbf{\lambda }=\mathbf{0}.\mathbf{3}$		$\mathbf{\lambda }=\mathbf{0}.\mathbf{5}$
$1/20$	3.39429 × 10${ }^{-4}$	⋯	3.39353 × 10${ }^{-4}$	⋯	3.39557 × 10${ }^{-4}$	⋯
$1/40$	8.88467 × 10${ }^{-5}$	1.93372	8.88382 × 10${ }^{-5}$	1.93353	8.88819 × 10${ }^{-5}$	1.93369
$1/80$	2.22587 × 10${ }^{-5}$	1.99695	2.22520 × 10${ }^{-5}$	1.99725	2.22364 × 10${ }^{-5}$	1.99897
$1/160$	5.59571 × 10${ }^{-6}$	1.99198	5.58911 × 10${ }^{-6}$	1.99324	5.55831 × 10${ }^{-6}$	2.00021
$1/320$	1.41227 × 10${ }^{-6}$	1.98632	1.40599 × 10${ }^{-6}$	1.98461	1.37167 × 10${ }^{-6}$	2.01871

and

Table 4. Absolute error and order of convergence of $U(x,t)$ when $\lambda =0.7,0.8,0.9$ and $\Delta t=0.001$ for Example 1.

h	${\Vert \mathit{L}\Vert }_{\mathit{\infty }}$	Order	${\Vert \mathit{L}\Vert }_{\mathit{\infty }}$	Order	${\Vert \mathit{L}\Vert }_{\mathit{\infty }}$	Order
	$\mathbf{\lambda }=\mathbf{0}.\mathbf{7}$		$\mathbf{\lambda }=\mathbf{0}.\mathbf{8}$		$\mathbf{\lambda }=\mathbf{0}.\mathbf{9}$
$1/20$	3.39995 × 10${ }^{-4}$	⋯	3.40177 × 10${ }^{-4}$	⋯	3.40102 × 10${ }^{-4}$	⋯
$1/40$	8.88670 × 10${ }^{-5}$	1.93579	8.86860 × 10${ }^{-5}$	1.93951	8.81345 × 10${ }^{-5}$	1.94819
$1/80$	2.20861 × 10${ }^{-5}$	2.00851	2.18047 × 10${ }^{-5}$	2.02407	2.11294 × 10${ }^{-5}$	2.06046
$1/160$	5.37405 × 10${ }^{-6}$	2.03906	5.06770 × 10${ }^{-6}$	2.10524	4.36195 × 10${ }^{-6}$	2.27621
$1/320$	1.17911 × 10${ }^{-6}$	2.18831	8.66987 × 10${ }^{-7}$	2.54725	1.63195 × 10${ }^{-6}$	1.88726

, the ${\Vert L\Vert }_{\infty }$ of $U(x,t)$ are estimated on $\lambda =0.1,0.3$ and $0.5$ for different values of N and provide an analysis of the convergence order between stages. In

Table 5. Absolute error and order of convergence of $U(x,t)$ when $\lambda =0.1,0.05$ and $N=512$ for Example 1.

$\mathit{\tau }$	${\Vert \mathit{L}\Vert }_{\mathit{\infty }}$	Order	${\Vert \mathit{L}\Vert }_{\mathit{\infty }}$	Order
	$\mathbf{\lambda }=\mathbf{0}.\mathbf{1}$		$\mathbf{\lambda }=\mathbf{0}.\mathbf{05}$
$1/16$	4.41715 × 10${ }^{-4}$	⋯	4.41624 × 10${ }^{-4}$	⋯
$1/32$	1.14146 × 10${ }^{-4}$	1.95224	1.14119 × 10${ }^{-4}$	1.95228
$1/64$	2.89674 × 10${ }^{-5}$	1.97838	2.89596 × 10${ }^{-5}$	1.97843
$1/128$	7.26223 × 10${ }^{-6}$	1.99595	7.26003 × 10${ }^{-6}$	1.99599

, ${\Vert L\Vert }_{\infty }$ and an order of convergence assessment are conducted for $U(x,t)$ at different values of $\tau$ when $\lambda =0.1,0.005$.

Figure 1 shows the exact 3D solution, while Figure 2 represents the comparison of 2D exact and approximate values U and V using $N=100$, $\Delta t=0.001$, and $\lambda =0.1$. The convergence of the exact and approximate solutions is illustrated in Figure 3 at different time stages for Example 1. In Figure 4, the graphs display the function error for different values of N and $\lambda$.

In Figure 4, graphs show the error function (EF) for different value of N and $\lambda$.

Example 2.

Consider the TFCBE in the Caputo sense, when $\gamma =1000$ and ${\alpha }_1={\alpha }_2=0.001$,

$$\left\{\begin{array}{c}\frac{{\partial }^{\lambda }U}{\partial t^{\lambda }}-\frac{{\partial }^{2}U}{\partial x^2}+\gamma U\frac{\partial U}{\partial x}+{\alpha }_1\frac{\partial \left(UV\right)}{\partial x}=Q_1\hfill \\ \frac{{\partial }^{\lambda }V}{\partial t^{\lambda }}-\frac{{\partial }^{2}V}{\partial x^2}+\gamma V\frac{\partial V}{\partial x}+{\alpha }_2\frac{\partial \left(UV\right)}{\partial x}=Q_2\hfill \end{array}\right.a\le x\le b,0\le t\le T,0<\lambda <1$$

(42)

where BCs and ICs are $\left\{\begin{array}{c}u(0,t)=v(o,t)=t^2\hfill \\ u(1,t)=v(1,t)=t^{2}e\hfill \end{array}\right.$ and $\left\{\begin{array}{c}u(x,0)=0\hfill \\ v(x,0)=0\hfill \end{array}\right.$, respectively.

The exact solutions are $U(x,t)=V(x,t)=t^2{e}^x$. For Example 2,

Table 6. Absolute error of $U(x,t)$ and $V(x,t)$, when $\lambda =0.1$, $\Delta t=0.001$, and $N=100$, for Example 2.

		For $\mathit{U}(\mathit{x},\mathit{t})$		For $\mathit{V}(\mathit{x},\mathit{t})$
$\mathit{x}$	Exact	Approximated	Error	Approximated	Error
	Solution	Solution		Solution
$0.1$	1.10517	1.10517	2.99571 × 10${ }^{-7}$	1.10517	2.99571 × 10${ }^{-7}$
$0.2$	1.22140	1.22140	6.01967 × 10${ }^{-7}$	1.22140	6.01967 × 10${ }^{-7}$
$0.3$	1.34986	1.34986	9.10470 × 10${ }^{-7}$	1.34986	9.10470 × 10${ }^{-7}$
$0.4$	1.49182	1.49183	1.22815 × 10${ }^{-6}$	1.49183	1.22815 × 10${ }^{-6}$
$0.5$	1.64872	1.64872	1.55804 × 10${ }^{-6}$	1.64872	1.55804 × 10${ }^{-6}$
$0.6$	1.82212	1.82212	1.90185 × 10${ }^{-6}$	1.82212	1.90185 × 10${ }^{-6}$
$0.7$	2.01375	2.01375	2.25080 × 10${ }^{-6}$	2.01375	2.25080 × 10${ }^{-6}$
$0.8$	2.22554	2.22554	2.53167 × 10${ }^{-6}$	2.22554	2.53167 × 10${ }^{-6}$
$0.9$	2.71828	2.71828	2.35147 × 10${ }^{-6}$	2.71828	2.35147 × 10${ }^{-5}$

displays the computational results showing the values of the function at various stages, while

Table 7. Absolute error and order of convergence of $U(x,t)$ when $\lambda =0.1,0.05$ and $N=512$ for Example 2.

$\mathit{\tau }$	${\Vert \mathit{L}\Vert }_{\mathit{\infty }}$	Order	${\Vert \mathit{L}\Vert }_{\mathit{\infty }}$	Order
	$\mathbf{\lambda }=\mathbf{0}.\mathbf{1}$		$\mathbf{\lambda }=\mathbf{0}.\mathbf{05}$
$1/64$	1.63599 × 10${ }^{-3}$	⋯	1.63597 × 10${ }^{-3}$	⋯
$1/128$	4.10724 × 10${ }^{-4}$	1.99392	4.10713 × 10${ }^{-4}$	2.01259
$1/256$	1.01791 × 10${ }^{-4}$	2.01256	1.01786 × 10${ }^{-4}$	2.01259
$1/512$	2.42205 × 10${ }^{-5}$	2.07131	2.42145 × 10${ }^{-5}$	2.07159

represents the behaviour of the error norm for different values of k at $\lambda =0.1$ and $0.05$.

Figure 5 shows the exact 3D solution, while Figure 6 represents the comparison of the exact and approximate 2D solutions for U and V using $N=100$, $\Delta t=0.001$, and $\lambda =0.1$. For Example 2, Figure 7 illustrates the convergence of the exact and approximate solution at different stages. In Figure 8, the graphs display the function error for different values of N and $\lambda$.

7. Conclusion Remarks

In the conducted research, we have developed the efficient approximate method for TFCBEs. It is used to study turbulent fluids, suspensions, and the propagation of shallow water waves. Here, we obtain a approximate solution for TFCBEs using the CBS and Crank–Nicolson method. The time FD has been discretized using Caputo’s formula. The numerical algorithm shows that the system is unconditionally stable. The numerical order of convergence has also been determined. Two numerical test problems have been considered in order to evaluate the effectiveness of the delivered method. The results presented in the tables and graphs demonstrate the applicability and accuracy of the presented technique. Approximated values have been compared with exact values, and their errors have been determined. The numerical results were calculated using Mathematica 12.3, and our method yielded acceptable outcomes.