Dynamics and Simulations of Impulsive Population Models Involving Integrated Mosquito Control Strategies and Fractional Derivatives for Dengue Control
Abstract
1. Introduction
- Integrated mosquito management. Traditional chemical pesticide control and Wolbachia-based biological control each has its distinct advantages and disadvantages. Integrated mosquito management that combines the advantages of both approaches is beneficial for quickly and effectively controlling mosquito populations and the transmission of dengue fever. However, current studies on population replacement strategies for controlling mosquitoes or dengue transmission mostly only consider Wolbachia control, while neglecting integrated mosquito management.
- Population replacement with low total mosquito amount. Introducing Wolbachia into wild mosquitoes has the potential to decrease their capacity for transmitting the dengue virus. Nevertheless, the replacement of wild mosquitoes with Wolbachia mosquitoes can cause annoying mosquito bites and the potential risk of transmitting other mosquito-borne viruses. Therefore, during dengue outbreak seasons, it is desirable to achieve population replacement while keeping the overall mosquito population at a lower threshold, or even aiming for eradication. Moreover, the combination of releasing Wolbachia-carrying mosquitoes and spraying insecticide may help to realize the mentioned control objective. Based on a single Wolbachia-based biological control approach, this work aims to further explore integrated mosquito management through modeling. To this end, an integer-order impulsive differential model is proposed to depict the periodic use of insecticides and explore the dynamics of the spread of Wolbachia in wild mosquito populations. We will investigate the threshold dynamics of periodic solutions and the effects of control parameters on strategies for mosquito eradication and replacement.
- Mosquito memory effects. Mosquitoes serve as the vectors for dengue virus transmission, and due to memory effects related to past environmental resources and climate changes throughout their life cycle, their behaviors—such as mating, blood-feeding, and oviposition—may change. These behavioral changes can influence mosquito control strategies. However, most current modeling studies on the spread of Wolbachia in mosquito populations overlook the memory factors within the mosquito life cycle and their effects on mosquito dynamics and control strategies. To further investigate the impact of mosquito memory factors on strategies for mosquito eradication and replacement, we will extend the established integer-order impulsive differential equation model to a Caputo fractional-order impulsive model. We will numerically examine the impact of varying orders on the periodic solutions of the system and the performance of the two control strategies.
2. Model Formulation and Dynamical Analysis
2.1. Model Formulation
2.2. Stability and Permanence Analysis
3. Simulations
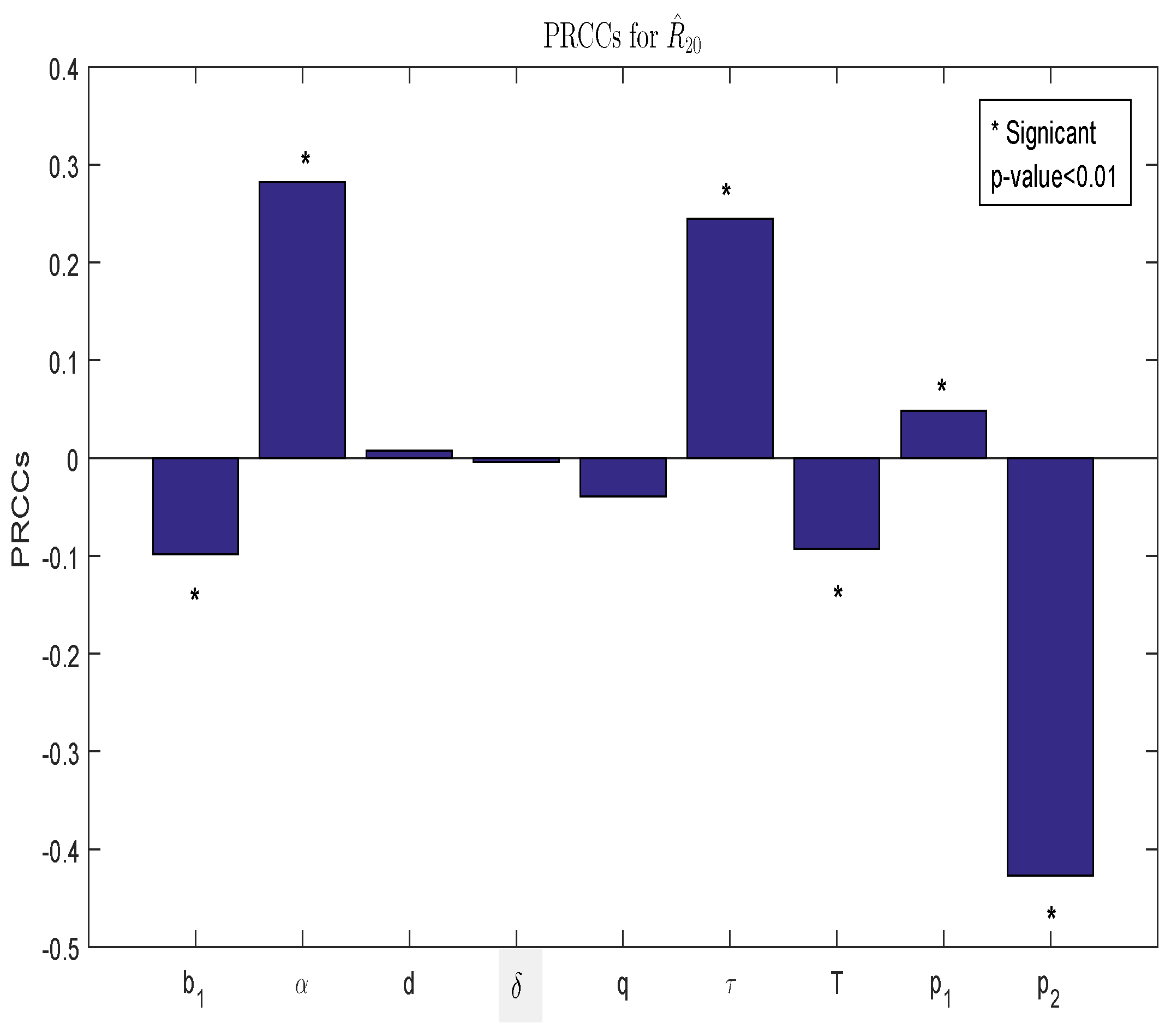
3.1. Sensitivity Analysis

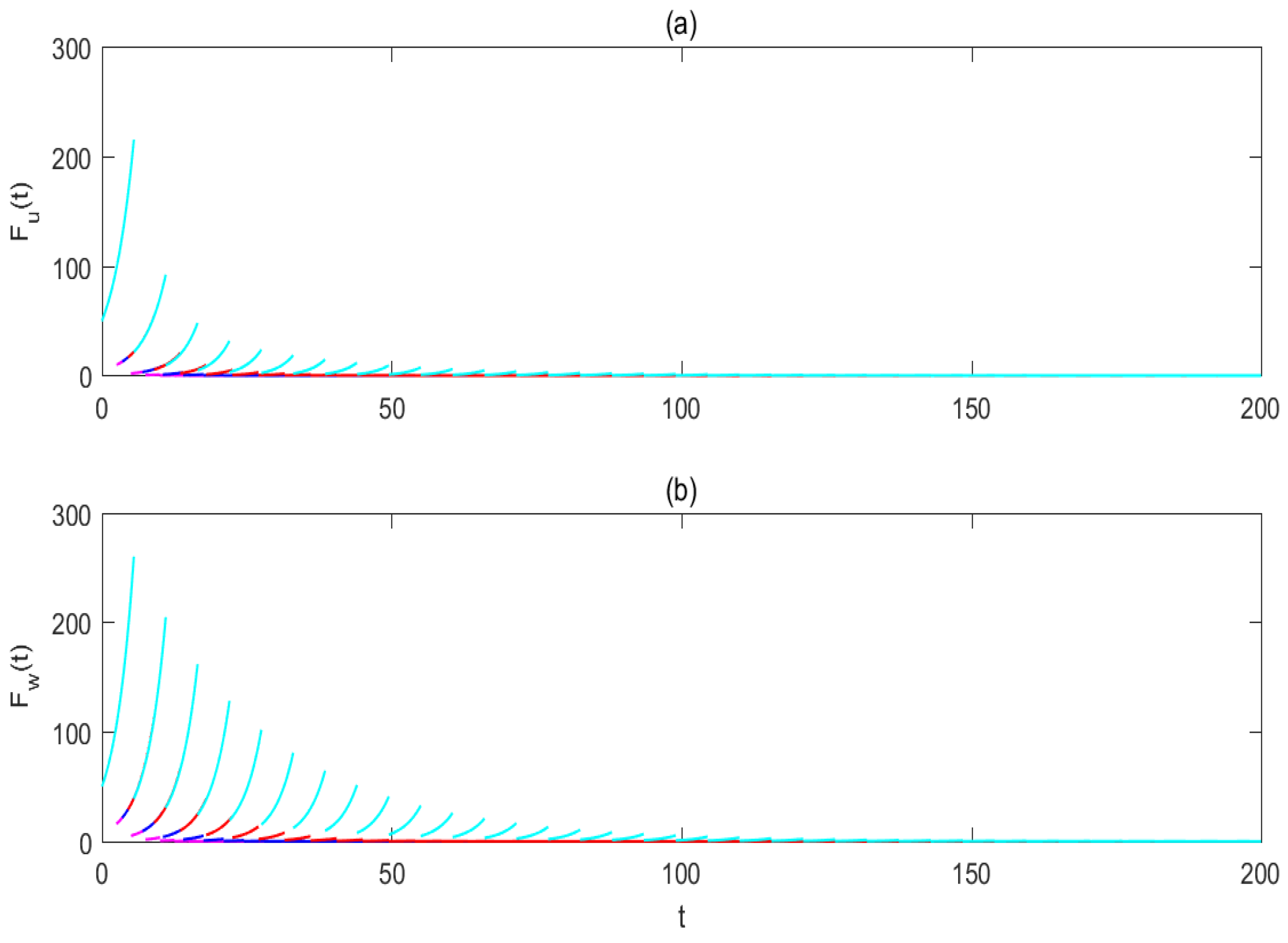
3.2. Effectiveness of Pulse-Spraying Insecticide on Control Strategies
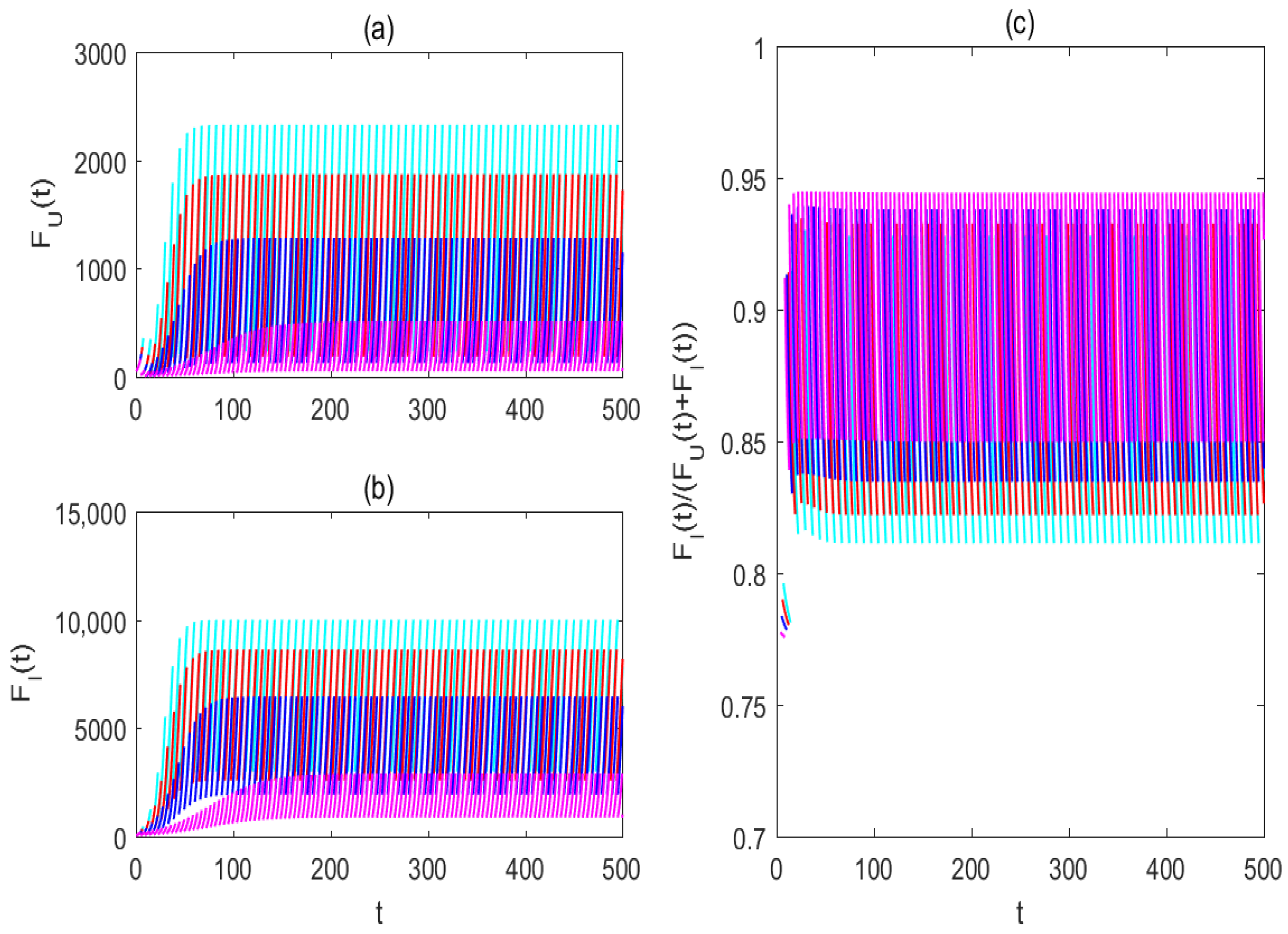

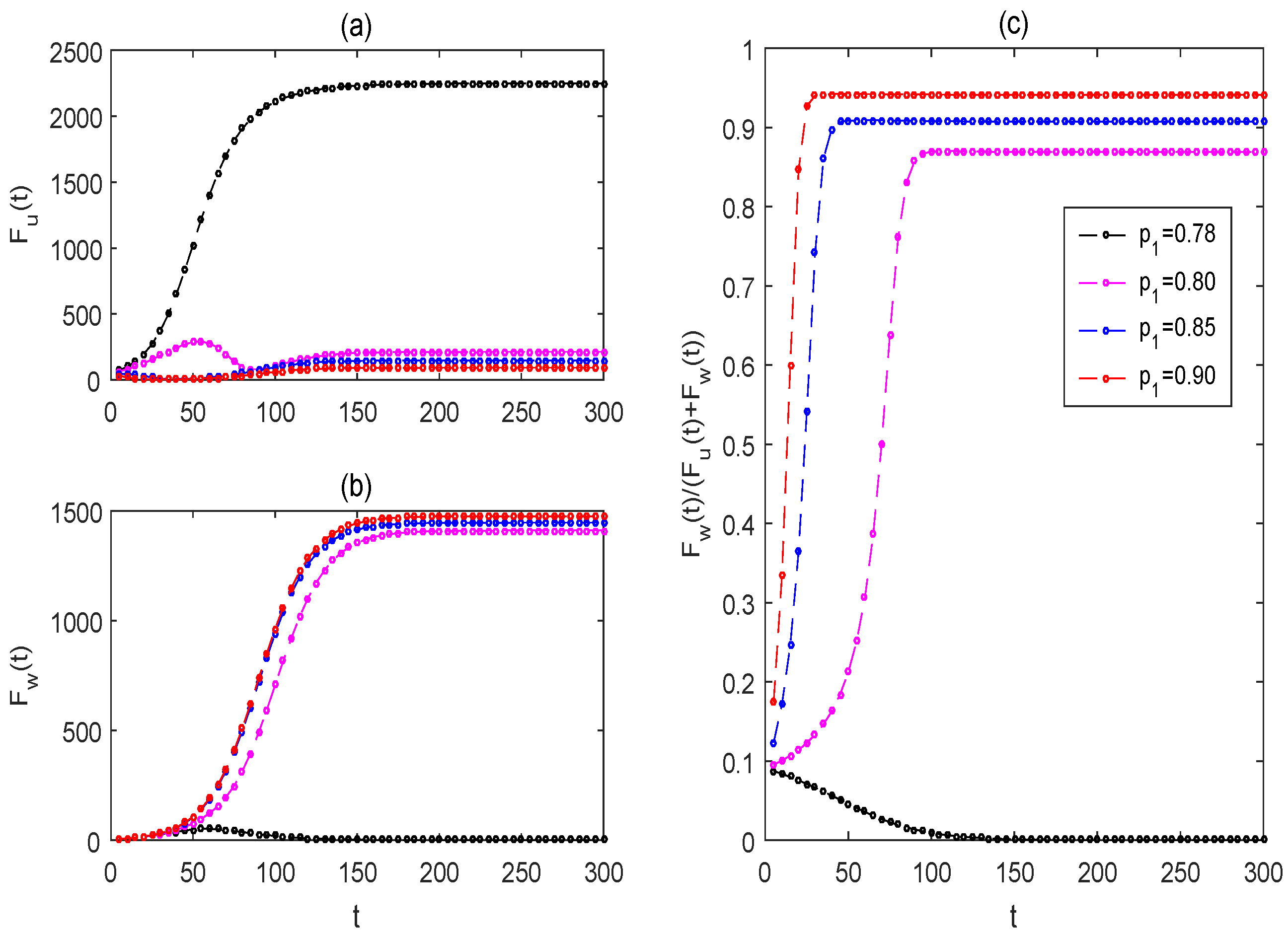
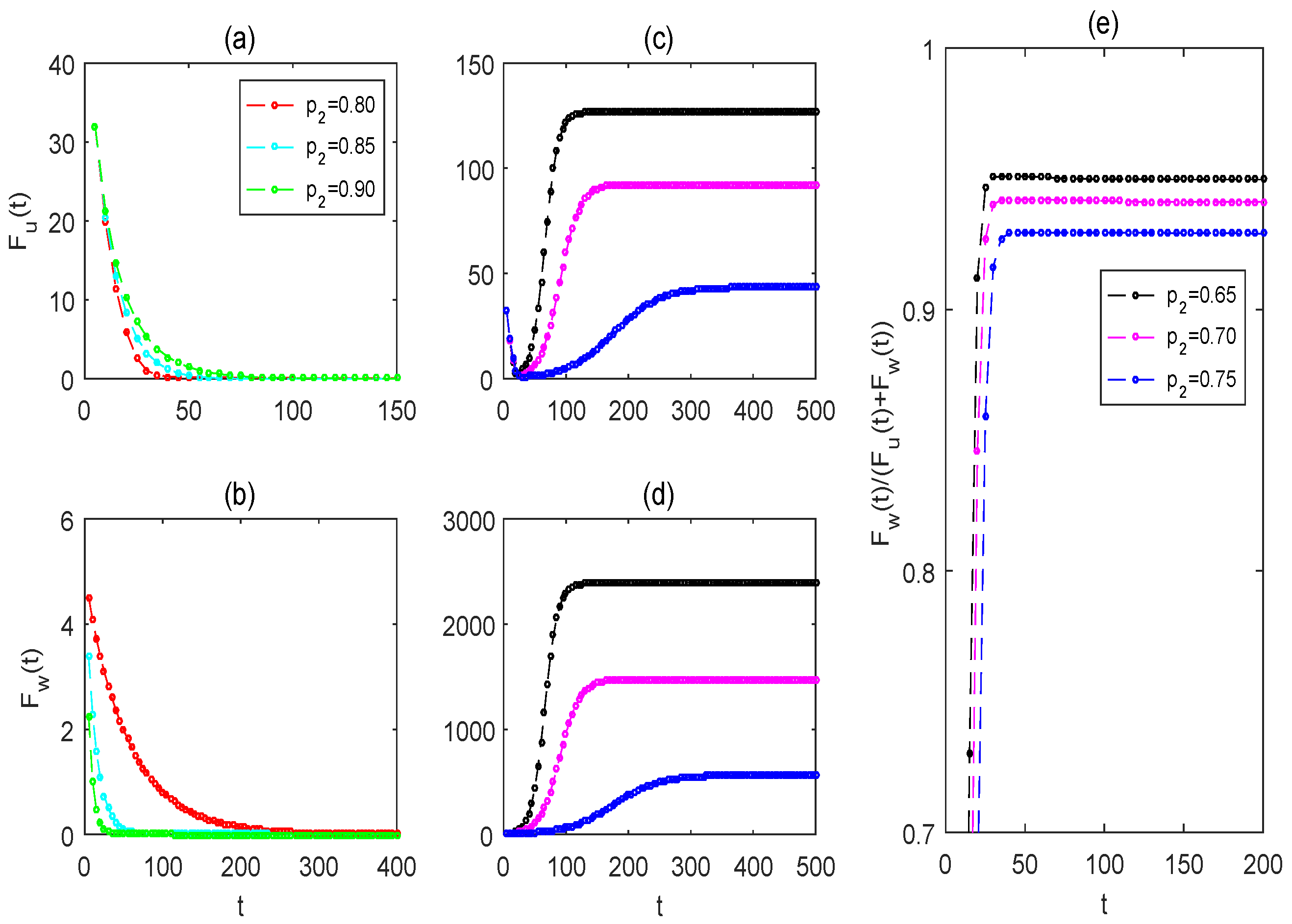
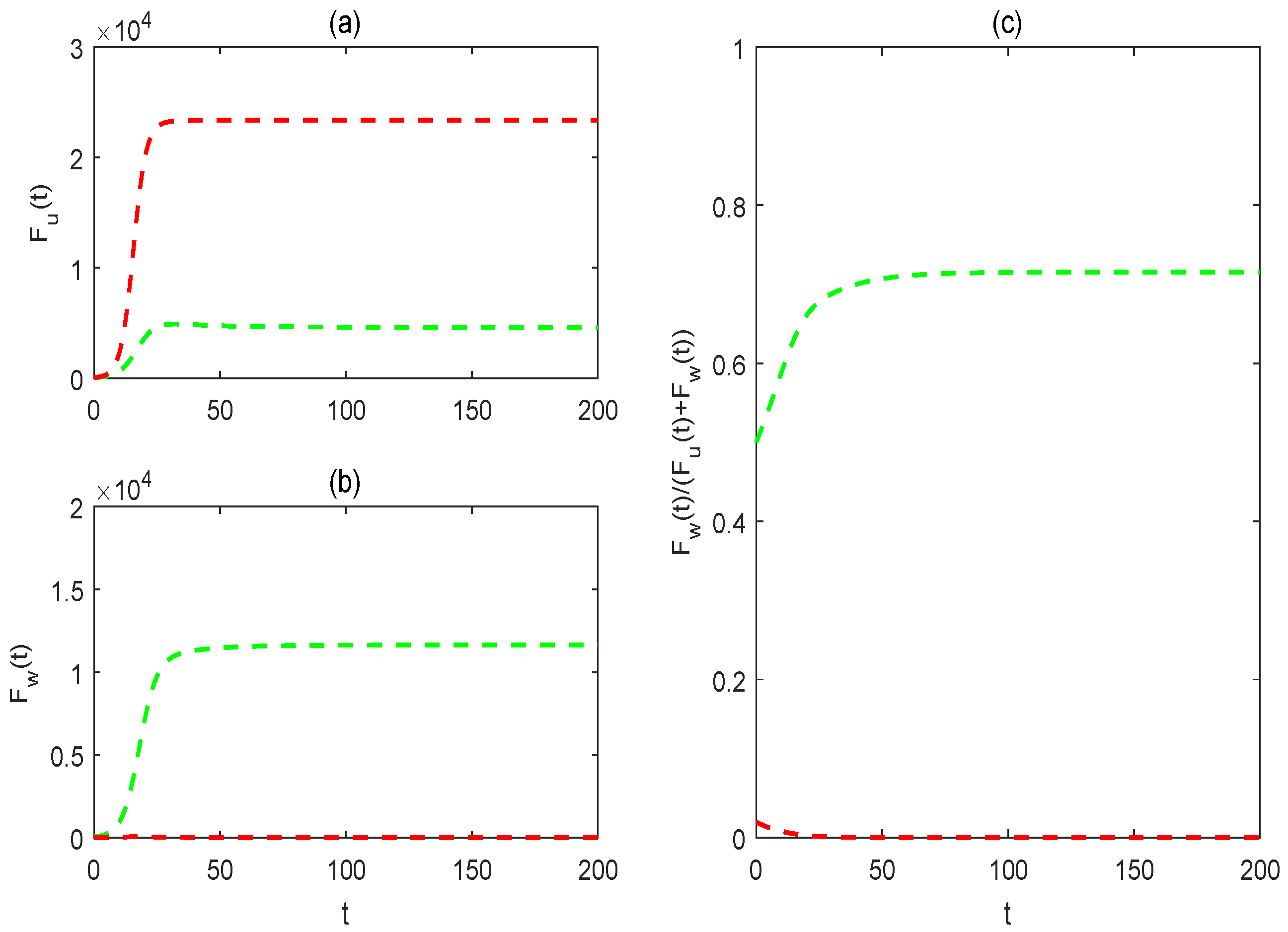
3.3. Impacts of Mosquito Memory on the Two Control Strategies

4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gubler, D.J. Dengue. In The Arboviruses; CRC Press: Boca Raton, FL, USA, 2019; pp. 223–260. [Google Scholar]
- Li, Y.; Dou, Q.; Lu, Y.; Xiang, H.; Yu, X.; Liu, S. Effects of ambient temperature and precipitation on the risk of dengue fever: A systematic review and updated meta-analysis. Environ. Res. 2020, 191, 110043. [Google Scholar] [CrossRef] [PubMed]
- Meetei, M.Z.; Zafar, S.; Zaagan, A.A.; Mahnashi, A.M.; Idrees, M. Dengue transmission dynamics: A fractional-order approach with compartmental modeling. Fractal Fract. 2024, 8, 207. [Google Scholar] [CrossRef]
- Lambrechts, L.; Ferguson, N.M.; Harris, E.; Holmes, E.C.; McGraw, E.A.; O’Neill, S.L.; Ooi, E.E.; Ritchie, S.A.; Ryan, P.A.; Scott, T.W.; et al. Assessing the epidemiological effect of Wolbachia for dengue control. Lancet Infect. Dis. 2015, 15, 862–866. [Google Scholar] [CrossRef]
- Walker, T.; Johnson, P.; Moreira, L.; Iturbe-Ormaetxe, I.; Frentiu, F.; McMeniman, C.; Leong, Y.S.; Dong, Y.; Axford, J.; Kriesner, P.; et al. The wMel Wolbachia strain blocks dengue and invades caged Aedes aegypti populations. Nature 2011, 476, 450–453. [Google Scholar] [CrossRef]
- Hoffmann, A.A.; Montgomery, B.; Popovici, J.; Iturbe-Ormaetxe, I.; Johnson, P.; Muzzi, F.; Greenfield, M.; Durkan, M.; Leong, Y.; Dong, Y.; et al. Successful establishment of Wolbachia in Aedes populations to suppress dengue transmission. Nature 2011, 476, 454–457. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, D.; Li, Y.; Yang, C.; Wu, Y.; Liang, X.; Liang, Y.; Pan, X.; Hu, L.; Sun, Q.; et al. Incompatible and sterile insect techniques combined eliminate mosquitoes. Nature 2019, 572, 56–61. [Google Scholar] [CrossRef]
- Landmann, F. The Wolbachia endosymbionts. Microbiol. Spectr. 2019, 7, 10–128. [Google Scholar] [CrossRef]
- Perlmutter, J.I.; Meyers, J.E.; Bordenstein, S.R. Transgenic testing does not support a role for additional candidate genes in Wolbachia male killing or cytoplasmic incompatibility. mSystems 2020, 5, e00658-19. [Google Scholar] [CrossRef]
- Caspari, E.; Watson, G. On the evolutionary importance of cytoplasmic sterility in mosquitoes. Evolution 1959, 13, 568–570. [Google Scholar] [CrossRef]
- Gan, Y.; Xiang, T.; Ouyang, D.; Zhou, M.; Ye, M. SPGAN: Siamese projection generative adversarial networks. Knowl. Based Syst. 2024, 285, 111353. [Google Scholar] [CrossRef]
- Gan, Y.; Yang, C.; Ye, M.; Huang, R.; Ouyang, D. Generative Adversarial Networks with Learnable Auxiliary Module for Image Synthesis. ACM Trans. Multimed. Comput. Commun. Appl. 2024, 1–21. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Tuyet-Hanh, T.T.; Mulhall, J.; Minh, H.V.; Duong, T.Q.; Chien, N.V.; Nhung, N.T.T.; Lan, V.H.; Minh, H.B.; Cuong, D.; et al. Deep learning models for forecasting dengue fever based on climate data in Vietnam. PLoS Negl. Trop. Dis. 2022, 16, e0010509. [Google Scholar] [CrossRef] [PubMed]
- Tantowijoyo, W.; Andari, B.; Arguni, E.; Budiwati, N.; Nurhayati, I.; Fitriana, I.; Ernesia, I.; Daniwijaya, E.W.; Supriyati, E.; Yusdiana, D.H.; et al. Stable establishment of wMel Wolbachia in Aedes aegypti populations in Yogyakarta, Indonesia. PLoS Negl. Trop. D 2020, 14, e0008157. [Google Scholar] [CrossRef]
- Gesto, J.S.M.; Pinto, S.B.; Dias, F.B.S.; Peixoto, J.; Costa, G.; Kutcher, S.; Montgomery, J.; Green, B.R.; Anders, K.L.; Ryan, P.A.; et al. Large-scale deployment and establishment of Wolbachia into the Aedes aegypti population in Rio de Janeiro, Brazil. Front. Microbiol. 2021, 12, 711107. [Google Scholar] [CrossRef]
- Velez, I.D.; Uribe, A.; Barajas, J.; Uribe, S.; Ángel, S.; Suaza-Vasco, J.D.; Mejia Torres, M.C.; Arbeláez, M.P.; Santacruz-Sanmartin, E.; Duque, L.; et al. Large-scale releases and establishment of wMel Wolbachia in Aedes aegypti mosquitoes throughout the Cities of Bello, Medellín and Itagüí, Colombia. PLoS Negl. Trop. D 2023, 17, e0011642. [Google Scholar] [CrossRef]
- Turelli, M. Evolution of incompatibility-inducing microbes and their hosts. Evolution 1994, 48, 1500–1513. [Google Scholar]
- Haygood, R.; Turelli, M. Evolution of incompatibility-inducing microbes in subdivided host populations. Evolution 2009, 63, 432–447. [Google Scholar] [CrossRef]
- Keeling, M.J.; Jiggins, F.; Read, J.M. The invasion and coexistence of competing Wolbachia strains. Heredity 2003, 91, 382–388. [Google Scholar] [CrossRef]
- Zheng, B.; Tang, M.; Yu, J. Modeling Wolbachia spread in mosquitoes through delay differential equations. SIAM J. Appl. Math. 2014, 74, 743–770. [Google Scholar] [CrossRef]
- Hancock, P.A.; Sinkins, S.P.; Godfray, H.C.J. Population dynamic models of the spread of Wolbachia. Am. Nat. 2011, 177, 323–333. [Google Scholar] [CrossRef]
- Farkas, J.Z.; Gourley, S.A.; Liu, R.; Yakubu, A.A. Modelling Wolbachia infection in a sex-structured mosquito population carrying West Nile virus. J. Math. Biol. 2017, 75, 621–647. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Zheng, B.; Zou, X. Wolbachia dynamics in mosquitoes with incomplete CI and imperfect maternal transmission by a DDE system. Bull. Math. Biol. 2022, 84, 95. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Liu, Q.; Zhu, H. Modeling and dynamics of Wolbachia-infected male releases and mating competition on mosquito control. J. Math. Biol. 2020, 81, 243–276. [Google Scholar] [CrossRef] [PubMed]
- Jansen, V.A.; Turelli, M.; Godfray, H.C.J. Stochastic spread of Wolbachia. Proc. R. Soc. B Biol. Sci. 2008, 275, 2769–2776. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Supriatna, A.K. Stochastic dengue mathematical model in the presence of Wolbachia: Exploring the disease extinction. Nonlinear Dyn. Syst. Theory 2020, 20, 214–227. [Google Scholar]
- Chan, M.H.; Kim, P.S. Modelling a Wolbachia invasion using a slow–fast dispersal reaction–diffusion approach. Bull. Math. Biol. 2013, 75, 1501–1523. [Google Scholar] [CrossRef]
- Huang, M.; Tang, M.; Yu, J. Wolbachia infection dynamics by reaction-diffusion equations. Sci. China Math. 2015, 58, 77–96. [Google Scholar] [CrossRef]
- Qu, Z.; Wu, T.; Hyman, J.M. Modeling spatial waves of Wolbachia invasion for controlling mosquito-borne diseases. SIAM J. Appl. Math. 2022, 82, 1903–1929. [Google Scholar] [CrossRef]
- Xue, L.; Cao, X.; Wan, H. Releasing Wolbachia-infected mosquitos to mitigate the transmission of zika virus. J. Math. Anal. Appl. 2021, 496, 124804. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Li, Y.; Liu, Q.; Zhu, H. Modelling the effects of Wolbachia-carrying male augmentation and mating competition on the control of dengue fever. J. Dyn. Differ. Equ. 2023, 1–41. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, S.; Cheke, R.A. Models to assess how best to replace dengue virus vectors with Wolbachia-infected mosquito populations. Math. Biosci. 2015, 269, 164–177. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Tang, S.; Cheke, R.A.; Zhu, H. Modeling the effects of augmentation strategies on the control of dengue fever with an impulsive differential equation. Bull. Math. Biol. 2016, 78, 1968–2010. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, X. Modeling and control of mosquito-borne diseases with Wolbachia and insecticides. Theor. Popul. Biol. 2020, 132, 82–91. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Tang, M.; Wu, Z.; Xi, Z.; Yu, J. The threshold infection level for Wolbachia invasion in random environments. J. Differ. Equ. 2019, 266, 4377–4393. [Google Scholar] [CrossRef]
- Yu, J. Existence and stability of a unique and exact two periodic orbits for an interactive wild and sterile mosquito model. J. Differ. Equ. 2020, 269, 10395–10415. [Google Scholar] [CrossRef]
- Zheng, B.; Yu, J.; Li, J. Modeling and analysis of the implementation of the Wolbachia incompatible and sterile insect technique for mosquito population suppression. SIAM J. Appl. Math. 2021, 81, 718–740. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.M.; El-Saka, H.A. Equilibrium points, stability and numerical solutions of fractional-order predator–prey and rabies models. J. Math. Anal. Appl. 2007, 325, 542–553. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, Y.; Lu, J.; Li, Y. Stability and bifurcation of a delayed generalized fractional-order prey–predator model with interspecific competition. Appl. Math. Comput. 2019, 347, 360–369. [Google Scholar] [CrossRef]
- Li, S.; Huang, C.; Yuan, S. Hopf bifurcation of a fractional-order double-ring structured neural network model with multiple communication delays. Nonlinear Dyn. 2022, 108, 379–396. [Google Scholar] [CrossRef]
- Jajarmi, A.; Arshad, S.; Baleanu, D. A new fractional modelling and control strategy for the outbreak of dengue fever. Physica A 2019, 535, 122524. [Google Scholar] [CrossRef]
- Yangla, J.; Abboubakar, H.; Dangbe, E.; Yankoulo, R.; Ari, A.A.A.; Damakoa, I.; Nisar, K.S. Fractional dynamics of a Chikungunya transmission model. Sci. Afr. 2023, 21, e01812. [Google Scholar] [CrossRef]
- Farman, M.; Ahmad, A.; Akgül, A.; Saleem, M.U.; Rizwan, M.; Ahmad, M.O. A mathematical analysis and simulation for Zika virus model with time fractional derivative. Math. Methods Appl. Sci. 2024, 47, 11135–11146. [Google Scholar] [CrossRef]
- Dianavinnarasi, J.; Raja, R.; Alzabut, J.; Cao, J.; Niezabitowski, M.; Bagdasar, O. Application of Caputo–Fabrizio operator to suppress the Aedes Aegypti mosquitoes via Wolbachia: An LMI approach. Math. Comput. Simul. 2022, 201, 462–485. [Google Scholar] [CrossRef]
- Joseph, D.; Ramachandran, R.; Alzabut, J.; Jose, S.A.; Khan, H. A fractional-order density-dependent mathematical model to find the better strain of Wolbachia. Symmetry 2023, 15, 845. [Google Scholar] [CrossRef]
- Lakshmikantham, V.; Simeonov, P.S. Theory of Impulsive Differential Equations; World Scientific: Singapore, 1989. [Google Scholar]
- Bainov, D.; Simeonov, P. Impulsive Differential Equations: Periodic Solutions and Applications; Routledge: London, UK, 2017. [Google Scholar]
- Blower, S.M.; Dowlatabadi, H. Sensitivity and uncertainty analysis of complex models of disease transmission: An HIV model, as an example. Int. Stat. Rev. 1994, 62, 229–243. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef]
- Diethelm, K. A fractional calculus based model for the simulation of an outbreak of dengue fever. Nonlinear Dyn. 2013, 71, 613–619. [Google Scholar] [CrossRef]

| Parameter | Definition | Value (Range) | Unit | Source |
|---|---|---|---|---|
| The ratio of natural birth rates of W to wild mosquitoes, | 0.9 [0.5, 1] | N/A | [5] | |
| The ratio of death rates of W to wild mosquitoes, | 1.1 [0, 2] | N/A | [5,33] | |
| Natural birth rate of wild mosquitoes | 0.4 [0.25, 0.76] | [20,33] | ||
| Natural birth rate of W mosquitoes | 0.36 [0.13, 0.76] | [20,33] | ||
| d | Density-dependent mortality rate of mosquitoes | [20,33] | ||
| Maternal inheritance rate | N/A | [20,33] | ||
| Fitness cost of W mosquitoes, | [20,33] | |||
| q | CI intensity | 0.9 [0.6, 1] | N/A | [24] |
| T | Pulse period of spraying insecticide | 4 [2, 15] | day | Assumed |
| Insecticide killing rate of wild mosquitoes | 0.8 [0.4, 1] | N/A | Assumed | |
| Insecticide killing rate of W mosquitoes | 0.8 [0.4, 1] | N/A | Assumed |
| Parameter | d | q | T | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PRCCs | |||||||||
| p-values | 0 | 0 | 0 | 0 | 0 |
| Scenarios | Strategy | RST | No. of | No. of | No. of | Repl. Level | |
|---|---|---|---|---|---|---|---|
| , (low fecundity of individuals) | Erad. | 85 | 0 | 0 | 0 | / | |
| 70 | |||||||
| Erad. | 190 | 0 | 0 | 0 | / | ||
| 140 | |||||||
| Repl. | 275 | 26 | 113 | 139 | |||
| 155 | 4 | 18 | 22 | ||||
| , (high fecundity of individuals) | Repl. | 165 | 998 | 4798 | 5796 | ||
| 155 | 157 | 1437 | 1594 | ||||
| Repl. | 90 | 499 | 2317 | 2766 | |||
| 85 | 78 | 693 | 771 | ||||
| Repl. | 50 | 207 | 937 | 1144 | |||
| 50 | 32 | 280 | 312 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; He, H.; Wang, K.; Zhu, H. Dynamics and Simulations of Impulsive Population Models Involving Integrated Mosquito Control Strategies and Fractional Derivatives for Dengue Control. Fractal Fract. 2024, 8, 624. https://doi.org/10.3390/fractalfract8110624
Zhang X, He H, Wang K, Zhu H. Dynamics and Simulations of Impulsive Population Models Involving Integrated Mosquito Control Strategies and Fractional Derivatives for Dengue Control. Fractal and Fractional. 2024; 8(11):624. https://doi.org/10.3390/fractalfract8110624
Chicago/Turabian StyleZhang, Xianghong, Hua He, Kaifa Wang, and Huaiping Zhu. 2024. "Dynamics and Simulations of Impulsive Population Models Involving Integrated Mosquito Control Strategies and Fractional Derivatives for Dengue Control" Fractal and Fractional 8, no. 11: 624. https://doi.org/10.3390/fractalfract8110624
APA StyleZhang, X., He, H., Wang, K., & Zhu, H. (2024). Dynamics and Simulations of Impulsive Population Models Involving Integrated Mosquito Control Strategies and Fractional Derivatives for Dengue Control. Fractal and Fractional, 8(11), 624. https://doi.org/10.3390/fractalfract8110624





