Abstract
Dengue fever, a mosquito-borne disease caused by the dengue virus, imposes a substantial disease burden on the world. Wolbachia not only manipulates the reproductive processes of mosquitoes through maternal inheritance and cytoplasmic incompatibility (CI) but also restrain the replication of dengue viruses within mosquitoes, becoming a novel approach for biologically combating dengue fever. A combined use of Wolbachia and insecticides may help to prevent pesky mosquito bites and dengue transmission. A model with impulsive spraying insecticide is introduced to examine the spread of Wolbachia in wild mosquitoes. We prove the stability and permanence results of periodic solutions in the system. Partial rank correlation coefficients (PRCCs) can determine the importance of the contribution of input parameters on the value of the outcome variable. PRCCs are used to analyze the influence of input parameters on the threshold condition of the population replacement strategy. We then explore the impacts of mosquito-killing rates and pulse periods on both population eradication and replacement strategies. To further investigate the effects of memory intensity on the two control strategies, we developed a Caputo fractional-order impulsive mosquito population model with integrated control measures. Simulation results show that for the low fecundity scenario of individuals, as memory intensity increases, the mosquito eradication strategy will occur at a slower speed, potentially even leading to the mosquito replacement strategy with low female numbers. For the high fecundity scenario of individuals, with increasing memory intensity, the mosquito replacement strategy will be achieved more quickly, with lower mosquito population amplitudes and overall numbers. It indicates that although memory factors are not conducive to implementing a mosquito eradication strategy, achieving the replacement strategy with a lower mosquito amount is helpful. This work will be advantageous for developing efficient integrated control strategies to curb dengue transmission.
1. Introduction
Dengue, recognized as a major mosquito-borne disease, places a substantial socioeconomic burden on numerous tropical and subtropical regions. Over of the global population is vulnerable to this disease, leading to nearly 400 million infections annually and causing more than 25,000 deaths [1,2]. Dengue viruses (DENVs) are part of the genus Flavivirus and comprise four different serotypes (DENV1-4), each with distinct serological and genetic characteristics [1]. Developing effective vaccines against all dengue virus serotypes is challenging due to the antibody-dependent enhancement [3]. Currently, dengue prevention methods focus on controlling the primary mosquito vectors or altering human behaviors. These strategies include using insecticides, introducing predators, destroying breeding sites, and enhancing personal protection. Specifically, the suitable application of insecticides prevents dengue transmission by rapidly reducing mosquito populations in the short term [4].
Wolbachia not only manipulates mosquito reproductive processes but also inhibits the replication of dengue viruses within mosquitoes, making it a novel approach for biologically combating dengue fever. The reproductive manipulation of mosquitoes by Wolbachia is mainly reflected in maternal inheritance and cytoplasmic incompatibility (CI). Maternal inheritance means that females carrying Wolbachia can pass the bacteria to their offspring. CI occurs when males carrying Wolbachia mate with uninfected females, resulting in non-viable offspring. Such female-skewed reproductive mechanisms can promote Wolbachia infections in wild populations. Some Wolbachia strains can inhibit mosquitoes from replicating the dengue virus, thereby interrupting the transmission of the virus among mosquitoes and humans [5,6]. Therefore, to suppress the transmission of the dengue virus, there are two main control strategies for mosquito vectors: population replacement and suppression. Population replacement relies on maternal inheritance and CI to establish and replace wild mosquitoes through the release of Wolbachia-carrying female mosquitoes (or together with Wolbachia-carrying males) [6]. Meanwhile, population suppression, based on CI, aims to suppress or eradicate wild mosquitoes by releasing only Wolbachia-carrying male mosquitoes, which can be regarded as a biological pesticide [7]. In this work, we will focus on the strategy of population replacement through the mixed releases of Wolbachia-carrying female and male mosquitoes. Moreover, Wolbachia bacterium is widely distributed within insects and certain nematodes. It does not infect humans and other mammals and it is one of the most common symbiotic microorganisms. They may manipulate the reproductive processes of their hosts to promote their own survival through maternal inheritance, CI, male killing, and parthenogenesis [8,9]. The resulting phenotype depends on both host species and Wolbachia strains [9,10].
Research on dengue fever transmission and control has explored numerous approaches, from dynamic models to deep learning methods [11,12,13]. Wolbachia, as an innovative approach to biological control of mosquito vectors, has also drawn the attention of scholars across both biological and mathematical disciplines. Lately, scientists in dengue-epidemic countries have been exploring the release of mosquitoes carrying various Wolbachia strains to prevent the transmission of dengue virus [6,7,14,15,16]. Many modeling studies have been conducted to explore the spread of various Wolbachia strains among a wide range of wild mosquito species. Considering diverse reproductive mechanisms, discrete difference systems were proposed to depict the frequency of Wolbachia in wild mosquitoes and explore the potential coexistence of multiple Wolbachia strains [17,18]. Assuming that Wolbachia-carrying mosquitoes are already present in wild mosquitoes or are being consistently released into the wild mosquitoes, a variety of continuous-time differential models [19,20,21,22,23,24], stochastic dynamic models [25,26], and reaction-diffusion equations [27,28,29] have been established to primarily examine the spread of Wolbachia among wild mosquito populations. Moreover, several epidemic models have been proposed to explore the impact of Wolbachia on the prevention of mosquito-borne diseases [22,30,31].
Impulsive differential equation, as an extension of differential equation, can be used to describe the dynamic phenomena of a system subjected to instantaneous interventions at specific moments. It is widely applied in pest control, engineering control, and signal processing. Since Wolbachia-carrying mosquitoes are typically released periodically in real-world applications, various impulsive differential equation models have been employed to analyze the influence of introducing Wolbachia on the dynamics behaviors of mosquito populations [32,33,34,35,36,37].
A fractional-order differential equation is a differential equation with fractional-order derivatives. As an extension of traditional integer-order differential equations, fractional-order differential equations have attracted much attention in recent years. Since they can describe the memory effects and complex dynamical behaviors of systems, they have been widely used in various fields, particularly in ecology and biology [38,39,40]. It is widely acknowledged that the reproductive and migratory behaviors of mosquitoes are strongly influenced by their past experiences in environmental resources and climate change, which has a significant impact on the population dynamics [41,42,43,44,45]. Currently, there has been considerable research on mosquito population dynamics and the transmission of mosquito-borne diseases utilizing fractional differential equations to depict the above-mentioned mosquito memory factors [41,42,43]. However, research specifically focusing on modeling Wolbachia-based biological control through a fractional framework remains relatively scarce [44,45]. In [44], the authors established a Caputo–Fabrizio fractional-order mosquito population model by releasing mosquitoes at different life stages carrying Wolbachia to explore the spread of Wolbachia in wild mosquito populations. They investigated the existence, uniqueness, and -exponential stability of the system’s solution. In [45], the authors developed a fractional-order epidemiological model to study the spreading dynamics of different Wolbachia strains and their impact on disease transmission, aiming to identify the most effective strain for disease control. The research motivation and novelty are mainly reflected in the following aspects.
- Integrated mosquito management. Traditional chemical pesticide control and Wolbachia-based biological control each has its distinct advantages and disadvantages. Integrated mosquito management that combines the advantages of both approaches is beneficial for quickly and effectively controlling mosquito populations and the transmission of dengue fever. However, current studies on population replacement strategies for controlling mosquitoes or dengue transmission mostly only consider Wolbachia control, while neglecting integrated mosquito management.
- Population replacement with low total mosquito amount. Introducing Wolbachia into wild mosquitoes has the potential to decrease their capacity for transmitting the dengue virus. Nevertheless, the replacement of wild mosquitoes with Wolbachia mosquitoes can cause annoying mosquito bites and the potential risk of transmitting other mosquito-borne viruses. Therefore, during dengue outbreak seasons, it is desirable to achieve population replacement while keeping the overall mosquito population at a lower threshold, or even aiming for eradication. Moreover, the combination of releasing Wolbachia-carrying mosquitoes and spraying insecticide may help to realize the mentioned control objective. Based on a single Wolbachia-based biological control approach, this work aims to further explore integrated mosquito management through modeling. To this end, an integer-order impulsive differential model is proposed to depict the periodic use of insecticides and explore the dynamics of the spread of Wolbachia in wild mosquito populations. We will investigate the threshold dynamics of periodic solutions and the effects of control parameters on strategies for mosquito eradication and replacement.
- Mosquito memory effects. Mosquitoes serve as the vectors for dengue virus transmission, and due to memory effects related to past environmental resources and climate changes throughout their life cycle, their behaviors—such as mating, blood-feeding, and oviposition—may change. These behavioral changes can influence mosquito control strategies. However, most current modeling studies on the spread of Wolbachia in mosquito populations overlook the memory factors within the mosquito life cycle and their effects on mosquito dynamics and control strategies. To further investigate the impact of mosquito memory factors on strategies for mosquito eradication and replacement, we will extend the established integer-order impulsive differential equation model to a Caputo fractional-order impulsive model. We will numerically examine the impact of varying orders on the periodic solutions of the system and the performance of the two control strategies.
The structure of this paper is as follows: In Section 2, an integer-order mosquito population model incorporating impulsive insecticide spraying is presented to illustrate the spread of Wolbachia in the wild mosquito population. The stability and persistence of the periodic solutions are proved. Section 3 examines the effects of pulse periods and killing rates on the two control strategies, as well as a global sensitivity analysis. Also, a Caputo fractional-order impulsive model is developed to investigate the impact of memory factors on the two control strategies. Section 4 provides some discussions and insights for future research. The Section 5 presents the main conclusion of this work. The specific methodological flow chart is shown in Figure 1.
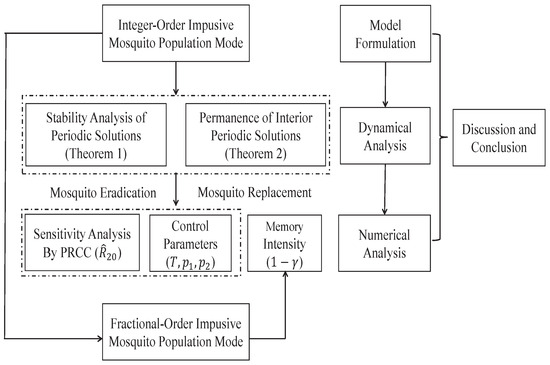
Figure 1.
The specific methodological flow chart of this research work.
2. Model Formulation and Dynamical Analysis
2.1. Model Formulation
Divide the total mosquito population into four categories: Wolbachia-free (i.e., wild) females , Wolbachia-carrying females , Wolbachia-free males , and Wolbachia-carrying males . It is assumed that parent mosquitoes produce an equal ratio of female and male offspring and that Wolbachia-free and -carrying individuals exhibit distinct natural birth rates ( and , respectively) while sharing a common natural death rate . Wolbachia-carrying mosquitoes might experience an extra fitness cost , influenced by mosquito species and Wolbachia strains. Assume that maternal inheritance is incomplete. It refers to the phenomenon where only a proportion of the offspring from Wolbachia-carrying female mosquitoes can carry the bacteria, while the remaining proportion of the offspring does not carry the bacteria [19,20,23]. CI leads to a probability q of fertilized eggs not hatching when a wild female mates with a Wolbachia-carrying male. Thus, we obtain the following mosquito population model without impulsive insecticide spraying:
where Moreover, this mechanistic model has been developed to explore the spread of Wolbachia in wild mosquitoes following the release of Wolbachia-carrying mosquitoes [19,20,32,33].
Despite females carrying Wolbachia being unable to transmit the dengue virus, they can still cause bothersome mosquito bites and present the potential risk of transmitting other mosquito-borne viruses. Thus, to effectively control dengue disease and reduce annoying mosquito bites simultaneously, it is necessary to achieve population replacement (through Wolbachia biological control) while maintaining a low total mosquito population (through chemical pesticides). This can be accomplished by combining the use of Wolbachia and insecticides. An important aspect of this integrated strategy is the need to mitigate the effects of pesticides on newly released Wolbachia-carrying mosquitoes. Therefore, the timing of Wolbachia-carrying mosquito releases should differ from the timing of insecticide spraying. This paper is our first work about the integrated control strategy; we simply take into account the scenario that Wolbachia-carrying mosquitoes have already been released, and then periodically spray insecticides to achieve population replacement with a low total mosquito population. The combined use of Wolbachia and insecticides in managing mosquito populations is illustrated by the following integer-order impulsive differential equation model:
where the parameter T represents the impulsive period. The parameters and denote the insecticide killing rates for Wolbachia-free and -carrying mosquitoes, respectively. Furthermore, when , the four categories of mosquito population without insecticide impulsive spraying remain the same as in model (1), while impulsive spraying occurs at . More details about the definitions, values, and sources of the parameters for systems (1) and (2) are provided in Table 1.
2.2. Stability and Permanence Analysis
The subsystem of system (2) in the subspace without Wolbachia is as follows:
Solving subsystem (3) within the impulsive interval yields the following:
Let From (4) and system (3), we have the stroboscopic map of system (3):
To determine the fixed points of system (5), one needs to address the following equations:
By simple calculations, there are three possible roots, including , and with the following:
Only the fix points and will be considered due to biological meaning. It is easy to verify that and will be positive if and only if
Denote the eigenvalues of and as then we have the following:
For convenience, we define the following:
which indicates the basic offspring number of wild mosquitoes in the absence of Wolbachia-carrying mosquitoes.
Thus, system (5), if the unique equilibrium is locally asymptotically stable (LAS). If then is unstable, while the unique interior equilibrium is LAS. Note that the unique equilibrium being LAS signifies its global stability. From the relation between systems (3) and (5), the local stability of the equilibrium of system (5) indicates the local stability of the corresponding periodic solution of system (3). Thus, we have the following lemma about the stability of periodic solutions of system (3).
Lemma 1.
For system (3), if then there exists a unique mosquito eradication periodic solution and as If then a mosquito eradication periodic solution and a positive periodic solution exist, and as with
From Lemma 1, it is obvious that system (2) consistently exhibits a mosquito-eliminating periodic solution If system (2) also has a boundary periodic solution Subsequently, our primary focus is to examine the stability of these two boundary periodic solutions and the permanence of the interior periodic solution.
Similarly, the stroboscopic map of system (6) is as follows:
System (7) has two meaningful fixed points, including and where
with Denote the eigenvalues of and as then we have the following:
Define
which indicates the basic offspring number of Wolbachia mosquitoes in the absence of wild mosquitoes. For system (7), if then the unique equilibrium is LAS. If then is unstable and the unique interior equilibrium is LAS. Similarly, based on the relationship between systems (6) and (7), we have the following lemma regarding the stability of periodic solutions of system (6).
Lemma 2.
For system (6), if then there exists a unique Wolbachia-carrying mosquito eradication periodic solution and as if then there is a Wolbachia-carrying mosquito eradication periodic solution , a positive periodic solution and , as with
Next, the stability and permanence of periodic solutions for system (2) are summarized below.
Theorem 1.
For system (2), if and then the mosquito-eliminating periodic solution is LAS. If then Wolbachia-free periodic solution is LAS.
Proof.
Note that the stability analysis of cannot directly employ the Floquet multiplier theory due to the presence of term derived from As a result of system (2), variables and maybe equal to zero only if From Lemmas 1 and 2, one can obtain a sufficient condition for the local asymptotic stability of is and
Next, we will prove the local stability of . Let , . Then, the linear system of (2) at is as follows:
where
the square matrix is a 2nd-order zero matrix.
Suppose that the fundamental solution matrix of is The initial value problem with can be solved as follows:
Then, the fundamental solution matrix of system (8) on is as follows:
Thus, eigenvalues of matrix are defined as the Floquet multipliers of system (8). According to the Floquet multiplier theory of impulsive differential equations [46,47], if the absolute values of all the Floquet multipliers are less than one, then the periodic solution is LAS; if the absolute values of some Floquet multipliers are larger than one, then the periodic solution is unstable.
Denote
where is the spectral radius of and a similar case is for It is worth mentioning that is equivalent to since they both are the threshold criteria for the stability of indicates the basic offspring number of Wolbachia mosquitoes in the presence of wild mosquitoes. Then, and indicate that all four Floquet multipliers are less than one. Thus, by using the Floquet multiplier theory, the periodic solution is LAS when and □
Theorem 2.
For system (2), if and then both Wolbachia-free and -carrying mosquitoes are permanent, i.e., there exist constants satisfying
Proof.
From system (2), one can deduce that when Our initial step is to prove the weak permanence of Wolbachia-carrying mosquitoes. That is, we need to prove the existence of a positive constant such that we have the following:
On the contrary, if there is a , such that for all then according to system (2), we can express the following:
Take the following comparison system:
System (10) has a unique positive periodic solution, denoted as follows: If then So, for any there exists , small enough such that and By applying the comparison theorem, one can find and such that we have the following: and for
From system (2), we have the following:
When and are sufficiently small, we consider the following system:
where Then, we have the following:
If we can find so that for each both and So which contradicts with for all Thus, the weak persistence of Wolbachia-carrying mosquitoes is proved. It indicates that there exits such that i.e., When for all sufficiently large with we have demonstrated the permanence of Wolbachia-carrying mosquitoes.
We now assume that and fluctuate around for all sufficiently large Since there is a such that Similarly, another exists, ensuring Based on system (2) for we have the following:
If i.e., then the variables and of system (2) can either be finite or infinite. In this case, there must exist positive constants such that for any or at least one of the variables and tends to infinity.
According to system (11), if then we obtain the following:
From (12), we have the following:
where such that is the maximum.
Similarly,
where such that is the maximum. Take When is finite, then cannot be infinitely small. Thus,
For we continue the same process, and then obtain a finite positive constant In this manner, we can sequentially acquire the series where is non-infinitesimal because is finite. For system (2), both and in Let Hence, and for all
If either and tends to infinity, then there exists a sufficiently large constant and
Similarly, the series can be obtained, where
and and hold true in Take It is obvious that is the positively invariant of system (2). If for each it contradicts with the assumption (i.e., and fluctuate around for all sufficiently large (t). If and then one can find a constant ensuring and for all Therefore, there exists a constant , such that
Similarly, the existence of a constant can be proved such that we have the following:
Take we then have the following:
□
Remark.
If system (2) exhibits a complete transmission rate then there is a similar conclusion to Theorem 1, but the interior periodic solution is degenerated as a boundary periodic solution where we have the following:
with
3. Simulations
In this section, we will evaluate the effectiveness of integrated control measures on the strategies of mosquito eradication and mosquito replacement. Global sensitivity analysis of parameters is used to evaluate the influence of various input parameters on the output variable and population replacement, as shown in Figure 2 and Figure 3. We also explore the impacts of varying pulse periods and the killing rates on the mosquito dynamics of system (2) in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. To compare the solutions of system (2) with that of no impulsive spraying control, the impacts of initial states on the solutions of system (1) are as shown in Figure 9. Moreover, a Caputo fractional-order impulsive model will be used to assess the impact of memory factors on the strategies of mosquito eradication and replacement, as shown in Figure 10.
3.1. Sensitivity Analysis
Uncertainty analysis of input parameters is explored by using a Latin hypercube sampling (LHS) method. Global sensitivity analysis is conducted by assessing the partial rank correlation coefficients (PRCCs) between various input parameters (generated from the LHS method with 3000 samples) and the output variable PRCC values can determine the importance of the contribution of each input parameter on the value of the outcome variable. A positive or negative PRCC value indicates the positive or negative correlation between the input parameter and the output variable, respectively. Generally, the absolute of PRCC within , or indicates an insignificant difference from zero, a moderate correlation, or a high correlation between the input parameter and the output variable, respectively. Interested readers can refer to reference [48,49] for a more detailed definition and explanation of the LHS method and PRCCs.
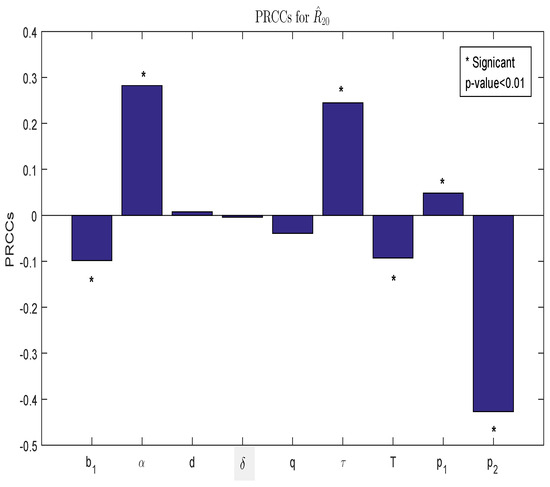
Figure 2.
PRCC histogram describing the dependence of with respect to input parameters.
From Theorem 1, the stability and persistence of interior periodic solutions are determined by threshold value playing a critical role in whether or not the population replacement strategy can succeed. Although the explicit value of cannot be directly calculated, it can be determined numerically. We then concentrate on examining the influence of each parameter on , as depicted in Figure 2. The PRCC values and p-values of each parameter are presented in Table 2. Based on Figure 2 and Table 2, the highest contribution on is the killing rate The ratio and the transmission rate have moderate contributions, and other parameters only have slight contributions. In particular, we can increase by decreasing or increasing which is conducive to achieving partial population replacement.

Table 2.
PRCCs describing the dependence of with respect to each input parameter. We assign a p-value as zero if and consider it significant if .
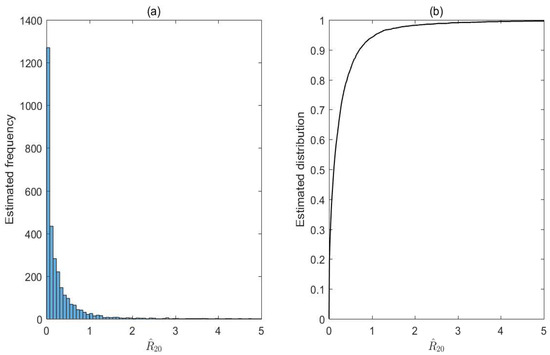
Figure 3.
Frequency histogram (a) and cumulative distribution (b) of based on the 3000 LHS samples.
Figure 3 show the frequency and cumulative distribution of based on the 3000 samples of LHS to analyze its sample results. It follows from Figure 3 that the mean of is with the standard deviation being The coefficient of variation (CV) is calculated by dividing a variable’s standard deviation by its mean, which helps assess the concentration extent of the variable. If the CV exceeds 10%, the frequency distribution is considered dispersed; otherwise, it is deemed concentrated. Figure 3 reveals that the frequency of is significantly dispersed (), with the lowest and the highest estimates being and respectively. Our estimates from the replicated LHS shows that of these estimates of are less than and the probability of is about Moreover, based on the sensitivity analysis of the probability of can be improved by reducing and increasing
3.2. Effectiveness of Pulse-Spraying Insecticide on Control Strategies
To assess the effectiveness of pulse-spraying insecticide on mosquito eradication or partial replacement, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 illustrate the impacts of varying pulse periods and killing rates on the mosquito dynamics of system (2). From Figure 4, the solutions of system (2) can stabilize at the mosquito eradication periodic solution more quickly with decreasing impulsive periods successively from to From Figure 5, with successively decreasing impulsive periods from to the solutions of both Wolbachia-free and -carrying females can be successively decreased, and the mosquito replacement level is slightly increased. This indicates that an increase in the frequency of impulsive periods contributes to reducing annoying mosquito bites while improving the level of mosquito replacement.
From Figure 6, if the killing rate is too low, the mosquito eradication strategy cannot succeed (as observed in the black curves). Only if the killing rate is adequately high is it possible to achieve the mosquito eradication strategy. By increasing the killing rate (see magenta, blue, and red curves), the mosquito eradication strategy can be achieved more quickly. From Figure 7, if the killing rate is too low, the mosquito replacement strategy will not succeed (see black curves), and the strategy may be achieved only if the killing rate is adequately high. When the partial replacement strategy succeeds, the total number of wild and Wolbachia-carrying female mosquitoes is much lower than the total number of females when the mosquito population replacement strategy fails. As increasing the killing rate from to , the solutions of Wolbachia-free and -carrying mosquitoes can be increased and reduced, respectively, while the strategy of mosquito replacement can reach higher levels more quickly. It indicates that appropriately increasing the killing rate helps to quicker achieve a high level of mosquito replacement and also helps to reduce annoying mosquito bites.
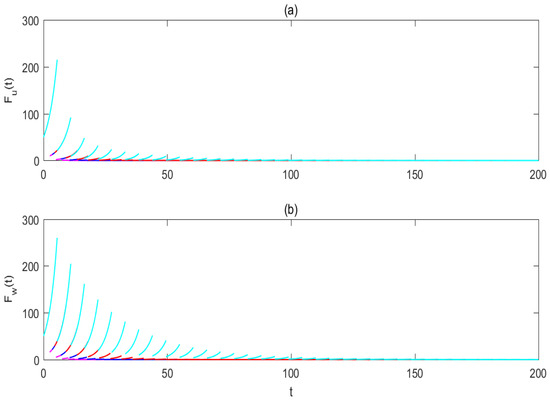
Figure 4.
The impacts of pulse periods on the mosquito eradication strategy. (a) For the solution of wild female mosquitoes ; (b) for the solution of Wolbachia-carrying female mosquitoes . The magenta, blue, red, and cyan lines represent the solutions of the system (2) corresponding to T values of and respectively. Baseline parameter values are set as , . The initial values of the solution curves are taken by .
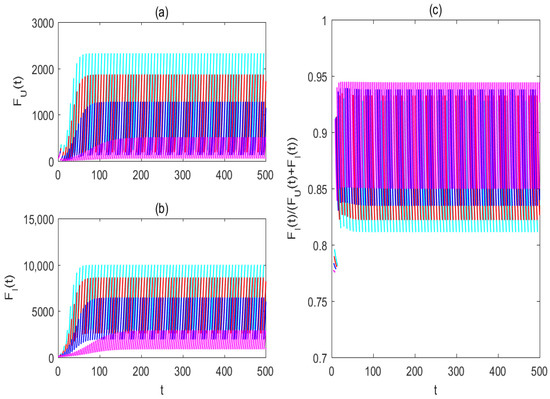
Figure 5.
The impacts of impulsive periods on the mosquito replacement strategy. (a) For the solution of wild female mosquitoes ; (b) for the solution of Wolbachia-carrying female mosquitoes (c) for the proportion of Wolbachia-carrying female mosquitoes to the total female mosquitoes The cyan, red, blue, and magenta lines, respectively, represent the solution of system (2) by taking The values of the baseline parameters are consistent with those in Figure 4, but .
From Figure 8a,b, when the killing rate is relatively large, the solutions of Wolbachia-free and -carrying mosquitoes stabilize more slowly and quickly, respectively, to the mosquito eradication periodic solution as is increased (see red, cyan, and green curves). As shown in Figure 8c–e, when the killing rate is relatively small, decreasing allows the solution of system (2) to stabilize faster to the partial replacement periodic solution, and the partial replacement can reach higher levels more quickly (see blue, magenta, and black curves).
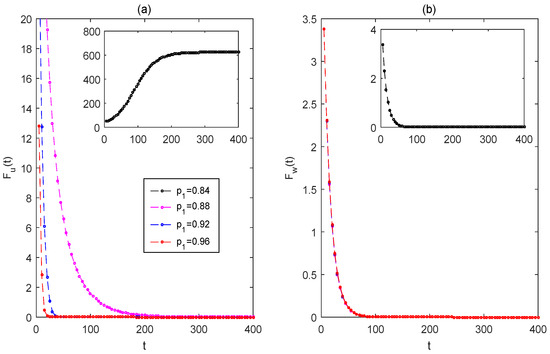
Figure 6.
The effects of impulsive killing rates on the mosquito eradication strategy. (a) For the solution of wild female mosquitoes ; (b) for the solution of Wolbachia-carrying female mosquitoes . The values of the baseline parameters are consistent with those in Figure 4, but For black lines, for the magenta, blue, and red lines, .
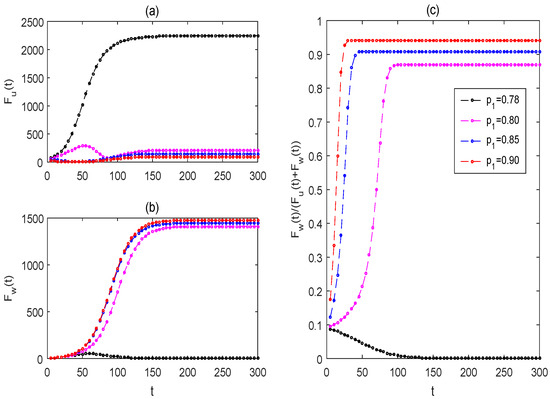
Figure 7.
The effects of impulsive killing rates on the strategy of mosquito replacement. (a) For the solution of wild female mosquitoes ; (b) for the solution of Wolbachia-carrying female mosquitoes (c) for the proportion of Wolbachia-carrying female mosquitoes to the total female mosquitoes The values of the baseline parameters are consistent with those in Figure 4, but For black lines, for the magenta, blue, and red lines, .
Figure 9 shows that system (2), without impulsive spraying insecticide, shows bistable equilibria, with the system’s stabilization at one of the equilibria depending on the initial conditions. The green and red solution curves indicate the success or failure of the partial replacement strategy. For more details about the bistable equilibria of system (2), without impulsive spraying insecticide, interested readers can refer to our previous work [32]. However, when the combination of Wolbachia and impulsive spraying insecticide is considered, even in the same non-impulsive control parameters, the mosquito eradication strategy or replacement may be achieved, depending on the values of pulse control parameters or the initial mosquito densities. This indicates that, compared to the sole use of Wolbachia, the integrated use of Wolbachia and insecticide can bring diverse control strategies. Moreover, regardless of the case of dynamical behaviors and the initial values, the total quantities of female mosquitoes in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 are consistently much lower than those in Figure 9. This indicates that the integrated control measure can help reduce annoying mosquito bites while implementing a mosquito replacement strategy, and potentially even eliminate mosquitoes.
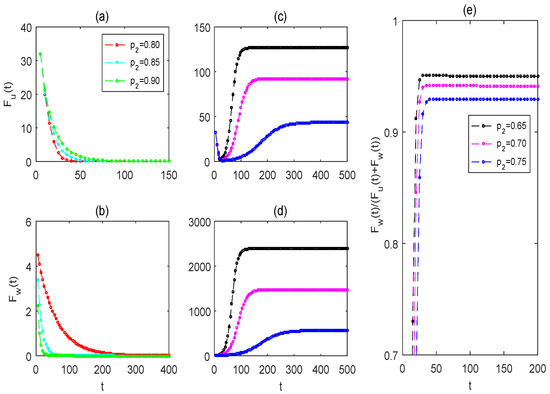
Figure 8.
The effects of impulsive killing rates on the strategies of mosquito eradication and replacement. (a,c) For the solution of wild female mosquitoes ; (b,d) for the solution of Wolbachia-carrying female mosquitoes (e) for the proportion of Wolbachia-carrying female mosquitoes to the total female mosquitoes The values of the baseline parameters are consistent with those in Figure 4, but .
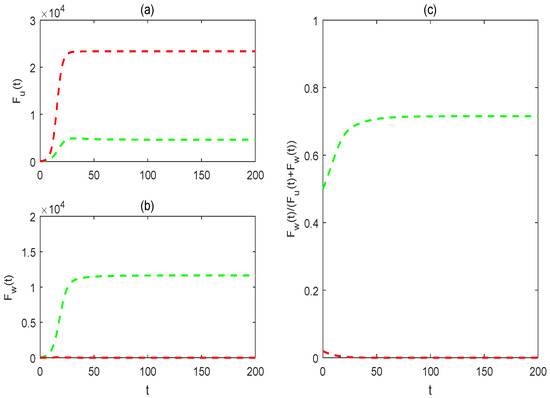
Figure 9.
The impacts of initial states on the solutions of system (1). (a) For the solution of wild female mosquitoes ; (b) for the solution of Wolbachia-carrying female mosquitoes (c) for the proportion of Wolbachia-carrying female mosquitoes to the total female mosquitoes The red and green lines, respectively, are the solutions from the initial values and Baseline parameter values are taken as the same as in Figure 4.
3.3. Impacts of Mosquito Memory on the Two Control Strategies
The memory effect of mosquitoes on past environmental resources, climate changes, and other factors has a significant impact on mosquito population dynamics. This suggests that the future state of the mosquito population depends not only on its current state but also on its past states. Fractional differential equations can effectively describe this memory effect and the complex dynamical behavior of such systems. Many notable definitions of fractional derivatives have been developed and discussed, with the most well-known being the Riemann–Liouville and Caputo definitions.
The integer-order derivative and Caputo derivative of a constant are both zero, whereas the Riemann–Liouville derivative of a constant is not. Thus, the Riemann–Liouville differential operator fails to handle differential equations when they involve constant values. Additionally, the Riemann–Liouville fractional derivative cannot be paired with initial conditions defined in classical integer-order models. Caputo fractional differential equations can effectively represent the memory effect and historical dependence in mosquito populations and allow the initial values from the integer-order equation to be directly used as initial conditions. This makes Caputo’s approach more comparable to the solution of the integer-order model. Therefore, we will extend the integer-order impulsive differential equation model (2) into a Caputo fractional-order impulsive model to assess and compare the impact of memory factors on strategies for mosquito eradication and replacement. The modified model can be obtained by replacing the integer derivative in model (2) with the Caputo derivative of order , as follows:
where is the order of a Caputo-type fractional derivative.
Through a straightforward dimensional analysis, it becomes evident that the first four equations of system (13) exhibit a dimensional mismatch between the left-hand and right-hand sides of the equations. By careful examination, the left-hand side of the first four equations of system (13) exhibits a dimension of day−γ. On the right-hand side, the terms and share the same dimensions of Cap−1day−1, the terms d and share the same dimensions of Cap−2day−1, the variables , and share the same dimensions of Cap, while the remaining terms are identified as dimensionless, as shown in Table 1. Thus, the right-hand side of the first four equations of system (13) has the dimension of day−1. Note that the right-hand side of the equations of the system must have the same dimensions as the left-hand side. Moreover, Diethelm addressed the dimensional mismatch associated with direct fractionation in [50], where he proposed a fractional-order system with the same dimensions on both sides of the equations. We attempt to follow the procedure proposed by Diethelm to overcome the dimensional mismatch in system (13) and improve the system as follows:
where is the order of a Caputo-type fractional derivative, the fractional operator is identical to the first integer-order derivative when Generally, the term denotes the memory intensity of mosquitoes, so indicates no memory effect. The definitions, units, and values of parameters are the same as those in system (2). It is noteworthy that both systems (2) and (14) share identical initial values and parameter values, thereby offering a solid foundation for our subsequent investigation into the impact of memory factors on the strategies of mosquito eradication and replacement, as shown in Figure 10.
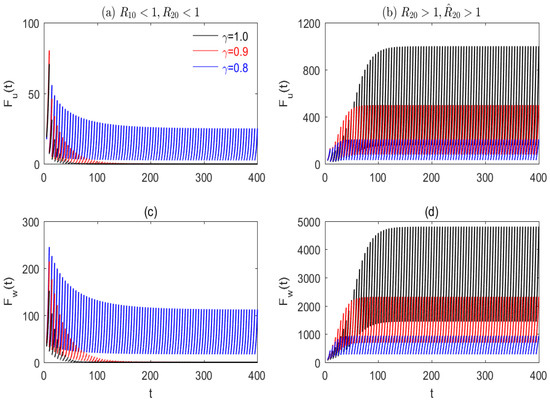
Figure 10.
The impacts of memory on the strategies of mosquito eradication and replacement. (a,c) For and with ; (b,d) for , and with . The black, red, and blue curves represent the solution of system (14) by taking respectively. Other parameter values and the initial values are taken as the same as in Figure 4, except for .
According to Section 3, we denote the two cases and as the low fecundity of individuals and the high fecundity of individuals, respectively. Figure 10 shows the impacts of the memory intensity of mosquitoes on the strategies of mosquito eradication and replacement for both the low and high fecundity of individuals. To provide a more intuitive and precise comparison of the impact of memory intensity on control strategies, we have compiled a table (see Table 3) that summarizes the key aspects from Figure 10 under different threshold conditions and three distinct levels of memory intensity. The key aspects include the control strategies, the time required for the system to reach stable periodic solutions, the number of wild females, Wolbachia-carrying females, and total females at stabilization, as well as the replacement levels at stabilization. This table offers a clear and concise representation of the relationship between memory intensity and the effectiveness of control strategies.

Table 3.
The key aspects from Figure 10 under low and high fecundity of individuals with different memory intensities. The key aspects include the control strategies, the time required for the solution sequences to stabilize before and after the pulse controls, the numbers of wild females , Wolbachia-carrying females , total females , and the replacement levels at stabilization for the solution sequences before and after the pulse controls.
From Figure 10a,c and Table 3 for and if there is no memory effect from mosquitoes (), then about 85 and 70 days later, the solution sequences of both wild and Wolbachia-carrying females before and after the pulse control, will, respectively, tend to zero. This indicates that the mosquito eradication strategy can be swiftly achieved. Compared to the scenario without memory effect, when the memory intensity of mosquitoes is increased to 0.1, i.e., then 190 and 140 days later, the solutions for both wild females and Wolbachia-carrying females before and after the pulse control will, respectively, converge to zero, implying that the speed of mosquito eradication has slowed down. When we continue to increase the memory intensity to 0.2, i.e., then it, respectively, requires about 275 and 155 days for the solution sequences before and after the pulse control, and solutions of both wild and Wolbachia-carrying females will converge to stable interior periodic solutions with low female mosquito numbers. This implies that mosquito eradication is replaced by mosquito replacement with a low amount of mosquitoes.
Similarly, from Figure 10b,d and Table 3 for and if there is no memory effect from mosquitoes for then about 165 and 155 days later, the solution sequences of both wild and Wolbachia-carrying females, before and after the pulse control, will tend to interior equilibria, with the total number of females being, respectively, 5796 and and the corresponding replacement levels being, respectively, and This indicates that the strategy of mosquito replacement—with high numbers of females, high amplitudes of females, and high replacement levels—can be achieved gradually. Compared to the scenario with no memory effect, when the memory intensity of mosquitoes is progressively increased from 0.1, i.e., γ =0.9, to 0.2 i.e., γ = 0.8, then the solution sequences of both wild and Wolbachia-carrying females, before and after the pulse control, will converge more quickly to the interior equilibria. These equilibria will have both lower numbers and amplitudes of females, though the replacement levels will only increase slightly.
4. Discussion
In this work, a four-dimensional impulsive differential model with pulse-spraying insecticides was developed to explore the impact of the integrated application of Wolbachia and chemical insecticides on the spread of Wolbachia in mosquito populations. We investigated the stability of the mosquito elimination periodic solution and Wolbachia-free periodic solution by using the stability analysis of the equivalent difference systems and the Floquet multiplier theory, as shown in Theorem 1. Then, we proved the permanence of Wolbachia partially established periodic solution, as shown in Theorem 2. These threshold conditions of stability and permanence can determine the success or failure of mosquito eradication or replacement strategy.
Sensitivity analysis was conducted by using PRCCs to reveal the contributions of input parameters to the threshold value . The first three contribution parameters are the insecticide killing rate of Wolbachia mosquitoes , the ratio of natural birth rates, and transmission rate Moreover, can be increased by decreasing or increasing and which is conducive to achieving partial population replacement. We also numerically explored the effects of pulse periods and insecticide killing rates on the strategies of mosquito eradication and replacement. For the mosquito eradication strategy, increasing the frequency of insecticide spraying can rapidly reduce mosquito populations. Increasing the kill rate of insecticides against wild mosquitoes, or moderately reducing the kill rate of Wolbachia-carrying mosquitoes, can help to rapidly reduce the population of wild mosquitoes that transmit dengue disease. As for the strategy of mosquito replacement, increasing the spraying frequency of insecticides is beneficial to achieve a high level of mosquito replacement with a low total amount and low amplitude. Increasing the kill rate of insecticides against wild mosquitoes will help rapidly reduce their population and improve the level of mosquito population replacement. Appropriately reducing the kill rate of insecticides against Wolbachia-carrying mosquitoes may slightly lower the mosquito replacement level, but can significantly reduce the total number of both types of mosquitoes.
The solutions of system (2), both with and without pulse-spraying insecticide, were compared to assess the effectiveness of mosquito control between the combined use of Wolbachia and insecticides versus using only Wolbachia. Numerical results indicate that the mosquito elimination strategy cannot be achieved by using only Wolbachia. However, the integrated use of Wolbachia and insecticide can successfully lead to either mosquito eradication or replacement. Compared to solely using Wolbachia, the integrated control measure can reduce annoying mosquito bites by significantly lowering the total mosquito population, while also achieving mosquito replacement or even complete eradication.
Moreover, the integer-order impulsive differential equation model was extended into a Caputo fractional-order impulsive model to assess the impacts of memory factors on the strategies of mosquito eradication and replacement. Under both the low and high fecundity of individuals, we numerically compared the impacts of three different memory intensities on the effectiveness of mosquito eradication and replacement from several critical aspects, including the control strategy, the required stable time of the periodic solution, the numbers of wild, Wolbachia-carrying, and total females, and the replacement level.
When the basic offspring numbers of wild mosquitoes in the absence of Wolbachia mosquitoes and the basic offspring number of Wolbachia mosquitoes in the absence of wild mosquitoes are both less than one (i.e., for and ), an increase in mosquito memory intensity is not conducive to achieving the eradication strategy, both in terms of the required stabilization time and the number of female mosquitoes at stabilization. The reason for this phenomenon is that when the fecundity of individuals is relatively low or the mosquito population is relatively low, then mosquitoes will choose more suitable places to breed in response to their memories of the environment and resource availability, in order to support their own development and thereby increase their population size.
When the basic offspring numbers of Wolbachia mosquitoes in the absence or presence of wild mosquitoes are both larger than one (i.e., for and ), then the increase in mosquito memory intensity is beneficial to the implementation of a replacement strategy from the perspectives of the required stable time, the number of female mosquitoes, and replacement levels at stabilization. The primary reason for this phenomenon is that when the fecundity of individuals is relatively high or the mosquito population is relatively large, adult mosquitoes will reduce their oviposition behavior to allocate more resources to each individual, based on their memory evaluation, the living environment, and resources. This results in a decrease in the overall mosquito population.
At present, modeling studies on the effects of Wolbachia biological control on the transmission and control of mosquitoes and mosquito-borne diseases using fractional differential equations are notably scarce [44,45]. In [44], Dianavinnarasi et al. developed a stage-structured mosquito population model that continuously releases various stages of Wolbachia-carrying female and male mosquitoes to explore how Wolbachia spreads in wild mosquito populations. They examined the existence, uniqueness, and α-exponential stability properties of the solutions were examined. In [45], the authors further expanded the model to include the dynamics of the human population and dengue virus transmission, building upon the work of Dianavinnarasi et al. They established a Caputo fractional-order epidemiological model. By analyzing the local and global stability of the system’s equilibrium points, they investigated the dynamics of Wolbachia transmission and its impact on dengue transmission. Additionally, they used numerical analysis methods to identify the most effective strain for disease control.
When comparing this work with the above-mentioned modeling studies, the main differences are as follows. The two previous studies primarily utilized fractional-order models of mosquito populations or dengue transmission to investigate the impact of solely using Wolbachia-based biological control on the strategy of mosquito replacement, and the transmission and control of dengue diseases. When the fractional order degrades to one, both systems transform into continuous differential equation models. In this work, we considered the fact that replacing wild mosquitoes with Wolbachia-infected mosquitoes can cause annoying mosquito bites and pose a potential risk of transmitting other mosquito-borne viruses. During dengue outbreak seasons, it is ideal to achieve population replacement while maintaining the overall mosquito population at a lower threshold or even achieving eradication. Therefore, we aimed to go beyond using Wolbachia biological control alone by further exploring the modeling of integrated mosquito management. This approach combines the advantages of Wolbachia with chemical insecticides and considers the memory effect of mosquito populations. Consequently, we established integer-order and fractional-order differential equation models of mosquito populations with impulsive insecticide spraying to study the impact of integrated mosquito management on both population replacement and eradication strategies. We also conducted numerical comparisons between integer-order and fractional-order models to investigate the specific impact of memory intensity on these two control strategies under different control thresholds. Moreover, when the fractional order reduces to one, the primary difference between our impulsive model and the previous continuous models lies in the fact that the function on the right-hand side of our model is neither continuous nor smooth, which increases the theoretical analysis challenges for such impulsive systems.
Our model focuses on the spread of Wolbachia in mosquito populations through the combined use of Wolbachia and insecticide. To simplify, we only consider the dynamic behaviors of adult mosquitoes but ignore the life cycle of mosquitoes. Moreover, mosquitoes experience four distinct stages, and each stage may have different birth and death rates and dynamic behaviors. In addition, this paper investigates the impact of memory intensity on the two control strategies. Due to space limitations, we have not conducted a theoretical investigation of the threshold dynamic conditions for the extended Caputo fractional-order differential equations. Instead, we have numerically compared the solutions of the integer-order impulsive differential equation model with those of the fractional-order impulsive model. We assume that this fractional-order model possesses threshold dynamics similar to those of integer-order models. Therefore, in future work, we will attempt to theoretically derive the precise threshold dynamic conditions for the fractional-order impulsive model with stage structures, and investigate the spread of Wolbachia and integrated control strategies.
5. Conclusions
In this work, we established integer-order and fractional-order impulsive differential models to study the effects of integrated mosquito management and mosquito memory factors on mosquito population dynamics, as well as strategies for mosquito replacement and eradication. In conclusion, while maintaining the safety of chemical pesticide use, appropriately increasing the frequency of pesticide spraying and selecting pesticides that are effective against wild mosquitoes but relatively less effective against Wolbachia-carrying mosquitoes can be more conducive to achieving a low overall mosquito population under high-level replacement, and even to achieving mosquito eradication. Compared to using only Wolbachia, the integrated control measure offers diverse control strategies. It can help reduce annoying mosquito bites while achieving a mosquito replacement strategy, and potentially even eliminate mosquitoes. For cases with low fecundity, with the increase in memory intensity, the time required to achieve eradication strategies will be prolonged, and it may even result in the replacement strategy with a low total number of female mosquitoes. However, for cases with high fecundity, with the increase in memory intensity, the time required to achieve replacement strategies will be shortened, and the number and amplitude of female mosquitoes will decrease, although the replacement level only undergoes slight changes.
Author Contributions
Conceptualization, X.Z. and K.W.; methodology, X.Z., H.H. and H.Z.; software, X.Z. and H.H.; validation, H.Z.; writing—original draft preparation, X.Z.; writing—review and editing, H.Z. and X.Z.; supervision, K.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (12471473, 12171396), Fundamental Research Funds for the Central Universities (SWU-KT24004), and Natural Sciences and Engineering Research Council of Canada and Public Health Agency of Canada (NSERC-PHAC).
Data Availability Statement
Data are contained within the article.
Acknowledgments
We are grateful to the editor and reviewers for their valuable comments and suggestions, which greatly improved the presentation of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gubler, D.J. Dengue. In The Arboviruses; CRC Press: Boca Raton, FL, USA, 2019; pp. 223–260. [Google Scholar]
- Li, Y.; Dou, Q.; Lu, Y.; Xiang, H.; Yu, X.; Liu, S. Effects of ambient temperature and precipitation on the risk of dengue fever: A systematic review and updated meta-analysis. Environ. Res. 2020, 191, 110043. [Google Scholar] [CrossRef] [PubMed]
- Meetei, M.Z.; Zafar, S.; Zaagan, A.A.; Mahnashi, A.M.; Idrees, M. Dengue transmission dynamics: A fractional-order approach with compartmental modeling. Fractal Fract. 2024, 8, 207. [Google Scholar] [CrossRef]
- Lambrechts, L.; Ferguson, N.M.; Harris, E.; Holmes, E.C.; McGraw, E.A.; O’Neill, S.L.; Ooi, E.E.; Ritchie, S.A.; Ryan, P.A.; Scott, T.W.; et al. Assessing the epidemiological effect of Wolbachia for dengue control. Lancet Infect. Dis. 2015, 15, 862–866. [Google Scholar] [CrossRef]
- Walker, T.; Johnson, P.; Moreira, L.; Iturbe-Ormaetxe, I.; Frentiu, F.; McMeniman, C.; Leong, Y.S.; Dong, Y.; Axford, J.; Kriesner, P.; et al. The wMel Wolbachia strain blocks dengue and invades caged Aedes aegypti populations. Nature 2011, 476, 450–453. [Google Scholar] [CrossRef]
- Hoffmann, A.A.; Montgomery, B.; Popovici, J.; Iturbe-Ormaetxe, I.; Johnson, P.; Muzzi, F.; Greenfield, M.; Durkan, M.; Leong, Y.; Dong, Y.; et al. Successful establishment of Wolbachia in Aedes populations to suppress dengue transmission. Nature 2011, 476, 454–457. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, D.; Li, Y.; Yang, C.; Wu, Y.; Liang, X.; Liang, Y.; Pan, X.; Hu, L.; Sun, Q.; et al. Incompatible and sterile insect techniques combined eliminate mosquitoes. Nature 2019, 572, 56–61. [Google Scholar] [CrossRef]
- Landmann, F. The Wolbachia endosymbionts. Microbiol. Spectr. 2019, 7, 10–128. [Google Scholar] [CrossRef]
- Perlmutter, J.I.; Meyers, J.E.; Bordenstein, S.R. Transgenic testing does not support a role for additional candidate genes in Wolbachia male killing or cytoplasmic incompatibility. mSystems 2020, 5, e00658-19. [Google Scholar] [CrossRef]
- Caspari, E.; Watson, G. On the evolutionary importance of cytoplasmic sterility in mosquitoes. Evolution 1959, 13, 568–570. [Google Scholar] [CrossRef]
- Gan, Y.; Xiang, T.; Ouyang, D.; Zhou, M.; Ye, M. SPGAN: Siamese projection generative adversarial networks. Knowl. Based Syst. 2024, 285, 111353. [Google Scholar] [CrossRef]
- Gan, Y.; Yang, C.; Ye, M.; Huang, R.; Ouyang, D. Generative Adversarial Networks with Learnable Auxiliary Module for Image Synthesis. ACM Trans. Multimed. Comput. Commun. Appl. 2024, 1–21. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Tuyet-Hanh, T.T.; Mulhall, J.; Minh, H.V.; Duong, T.Q.; Chien, N.V.; Nhung, N.T.T.; Lan, V.H.; Minh, H.B.; Cuong, D.; et al. Deep learning models for forecasting dengue fever based on climate data in Vietnam. PLoS Negl. Trop. Dis. 2022, 16, e0010509. [Google Scholar] [CrossRef] [PubMed]
- Tantowijoyo, W.; Andari, B.; Arguni, E.; Budiwati, N.; Nurhayati, I.; Fitriana, I.; Ernesia, I.; Daniwijaya, E.W.; Supriyati, E.; Yusdiana, D.H.; et al. Stable establishment of wMel Wolbachia in Aedes aegypti populations in Yogyakarta, Indonesia. PLoS Negl. Trop. D 2020, 14, e0008157. [Google Scholar] [CrossRef]
- Gesto, J.S.M.; Pinto, S.B.; Dias, F.B.S.; Peixoto, J.; Costa, G.; Kutcher, S.; Montgomery, J.; Green, B.R.; Anders, K.L.; Ryan, P.A.; et al. Large-scale deployment and establishment of Wolbachia into the Aedes aegypti population in Rio de Janeiro, Brazil. Front. Microbiol. 2021, 12, 711107. [Google Scholar] [CrossRef]
- Velez, I.D.; Uribe, A.; Barajas, J.; Uribe, S.; Ángel, S.; Suaza-Vasco, J.D.; Mejia Torres, M.C.; Arbeláez, M.P.; Santacruz-Sanmartin, E.; Duque, L.; et al. Large-scale releases and establishment of wMel Wolbachia in Aedes aegypti mosquitoes throughout the Cities of Bello, Medellín and Itagüí, Colombia. PLoS Negl. Trop. D 2023, 17, e0011642. [Google Scholar] [CrossRef]
- Turelli, M. Evolution of incompatibility-inducing microbes and their hosts. Evolution 1994, 48, 1500–1513. [Google Scholar]
- Haygood, R.; Turelli, M. Evolution of incompatibility-inducing microbes in subdivided host populations. Evolution 2009, 63, 432–447. [Google Scholar] [CrossRef]
- Keeling, M.J.; Jiggins, F.; Read, J.M. The invasion and coexistence of competing Wolbachia strains. Heredity 2003, 91, 382–388. [Google Scholar] [CrossRef]
- Zheng, B.; Tang, M.; Yu, J. Modeling Wolbachia spread in mosquitoes through delay differential equations. SIAM J. Appl. Math. 2014, 74, 743–770. [Google Scholar] [CrossRef]
- Hancock, P.A.; Sinkins, S.P.; Godfray, H.C.J. Population dynamic models of the spread of Wolbachia. Am. Nat. 2011, 177, 323–333. [Google Scholar] [CrossRef]
- Farkas, J.Z.; Gourley, S.A.; Liu, R.; Yakubu, A.A. Modelling Wolbachia infection in a sex-structured mosquito population carrying West Nile virus. J. Math. Biol. 2017, 75, 621–647. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Zheng, B.; Zou, X. Wolbachia dynamics in mosquitoes with incomplete CI and imperfect maternal transmission by a DDE system. Bull. Math. Biol. 2022, 84, 95. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Liu, Q.; Zhu, H. Modeling and dynamics of Wolbachia-infected male releases and mating competition on mosquito control. J. Math. Biol. 2020, 81, 243–276. [Google Scholar] [CrossRef] [PubMed]
- Jansen, V.A.; Turelli, M.; Godfray, H.C.J. Stochastic spread of Wolbachia. Proc. R. Soc. B Biol. Sci. 2008, 275, 2769–2776. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Supriatna, A.K. Stochastic dengue mathematical model in the presence of Wolbachia: Exploring the disease extinction. Nonlinear Dyn. Syst. Theory 2020, 20, 214–227. [Google Scholar]
- Chan, M.H.; Kim, P.S. Modelling a Wolbachia invasion using a slow–fast dispersal reaction–diffusion approach. Bull. Math. Biol. 2013, 75, 1501–1523. [Google Scholar] [CrossRef]
- Huang, M.; Tang, M.; Yu, J. Wolbachia infection dynamics by reaction-diffusion equations. Sci. China Math. 2015, 58, 77–96. [Google Scholar] [CrossRef]
- Qu, Z.; Wu, T.; Hyman, J.M. Modeling spatial waves of Wolbachia invasion for controlling mosquito-borne diseases. SIAM J. Appl. Math. 2022, 82, 1903–1929. [Google Scholar] [CrossRef]
- Xue, L.; Cao, X.; Wan, H. Releasing Wolbachia-infected mosquitos to mitigate the transmission of zika virus. J. Math. Anal. Appl. 2021, 496, 124804. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Li, Y.; Liu, Q.; Zhu, H. Modelling the effects of Wolbachia-carrying male augmentation and mating competition on the control of dengue fever. J. Dyn. Differ. Equ. 2023, 1–41. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, S.; Cheke, R.A. Models to assess how best to replace dengue virus vectors with Wolbachia-infected mosquito populations. Math. Biosci. 2015, 269, 164–177. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Tang, S.; Cheke, R.A.; Zhu, H. Modeling the effects of augmentation strategies on the control of dengue fever with an impulsive differential equation. Bull. Math. Biol. 2016, 78, 1968–2010. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, X. Modeling and control of mosquito-borne diseases with Wolbachia and insecticides. Theor. Popul. Biol. 2020, 132, 82–91. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Tang, M.; Wu, Z.; Xi, Z.; Yu, J. The threshold infection level for Wolbachia invasion in random environments. J. Differ. Equ. 2019, 266, 4377–4393. [Google Scholar] [CrossRef]
- Yu, J. Existence and stability of a unique and exact two periodic orbits for an interactive wild and sterile mosquito model. J. Differ. Equ. 2020, 269, 10395–10415. [Google Scholar] [CrossRef]
- Zheng, B.; Yu, J.; Li, J. Modeling and analysis of the implementation of the Wolbachia incompatible and sterile insect technique for mosquito population suppression. SIAM J. Appl. Math. 2021, 81, 718–740. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.M.; El-Saka, H.A. Equilibrium points, stability and numerical solutions of fractional-order predator–prey and rabies models. J. Math. Anal. Appl. 2007, 325, 542–553. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, Y.; Lu, J.; Li, Y. Stability and bifurcation of a delayed generalized fractional-order prey–predator model with interspecific competition. Appl. Math. Comput. 2019, 347, 360–369. [Google Scholar] [CrossRef]
- Li, S.; Huang, C.; Yuan, S. Hopf bifurcation of a fractional-order double-ring structured neural network model with multiple communication delays. Nonlinear Dyn. 2022, 108, 379–396. [Google Scholar] [CrossRef]
- Jajarmi, A.; Arshad, S.; Baleanu, D. A new fractional modelling and control strategy for the outbreak of dengue fever. Physica A 2019, 535, 122524. [Google Scholar] [CrossRef]
- Yangla, J.; Abboubakar, H.; Dangbe, E.; Yankoulo, R.; Ari, A.A.A.; Damakoa, I.; Nisar, K.S. Fractional dynamics of a Chikungunya transmission model. Sci. Afr. 2023, 21, e01812. [Google Scholar] [CrossRef]
- Farman, M.; Ahmad, A.; Akgül, A.; Saleem, M.U.; Rizwan, M.; Ahmad, M.O. A mathematical analysis and simulation for Zika virus model with time fractional derivative. Math. Methods Appl. Sci. 2024, 47, 11135–11146. [Google Scholar] [CrossRef]
- Dianavinnarasi, J.; Raja, R.; Alzabut, J.; Cao, J.; Niezabitowski, M.; Bagdasar, O. Application of Caputo–Fabrizio operator to suppress the Aedes Aegypti mosquitoes via Wolbachia: An LMI approach. Math. Comput. Simul. 2022, 201, 462–485. [Google Scholar] [CrossRef]
- Joseph, D.; Ramachandran, R.; Alzabut, J.; Jose, S.A.; Khan, H. A fractional-order density-dependent mathematical model to find the better strain of Wolbachia. Symmetry 2023, 15, 845. [Google Scholar] [CrossRef]
- Lakshmikantham, V.; Simeonov, P.S. Theory of Impulsive Differential Equations; World Scientific: Singapore, 1989. [Google Scholar]
- Bainov, D.; Simeonov, P. Impulsive Differential Equations: Periodic Solutions and Applications; Routledge: London, UK, 2017. [Google Scholar]
- Blower, S.M.; Dowlatabadi, H. Sensitivity and uncertainty analysis of complex models of disease transmission: An HIV model, as an example. Int. Stat. Rev. 1994, 62, 229–243. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef]
- Diethelm, K. A fractional calculus based model for the simulation of an outbreak of dengue fever. Nonlinear Dyn. 2013, 71, 613–619. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).