Event-Triggered Fuzzy Adaptive Predefined-Time Control for Fractional-Order Nonlinear Systems with Time-Varying Deferred Constraints and Its Application
Abstract
1. Introduction
2. System Description and Preliminaries
2.1. System Description
2.2. Preliminaries
2.3. Predefined-Time Stability Theory
2.4. Time-Varying Deferred Constraints
2.5. Interval Type-2 Fuzzy Logic Systems
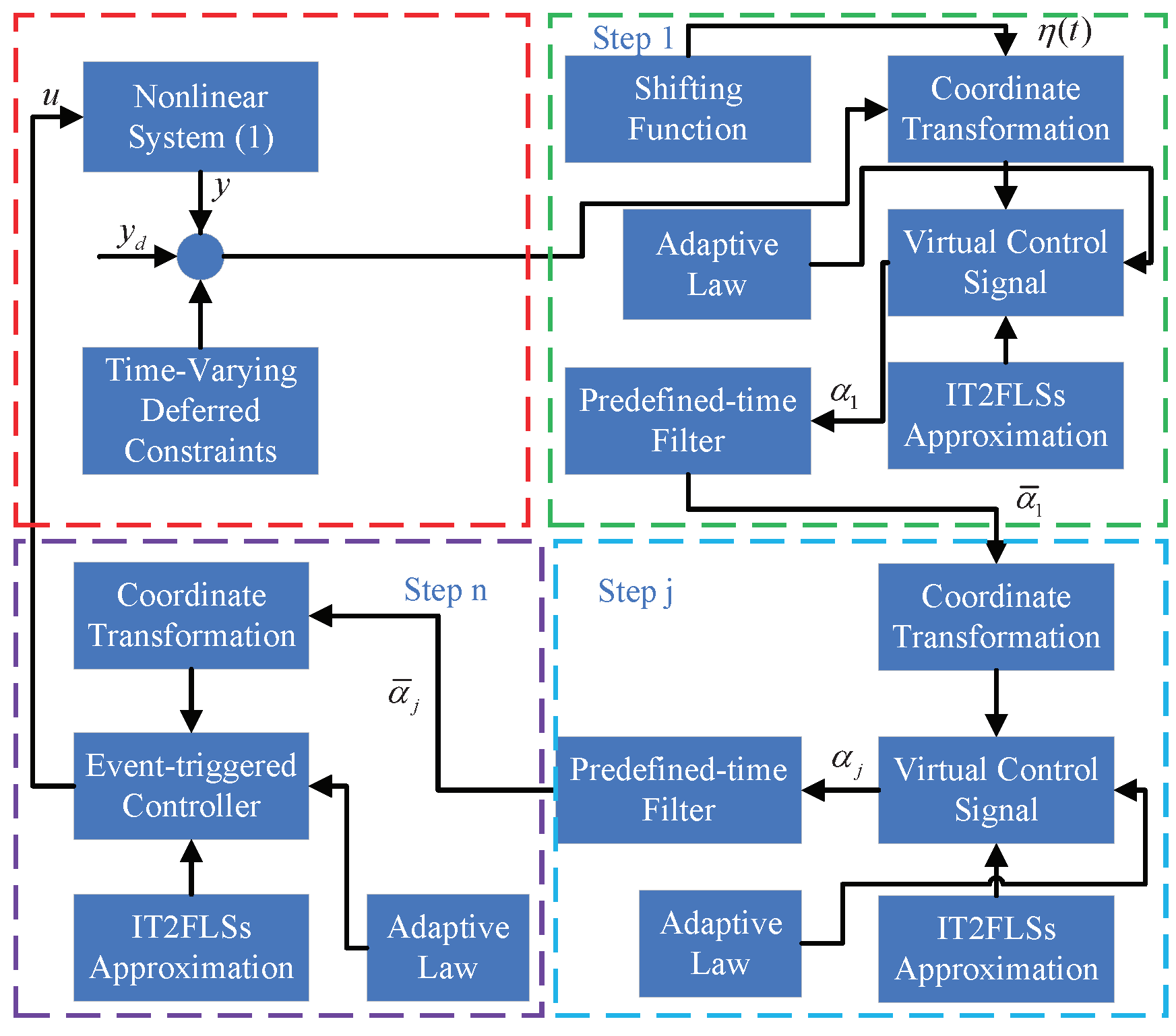
3. Main Results
3.1. Controller Design
- Step 1.
- Taking the qth time derivative of , one can derive
- Step 2.
- An enhanced FO nonlinear filter is designed as:
3.2. Stability Analysis
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tejado, I.; Pérez, E.; Valério, D. Fractional calculus in economic growth modeling of the group of seven. Fract. Calc. Appl. Anal. 2019, 22, 139–157. [Google Scholar] [CrossRef]
- Wei, Y.; Tse, P.W.; Yao, Z.; Wang, Y. Adaptive backstepping output feedback control for a class of nonlinear fractional order systems. Nonlinear Dyn. 2016, 86, 1047–1056. [Google Scholar] [CrossRef]
- Liu, H.; Pan, Y.; Li, S.; Chen, Y. Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2209–2217. [Google Scholar] [CrossRef]
- Lin, C.; Chen, B.; Shi, P.; Yu, J. Necessary and sufficient conditions of observer-based stabilization for a class of fractional-order descriptor systems. Syst. Control Lett. 2018, 112, 31–35. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, W. Adaptive Neural Network Sliding Mode Control for Nonlinear Singular Fractional Order Systems with Mismatched Uncertainties. Fractal Fract. 2020, 4, 50. [Google Scholar] [CrossRef]
- Zouari, F.; Ibeas, A.; Boulkroune, A.; Cao, J.; Arefi, M.M. Adaptive neural output-feedback control for nonstrict-feedback time-delay fractional-order systems with output constraints and actuator nonlinearities. Neural Netw. 2018, 105, 256–276. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Ma, H. Adaptive fuzzy backstepping dynamic surface control of strict-feedback fractional-order uncertain nonlinear systems. IEEE Trans. Fuzzy Syst. 2020, 28, 122–133. [Google Scholar] [CrossRef]
- Zhan, Y.; Sui, S.; Tong, S. Adaptive fuzzy decentralized dynamic surface control for fractional-order nonlinear large-scale systems. IEEE Trans. Fuzzy Syst. 2022, 30, 3373–3383. [Google Scholar] [CrossRef]
- Song, S.; Park, J.H.; Zhang, B.; Song, X. Observer-based adaptive hybrid fuzzy resilient control for fractional-order nonlinear systems with time-varying delays and actuator failures. IEEE Trans. Fuzzy Syst. 2021, 29, 471–485. [Google Scholar] [CrossRef]
- Bi, W.; Wang, T.; Yu, X. Fuzzy adaptive decentralized control for nonstrict-feedback large-scale switched fractional-order nonlinear systems. IEEE Trans. Cybern. 2022, 52, 8887–8896. [Google Scholar] [CrossRef]
- Mendel, J. Computing derivatives in interval type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 2004, 12, 84–98. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Hwang, J.H.; Kwak, H.J.; Park, J.T. Adaptive interval type-2 fuzzy sliding mode control for unknown chaotic system. Nonlinear Dyn. 2011, 63, 491–502. [Google Scholar] [CrossRef]
- Jafari, A.A.; Mohammadi, S.M.A.; Naseriyeh, M.H. Adaptive type-2 fuzzy backstepping control of uncertain fractional-order nonlinear systems with unknown dead-zone. Appl. Math. Model. 2019, 69, 506–532. [Google Scholar] [CrossRef]
- Shao, S.; Chen, M.; Zheng, S.; Lu, S.; Zhao, Q. Event-triggered fractional-order tracking control for an uncertain nonlinear system with output saturation and disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 5857–5869. [Google Scholar] [CrossRef]
- Tang, L.; He, K.; Liu, Y. Adaptive output feedback fuzzy event-triggered control for fractional-order nonlinear switched systems. IEEE Trans. Fuzzy Syst. 2023, 31, 3459–3469. [Google Scholar] [CrossRef]
- Zhang, H.; Cai, Y.; Wang, Y.; Su, H. Adaptive bipartite event-triggered output consensus of heterogeneous linear multiagent systems under fixed and switching topologies. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4816–4830. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Dong, J. Adaptive fuzzy consensus tracking control for uncertain fractional-order multiagent systems with event-triggered input. IEEE Trans. Fuzzy Syst. 2022, 30, 310–320. [Google Scholar] [CrossRef]
- Cui, M.; Tong, S. Event-triggered predefined-time output feedback control for fractional-order nonlinear systems with input saturation. IEEE Trans. Fuzzy Syst. 2023, 31, 4397–4409. [Google Scholar] [CrossRef]
- Song, X.; Sun, P.; Song, S.; Stojanovic, V. Finite-time adaptive neural resilient DSC for fractional-order nonlinear large-scale systems against sensor-actuator faults. Nonlinear Dyn. 2023, 111, 12181–12196. [Google Scholar] [CrossRef]
- Wu, W.; Tong, S. Observer-based fixed-time adaptive fuzzy consensus DSC for nonlinear multiagent systems. IEEE Trans. Cybern. 2023, 53, 5881–5891. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.; Chen, Q.; Yang, Q. Adaptive fuzzy predefined-time dynamic surface control for attitude tracking of spacecraft with state constraints. IEEE Trans. Fuzzy Syst. 2022, 31, 2292–2304. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Tong, S. Observer-based neuro-adaptive optimized control of strict-feedback nonlinear systems with state constraints. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3131–3145. [Google Scholar] [CrossRef]
- Song, S.; Zhang, B.; Song, X.; Zhang, Z. Neuro-fuzzy-based adaptive dynamic surface control for fractional-order nonlinear strict-feedback systems with input constraint. IEEE Trans. Syst. Man Cybern. Syst. 2021, 50, 3575–3586. [Google Scholar] [CrossRef]
- Pishro, A.; Shahrokhi, M.; Sadeghi, H. Fault-tolerant adaptive fractional controller design for incommensurate fractional-order nonlinear dynamic systems subject to input and output restrictions. Chaos Solut. Fractals 2022, 157, 111930. [Google Scholar] [CrossRef]
- Tee, K.P.; Ren, B.; Ge, S.S. Control of nonlinear systems with time-varying output constraints. Auotomatica 2011, 47, 2511–2516. [Google Scholar] [CrossRef]
- Sun, J.; Yi, J.; Pu, Z. Fixed-time adaptive fuzzy control for uncertain nonstrict-feedback systems with time-varying constraints and input saturations. IEEE Trans. Fuzzy Syst. 2022, 30, 1114–1128. [Google Scholar] [CrossRef]
- Song, Y.; Zhou, S. Tracking control of uncertain nonlinear systems with deferred asymmetric time-varying full state constraints. Automatica 2018, 98, 314–322. [Google Scholar] [CrossRef]
- Wang, A.; Liu, L.; Qiu, J.; Feng, G. Event-triggered adaptive fuzzy output-feedback control for nonstrict-feedback nonlinear systems with asymmetric output constraint. IEEE Trans. Cybern. 2022, 52, 712–722. [Google Scholar] [CrossRef]
- Wang, Q.; Pan, Y.; Cao, J.; Liu, H. Adaptive fuzzy echo state network control of fractional-order large-scale nonlinear systems with time-varying deferred constraints. IEEE Trans. Fuzzy Syst. 2024, 32, 632–648. [Google Scholar] [CrossRef]
- Chen, M.; Li, Y.; Wang, H.; Peng, K.; Wu, L. Adaptive fixed-time tracking control for nonlinear systems based on finite-time command filtered backstepping. IEEE Trans. Fuzzy Syst. 2023, 31, 1604–1613. [Google Scholar] [CrossRef]
- Yang, X.; Cao, J.; Liu, H.; Huang, C.; Xue, G. Composite adaptive fuzzy bipartite consensus of fractional-order multiagent systems with a switched event-triggered mechanism. ISA Trans. 2024, 148, 224–236. [Google Scholar] [CrossRef] [PubMed]
- Podlubny, L. Fractional Differential Equations; Academic: New York, NY, USA, 1998. [Google Scholar]
- Li, A. Convexity preserving interpolation. Comput. Aided Geom. Des. 1999, 16, 127–147. [Google Scholar] [CrossRef]
- Munoz-Vazquez, A.J.; Sánchez-Torres, J.D.; Jimenez-Rodriguez, E.; Loukianov, A.G. Predefined-time robust stabilization of robotic manipulators. IEEE/ASME Trans. Mechatron. 2019, 24, 1033–1040. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Sun, J.; Wang, Y. Event-triggered adaptive finite-time containment control for fractional-order nonlinear multiagent systems. IEEE Trans. Cybern. 2022, 54, 1250–1260. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, X.; Li, Y. Type-2 fuzzy adaptive output feedback saturation control for photovoltaic grid-connected power systems. Int. J. Control Autom. Syst. 2021, 19, 2759–2768. [Google Scholar] [CrossRef]
- Li, Y.; Tong, S. A bound estimation approach for adaptive fuzzy asymptotic tracking of uncertain stochastic nonlinear systems. IEEE Trans. Cybern. 2022, 52, 5333–5342. [Google Scholar] [CrossRef]
- You, X.; Shi, M.; Guo, B.; Zhu, Y.; Lai, W.; Dian, S.; Liu, K. Event-triggered adaptive fuzzy tracking control for a class of fractional-order uncertain nonlinear systems with external disturbance. Chaos Solut. Fractals 2022, 161, 112393. [Google Scholar] [CrossRef]
- Wang, X.; Xia, J.; Zhang, N.; Yu, M.; Guo, X. Dynamic event-triggered adaptive control for uncertain nonlinear switched systems based on MDADT method. Int. J. Control Autom. Syst. 2023, 21, 84–93. [Google Scholar] [CrossRef]
- Liang, Z.; Gao, J. Chaos in a fractional-order single-machine infinite-bus power system and its adaptive backstepping control. Int. J. Mod. Nonlinear Theory Appl. 2016, 5, 122–131. [Google Scholar] [CrossRef]
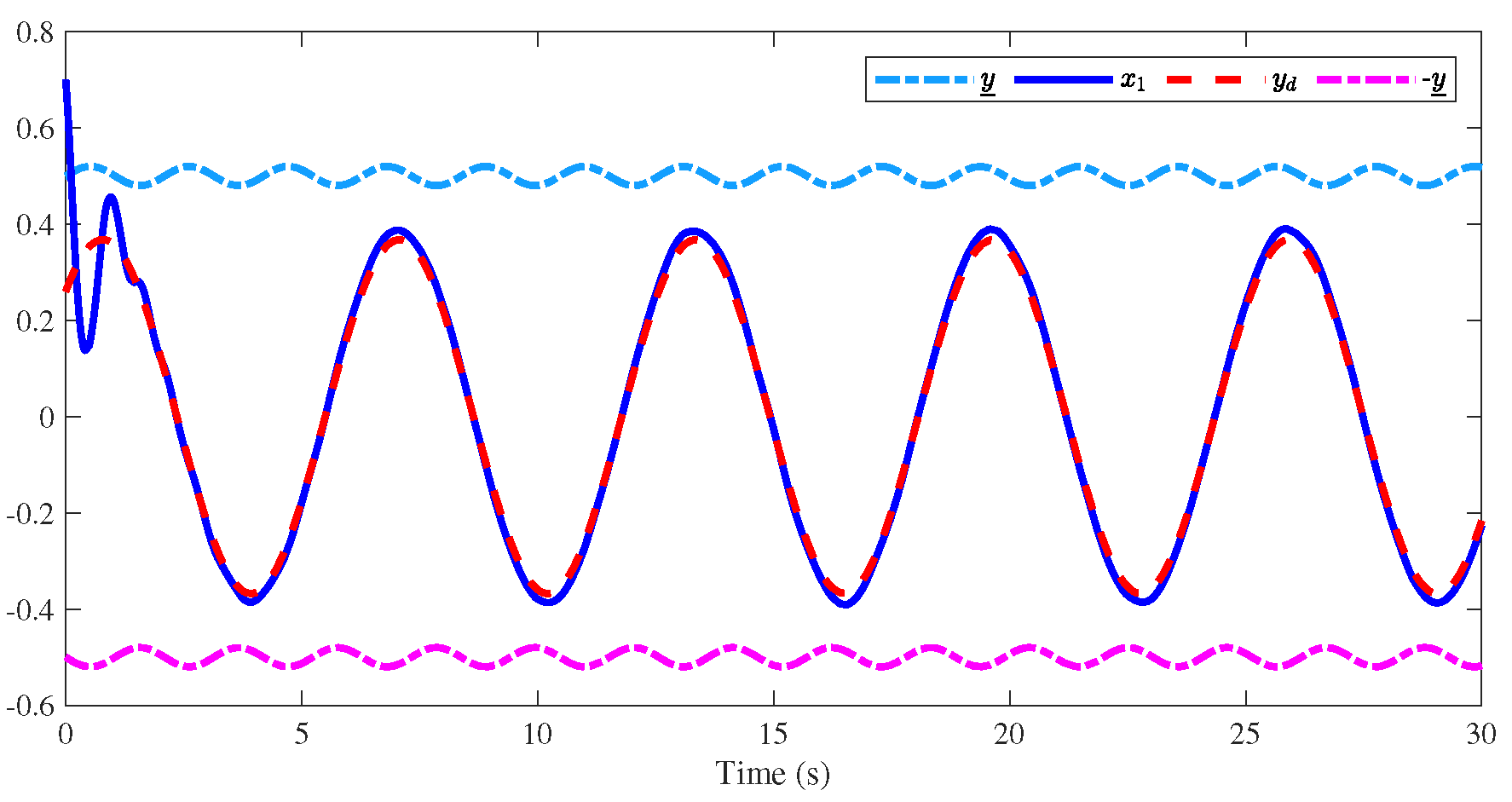
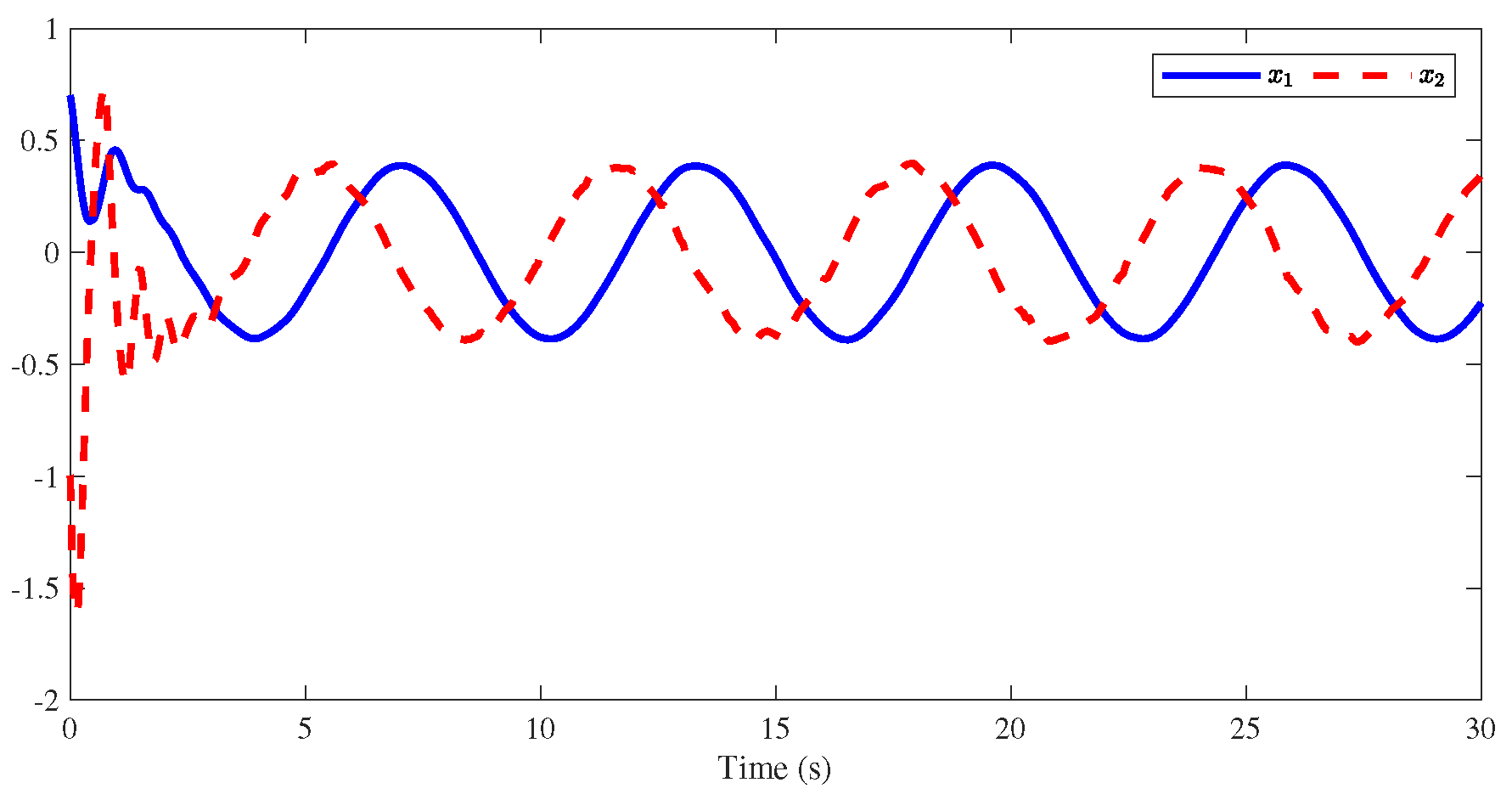
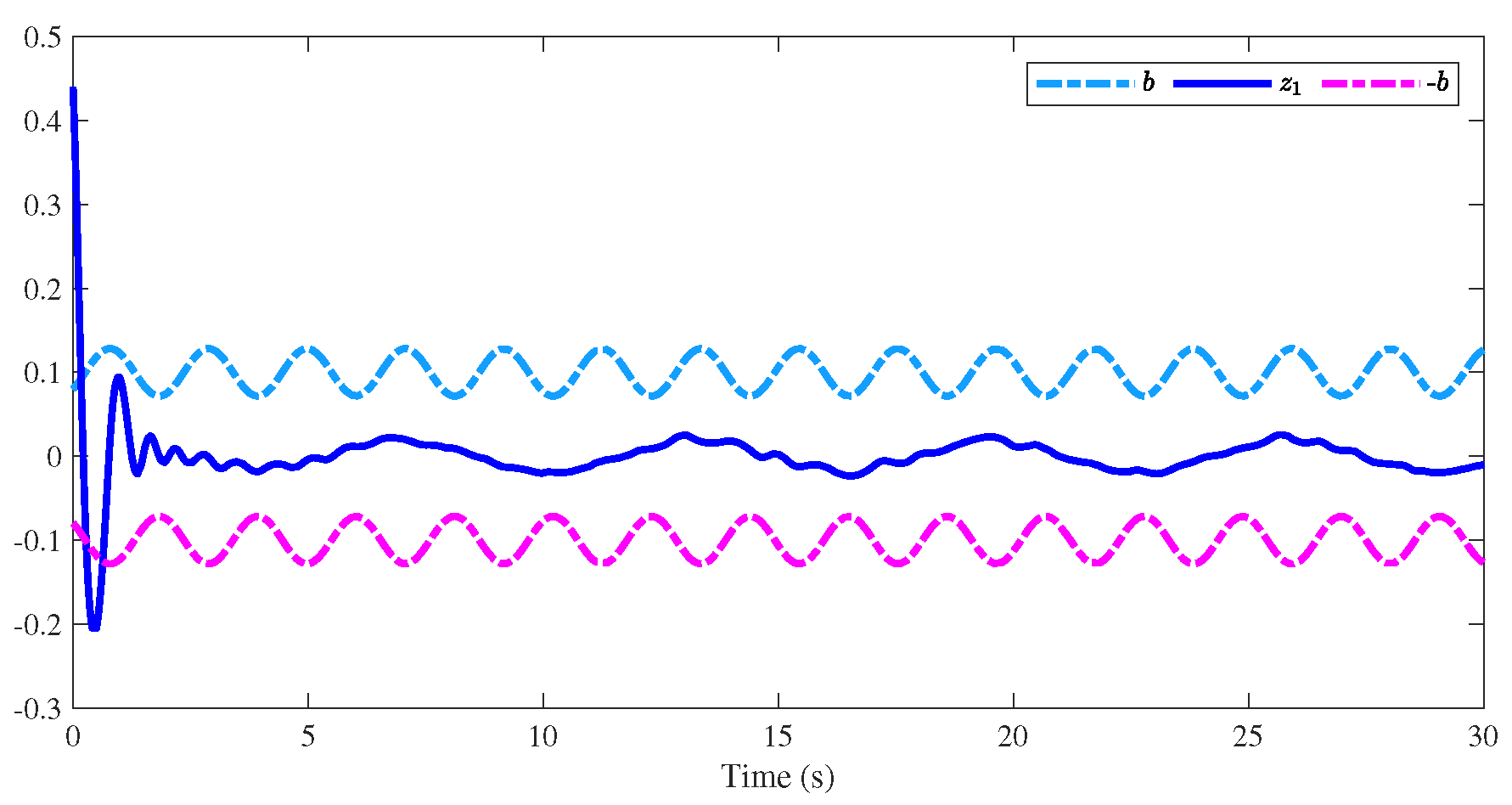
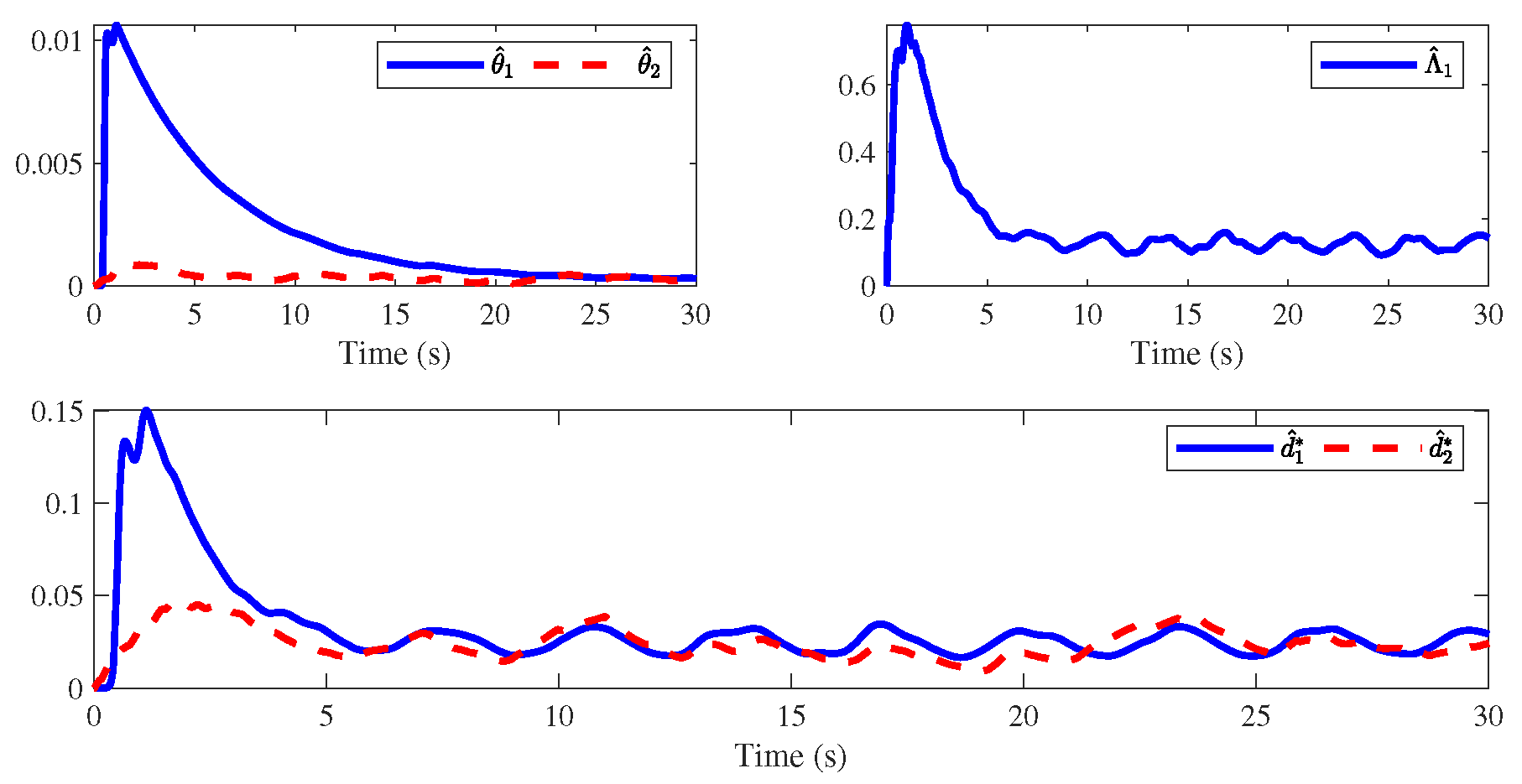
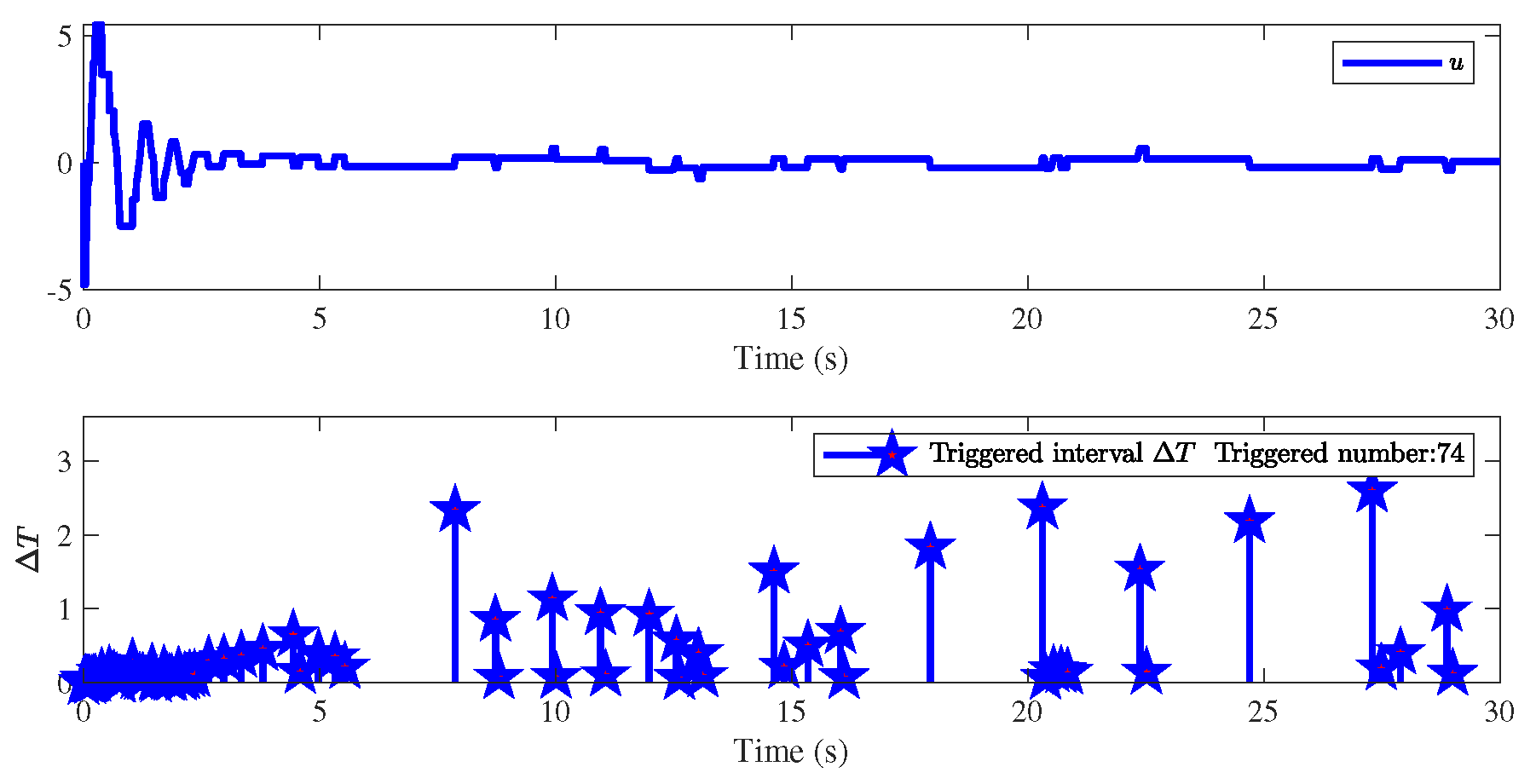
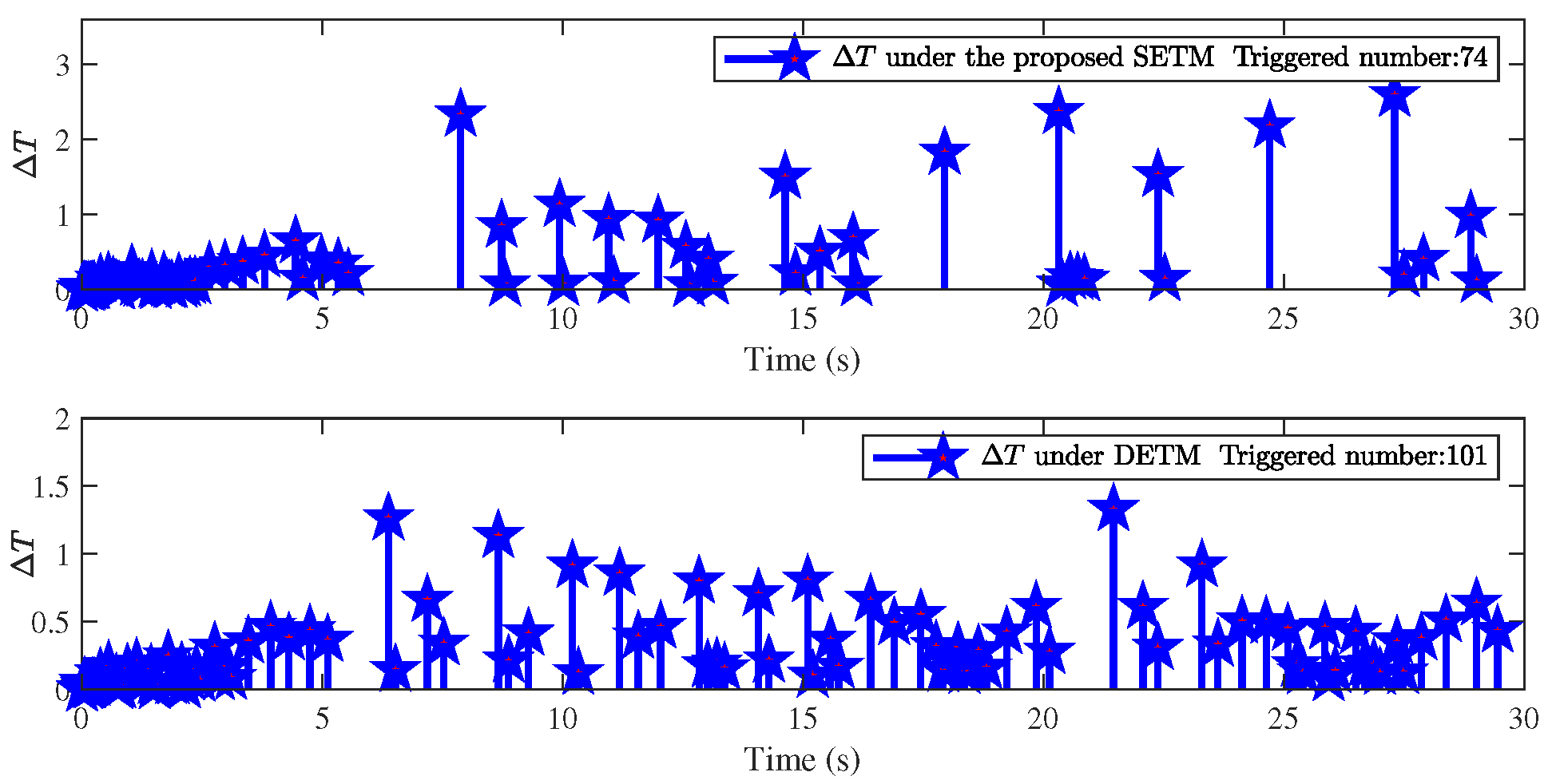


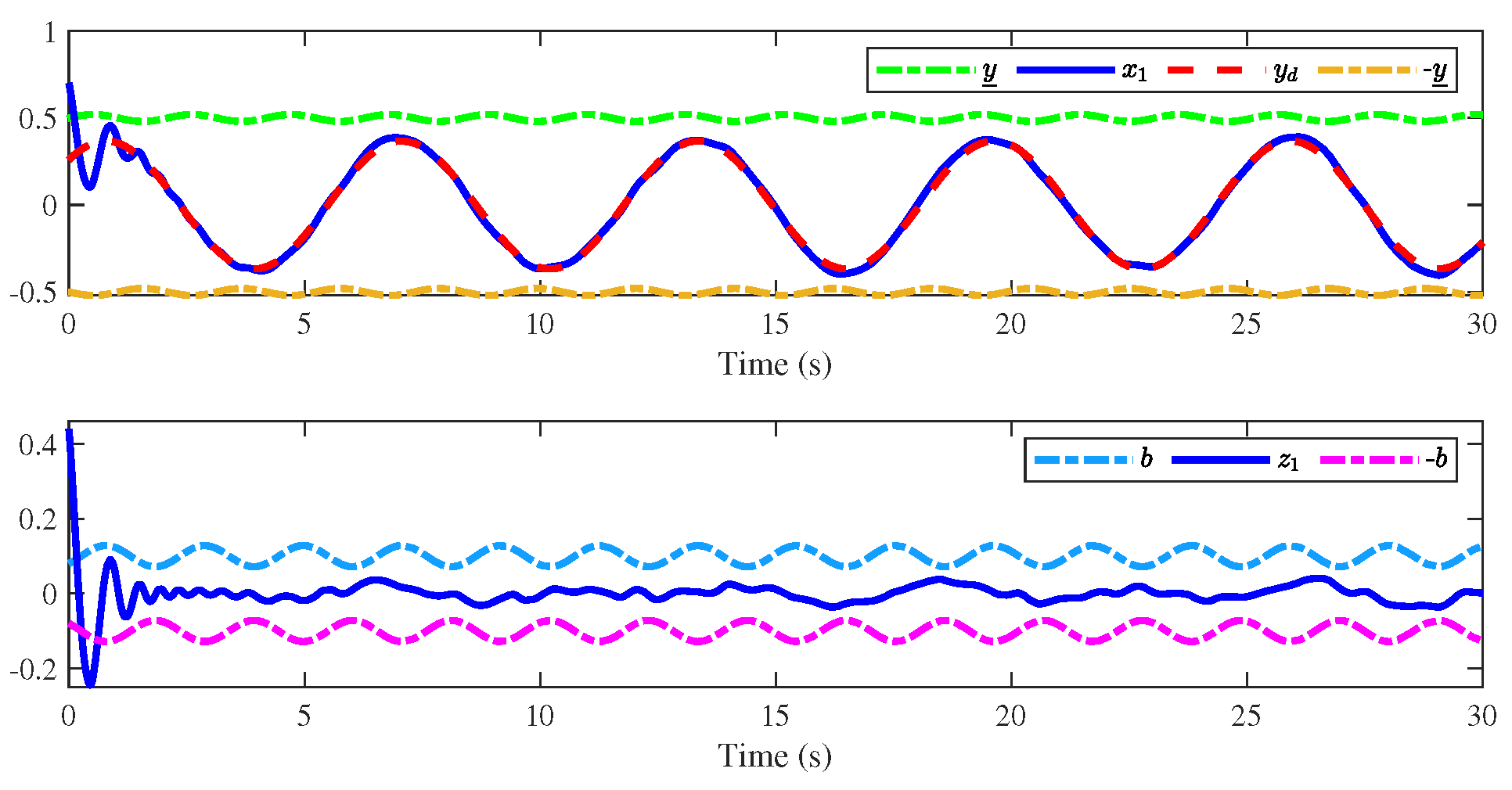
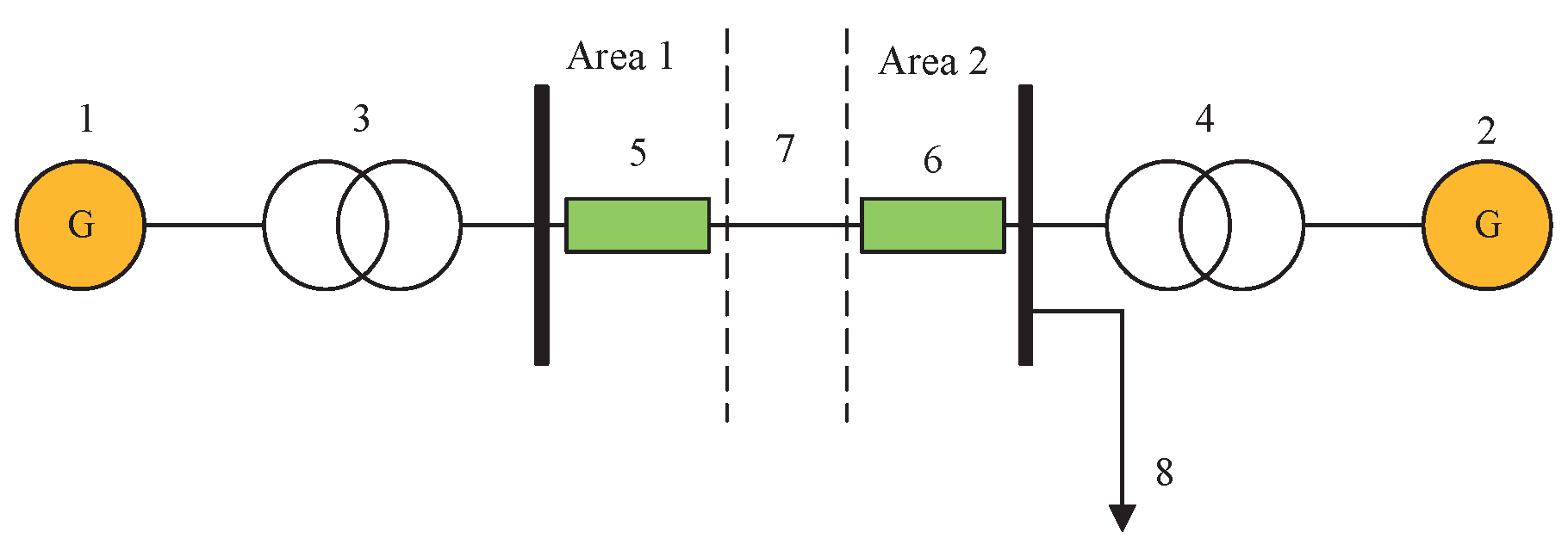
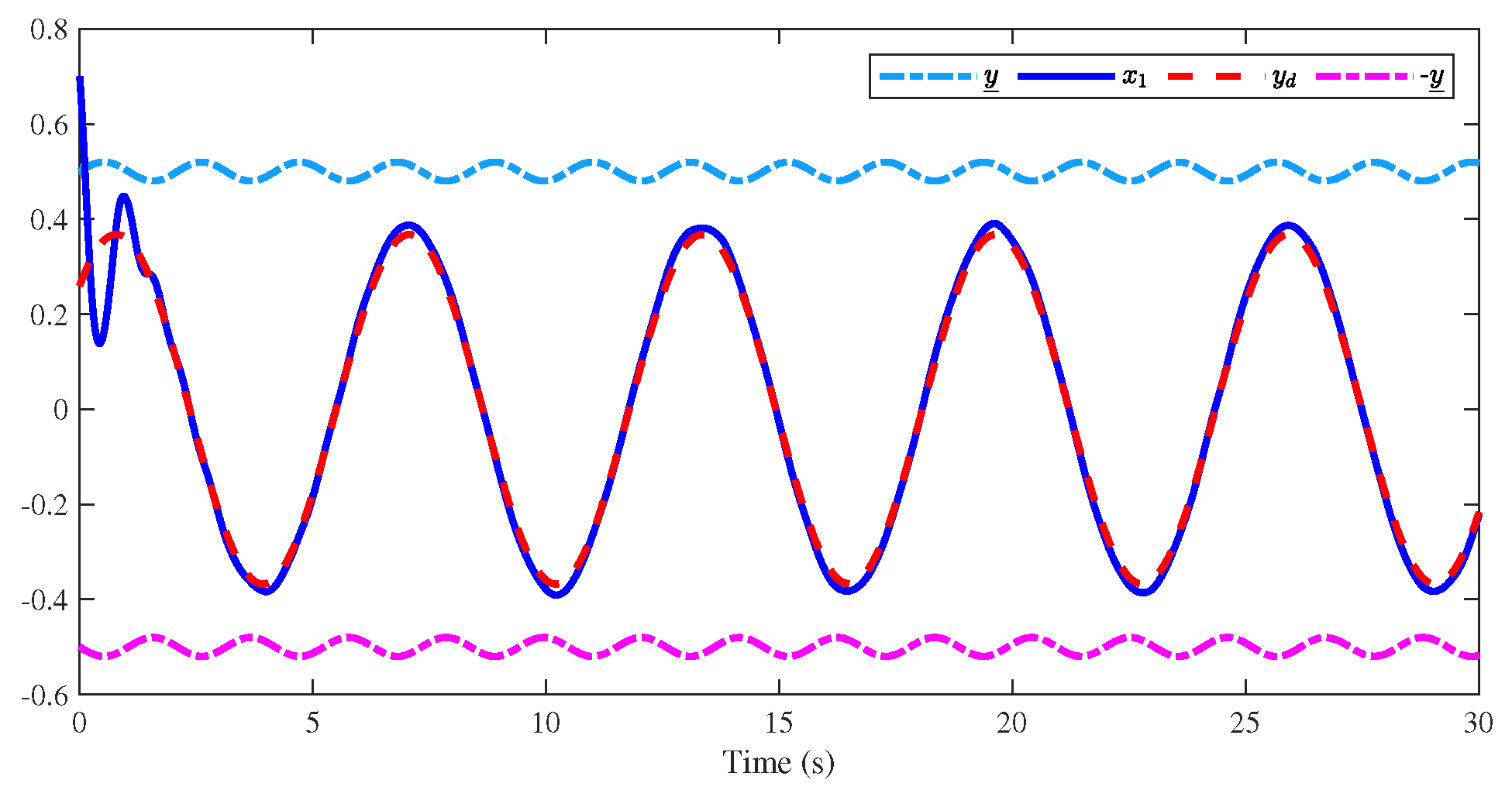

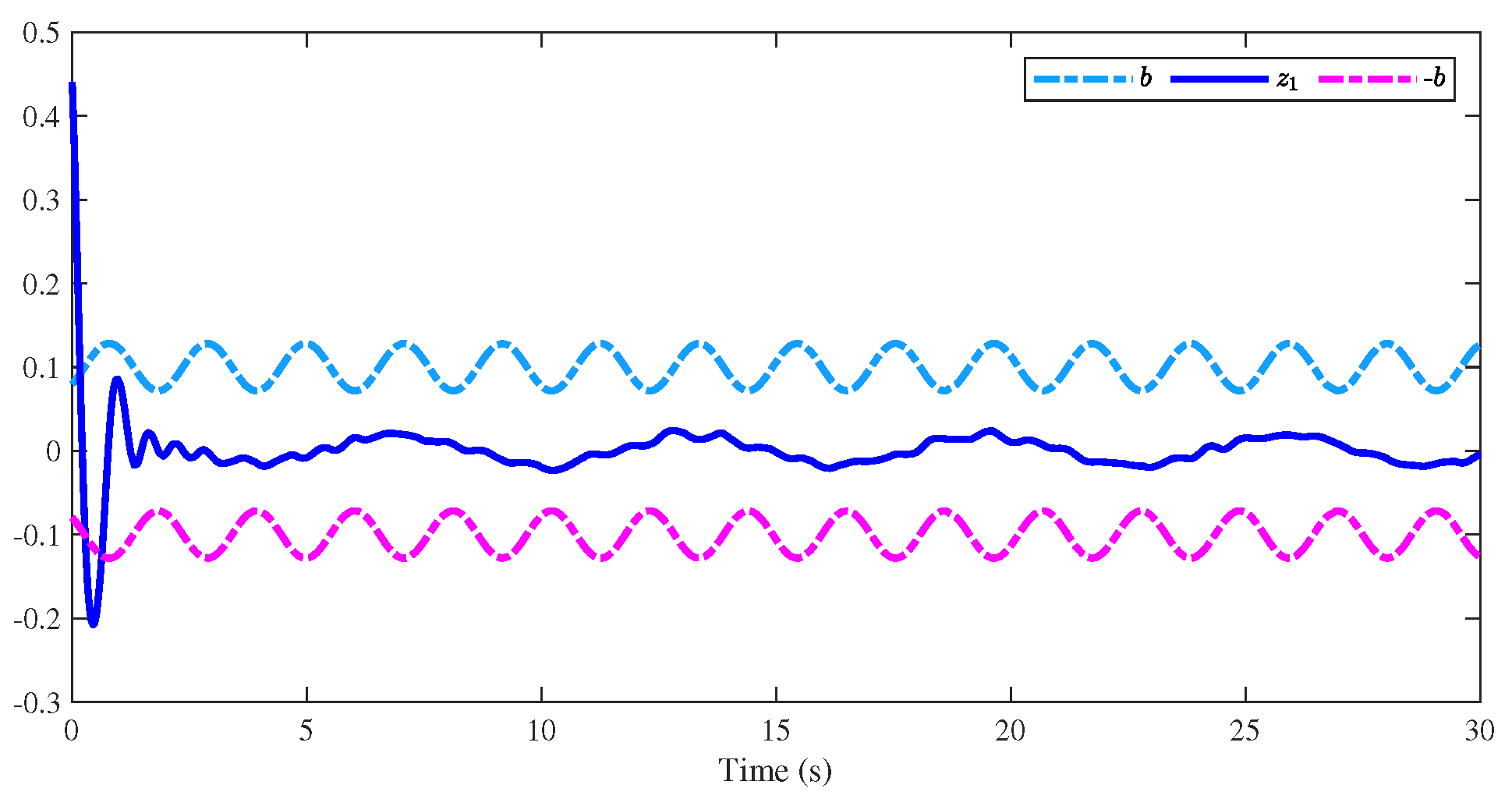

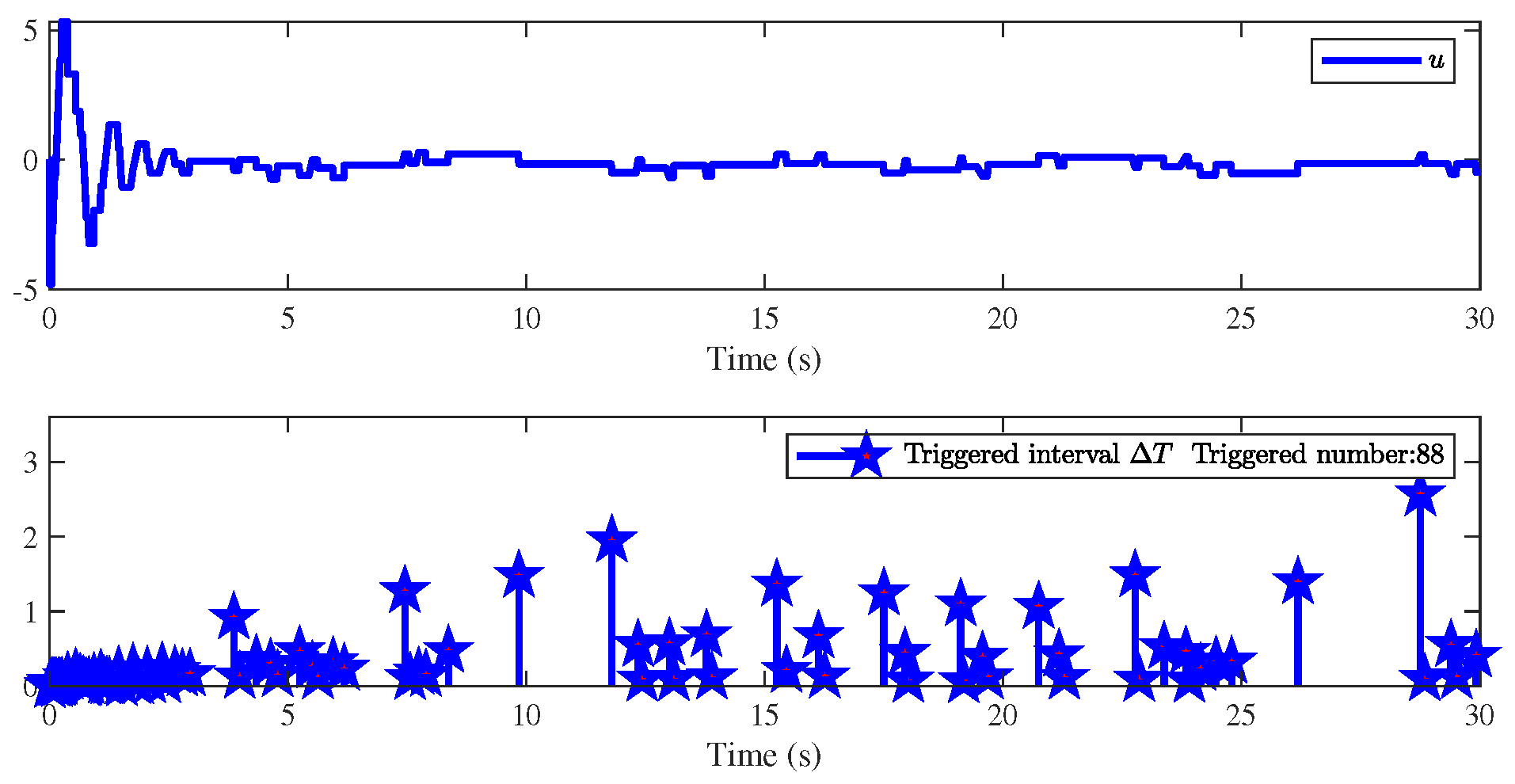
| The Initial Conditions |
| The Design Parameters |
| The Membership Functions |
| . |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Xing, L.; Song, X.; Tejado, I. Event-Triggered Fuzzy Adaptive Predefined-Time Control for Fractional-Order Nonlinear Systems with Time-Varying Deferred Constraints and Its Application. Fractal Fract. 2024, 8, 613. https://doi.org/10.3390/fractalfract8100613
Song S, Xing L, Song X, Tejado I. Event-Triggered Fuzzy Adaptive Predefined-Time Control for Fractional-Order Nonlinear Systems with Time-Varying Deferred Constraints and Its Application. Fractal and Fractional. 2024; 8(10):613. https://doi.org/10.3390/fractalfract8100613
Chicago/Turabian StyleSong, Shuai, Longhang Xing, Xiaona Song, and Inés Tejado. 2024. "Event-Triggered Fuzzy Adaptive Predefined-Time Control for Fractional-Order Nonlinear Systems with Time-Varying Deferred Constraints and Its Application" Fractal and Fractional 8, no. 10: 613. https://doi.org/10.3390/fractalfract8100613
APA StyleSong, S., Xing, L., Song, X., & Tejado, I. (2024). Event-Triggered Fuzzy Adaptive Predefined-Time Control for Fractional-Order Nonlinear Systems with Time-Varying Deferred Constraints and Its Application. Fractal and Fractional, 8(10), 613. https://doi.org/10.3390/fractalfract8100613







