Adaptive Fault-Tolerant Control of Mobile Robots with Fractional-Order Exponential Super-Twisting Sliding Mode
Abstract
1. Introduction
- •
- Addressing LIP and LOE actuator faults of the NMR system, a new adaptive FTC scheme is presented based on a chattering-free BF-FOESTSMC algorithm. This method can achieve fast convergence and maintain the sliding variable in a predetermined neighborhood of the sliding manifold due to the newly designed barrier function, which is different from the UUB guaranteed in [27,28] as such boundaries are related to unknown faults.
- •
- Inspired by [33], an exponential term associated with a sliding variable is established to accelerate the convergence of the STA and further reduce chattering. Furthermore, a FO sliding surface is designed to improve the control performance.
- •
- •
- Unlike [35], the proposed barrier function gain strategy provides sufficient adaptability to the LIP fault and uncertainties while avoiding gain overestimation.
- •
- The proposed method compensates for the partial LOE actuator faults by designing an estimator to estimate the boundaries of the LOE fault coefficient, hence only one constant needs to be estimated, which requires fewer computing resources.
2. Preliminaries and Problem Statement
2.1. Preliminaries
2.2. Kinematic and Dynamic Models of NMR System
2.3. Actuator Fault Model of NMR
2.4. Problem Statement
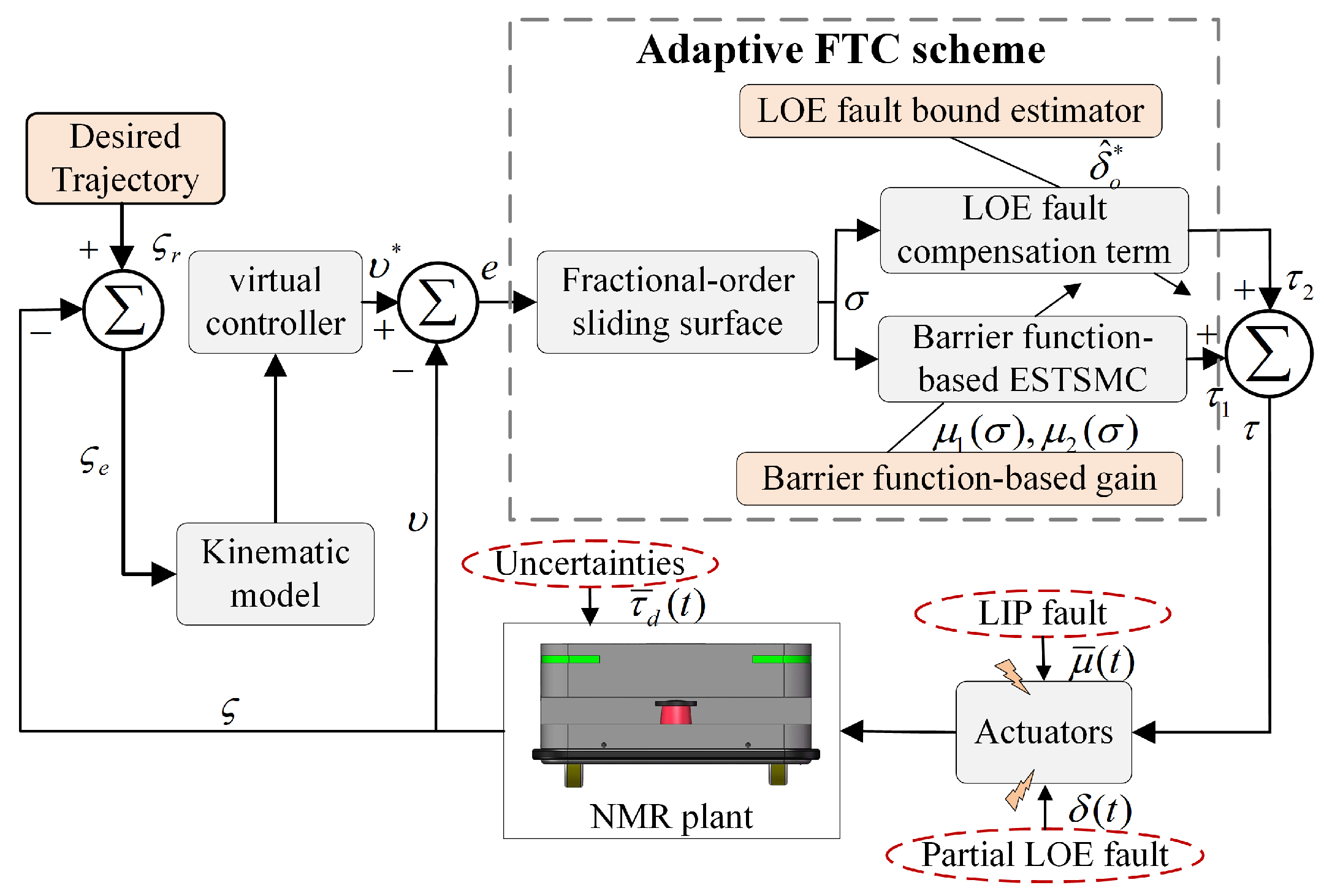
3. Methodology
4. Verification Examples
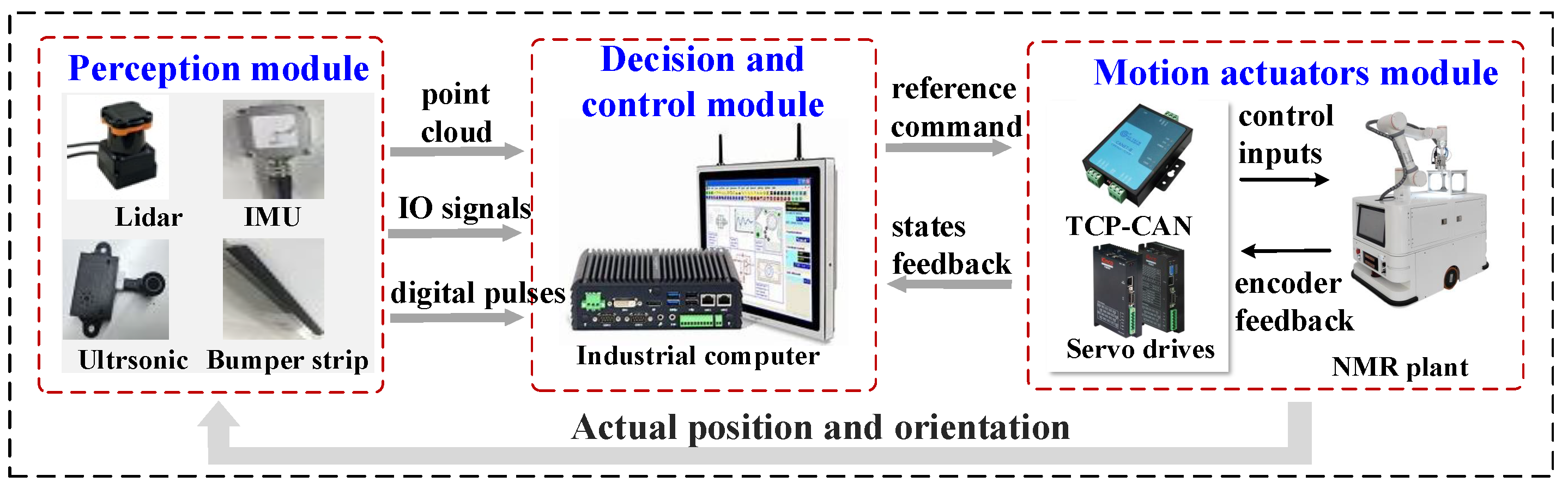
4.1. Parameter Determination and Experimental Setup
4.2. Implementation of the Proposed Controller and Comparison Methods
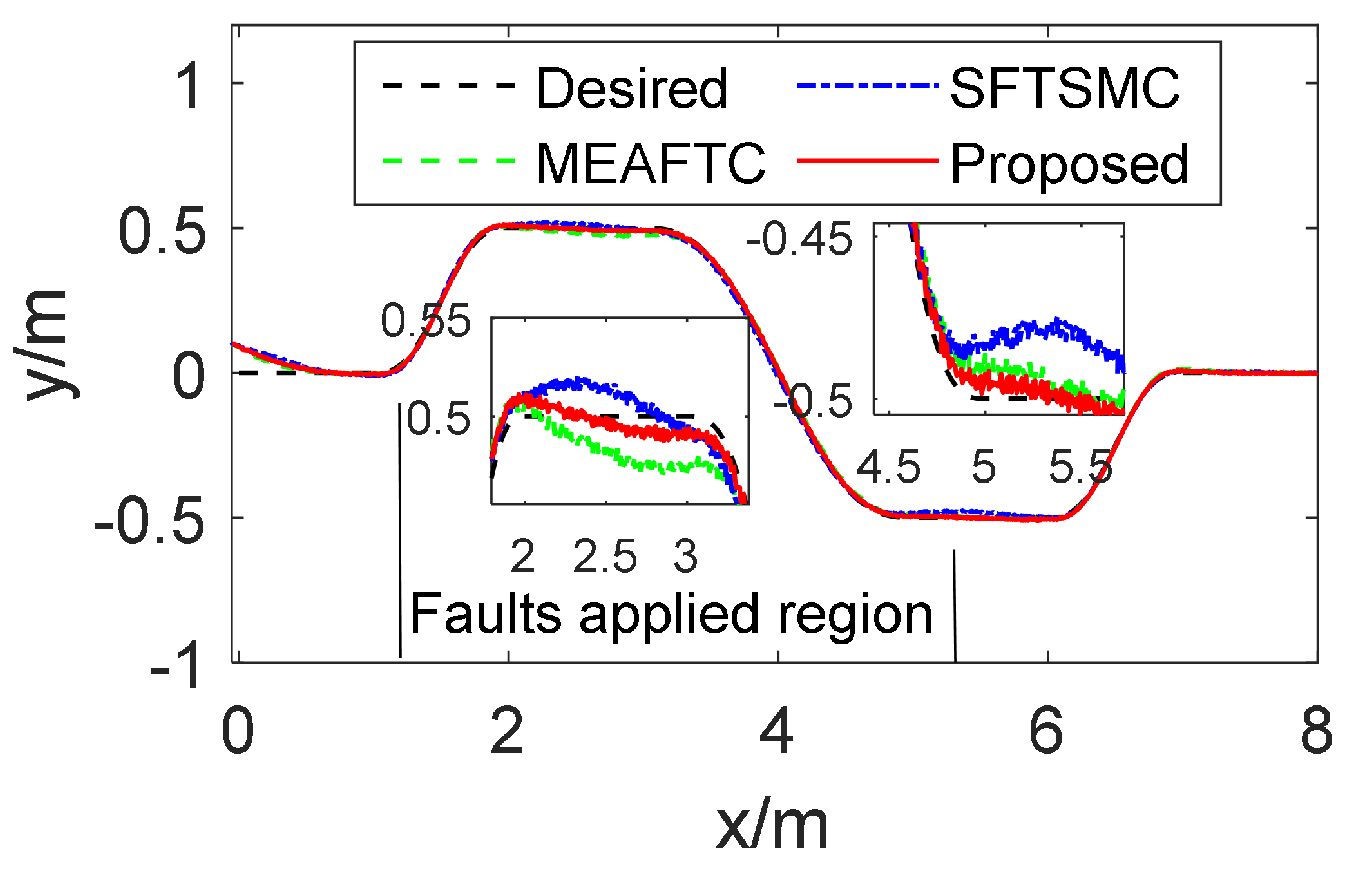
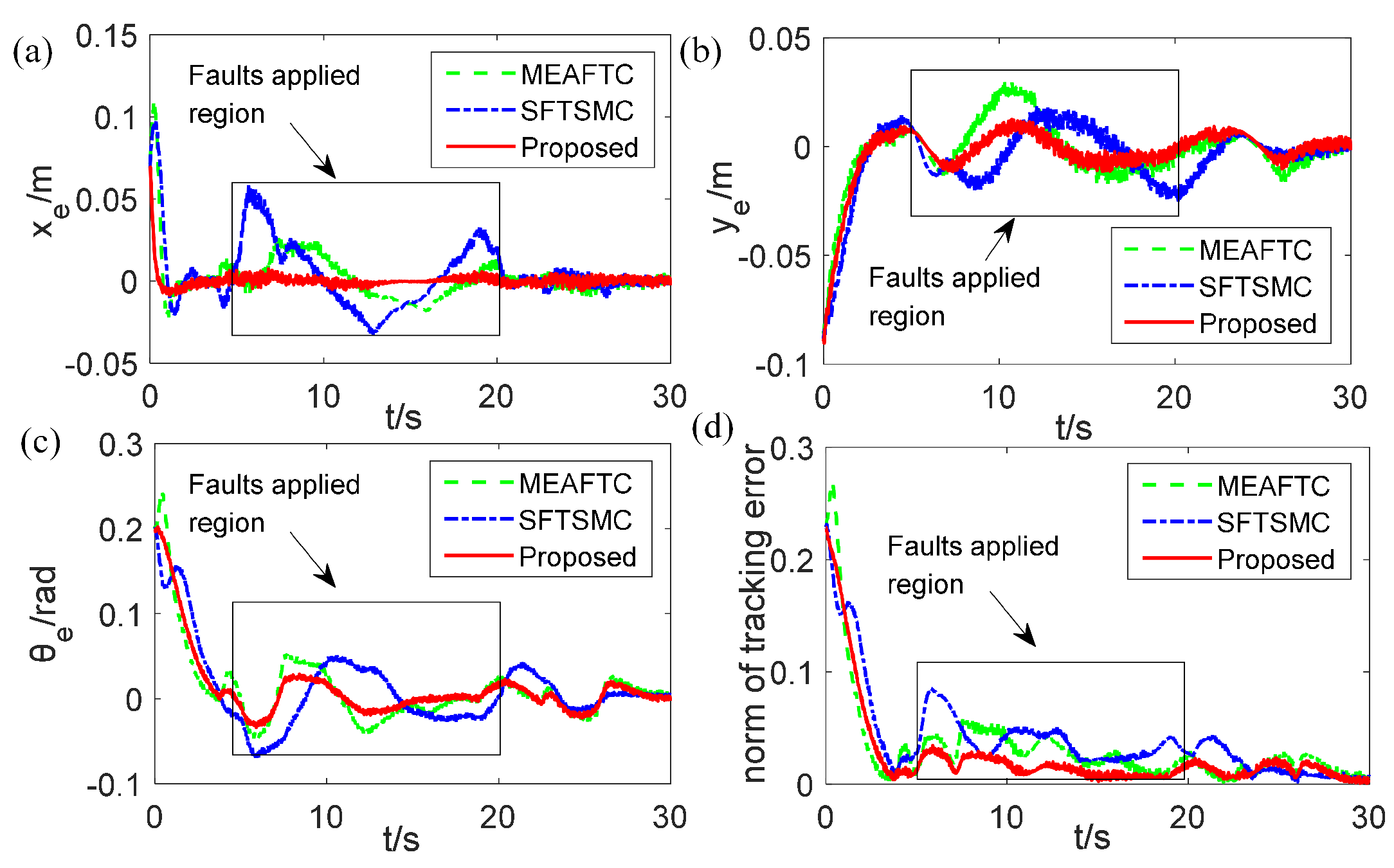
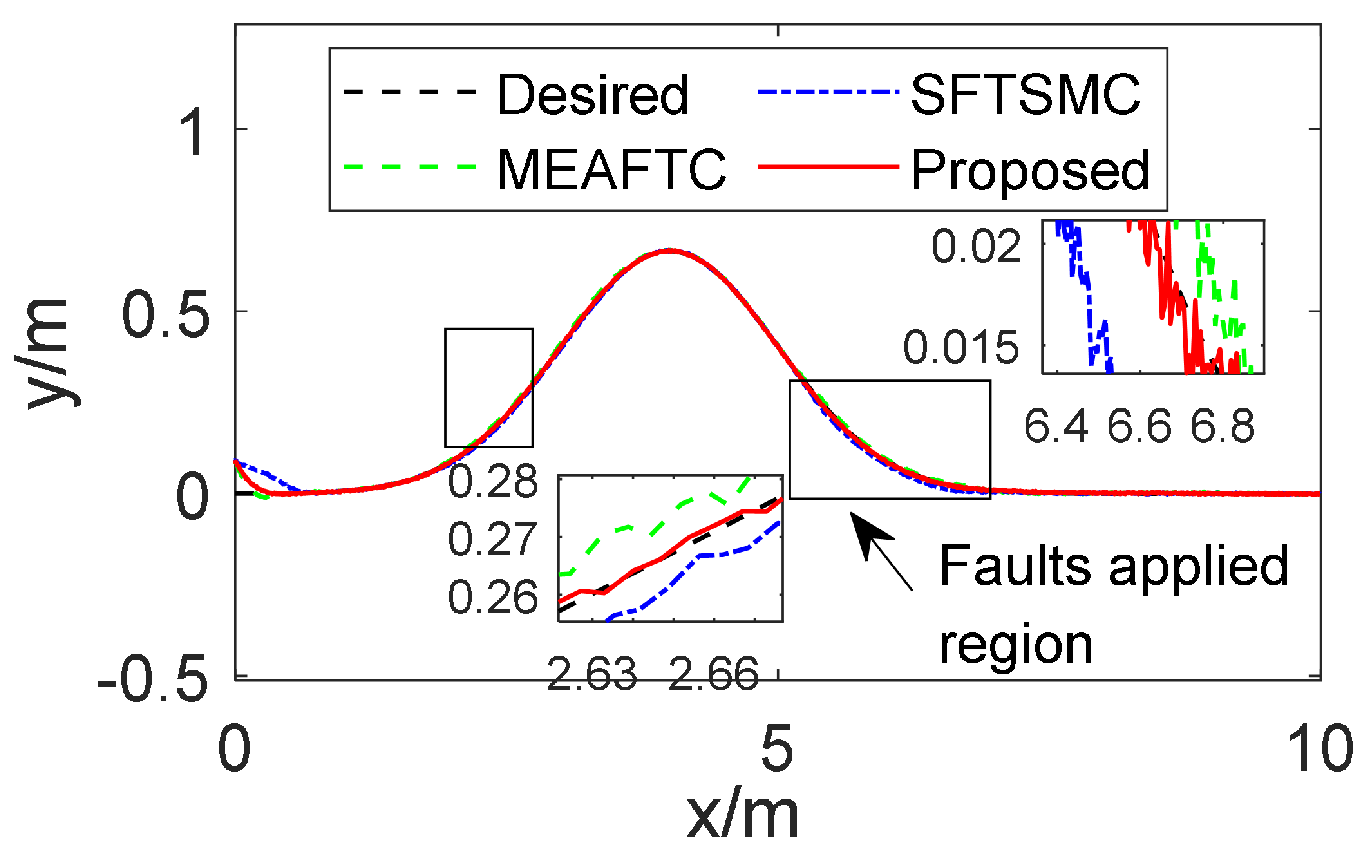
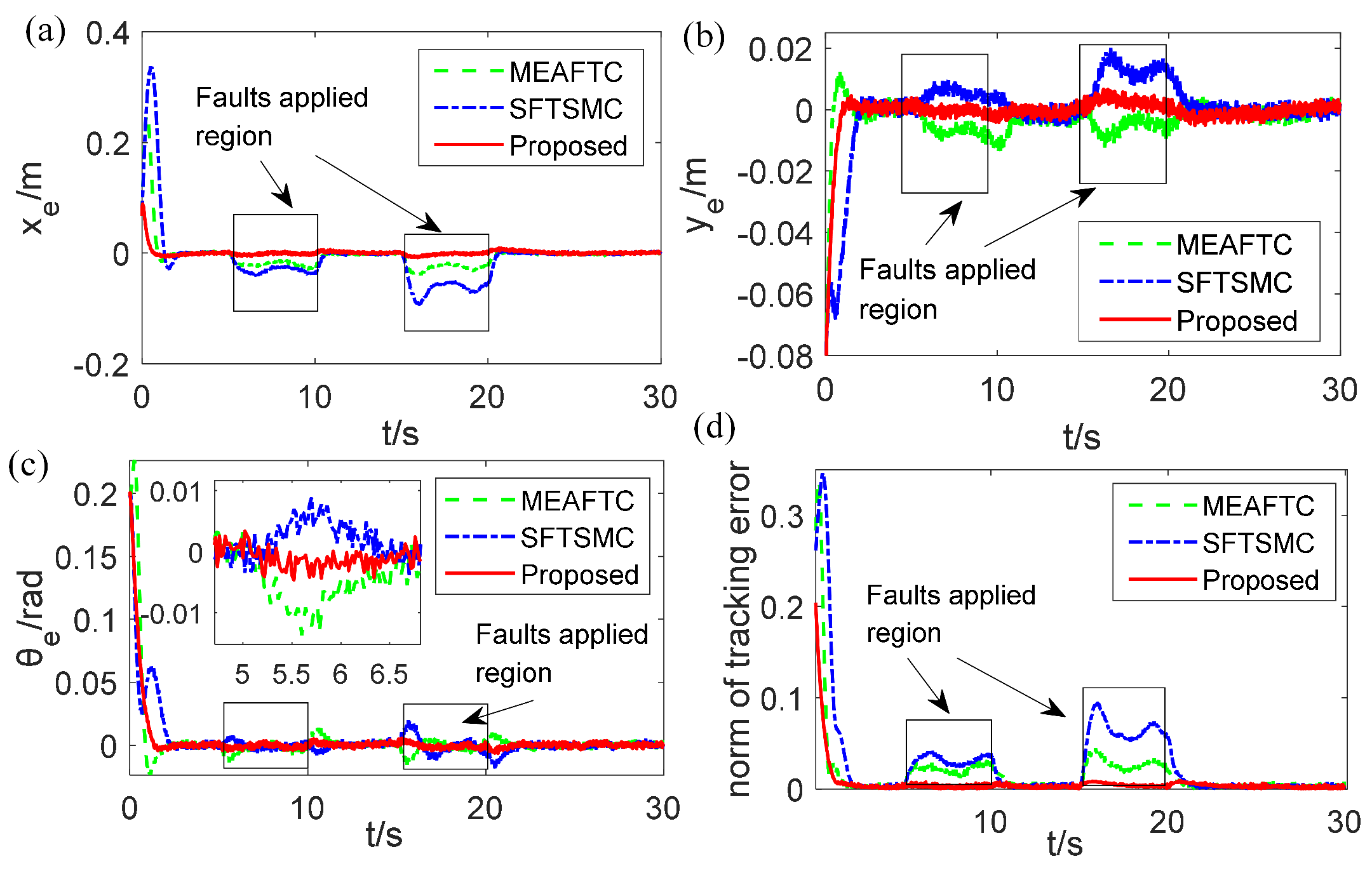
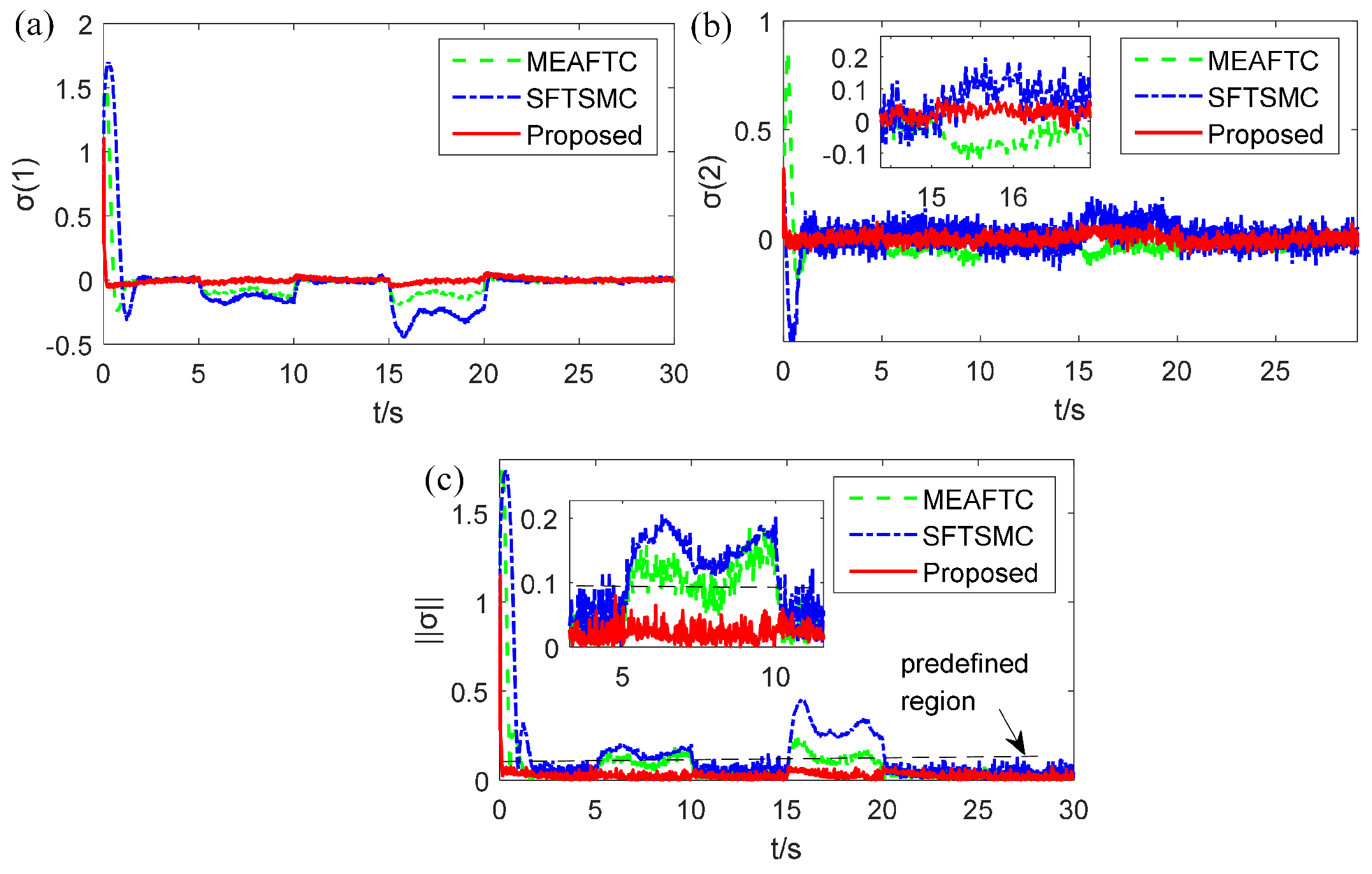
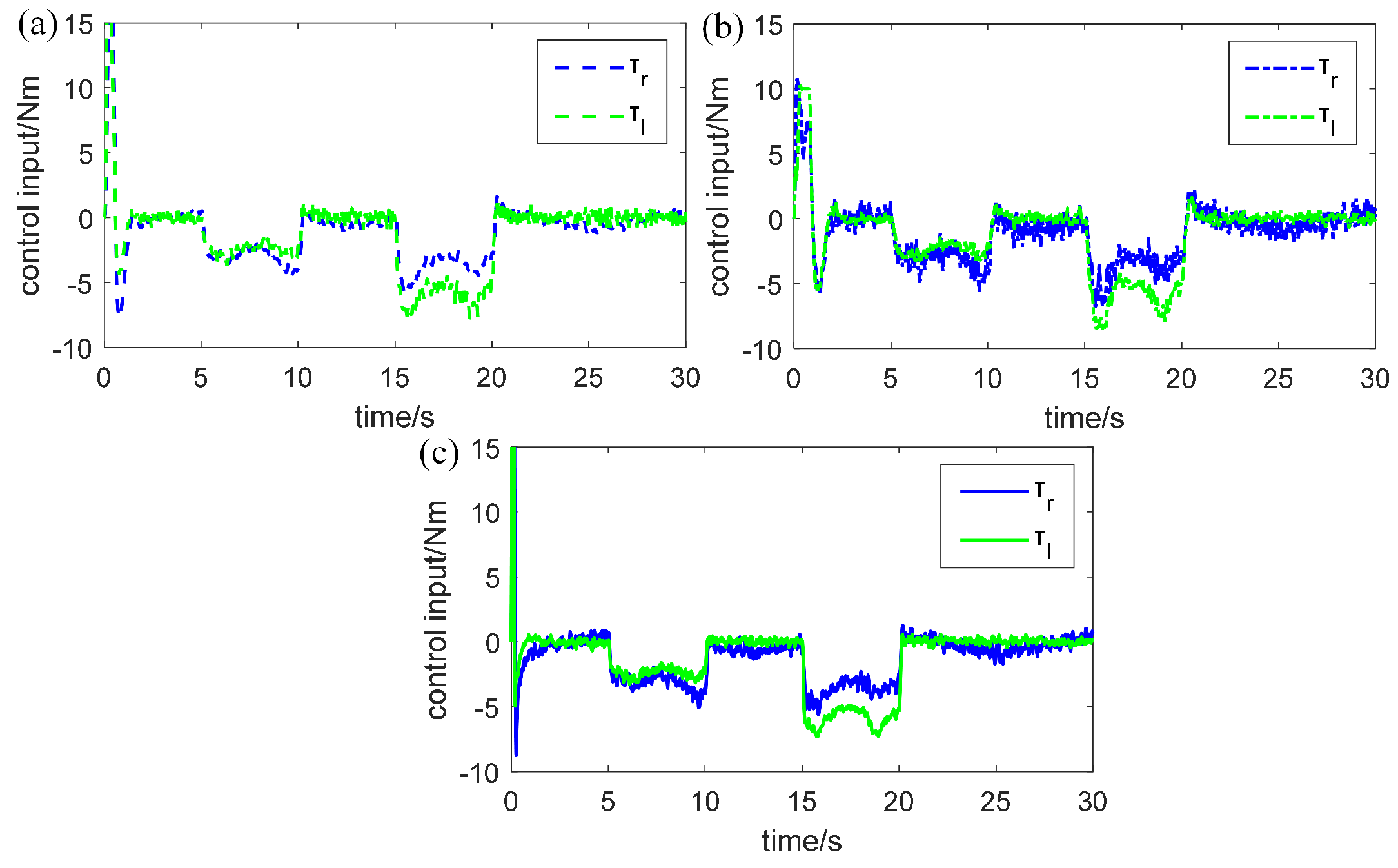
4.3. Results
- (1)
- The SFTSMC scheme has the largest MAX errors, which means that it cannot effectively handle the transient errors due to that MAX focuses on the worst-case deviation. In contrast, our proposed controller achieves a great reduction in MAX error in both case 1 and case 2, and the MAX error of is less than 0.1.
- (2)
- The RMSE indicator shows that the tracking state of our method has much less average deviation in case 1 and case 2 (i.e., time-varying or step-like additive faults), which reflects smoother trajectory tracking, since that RMSE emphasizes larger errors and provides a measure of average performance.
- (3)
- The MAE of the proposed method can be improved by more than 80% compared to SFTSMC in case 1 and more than 78.2 % in case 2. This indicates that the proposed controller can quickly reduce the error that deviates from the actual values on average, thereby effectively suppressing time-varying LIP or step-like faults.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| the state vector of pose, velocity and acceleration of the NMR | |
| , | the position, the orientation of NMR |
| , | the desired state vector, the tracking error vector |
| , | position tracking error, the orientation tracking error of NMR |
| , | the symmetric positive definite inertia matrix, centripetal and Coriolis matrix |
| , , A | surface friction, input transformation matrix, constraints matrix |
| transformation matrix of M, C, B, full rank Jacobian transformation matrix | |
| the designed controller, the faulty control input | |
| control inputs of the right motor, control inputs of the left motor |
Appendix A
Appendix B
References
- Jiang, L.; Wang, S.; Xie, Y.; Xie, S.; Zheng, S.; Meng, J.; Ding, H. Decoupled fractional supertwisting stabilization of interconnected mobile robot under harsh terrain conditions. IEEE Trans. Ind. Electron. 2022, 69, 8178–8189. [Google Scholar] [CrossRef]
- Ao, W.; Zhang, L.; Zhang, H.; Li, Z.; Huang, G. Structure design and event-triggered control of a modular omnidirectional mobile chassis of life support robotics. Fractal Fract. 2023, 7, 121. [Google Scholar] [CrossRef]
- Gupta, M.; Kumar, S.; Behera, L.; Subramanian, V.K. A novel vision-based tracking algorithm for a human-following mobile robot. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1415–1427. [Google Scholar] [CrossRef]
- Labbadi, M.; Boubaker, S.; Djemai, M.; Mekni, S.K.; Bekrar, A. Fixed-time fractional-order global sliding mode control for nonholonomic mobile robot systems under external disturbances. Fractal Fract. 2022, 6, 177. [Google Scholar] [CrossRef]
- Jia, F.; Huang, J.; He, X. Predefined-time fault-tolerant control for a class of nonlinear systems with actuator faults and unknown mismatched disturbances. IEEE Trans. Autom. Sci. Eng. 2024, 21, 3801–3815. [Google Scholar] [CrossRef]
- Kamel, M.; Yu, X.; Zhang, Y. Fault-tolerant cooperative control design of multiple wheeled mobile robots. IEEE Trans. Control Syst. Technol. 2018, 26, 756–764. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite time fault tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control. IEEE Trans. Cybern. 2016, 47, 1681–1693. [Google Scholar] [CrossRef]
- Guo, B.; Chen, Y. Robust adaptive fault-tolerant control of fourwheel independently actuated electric vehicles. IEEE Trans. Ind. Informat. 2020, 16, 2882–2894. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, S.; Zhang, X. Adaptive distributed fault-tolerant control for underactuated surface vehicles with bridge-to-bridge event-triggered mechanism. Ocean Eng. 2022, 262, 112205. [Google Scholar] [CrossRef]
- Wu, F.; Liu, Y.; Fang, Y.; Liu, L.; Lei, Z. Fault estimation and active fault-tolerant control for a class of nonlinear systems with actuator and sensor faults based on unknown input iterative learning. Asian J. Control 2024, 26, 376–392. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, X.; Li, J.; Ma, F.; Zhang, Z.; Brunauer, G.; Steyskal, F. Fault estimation and H∞ fuzzy active fault-tolerant control design for ship steering autopilot subject to actuator and sensor faults. IEEE Sens. J. 2023, 23, 28110–28119. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, Y.; Guo, G. Finite-time fault-tolerant prescribed performance control of connected vehicles with actuator saturation. IEEE Trans. Veh. Technol. 2022, 72, 1438–1448. [Google Scholar] [CrossRef]
- Wu, K.; Hu, J.; Ding, Z.; Arvin, F. Finite-time fault-tolerant formation control for distributed multi-vehicle networks with bearing measurements. IEEE Trans. Autom. Sci. Eng. 2023, 21, 1346–1357. [Google Scholar] [CrossRef]
- Gong, J.; Jiang, B.; Ma, Y.; Mao, Z. Distributed adaptive fault-tolerant formation—Containment control with prescribed performance for heterogeneous multiagent systems. IEEE Trans. Cybern. 2022, 53, 7787–7799. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Yang, G. Backstepping adaptive fuzzy control of uncertain nonlinear systems against actuator faults. J. Control Theory Appl. 2009, 7, 248–256. [Google Scholar] [CrossRef]
- Xiao, B.; Hu, Q.; Shi, P. Attitude stabilization of spacecraft under actuator saturation and partial loss of control effectiveness. IEEE Trans. Control Syst. Technol. 2013, 21, 2251–2263. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, Y.; Jiang, L.; Li, G.; Meng, J.; Huang, Y. Fault-tolerant dynamic control of a four-wheel redundantly-actuated mobile robot. IEEE Access 2019, 7, 157909–157921. [Google Scholar] [CrossRef]
- Singh, P.; Nandanwar, A.; Behera, L.; Verma, N.K.; Nahavandi, S. Uncertainty compensator and fault estimator-based exponential supertwisting sliding-mode controller for a mobile robot. IEEE Trans. Cybern. 2021, 52, 11963–11976. [Google Scholar] [CrossRef]
- Ijaz, S.; Galea, M.; Hamayun, M.T.; Ijaz, H.; Javaid, U. A new output integral sliding mode fault-tolerant control and fault estimation scheme for uncertain systems. IEEE Trans. Autom. Sci. Eng. 2024, 21, 4214–4225. [Google Scholar] [CrossRef]
- Rotondo, D.; Puig, V.; Nejjari, F.; Romera, J. A fault-hiding approach for the switching quasi-LPV fault-tolerant control of a four-wheeled omnidirectional mobile robot. IEEE Trans. Ind. Electron. 2014, 62, 3932–3944. [Google Scholar] [CrossRef]
- Yang, H.; Yin, S.; Kaynak, O. Neural network-based adaptive fault-tolerant control for Markovian jump systems with nonlinearity and actuator faults. IEEE Trans. Syst., Man, Cybern., Syst. 2020, 51, 3687–3698. [Google Scholar] [CrossRef]
- Diao, S.; Sun, W.; Su, S.F.; Xia, J. Adaptive fuzzy event-triggered control for single-link flexible-joint robots with actuator failures. IEEE Trans. Cybern. 2021, 52, 7231–7241. [Google Scholar] [CrossRef] [PubMed]
- Argha, A.; Su, S.W.; Celler, B.G. Static output feedback fault tolerant control using control allocation scheme. Int. J. Robust Nonlinear Control 2019, 29, 98–116. [Google Scholar] [CrossRef]
- Qin, M.; Dian, S.; Guo, B. Fractional-order SMC controller for mobile robot trajectory tracking under actuator fault. Syst. Sci. Control Eng. 2022, 10, 312–324. [Google Scholar] [CrossRef]
- Ma, Y.; Jiang, B.; Cocquempot, V. Modeling and adaptive fault compensation for two physically linked 2WD mobile robots. IEEE/ASME Trans. Mech. 2021, 26, 1161–1171. [Google Scholar] [CrossRef]
- Ma, Y.; Cocquempot, V.; El Najjar, M.E.; Jiang, B. Adaptive compensation of multiple actuator faults for two physically linked 2WD robots. IEEE Trans. Robot. 2017, 34, 248–255. [Google Scholar] [CrossRef]
- Shen, Z.; Ma, Y.; Song, Y. Robust adaptive fault-tolerant control of mobile robots with varying center of mass. IEEE Trans. Ind. Electron. 2017, 65, 2419–2428. [Google Scholar] [CrossRef]
- Xiao, B.; Cao, L.; Xu, S.; Liu, L. Robust tracking control of robot manipulators with actuator faults and joint velocity measurement uncertainty. IEEE/ASME Trans. Mech. 2020, 25, 1354–1365. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, J.; Li, H.; Liu, J.; Tian, D. Adaptive sliding mode current control with sliding mode disturbance observer for PMSM drives. ISA Trans. 2019, 88, 113–126. [Google Scholar] [CrossRef]
- Song, Z.; Liu, J.; Liu, Y.; Hu, Y.; Fang, F. Fault-tolerant control of floating wind turbine with switched adaptive sliding mode controller. IEEE Trans. Autom. Sci. Eng. 2024, 21, 3705–3718. [Google Scholar] [CrossRef]
- Relaño, C.; Muñoz, J.; Monje, C.A.; Martínez, S.; González, D. Modeling and control of a soft robotic arm based on a fractional order control approach. Fractal Fract. 2022, 7, 8. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, X.; Meng, W.; Zheng, S.; Jiang, L.; Meng, J.; Wang, S. Coupled fractional-order sliding mode control and obstacle avoidance of a four-wheeled steerable mobile robot. ISA Trans. 2021, 108, 282–294. [Google Scholar] [CrossRef] [PubMed]
- Fallaha, C.J.; Saad, M.; Kanaan, H.Y.; Al-Haddad, K. Sliding-mode robot control with exponential reaching law. IEEE Trans. Ind. Electron. 2010, 58, 600–610. [Google Scholar] [CrossRef]
- Saied, H.; Chemori, A.; Bouri, M.; Rafei, M.E.; Francis, C. Feedforward super-twisting sliding mode control for robotic manipulators: Application to PKMs. IEEE Trans. Robot. 2023, 39, 3167–3184. [Google Scholar] [CrossRef]
- Obeid, H.; Laghrouche, S.; Fridman, L.; Chitour, Y.; Harmouche, M. Barrier function-based adaptive super-twisting controller. IEEE Trans. Autom. Control 2020, 65, 4928–4933. [Google Scholar] [CrossRef]
- Mendoza-Avila, J.J.; Moreno, A.; Fridman, L.M. Continuous Twisting Algorithm for Third-Order Systems. IEEE Trans. Autom. Control 2020, 65, 2814–2825. [Google Scholar] [CrossRef]
- Xie, Y.; Tang, X.; Song, B.; Zhou, X.; Guo, Y. Data-driven adaptive fractional order PI control for PMSM servo system with measurement noise and data dropouts. ISA Trans. 2018, 75, 172–188. [Google Scholar] [CrossRef]
- Obeid, H.; Fridman, L.M.; Laghrouche, S.; Harmouche, M. Barrier function-based adaptive sliding mode control. Automatica 2018, 93, 540–544. [Google Scholar] [CrossRef]
- Chen, J.; Wu, C.; Yu, G.; Narang, D.; Wang, Y. Path following of wheeled mobile robots using online-optimization-based guidance vector field. IEEE/ASME Trans. Mech. 2021, 26, 1737–1744. [Google Scholar] [CrossRef]
- Fierro, R.; Lewis, F.L. Control of a nonholonomic mobile robot using neural networks. IEEE Trans. Neural Netw. 1998, 9, 589–600. [Google Scholar] [CrossRef]
- Li, J.W. Adaptive tracking and stabilization of nonholonomic mobile robots with input saturation. IEEE Trans. Autom. Control 2021, 67, 6173–6179. [Google Scholar] [CrossRef]
- Nagesh, I.; Edwards, C. A multivariable super-twisting sliding mode approach. Automatica 2014, 50, 984–988. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, Y.; He, W.; Qiao, H.; Ji, H. Adaptive-neural-network-based trajectory tracking control for a nonholonomic wheeled mobile robot with velocity constraints. IEEE Trans. Ind. Electron. 2021, 68, 5057–5067. [Google Scholar] [CrossRef]
- Wu, H.; Wang, S.; Xie, Y.; Li, H.; Zheng, S.; Jiang, L. Adaptive abrupt disturbance rejection tracking control for wheeled mobile robots. IEEE Robot. Autom. Lett. 2024, 9, 7787–7794. [Google Scholar] [CrossRef]




| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Max speed | 1.5 m/s | Robot length | 0.8 m |
| RAM of PC | 8 G | Robot width | 0.52 m |
| Encoder | 2500 ppr | Total mass m | 80 kg |
| Laser sweep distance | 30 m | Wheel diameter | 0.16 m |
| Signals | Errors | Schemes | MAX () | RMSE () | MAE () |
|---|---|---|---|---|---|
| case 1: simultaneously partial LOE and time- varying LIP faults | MEAFTC | 26.1 | 9.9 | 7.4 | |
| SFTSMC | 55.7 | 16.1 | 11.6 | ||
| Proposed | 7.3 | 2.0 | 1.6 | ||
| MEAFTC | 29.7 | 11.1 | 8.6 | ||
| SFTSMC | 25.3 | 10.0 | 8.5 | ||
| Proposed | 12.5 | 5.5 | 4.8 | ||
| MEAFTC | 52.4 | 21.8 | 17.5 | ||
| SFTSMC | 68.9 | 26.9 | 21.7 | ||
| Proposed | 31.6 | 13.2 | 10.7 | ||
| MEAFTC | 230.4 | 47.3 | 62.1 | ||
| SFTSMC | 496.4 | 94.5 | 122.4 | ||
| Proposed | 81.4 | 15.8 | 31.5 | ||
| case 2: simultaneously partial LOE and unknown bias LIP faults | MEAFTC | 42.3 | 11.7 | 10.3 | |
| SFTSMC | 92.7 | 26.0 | 20.0 | ||
| Proposed | 9.1 | 2.8 | 2.1 | ||
| MEAFTC | 14.3 | 3.5 | 3.9 | ||
| SFTSMC | 20.1 | 5.5 | 4.5 | ||
| Proposed | 6.6 | 2.1 | 1.6 | ||
| MEAFTC | 15.6 | 3.9 | 2.8 | ||
| SFTSMC | 21.0 | 4.5 | 3.0 | ||
| Proposed | 6.4 | 1.8 | 1.5 | ||
| MEAFTC | 238.5 | 53.1 | 62.2 | ||
| SFTSMC | 456.8 | 107.7 | 117.7 | ||
| Proposed | 75.2 | 15.4 | 25.6 |
| SFTSMC | MEAFTC | Proposed | |
|---|---|---|---|
| MAX of in case 1 | 0% | 53.6% | 83.6% |
| RMSE of in case 1 | 0% | 49.9% | 83.3% |
| MAE of in case 1 | 0% | 49.3% | 74.3% |
| MAX of in case 2 | 0% | 47.8% | 83.5% |
| RMSE of in case 2 | 0% | 50.7% | 85.7% |
| MAE of in case 2 | 0% | 47.2% | 78.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Wang, S.; Xie, Y.; Li, H. Adaptive Fault-Tolerant Control of Mobile Robots with Fractional-Order Exponential Super-Twisting Sliding Mode. Fractal Fract. 2024, 8, 612. https://doi.org/10.3390/fractalfract8100612
Wu H, Wang S, Xie Y, Li H. Adaptive Fault-Tolerant Control of Mobile Robots with Fractional-Order Exponential Super-Twisting Sliding Mode. Fractal and Fractional. 2024; 8(10):612. https://doi.org/10.3390/fractalfract8100612
Chicago/Turabian StyleWu, Hao, Shuting Wang, Yuanlong Xie, and Hu Li. 2024. "Adaptive Fault-Tolerant Control of Mobile Robots with Fractional-Order Exponential Super-Twisting Sliding Mode" Fractal and Fractional 8, no. 10: 612. https://doi.org/10.3390/fractalfract8100612
APA StyleWu, H., Wang, S., Xie, Y., & Li, H. (2024). Adaptive Fault-Tolerant Control of Mobile Robots with Fractional-Order Exponential Super-Twisting Sliding Mode. Fractal and Fractional, 8(10), 612. https://doi.org/10.3390/fractalfract8100612







