A Fractional-Order Model Predictive Control Strategy with Takagi–Sugeno Fuzzy Optimization for Vehicle Active Suspension System
Abstract
1. Introduction
2. Design of a Fractional-Order MPC Controller for Active Suspension
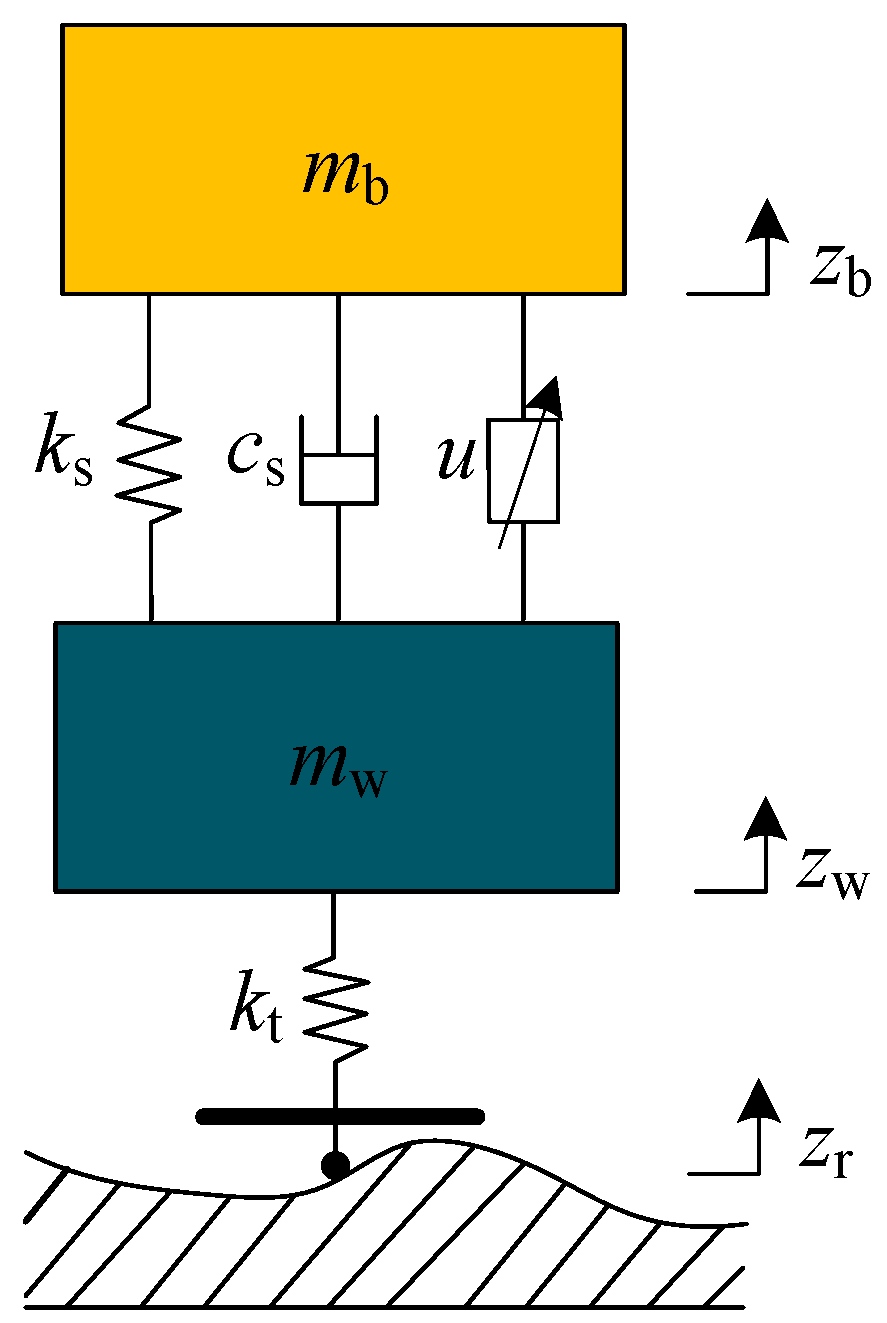
2.1. Dynamics Modeling for Active Suspension
2.2. Predictive Model of MPC
2.3. Fractional Objective Function of MPC
3. Fractional-Order MPC Strategy with Takagi–Sugeno Fuzzy Optimization
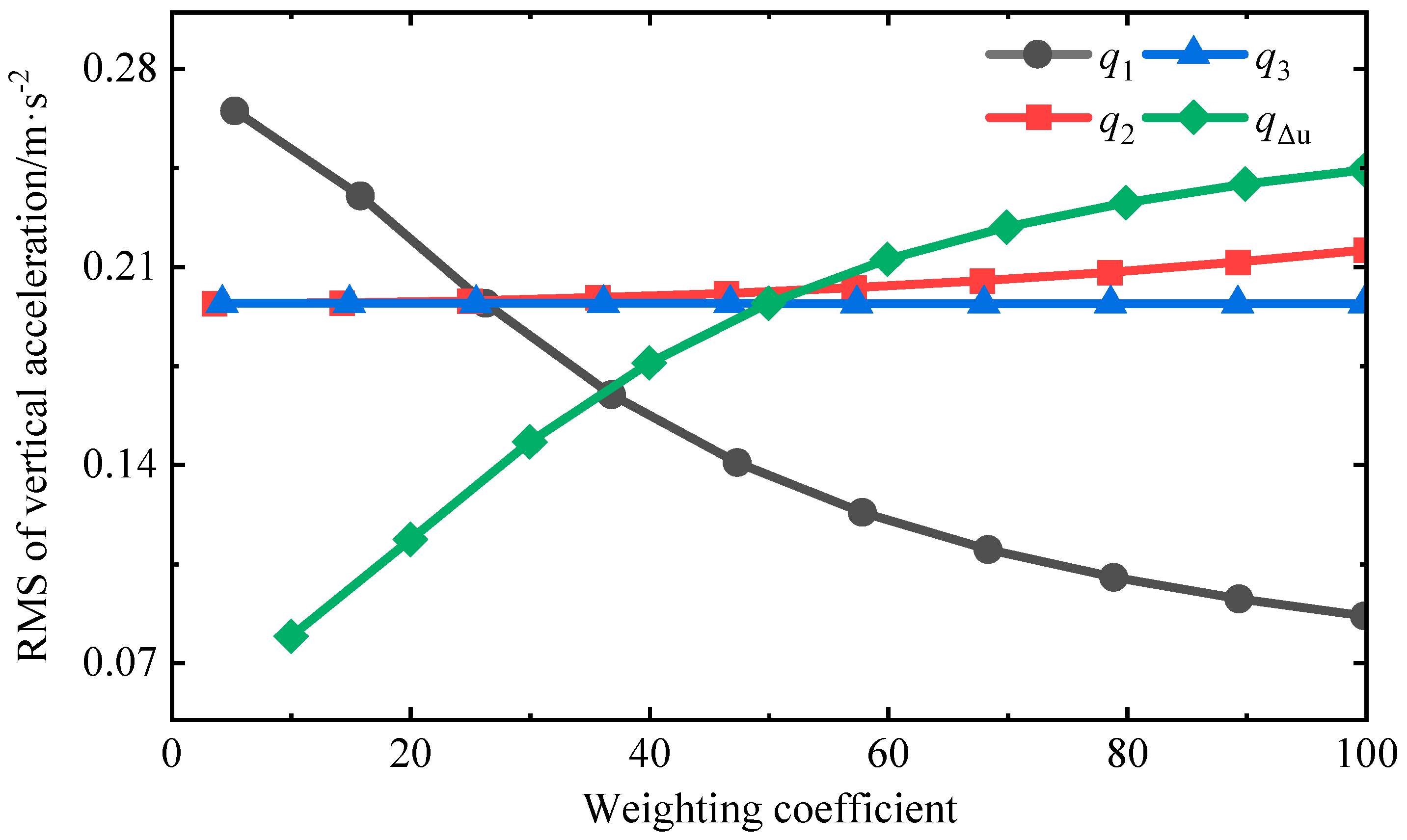
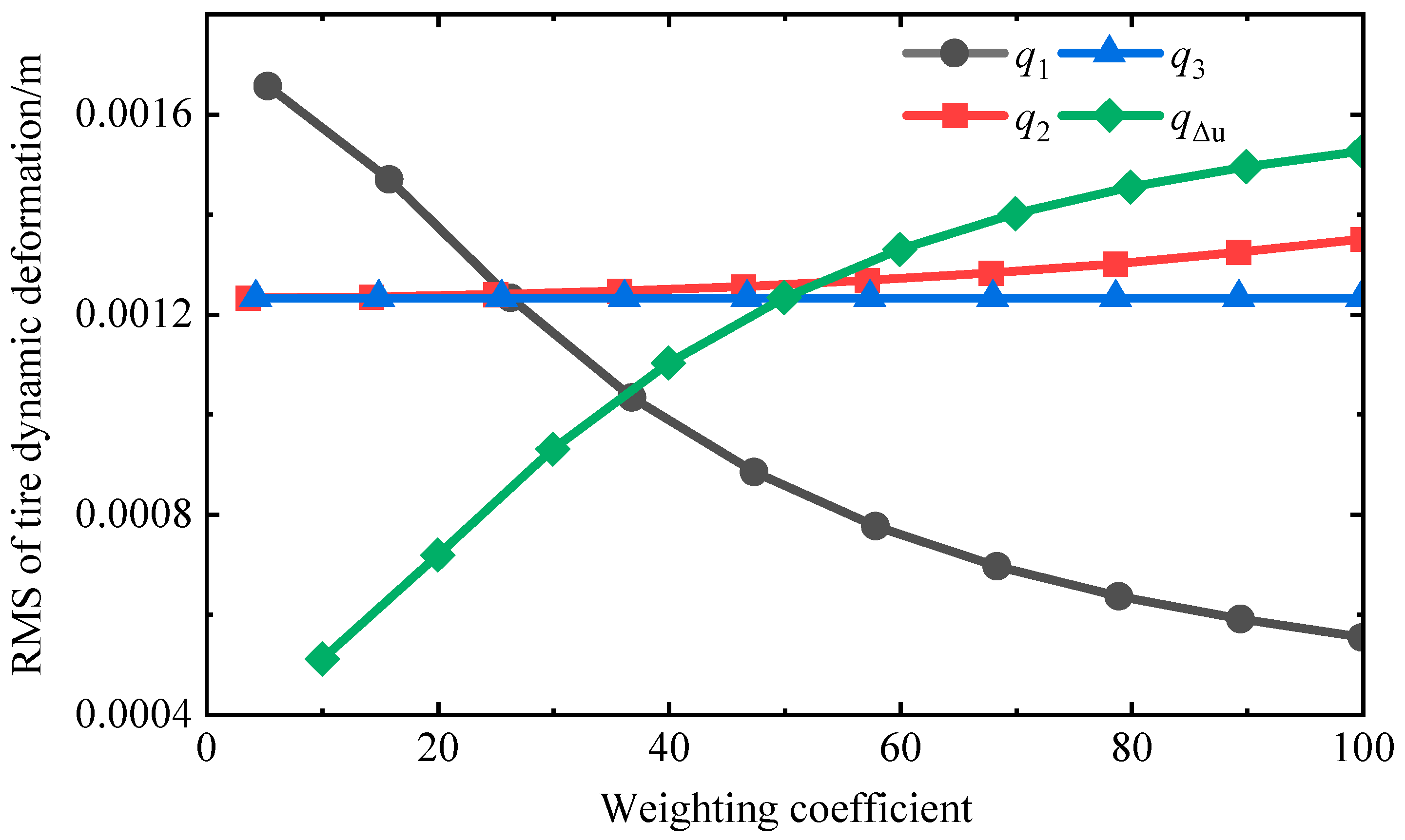
3.1. The Effect of Different Weights on Suspension Performance
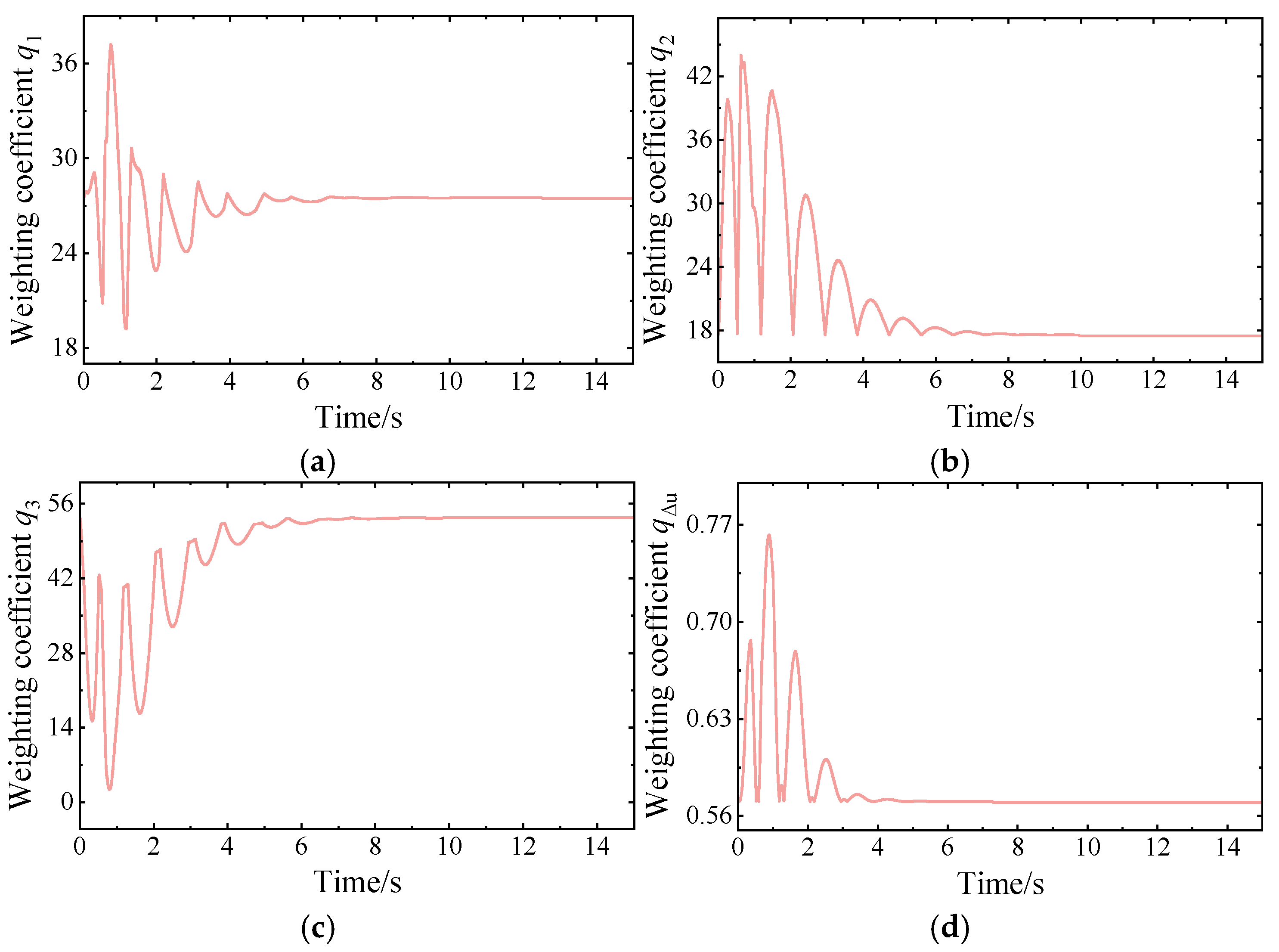
3.2. Establishment of Takagi–Sugeno Fuzzy Optimization
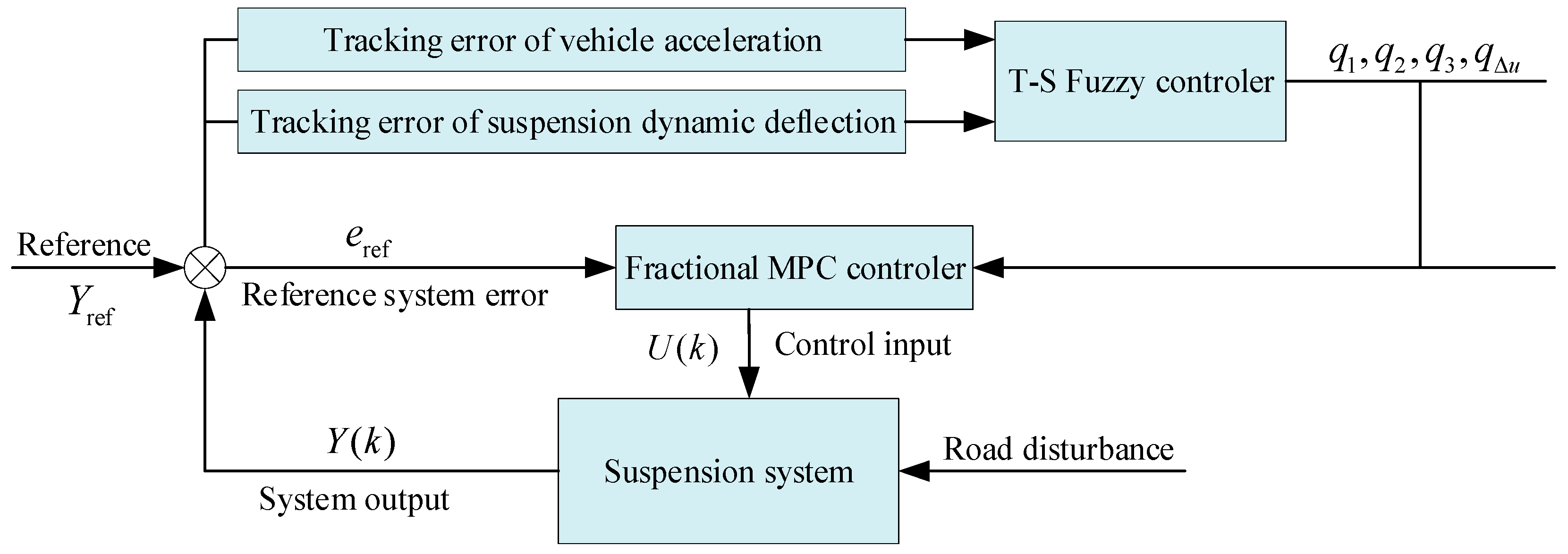
3.3. Design of T–SFO MPC
4. Simulation Result
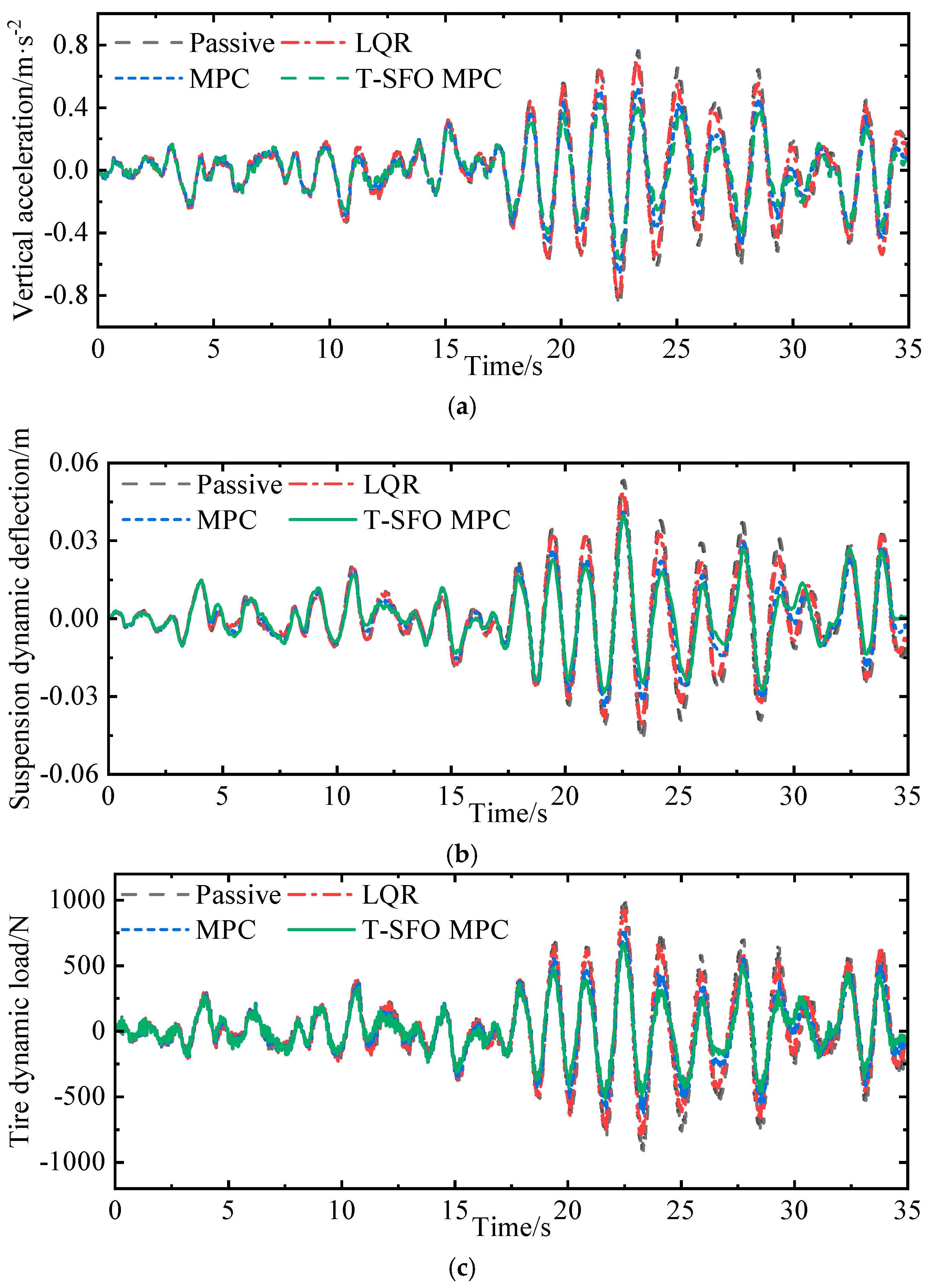
4.1. Random Terrain Road
4.2. Bump Road
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Soliman, A.M.A.; Kaldas, M.M.S. Semi-active suspension systems from research to mass-market—A review. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1005–1023. [Google Scholar] [CrossRef]
- Liu, Q.J.; Chen, W.; Hu, H.S.; Hu, G.L.; Zhu, Q.Y. Effect of magnetorheological damper parameters on dynamic responses of a full-vehicle suspension system. Int. J. Appl. Electromagn. Mech. 2020, 63, 483–503. [Google Scholar] [CrossRef]
- Theunissen, J.; Tota, A.; Gruber, P.; Dhaens, M.; Sorniotti, A. Preview-based techniques for vehicle suspension control: A state-of-the-art review. Annu. Rev. Control 2021, 51, 206–235. [Google Scholar] [CrossRef]
- Rana, R.S.; Dipak, M.A. Two-degree of freedom-based control model for active suspension system to mitigate the nonlinear disturbance. J. Circuits Syst. Comput. 2023, 32, 2350312. [Google Scholar] [CrossRef]
- Al-Ashmori, M.; Wang, X. A systematic literature review of various control techniques for active seat suspension systems. Appl. Sci. 2020, 10, 1148. [Google Scholar] [CrossRef]
- Zhao, Z.K.; Wang, C.W.; Zhao, J.Q.; Du, W. LQR force command planning–based sliding mode control for active suspension system. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2024, 238, 373–385. [Google Scholar] [CrossRef]
- Bai, R.; Wang, H.B. Robust optimal control for the vehicle suspension system with uncertainties. IEEE Trans. Cybern. 2021, 52, 9263–9273. [Google Scholar] [CrossRef]
- Liu, Y.J.; Chen, H. Adaptive sliding mode control for uncertain active suspension systems with prescribed performance. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6414–6422. [Google Scholar] [CrossRef]
- Wang, C.; Cui, X.X.; Zhao, S.J.; Zhou, X.R.; Song, Y.Q.; Wang, Y.; Guo, K.H. Enhancing vehicle ride comfort through deep reinforcement learning with expert-guided soft-hard constraints and system characteristic considerations. Adv. Eng. Inform. 2024, 59, 102328. [Google Scholar] [CrossRef]
- Lee, D.; Jin, S.; Lee, C. Deep reinforcement learning of semi-active suspension controller for vehicle ride comfort. IEEE Trans. Veh. Technol. 2022, 72, 327–339. [Google Scholar] [CrossRef]
- Papadimitrakis, M.; Alexandridis, A. Active vehicle suspension control using road preview model predictive control and radial basis function networks. Appl. Soft Comput. 2022, 120, 108646. [Google Scholar] [CrossRef]
- Zhang, N.N.; Yang, S.; Wu, G.Y.; Ding, H.T.; Zhang, Z.; Guo, K.H. Fast distributed model predictive control method for active suspension systems. Sensors 2023, 23, 3357. [Google Scholar] [CrossRef] [PubMed]
- Ricco, M.; Alshawi, A.; Gruber, P.; Dhaens, M.; Sorniotti, A. Nonlinear model predictive control for yaw rate and body motion control through semi-active and active suspensions. Veh. Syst. Dyn. 2024, 62, 1587–1620. [Google Scholar] [CrossRef]
- Li, W.; Liang, H.J.; Xia, D.B.; Fu, J.; Yu, M. Explicit model predictive control of magnetorheological suspension for all-terrain vehicles with road preview. Smart Mater. Struct. 2024, 33, 035037. [Google Scholar] [CrossRef]
- Yaghini, H.H.; Kharrati, H.; Rahimi, A. Linear time-varying fractional-order model predictive attitude control for satellite using two reaction wheels. Aerosp. Sci. Technol. 2024, 145, 108901. [Google Scholar] [CrossRef]
- Yang, T.; Li, P.; Li, Q.; Li, Z. Active suspension control strategy for vehicles based on road surface recognition. Nonlinear Dyn. 2024, 112, 11043–11065. [Google Scholar] [CrossRef]
- Zhang, B.; Zong, C.; Chen, G.; Zhang, B. Electrical vehicle path tracking based model predictive control with a Laguerre function and exponential weight. IEEE Access 2019, 7, 17082–17097. [Google Scholar] [CrossRef]
- Batta, N.A.; Daniel, P.D. Model predictive control of a multi-mode suspension system using preview information and weight optimization. J. Dyn. Syst. Meas. Control 2023, 145, 065001. [Google Scholar] [CrossRef]
- Sun, X.; Wu, M.; Yin, C.; Wang, S. Model predictive thrust force control for linear motor actuator used in active suspension. IEEE Trans. Energy Convers. 2021, 36, 3063–3072. [Google Scholar] [CrossRef]
- Dogruer, C.U. Constrained model predictive control of a vehicle suspension using Laguerre polynomials. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1253–1268. [Google Scholar] [CrossRef]
- Hsiao, C.Y.; Wang, Y.H. Evaluation of ride comfort for active suspension system based on self-tuning fuzzy sliding mode control. Int. J. Control Autom. Syst. 2022, 20, 1131–1141. [Google Scholar] [CrossRef]
- Dehghan, M.; Fateh, M.M.; Ghalehnoie, M. A fuzzy-supervised impedance control for an active suspension system. J. Vib. Eng. Technol. 2023, 11, 3257–3266. [Google Scholar] [CrossRef]
- Kim, J.; Lee, T.; Kim, C.J.; Yi, K. Model predictive control of a semi-active suspension with a shift delay compensation using preview road information. Control Eng. Pract. 2023, 137, 105584. [Google Scholar] [CrossRef]
- Mohanty, D.; Panda, S. Modified salp swarm algorithm-optimized fractional-order adaptive fuzzy PID controller for frequency regulation of hybrid power system with electric vehicle. J. Control Autom. Electr. Syst. 2021, 32, 416–438. [Google Scholar] [CrossRef]
- Safari, A.; Yaghini, H.H.; Kharrati, H.; Rahimi, A.; Oshnoei, A. Voltage controller design for offshore wind turbines: A machine learning-based fractional-order model predictive method. Fractal Fract. 2024, 8, 463. [Google Scholar] [CrossRef]
- Vassilyev, S.N.; Kudinov, Y.I.; Pashchenko, F.F.; Durgaryan, I.S.; Kelina, A.Y.; Kudinov, I.Y.; Pashchenko, A.F. Intelligent control systems and fuzzy controllers. II. trained fuzzy controllers, fuzzy PID controllers. Autom. Remote Control 2020, 81, 922–934. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhou, H.L.; Chen, S.L.; Miao, W.W.; Jiang, Y.F. Designing a Switched Takagi-Sugeno Fuzzy controller for CDC semi-active suspensions with current input constraint. Mech. Syst. Signal Process. 2023, 199, 110450. [Google Scholar]
- Shi, J.Z.; Huang, W.W.; Zhou, Y. T–S fuzzy control of travelling-wave ultrasonic motor. J. Control Autom. Electr. Syst. 2020, 31, 319–328. [Google Scholar]






| Parameter | Value |
|---|---|
| The weight of vertical acceleration | 10:20:190 |
| The weight of suspension dynamic deflection | 50:150:1400 |
| The weight of tire dynamic deformation | 10:25:235 |
| The weight of control input | 0.01 |
| The weight of control input incremental | 0.3:0.3:3 |
| VL | L | M | H | VH | |
|---|---|---|---|---|---|
| VL | 0.66 | 0.55 | 0.28 | 0.55 | 0.66 |
| L | 0.85 | 0.55 | 0.28 | 0.55 | 0.85 |
| M | 0.98 | 0.66 | 0.55 | 0.66 | 0.98 |
| H | 0.85 | 0.55 | 0.28 | 0.55 | 0.85 |
| VH | 0.66 | 0.55 | 0.28 | 0.55 | 0.66 |
| VL | L | M | H | VH | |
|---|---|---|---|---|---|
| VL | 0.75 | 0.35 | 0.23 | 0.35 | 0.75 |
| L | 0.94 | 0.75 | 0.35 | 0.75 | 0.94 |
| M | 0.94 | 0.94 | 0.35 | 0.94 | 0.94 |
| H | 0.94 | 0.75 | 0.35 | 0.75 | 0.94 |
| VH | 0.75 | 0.35 | 0.23 | 0.35 | 0.75 |
| VL | L | M | H | VH | |
|---|---|---|---|---|---|
| VL | 0 | 0.25 | 0.53 | 0.25 | 0 |
| L | 0 | 0.25 | 0.53 | 0.25 | 0 |
| M | 0.25 | 0.53 | 0.89 | 0.53 | 0.25 |
| H | 0 | 0.25 | 0.53 | 0.25 | 0 |
| VH | 0 | 0.25 | 0.53 | 0.25 | 0 |
| VL | L | M | H | VH | |
|---|---|---|---|---|---|
| VL | 0.58 | 0.58 | 0.4 | 0.58 | 0.58 |
| L | 0.4 | 0.4 | 0.3 | 0.4 | 0.4 |
| M | 0.4 | 0.3 | 0.3 | 0.3 | 0.4 |
| H | 0.4 | 0.4 | 0.3 | 0.4 | 0.4 |
| VH | 0.58 | 0.58 | 0.4 | 0.58 | 0.58 |
| Parameter | Value |
|---|---|
| Spring loaded mass /(kg) | 390 |
| Unsprung mass /(kg) | 40 |
| Tire stiffness /(N·m−1) | 185,000 |
| Suspension stiffness /(N·m−1) | 19,500 |
| Suspension damping /(N·s·m−1) | 1900 |
| Parameter | Value |
|---|---|
| Prediction step (Np)/control step (Nc) | 10/2 |
| Sampling time/(s) | 0.01 |
| Control constraints/(N) | |
| Constraint of suspension dynamic deflection/(m) | |
| Constraint of tire dynamic load/(N) |
| Control Strategy | /m·s−2 | /m | )]/N |
|---|---|---|---|
| Passive | 0.2739 | 0.0170 | 316.83 |
| LQR (Compared to passive) | 0.2499 (↓ 8.76%) | 0.0150 (↓ 11.76%) | 282.61 (↓ 10.80%) |
| MPC (Compared to passive) | 0.1988 (↓ 27.42%) | 0.0127 (↓ 25.29%) | 230.30 (↓ 27.31%) |
| T–SFO MPC (Compared to passive) | 0.1699 (↓ 37.97%) | 0.0114 (↓ 32.94%) | 197.07 (↓ 37.80%) |
| Control Strategy | /m·s−2 | /m | )]/N |
|---|---|---|---|
| Passive | 0.3185 | 0.0196 | 364.98 |
| LQR (Compared to passive) | 0.3035 (↓ 4.71%) | 0.0180 (↓ 8.16%) | 339.62 (↓ 6.95%) |
| MPC (Compared to passive) | 0.2536 (↓ 20.38%) | 0.0159 (↓ 18.88%) | 289.92 (↓ 20.57%) |
| T–SFO MPC (Compared to passive) | 0.2223 (↓ 30.20%) | 0.0147 (↓ 25.00%) | 253.71 (↓ 30.49%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Hu, B.; Liu, W.; Li, J.; Yu, W.; Li, G.; Hu, G. A Fractional-Order Model Predictive Control Strategy with Takagi–Sugeno Fuzzy Optimization for Vehicle Active Suspension System. Fractal Fract. 2024, 8, 610. https://doi.org/10.3390/fractalfract8100610
Liu Q, Hu B, Liu W, Li J, Yu W, Li G, Hu G. A Fractional-Order Model Predictive Control Strategy with Takagi–Sugeno Fuzzy Optimization for Vehicle Active Suspension System. Fractal and Fractional. 2024; 8(10):610. https://doi.org/10.3390/fractalfract8100610
Chicago/Turabian StyleLiu, Qianjie, Bo Hu, Wei Liu, Jiantao Li, Wenwen Yu, Gang Li, and Guoliang Hu. 2024. "A Fractional-Order Model Predictive Control Strategy with Takagi–Sugeno Fuzzy Optimization for Vehicle Active Suspension System" Fractal and Fractional 8, no. 10: 610. https://doi.org/10.3390/fractalfract8100610
APA StyleLiu, Q., Hu, B., Liu, W., Li, J., Yu, W., Li, G., & Hu, G. (2024). A Fractional-Order Model Predictive Control Strategy with Takagi–Sugeno Fuzzy Optimization for Vehicle Active Suspension System. Fractal and Fractional, 8(10), 610. https://doi.org/10.3390/fractalfract8100610






