1. Introduction
The Banach fixed-point theorem stands as a cornerstone in operator theory and nonlinear analysis, offering profound insight into a broad spectrum of equations. Detailed elucidation of this theorem can be found in [
1]. This theorem serves as a testament to the interdisciplinary nature of fixed-point theory. Furthermore, the evolution of the Banach contraction mapping theorem, as extended by Edelstein in his seminal work [
2] in 1961, marks a significant advancement. Fuzzy sets, introduced by Lotfi A. Zadeh [
3] in 1965, have seen significant evolution and expanded applications in various fields, particularly in decision making, artificial intelligence, and mathematical modeling. The development of fuzzy sets has led to various generalizations, extensions, and applications, making it a highly versatile tool in computational intelligence. The original concept of fuzzy sets was based on handling uncertainty and imprecision. Over time, this foundational work led to the creation of multiple generalizations, such as intuitionistic fuzzy sets by Atanassov [
4] in 1986, which account for a degree of hesitation in membership functions, and neutrosophic sets by Smarandache [
5] in 1998, which introduce the concept of indeterminacy alongside truth and falsity values. More recent advances include hesitant fuzzy sets, introduced by Torra and Narukawa [
6] in 2009, which allow for multiple membership values, and Pythagorean fuzzy sets developed by Yager [
7] in 2013, which provide a more flexible approach to multi-criteria decision making. The spherical fuzzy sets, proposed in 2018, extend this idea into a 3D membership function space, offering a richer framework for addressing real-world problems. Based on the theory of fuzzy sets introduced by Zadeh [
3], a significant expansion of classical metric spaces, the notion of fuzzy metric spaces (developed by Kramosil and Michalek [
8]) allows for a more adaptable and comprehensive treatment of distances and continuity. There are uses for fuzzy metric spaces in many domains, such as fixed-point theory and topology. The concepts of fuzzy metric spaces and Hausdorff topology on fuzzy metric spaces were proposed by George and Veeramani [
9,
10]. It was demonstrated that this topology is metrizable when applied to specific fuzzy metric spaces, offering a more reliable framework for researching topological characteristics. It is observed that related fuzzy metric spaces may be generated from any classical metric space. This connection demonstrates how flexible fuzzy metric spaces represent various notions of distance. The adaption of Banach fixed-point theorem to the fuzzy setting described in reference [
11] is a crucial step in the study of FFPT. This fuzzy version of the Banach contraction theorem (BCT) is an essential and foundational work that has significant implications and applications in a number of mathematical fields. Its ability to solve a wide variety of mathematical problems from linear to nonlinear ordinary and integral equations is its essential characteristic. Mathematicians can tackle complex problems in various domains by using this theorem, which offers a structure for proving the presence and uniqueness of fixed points in FMS. Its usefulness goes past pure mathematics; engineering is one field in which it has value. In engineering, fuzzy sets and fuzzy logic are used to manage uncertainty and imprecision, which helps in modeling and solving optimization problems. The theorem also has a significant impact on fractal theory, providing deep knowledge about the creation and study of fractals with their complex geometric structures and self-similarities. This mathematical tool helps to create fractals and offers a way to explore their characteristics. For modeling and evaluating events that resist traditional approaches, the fuzzy Banach contraction (FBC) theorem provides a useful tool in areas like physics, biology, and image processing, where uncertainty and complexity are common. It is especially well-suited for handling ambiguous and vague real-world problems because of its ability to handle fuzzy sets and fuzzy logic. Essentially, the fuzzy form of the BC theorem works as a unifying principle that connects mathematical concepts with real-world applications in a variety of scientific fields. Its influence on mathematics and wide range of applications indicate its ongoing importance in modern science.
Theorem 1. ([
11]).
Consider a complete fuzzy metric space
where the fuzziness measure Ψ satisfies the condition Let
be a mapping that fulfills the inequality Under these conditions, it follows that T possesses a unique FP. Subsequently, Gregori [
12] and Huang [
13] introduced a variety of fuzzy contractive mappings in fuzzy metric spaces. Lopez [
14] defined the Hausdorff fuzzy metric on compact sets in 2004.
Fuzzy enriched contraction extends the fuzzy Banach contraction by introducing a parameter
, allowing for greater flexibility in controlling the contraction’s strength. Specifically, when
, our newly defined contraction reduces to the classical fuzzy Banach contraction, making it a special case of our more generalized form. To better illustrate the behavior of this contraction, we have provided a graphical visualization for different values of
. These visualizations offer insight into how the contraction changes as
varies, highlighting the versatility and applicability of the newly defined contraction in different contexts. Because FEC mappings can include both FBC mappings and fuzzy non-expansive (FNE) mappings, they are significant. Unlike FNE mappings, which might not always ensure FP, FEC mappings typically display distinct FPs. This work highlights the importance of FEC mappings in FFPT. The framework facilitates the analysis and understanding of FP features in FMS by providing a thorough coverage of various contractive mappings, including fuzzy versions. Moreover, the finding that distinct FPs exist for FEC opens up fresh avenues for iterative approaches to FFP problems. A significant advancement in FFPT, FEC mappings offer a useful tool for delving into and resolving complex problems in a variety of areas. A novel approach was recently presented by Zahid in [
15].
Self-similar sets are essential to the study of fractals because they provide a powerful way to include a wide range of physical phenomena into mathematical models. A major advance in this field was made by Hutchinson’s groundbreaking study [
16], which explored things with self-similarity. His groundbreaking work resulted in the creation of iterated function systems (IFS), which have become an essential tool for creating self-similar fractals. Barnsley [
17] built on Hutchinson’s foundational work to further advance the theory of iterated function systems, which led to its broad acceptance and use. Barnsley proved that it is possible to create fractal sets in any MS by using a finite set of BCs. This groundbreaking work expanded the field of fractal formation and advanced our knowledge of the fundamental mathematical ideas guiding self-similar structures. The idea of shift dynamical systems, which came forth from the study of iterated function systems, was one of the major contributions made by Barnsley. Researchers learned a great deal about the dynamics of fractals and their underlying symmetries by analyzing the orbits of these systems. This expanded the theoretical foundations of fractal geometry and opened up new directions for research and application. The theory of iterated function systems has been developing ever since Hutchinson and Barnsley’s seminal publications, and further research has looked at adaptations and extensions in a variety of mathematical contexts. These advancements have improved our theoretical understanding of fractals and opened up new avenues for application in data analysis, computer graphics, and picture compression, among other areas. The theory and use of fractals have advanced greatly as a result of the work of Hutchinson and Barnsley as well as later research projects. These innovators have created a dynamic and diverse subject that continues to enthrall and excite mathematicians, physicists, and artists alike through their studies of self-similar sets and the creation of iterated function systems. Recently, Nazir [
18] generated fractals using common attractors in G-metric spaces.
Given the pivotal role of the fuzzy BC mapping principle in both theory and practice, this article seeks to presenters a broader class of fuzzy Picard operators termed fuzzy enriched BCs. This class not only encompasses fuzzy Picard BCs as a specific case but also encompasses certain fuzzy nonexpansive mappings. Our primary objective is to investigate the existence and uniqueness of FPs associated with fuzzy enriched BCs. Furthermore, we aim to establish a strong convergence theorem for the Kransnoselskij iteration, a powerful tool utilized for approximating the fixed points of these contractions. Moving forward, we plan to construct a novel iterated function system (IFS) and the related H–B operator, integrating the concept of fuzzy enriched contractions within fuzzy Banach spaces (FBS). By leveraging the demonstrated FP theorem, we seek to establish the presence of a single attractor for the IFS. To elucidate the proposed construction, we provide a concrete example that showcases the application of fuzzy enriched contractions in generating fractals. Through this illustrative demonstration, we aim to underscore the efficacy of our approach in generating intricate geometric structures with self-similar properties. In summary, this paper aims to advance the understanding and application of fuzzy Banach contraction mappings by introducing the concept of fuzzy enriched contractions. By exploring their properties and employing them within the framework of iterated function systems, we aim to contribute to the field of fractal geometry and provide valuable insights into the generation of complex fractal patterns.
3. Results
We introduce fuzzy enriched contraction (FEC) and establish some fixed-point (FP) results for this newly defined contraction. In the context of fuzzy Banach spaces (FBS), we generate fractals using a generalized fuzzy enriched Hutchinson–Barnsley (H-B) operator with a finite family of FECs. Additionally, we apply FEC to study dynamic market equilibrium, demonstrating their utility in analyzing stability and convergence within economic models.
Definition 8. Suppose
is an FNLS, and
is any mapping, then
is fuzzy enriched contraction (FEC) if there exist
and
such thatWe will also refer to
as
-FEC. Note that every FEC mapping is continuous.
Example 1. Any FC
with contraction constant λ is a
-FEC, i.e.,
satisfies inequality (1) with
and
. Let
be equipped with the fuzzy norm characterized by
Consider the function
defined by
, where I denotes the interval
. It is evident that
preserves distances, making it fuzzy nonexpansive, essentially acting as an isometry.
However,
does not meet the criteria of being a fuzzy contraction. However, it does fulfill the conditions of being a fuzzy enriched contraction. This assertion is supported by the hypothetical scenario where
is a fuzzy contraction, implying the existence of
such thatfor any
. However, this assumption leads to a contradiction for any
. Alternatively, the FEC condition in inequality (1) may be stated asfor all
, where
. This inequality applies for every
when
and
. Therefore, for any
,
constitutes a
-FEC. It is noteworthy that
=
. Remark 1. In Example 1 (2), we observe that, for any starting guess
other than
, the unique FP of
, the Picard iteration
related to
, referred to as the sequence
for
, fails to converge. This discovery suggests that in order to estimate FPs of FECs, more advanced FP iterative techniques are required. We prove a strong convergence theorem for the Krasnoselskij iterative method, which is one such approach in the category of fuzzy enriched contractions. However, before delving into the theorem, it is essential to revisit a crucial property.
Remark 2. When examining a self-mapping
on a convex subset C inside a linear space X, it is worth noting that for any
, the averaged transformation, denoted as
(a term introduced in [22]), is defined asfor all
. Notably, this mapping has the characteristic that Fix(
)=Fix(
).
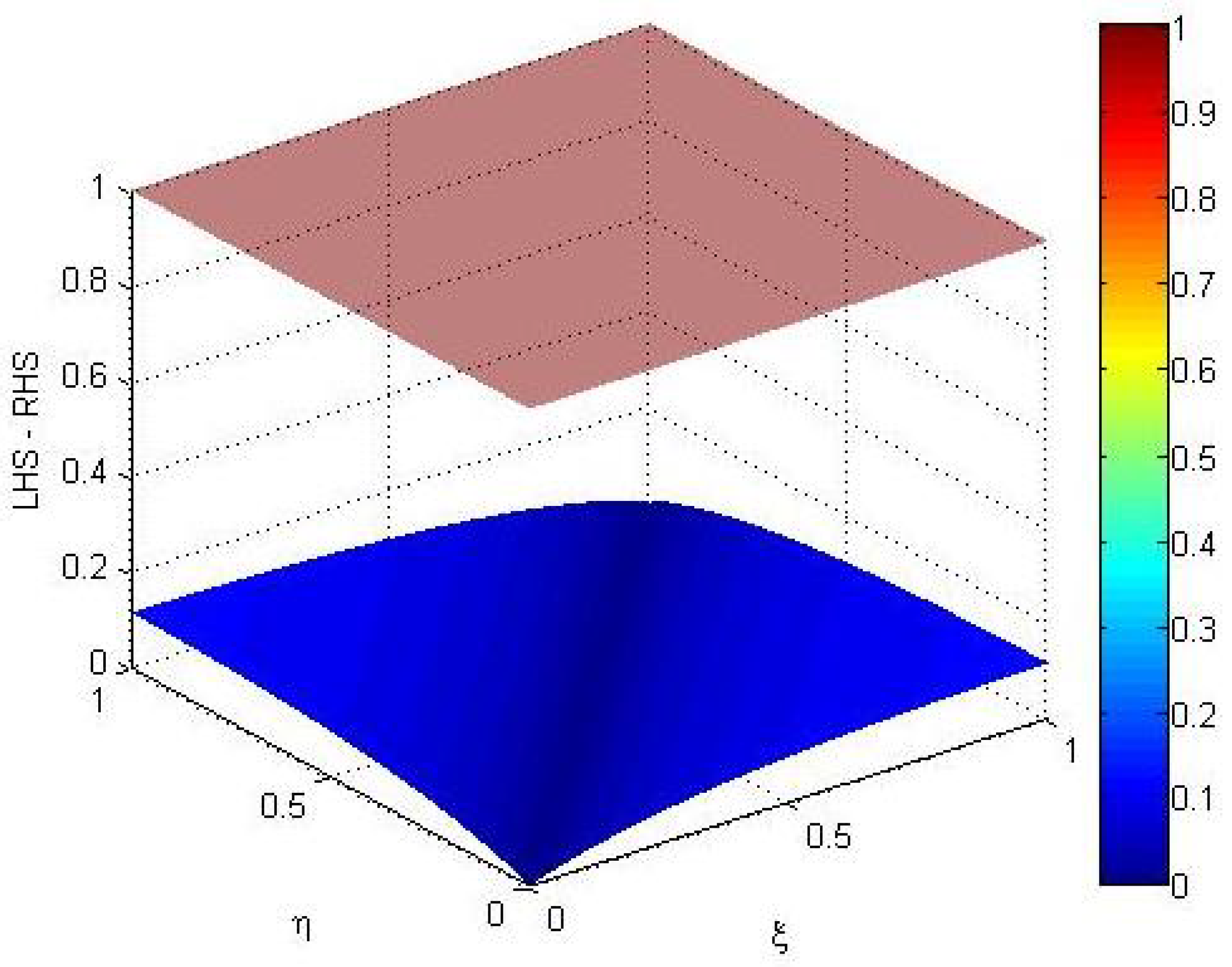
In
Figure 1, the blue region indicates areas where the fuzzy enriched contraction does not hold, whereas the light brown region shows that in those areas, the fuzzy enriched contraction holds with a 0.7 degree of membership.
Figure 1 corresponds to the case where beta is equal to zero, and in this scenario, the fuzzy enriched contraction and the fuzzy Banach contraction become the same.
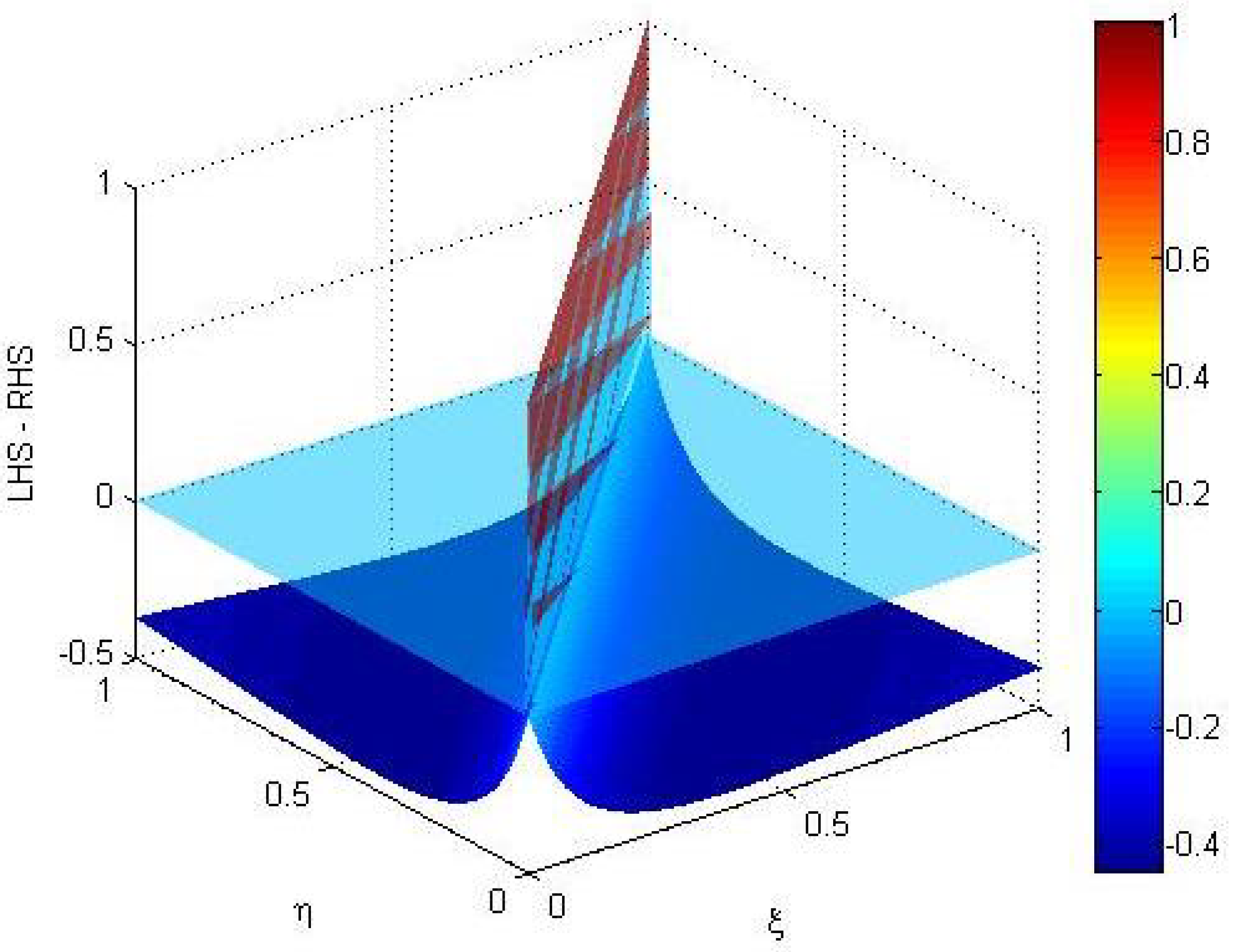
In
Figure 2, readers can observe that in the region where the fuzzy Banach contraction does not hold, the fuzzy enriched contraction does hold for beta equal to 0.3.
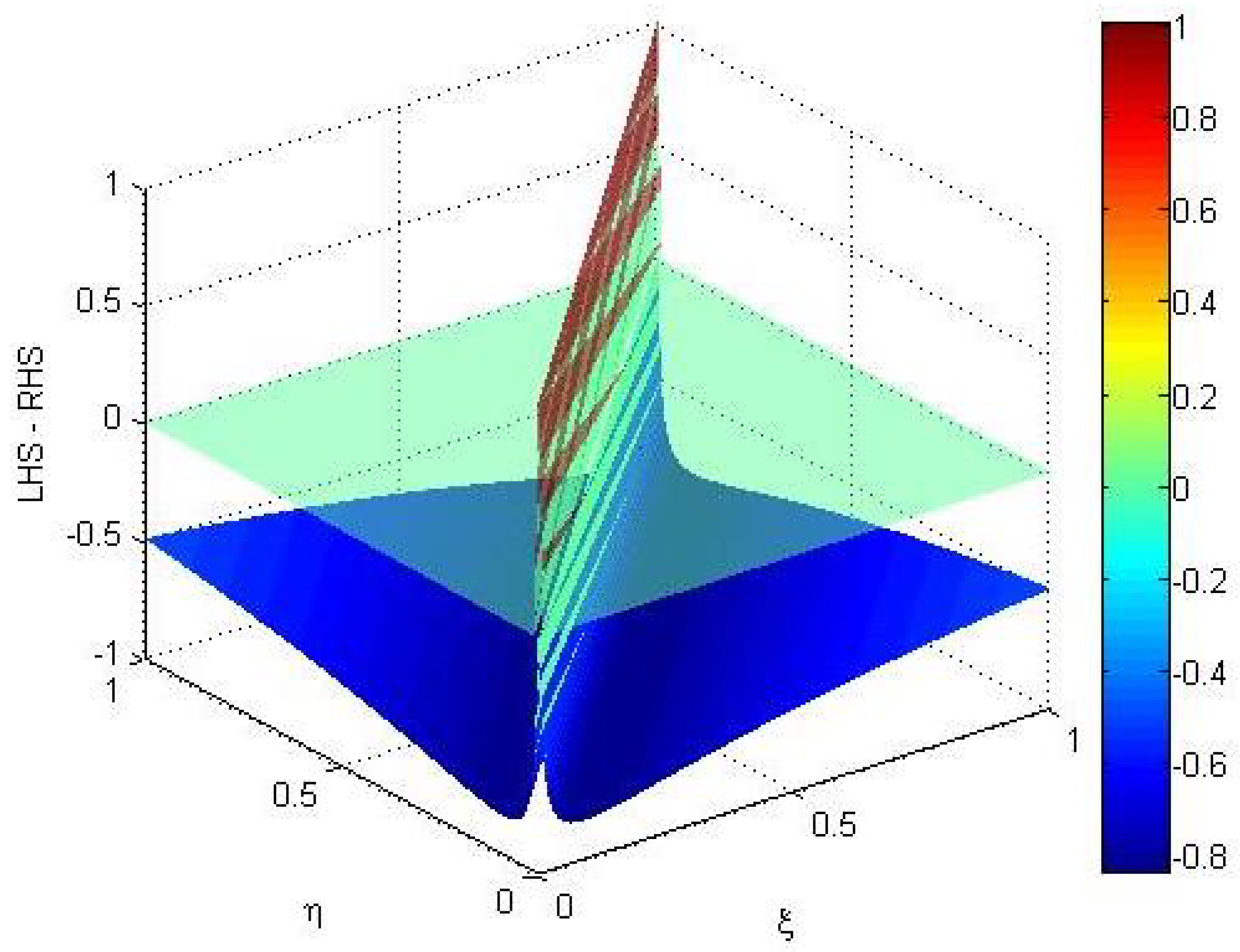
If readers closely examine
Figure 3, they will notice that the region where the contraction does not hold is gradually starting to disappear. This indicates a progressive change in the behavior of the contraction over this region.
In
Figure 4, the sky blue color represents the region where the fuzzy enriched contraction does not hold, whereas the blue and dark brown colors indicate regions where the fuzzy enriched contraction holds at 40 percent and 90 percent, respectively.
In
Figure 5, readers can observe that as the value of beta increases, the region where the fuzzy enriched contraction does not hold gradually disappears. This shows how increasing beta improves the contraction’s hold over the region. Regions where the inequality (
1) holds are highlighted, helping to visually interpret the inequality.
Theorem 2. Let
be an FBS and
a
-FEC. Then
Proof. Case(i):. Let us write
in this instance. The FEC condition (
1) with
is evidently
for every
, where the averaged transformation represented by
is found in Equation (
2);
is a fuzzy contraction since
, which implies that
.
Using Equation (
2), the Krasnoselskij iterative process
, as stated by Equation (
3), is precisely the Picard iteration linked to
.
Take
and
in inequality (
4) to get
From inequality (
6), one routinely obtains the estimate:
Let
. Observe that
Thus, using inequality (
8), we have
As a result,
is convergent in fuzzy Banach space
since it is a G-V Cauchy sequence. Let us indicate
Using the continuity of
and letting
in Equation (
5), we quickly obtain
hence
. We then show that
y is
’s unique FP. Suppose that second FP of
is
z. Next, by inequality (
4)
a contradiction. Because of this, Fix(
and since, by Remark 2, Fix(
) = Fix(
).
Case(ii):. Let
, and we continue as in Case (i) but substitute
for
, when Equation (
3) shrinks, in fact, to the Picard iteration linked with
,
□
Remark 3. By virtue of Theorem (2), we obtain the classical FBC FP theorem [11] in the specific situation
. Definition 9. Let
be an FNLS and
be
-FECs. The operator
defined byfor all
, is fuzzy enriched H-B operator (FEHBO). Definition 10. Let
be an FBS. If
are FECs, then
is called the fuzzy enriched
IFS (
-FIFS).
Definition 11. A non-empty compact set
is an attractor of the
-FIFS) if
We prove the subsequent lemmas in order to support our next result.
Lemma 1. Consider the FNLS
for all
. Then, the following hold:
- (i)
If
, then
,
- (ii)
,
- (iii)
.
Proof. To prove (i): Since
, for all
, we have
which implies that
To prove (ii):
To prove (iii): Note that, by using (ii)
In the similar way, we obtain that
Hence, it follows that
□
Lemma 2. If T is FEHBO, thenfor all
. Proof. Since
T is FEHBO, for every
, we have
Now, using set theory concepts, we obtain
□
Theorem 3. Let
be an FNLS and
a finite family of FEC mappings on I. Define
byfor each
. Then T is FEC on
. Proof. It is sufficient to prove the statement for
Let
be two fuzzy enriched
contractions. Take
with
It is evident from Lemma 1 (iii) that
Hence,
T is fuzzy enriched
contraction on
. □
Theorem 4. Let
be a fuzzy Banach space and
a finite family of FEC mappings on I. Define a mapping on
asfor each
Then - (i)
,
- (ii)
T has a unique fixed point
that is
.
Proof. - (i)
Since every
is a FEC, the result from Theorem 3 and the definition of T follows right away.
- (ii)
From Theorem 3
is FEC. Furthermore,
is a fuzzy Banach space, as implied by the completeness of
. Consequently, (ii) follows from Theorem 2.
□
Definition 12. Let
be an FNLS. A mapping
is generalized FEC if there exist
and
such that the following is valid for each
with
where
. The generalized fuzzy enriched contraction operator is another name for the above-described operator T. It should be noted that T is a trivially generalized fuzzy enriched contraction if T as stated in Theorem 3 is a fuzzy enriched contraction.
Theorem 5. Let
be an FBS and
be a fuzzy enriched iterated function system. Let
be a generalized fuzzy enriched contraction operator defined byThen Proof. We divided the proof into two instances.
Case(i):. In this case, let us denote
. Obviously,
. Since
T is a generalized fuzzy enriched contraction operator, therefore, for each
with
0, holds
where
Now consider,
By using inequality (
12), we have
Let
be any element within
. If
the evidence is complete. Therefore, we presume that
. Define
for
.
For all
, we can assume that
. If not, then for some
,
indicates
, which completes the evidence. Take into account
for all
.
where
This implies that
From the above inequality, one routinely obtains the estimate:
Let
and
. Observe that
Thus, using inequality (
15), we have
The G-V Cauchy sequence
is therefore convergent in the FBS
. Let us denote
By letting
in Equation (
11), we quickly acquire
that is,
. We then demonstrate that
U is
’s unique FP. Let
be another FP of
. Subsequently, by inequality (
13)
a contradiction. Hence, Fix(
and since, by Remark (
2), Fix(
T) = Fix(
).
Case(ii):. Let
, and we continue as in Case (i) but substitute
for
, when the iteration in Equation (
3) shrinks, in fact, to the Picard iteration linked with
,
□
Remark 4. Observe that, if we consider
, the class of all singleton subsets of I in Theorem 5, then
is a subclass of
. Furthermore, for each
, consider
. In such case, the mapping T becomesNext, we present the following corollaries as some fixed-point results using the assumptions given in Remark 4. Corollary 1. Let
be an FBS and
a generalized FEIFS. Let
be a self mapping as defined in Remark 4. if there exist
and
such that the following is valid for each
where
then
has a unique FP. Moreover, for any
and
, the sequence
defined byconverges to the FP. Example 2. Let
and
be the fuzzy norm defined byLet
defined byLet
and
, thenSimilarly, let
and
, thenThis implies that
and
are fuzzy enriched contraction mappings. Consider the generalized fuzzy enriched iterated function system
with the mapping
given asfor all
, we have, by Theorem 5:Therefore, Theorem 5 requirements are all met. Furthermore, the sequence of compact sets
is convergent and has a limit that is the attractor of T for any initial set
.
Example 3. Let
and
be the fuzzy norm defined byLet
defined byLet
and
, thenSimilarly, let
and
, thenThis implies that
and
are fuzzy enriched contraction mappings. Consider the generalized fuzzy enriched iterated function system
with the mapping
given asfor all
, we have, by Theorem 5:Consequently, every need stated in Theorem 5 is met. Furthermore, the sequence of compact sets {
is convergent and has a limit that is the attractor of T for any initial set
.
Example 4. Let
and
be the fuzzy norm defined byLet
defined byLet
and
, thenNow,Similarly,This implies that
,
, and
are fuzzy enriched contraction mappings. Consider the generalized fuzzy enriched iterated function system
with the mapping
given asfor all
, we have, by Theorem 5:Consequently, every need stated in Theorem 5 is met. Furthermore, the sequence of compact sets {
is convergent and has a limit that is the attractor of T for any initial set
.
We aim to explain how fuzzy metrics can be used to color fractals based on the degree of nearness to the origin, influenced by a parameter “t” that governs distance. Here is a breakdown of how this process works conceptually, and how it is applied when generating and coloring fractals. We begin with the origin as the initial reference point. The origin serves as the base object from which we will calculate distances as transformations (contractions) are applied to generate fractal patterns. When creating fractals, we use a set of contraction mappings (transformations) to apply recursive patterns. Each transformation slightly alters the position of points, repeating the process over multiple iterations to create a complex fractal structure. Each point on the fractal will now have a unique location based on how far it has been transformed from the origin. After applying these transformations, we calculate the distance of each point from the origin. This is a key part of measuring nearness. This distance measures how far the point has moved from the origin during the transformation process. To control how we assess nearness, we introduce a parameter “t”, which can range from 0 to infinity. This parameter acts as a threshold, allowing us to decide whether a point is considered “near” or “far” from the origin. If the distance of a point from the origin is less than “t”, we consider the point to be relatively near the origin. If the distance exceeds “t”, the point is considered farther from the origin. In the context of fuzzy logic, instead of using hard boundaries (like either near or far), we use a membership function to assign a membership grade or degree of nearness. This grade indicates how “near” a point is to the origin with respect to the threshold “t”. For points very close to the origin, the degree of nearness will be high (close to 1). As the distance increases, the degree of nearness gradually decreases. For points far from the origin, the degree of nearness approaches 0. This gives us a way to quantify both how near or far a point is from the origin. When visualizing fractals, we can use these degrees of nearness to assign colors to each point on the fractal. Here is how it works: High Nearness: Points close to the origin (or within the threshold “t”) are assigned one color (e.g., blue), representing a high degree of nearness. Low Nearness (High Non-Nearness): Points far from the origin are assigned a different color (e.g., red). The color gradient is smooth, meaning points closer to the origin gradually transition from one color to another as their distance increases, providing a visually appealing fractal pattern. This approach combines fuzzy logic with fractal geometry to create intricate, color-coded visual representations. By controlling the parameter “t”, we can adjust the sensitivity of the nearness calculation and influence how the fractal’s colors are distributed. This makes the fractal not only a mathematical object but also an aesthetically rich one, where each point’s visual appearance is determined by how close it is to the origin, giving deeper insight into the underlying structure.
5. Conclusions
We present fuzzy enriched contractions, an entirely new class of mappings, which extends the concept of fuzzy Banach contractions and encompasses certain fuzzy non-expansive mappings. Our investigation has revealed that every FEC has a single fixed point that could be found using Kransnoselskij iterations. Notably, our fixed-point results establish a classical fuzzy BCP within the framework of fuzzy Banach spaces.
Moreover, we have provided illustrative examples demonstrating that the spectrum of fuzzy enriched contractions is broader than fuzzy Banach contractions. These examples show mappings that fall within the fuzzy enriched contraction spectrum but are not fuzzy contractions. Notably, fuzzy enriched contractions share essential properties with fuzzy Banach contractions, including the presence of a unique fixed point and continuity, as evidenced by their definition.
We have applied these fuzzy enriched contractions in constructing fractals using Hutchinson–Barnsley operators, showcasing their versatility in creating intricate fractal structures. Our findings extend beyond traditional methods of fractal construction by utilizing fixed-point theorems via fuzzy enriched contractions. We have tried to determine their basic features by investigating trajectories generated by sequences of countable transformations.
In the future, we plan to investigate the trajectories of fuzzy enriched contractions that are represented by function systems, which are generalizations of the iterated function system that is presented in this study. This exploration promises to broaden the scope of feasible solutions and provide new insights into this field of study.