Abstract
This research introduces a fractional high-order sliding mode control (FHOSMC) method that utilises an inverse integral fractional order,
, as the high order on the FHOSMC reaching law, exhibiting a novel contribution in the related field of study. The application of the proposed approach into a bioreactor system via diffeomorphism operations demonstrates a notable improvement in the management of the bioreactor dynamics versus classic controllers. The numerical findings highlight an improved precision in tracking reference signals and an enhanced plant stability compared to proportional–integral–derivative (PID) controller implementations within challenging disturbance scenarios. The FHOSMC effectively maintains the biomass concentration at desired levels, reducing the wear of the system as well as implementation expenses. Furthermore, the theoretical analysis of the convergence within time indicates substantial potential for further enhancements. Subsequent studies might focus on extending this control approach to bioreactor systems that integrate sensor technologies and the formulation of adaptive algorithms for real-time adjustments of
-type fractional-orders.
1. Introduction
Bioengineering involves a mixture of biology, engineering, and technology to promote relevant scientific advances. Diverse approaches to bioengineering promote sustained growth in sectors such as healthcare, agriculture, and chemical production, to mention a few. It has caused a transformative change in these areas, marking the beginning of a new development stage for scientific and industrial applications [1,2]. The progress of biotechnology has been driven by its integration into real-world practices. By commercialising biotechnology, scientific findings are transformed into real-world solutions, connecting research studies with market needs. This approach has not only boosted economic growth, but it has also addressed important social challenges, including the healthcare crisis and environmental concerns [3].
Further studies deal with bioreactor control systems by addressing nonlinearities, high sensitivity to critical variables, and unpredictable disturbances, as well as the challenge of designing effective control laws. By incorporating sensors, actuators, and sophisticated control algorithms, the performance, efficiency, and reproducibility of biotechnological processes can be refined to sustainably optimise biomedical production [4]. Sliding mode control (SMC) and adaptive control approaches have made notable advances in the field of nonlinear bioprocesses. These are designed to effectively handle uncertainties in parameters and external disturbances, with the aim of achieving long-term stability in the production of bioprocesses [5]. SMC-based controllers are crucial for bioreactor systems to address the nonlinear and dynamic characteristics of biological processes. The implementation of SMC schemes in bioreactors ensures the preservation of the system stability and robust performance, even in the presence of uncertainties and external disturbances. Several research studies have explored the use of SMC in bioreactor setups. Studies such as that reported in [6,7] suggested sliding mode controllers for biogas generation, focussing on metabolism, and Zlateva on the addition of acetate. The investigations in [8,9] expanded on this idea by exploring the control of microalgae photobioreactors and methane fermentation processes. Other works, such as the study presented in [10], introduced a dual switch tilt panel arrangement for membrane bioreactors, while in [11] a rotating bioreactor for biofilm production was devised. In [12], the effectiveness of an SMC-based method was evaluated in a pasteurisation facility. Together, these investigations show how such controllers can improve the efficiency and reliability of bioreactor systems.
Sliding mode control (SMC) has become widely recognised in fractional-order systems for its ability to handle uncertainties and disturbances effectively. Researchers have used SMC in a range of applications, including circulation models [13], chaotic systems [14,15], satellite attitude control [16], and power distribution systems [17]. Recent progress includes the utilisation of time-varying sliding surfaces [18] and order sliding surfaces [19] to enhance system performance. These methods have shown stability, faster convergence, and reduced chattering compared to controllers. SMC has found application in power converters, offering benefits such as rapid dynamic response and ease of implementation [20]. The fractional-order SMC has the potential to address control issues in all fields, and ongoing research is focused on further enhancing its efficiency and robustness. The combination of sliding mode control with fractional-order systems brings advantages such as reduced chattering, lower energy usage, and improved overall system performance by leveraging the strengths of both approaches to offer solutions for applications.
Recent research has delved into the use of fractional-order controllers in the regulation of bioreactor temperatures, highlighting their effectiveness and benefits compared to other approaches. Fractional-order PID (FOPID) controllers offer performance, resilience, and adaptability in temperature regulation systems [21]. Studies show that these controllers can maintain desired temperature levels in bioreactors despite model disturbances and uncertainties [22,23]. The proposals of the cascade method have shown superior efficacy compared to conventional PID controllers [24]. We have developed advanced nonlinear control tactics that incorporate control principles and estimation algorithms to optimise ethanol production efficiency while mitigating impacts [25]. Fractional-order model predictive control (FOMPC) has also been shown to improve the accuracy of tracking references and reduce disturbances in temperature regulation settings [26]. Ongoing advances in auto-tuning techniques for fractional-order controllers aim to enhance their acceptance within applications [27]. Together, these studies describe the potential of fractional-order controllers in bioreactor management, particularly in temperature regulation and biochemical reactor control.
Integration of SMC schemes and fractional-order calculus in bioprocesses is an area that has not been extensively studied, although research papers have delved into this topic. The studies in [8,28] suggest the use of sliding mode controllers for chemical processes and microalgae photobioreactors, respectively. In both studies, increasing the fractional order was shown to have a direct impact on convergence within the sliding surface, improving the durability and energy efficiency of the actuators, typically represented by the dilution rate. One challenge can be that often a negative dilution rate is required, which can be impractical under real circumstances. The presence of a discontinuous control signal causes an undesired chattering effect, which complicates practical control implementations. The regulation task of a plant output subject to setpoint variations is particularly difficult when the initial state of the process evolves above the function’s maximum, where
exceeds
. By selecting suitable values for the relevant system parameters, the fermentation process produces a better output behaviour and smoother control input when the setpoint is left below the maximum value. Moreover, in [9] a discontinuous control signal which causes positive sutured chattering making control difficult to implement is investigated. Adjusting the system output in response to setpoint variations represents a difficult task when the process’s initial state is above that of the function’s maximum. The fermentation process performs better with relevant parameter values and smoother control input when the setpoint is below the maximum.
In the work reported in [8], it is demonstrated how using fractional order can help reduce erratic behaviour in bioreactors produced by chattering. However, such control design faces limitations because of its reliance on a simplified model focussing on the control of biomass and the dilution rate. This study suggests improving a control algorithm which integrates a comprehensive diffeomorphism for the nonlinear model and an intermediate nutrient mixing stage to allow nutrient concentration control. By incorporating a logarithmic diffeomorphic base shift, an efficient control method can be developed for plants, described by the classical full Monod model, offering a robust strategy to manage both internal and external variations effectively. This demonstrates the significant impact of fractional action on simplifying the future implementations of such controllers applied to industrial processes.
This study introduces a novel control strategy for bioreactors, utilising fractional sliding mode control (FSMC), with an emphasis on input concentration as the principal control variable. To the best of our knowledge, this methodology has not been previously investigated in the literature. Previous studies have focused on output regulation or intermediate control variables; our contribution involves directly manipulating the input substrate concentration to enhance system performance and stability. This innovative method facilitates enhanced regulation of the bioreactor’s dynamic behaviour, essential for optimising biological processes.
Our results demonstrate that fractional-order sliding mode control significantly outperforms conventional PID and integer-order sliding mode controllers in terms of settling time, robustness, and input tracking. Specifically, we observe that the proposed FSMC method minimises overshoot and reduces the steady-state error, contributing to a more efficient control process. Moreover, this approach provides a higher degree of flexibility in system design, which is essential for managing the complex dynamics of bioreactors. These findings suggest that FSMC is a promising alternative for future bioreactor control strategies.
The manuscript is structured into multiple sections. Section 1 provides a concise overview of current advances and their key benefits. Section 2 explores the mathematical modelling and challenges in robust bioreactor control, focussing on graphical tools used in design analysis. Section 3 outlines the key theoretical development based on various theorems, determining the foundation for designing primary sliding mode controllers. In Section 4, numerical simulations are displayed to demonstrate the superior effectiveness of the suggested controller compared to both PID control and standard sliding modes. Section 5 provides an assessment of the results that leads to final conclusions.
2. Model and Statement Problem
Monod kinetics holds great importance in the field of biotechnology, as it is employed for the development of controllers to effectively regulate biomass, nutrients, and by-products. Valued for its simple approach and useful functionality, it is inherently straightforward and highly preferred for creating control systems due to its capacity to efficiently convey essential information about biotechnological processes, particularly in fermentations. This model simplifies the complex bioreactor management process, enhancing its availability to academic researchers and industry practitioners [29,30]. Although there are more intricate models available that offer a more comprehensive analytical understanding, the simplicity of the Monod model is advantageous, particularly in time-critical scenarios, where quick decision making is essential. Incorporation of this tool into feedback control systems yields an optimal fusion of theoretical simplicity and practical adaptability. Feedback effectively compensates for the limited information offered by the basic Monod model, making it a reliable instrument in the dynamic realm of bioreactors control. The Monod model continues to serve as a reliable foundation for the implementation of efficient control strategies in modern bioreactors, particularly as biotechnological processes become more complex [31,32,33].
Certain recent research outputs still employ the Monod model for designing their processes. Advancements in dense cell culture systems such as the Monod bioreactor have boosted monoclonal antibody production, and are a crucial element in biopharmaceuticals [34]. The Monod growth model, which considers factors such as limited nutrients and system capacity, is effective in batch and continuous stirred-tank reactor setups [35]. Bioreactors that use Monod growth kinetics aim to reduce the concentration and volume of the effluent substrate when operating in steady state [36]. A revised Droop model applied in microalgae-based photobioreactors addresses the limitations of internal substrate utilisation seen in the Monod model [37]. Additionally, a continuous flow bioreactor based on hierarchically porous cellulose monoliths has been suggested for rapid enzymatic esterification/transesterification processes without interruptions [38]. Lastly, the use of microreactor technology can improve biodiesel production by focussing on factors such as the ratio of alcohol to triglyceride, microchannel dimensions, residence time, reaction temperature, and mixing techniques [39].
The following is an in-depth description of the standard fundamental metabolic model. This model is commonly used to demonstrate the behaviour of a group of microorganisms in a continuous reactor. It encompasses the fundamental biological and chemical interactions within the reactor, providing a theoretical framework to predict and understand behaviour under various conditions. It serves as a crucial instrument for designing, evaluating, and improving biotechnological processes. A Monod-type model, similar to the one used in [30], is applied to describe the dynamics of microbial growth. This approach incorporates specific growth rates and substrate limitations, making it suitable for processes involving photobioreactors and similar systems.
where
and
are the state variables for biomass () and nutrients (), respectively. The parameters
,
, and
represent the maximum growth rate, the saturation constant, and the metabolic stoichiometry constant, respectively. The function
is considered a variable parameter with
being a bounded parametric disturbance smaller than the fixed and nominal maximum value
, and
represents the dilution rate. The element
represents the concentration of nutrients at the input of the reactor. In this study, it is proposed that this concentration, represented as
, serves as the control input variable. Therefore, it is suggested that there exists a function
,
to represent the total impact and sum of all these unidentified nonlinear uncertainties. In this study, it is proposed, based on experimental observations, that these time, state, and new parameter constraints are bounded as shown below. Integrating these nonlinear uncertainties into (1), we have
Since the biomass is a function of nutrients, it can be arrived at as follows: it will say that
, where
is the high criticality concentration used in the bioreactor used in the control input, and it is proposed that this function is quadratic Lispchitz-bounded in the x-state.
It is essential to convert the model into a chain of integrators to design fractional controllers using sliding modes based on the Lyapunov stability theory. The chain-of-integrators form enables the use of SMC techniques to ensure that the system is insensitive to disturbances and uncertainties, and ensure that the bioreactor works best and with the least amount of damage. This formulation makes it easier to study and design fractional-type controllers. In order to carry out the further analysis, we consider that the function
can be approximated by its associated nominal dilution rate value
. We start by proposing the following diffeomorphism:
We now define
as
Hence, we can rearrange this to obtain
with the condition that
for all
. Therefore, we differentiate this expression with respect to time:
This derivative is obtained by applying the quotient rule for differentiation, where the numerator is the derivative of the function involving
,
, and
, and the denominator is the square of
. Specifically,
After simplifying, we obtain
We now introduce an auxiliary function to simplify the expression:
Next, we define constants
,
, and
:
Using these constants, we can now rewrite the system dynamics as
The function
was defined to simplify terms that involve
, and the constants
,
, and
help organise the system equations into more manageable terms for analysis.
Finally, the system can be further rewritten as
where
represents an unknown disturbance term, corresponding to a bounded disturbance caused by pre-diffeomorphism modelling errors, which must be considered to ensure robust control performance:
Thus, the system is expressed in an input affine form subject to disturbances as
where the functions
and
are defined as
Here,
with
represents a vector composed of the system parameters
, and
with
represents the state of the system.
Thus, we can rewrite the system (2) in the following input affine form subject to disturbances:
where
and
Let
with
represent a vector comprised by the system parameters (in this case these parameters are
,
), and let
with
be the system state.
When examining the bioreactor it is important to take into account the uncertainties in the system parameters. Let
represent the system with approximated parameters
and
describe the system with the real parameters. The discrepancy caused by parameter adjustments can be described as follows:
Similarly, if
represents the function with parameter uncertainties and
the function with the real parameters, the corresponding error is
These error functions,
and
, must be bounded to ensure the system’s stability against unexpected parameter variations. The error summation
is considered in the further analysis for a complete evaluation of the impact of uncertainties on the system. Such a summation is supposed to fulfil the following boundary condition:
where
is a positive upper limit that represents the maximum value for the sum of such errors.
The restrictions introduced for the
and
functions within defined limits provide a feasible approach to ensure that the bioreactor dynamics remain bounded over time, although unexpected parameter changes may still occur.
The global system can be expressed as
Based on the definitions of
and
, (23) can be reformulated as
Therefore, the dynamics of the system with parameter uncertainties and disturbances can be expressed as
Assumption 1.
It is assumed that there exists a bounded function
. To show this, we use the fact that the control input
is bounded by the system nature, that is,
, which is the maximum concentration of nutrients of the mixer.
Given that
and
, we use the Cauchy–Schwarz inequality, the triangle inequality, and the properties of bounded functions to establish the following bounds:
Since
, it follows that
Now, due to
being a bounded disturbance (16), we have
Therefore,
can be bounded as follows:
In order to simplify the notation and for clarity throughout the document, a single bound for
is defined
where
This definition allows us to represent the total impact of uncertainties and disturbances with a single bounded term
, which is crucial for stability analysis and controller design. Therefore, the main model is as follows:
The entire bioreactor can be represented by a diffeomorphic form. The whole effect of uncertainties and disturbances is contained within the term
, which has been shown to be bounded. This thorough representation guarantees that the disturbance effect on the bioreactor’s operation is accurately characterised by
, facilitating the stability analysis and the control design.
3. Fractional Robust Control Design
This section presents the development of a study focused on designing and implementing a combination of sliding mode control (SMC) strategies and fractional computation in bioprocess systems. Thus, a new approach, a sliding mode controller based on integrator chain input concentration, is introduced. To the best of our knowledge this concept has not been explored before. The section starts by discussing a sliding mode control design followed by the procedure to incorporate several calculus into the control process. The primary goal of SMC is to maintain system stability by a robust control action and ensure the desired performance facing uncertainties and external disturbances. To enhance the system states’ performance, a transition from using the dilution rate as the control variable to the concentration of nutrients through a mixing step is suggested. Bioreactor management typically relied on the dilution rate as a control parameter. However, this parameter has a lack of dynamism, and fails to respond to rapid changes in system conditions. Thus, changing the control variable to concentration improves the system response [13].
Fractional calculus incorporates integration operations with noninteger orders. In the realm of time, fractional derivatives and integrals are introduced via convolution operations, serving to represent memory-related phenomena. This approach finds a range of uses in engineering domains [40].
Fractional derivatives and integrals have characteristics that make them valuable tools for capturing memory effects in fields like science and engineering when applied through convolution in the time domain. These mathematical concepts are not limited to these areas. Here, a sliding mode order controller designed to track the trajectory of a bioreactor modelled as a series of integrators is introduced. The Caputo fractional derivative, defined for a function
at times, is denoted by the order
. It is as follows:
where
is a function that is assumed to be sufficiently smooth and locally integrable;
is the gamma function defined as
; and
, with n being an integer. This definition of the Caputo fractional derivative is the most commonly used in engineering applications because it incorporates initial conditions for
and its integer-order derivatives. These initial conditions are traditionally physically appealing. Note that
represents the nth-order integer derivative of the function
in Equation (34). To simplify notation, the Caputo fractional derivative of order
of the function
is denoted as
, which can be written as
. Furthermore, the fractional integral of order
of the function
on the positive real semi-axis is
where
is the fractional order previously defined. It is important to note that the notation
is also used to denote the fractional integral of order
of the function
, more precisely,
.
In the mathematical design of robust controllers based on sliding modes, there is an extremely important mathematical concept, the sliding surface (). This abstract concept describes how, via a controller
(defined in (33)), a system converges to a dynamic surface, that is usually asymptotically stable, using an abstract conceptual function, the reaching law. Another main term is the named "reaching law", that can be designed using classical integer-order control methodologies. In this context, one of the most important contributions of fractional control to the mathematical design of robust sliding mode controllers is the incorporation of the abstract concept of fractional order () on the reaching law
and sliding surface (), where
is a function that, when set to
, has a dynamic that converges to zero, and s depends on the control error
. In this particular case study on bioreactors, the focus is on concentration mixers
.
The sliding surface is proposed as follows:
where
is a gain selected such that the corresponding first-order differential equation is the bioreactor’s exponential growth rate (see (33)), and
is the dilution rate of the main system (33). The controller and its design are defined on the basis of real process conditions. Hence,
has a solution that converges exponentially to zero; consequently, x, the solution of (33), converges exponentially to
, where
is the desired tracking of the dynamics, which is the reference dynamics. When the system dynamics are restricted to the fractional reaching law
the fractional high-order sliding reaching law follows:
It is defined that
represents the main fractional sliding reaching law, which serves as the fractional convergence function. Through the design of a sliding mode controller, the system is desired to converge. The natural dynamics of the system are utilised, employing the parameter
as an exponent. This fractional sliding reaching law introduces a more flexible and robust approach to ensure system convergence, accommodating the unique characteristics of fractional-order systems. By incorporating
into the fractional power term, the inherent properties of the system are exploited to achieve more effective control and stability. Using the second-order system Equation (33), the synthesis of the error signal
with
as the reference signal is described. The reference signal
can be constant or variable and it is usually proposed that this dynamic follows a reference biomass model. It is desired that the system converges according to a fractional sliding reaching law. Therefore, the dynamic error
is derived from the system model (33), which represents the final plant with the desired properties. Similarly,
in Equation (31) captures the various phases of disturbances considered in the previous section, ensuring the system accounts for all possible perturbations.
Thus, in
, the following is obtained:
Therefore, substituting the dynamic error into the previous equation,
When the controller
is designed to ensure that
asymptotically, it is always designed assuming that
. However, this design must be robust when, in reality,
. Therefore, solving for the saturated control term
, the following is obtained, the main control FHOSMC:
If the main control (42) is substituted into the closed-loop system in the presence of perturbations shown in (40), after some simplifications, the following closed-loop equation is obtained:
To ensure robust control performance, it is crucial to establish bounds on the fractional integral terms involved in the control law. The following assumption is proposed to guarantee that the fractional integral term
is properly bounded.
Assumption 2.
Bounding the Fractional Integral Term of
.
In this study, the primary assumption regarding the bounding of the fractional integral term within the sliding mode control framework is introduced. The fractional integral of order
for the function
is defined as in (35). To achieve this, the function
is substituted into the definition of the fractional integral, resulting in
Given that the initial conditions of the system are non-zero, the sliding surface is defined as
, and it is always bounded by a constant
. Mathematically, this implies that the norm
satisfies
, where M represents the maximum allowable deviation on the sliding surface [41].
The term
is consequently bounded by
, since the sliding surface
is restricted to a maximum value of M, and the sign function
merely reflects the direction of the error without affecting its magnitude. This guarantees that the dynamics associated with the sliding mode control do not diverge, keeping the system’s behaviour predictable and stable under the presence of bounded disturbances.
Using the properties of the fractional integral, we derive the following inequality:
The integral is evaluated as follows:
Combining the derived expressions, the final bound is established:
Theorem 1.
FHOSM Control
Proof.
Consider the classical Lyapunov candidate function to demonstrate the stability of the proposed FHOSMC controller for the error dynamics, where
represents the sliding surface:
Take the time derivative of
:
Substitute the error dynamics
into the equation:
Since
cancels out, we obtain
Now, substitute the fractional-order reaching law for
:
The fractional integral term is bounded by
where M is the bound of the sliding surface
. Therefore, the inequality becomes
Next, when the term
approaches zero at time
the control law simplifies to
At this point, the system exhibits classical sliding mode behaviour, where the term
dominates, ensuring that
is strictly negative and the system converges asymptotically to the sliding surface, guaranteeing the stability of the closed-loop system. To verify the robustness and stability of the FHOSMC controller under perturbations, we observe that the system remains stable as long as
and
is bounded by
. This shows that the fractional controller not only generalises the traditional sliding mode control for
, but also offers superior performance in terms of energy consumption and reduction of control effort, as demonstrated in the numerical analysis.
Furthermore, in the particular case where
, the fractional integral term simplifies to
leading to the classical sliding mode control law
thus recovering the conventional sliding mode control law. Therefore, the fractional high-order sliding mode control (FHOSMC) presented here not only extends but also improves upon the classical approach, particularly in systems with disturbances.
By establishing these results, the proof concludes that the FHOSMC controller achieves finite-time stability for the system, with a convergence time bounded by
□
Therefore, the above demonstrates that the robustness and reliability of the closed loop using the FHOSMC controller; and in the next section we propose a long-term numerical experimental approach for the demonstration of the feasibility of the proposed results.
4. Numerical Simulation
In this part, an in depth simulation is shown to assess how well fractional high-order sliding mode control (FHOSMC) performs in tracking control trajectories in a robust manner. The simulation is divided into two stages to thoroughly examine how the control strategy functions across scenarios. The main goal of the simulation is to achieve robust trajectory tracking using FHOSMC. The control equation for FHOSMC is as shown in Equation (42). This control approach is designed to manage the bioreactor trajectory tracking. The system modelled in this scenario is expressed using Equation (33).
The standard reference plant is a plant of disturbances of parameters, and managed with open-loop control. This baseline plant acts as a reference for evaluating control strategies in these circumstances.
The system represented by Equation (33) is subject to a variation of 10% in all parameters
,
,
, and
. This level of change is realistic. It mirrors scenarios where environmental or operational factors cause variations in system parameters. In addition, the system encounters disturbances that mimic real-world uncertainties and disturbances. The random disturbance shown in Figure 1 is utilised in simulation tests to assess how both the fractional high-order sliding mode control (FHOSMC) with fractional order and the traditional PID controller perform. This method enables an evaluation of the resilience and efficiency of each control strategy under disturbance conditions. In addition, the plant experiences two types of disturbances: parametric and arbitrary. This scenario involving disturbances aims to use the characteristics defined by equations
and
, resulting in a combined perturbation, within limits as illustrated in Equation (31). The following Table 1 are the parameters used in the numerical simulation.
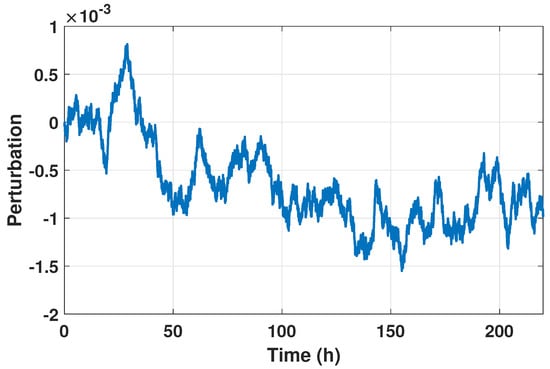
Figure 1.
The figure illustrates the dynamics
of the arbitrary perturbation impacting the general dynamics of the plant represented in Equation (33). The perturbation varies over time, reaching its maximum value of 0.00813765 at approximately 28.87 h.

Table 1.
Simulation parameters with nominal and perturbed values.
Figure 1 illustrates how an arbitrary disturbance, denoted as
affects the behaviour of the system described in Equation (2). This visual representation demonstrates the fluctuation of the disturbance over time, peaking at 0.00813765 around 28.87 h. It is important to note that both functions
and
are influenced by parameter value k, which is subject to perturbations of up to 10% from its value. These perturbations aim to mimic real-world scenarios in which system parameters may change due to operational factors. By introducing these variations, the simulation can evaluate how well the control strategies maintain system performance in the presence of disruptions.
The arbitrary disturbance shown in Figure 1 is used in simulation experiments to assess the performance of two control methods: fractional high-order sliding mode control (FHOSMC) with fractional order and a traditional PID controller. This approach enables an evaluation of how each control strategy handles disturbance scenarios. After determining the values of
and
, from the simulation findings, referred to as
and
under circumstances and
and
under altered conditions, functions
and
are assessed. The errors
and
are calculated by measuring the discrepancies between the modified assessments of f and g.
With the maximum value of the control input
taken as
from the nominal conditions, and considering the maximum arbitrary disturbance
, the total maximum disturbance
is determined using the inequality
leading to the final calculation of
:
The values for
and
were calculated using both the adjusted parameters of the bioreactor system. Initially, the standard values for the parameters
,
,
, and
were assigned as 0.023, 0.018, 3.45, and 0.018, respectively. The adjusted values reflect an increase of 10%, and were set at 27.5, 3.795, 0.0198, and 0.0198, respectively.
The upper limits of the state variables
and
were derived from the simulation results. By evaluating the function
with both adjusted parameters, a norm difference of
was obtained. Similarly, evaluating the function
resulted in a norm difference of
. These values indicate the extent of the error caused by parameter adjustments. To compute the perturbation value (), the formula
was used, where
denotes the maximum control input saturation and
signifies an arbitrary disturbance. The calculated value for
was determined to be approximately 52.233348. The outcome measures the influence of the changes and disturbance on the bioreactor system, showing how well the control plan maintains system efficiency when faced with major parameter changes and external interferences.
4.1. Experimental Methodology
The numerical simulations are executed in MATLAB Simulink 2021a using the Dormand–Prince method (ode45). This method is chosen because of its robustness and efficiency in solving differential equations, making it suitable for simulating the dynamic behaviour of the bioreactor under different control strategies. In the first step, the effect of fractional order
of the FHOSMC controller is simulated (see (42)). The goal is to determine the optimal high-order fractional
that provides the best performance in terms of tracking the trajectory and rejecting disturbances. By varying the fractional order, the sensitivity of the controller to different system dynamics and perturbations can be assessed, allowing for the identification of the most effective fractional order. In the second phase of the study, the best-performing fractional high-order sliding mode control (FHOSMC) from the initial analysis is systematically compared with a classical proportional–integral–derivative (PID) controller. This comparison aims to underscore the benefits of FHOSMC over traditional control methodologies. The PID controller is widely used across various industrial applications due to its simplicity and effectiveness in managing linear and mildly nonlinear systems. However, it often falls short when handling highly nonlinear and perturbed environments, making it an ideal benchmark for evaluating the performance of FHOSMC. In this phase, all the key parameters,
,
,
, and
, of the bioreactor system are increased by 50%. This substantial increase in parameter values is intended to simulate significant parametric uncertainties, reflecting real-world scenarios, where system parameters can vary widely due to environmental and operational conditions. The combined effect of doubling the disturbance function and introducing a positive perturbation of 50% into the system parameters creates a challenging environment for the controllers, providing a rigorous test of their robustness and adaptability. The specific gains for the PID controller employed in this study are as follows:
- Proportional gain (): 232392.38;
- Integral gain (): 8961.848;
- Derivative gain (): 778077.82;
- Filter coefficient: 14.175.
The high PID coefficients were determined as optimal through MATLAB’s self-tuning algorithm (see [42]). Lower values reduced system performance, so these gains were necessary for the best results. This ensures a fair comparison between the PID and our FHOSMC controller, further validating our findings. These simulations aim to demonstrate the robustness and efficacy of FHOSMC under various conditions, including parameter perturbations and external disturbances. The findings are expected to offer valuable insight into the practical applicability of FHOSMC in real-world bioreactor control scenarios, potentially revolutionising control strategies in complex and dynamic environments.
4.2. First Step Results
In the first step of the simulation, the effect of the fractional order
on the performance of the fractional high-order sliding mode controller (FHOSMC) was examined. The tested values of
included
,
,
,
, and
. These values represent different degrees of memory and nonlocality in the fractional derivative, which significantly affect the system’s response and robustness to perturbations.
The biomass concentration over time was plotted for each value of
(Figure 2). It was observed how different fractional orders impacted the controller’s ability to maintain the desired biomass level. Higher values of
generally led to smoother responses, while lower values resulted in more rapid adjustments but with increased oscillations. This behaviour highlights the trade-off between response speed and stability inherent in fractional-order control. The sliding surface, indicating the deviation from the desired trajectory, was also plotted for different values of
(Figure 2). The sliding surface analysis provided information about the robustness and accuracy of the controller. Lower values of
resulted in more pronounced deviations, indicating higher sensitivity to disturbances. In contrast, higher values of
showed more gradual convergence to the desired sliding surface, suggesting better overall stability and control performance. These results inform the selection of the optimal fractional order for the subsequent comparison with the PID controller.
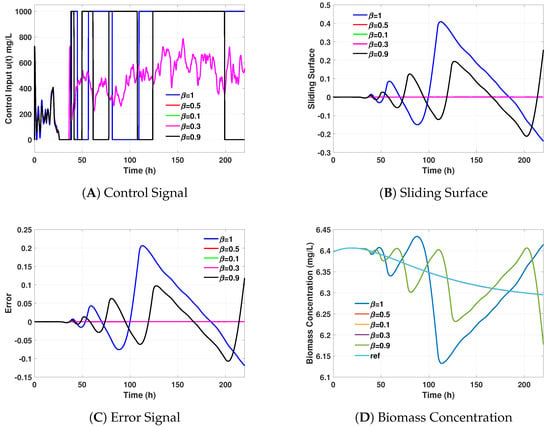
Figure 2.
The figures illustrate the performance metrics for the FHOSMC controller with different
values. (A) Control signal shows the input to the system. (B) Sliding surface depicts the evolution of the sliding mode surface. (C) Error signal represents the deviation from the reference trajectory. (D) Biomass concentration shows the state variable representing the biomass in the bioreactor. These metrics are crucial for evaluating the control strategy’s effectiveness and stability.
4.3. Analysis of Step 1 Results
The performance of the fractional high-order sliding mode control (FHOSMC) was evaluated for different values of fractional order
(0.1, 0.3, 0.5, 0.9, and 1) using various error indices. The indices used in this analysis were the integral absolute error (IAE), the integral absolute input (IAI), the integral squared error (ISE), the integral squared input (ISI), and the integral time absolute error (ITAE). Furthermore, maximum values of biomass concentration (), control input (u), and sliding surface (s) were recorded for each
value. The results are summarised in the following tables (see Figure 3, Table 2 and Table 3).
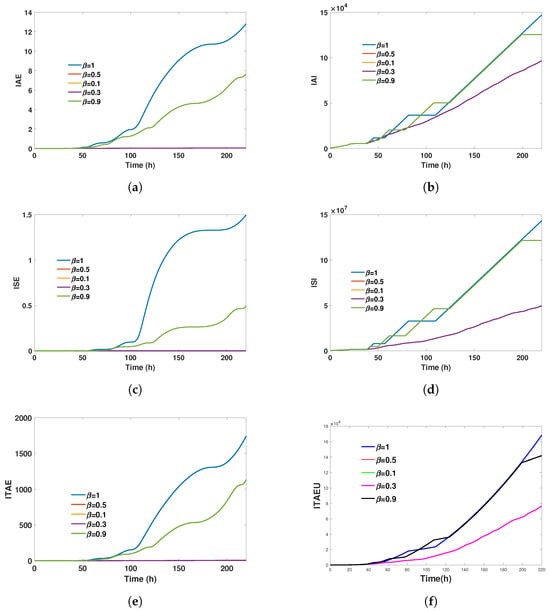
Figure 3.
Performance indices and control metrics during step 1 for various values of fractional order
. These metrics provide a comprehensive assessment of control performance, including error accumulation, control effort, and smoothness of control signals. The results indicate that lower
values generally yield better performance in these indices, highlighting the robustness and efficiency of the FHOSMC with fractional orders
and
. (a) Integral absolute error (IAE) during step 1. (b) Integral absolute input (IAI) during step 1, which measures the total control effort exerted over time. (c) Integral squared error (ISE) during step 1, heavily penalising larger errors by squaring the error values. (d) Integral squared input (ISI) during step 1, evaluating the total control effort squared and emphasising the importance of avoiding excessive control actions. (e) Integral time absolute error (ITAE) during step 1, which penalises errors that persist over time, promoting rapid error correction. (f) Integral time absolute error of control (ITEAU) during step 1, a novel metric introduced to measure the deviation from the open-loop control value.

Table 2.
Steady-state error indices for different
values to 220 h.

Table 3.
Maximum values of state variables for different
values.
4.3.1. Integral Absolute Error
This quantifies the total accumulated error over time without considering its direction. It is particularly useful for understanding the overall magnitude of the error. Lower IAE values indicate better performance, as seen with
and
, which achieved IAE values of 0.05, significantly lower than the other
values.
4.3.2. Integral Absolute Input (IAI)
This measures the total control effort exerted over time. A lower IAI implies more efficient control, as excessive control actions can lead to increased wear and energy consumption. The results show that
and
had the lowest IAI values, suggesting efficient control efforts.
4.3.3. Integral Squared Error (ISE)
This heavily penalises larger errors by squaring the error values. This index is crucial for applications where large errors are particularly undesirable. Both
and
achieved ISE values of 0.00, indicating minimal significant errors.
4.3.4. Integral Squared Input (ISI)
This assesses the squared control effort, emphasising the importance of avoiding excessive control actions. Lower ISI values indicate better performance.
The results show that
and
performed the best, with ISI values of 49,318,035.17 and 49,318,038.94, respectively.
4.3.5. Integral Time Absolute Error (ITAE)
This penalises errors that persist over time, promoting rapid error correction. This is particularly useful for ensuring quick response to disturbances.
and
had the lowest ITAE values, demonstrating their effectiveness in minimising prolonged errors.
In addition to the standard error indices, the curvature of the control signal and the sliding surface was analysed to determine the smoothness of the control action. The curvature was calculated using the second derivative of the control signals and the sliding surface. Lower curvature values indicate smoother control actions, which are desirable to reduce wear and improve the longevity of the system components. The curvature () is calculated as follows:
To quantify the deviation of the control input from its open-loop value (205 mg/L), a new index called the integral time absolute error of the control input (ITAEU) was introduced. This index is calculated as follows (see Figure 3):
where
is the open-loop control input value (205 mg/L).
Figure 3 lacks a comment explaining why all the above errors increase over time. It is important to mention that the error indices we propose to demonstrate convergence and compare different controllers are cumulative and always increasing. Therefore, the goal is to determine which controller produces the least growth in error. This behaviour arises because the indices are derived from the integral of strictly positive terms, since they involve norms and squared values. As shown in Figure 3, this leads to increasing trends in all cases.
High-order sliding mode controllers, as illustrated in [43], are recognised for their ability to attain quasi-finite time convergence, facilitating a rapid decrease in error. This attribute directly influences the system’s performance, resulting in markedly reduced error metrics, including ISE and IAE, as illustrated in Table 2. Although the reference does not specify particular error indices, the controller’s rapid convergence behaviour accounts for the significant decrease in these values. Theorem 1 indicates that the convergence time is contingent on the fractional order, which explains why the controller with a fractional order of
achieves rapid convergence. Although attaining such minimal errors may prove difficult in practical applications, this finite-time convergence characteristic underpins these outcomes. In the second phase, we designate
as the most effective configuration and compare it with an optimised PID controller under more realistic conditions, which includes greater perturbations and noise. This configuration is expected to produce elevated ISE and IAE values, making the results more congruent with real-world scenarios where flawless convergence is challenging to achieve. Based on the statistical results shown in Table 4,
shows superior performance compared to other fractional orders. This preference is due to its lower mean error, reduced standard deviation, and minimal variance. These metrics indicate a more consistent and stable control performance, making
the optimal choice for robust and efficient bioreactor control. The fractional orders
and
demonstrated superior performance in controlling the bioreactor system, as evidenced by error indices and statistical measures. These values achieved the lowest error and control efforts, indicating efficient and effective control.

Table 4.
Statistical analysis of control error for different
values.
Given the analysis of the error indices and statistical measures,
is the preferred choice. This selection is based on its superior performance in minimising the integral absolute error (IAE), integral squared error (ISE), and integral time absolute error (ITAE), which are critical for efficient and effective control (for example, see Table 5). Furthermore,
showed lower standard deviation and variance in the control error, indicating more consistent and stable performance. Despite
also showing strong results, the marginal improvements with
make it the optimal choice for robust and efficient control in practical applications.

Table 5.
Curvature and ITAEU for control signals with different
values.
4.4. Step 2: Comparison of FHOSMC and PID Controller
In this step, the performance of the fractional high-order sliding mode control (FHOSMC) with
is compared against a traditional proportional–integral–derivative (PID) controller. Both controllers are subjected to the same plant dynamics and perturbations as described previously. The PID controller is tuned using MATLAB 2023’s auto-tuning algorithm, which employs a frequency-response estimation experiment to determine the optimal PID gains based on the plant’s frequency. This comprehensive analysis aims to determine whether the FHOSMC with
demonstrates superior performance over the PID controller, which is traditionally known for its robustness and effectiveness in such processes.
To further challenge the robustness of the proposed controller, the maximum perturbation bound is doubled, with
used in step 1. Furthermore, a positive perturbation of 50% is applied to all parameters,
and
. This rigorous testing provides a more conclusive evaluation of the FHOSMC’s performance compared to the PID controller, which is tuned based on the nominal plant model (see Figure 4).
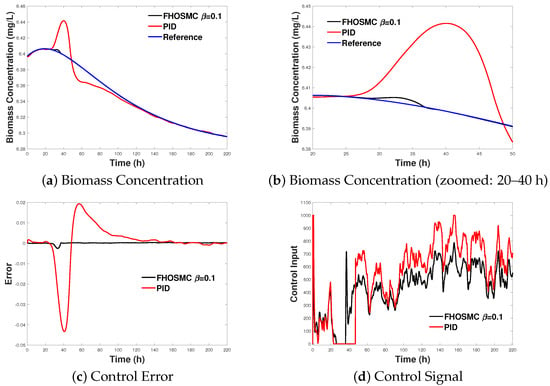
Figure 4.
Comparison of the FHOSMC and PID controllers for the bioreactor system. (a) Biomass concentration over time. (b) Zoomed-in view of biomass concentration between 20 and 40 h. (c) Control error over time. (d) Control signal over time. These plots demonstrate the dynamic performance of both controllers under the same plant and perturbation conditions, with the PID controller tuned using the MATLAB 2023 auto-tuning algorithm.
The results of this comparative analysis highlight the strengths and weaknesses of each control strategy, providing insight into their suitability for practical applications in controlling the bioreactor system under study. The subsequent sections present the dynamic responses of the error, biomass concentration, and control input for both the FHOSMC and PID controllers. These comparisons are illustrated through detailed plots, showing the time evolution of each variable and the effectiveness of each control strategy in managing the bioreactor’s behaviour under the specified perturbations.
In the following figures, further comparisons of the error, biomass dynamics, and control dynamics are presented.
4.5. Analysis of Step 2 Results
The second phase of the analysis concentrated on comparing the fractional high-order sliding mode control (FHOSMC) with
to a proportional–integral–derivative (PID) controller. Both controllers were installed in the same bioreactor system under identical disturbance conditions. The PID controller was calibrated using the auto-tuning algorithm provided in MATLAB 2023, guaranteeing optimal parameter selection. To improve the robustness stress test of the controllers, the magnitude of the disturbance was increased to
, and an increase of 50% was implemented for the system parameters
, and
. Performance assessment was based on various control metrics, including integral absolute error (IAE), integral absolute input (IAI), integral squared error (ISE), integral squared input (ISI), and integral absolute time error (ITAE). Furthermore, the maximum values of the control input (u) and the biomass concentration (x) were documented. The findings are displayed in Table 6.

Table 6.
Performance metric comparison between FHOSMC (
) and PID.
The experimental data indicate that the FHOSMC with
consistently surpasses the PID controller in control accuracy and efficiency. The FHOSMC achieves an IAE of
, markedly lower than PID,
, indicating a considerable decrease in cumulative error. The enhancement in accuracy is evident in the ITAE values, with FHOSMC achieving
, in contrast to the PID’s
. The reduced ITAE for FHOSMC indicates a more rapid and effective rectification of deviations from the setpoint, which is essential to preserve bioreactor stability amid disturbances. FHOSMC demonstrates a distinct advantage in error minimisation, which directly influences the overall stability of the system, as indicated in Table 6.
Furthermore, FHOSMC requires reduced control effort relative to the PID, as demonstrated by the diminished IAI and ISI values. The IAI for FHOSMC was
, while PID required
, indicating that FHOSMC can maintain effective control with diminished input action. The ISI for FHOSMC was
, significantly lower than the PID’s
, indicating that FHOSMC utilises less energy and exerts reduced stress on system components, potentially leading to an extended operational lifespan and reduced equipment wear. The highest control input observed for FHOSMC was
mg/L, while PID achieved
mg/L, thus highlighting the superior efficiency of FHOSMC in regulating the bioreactor with reduced extreme control actions (Table 6).
An in-depth examination of the statistical data in Table 7 uncovers essential insights into the superior performance of the FHOSMC compared to the PID controller in this bioreactor system. The reduced mean control effort for FHOSMC ( mg/L) in contrast to PID ( mg/L) indicates that the fractional-order controller attains the requisite system performance with reduced energy consumption. This is essential in practical applications, as it results in decreased operational expenses and reduced stress on system components, thereby potentially extending equipment longevity. Furthermore, the standard deviation of the control signal for FHOSMC ( mg/L) is markedly lower than that of the PID ( mg/L), suggesting that control actions under FHOSMC exhibit greater consistency and reduced susceptibility to extreme variations. Although both controllers demonstrate comparable ranges, the lower variance of FHOSMC (33,039.00) compared to the PID () indicates that the fractional-order controller yields a more stable and predictable response, even in the presence of disturbances. The stability is further highlighted by the values of skewness and kurtosis. The skewness values for FHOSMC (
) and the PID () are similar; however, the marginally elevated kurtosis for FHOSMC () relative to the PID (
) indicates a more concentrated distribution of control actions around the mean, signifying enhanced control precision. The statistical characteristics of FHOSMC, characterised by lower mean values, reduced variability, and more predictable control actions, facilitate its capacity to diminish energy consumption and improve long-term stability in bioreactor systems, especially under challenging conditions. The diminished variance and uniform control actions mitigate wear on the system, rendering FHOSMC a more sustainable and efficient approach for sustaining stable system performance over prolonged durations.

Table 7.
Statistical analysis of control variables for FHOSMC (
) and PID.
The outstanding efficiency of FHOSMC is due to its intrinsic capacity to reduce control efforts while preserving accuracy, which is particularly vital in systems exposed to frequent disturbances. In contrast to PID controllers, which typically respond more aggressively to disturbances, the fractional-order characteristic of FHOSMC facilitates smoother control actions with reduced extreme interventions. This not only reduces the wear on system components but also enhances long-term stability. By mitigating significant variations in the control input, FHOSMC guarantees a more stable operational environment, thereby decreasing energy consumption and extending the longevity of the bioreactor system. The equilibrium between precision and efficiency renders FHOSMC a more resilient choice in situations where consistent performance and dependability are essential.
5. Main Conclusions
The research findings demonstrate that employing fractional high-order sliding mode control (FHOSMC) with a setting of
outperforms a proportional–integral–derivative (PID) controller, in managing a bioreactor system during significant disturbances. The study reveals a decrease in error metrics such as absolute error (IAE), integral squared error (ISE), and integral time absolute error (ITAE), indicating enhanced precision and efficiency in control operations.
Although some fluctuation was observed in the FHOSMC control signal, overall control effort was found to be more effective compared to PID, leading to reduced equipment wear and operating expenses. Moreover, FHOSMC consistently kept the biomass concentration closer to the target values than the PID controller under challenging disturbances and changes in parameters. This highlights the robustness of FHOSMC in ensuring system stability and performance.
Although acknowledging the reputation of PID controllers for their resilience and effectiveness across applications, this study has tested their capabilities under disturbance scenarios. However, when using FHOSMC with a value of
of 0.1 it not only offered precise and effective control but also showed increased resilience against disturbances and variations in parameters. This has solidified its position as the preferred control strategy for use in bioreactors.
Moreover, it has been observed that no prior research has proposed the reach-law function of the sliding mode order with respect to the fractional order. This research has highlighted that this method significantly improves convergence in the presence of disruptions. There are also hints that studying convergence within a time frame is possible, although further investigation into this concept is required.
6. Future Work
In the future, it would be beneficial to study how FHOSMC can be used in types of bioreactor setups and different environmental conditions to confirm its strength and flexibility. Furthermore, exploring how FHOSMC can be combined with cutting-edge sensor technologies and real-time monitoring systems might improve control accuracy and responsiveness. Comparative analyses with control methods could offer valuable insight into the pros and cons of using FHOSMC. Lastly, creating algorithms to tweak the fractional order
based on real-time feedback from the system could further improve performance and resilience.
Author Contributions
Conceptualisation, A.E.R.-M., J.A.M.-H. and P.A.L.-P.; methodology, P.A.L.-P.; software, V.A.G.-H.; validation, R.C.-L., J.S.C.-R. and V.A.G.-H.; formal analysis, A.E.R.-M. and P.A.L.-P.; investigation, V.A.G.-H. and A.E.R.-M.; resources, J.A.M.-H.; writing—original draft preparation, A.E.R.-M., P.A.L.-P., J.A.M.-H. and R.C.-L.; writing—review and editing, A.E.R.-M., P.A.L.-P., J.A.M.-H. and R.C.-L.; supervision, P.A.L.-P.; project administration, P.A.L.-P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by “Convocatoria 2024: Proyectos de Investigación Cientfica, Desarrollo Tecnológico y Innovación” of “Tecnólogico Nacional de México”.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
CONACYT for the Master’s scholarship awarded to E.A.G.V. with registration number 902332.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| Variable | Description |
| s | Sliding surface |
| Error function, defined as | |
| Maximum growth rate | |
| Saturation constant | |
| Metabolic stoichiometry constant | |
| Dilution rate | |
| Integral of the error function | |
| Second derivative of the error | |
| Positive real parameter | |
| First derivative of the error | |
| Time derivative of the sliding surface | |
| Fractional integral of order | |
| Fractional order | |
| Sign function | |
| Coefficients in the bioreactor dynamics | |
| State variables of the system | |
| Function dependent on the state variable | |
| Control input | |
| Disturbance function | |
| Maximum bound of the disturbance | |
| V | Lyapunov function |
| Fractional control gain | |
| Fractional order of the controller | |
| Function in the fractional sliding mode controller | |
| Function in the fractional sliding mode controller | |
| Function in the fractional sliding mode controller | |
| First derivative of the reference trajectory |
References
- Barragán-Ocaña, A.; Silva-Borjas, P.; Olmos-Peña, S.; Polanco-Olguín, M. Biotechnology and bioprocesses: Their contribution to sustainability. Processes 2020, 8, 436. [Google Scholar] [CrossRef]
- Wei, X.; Luo, J.; Pu, A.; Liu, Q.; Zhang, L.; Wu, S.; Long, Y.; Leng, Y.; Dong, Z.; Wan, X. From biotechnology to bioeconomy: A review of development dynamics and pathways. Sustainability 2022, 14, 10413. [Google Scholar] [CrossRef]
- Yıldız-Ozturk, E.; Askin-Uzel, R. Advanced Bioengineering Applications with Eco-Technology Approach for Sustainable Development. In Proceedings of the International Conference on Sustainable, Circular Management and Environmental Engineering; Springer: Berlin/Heidelberg, Germany, 2022; pp. 182–208. [Google Scholar]
- Zhong, Z.; Huo, H.; Zhu, X.; Cao, G.y.; Ren, Y. Adaptive maximum power point tracking control of fuel cell power plants. J. Power Sources 2008, 177, 457–464. [Google Scholar] [CrossRef]
- Selișteanu, D.; Petre, E.; Răsvan, V. Sliding mode and adaptive sliding-mode control of a class of nonlinear bioprocesses. Int. J. Adapt. Control Signal Process. 2007, 21, 707–722. [Google Scholar] [CrossRef]
- Zlateva, P. Sliding mode control of biogas production by anaerobic digestion with addition of acetate. E3S Web Conf. 2019, 93, 03002. [Google Scholar] [CrossRef]
- Lopéz-Peréz, P.A.; Rodriguez-Mata, A.E.; Hernández-González, O.; Amabilis-Sosa, L.E.; Baray-Arana, R.; Leon-Borges, J. Design of a Robust sliding mode controller for bioreactor cultures in overflow metabolism via an interdisciplinary approach. Open Chem. 2022, 20, 120–129. [Google Scholar] [CrossRef]
- Rodríguez-Mata, A.E.; Luna, R.; Pérez-Correa, J.R.; Gonzalez-Huitrón, A.; Castro-Linares, R.; Duarte-Mermoud, M.A. Fractional Sliding Mode Nonlinear Procedure for Robust Control of an Eutrophying Microalgae Photobioreactor. Algorithms 2020, 13, 50. [Google Scholar] [CrossRef]
- Zlateva, P. A modified sliding mode control of a nonlinear methane fermentation process. E3S Web Conf. 2020, 167, 05007. [Google Scholar] [CrossRef]
- Eliseus, A.; Bilad, M.; Nordin, N.; Khan, A.L.; Putra, Z.; Wirzal, M.; Aslam, M.; Aqsha, A.; Jaafar, J. Two-way switch: Maximizing productivity of tilted panel in membrane bioreactor. J. Environ. Manag. 2018, 228, 529–537. [Google Scholar] [CrossRef]
- Kretschmer, M.; Hayta, E.N.; Ertelt, M.J.; Würbser, M.A.; Boekhoven, J.; Lieleg, O. A rotating bioreactor for the production of biofilms at the solid–air interface. Biotechnol. Bioeng. 2022, 119, 895–906. [Google Scholar] [CrossRef]
- Espin, J.; Estrada, S.; Caiza, L.; Aguirre, O.; Benitez, D.S.; Camacho, O. Sliding Mode Control Applied to a Pasteurization Plant: A Performance Evaluation. In Proceedings of the 2022 IEEE Biennial Congress of Argentina (ARGENCON), San Juan, Argentina, 7–9 September 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Premakumari, R.N.; Baishya, C.; Veeresha, P.; Akinyemi, L. A Fractional Atmospheric Circulation System under the Influence of a Sliding Mode Controller. Symmetry 2022, 14, 2618. [Google Scholar] [CrossRef]
- Haghighi, A.; Ziaratban, R. A non-integer sliding mode controller to stabilize fractional-order nonlinear systems. Adv. Differ. Equ. 2020, 2020, 503. [Google Scholar] [CrossRef]
- Modiri, A.; Mobayen, S. Adaptive terminal sliding mode control scheme for synchronization of fractional-order uncertain chaotic systems. ISA Trans. 2020, 105, 33–50. [Google Scholar] [CrossRef] [PubMed]
- Ismail, Z.; Varatharajoo, R.; Chak, Y. A fractional-order sliding mode control for nominal and underactuated satellite attitude controls. Adv. Space Res. 2020, 66, 321–334. [Google Scholar] [CrossRef]
- Ahmed, T.; Waqar, A.; Elavarasan, R.M.; Imtiaz, J.; Premkumar, M.; Subramaniam, U. Analysis of Fractional Order Sliding Mode Control in a D-STATCOM Integrated Power Distribution System. IEEE Access 2021, 9, 70337–70352. [Google Scholar] [CrossRef]
- Eray, O.; Tokat, S. The design of a fractional-order sliding mode controller with a time-varying sliding surface. Trans. Inst. Meas. Control 2020, 42, 3196–3215. [Google Scholar] [CrossRef]
- Özbek, N.S. Design and real-time implementation of a robust fractional second-order sliding mode control for an electromechanical system comprising uncertainties and disturbances. Eng. Sci. Technol. Int. J. 2022, 35, 101212. [Google Scholar] [CrossRef]
- Komurcugil, H.; Biricik, S.; Bayhan, S.; Zhang, Z. Sliding Mode Control: Overview of Its Applications in Power Converters. IEEE Ind. Electron. Mag. 2021, 15, 40–49. [Google Scholar] [CrossRef]
- Jamil, A.A.; Tu, W.F.; Ali, S.W.; Terriche, Y.; Guerrero, J.M. Fractional-Order PID Controllers for Temperature Control: A Review. Energies 2022, 15, 3800. [Google Scholar] [CrossRef]
- Tusset, A.M.; Inacio, D.; Fuziki, M.E.K.; Costa, P.M.L.Z.; Lenzi, G.G. Dynamic Analysis and Control for a Bioreactor in Fractional Order. Symmetry 2022, 14, 1609. [Google Scholar] [CrossRef]
- Tang, X.; Xu, B.; Xu, Z. Reactor Temperature Control Based on Improved Fractional Order Self-Anti-Disturbance. Processes 2023, 11, 1125. [Google Scholar] [CrossRef]
- Mohan, V.; Pachauri, N.; Panjwani, B.; Kamath, D.V. A novel cascaded fractional fuzzy approach for control of fermentation process. Bioresour. Technol. 2022, 357, 127377. [Google Scholar] [CrossRef] [PubMed]
- Petre, E.; Selişteanu, D.; Roman, M. Advanced nonlinear control strategies for a fermentation bioreactor used for ethanol production. Bioresour. Technol. 2021, 328, 124836. [Google Scholar] [CrossRef] [PubMed]
- Cajo, R.; Zhao, S.; Birs, I.; Espinoza, V.; Fernández, E.; Plaza, D.; Salcan-Reyes, G. An advanced fractional order method for temperature control. Fractal Fract. 2023, 7, 172. [Google Scholar] [CrossRef]
- Muresan, C.I.; Birs, I.; Ionescu, C.; Dulf, E.H.; De Keyser, R. A review of recent developments in autotuning methods for fractional-order controllers. Fractal Fract. 2022, 6, 37. [Google Scholar] [CrossRef]
- Di Teodoro, A.; Ochoa-Tocachi, D.; Aboukheir, H.; Camacho, O. Sliding-Mode Controller Based on Fractional Order Calculus for Chemical Processes. In Proceedings of the 2022 IEEE International Conference on Automation/XXV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Curico, Chile, 24–28 October 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Prasad, D.; Kumar, M.; Srivastav, A.; Singh, R. Modelling of Multiple Steady-state Behaviour and Control of a Continuous Bioreactor. Indian J. Sci. Technol 2019, 12, 1–12. [Google Scholar] [CrossRef]
- Nausch, H.; Baldan, M.; Teichert, K.; Lutz, J.; Claussen, C.; Bortz, M.; Buyel, J.F. Simulation and optimization of nutrient uptake and biomass formation using a multi-parameter Monod-type model of tobacco BY-2 cell suspension cultures in a stirred-tank bioreactor. Front. Plant Sci. 2023, 14, 1183254. [Google Scholar] [CrossRef]
- Hartmann, F.S.; Udugama, I.A.; Seibold, G.M.; Sugiyama, H.; Gernaey, K.V. Digital models in biotechnology: Towards multi-scale integration and implementation. Biotechnol. Adv. 2022, 60, 108015. [Google Scholar] [CrossRef]
- Pajčin, I.; Knežić, T.; Savic Azoulay, I.; Vlajkov, V.; Djisalov, M.; Janjušević, L.; Grahovac, J.; Gadjanski, I. Bioengineering outlook on cultivated meat production. Micromachines 2022, 13, 402. [Google Scholar] [CrossRef]
- Garza, D.R.; Gonze, D.; Zafeiropoulos, H.; Liu, B.; Faust, K. Metabolic models of human gut microbiota: Advances and challenges. Cell Syst. 2023, 14, 109–121. [Google Scholar] [CrossRef]
- Jyothilekshmi, I.; Jayaprakash, N.S. Trends in Monoclonal Antibody Production Using Various Bioreactor Syst. J. Microbiol. Biotechnol. 2021, 31, 349–357. [Google Scholar] [CrossRef] [PubMed]
- Xu, P. Analytical solution for a hybrid LogisticMonod cell growth model in batch and continuous stirred tank reactor culture. Biotechnol. Bioeng. 2019, 117, 873–878. [Google Scholar] [CrossRef] [PubMed]
- Zambrano, J.; Carlsson, B.; Diehl, S. Optimal steady-state design of zone volumes of bioreactors with Monod growth kinetics. Biochem. Eng. J. 2015, 100, 59–66. [Google Scholar] [CrossRef]
- Vo, H.N.P.; Ngo, H.H.; Guo, W.; Nguyen, T.M.H.; Liu, Y.; Liu, Y.; Nguyen, D.D.; Chang, S.W. A critical review on designs and applications of microalgae-based photobioreactors for pollutants treatment. Sci. Total Environ. 2019, 651, 1549–1568. [Google Scholar] [CrossRef]
- Xiao, Y.; Zheng, M.; Liu, Z.; Shi, J.; Huang, F.; Luo, X. Constructing a Continuous Flow Bioreactor Based on a Hierarchically Porous Cellulose Monolith for Ultrafast and Nonstop Enzymatic Esterification/Transesterification. ACS Sustain. Chem. Eng. 2018, 7, 2056–2063. [Google Scholar] [CrossRef]
- Madhawan, A.; Arora, A.; Das, J.; Kuila, A.; Sharma, V. Microreactor technology for biodiesel production: A review. Biomass Convers. Biorefinery 2017, 8, 485–496. [Google Scholar] [CrossRef]
- Vellappandi, M.; Kumar, P.; Govindaraj, V.; Albalawi, W. An optimal control problem for mosaic disease via Caputo fractional derivative. Alex. Eng. J. 2022, 61, 8027–8037. [Google Scholar] [CrossRef]
- Khaledi, G.; Mirhosseini-Alizamini, S.; Khaleghizadeh, S. Sliding Mode Control Design for a Class of Uncertain Time-Delay Conic Nonlinear Systems. Iran. J. Sci. Technol. Trans. Electr. Eng. 2022, 46, 583–593. [Google Scholar] [CrossRef]
- Gade, S.; Shendage, S.; Uplane, M. MATLAB Based Response of Systems Using Auto Tune PID Controller. Int. J. Emerg. Technol. Adv. Eng. 2012, 2, 157–162. [Google Scholar]
- Mishra, J.P.; Yu, X.; Jalili, M. Arbitrary-order continuous finite-time sliding mode controller for fixed-time convergence. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1988–1992. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).