Abstract
This paper presents an extensive investigation into the state feedback stabilization, observer design, and observer-based controller design for a specific category of nonlinear Hadamard fractional-order systems. The research extends the conventional integer-order derivative to the Hadamard fractional-order derivative, offering a more universally applicable method for system analysis. Furthermore, the traditional Lipschitz condition is adapted to a one-sided Lipschitz condition, broadening the range of systems amenable to analysis using these techniques. The efficacy of the proposed theoretical findings is illustrated through several numerical examples. For instance, in Example 1, we select an order of derivative r = 0.8; in Example 2, r is set to 0.9; and in Example 3, r = 0.95. This study enhances the comprehension and regulation of nonlinear Hadamard fractional-order systems, setting the stage for future explorations in this domain.
1. Introduction
Fractional-order systems have garnered significant attention in recent years due to their ability to more accurately model real-world phenomena compared to integer-order systems. These systems have found applications in diverse fields such as control engineering, signal processing, and bioengineering, where their inherent memory and hereditary properties provide superior modeling capabilities [1,2,3,4,5,6,7,8]. Among the various types of fractional derivatives, Hadamard fractional derivatives offer distinct mathematical features, making them well suited to a range of practical problems [9,10,11]. Recent studies have emphasized the importance of fractional-order control systems in areas such as robotics, electric drives, and power electronics, where fractional calculus provides more robust stability and control compared to traditional methods [12,13,14,15].
Despite these advancements, there remain significant challenges in designing and implementing effective observer-based controllers for nonlinear systems governed by fractional-order dynamics. Existing studies have explored various approaches to linear fractional-order systems [16,17,18,19], but research on nonlinear systems, particularly those involving Hadamard fractional derivatives, remains sparse. This paper aims to address these challenges by extending classical control methodologies to nonlinear Hadamard fractional-order systems.
In addition to fractional-order derivatives, the Lipschitz condition has been extensively used in control system analysis to address system nonlinearity [20,21,22]. However, the classical Lipschitz condition is often too restrictive, particularly for systems with large Lipschitz constants. Recent research has introduced the one-sided Lipschitz condition, which allows for the more flexible and less conservative analysis of nonlinear systems [23,24,25]. This study adopts the one-sided Lipschitz condition to expand the range of systems that can be analyzed and controlled.
In terms of control design for nonlinear systems, several researchers have contributed to observer-based control methods. Ref. [20] presented adaptive observers for nonlinear fractional-order systems, while more recent works such as [23,24] have introduced unknown input observer schemes and state feedback controller designs for generalized fractional-order systems. These approaches have proven effective in specific scenarios, but often rely on restrictive conditions such as the classical Lipschitz condition, which limits their applicability to systems with more complex dynamics.
Our study builds upon this growing body of work by addressing the limitations of traditional approaches. While most existing methods apply to Caputo or Riemann–Liouville derivatives, our focus on Hadamard fractional derivatives provides a novel extension, particularly in the context of nonlinear systems. Furthermore, by incorporating the one-sided Lipschitz condition, as explored by Borthagaray et al. (2024) [18] and N’doye et al. (2017) [20], we extend the range of systems that can be analyzed and controlled. This approach is more flexible and less restrictive, allowing for broader applicability in complex real-world systems.
Compared to the state of the art, our proposed method offers several advantages:
- •
- It provides greater flexibility in handling nonlinearities due to the one-sided Lipschitz condition.
- •
- It expands the range of fractional-order systems analyzed by focusing on Hadamard derivatives.
- •
- Our method is demonstrated through various numerical examples, illustrating its effectiveness in stabilizing nonlinear systems, which further sets it apart from other approaches focused primarily on linear or simplified systems [22,25].
The aim of this work is to develop novel state feedback stabilization techniques, observer design methods, and observer-based controllers for nonlinear systems using Hadamard fractional-order derivatives. By integrating the one-sided Lipschitz condition, we enhance the stability and performance of these systems, as demonstrated through various numerical examples. Future work will focus on the application of these methods to real-world systems, particularly in control engineering, to validate their practical utility.
The main contributions of this work are as follows:
- •
- Novel Observer and Controller Design: We propose a new method for designing both a state feedback controller and an observer for nonlinear Hadamard fractional-order systems. This approach ensures the Mittag-Leffler stability of the system states, extending classical control methods to fractional-order systems with complex dynamics.
- •
- Extension of the Lipschitz Condition: The research adapts the classical Lipschitz condition to the one-sided Lipschitz condition, significantly broadening the range of systems that can be analyzed and controlled. This modification allows for greater flexibility and applicability to real-world systems with larger Lipschitz constants.
- •
- Application to Hadamard Fractional Derivatives: Unlike many existing works focused on Caputo or Riemann–Liouville derivatives, this work specifically addresses Hadamard fractional derivatives, providing insights and solutions that are more applicable to systems with long-term memory effects.
- •
- Numerical Validation: The theoretical findings are validated through several numerical examples, demonstrating the robustness and effectiveness of the proposed observer and controller designs in stabilizing nonlinear systems.
The paper is systematically and comprehensively structured to explore the research topic. It begins with Section 2, which introduces the basic concepts and problem statement, and is further divided into two subsections. Section 2.1 provides the necessary background and foundational knowledge, while Section 2.2 presents a clear statement of the problem. Following this, Section 3 delves into the state feedback stabilization of nonlinear Hadamard fractional-order systems. Section 4 discusses the design of observers for the considered systems, presenting the theoretical development, algorithms, and results related to observer design. Section 5 focuses on the design of observer-based controllers for the systems under consideration, presenting the theoretical development, algorithms, and results related to controller design. Section 6 presents the numerical examples. Section 7 offers a discussion section. The paper concludes with Section 8, summarizing the main findings of the research, discussing their implications, and suggesting directions for future research.
2. Preliminaries and Problem Statement
2.1. Preliminaries
Definition 1
([26]). The Hadamard integral of a locally integrable function x of order is given by the following:
Definition 2
([26]). The Caputo–Hadamard fractional derivative of an absolutely continuous function x of order is given by the following:
Lemma 1
([25]). Let and be a constant and symmetric, definite the positive matrix. Then,
Definition 3
([26]). The Mittag-Leffler (ML) functions can be defined with one or two parameters, respectively, as follows:
Consider the following system:
Definition 4
([26]). The equilibrium point
of (4) is called GML stable if
such that for
of (4), the inequality
is satisfied, where is the ML function with one parameter,, and is a given locally Lipschitz function.
Definition 5.
The nonlinear function
is said to be one-sided Lipschitz in a region
, if there exists
s.t
:
where the term <> denotes the inner product between two vectors.
Definition 6.
The nonlinear function
is said to be quadratically inner bounded in a region
, if there exists
s.t
:
2.2. Problem Statement
Consider a class of continuous-time nonlinear systems described by the following:
where
is the state,
is the input,
is the output, and
,
and
.
represent the system nonlinearity. We assume that
.
In this study, the nonlinear function
) is assumed to satisfy the conditions described in Definitions 5 and 6. Specifically,
) is considered to be one-sided Lipschitz (Definition 5) and quadratically inner bounded (Definition 6). These conditions are used to ensure the stability of the proposed observer and controller design methods in the subsequent theorems.
3. State Feedback Stabilization
Consider the state feedback controller given by the following:
In (8),
and
are two feedback gain matrices, where
is fixed such that
is a Hurwitz matrix, and
is to be computed later. Under this control law, the system equation becomes the following:
Theorem 1.
Consider the system (7) with the state feedback controller (8), under conditions (5) and (6), system (7) is Mittag-Leffler stable if
where
and
,
.
Proof.
For simplicity, denote:
,
Consider the Lyapunov function
Then, using Lemma 1, one can obtain the following:
Now, from inequality (5) and for any positive scalar
, it follows that
Similarly, for any
, condition (6) yields the following:
Then, adding the terms on the left-hand side of (12) and (13) to the right-hand side of (11) yields the following:
where
.
Then,
ensures that
. Then, the origin
is globally Mittag-Leffler stable. This ends the proof. □
4. Observer Design
Consider the following observer for system (7):
where
is chosen such that
is Hurwitz, and
is the observer gain matrix.
Theorem 2.
Consider system (7) with the proposed state observer system (14). Under conditions (5) and (6), system (14) is a Mittag-Leffler observer for system (7), if
where
and
,
.
Proof.
Let the estimation error be
. The error dynamics are
Consider the following Lyapunov function candidate
The time derivative of
along the trajectory is
Choosing
One supposes that
.
Now, from inequality (5) and for any positive scalar
, it follows that
Similarly, for any
, condition (5) yields:
Then, adding the terms on the left-hand side of (19) and (20) to the right-hand side of (16) yields the following:
where
.
Then,
ensures that
. Then, the origin
is globally Mittag-Leffler stable. This ends the proof. □
5. Observer-Based Controller Design
Combining the full-state feedback control design of Section 3 and the observer design of Section 4, we design an observer-based controller for system (7).
where
is the estimate of
generated by (18), and
is the gain matrix that will be defined later. We should prove that the state
and the observation error
converge to zero, in the Mittag-Leffler stability sense. Thus, we give the following theorem:
Theorem 3.
Consider the system (7) with conditions (5) and (6) and the state feedback controller (22) with the state observer (14). If (23)–(25) hold, then
and
are Mittag-Leffler stable.
where
,
,
and
,
,
, and
.
Proof.
Define the following:
By substituting the observer-based control law given by (19) into (6) and simplifying it, we obtain
The time derivative of the Lyapunov function candidate
is as follows:
One can obtain the following:
with
,
One supposes
, where
.
If (23) and (24) hold, then
If (25) holds, then we can conclude that
is Mittag-Leffler stable. This ends the proof. □
6. Numerical Examples
The examples presented in this study were chosen with the objective of validating the theoretical contributions made in the design of the observer and controller for nonlinear Hadamard fractional-order systems. The aim was to demonstrate the effectiveness of the proposed methods in a simulation-based manner. Each example illustrates a specific aspect of the theoretical results:
- •
- Example 1 validates the theoretical findings of Theorem 1 by applying the proposed state feedback stabilization method to a nonlinear system with a given set of initial conditions and nonlinearity.
- •
- Example 2 demonstrates the applicability of the observer design from Theorem 2, showing how the system’s estimated states closely track the actual states.
- •
- Example 3 extends the approach to an observer-based controller design, illustrating the effectiveness of the combined observer and controller in ensuring Mittag-Leffler stability for the system.
The choice of these examples ensures that the theoretical findings are effectively validated and that the simulations provided are clear.
6.1. Example 1
This example validates the theoretical finding of Theorem 1.
One supposes
and
. The matrix
is chosen such that
is a Hurwitz matrix; by pole placement, we obtain
. We have
.
With regard to the nonlinear part, we use the following:
. Then, conditions (5) and (6) are fulfilled, with the following:
,
and
. The condition
is not LMI. So, to transform it into an LMI, we will make the following derivations:
When replacing
by its expression into
and
by its value, we obtain the following:
We have:
where
,
and
.
One supposes
.
By multiplying the left side and the right side of
by
, we obtain the following:
Applying the Schur complement lemma, we obtain the following:
If one supposes
, we have the following:
By using the LMI control toolbox, we find the following:
In this example, one considers the initial condition of
as
and the order of the fractional derivative equals 0.8. We obtain the following simulation result:
Drawing from Figure 1, it is evident that as time approaches infinity, all states converge towards zero. This observation confirms the validity of the outcome outlined in Theorem 1.
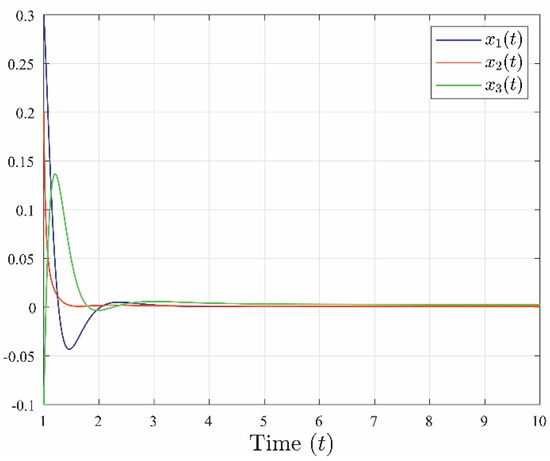
Figure 1.
The evolution of the system states
,
and
related to system (5).
6.2. Example 2
This example validates the theoretical finding of Theorem 2. One supposes
and
.
is chosen such that
is a Hurwitz matrix; by pole placement, we obtain
. We have
. With regard to the nonlinear part, we take the following:
. Then, conditions (5) and (6) are fulfilled, with the following:
,
and
. By using Equation (14) in the condition
, we obtain an LMI condition. So, by using the LMI control toolbox, we find the following:
In this example, one considers the initial condition of
as
and the initial condition of
as
The order of the fractional derivative equals 0.9. We have the following simulation results:
It is evident from Figure 2 and Figure 3 that the system’s estimated state closely tracks its actual state. This relationship is further illustrated in Figure 4, where the errors between the actual state and the estimated state converge towards zero as time approaches infinity.
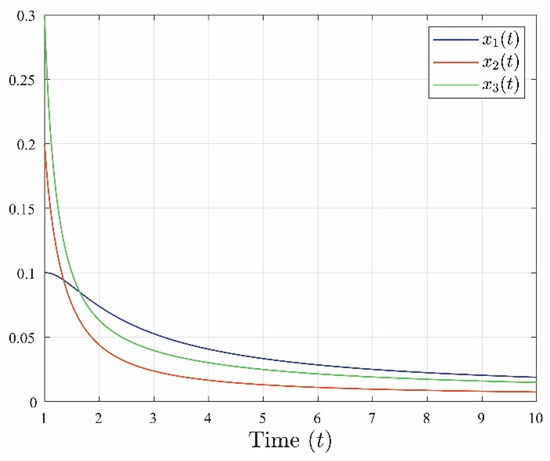
Figure 2.
The evolution of the system states
,
and
related to system (3).
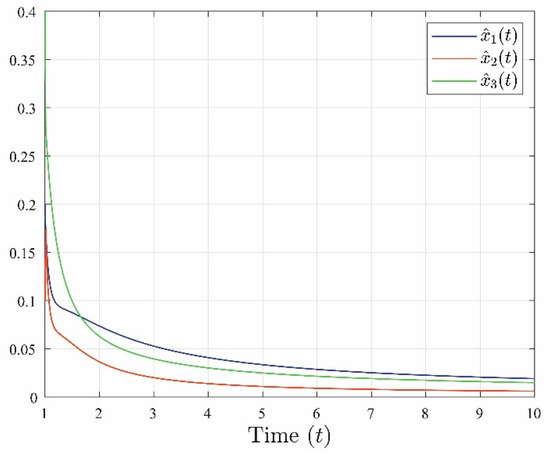
Figure 3.
The evolution of the system states
,
and
related to system (10).
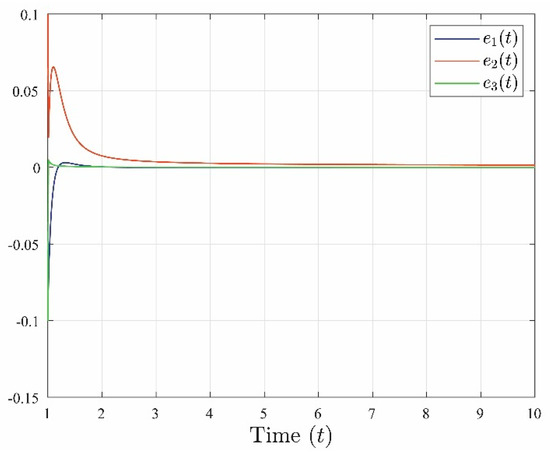
Figure 4.
The evolution of the system errors
,
and
related to system (11).
6.3. Example 3
This example validates the theoretical finding of Theorem 1. One supposes
and
.
is chosen such that
is a Hurwitz matrix; by pole placement, we obtain
. We have
. With regard to the nonlinear part, we use the following:
. Then, conditions (5) and (6) are fulfilled, with the following:
,
and
. The resolution of the LMI stability condition of Theorem 2 (condition (24)) is still the same as example 2.
To facilitate the resolution of condition (23), we make the following derivations.
By replacing
and
by its expression into (23) and
by its value, and by multiplying the left side and the right side of
by
, we obtain the following:
Applying the Schur complement lemma, we obtain the following:
In order to get a feasible solution, we first set the following constants:
. Note that, with
, the necessary condition (25) is well satisfied. By using the LMI control toolbox, we find the feasibility of LMI (23), with the following solution:
Then, we conclude the gain matrix
:
.
In this example, one considers the initial condition of
as
and the initial condition of
as
The order of the fractional derivative equals 0.95. We have the following simulation results:
Figure 5 denotes the disparity between the evolution of the system states in system (23) and the observer state in Equation (10).

Figure 5.
The evolution of the system states
,
and
related to system (23).
Observing Figure 5 and Figure 6 reveals that both the state and the error exhibit Mittag-Leffler stability, thus confirming the theoretical findings of Theorem 3.
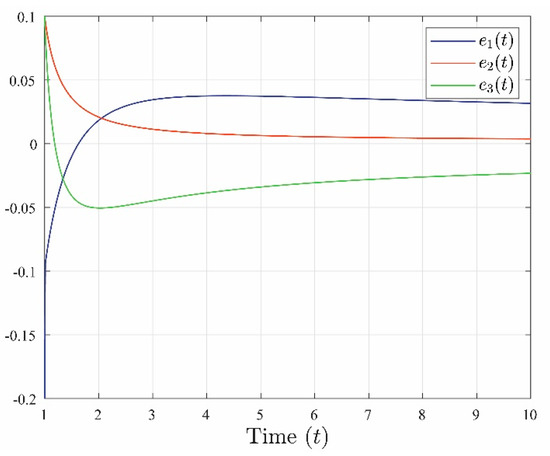
Figure 6.
The progression of the system errors
,
, and
.
7. Design Algorithm and Discussion
Figure 7 depicts the observer-based control diagram.
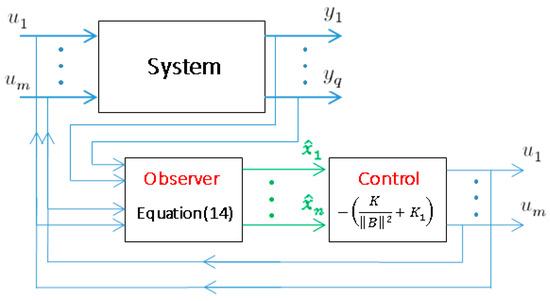
Figure 7.
The control block diagram.
In order to implement the observer-based control law (22), the steps of the following design algorithm can be followed:
Design Algorithm
- •
- Step 1: The gain matrices and are chosen such that is a Hurwitz matrix and is a Hurwitz matrix.
- •
- Step 2: Solve the LMI stability condition of Theorem 2 to find the observer gain matrix .
- •
- Step 3: The controller stability condition (23) is a Nonlinear Matrix Inequality (NMI). It should be transformed into an LMI, as performed in simulation example 3, just above (LMI (28)).
- •
- Step 4: Chose a value for the variable , such that the stability condition (25) is well satisfied.
- •
- Step 5: Solve the LMI (28), and obtain the control gain matrix .
- •
- Step 6: Use these results to develop the MATLAB simulation code, and obtain the simulation figures.
The variable
represents the order of the fractional derivative. In Example 1, we select
= 0.8; in Example 2,
is set to 0.9; and in Example 3,
= 0.95. The order of the fractional derivative does not significantly affect the results; we chose these values randomly to generate curves and simulations. We can adjust the order and produce different curves, which will yield similar results. The primary difference may lie in the transient regime, which is not the main focus of this work. Our primary objective is to demonstrate Mittag-Leffler stability, irrespective of the transient regime duration and behaviors.
Theoretically, the Mittag-Leffler convergence in our case study exhibits a relatively long transient phase, particularly due to the logarithmic term in the definition of the Hadamard fractional-order derivative. This characteristic is inherent to the Hadamard derivative, which accounts for long-term memory effects in the system. The logarithmic nature of the fractional-order derivative introduces a slower convergence rate, especially in the transient phase, compared to systems governed by other types of fractional derivatives such as Caputo or Riemann–Liouville. In Example 3, the curves generated and displayed reflect this behavior. The system states and errors converge toward zero but do so gradually over an extended period, aligning with the expected behavior dictated by the Mittag-Leffler stability criterion. This slow convergence is not a limitation of the control design but a natural outcome of the system’s inherent dynamics under the Hadamard fractional derivative. The long transient period observed in the numerical simulations is entirely consistent with the theoretical findings. It confirms that the system is Mittag-Leffler stable, even though the convergence takes more time due to the logarithmic function in the derivative definition. The simulation results, therefore, validate the theoretical predictions and demonstrate the robustness of the proposed control method in achieving stability for nonlinear Hadamard fractional-order systems. This alignment between theory and simulation underscores the importance of considering the specific nature of the fractional derivative when analyzing the convergence behavior. The longer settling time should be interpreted as a characteristic feature of the Hadamard fractional system, providing deeper insights into how such systems behave over time.
8. Conclusions
This research has made significant strides in the field of nonlinear Hadamard fractional-order systems. By generalizing the classical integer-order derivative to the Hadamard fractional-order derivative and the classical Lipschitz condition to a one-sided Lipschitz condition, we have broadened the range of systems that can be analyzed. The development of state feedback stabilization, observer design, and observer-based controller design for these systems has further contributed to the understanding and control of such systems. The effectiveness of the proposed theoretical results has been demonstrated through several numerical examples. This work not only contributes to the existing body of knowledge but also opens up new avenues for future research in this field. While the focus of this work has been on the theoretical exploration and numerical validation of the proposed methodologies, we recognize the importance of applying these results to actual engineering systems. Future research will explore potential applications in real-world scenarios, such as control engineering and signal processing, to demonstrate the practical utility of the proposed observer and controller design. This will help bridge the gap between theory and practice, further solidifying the relevance of fractional-order systems in engineering and technology.
Author Contributions
Conceptualization, Visualization, A.J.; Methodology, Supervision, O.N., M.R.; Formal analysis, A.B.M.; Writing—original draft, L.M.; Writing—review and editing, A.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by King Saud University in Riyadh, Saudi Arabia through researchers supporting project number (RSPD2024R683).
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors acknowledge “Researchers Supporting Project number (RSPD2024R683), King Saud University, Riyadh, Saudi Arabia”.
Conflicts of Interest
The authors declare that they have no conflicts of interest regarding the publication of this paper.
References
- Benbouhenni, H.; Bizon, N.; Mosaad, M.I.; Colak, I.; Djilali, A.B.; Gasmi, H. Enhancement of the power quality of DFIG-based dual-rotor wind turbine systems using fractional order fuzzy controller. Expert Syst. Appl. 2024, 238, 121695. [Google Scholar] [CrossRef]
- Singh, J.; Agrawal, R.; Baleanu, D. Dynamical analysis of fractional order biological population model with carrying capacity under Caputo-Katugampola memory. Alex. Eng. J. 2024, 91, 394–402. [Google Scholar] [CrossRef]
- Li, J.; Yan, Z.; Shi, X.; Luo, X. Distributed Adaptive Formation Control for Fractional-Order Multi-Agent Systems with Actuator Failures and Switching Topologies. Fractal Fract. 2024, 8, 563. [Google Scholar] [CrossRef]
- Sharafian, A.; Ali, A.; Ullah, I.; Khalifa, T.R.; Bai, X.; Qiu, L. Fuzzy adaptive control for consensus tracking in multiagent systems with incommensurate fractional-order dynamics: Application to power systems. Inf. Sci. 2024, 689, 121455. [Google Scholar] [CrossRef]
- Liu, H.; He, L.; Cheng, B. A Powerless Fractional-Order WPT System With Extended Zero Voltage Switching Region. IEEE Trans. Ind. Electron. 2024, 1–9. [Google Scholar] [CrossRef]
- Liu, H.; He, L.; Cheng, B. Powerless Fractional-Order Tuning Wireless Power Transfer System With Zero Phase Angle Input. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 1–10. [Google Scholar] [CrossRef]
- Zhou, H.; He, L.; Yang, Z.; Lin, Z. Virtual Fractional-Order-Inductor Based Second Harmonic Current Suppression Method. IEEE Trans. Ind. Electron. 2023, 1–11. [Google Scholar] [CrossRef]
- Zhou, H.; He, L.; Lu, F. Impedance Editing Based Second Harmonic Current Reduction for New Energy Access System. IEEE Trans. Ind. Electron. 2023, 71, 2638–2649. [Google Scholar] [CrossRef]
- Ma, L. On the kinetics of Hadamard-type fractional differential systems. Fract. Calc. Appl. Anal. 2020, 23, 553–570. [Google Scholar] [CrossRef]
- Ma, L.; Li, C. On hadamard fractional calculus. Fractals 2017, 25, 1750033. [Google Scholar] [CrossRef]
- He, B.B.; Zhou, H.C. Caputo-Hadamard fractional Halanay inequality. Appl. Math. Lett. 2022, 125, 107723. [Google Scholar] [CrossRef]
- Singh, A.P.; Bingi, K. Applications of Fractional-Order Calculus in Robotics. Fractal Fract. 2024, 8, 403. [Google Scholar] [CrossRef]
- Prabhakaran, A.; Ponnusamy, T.; Janarthanan, G. Optimized fractional order PID controller with sensorless speed estimation for torque control in induction motor. Expert Syst. Appl. 2024, 249, 123574. [Google Scholar] [CrossRef]
- Mseddi, A.; Wali, K.; Abid, A.; Naifar, O.; Rhaima, M.; Mchiri, L. Advanced modeling and control of wind conversion systems based on hybrid generators using fractional order controllers. Asian J. Control 2024, 26, 1103–1119. [Google Scholar] [CrossRef]
- Mseddi, A.; Abid, A.; Naifar, O.; Rhaima, M.; Ben Makhlouf, A.; Mchiri, L. Investigation of the Robust Fractional Order Control Approach Associated with the Online Analytic Unity Magnitude Shaper: The Case of Wind Energy Systems. Fractal Fract. 2024, 8, 187. [Google Scholar] [CrossRef]
- Naifar, O.; Nagy, A.M.; Makhlouf, A.B.; Kharrat, M.; Hammami, M.A. Finite-time stability of linear fractional-order time-delay systems. Int. J. Robust Nonlinear Control 2019, 29, 180–187. [Google Scholar] [CrossRef]
- Lu, Q.; Zhu, Y. Finite-time stability in measure for nabla uncertain discrete linear fractional order systems. Math. Sci. 2024, 18, 55–62. [Google Scholar] [CrossRef]
- Borthagaray, J.P.; Li, W.; Nochetto, R.H. Quasi-linear Fractional-Order Operators in Lipschitz Domains. SIAM J. Math. Anal. 2024, 56, 4006–4039. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Gallegos, J.A. Error-Based Switched Fractional Order Model Reference Adaptive Control for MIMO Linear Time Invariant Systems. Fractal Fract. 2024, 8, 109. [Google Scholar] [CrossRef]
- N’doye, I.; Laleg-Kirati, T.M.; Darouach, M.; Voos, H. Adaptive observer for nonlinear fractional-order systems. Int. J. Adapt. Control Signal Process. 2017, 31, 314–331. [Google Scholar] [CrossRef]
- Naifar, O.; Assaad, J.; Ben Makhlouf, A. Non-fragile H∞ observer for Lipschitz conformable fractional-order systems. Asian J. Control 2022, 24, 2202–2212. [Google Scholar] [CrossRef]
- Thuan, M.V.; Huong, D.C.; Sau, N.H.; Ha, Q.T. Unknown input fractional-order functional observer design for one-side Lipschitz time-delay fractional-order systems. Trans. Inst. Meas. Control 2019, 41, 4311–4321. [Google Scholar] [CrossRef]
- Alsharif, A.O.M.; Jmal, A.; Naifar, O.; Ben Makhlouf, A.; Rhaima, M.; Mchiri, L. Unknown Input Observer Scheme for a Class of Nonlinear Generalized Proportional Fractional Order Systems. Symmetry 2023, 15, 1233. [Google Scholar] [CrossRef]
- Alsharif, A.O.M.; Jmal, A.; Naifar, O.; Ben Makhlouf, A.; Rhaima, M.; Mchiri, L. State Feedback Controller Design for a Class of Generalized Proportional Fractional Order Nonlinear Systems. Symmetry 2023, 15, 1168. [Google Scholar] [CrossRef]
- Issaoui, R.; Naifar, O.; Tlija, M.; Mchiri, L.; Ben Makhlouf, A. Practical Stability of Observer-Based Control for Nonlinear Caputo–Hadamard Fractional-Order Systems. Fractal Fract. 2024, 8, 531. [Google Scholar] [CrossRef]
- He, B.-B.; Zhou, H.-C.; Kou, C.-H. Stability analysis of Hadamard and Caputo-Hadamard fractional nonlinear systems without and with delay. Fract. Calc. Appl. Anal. 2022, 25, 2420–2445. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).