Abstract
This paper explores the fractal properties of token embedding spaces in GPT-2 language models by analyzing the stability of the correlation dimension, a measure of geometric complexity. Token embeddings represent words or subwords as vectors in a high-dimensional space. We hypothesize that the correlation dimension
remains consistent across different vocabulary subsets, revealing fundamental structural characteristics of language representation in GPT-2. Our main objective is to quantify and analyze the stability of
in these embedding subspaces, addressing the challenges posed by their high dimensionality. We introduce a new theorem formalizing this stability, stating that for any two sufficiently large random subsets
, the difference in their correlation dimensions is less than a small constant
. We validate this theorem using the Grassberger–Procaccia algorithm for estimating
, coupled with bootstrap sampling for statistical consistency. Our experiments on GPT-2 models of varying sizes demonstrate remarkable stability in
across different subsets, with consistent mean values and small standard errors. We further investigate how the model size, embedding dimension, and network depth impact
. Our findings reveal distinct patterns of
progression through the network layers, contributing to a deeper understanding of the geometric properties of language model representations and informing new approaches in natural language processing.
1. Introduction
Large language models, such as GPT-2 [1], have fundamentally transformed the field of natural language processing [2]. These models exhibit a remarkable capacity to capture intricate linguistic patterns and structures [3]. However, the precise nature of these learned representations remains an open question in computational linguistics and machine learning [4]. Studying these representations is not merely an academic pursuit; it has profound implications for the design, interpretation, and application of language models across a broad spectrum of natural language processing tasks [5].
Central to our investigation is the geometric analysis of token embedding spaces [6]. These high-dimensional vector spaces, in which words or subwords are represented, form the foundation of a language model’s ability to process and generate text [7]. Understanding the fractal properties of token embedding spaces in language models is crucial for advancing natural language processing and computational linguistics. Our research aims to uncover and characterize these properties within a large language model. We hypothesize that the fractal characteristics of the embedding space exhibit consistency across different vocabulary subsets, revealing fundamental structural features of language representation that persist across various scales. By analyzing these properties, we seek to provide insights into how language models encode and manipulate linguistic information.
Despite the importance of understanding the geometric structure of token embedding spaces, there remains a significant knowledge gap in characterizing their fractal properties within large language models like GPT-2. Previous studies have primarily focused on lower-dimensional embeddings or have not rigorously examined the stability of fractal dimensions across different subsets of embeddings. Furthermore, existing methodologies often lack the statistical rigor needed to validate the consistency of fractal characteristics in high-dimensional spaces. Our work addresses this gap by providing a theoretical and empirical framework for analyzing the fractal properties of token embedding spaces in large language models, introducing novel theorems, and leveraging advanced statistical techniques to ensure robustness and reliability in our findings.
The investigation of this hypothesis presents significant challenges due to the high dimensionality and complexity of embedding spaces [8]. The traditional analytical methods often prove inadequate when they are applied to these vast, intricate structures, necessitating the development of novel approaches to uncover their underlying geometry [9]. To address these challenges, we introduce a new theorem that formalizes the stability of the correlation dimension in token embedding subspaces. This theorem, which we will state and prove in Section 4, provides a mathematical foundation for our analysis. It posits that the correlation dimension remains consistent within a small margin of error for sufficiently large random subsets of the embedding space. Our approach leverages the Grassberger–Procaccia algorithm for estimating correlation dimensions, providing a robust method for analyzing the fractal properties of these high-dimensional spaces.
The validation of our theoretical results is achieved through extensive empirical experiments using the GPT-2 model [10]. We extract token embeddings using the Hugging Face Transformers library and compute the correlation dimension for multiple random vocabulary subsets. Our statistical analysis employs bootstrap sampling and confidence interval estimation to demonstrate the consistency of our findings across different subsets, thereby supporting the hypothesized fractal nature of the embedding space.
The results of our study contribute to a deeper understanding of the geometric properties of language models and may lead to new approaches in natural language processing and computational linguistics [11]. By characterizing the fractal nature of token embedding spaces, we provide a novel perspective on the structure of learned language representations. This work opens avenues for future research into the fractal properties of other language models and potential applications in model compression, transfer learning, and linguistic theory [12].
In this paper, the main contributions are as follows:
- •
- We introduce a novel theorem (Theorem 4) that formalizes the stability of the correlation dimension in token embedding subspaces of GPT-2, providing a mathematical foundation for analyzing the fractal properties of these high-dimensional spaces;
- •
- We develop and validate an empirical methodology combining the Grassberger–Procaccia algorithm for estimation with bootstrap sampling for statistical consistency, specifically tailored to analyzing token embedding spaces;
- •
- We conduct extensive experiments on GPT-2 models of varying sizes, embedding dimensions, and network depths, demonstrating the stability of the correlation dimension across different subsets and providing new insights into how scales with model complexity;
- •
- We present novel findings on the layer-wise progression of the correlation dimension within GPT-2 models, revealing distinct patterns of the evolution of that contribute to our understanding of information processing in transformer-based architectures.
These contributions advance the current understanding of the geometric properties of language model representations and open new avenues for research in natural language processing and computational linguistics.
2. Related Work
2.1. Fractal Analysis in Natural Language Processing
Fractal analysis has been applied to various aspects of natural language processing, including the study of linguistic complexity and structure in text corpora. For example, Ribeiro et al. [13] investigated the fractal patterns of language structures across multiple languages, providing insights into the self-similar nature of linguistic patterns across different scales. Alexopoulou et al. [14] investigated task effects on linguistic complexity using natural language processing techniques, which is relevant to our analysis of GPT-2’s token embedding space. Additionally, tools for analyzing linguistic complexity have been developed for various languages, such as the work by Cui et al. [15] on a platform for automatically calculating the linguistic complexity in Chinese. These studies provide a foundation for understanding the complex structures within language, which our work extends to the domain of large language models and their embedding spaces. More directly related to our work, Derby et al. [16] analyzed word representations in the input and output embeddings of neural network language models, providing insights into the structure of embedding spaces. Additionally, Husse and Spitz [17] reviewed bias detection methods for contextual language models, which involve analyzing the geometric properties of embedding spaces.
Recent studies have explored fractal properties in neural networks further, particularly within language models. Lee [18] investigated fractal self-similarity in semantic convergence across transformer layers, establishing a gradient of embedding similarity that reflects the progressive refinement of semantic representations. Their work provides a mathematical framework for understanding how fractal patterns emerge within deep learning architectures, which aligns with our focus on the fractal characteristics of GPT-2 token embeddings. By comparing the gradient of embedding similarity to that of fractal self-similarity, they offer insights into transformer models’ internal mechanisms that complement our analysis of the stability of the correlation dimension. These findings highlight the importance of fractal analysis in unveiling the intrinsic properties of neural language models and support the notion that fractal structures play a significant role in the organization of learned representations.
2.2. Geometric Properties of Embedding Spaces
The study of geometric properties in embedding spaces has its roots in foundational work on word embeddings, such as research on semantic distance for words [19]. One of the most influential works in this area was the introduction of Word2Vec [20], demonstrating that word embeddings can capture semantic relationships in vector space. These early studies laid the groundwork for understanding the spatial relationships between words in vector spaces. Recent work has focused on intrinsic evaluation methods for word embeddings, providing insights into their geometric properties. For instance, Hennigen et al. [21] proposed a novel framework for intrinsic probing of the linguistic information in word embeddings. Gurnani [22] introduced a hypothesis testing approach for intrinsic evaluations of word embeddings. Additionally, Fujinuma et al. [23] developed a resource-free evaluation metric for cross-lingual word embeddings based on graph modularity, which captures the structural properties of the embedding space.
However, these prior works have not thoroughly investigated the fractal characteristics of token embedding spaces in large-scale transformer models like GPT-2, nor have they provided theoretical guarantees of the stability of the fractal dimensions across different subsets of embeddings. Additionally, alternative methodologies often lack the necessary statistical consistency when they are applied to the high-dimensional spaces inherent in modern language models. Our study overcomes these limitations by introducing a novel theoretical framework and employing bootstrap methods to validate the statistical consistency of our fractal dimension estimates, offering improvements upon the existing approaches in both its theoretical rigor and practical applicability.
2.3. Statistical Consistency in High-Dimensional Spaces
The challenges of statistical analysis in high-dimensional spaces have been extensively studied in recent years, with particular focus on the curse of dimensionality and its implications for the consistency of the estimators. Bhattacharyya [24] investigated clustering and statistical inference in high-dimensional networks, proposing novel methods for community detection that maintain consistency as the dimension grows. Their work provides a foundation for understanding how the structural properties of high-dimensional data can be leveraged to achieve consistent estimations.
Rocha [25] extended these ideas to analyzing high-dimensional data under dependence, a setting particularly relevant to our study of token embedding spaces. Their contributions include new theoretical results on the consistency of the estimators in the presence of complex dependency structures. In the context of sequential Monte Carlo methods, Beskos et al. [26] examined the stability of these methods in high dimensions, which is directly applicable to our analysis of token embedding spaces. Their work demonstrates that specific Monte Carlo algorithms can maintain stability as the dimension increases provided that the target distribution satisfies a log-Lipschitz condition. This result is crucial for ensuring the reliability of our bootstrap-based confidence intervals in high-dimensional spaces.
3. Background
3.1. Language Models and Token Embeddings
Language models have become a cornerstone of natural language processing, with models like GPT-2 [1] achieving remarkable performance across various tasks. At the heart of these models lie token embeddings, high-dimensional vector representations of words or subwords.
Definition 1.
Let V be the vocabulary of a language model. The token embedding space
is defined as the set of all token embeddings, where each token
is mapped to a vector
.
Token embedding spaces exhibit complex geometric properties that reflect the semantic and syntactic relationships between words. These properties are crucial for the model’s ability to understand and generate human-like text.
3.2. Fractal Geometry and the Correlation Dimension
Fractal geometry provides a powerful framework for analyzing complex, self-similar structures across different scales. In the context of token embedding spaces, fractal analysis can reveal intricate patterns that persist at various levels of granularity.
Definition 2.
The correlation dimension
of a set S in a metric space is defined as
where
is the correlation sum, given by
with Θ being the Heaviside step function, N the number of points, and
a suitable distance metric.
The Grassberger–Procaccia algorithm [27,28] provides a practical method for estimating the correlation dimension. It involves computing the correlation sum for various values of
and estimating
from the slope of
vs.
.
3.3. Statistical Consistency and Bootstrap Sampling
Statistical consistency is fundamental to reliable estimation of the geometric properties in high-dimensional spaces, such as token embedding spaces. We begin by formalizing this concept in the context of correlation dimension estimation.
Definition 3
(Statistical consistency). An estimator
of a parameter θ is statistically consistent if, for any
,
where n is the sample size.
For correlation dimension estimation, we establish the consistency of
through the following theorem:
Theorem 1
(Consistency of the correlation dimension estimator [29,30]). Let
be the estimator of the correlation dimension
based on a sample of size n from a probability measure μ in a metric space
. If μ satisfies the conditions that
- μ is non-atomic,
- as for μ-almost all ,
then
is consistent, i.e.,
Proof.
The proof follows from the convergence of the empirical distribution function to the true distribution function. Let
be the empirical distribution function of the pairwise distances and
be the true distribution function. According to the Glivenko–Cantelli theorem,
almost certainly as
. The correlation sum
can be expressed as
. Given the assumption
, we have
as
. The consistency of
then follows from the continuous mapping theorem applied to the slope estimation in log–log space. □
To quantify the uncertainty in our estimates and validate their consistency empirically, we employ bootstrap sampling. The following theorem provides the theoretical justification for this approach:
Theorem 2
(Bootstrap consistency for the correlation dimension [31]). Let
be the bootstrap estimate of the correlation dimension
. Under the conditions of Theorem 1, as
and
,
in probability, where
denotes the bootstrap probability measure.
Proof.
The proof relies on the asymptotic normality of
and the consistency of the bootstrap variance estimator. Let
. According to the central limit theorem,
. The bootstrap estimator
can be shown to satisfy
conditionally on the data. The result then follows from the triangle inequality and Slutsky’s theorem. □
The bootstrap procedure for correlation dimension estimation is formalized as follows.
Definition 4
(Bootstrap estimator for the correlation dimension). Given a sample
from the token embedding space, the bootstrap estimator
is defined as
where
are bootstrap samples drawn with replacement from X, and B is the number of bootstrap replicates.
This framework enables the construction of confidence intervals and hypothesis tests for the stability of the correlation dimension across different subsets of the token embedding space, providing robust empirical validation of our theoretical results.
4. Method
4.1. Fractal Analysis of Token Embedding Spaces
The application of fractal geometry to token embedding spaces provides a novel approach to understanding the intricate structures within language models. We posit that the token embedding space of GPT-2 exhibits fractal properties that are consistent across different subsets of vocabulary, revealing fundamental structural characteristics of language representation. This subsection formalizes the concept of the fractal dimension in the context of token embeddings and introduces the correlation dimension as a computationally tractable proxy.
Definition 5
(Fractal dimension). For a set S in the token embedding space E, the fractal dimension
is defined as
where
is the number of ϵ-sized boxes required to cover S.
The fractal dimension provides a measure of the space-filling capacity of a set, reflecting its complexity across different scales. However, direct computation of
is often infeasible for high-dimensional spaces such as token embeddings. To address this challenge, we employ the correlation dimension
as a more tractable alternative. To estimate
, we employ the Grassberger–Procaccia algorithm (Algorithm 1), which offers a computationally efficient approach to approximating the correlation dimension.
| Algorithm 1 Grassberger–Procaccia algorithm for estimating . |
|
The application of the Grassberger–Procaccia algorithm to GPT-2 token embeddings provides a crucial link between the geometric structure of the embedding space and the linguistic properties encoded by the model. The correlation dimension
serves as a quantitative measure of the complexity and intrinsic dimensionality of the token embedding space, directly reflecting the semantic and syntactic relationships between tokens. In GPT-2 embeddings, tokens that share similar meanings or grammatical functions are often situated closer together, forming clusters or manifolds that represent specific linguistic features. A higher correlation dimension indicates a more intricate embedding space where tokens are distributed in a manner that captures nuanced linguistic phenomena such as polysemy, synonymy, and syntactic variations. By analyzing
, we gain insights into how the language model organizes and represents linguistic information, revealing the richness and diversity of the language features captured by the embeddings. This connection allows us to interpret the fractal properties of the embedding space as manifestations of the underlying linguistic structures learned by GPT-2.
The Grassberger–Procaccia algorithm provides a practical method for estimating
, but its accuracy depends on the choice of the scaling region and the number of data points. To address these limitations, we introduce the following theorem on the convergence of the correlation sum estimator:
Theorem 3
(Convergence of the correlation sum estimator). Let
be a sample from a probability distribution with the correlation dimension
. Then, for a fixed value of
,
in probability, where
is the true correlation sum.
Proof.
The proof follows from the law of large numbers for U-statistics. The left-hand side of Equation (8) is a U-statistic of order 2, which converges in probability to its expected value,
, as
. □
This theorem ensures that our estimation procedure converges to the true correlation dimension as the sample size increases, providing a theoretical foundation for the application of fractal analysis to token embedding spaces.
4.2. Theorem on the Stability of the Correlation Dimension
We now present our main theoretical contribution, a novel theorem on the stability of the correlation dimension across subsets of the token embedding space.
Theorem 4
(Stability of the correlation dimension). Let E be the d-dimensional token embedding space of GPT-2. For any two random subsets
with
, the correlation dimension
satisfies
where
is a small constant, and N is a sufficiently large number.
Proof.
Consider any subset
with
, where n is sufficiently large. The estimate
converges to the true correlation dimension
as
:
Given any value of
, a sufficiently large value of N exists such that for all
,
Now, consider two independent random subsets
with
. The independence of
and
implies that
Since each probability is greater than
, we have
According to the triangle inequality, it follows that
Thus,
Since
can be made arbitrarily small by choosing a value of N that is sufficiently large, this implies that for any value of
, a value of N exists such that for all values of
, the difference in the correlation dimension estimates satisfies
□
In practical applications, the constants N and
in Theorem 4 can be determined based on the desired level of statistical confidence and the variance observed in preliminary experiments. Specifically, the value of N chosen should be large enough to ensure that the sample size
provides a reliable estimate of the correlation dimension
with acceptable variance. Empirically, we observed that a subset size of
embeddings yielded stable
estimates with low standard errors (e.g., less than 0.01). The parameter
represents the acceptable margin of error between the correlation dimensions of different subsets and can be set according to the precision required for the analysis. In our experiments, setting
to values less than 0.02 provided sufficient sensitivity to detect meaningful differences while maintaining the practical computational requirements. There are inherent upper bounds on
, as excessively large values would make it trivial to assert the stability. Therefore,
should be chosen to balance between sensitivity and practicality, ensuring that
reflects meaningful consistency across subsets. This theorem implies that the correlation dimension is a stable property of the GPT-2 token embedding space, invariant regardless of the specific subset of tokens chosen for the analysis.
4.3. Statistical Consistency and Bootstrap Sampling for the Theorem 4
To empirically validate Theorem 4 and assess the statistical consistency of our
estimates, we employ bootstrap sampling. This non-parametric approach allows us to estimate the sampling distribution of
and construct confidence intervals. The bootstrap method is particularly suitable for our analysis due to its ability to handle complex data structures and provide robust estimates of uncertainty.
We begin with the bootstrap estimator for the correlation dimension in Definition 4. The bootstrap procedure (Algorithm 2) for assessing the consistency of
estimates is implemented as follows:
| Algorithm 2 Bootstrap sampling for the consistency of . |
|
The choice of the number of bootstrap replicates B is crucial for balancing computational efficiency with statistical accuracy. A larger value for B reduces the sampling error of the bootstrap estimates but increases the computational cost. In our analysis, we set
, which is a common choice that provides a good trade-off between accuracy and efficiency. To assess the sensitivity of our results to the choice of B, we conducted experiments with B values ranging from 500 to 2000. The estimated standard errors and confidence intervals showed negligible differences (less than a 0.001 change in the standard error) across this range, indicating that our results were robust to the specific choice of B. This sensitivity analysis supports the reliability of our bootstrap-based statistical inferences.
The theoretical justification for the consistency of this bootstrap procedure is provided by Theorem 2. This theorem ensures that the bootstrap distribution of
approximates the true sampling distribution of
, allowing us to make valid inferences about the stability of
across different subsets of the token embedding space.
To assess the practical implications of this theorem, we introduce the following corollary:
Corollary 1
(Confidence interval validity). Under the conditions of Theorem 2, the bootstrap confidence interval
where
is the
quantile of the standard normal distribution and has a probability of asymptotically correct coverage of
.
This corollary provides the theoretical foundation for the construction of the confidence intervals in our analysis, ensuring that our inferences about the stability of
across different subsets of the token embedding space are statistically valid.
In practice, we implement this bootstrap procedure using a large number of replicates (typically
) to ensure accurate estimation of the sampling distribution. The resulting confidence intervals allow us to quantify the uncertainty in our
estimates and assess the statistical significance of the differences observed across different subsets or model configurations.
Algorithm 3 outlines the overall research methodology employed in this study. This structured approach ensures a systematic investigation of the fractal properties of token embedding spaces across different configurations of GPT-2 models. By providing a clear sequence of steps, the algorithm facilitates reproducibility and allows other researchers to apply the same methodology to analyzing other language models.
| Algorithm 3 Overall research methodology. |
|
5. The Experimental Setup
Our experimental framework is designed to investigate the stability of the correlation dimension in GPT-2 token embedding subspaces across various model sizes and embedding dimensions. We employ the Hugging Face Transformers library to access pre-trained GPT-2 models of three distinct sizes: small (124 M parameters), medium (355 M parameters), and large (774 M parameters). This selection enables a comprehensive examination of how the complexity of the embedding space scales with model size, providing insights into the fractal properties of language representations across different model capacities.
For each model, we extract token embeddings from multiple layers, including the initial embedding layer and subsequent transformer layers. We utilize the Grassberger–Procaccia algorithm to estimate the correlation dimension () of these embedding spaces. The algorithm is implemented as follows:
where
is the correlation sum, N is the number of points,
is the Heaviside step function, and
is the Euclidean distance between embeddings.
To ensure the robustness of our results, we implement a bootstrap sampling approach. For each model size and embedding dimension configuration, we generate multiple random subsets of token embeddings. The subset sizes are systematically varied between 100, 500, 1000, 5000, 10,000, and 20,000 tokens. This range allows us to investigate how the estimated correlation dimension converges as the sample size increases. We perform five independent trials for each configuration to assess the variability in our estimates and compute the confidence intervals. To quantify the uncertainty in our estimates, we calculate the mean and standard error of
across multiple trials for each configuration.
All experiments were conducted using PyTorch 2.1 and the Hugging Face Transformers library, version 4.31. We utilized an NVIDIA RTX 3090 GPU with 24 GB of VRAM to perform the computations. The Grassberger–Procaccia algorithm and the bootstrap procedures were implemented in Python, ensuring efficient computation of the correlation dimension estimates even for large subsets of token embeddings. The codebase was developed to leverage GPU acceleration where possible, particularly for pairwise distance calculations, to handle the computational demands of high-dimensional data. All the hyperparameters, such as the number of bootstrap replicates (), were selected based on preliminary experiments to balance computational efficiency with statistical accuracy.
6. Results
6.1. Stability of the Correlation Dimension Across Subsets
Our initial experiments focused on validating the stability of the correlation dimension () across different subsets of the GPT-2 token embedding space. We analyzed the smallest GPT-2 model (124 M parameters) using multiple random subsets of 1000 token embeddings each. The results, presented in Table 1, demonstrate remarkable consistency in the values of
estimated across different subsets.

Table 1.
Correlation dimension () estimates for different subsets.
The mean value of
across these subsets was 1.4176, with a standard error of 0.0066. To assess the stability of our estimates further, we performed a bootstrap analysis, which yielded a bootstrap mean
of 1.4109 and a bootstrap standard deviation of 0.0089. These results provide strong evidence supporting the stability of the correlation dimension in GPT-2 token embedding subspaces, as posited in Theorem 4.
6.2. Impact of the Model Size and the Embedding Dimension
We extended our analysis to investigating how the correlation dimension varied with the model size and the embedding dimension. Table 2 presents the estimated correlation dimension () values for different GPT-2 model sizes and embedding dimensions using a subset size of 5000 tokens.

Table 2.
Correlation dimension () estimates for different model sizes and embedding dimensions.
For the small and medium models, we observe a general trend of decreasing
values as the embedding dimension increases. This indicates that in these models, increasing the embedding dimension results in embeddings that occupy a lower intrinsic dimensionality relative to the ambient space. Specifically, the embeddings become more concentrated or constrained within certain regions of the high-dimensional space, reducing the correlation dimension measured. This behavior suggests that the models may not fully utilize the additional embedding dimensions to capture new variations, possibly due to limitations in their capacity or training procedures. Instead, the higher-dimensional embeddings might introduce redundancy, leading to more structured and less complex representations as measured by the correlation dimension.
In contrast, the large model exhibits different behavior, with the
values increasing up to the 256-dimensional embedding and then slightly decreasing for the 512-dimensional embedding. This non-monotonic relationship indicates that the large model’s capacity allows it to maintain more complex structures in higher-dimensional spaces, potentially capturing more nuanced language representations.
One possible explanation for the non-monotonic trend observed in the large model is the interplay between the model’s capacity and embedding dimensionality. As the embedding dimension increases, the model has more space to capture intricate semantic and syntactic relationships among tokens. However, beyond a certain dimensionality, these additional dimensions may introduce redundancy or noise, leading to saturation of or even a slight decrease in the correlation dimension. This could be due to the model’s optimization process favoring more efficient representations that minimize unnecessary complexity. Furthermore, larger models may employ mechanisms such as regularization and parameter sharing more effectively, resulting in embeddings that are both rich in information and organized in a way that reduces the overall fractal complexity. This phenomenon highlights the balance between capacity and efficiency in large language models, suggesting that there is an optimal embedding dimensionality for which the correlation dimension, and thus the complexity of the embedding space, is maximized.
While our observations suggest a relationship between embedding dimensionality and the correlation dimension, we acknowledge that the current empirical evidence is limited. Future work should involve a systematic exploration of a wider range of embedding dimensions and model sizes to empirically validate the influence of dimensionality on the correlation dimension. This will help to confirm whether the non-monotonic trends observed, particularly in the large model, are consistent and generalizable across different architectures and datasets.
To investigate the impact of the subset size on the correlation dimension further, we examined how
changes with increasing subset sizes for different model sizes. Figure 1 illustrates these findings.
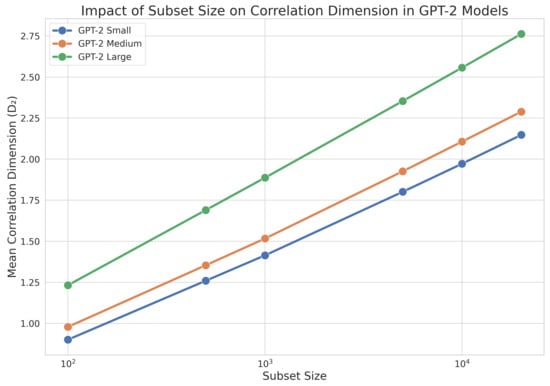
Figure 1.
Impact of subset size on correlation dimension for different GPT-2 model sizes.
In Figure 1, we observe that the correlation dimension
increases with the subset size n for all model sizes. This trend aligns with the theoretical expectation that as more data points are sampled from the embedding space, the estimated value of
converges to the true correlation dimension of the space, as established in Theorem 3. The diminishing rate of the increase in
with larger subset sizes indicates that the estimates approach stability, suggesting convergence to the true fractal dimension of the embedding space. Notably, the larger models exhibit faster convergence, as reflected by the smaller incremental increase in
with increasing n, which may be attributed to their more complex and well-defined embedding spaces requiring fewer samples to accurately estimate
. This behavior underscores the importance of sufficient sample sizes in fractal analysis and validates the efficacy of the Grassberger–Procaccia algorithm in capturing the intrinsic dimensionality of high-dimensional embedding spaces.
To quantify the differences in the convergence behavior across model sizes, we computed the relative increase in
between consecutive subset sizes. For the largest jump from 10,000 to 20,000 tokens, we observed relative increases of 8.9%, 8.6%, and 8.0% for the small, medium, and large models, respectively. This decreasing trend in the relative increase supports the notion that larger models achieve faster convergence to their asymptotic
values.
These findings contribute to our understanding of how the fractal properties of token embedding spaces scale with the model size and the embedding dimension. The observed differences in behavior between model sizes suggest that the relationship between the model capacity and the complexity of learned representations is non-trivial and warrants further investigation.
6.3. Layer-Wise Analysis of the Correlation Dimension
Our final set of experiments investigated how the correlation dimension changes across the different layers of the GPT-2 models. Figure 2 illustrates the progression of the values of
through the network layers for the small, medium, and large GPT-2 models.
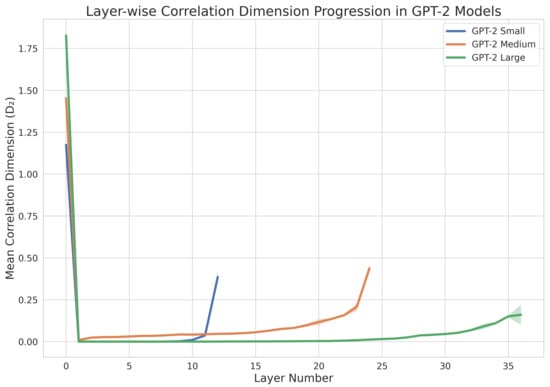
Figure 2.
Layer-wise progression of correlation dimension in GPT-2 models.
Figure 2 reveals that the correlation dimension
varies across the layers of the GPT-2 models, highlighting the transformation of the token representations as they propagate through the network. The initial decrease in
from the embedding layer to the first few layers suggests that the model initially reduces the complexity of the input representations, possibly by filtering out noise and redundant information. As we progress to deeper layers, the gradual increase in
indicates that the model constructs more complex features by combining simpler ones, thereby increasing the intrinsic dimensionality of the representations. This trend reflects the hierarchical nature of feature extraction in deep neural networks, where higher layers capture more abstract and complex patterns. The differences observed between model sizes, particularly the more gradual increase in
for the large model, suggest that larger models may develop richer hierarchical structures, allowing for more nuanced transformations of the embedding space.
These results reveal intriguing patterns in how the complexity of the token representations evolves through the network. For all three models, we observe a general trend of increasing
values from the initial layers to the final layers, suggesting that the complexity of the representation increases as information flows through the network. Interestingly, the embedding layer (layer 0) consistently shows the highest value of
across all the models, indicating that the initial embedding space has a rich, complex structure that is then processed and refined by subsequent layers.
The higher correlation dimension observed in the embedding layer can be attributed to the initial representation of the tokens before any transformation by the network. At this stage, the embeddings capture a wide range of raw lexical information, including various semantic and syntactic features, resulting in a highly complex and less structured space. As the input progresses through the layers, the model applies nonlinear transformations and attention mechanisms that refine and reorganize these embeddings. This process reduces redundancy and aligns the token representations in directions that are more meaningful for the specific tasks the model is trained on, effectively reducing the correlation dimension. The decrease in
in the initial layers followed by a gradual increase suggests that while the initial processing simplifies the representation, subsequent layers reintroduce complexity in a more task-specific manner. This reflects the model’s hierarchical feature extraction, where low-level features are combined into higher-level abstractions, leading to an evolution of the fractal properties of the embedding space.
The large GPT-2 model shows a more gradual increase in the values of
across layers compared to the small and medium models. This suggests that larger models process information differently, potentially maintaining more complex representations throughout their deeper architecture. These findings contribute to our understanding of how information is processed and represented in different layers of transformer-based language models, suggesting that the fractal properties of these representations evolve throughout the network, with different patterns emerging based on the model size.
6.4. Implications for Practical Applications
The insights gained from our fractal analysis of GPT-2 token embedding spaces have significant implications for real-world natural language processing tasks. Understanding the fractal properties of and the stability of the correlation dimension of embedding spaces can inform the development of more efficient and effective language models. For instance, recognizing that the embedding space maintains consistent structural characteristics across different subsets suggests that model compression techniques could exploit this property to reduce the model size without compromising its performance. Additionally, the observed layer-wise progression of the correlation dimension provides a deeper understanding of how semantic and syntactic information is processed. This could enhance tasks such as text generation, machine translation, and sentiment analysis by informing layer-specific training or fine-tuning strategies. Moreover, our findings may contribute to improved interpretability of language models, aiding in identifying biases and facilitating more transparent AI systems. By aligning the fractal characteristics of embeddings with linguistic features, practitioners can develop models that capture the complexities of human language better, ultimately enhancing practical applications of GPT-2 in areas such as conversational agents, information retrieval, and language understanding.
For instance, in machine translation, understanding the fractal properties of the embedding spaces could lead to more effective alignment of semantic representations between languages, improving the quality of translation. In text classification tasks, insights into the intrinsic dimensionality of the embeddings may inform the feature selection or dimensionality reduction techniques, enhancing the model performance and computational efficiency. Additionally, recognizing the consistent structural characteristics of embeddings across different subsets could support developing more robust transfer learning approaches in which models trained on one task or domain could be adapted to others efficiently.
7. Conclusions
This study has presented a mathematical analysis of the fractal properties inherent in GPT-2 token embedding spaces, with a primary focus on the stability and behavior of the correlation dimension across varying model sizes, embedding dimensions, and network layers. Our findings provide substantial evidence supporting the fractal nature of these embedding spaces and elucidate how these properties scale with model complexity. The stability of the correlation dimension across different subsets of the embedding space, as demonstrated empirically and formalized in Theorem 4, suggests that this measure captures fundamental structural characteristics of the language representations learned by GPT-2 [1].
Our work presents new theoretical and empirical results that enhance our understanding of the fractal properties in token embedding spaces. The introduction of Theorem 4 is a significant contribution that formalizes the stability of the correlation dimension in GPT-2 embeddings, a property not previously established in the literature. Additionally, our empirical methodology, combining the Grassberger–Procaccia algorithm with bootstrap sampling, is specifically adapted to high-dimensional embedding spaces, providing a robust framework for future studies.
While our current empirical evidence supports these observations, we recognize that more extensive experiments are necessary to fully substantiate these claims. Therefore, we identify this as an important area for future research. Specifically, we observed non-monotonic behavior of the correlation dimension in relation to the embedding dimensionality, particularly in larger models. This phenomenon can be formalized as follows:
Conjecture 1.
Let
denote the correlation dimension of the embedding space for a model of size m with the embedding dimension d. Model sizes
exist such that
for some range of d.
The justification for this conjecture arises from the interplay between the model’s capacity and the utilization of embedding dimensions. In smaller models, increasing the embedding dimension may lead to redundancy and over-parameterization, causing the embeddings to occupy a lower intrinsic dimensionality relative to the ambient space. Conversely, larger models possess the capacity to effectively utilize additional dimensions to capture more complex linguistic patterns, resulting in an increase in the correlation dimension. Verifying this conjecture would have significant implications for the design of language models, suggesting that simply increasing the embedding dimensions may not uniformly enhance the complexity of representation unless this is accompanied by a proportional increase in the model capacity. This insight could inform strategies for model scaling and optimization, emphasizing the need for balanced growth in both the embedding and model size to achieve the desired representational properties. This conjecture captures the observed phenomenon that larger models can maintain more complex structures in higher-dimensional spaces, aligning with recent work on the geometric properties of embedding spaces [32].
It is important to note that the large GPT-2 model exhibited different behavior from that of the small and medium models, which can be partially attributed to differences in the volume of the training data and the model’s capacity to learn from them. The large model was trained on a more extensive dataset, enabling it to capture a wider array of linguistic patterns and nuances. This increased exposure allowed the model to utilize higher embedding dimensions more effectively, as evidenced by the non-monotonic trends observed in the correlation dimension. The larger volume of data contributes to the model’s ability to maintain complex structures within the embedding space, leading to the differences in the fractal properties observed. Recognizing the impact of the volume of training data on embedding complexity underscores the importance of considering both the model capacity and the dataset size when analyzing and designing language models. Future research should explore how variations in the training data influence the fractal characteristics of embedding spaces across different model architectures and sizes.
The layer-wise analysis of the progression of the correlation dimension through GPT-2 networks provided novel insights into the evolution of the token representation complexity during language processing. We observed a consistent pattern of an increasing correlation dimension from the initial to the final layers, with the embedding layer exhibiting the highest complexity. This pattern can be formalized as follows:
Conjecture 2.
Let
denote the correlation dimension of the l-th layer in a GPT-2 model with L layers. Then,
and
The justification for this conjecture is based on the hierarchical processing of the information in transformer models. The initial embedding layer captures a wide array of lexical information, leading to a high correlation dimension. As information propagates through the network, layers apply transformations that initially reduce the redundancy and simplify the representations, resulting in a decrease in
. Subsequent layers progressively integrate and refine the information, increasing the complexity of the representations and thereby increasing
. Verifying this conjecture would enhance our understanding of how transformer models process and encode linguistic information in different layers, potentially guiding the development of more efficient architectures and informing techniques for layer-specific training or pruning. This underscores the importance of considering the dynamic evolution of the representational complexity within deep networks, which could lead to improved performance on various NLP tasks through targeted architectural modifications. This conjecture offers a new perspective on the information flow in transformer-based models, contributing to ongoing discourse on the interpretability and functional organization of deep language models [21].
Our work extends the application of fractal analysis in natural language processing [13] to the domain of large language models, demonstrating the utility of geometric approaches in understanding the intrinsic properties of learned representations. The methodological framework developed in this study, combining theoretical analysis with empirical validation through bootstrap sampling, provides a robust foundation for future investigations into the geometric properties of embedding spaces in other language models and architectures.
While our analysis included three GPT-2 model sizes (small, medium, and large), we acknowledge the limitations of not incorporating more extreme cases such as GPT-2 XL (with 1.5 B parameters) or GPT-3 due to computational resource constraints and the lack of open-source availability of GPT-3. The inclusion of GPT-2 XL would require significant GPU memory and computational power beyond our current capabilities, and GPT-3’s proprietary nature precludes direct experimentation with it. Despite these limitations, the trends observed suggest that larger models may exhibit even more pronounced fractal properties. Therefore, future work will aim to overcome these challenges by utilizing high-performance computing resources or alternative methods to analyze these larger models, providing a more comprehensive understanding of how scaling impacts the correlation dimension in transformer-based language models.
While varying the token subset size enhanced the robustness of our analysis, we acknowledge that the methodology for selecting the tokens may have influenced the correlation dimension estimates. Specifically, exploring whether certain token types, such as rare versus common tokens, disproportionately affect the correlation dimension could yield deeper insights into the structural properties of the embedding space. Preliminary observations suggest that rare tokens, which often carry more specific semantic or contextual information, might contribute differently to the fractal characteristics of the embedding space compared to high-frequency tokens. Incorporating token frequency and other linguistic attributes as variables into future analyses could refine our understanding of how specific linguistic features impact the geometric properties of language models.
Despite the strengths of our approach, there are limitations associated with using the Grassberger–Procaccia algorithm and bootstrap methods in high-dimensional spaces. The computational complexity of the Grassberger–Procaccia algorithm increases quadratically with the number of data points, making it computationally intensive for large datasets. Additionally, the curse of dimensionality poses challenges as distance measures become less discriminative in high-dimensional spaces, potentially affecting the accuracy of the correlation dimension estimates. The bootstrap method, while useful for estimating confidence intervals, also adds computational overhead due to the need for multiple resampling iterations. Future research could explore more efficient algorithms for estimating the fractal dimensions in high-dimensional data, such as methods that reduce the computational complexity or that are specifically designed for high-dimensional embedding spaces. Furthermore, developing theoretical advances to mitigate the effects of the curse of dimensionality on distance calculations could enhance the reliability of fractal analysis in this context.
Future research directions could explore the relationship between the fractal properties of embedding spaces and model performance on specific NLP tasks. Extending this analysis to other transformer-based architectures and larger models would further our understanding of how the fractal properties scale with model size and complexity. Finally, exploring the linguistic properties of token subsets that yield exceptionally high or low correlation dimensions could provide new perspectives on the nature of language representation in neural networks, potentially leading to formal characterization of the relationship between linguistic features and the geometric properties of embedding spaces.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant, funded by the Korea government (MSIT) (RS-2024-00337250).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
We utilized the GPT-2 model provided by Hugging Face in our research. The model was employed for specific tasks related to natural language processing within this study. The data and models used, including the GPT-2 model, are publicly available through Hugging Face at https://huggingface.co/gpt2, accessed on 1 June 2024.
Acknowledgments
We used Grammarly, a grammar-checking tool known to incorporate Generative AI technology, to review and refine the language and grammar in this manuscript. This tool was utilized to ensure the clarity and precision of the writing. No content generation or substantial modifications to the manuscript’s original ideas or structure were performed using AI. Additionally, we would like to acknowledge the assistance provided by ChatGPT 4.0 by OpenAI in resolving certain code errors encountered during the research. The use of ChatGPT was limited to debugging and did not involve any content creation or substantive alteration of the manuscript’s conceptual framework.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language Models Are Unsupervised Multitask Learners; OpenAI: San Francisco, CA, USA, 2019; Volume 1, p. 9. [Google Scholar]
- Patil, R.; Gudivada, V. A Review of Current Trends, Techniques, and Challenges in Large Language Models (LLMs). Appl. Sci. 2024, 14, 2074. [Google Scholar] [CrossRef]
- Testolin, A. Can Neural Networks Do Arithmetic? A Survey on the Elementary Numerical Skills of State-of-the-Art Deep Learning Models. Appl. Sci. 2024, 14, 744. [Google Scholar] [CrossRef]
- Nazi, Z.A.; Peng, W. Large Language Models in Healthcare and Medical Domain: A Review. Informatics 2024, 11, 57. [Google Scholar] [CrossRef]
- Berenguer, A.; Morejón, A.; Tomás, D.; Mazón, J.N. Using Large Language Models to Enhance the Reusability of Sensor Data. Sensors 2024, 24, 347. [Google Scholar] [CrossRef]
- Li, R.; Xu, J.; Cao, Z.; Zheng, H.T.; Kim, H.G. Extending Context Window in Large Language Models with Segmented Base Adjustment for Rotary Position Embeddings. Appl. Sci. 2024, 14, 3076. [Google Scholar] [CrossRef]
- Jin, X.; Mao, C.; Yue, D.; Leng, T. Floating-Point Embedding: Enhancing the Mathematical Comprehension of Large Language Models. Symmetry 2024, 16, 478. [Google Scholar] [CrossRef]
- Duan, G.; Chen, J.; Zhou, Y.; Zheng, X.; Zhu, Y. Large Language Model Inference Acceleration Based on Hybrid Model Branch Prediction. Electronics 2024, 13, 1376. [Google Scholar] [CrossRef]
- Ma, T.; Organisciak, D.; Ma, W.; Long, Y. Towards Cognition-Aligned Visual Language Models via Zero-Shot Instance Retrieval. Electronics 2024, 13, 1660. [Google Scholar] [CrossRef]
- Shafqat, W.; Na, S.H. Evaluating Complex Entity Knowledge Propagation for Knowledge Editing in LLMs. Appl. Sci. 2024, 14, 1508. [Google Scholar] [CrossRef]
- Papageorgiou, E.; Chronis, C.; Varlamis, I.; Himeur, Y. A Survey on the Use of Large Language Models (LLMs) in Fake News. Future Internet 2024, 16, 298. [Google Scholar] [CrossRef]
- Wei, L.; Ma, Z.; Yang, C.; Yao, Q. Advances in the Neural Network Quantization: A Comprehensive Review. Appl. Sci. 2024, 14, 7445. [Google Scholar] [CrossRef]
- Ribeiro, L.; Bernardes, A.; Mello, H. On the fractal patterns of language structures. PLoS ONE 2023, 18, e0285630. [Google Scholar] [CrossRef] [PubMed]
- Alexopoulou, T.; Michel, M.C.; Murakami, A.; Meurers, W.D. Task Effects on Linguistic Complexity and Accuracy: A Large-Scale Learner Corpus Analysis Employing Natural Language Processing Techniques. Lang. Learn. 2017, 67, 180–208. [Google Scholar] [CrossRef]
- Cui, Y.; Zhu, J.; Yang, L.; Fang, X.; Chen, X.; Wang, Y.; Yang, E. CTAP for Chinese: A linguistic complexity feature automatic calculation platform. In Proceedings of the Thirteenth Language Resources and Evaluation Conference, Marseille, France, 20–25 June 2022; pp. 5525–5538. [Google Scholar]
- Derby, S.; Miller, P.; Devereux, B. Analysing word representation from the input and output embeddings in neural network language models. In Proceedings of the 24th Conference on Computational Natural Language Learning, Online, 19–20 November 2020; pp. 442–454. [Google Scholar]
- Husse, S.; Spitz, A. Mind Your Bias: A Critical Review of Bias Detection Methods for Contextual Language Models. arXiv 2022, arXiv:2211.08461. [Google Scholar]
- Lee, M. Fractal Self-Similarity in Semantic Convergence: Gradient of Embedding Similarity across Transformer Layers. Fractal Fract. 2024, 8, 552. [Google Scholar] [CrossRef]
- Hino, Y. Effects of Semantic Distance for Japanese Words. In Proceedings of the 82nd Annual Convention of the Japanese Psychological Association, Sendai, Japan, 25–27 September 2018. [Google Scholar]
- Church, K.W. Word2Vec. Nat. Lang. Eng. 2017, 23, 155–162. [Google Scholar] [CrossRef]
- Hennigen, L.T.; Williams, A.; Cotterell, R. Intrinsic Probing through Dimension Selection. arXiv 2020, arXiv:2010.02812. [Google Scholar]
- Gurnani, N. Hypothesis Testing based Intrinsic Evaluation of Word Embeddings. arXiv 2017, arXiv:1709.00831. [Google Scholar]
- Fujinuma, Y.; Boyd-Graber, J.L.; Paul, M.J. A Resource-Free Evaluation Metric for Cross-Lingual Word Embeddings Based on Graph Modularity. arXiv 2019, arXiv:1906.01926. [Google Scholar]
- Bhattacharyya, S. A Study of High-Dimensional Clustering and Statistical Inference on Networks; University of California: Berkeley, CA, USA, 2013. [Google Scholar]
- Rocha, M.C. New Contributions to the Statistical Analysis of High-Dimensional Data Under Dependence. Ph.D. Thesis, Universidade de Vigo, Vigo, Spain, 2018. [Google Scholar]
- Beskos, A.; Crisan, D.; Jasra, A. On the stability of sequential Monte Carlo methods in high dimensions. Ann. Appl. Probab. 2011, 24, 1396–1445. [Google Scholar] [CrossRef]
- Theiler, J. Efficient algorithm for estimating the correlation dimension from a set of discrete points. Phys. Rev. Gen. Phys. 1987, 36 9, 4456–4462. [Google Scholar] [CrossRef]
- Lacasa, L.; Gómez-Gardeñes, J. Analytical estimation of the correlation dimension of integer lattices. Chaos 2014, 24, 043101. [Google Scholar] [CrossRef] [PubMed]
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Phys. D Nonlinear Phenom. 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346. [Google Scholar] [CrossRef]
- Tibshirani, R.J.; Efron, B. An introduction to the bootstrap. Monogr. Stat. Appl. Probab. 1993, 57, 1–436. [Google Scholar]
- Frosst, N.; Papernot, N.; Hinton, G.E. Analyzing and Improving Representations with the Soft Nearest Neighbor Loss. arXiv 2019, arXiv:1902.01889. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).