New Generalized Jacobi Galerkin Operational Matrices of Derivatives: An Algorithm for Solving Multi-Term Variable-Order Time-Fractional Diffusion-Wave Equations

Abstract

The current study discusses a novel approach for numerically solving MTVO-TFDWEs under various conditions, such as IBCs and DBCs. It uses a class of GSJPs that satisfy the given conditions (IBCs or DBCs). One of the important parts of our method is establishing OMs for Ods and VOFDs of GSJPs. The second part is using the SCM by utilizing these OMs. This algorithm enables the extraction of precision and efficacy in numerical solutions. We provide theoretical assurances of the treatment’s efficacy by validating its convergent and error investigations. Four examples are offered to clarify the approach’s practicability and precision; in each one, the IBCs and DBCs are considered. The findings are compared to those of preceding studies, verifying that our treatment is more effective and precise than that of its competitors.

1. Introduction

Fractional calculus has emerged as a subject of great interest among researchers from diverse fields in recent decades. The universal perspective that fractional operators offer for comprehending system dynamics is what primarily motivates this interest. Fractional derivatives offer a more precise and comprehensive description of various physical phenomena compared to traditional integer-order derivatives [1,2,3,4]. Consequently, there exists a wide range of definitions for fractional differentiation in the literature (for further details, refer to [5,6,7]). A list of abbreviations used in the paper is given in Abbreviations Section.

Researchers have made worthy progress in the field of fractional calculus, emphasizing the extension of the framework to encompass VOFDs. This extension facilitates an understanding of diverse dynamic systems. The authors in [8] conducted a specific study in which they investigated the characteristics of VOFD operators [9,10].

VOFC is a strong framework that obtains the nonlocal properties of different systems very well [11,12,13,14,15,16,17,18]. For instance, in study [19], the utilization of VOFD operators enabled the modeling of the microscopic structure of materials. As shown in an additional publication [20], continuum elasticity also made use of the Riesz–Caputo fractional derivative of space-dependent order. In [21], the authors recommend using collocation and tau spectral techniques to solve the time-fractional heat equation numerically. Studies [22,23] specifically focused on understanding and analyzing how the fractional order, which characterizes the system’s dynamics, evolves over time and influences its viscoelastic properties. By examining the time-dependent changes in the fractional order, valuable insights were gained into the complex behavior of such systems. Overall, VOFC has proven to be a valuable tool in engineering mechanics, providing a versatile approach to accurately describe and analyze a wide range of dynamic systems.

The pursuit of analytical solutions for FDEs poses a significant challenge, often necessitating reliance on numerical approximations. As a result, various numerical techniques have addressed the complexities associated with FDEs, enabling researchers to effectively tackle problems that would otherwise be challenging to solve analytically. Previous research has witnessed the utilization of a variety of approaches to create numerical solutions for FDEs through the use of both orthogonal and non-orthogonal polynomials. There are a number of papers [24,25,26,27,28,29,30] that talk about different OMs of JPs and some of their special cases. These papers use different spectral methods by utilizing these OMs to solve different kinds of DEs and FDEs numerically, subject to different kinds of IBCs. Additionally, researchers in [31,32,33,34,35,36] follow the same methodology to solve VOFDEs numerically. Additionally, in [37,38], Bernstein polynomials were employed to approximate solutions for FDEs. Another notable contribution in [39] proposed a numerical scheme based on Fourier analysis for solving FDEs. Furthermore, finite difference approximations were discussed in [40] as a means to construct numerical schemes for FDEs. In [41], the author uses a class of modified JPs to introduce a novel method for numerically solving MTVO-FDEs with initial conditions.

Many researchers [42,43,44] have shown that JPs have properties that make them very useful for solving different kinds of DEs, especially when spectral methods are used. Some of these properties are that they are orthogonal, have exponential accuracy, and have two parameters that allow us to shape approximate solutions in different ways. These inherent properties of JPs make them highly suitable for effectively solving a wide range of diverse problems encountered in various fields of study.

It is worth noting that a significant class of fractional partial differential equations that has received considerable attention in recent years is the TFDWE. This equation arises from the classical diffusion-wave equation by replacing the second-order time derivative term with a fractional derivative of order $1<\alpha <2$ [45]. The TFDWE describes important physical effects seen in many different types of systems, such as colloidal, amorphous, glassy, and porous materials, as well as dielectrics and semiconductors, comb structures, polymers, random and disordered media, biological systems, and geophysical and geological processes (see [46] and references therein).

Furthermore, it is worth mentioning that the TFDWE serves as an accurate model for many universal electromagnetic, acoustic, and mechanical responses [47,48]. A single TFDWE may not be able to fully describe the underlying processes in some real-life situations. This is why an MTFDWE was created, as shown in [46,49]. This MTFDWE formulation offers a more comprehensive representation of complex systems and their dynamic behavior, allowing for more accurate modeling of the underlying processes.

We considered the general form of MTVO-TFDE in our investigation as follows:

$$\left({\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}+{\displaystyle \sum _{j=1}^m}{\varrho }_j{\displaystyle {{}_0{}^c\mathcal{D}}_t^{{\nu }_j(x,t)}}\right)y(x,t)+\varrho y_t(x,t)=\kappa y_{xx}(x,t)+g(x,t),(x,t)\in [0,\ell ]\times [0,\mathcal{T}],$$

(1)

subject to the IBCs:

$$y(x,0)=f_1(x),y_t(x,0)=f_2(x),y(0,t)=f_3(t),y(\ell ,t)=f_4(t),$$

(2)

or the DBCs:

$$y(x,0)=f_1(x),y(x,\mathcal{T})=f_2(x),y(0,t)=f_3(t),y(\ell ,t)=f_4(t),$$

(3)

where ${\varrho }_j(j=1,2,\dots ,m,m\in \mathbb{N}),\varrho \ge 0$ and $\kappa >0$ are constants; $1<{\nu }_1(x,t)<{\nu }_2(x,t)<\dots <{\nu }_m(x,t)<\nu (x,t)\le 2$ holds; $f_0(x),f_1(x),f_2(x),f_3(t),f_4(t)$ and $g(x,t)$ are given functions; and ${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}and{\displaystyle {{}_0{}^c\mathcal{D}}_t^{{\nu }_j(x,t)}}(i=1,2,\dots ,m)$ are the VOFDs defined in the Caputo sense, as given in Section 2. The significance and difficulty of proving the existence, unicity, and dependency of parameters should be emphasized. The significance of determination of $\nu$ and ${\nu }_j$ in (1) is evident in theory and practice due to the strong relationship between them and the heterogeneity and associated physical features of media [50]. For instance, in the situation of a single term case, Cheng et al. [51] first demonstrated the uniqueness of $\nu$ using the boundary condition data that were provided.

We present a new Galerkin OM for Ods and new OMs for VOFDs of GSJPs in the sense of Caputo. This was made in order to find a new way to solve the problem shown by (1) and the conditions (2) or (3). These operational matrices are specifically tailored for the basis vectors of GSJPs. Leveraging these OMs, we have established a powerful tool that enables the accurate computation of numerical solutions using the SCM to solve a wide range of MTVO-TFDEs. This novel method opens up new ways to solve this type of FDE numerically and more effectively.

To summarize, the main article’s contributions are as follows:

(i)

We introduce two classes of GSJPs to satisfy the given IBCs and DBCs (see Section 3.2).

(ii)

We establish Galerkin OMs for the Ods and for VOFDs of the introduced GSJPs in the sense of Caputo (see Section 4 and Section 5).

(iii)

We address the presented MTVO-TFDE using the proposed GSJPs and their constructed OMs in conjunction with the SCM (see Section 6).

(iv)

We present a study of convergence and error analysis for the numerical solution obtained through the proposed scheme (see Section 7).

The paper has the following outline: Section 2 provides comprehensive coverage of the needed concepts of VOFC. Section 3 highlights the necessary attributes of JPs and GSJPs. Section 4 and Section 5 emphasize the development of new Galerkin OMs for Ods and VOFDs of GSJPs. These OMs are intended to address Equation (1) when IBCs (2) or DBCs (3) are considered. Section 6 explores the selection of newly generated OMs in the SCM to address the aforementioned issue. Section 7 analyzes convergence and error estimation. Section 8 includes four examples to clarify the approach’s practicability and precision, and the findings are compared to those of preceding studies, verifying that our treatment is more effective and precise than its competitors. Finally, Section 9 summarizes the key outcomes, implications derived from our investigation, and the scope of future work.

2. Basic Definition of Caputo VOFDs

This section serves to introduce and discuss important definitions and necessary assets that lay the groundwork for the development of our proposed technique. These tools are crucial building blocks that provide the necessary foundation for effectively handling the MTVO-TFDE under consideration.

Definition 1

([39,45]). Suppose $h(x,t)$ is a twice differentiable function. The Caputo derivative operator with the variable-order $\nu (x,t)$ is defined as:

$${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}h(x,t)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\Gamma (2-\nu (x,t))}}{\displaystyle \underset{0}{\overset{t}{\int }}}{(t-\tau )}^{1-\nu (x,t)}{\displaystyle \frac{{\partial }^{2}h(x,\tau )}{\partial {\tau }^2}}d\tau ,\hfill & 1<\nu (x,t)<2,\hfill \\ h_{tt}(x,t),\hfill & \nu (x,t)=2.\hfill \end{array}\right.$$

(4)

The Caputo VOFD exhibits the characteristics:

$${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}({\lambda }_1{h}_1(t)+{\lambda }_2{h}_2(t))={\lambda }_1{\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{h}_1(t)+{\lambda }_2{\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{h}_2(t),$$

(5)

$$\begin{array}{cc}\hfill {\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}(C)& =0,(\mathrm{C}\mathrm{is}\mathrm{a}\mathrm{constant}),\hfill \end{array}$$

(6a)

$$\begin{array}{cc}\hfill {\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{t}^k& =\left\{\begin{array}{cc}0,\hfill & k=0,1,\hfill \\ {\displaystyle \frac{\Gamma (k+1)}{\Gamma (k+1-\nu (x,t))}}{t}^{k-\nu (x,t)},\hfill & k=2,3,\dots .\hfill \end{array}\right.\hfill \end{array}$$

(6b)

Remark 1.

The reader who is interested may find several definitions and additional attributes of VOFDs in [4] (pp. 35–42).

3. An Overview of the Shifted JPs and Their Generalized Ones

Introducing the fundamental features of the JPs and their shifting form is the main objective of this section. Additionally, a group of GSJPs is introduced.

3.1. An Overview of the Shifted JPs

The orthogonal JPs, ${\displaystyle {\mathcal{J}}_n^{(\widehat{\alpha },\widehat{\beta })}}(x),\widehat{\alpha },\widehat{\beta }>-1$, satisfy the following relationship [52]:

$${\displaystyle {\int }_{-1}^1}{w}^{\widehat{\alpha },\widehat{\beta }}(x){\displaystyle {\mathcal{J}}_n^{(\widehat{\alpha },\widehat{\beta })}}(x){\displaystyle {\mathcal{J}}_m^{(\widehat{\alpha },\widehat{\beta })}}(x)dx=\left\{\begin{array}{cc}0,\hfill & m\ne n,\hfill \\ {\displaystyle h_n^{(\widehat{\alpha },\widehat{\beta })}},\hfill & m=n,\hfill \end{array}\right.$$

where $w^{\widehat{\alpha },\widehat{\beta }}(x)={(1-x)}^{\widehat{\alpha }}{(1+x)}^{\widehat{\beta }}$ and ${\displaystyle h_n^{(\widehat{\alpha },\widehat{\beta })}}={\displaystyle \frac{2^{\lambda }\Gamma (n+\widehat{\alpha }+1)\Gamma (n+\widehat{\beta }+1)}{n!(2n+\lambda )\Gamma (n+\lambda )}}, \lambda =\widehat{\alpha }+\widehat{\beta }+1$.

The shifted JPs, denoted as ${\displaystyle {\mathcal{J}}_{\ell ,n}^{(\widehat{\alpha },\widehat{\beta })}}(t)={\displaystyle {\mathcal{J}}_n^{(\widehat{\alpha },\widehat{\beta })}}(2t/\ell -1)$, are in accordance with:

$${\displaystyle {\int }_0^{\ell }}{\displaystyle w_{\ell }^{\widehat{\alpha },\widehat{\beta }}}(t){\displaystyle {\mathcal{J}}_{\ell ,n}^{(\widehat{\alpha },\widehat{\beta })}}(t){\displaystyle {\mathcal{J}}_{\ell ,m}^{(\widehat{\alpha },\widehat{\beta })}}(t)dt=\left\{\begin{array}{cc}0,\hfill & m\ne n,\hfill \\ {\left(\frac{\ell }{2}\right)}^{\lambda }{\displaystyle h_n^{(\widehat{\alpha },\widehat{\beta })}},\hfill & m=n,\hfill \end{array}\right.$$

where ${\displaystyle w_{\ell }^{\widehat{\alpha },\widehat{\beta }}}(t)={(\ell -t)}^{\widehat{\alpha }}{t}^{\widehat{\beta }}$.

The fundamental expansions that will be used in this paper are [53] (Section 11.3.4):

• The power form representations of ${\displaystyle {\mathcal{J}}_{\ell ,n}^{(\widehat{\alpha },\widehat{\beta })}}(t)$ are as follows:

  $${\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)={\displaystyle \sum _{k=0}^i}{\displaystyle c_k^{(i)}}{t}^k={\displaystyle \sum _{k=0}^i}{\displaystyle {\overline{c}}_k^{(i)}}{(\ell -t)}^k,$$

  (7)

  where

  $${\displaystyle c_k^{(i)}}=\frac{{(-1)}^{i-k}\Gamma (i+\widehat{\beta }+1)\Gamma (i+k+\lambda )}{{\ell }^{k}k!(i-k)!\Gamma (k+\widehat{\beta }+1)\Gamma (i+\lambda )}\mathrm{and}{\displaystyle {\overline{c}}_k^{(i)}}=\frac{{(-1)}^k{(\widehat{\alpha }+1)}_i{(\lambda +i)}_k}{{\ell }^{k}k!(i-k)!{(\widehat{\alpha }+1)}_k}.$$

  (8)
• Alternatively, the expressions for $t^k$ and ${(\ell -t)}^k$ in relation to ${\displaystyle {\mathcal{J}}_{\ell ,r}^{(\widehat{\alpha },\widehat{\beta })}}(t)$ have the forms:

  $$t^k={\displaystyle \sum _{r=0}^k}{\displaystyle b_r^{(k)}}{\displaystyle {\mathcal{J}}_{\ell ,r}^{(\widehat{\alpha },\widehat{\beta })}}(t),and{(\ell -t)}^k={\displaystyle \sum _{r=0}^k}{\displaystyle {\overline{b}}_r^{(k)}}{\displaystyle {\mathcal{J}}_{\ell ,r}^{(\widehat{\alpha },\widehat{\beta })}}(t),$$

  (9)

  where

  $${\displaystyle b_r^{(k)}}=\frac{{\ell }^{k}k!(\lambda +2r)\Gamma (k+\widehat{\beta }+1)\Gamma (r+\lambda )}{(k-r)!\Gamma (r+\widehat{\beta }+1)\Gamma (k+r+\lambda +1)}and{\displaystyle {\overline{b}}_r^{(k)}}=\frac{(2j+\lambda ){\ell }^k{(-k)}_j{(\lambda +1)}_{j-1}{(\widehat{\alpha }+1)}_k}{{(\widehat{\alpha }+1)}_j{(\lambda +1)}_k{(k+\lambda +1)}_j}.$$

  (10)

3.2. Introducing GSJPs

In this section, it is helpful to talk about two polynomials, ${\left\{{\displaystyle {\varphi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t)\right\}}_{j\ge 0}$ and ${\left\{{\displaystyle {\psi }_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t)\right\}}_{j\ge 0}$. These are needed to satisfy the homogeneous form of the given IBCs (2) and DBCs (3):

$${\displaystyle {\varphi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t^2{\displaystyle {\mathcal{J}}_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t),$$

(11)

$${\displaystyle {\psi }_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t(\ell -t){\displaystyle {\mathcal{J}}_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t).$$

(12)

Subsequently, these polynomials satisfy the orthogonality relations as follows:

$${\displaystyle {\int }_0^{\mathcal{T}}}\frac{{\displaystyle w_{\mathcal{T}}^{\widehat{\alpha },\widehat{\beta }}}(t)}{t^4}{\displaystyle {\varphi }_{\mathcal{T},i}^{(\widehat{\alpha },\widehat{\beta })}}(t){\displaystyle {\varphi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t)dt=\left\{\begin{array}{cc}0,\hfill & i\ne j,\hfill \\ {\left(\frac{\mathcal{T}}{2}\right)}^{\lambda }{\displaystyle h_i^{(\widehat{\alpha },\widehat{\beta })}},\hfill & i=j,\hfill \end{array}\right.$$

(13)

$${\displaystyle {\int }_0^{\ell }}\frac{{\displaystyle w_{\ell }^{\widehat{\alpha },\widehat{\beta }}}(t)}{t^2{(\ell -t)}^2}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t){\displaystyle {\psi }_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t)dt=\left\{\begin{array}{cc}0,\hfill & i\ne j,\hfill \\ {\left(\frac{\ell }{2}\right)}^{\lambda }{\displaystyle h_i^{(\widehat{\alpha },\widehat{\beta })}},\hfill & i=j,\hfill \end{array}\right.$$

(14)

where ${\displaystyle w_{\rho }^{\widehat{\alpha },\widehat{\beta }}}(t)={(\rho -t)}^{\widehat{\alpha }}{t}^{\widehat{\beta }}$.

4. Two OMs for Ods and VOFDs of ${\displaystyle {\mathit{\varphi }}_{\mathcal{T},\mathit{j}}^{(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }})}}(\mathit{t})$

In this part, we introduce two OMs related to ODEs and VOFDs of ${\displaystyle {\varphi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t)$. To facilitate this, we commence with Theorem 1:

Theorem 1

([41]). $\mathcal{D}(t^n{\displaystyle {\mathcal{J}}_{\mathcal{T},i}^{(\widehat{\alpha },\widehat{\beta })}}(t))$ for all $i\ge 0$ can be computed as follows:

$$\mathcal{D}(t^n{\displaystyle {\mathcal{J}}_{\mathcal{T},i}^{(\widehat{\alpha },\widehat{\beta })}}(t))={\displaystyle \sum _{j=0}^{i-1}}{\displaystyle {\theta }_{i,j}^{\widehat{\alpha },\widehat{\beta }}}(n,\mathcal{T})(t^n{\displaystyle {\mathcal{J}}_{\mathcal{T},i}^{(\widehat{\alpha },\widehat{\beta })}}(t))+{ϵ}_{n,i}(t),$$

(15)

where ${ϵ}_{n,i}(t)={\displaystyle \frac{n}{i!}}{(-1)}^i{(\widehat{\beta }+1)}_i{t}^{n-1}$,  and 

$${\displaystyle {\theta }_{i,j}^{\widehat{\alpha },\widehat{\beta }}}(n,\mathcal{T})={\displaystyle C_{i,j}^{\widehat{\alpha },\widehat{\beta }}}{\displaystyle \sum _{r=0}^{i-j-1}}\frac{{(-1)}^r(j+n+r+1){(i+j+\lambda +1)}_r}{r!(j+r+1)(j+r+\widehat{\beta }+1)\Gamma (i-j-r)\Gamma (2j+r+\lambda +1)},$$

(16)

where

$${\displaystyle C_{i,j}^{\widehat{\alpha },\widehat{\beta }}}=\frac{{(-1)}^{i+j-1}(\lambda +i){(\widehat{\beta }+1)}_i(\lambda +2j)\Gamma (j+\lambda ){(i+\lambda +1)}_j}{\mathcal{T}{(\widehat{\beta }+1)}_j}.$$

Then, the two desired OMs of

$${\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)={[{\displaystyle {\varphi }_{\mathcal{T},0}^{(\widehat{\alpha },\widehat{\beta })}}(t),{\displaystyle {\varphi }_{\mathcal{T},1}^{(\widehat{\alpha },\widehat{\beta })}}(t),\dots ,{\displaystyle {\varphi }_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)]}^T$$

(17)

can be computed as follows:

Corollary 1

([41]). The general derivative of ${\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)$ has the form:

$$\frac{d^m{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)}{d{t}^m}=G^m{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\displaystyle {\mathit{\eta }}_N^{(m)}}(t),$$

(18)

with ${\displaystyle {\mathit{\eta }}_N^{(m)}}(t)={\displaystyle \sum _{k=0}^{m-1}}{G}^k{\displaystyle {\mathit{ϵ}}_N^{(m-k-1)}}(t)$, where ${\mathit{ϵ}}_N(t)={\left[{ϵ}_{2,0}(t),{ϵ}_{2,1}(t),\dots ,{ϵ}_{2,N}(t)\right]}^T and G=(g_{i,j}{)}_{0\le i,j\le N}$,

$$g_{i,j}=\left\{\begin{array}{cc}{\displaystyle {\theta }_{i,j}^{\widehat{\alpha },\widehat{\beta }}}(2,\mathcal{T}),\hfill & i>j,\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Theorem 2.

$D^{\nu (x,t)}{\displaystyle {\varphi }_{\mathcal{T},i}^{(\widehat{\alpha },\widehat{\beta })}}(t)$ for all $i\ge 0$, has the form:

$${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{\displaystyle {\varphi }_{\mathcal{T},i}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t^{-\nu (x,t)}{\displaystyle \sum _{j=0}^i}{\Theta }_{i,j}(\nu (x,t)){\displaystyle {\varphi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t),$$

(19)

which leads to:

$${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t^{-\nu (x,t)}{\mathbf{D}}^{(\nu (x,t))}{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t),$$

(20)

where ${\mathbf{D}}^{(\nu (x,t))}=(d_{i,j}(\nu (x,t)))$ is a matrix of order $(N+1)\times (N+1)$, which can be expressed explicitly as:

$$\left(\begin{array}{cccccc}{\Theta }_{0,0}(\nu (x,t))& 0& \cdots & \cdots & \cdots & 0\\ \\ {\Theta }_{1,0}(\nu (x,t))& {\Theta }_{1,1}(\nu (x,t))& 0& \cdots & \cdots & 0\\ ⋮& & \ddots & & & ⋮\\ {\Theta }_{i,0}(\nu (x,t))& \cdots & {\Theta }_{i,i}(\nu (x,t))& 0& \cdots & 0\\ ⋮& & & \ddots & & ⋮\\ ⋮& & & & \ddots & 0\\ {\Theta }_{N,0}(\nu (x,t))& \cdots & \cdots & \cdots & \cdots & {\Theta }_{N,N}(\nu (x,t))\end{array}\right),$$

(21)

where

$$d_{i,j}(\nu (x,t))=\left\{\begin{array}{cc}{\Theta }_{i,j}(\nu (x,t)),\hfill & i\ge j,\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.$$

(22)

and

$${\Theta }_{i,j}(\nu (x,t))=\frac{{(-1)}^{i-j}(j+2)!\Gamma (i+\widehat{\beta }+1)\Gamma (j+\lambda )\Gamma (i+j+\lambda )}{(i-j)!\Gamma (j+\widehat{\beta }+1)\Gamma (2j+\lambda )\Gamma (i+\lambda )\Gamma (j-\nu (x,t)+3)}\times {}_3{F}_2\left(\begin{array}{c}j-i,j+3,i+j+\lambda \hfill \\ 2j+\lambda +1,j-\nu (x,t)+3\hfill \end{array};1\right).$$

(23)

Proof. 

By considering (7) and applying (6b), we obtain:

$${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{\displaystyle {\varphi }_{\mathcal{T},i}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t^{2-\nu (x,t)}{\displaystyle \sum _{k=0}^i}{\displaystyle c_k^{(i)}}\frac{\Gamma (k+3)}{\Gamma (k-\nu (x,t)+3)}{t}^k.$$

(24)

By utilizing (9), expanding and collecting similar terms, and using useful computational formulae of the Pochhammer symbol and the Gamma function (see [54] (p. 758)), it is possible to convert (24) to (19), which is represented as follows:

$${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{\displaystyle {\varphi }_{\mathcal{T},i}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t^{-\nu (x,t)}[{\Theta }_{i,0}(\nu (x,t)),{\Theta }_{i,1}(\nu (x,t)),\cdots ,{\Theta }_{i,i}(\nu (x,t)),0,\cdots ,0]{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t),$$

(25)

and this representation enables us to declare that (20) is proved and that the theorem is completely proved.    □

As an application of Theorem 2, for  $N=4,\widehat{\alpha }=-\widehat{\beta }=1/2$, and  $\nu (x,t)=xt$, the OM ${\mathbf{D}}^{(\nu (x,t))}$ has the form:

$${\mathbf{D}}^{(\nu (x,t))}={\left(\begin{array}{ccccc}\frac{2}{\Gamma (3-tx)}& 0& 0& 0& 0\\ \frac{tx}{\Gamma (4-tx)}& \frac{6}{\Gamma (4-tx)}& 0& 0& 0\\ \frac{3tx(tx+2)}{4\Gamma (5-tx)}& \frac{27tx}{2\Gamma (5-tx)}& \frac{24}{\Gamma (5-tx)}& 0& 0\\ \frac{5tx(tx+1)(tx+5)}{8\Gamma (6-tx)}& \frac{45tx(tx+1)}{2\Gamma (6-tx)}& \frac{100tx}{\Gamma (6-tx)}& \frac{120}{\Gamma (6-tx)}& 0\\ \frac{35tx(tx+1)(tx+2)(tx+9)}{64\Gamma (7-tx)}& \frac{525tx(tx+1)(tx+2)}{16\Gamma (7-tx)}& \frac{175tx(3tx+2)}{2\Gamma (7-tx)}& \frac{735tx}{\Gamma (7-tx)}& \frac{720}{\Gamma (7-tx)}\end{array}\right)}_{5\times 5}.$$

(26)

5. Two OMs for Ods and VOFDs of ${\displaystyle {\mathit{\psi }}_{\ell ,\mathit{i}}^{(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }})}}(\mathit{t})$

In this part, we establish two OMs for Ods and VOFDs of ${\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)$. In order to achieve this, we commence by proving the subsequent lemma:

Lemma 1.

The polynomials $t{\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t),i\ge 0$ have the following representation:

$$t{\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)=-{\displaystyle \sum _{j=0}^{i-1}}{\displaystyle {{\rm Y}}_{i,j}^{\widehat{\alpha },\widehat{\beta }}}(\ell ){\displaystyle {\psi }_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t)+\frac{{(\widehat{\alpha }+1)}_i}{i!}t,$$

(27)

where

$${\displaystyle {{\rm Y}}_{i,j}^{\widehat{\alpha },\widehat{\beta }}}=\frac{\Gamma (i+\widehat{\alpha }+1)\Gamma (j+\lambda )\Gamma (i+j+\lambda +1)}{\ell (j+1)\Gamma (i-j)\Gamma (j+\widehat{\alpha }+2)\Gamma (i+\lambda )\Gamma (2j+\lambda )}{}_4{F}_3\left(\begin{array}{c}-i+j+1,j+1,\widehat{\alpha }+j+1,\lambda +i+j+1\hfill \\ j+2,\widehat{\alpha }+j+2,\lambda +2j+1\hfill \end{array};1\right).$$

(28)

Proof. 

We have

$${\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)=(\ell -t)\left(\frac{{\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)-{\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(\ell )}{\ell -t}\right)+{\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(\ell ).$$

(29)

In view of (7) and (9), we obtain:

$$\frac{{\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)-{\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(\ell )}{\ell -t}={\displaystyle \sum _{k=0}^{i-1}}{\displaystyle {\overline{c}}_{k+1}^{(i)}}{(\ell -t)}^k={\displaystyle \sum _{k=0}^{i-1}}{\displaystyle {\overline{c}}_{k+1}^{(i)}}\left({\displaystyle \sum _{r=0}^k}{\displaystyle {\overline{b}}_r^{(k)}}{\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)\right),$$

(30)

consequently, through expansion, the accumulation of similar terms, and using useful computational formulae of the Pochhammer symbol and the Gamma function (see [54] (p. 758)), it becomes evident that:

$$\frac{{\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)-{\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(\ell )}{\ell -t}=-{\displaystyle \sum _{j=0}^{i-1}}{\displaystyle {{\rm Y}}_{i,j}^{\widehat{\alpha },\widehat{\beta }}}(\ell ){\displaystyle {\mathcal{J}}_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t).$$

(31)

Substitution of (31) and ${\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(\ell )=\frac{{(\widehat{\alpha }+1)}_i}{i!}$ into (29) leads to (27), and then the lemma is proved completely.    □

Theorem 3.

$\mathcal{D}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t),$ for all $i\ge 0$, has the form:

$$\mathcal{D}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)={\displaystyle \sum _{j=0}^{i-1}}{\displaystyle {\Omega }_{i,j}^{\widehat{\alpha },\widehat{\beta }}}(\ell ){\displaystyle {\psi }_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\vartheta }_{\ell ,i}(t),$$

(32)

where ${\vartheta }_{\ell ,i}(t)=\frac{1}{i!}({(-1)}^i(\ell -t){(\widehat{\beta }+1)}_i-t{(\widehat{\alpha }+1)}_i)$, and

$${\displaystyle {\Omega }_{i,j}^{\widehat{\alpha },\widehat{\beta }}}(\ell )={\displaystyle {\theta }_{i,j}^{\widehat{\alpha },\widehat{\beta }}}(1,\ell )+{\displaystyle {{\rm Y}}_{i,j}^{\widehat{\alpha },\widehat{\beta }}}(\ell ),$$

(33)

Proof. 

We have

$$\mathcal{D}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)=(\ell -t)\mathcal{D}(t{\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t))-t{\displaystyle {\mathcal{J}}_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t).$$

(34)

Using Theorem 1 and Lemma 1 leads to (32), and the proof of the theorem is complete.    □

Then, the desired two OMs of

$${\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(t)={[{\displaystyle {\psi }_{\ell ,0}^{(\widehat{\alpha },\widehat{\beta })}}(t),{\displaystyle {\psi }_{\ell ,1}^{(\widehat{\alpha },\widehat{\beta })}}(t),\cdots ,{\displaystyle {\psi }_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(t)]}^T$$

(35)

can be computed as follows:

Corollary 2.

The general derivative of ${\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(t)$ is expressed as:

$$\frac{d^m{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(t)}{d{t}^m}=H^m{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\displaystyle {\mathit{\xi }}_{\ell ,N}^{(m)}}(t),$$

(36)

with ${\displaystyle {\mathit{\xi }}_{\ell ,N}^{(m)}}(t)={\displaystyle \sum _{k=0}^{m-1}}{H}^k{\displaystyle {\mathit{\vartheta }}_{\ell ,N}^{(m-k-1)}}(t)$, where ${\mathit{\vartheta }}_{\ell ,N}(t)={\left[{\vartheta }_{\ell ,0}(t),{\vartheta }_{\ell ,1}(t),\dots ,{\vartheta }_{\ell ,N}(t)\right]}^{T}andH={\left(h_{i,j}\right)}_{0\le i,j\le N}$,

$$h_{i,j}=\left\{\begin{array}{cc}{\displaystyle {\Omega }_{i,j}^{\widehat{\alpha },\widehat{\beta }}}(\ell ),\hfill & i>j,\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Theorem 4.

${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)$ for all $i\ge 0$, has the expression

$${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t^{-\nu (x,t)}\left({\displaystyle \sum _{j=0}^i}{\Lambda }_{i,j}(\nu (x,t)){\displaystyle {\psi }_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\epsilon }_{\ell ,i}(x,t)\right),$$

(37)

which leads to

$${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t^{-\nu (x,t)}\left({\widehat{\mathbf{D}}}^{(\nu (x,t))}{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\mathit{\epsilon }}_{\ell ,N}(x,t)\right),$$

(38)

where ${\mathit{\epsilon }}_{\ell ,N}(x,t)={\left[{\epsilon }_{\ell ,0}(x,t),{\epsilon }_{\ell ,1}(x,t),\cdots ,{\epsilon }_{\ell ,N}(x,t)\right]}^T$ and ${\widehat{\mathbf{D}}}^{(\nu (x,t))}=({\widehat{d}}_{i,j}(\nu (x,t)))$ is a matrix of order $(N+1)\times (N+1)$, which can be expressed explicitly as:

$$\left(\begin{array}{cccccc}{\Lambda }_{0,0}(\nu (x,t))& 0& \cdots & \cdots & \cdots & 0\\ \\ {\Lambda }_{1,0}(\nu (x,t))& {\Lambda }_{1,1}(\nu (x,t))& 0& \cdots & \cdots & 0\\ ⋮& & \ddots & & & ⋮\\ {\Lambda }_{i,0}(\nu (x,t))& \cdots & {\Lambda }_{i,i}(\nu (x,t))& 0& \cdots & 0\\ ⋮& & & \ddots & & ⋮\\ ⋮& & & & \ddots & 0\\ {\Lambda }_{N,0}(\nu (x,t))& \cdots & \cdots & \cdots & \cdots & {\Lambda }_{N,N}(\nu (x,t))\end{array}\right),$$

(39)

where the matrix elements are defined as follows:

$${\widehat{d}}_{i,j}(\nu (x,t))=\left\{\begin{array}{cc}{\Lambda }_{i,j}(\nu (x,t)),\hfill & i\ge j,\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.$$

(40)

and the coefficients ${\Lambda }_{i,j}(\nu (x,t))$ have the form

$${\Lambda }_{i,j}(\nu (x,t))={\displaystyle {\Xi }_{i,j}^{(1)}}(\nu (x,t))+{\displaystyle {\Xi }_{i,j}^{(2)}}(\nu (x,t)),$$

(41)

where

$${\displaystyle {\Xi }_{i,j}^{(1)}}(\nu (x,t))=\frac{(j+2)!{(-1)}^{i-j}{(\lambda )}_j{(\lambda )}_{i+j}{(\widehat{\beta }+1)}_i}{(i-j)!{(\lambda )}_i{(\lambda )}_{2j}{(\widehat{\beta }+1)}_j\Gamma (j-\nu (x,t)+3)}\times {}_3{F}_2\left(\begin{array}{c}-i+j,j+3,i+j+\lambda \hfill \\ 2j+\lambda +1,3+j-\nu (x,t)\hfill \end{array};1\right),$$

(42)

$$\begin{array}{cc}\hfill {\displaystyle {\Xi }_{i,j}^{(2)}}(\nu (x,t))=& \frac{{(-1)}^{i+1}(2j+\lambda ){(\widehat{\beta }+1)}_i{(\lambda )}_j\nu (x,t)}{{(\widehat{\beta }+1)}_j{(\lambda )}_i}{\displaystyle \sum _{r=j}^i}\frac{{(-1)}^r(r+2)r!{(\lambda +1)}_{i+r}}{(\widehat{\beta }+r+1)(i-r-1)!(r-j)!{(\lambda +1)}_{j+r}\Gamma (r-\nu (x,t)+4)}\times \hfill \\ & {}_4{F}_3\left(\begin{array}{c}1,r+3,-i+r+1,i+\lambda +r+1\hfill \\ r+2,\widehat{\beta }+r+2,4+r-\nu (x,t)\hfill \end{array};1\right),\hfill \end{array}$$

(43)

and the functions ${\epsilon }_{\ell ,i}(x,t)$ have the form

$${\epsilon }_{\ell ,i}(x,t)=\frac{{(-1)}^{i+1}\ell {(\widehat{\beta }+1)}_i\nu (x,t)t}{i!\Gamma (3-\nu )}{}_3{F}_2\left(\begin{array}{c}-i,i+\lambda ,2\hfill \\ \widehat{\beta }+1,3-\nu (x,t)\hfill \end{array};1\right).$$

(44)

Proof. 

By considering (7) and applying (6b), it is easy to see that

$${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t^{-\nu (x,t)}{\displaystyle \sum _{s=0}^i}{\displaystyle c_k^{(i)}}\frac{\Gamma (s+2)t^{s+1}}{\Gamma (s+3-\nu (x,t))}((s+2)(\ell -t)-\ell \nu (x,t)),$$

(45)

which may be expressed as:

$${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t^{-\nu (x,t)}\left(\sum _1+\sum _2+\sum _3\right),$$

(46)

where

$$\sum _1={\displaystyle \sum _{s=0}^i}{\displaystyle c_s^{(i)}}\frac{\Gamma (s+3)}{\Gamma (s+3-\nu (x,t))}(t(\ell -t))t^s,$$

(47)

$$\sum _2={\displaystyle \sum _{s=0}^i}{\displaystyle c_s^{(i)}}\frac{\ell \Gamma (s+2)\nu (x,t)}{\Gamma (s+3-\nu (x,t))}t({\ell }^s-t^s),$$

(48)

and

$$\sum _3=-\left({\displaystyle \sum _{s=0}^i}{\displaystyle c_s^{(i)}}\frac{\Gamma (s+2)\nu (x,t)}{\Gamma (s+3-\nu (x,t))}{\ell }^{s+1}\right)t.$$

(49)

Using (9), through expansion, the accumulation of similar terms, and some algebraic manipulation (see [54] (p. 758)), it becomes evident that

$$\sum _1={\displaystyle \sum _{j=0}^i}{\displaystyle {\Xi }_{i,j}^{(1)}}(\nu (x,t)){\displaystyle {\psi }_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t).$$

(50)

Also, substitution of the form ${\displaystyle c_s^{(i)}}$ in (49)—after some simple algebraic manipulation—gives

$$\sum _3={\epsilon }_{\ell ,i}(x,t).$$

(51)

Now, it remains that we show that

$$\sum _2={\displaystyle \sum _{j=0}^i}{\displaystyle {\Xi }_{i,j}^{(2)}}(\nu (x,t)){\displaystyle {\psi }_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t).$$

(52)

Using ${\ell }^s-t^s={\ell }^{s-1}(\ell -t){\displaystyle {\sum }_{k=0}^{s-1}}{\ell }^{-k}{t}^k$ and ${\displaystyle c_{i+1}^{(i)}}=0$—after some algebraic manipulation—leads to:

$$\sum _2={\displaystyle \sum _{s=0}^i}{\displaystyle c_{s+1}^{(i)}}\frac{{\ell }^{s+1}\Gamma (s+3)\nu (x,t)}{\Gamma (s+4-\nu (x,t))}t(\ell -t)\left({\displaystyle \sum _{k=0}^s}{\ell }^{-k}{t}^k\right).$$

(53)

By expanding and collecting similar terms, we obtain:

$$\sum _2={\displaystyle \sum _{j=0}^i}{B}_{i,j}t(\ell -t)t^j,$$

(54)

where

$$B_{i,j}={\displaystyle \sum _{s=j}^i}{\displaystyle c_{s+1}^{(i)}}\frac{{\ell }^{s-j+1}\Gamma (s+3)\nu (x,t)}{\Gamma (s+4-\nu (x,t))}.$$

(55)

Again, using (9), expanding and collecting similar terms leads to:

$$\sum _2={\displaystyle \sum _{j=0}^i}\left({\displaystyle \sum _{r=j}^i}{B}_{i,r}{\displaystyle b_j^{(r)}}\right){\displaystyle {\psi }_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t).$$

(56)

Using the expressions of ${\displaystyle c_{s+1}^{(i)}}$ and ${\displaystyle b_j^{(r)}}$ after some algebraic manipulation leads to:

$${\displaystyle \sum _{r=j}^i}{B}_{i,r}{\displaystyle b_j^{(r)}}={\displaystyle {\Xi }_{i,j}^{(2)}}(\nu (x,t)),$$

(57)

then

$$\sum _2={\displaystyle \sum _{j=0}^i}{\displaystyle {\Xi }_{i,j}^{(2)}}(\nu (x,t)){\displaystyle {\psi }_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t).$$

(58)

In view of Equations (46), (50), (51), and (58), the proof of (37) is complete, which can be expressed as follows:

$${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t^{-\nu (x,t)}\left([{\Lambda }_{i,0}(\nu (x,t)),{\Lambda }_{i,1}(\nu (x,t)),\dots ,{\Lambda }_{i,i}(\nu (x,t)),0,\dots ,0]{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\epsilon }_{\ell ,i}(x,t)\right);$$

(59)

this gives (38), and the theorem is completely proved.    □

As an application of Corollary 2 and Theorem 4, for  $N=4,\widehat{\alpha }=-\widehat{\beta }=1/2$, and  $\nu (x,t)=xt$, the OMs H and ${\widehat{\mathbf{D}}}^{(\nu (x,t))}$ have the forms:

$$H=\frac{1}{\ell }{\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 6& 0& 0& 0& 0\\ -\frac{3}{2}& 12& 0& 0& 0\\ 10& -\frac{5}{2}& \frac{50}{3}& 0& 0\\ -\frac{35}{16}& \frac{315}{16}& -\frac{35}{12}& 21& 0\end{array}\right)}_{5\times 5},$$

(60)

and

$${\widehat{\mathbf{D}}}^{(\nu (x,t))}={\left(\begin{array}{ccccc}\frac{2}{\Gamma (3-tx)}& 0& 0& 0& 0\\ \frac{5tx}{\Gamma (4-tx)}& \frac{6}{\Gamma (4-tx)}& 0& 0& 0\\ \frac{3tx(13tx+14)}{4\Gamma (5-tx)}& \frac{63tx}{2\Gamma (5-tx)}& \frac{24}{\Gamma (5-tx)}& 0& 0\\ \frac{5tx(5tx(5tx+18)+41)}{8\Gamma (6-tx)}& \frac{15tx(13tx+9)}{2\Gamma (6-tx)}& \frac{180tx}{\Gamma (6-tx)}& \frac{120}{\Gamma (6-tx)}& 0\\ \frac{35tx(tx(tx(41tx+312)+481)+186)}{64\Gamma (7-tx)}& \frac{105tx(7tx(5tx+11)+38)}{16\Gamma (7-tx)}& \frac{35tx(43tx+22)}{2\Gamma (7-tx)}& \frac{1155tx}{\Gamma (7-tx)}& \frac{720}{\Gamma (7-tx)}\end{array}\right)}_{5\times 5}.$$

(61)

6. Numerical Handling for MTVO-TFDWEs Subject to IBCs (2) or DBCs (3)

OMs from Section 4 and Section 5 are used in this section to find numerical solutions for MTVO-TFDWEs (1) when IBCs (2) or DBCs (3) are present.

6.1. Homogeneous IBCs and DBCs

Suppose that the IBCs (2) or the DBCs (3) are homogeneous; that is, $f_1(x)=f_2(x)=f_3(t)=f_4(t)=0$. We can consider

$${\displaystyle y(x,t)\simeq y_N(x,t)={\displaystyle \sum _{i=0}^N}{\displaystyle \sum _{j=0}^N}{a}_{i,j}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x){\displaystyle {\varphi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t)={\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)}$$

(62)

in the case of IBCs, while in the case of DBCs, we have

$${\displaystyle y(x,t)\simeq y_N(x,t)={\displaystyle \sum _{i=0}^N}{\displaystyle \sum _{j=0}^N}{a}_{i,j}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x){\displaystyle {\psi }_{\ell ,j}^{(\widehat{\alpha },\widehat{\beta })}}(t)={\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}{\displaystyle {\mathsf{\Psi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t),}$$

(63)

where $\mathit{A}={(a_{i,j})}_{(N+1)\times (N+1)}$ is the unknown matrix.

Corollaries 1 and 2 and Theorems 2 and 4 allow us to approximate the derivatives of $y(x,t)$ that appear in Equation (1) according to the conditions considered, IBCs/DBCs, as follows:

$$\begin{array}{cc}& {\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{y}_N(x,t)=\hfill \\ & \left\{\begin{array}{cc}{\displaystyle {\displaystyle \sum _{i=0}^N}{\displaystyle \sum _{j=0}^N}{a}_{i,j}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x){\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{\displaystyle {\varphi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t^{-\nu (x,t)}{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}{\mathit{D}}^{(\nu (x,t))}{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t),}\hfill & \mathrm{for}\mathrm{IBCs},\hfill \\ {\displaystyle {\displaystyle \sum _{i=0}^N}{\displaystyle \sum _{j=0}^N}{a}_{i,j}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x){\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}{\displaystyle {\psi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t)=t^{-\nu (x,t)}{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}({\widehat{\mathit{D}}}^{(\nu (x,t))}{\displaystyle {\mathsf{\Psi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\mathit{\epsilon }}_{\mathcal{T},N}(x,t)),}\hfill & \mathrm{for}\mathrm{DBCs},\hfill \end{array}\right.\hfill \end{array}$$

(64)

$${\mathcal{D}}_t{y}_N(x,t)=\left\{\begin{array}{cc}{\displaystyle {\displaystyle \sum _{i=0}^N}{\displaystyle \sum _{j=0}^N}{a}_{i,j}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x){\mathcal{D}}_t{\displaystyle {\varphi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t)={\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}(G{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\displaystyle {\mathit{\eta }}_{\mathcal{T},N}^{(1)}}(t)),}\hfill & \mathrm{for}\mathrm{IBCs},\hfill \\ {\displaystyle {\displaystyle \sum _{i=0}^N}{\displaystyle \sum _{j=0}^N}{a}_{i,j}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x){\mathcal{D}}_t{\displaystyle {\psi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t)={\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}(H{\displaystyle {\mathsf{\Psi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\displaystyle {\mathit{\xi }}_{\mathcal{T},N}^{(1)}}(t)),}\hfill & \mathrm{for}\mathrm{DBCs},\hfill \end{array}\right.$$

(65)

and

$${\mathcal{D}}_{xx}{y}_N(x,t)=\left\{\begin{array}{cc}{\displaystyle {\displaystyle \sum _{i=0}^N}{\displaystyle \sum _{j=0}^N}{a}_{i,j}{\mathcal{D}}_{xx}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x){\displaystyle {\varphi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t)=(H^2{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)+{\displaystyle {\mathit{\xi }}_{\ell ,N}^{(2)}}(x))\mathit{A}{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t),}\hfill & \mathrm{for}\mathrm{IBCs},\hfill \\ {\displaystyle {\displaystyle \sum _{i=0}^N}{\displaystyle \sum _{j=0}^N}{a}_{i,j}{\mathcal{D}}_{xx}{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x){\displaystyle {\psi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t)=(H^2{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)+{\displaystyle {\mathit{\xi }}_{\ell ,N}^{(2)}}(x))\mathit{A}{\displaystyle {\mathsf{\Psi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t),}\hfill & \mathrm{for}\mathrm{DBCs}.\hfill \end{array}\right.$$

(66)

In this method, using the approximations (62)–(66) allows one to write the residual of Equation (1) as:

$$R_N(x,t)=\left({\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}+{\displaystyle \sum _{j=1}^m}{\varrho }_j{\displaystyle {{}_0{}^c\mathcal{D}}_t^{{\nu }_j(x,t)}}\right)y_N(x,t)+\varrho {\mathcal{D}}_t{y}_N(x,t)-\kappa {\mathcal{D}}_{xx}{y}_N(x,t)-g(x,t).$$

(67)

Now, we suggest a spectral approach called GSJCOPMM to obtain an approximate solution for (1) under the IBCs (2) or DBCs (3) (with $f_1(x)=f_2(x)=f_3(t)=f_4(t)=0$). The collocation points $x_i,t_i(0\le i\le N)$ are chosen to be either the zeros of ${\displaystyle {\mathcal{J}}_{\ell ,N+1}^{(\widehat{\alpha },\widehat{\beta })}}(x)$ and ${\displaystyle {\mathcal{J}}_{\mathcal{T},N+1}^{(\widehat{\alpha },\widehat{\beta })}}(t)$ or the points $x_i=\frac{\ell (i+1)}{N+2}$ and $t_i=\frac{\mathcal{T}(j+1)}{N+2},i,j=0,1,\dots ,N$, respectively. Therefore, we have

$$R_N(x_i,t_j)=0,i,j=0,1,\dots ,N.$$

(68)

We can compute $a_{i,j}$ (where $i,j=0,1,\dots ,N$) by using the right solver to work through a set of ${(N+1)}^2$ Equation (68). Achieving the target numerical solution relies heavily on these coefficients.

6.2. Non-Homogeneous IBCs and DBCs

Changing Equation (1) along with the non-homogeneous conditions (2) or (3) into a similar form with homogeneous conditions is an important part of creating the proposed algorithm. The following transformation accomplishes this change:

$$u(x,t)=y(x,t)-q(x,t),q(x,t)=q_1(x,t)+q_2(x,t),$$

(69)

where the two functions $q_1(x,t)$ and $q_2(x,t)$ are defined as follows:

• In the Case of IBCs:

$$\begin{array}{cc}\hfill q_1(x,t)=& {\displaystyle \frac{1}{\ell }}[(\ell -x)(f_3(t)-f_2(0)t-f_3(0))+x(f_4(t)-f_2(\ell )t-f_4(0))],\hfill \\ \hfill q_2(x,t)=& f_1(x)+f_2(x)t.\hfill \end{array}\}$$

(70)

• In the Case of DBCs:

$$\begin{array}{cc}\hfill q_1(x,t)=& {\displaystyle \frac{1}{\ell \mathcal{T}}}[(\ell -x)(\mathcal{T}{f}_3(t)-f_2(0)t-f_1(0)(\mathcal{T}-t))-f_1(\ell )x(\mathcal{T}-t)-f_2(\ell )xt+\mathcal{T}x{f}_4(t)],\hfill \\ \hfill q_2(x,t)=& {\displaystyle \frac{1}{\mathcal{T}}}[(\mathcal{T}-t)f_1(x)+t{f}_2(x)].\hfill \end{array}\}$$

(71)

As a result, the current issue may be simplified by solving the following updated equation:

$$\left({\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}+{\displaystyle \sum _{j=1}^m}{\varrho }_j{\displaystyle {{}_0{}^c\mathcal{D}}_t^{{\nu }_j(x,t)}}\right)u_N(x,t)+\varrho {\mathcal{D}}_t{u}_N(x,t)=\kappa {\mathcal{D}}_{xx}{u}_N(x,t)+\tilde{g}(x,t),$$

(72)

where

$$\tilde{g}(x,t)=g(x,t)+\left(\kappa {\mathcal{D}}_{xx}-{\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}-{\displaystyle \sum _{j=1}^m}{\varrho }_j{\displaystyle {{}_0{}^c\mathcal{D}}_t^{{\nu }_j(x,t)}}-\varrho {\mathcal{D}}_t\right)q(x,t),$$

subject to the homogeneous IBCs

$$u(x,0)=u_t(x,0)=u(0,t)=u(\ell ,t)=0,$$

(73)

or the homogeneous DBCs

$$u(x,0)=u(x,0)=u(0,t)=u(\ell ,t)=0.$$

(74)

Then,

$$y_N(x,t)=u_N(x,t)+q(x,t).$$

(75)

Remark 2.

Section 8 explains the algorithm that was used to solve various numerical examples. An Intel® Core™ i9-10850 CPU running at 3.60 GHz, with 10 cores and 20 logical processors and 64.0 GB RAM, was used to do the calculations on a computer system equipped with Mathematica 13.3.1.0 with GSJCOPMM, and the following algorithmic steps may be described to solve the MTVO-TFDWE (Algorithms 1 and 2):

Algorithm 1 GSJCOPMM algorithm to solve (1) subject to IBCs.
Stage 1.	Given $\widehat{\alpha },\widehat{\beta },\ell ,\mathcal{T},N,\nu (x,t),{\nu }_i(x,t)$ and $f_j,i=1,2,\dots ,m,j=1,2,3,4$.
Stage 2.	Define the basis ${\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x)$ and ${\displaystyle {\varphi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t)$, the matrices $\mathit{A},\mathit{G},\mathit{H},{\displaystyle {\mathit{\eta }}_N^{(m)}}(t),{\displaystyle {\mathit{\xi }}_{\ell ,N}^{(m)}}(x),{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)$,  ${\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)$, and calculate the elements of matrices   $\mathit{G},{\mathit{H}}^2,{\displaystyle {\mathit{\eta }}_N^{(1)}}(t),{\displaystyle {\mathit{\xi }}_{\ell ,N}^{(2)}}(x)$,  ${\mathbf{D}}^{(\nu (x,t))}$, and ${\mathbf{D}}^{({\nu }_i(x,t))},i=1,2,\dots ,m$.
Stage 3.	Calculate the matrices: 1. ${\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)$, 2. ${\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}(G{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\displaystyle {\mathit{\eta }}_N^{(1)}}(t))$, 3. $(H^2{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)+{\displaystyle {\mathit{\xi }}_{\ell ,N}^{(2)}}(x))\mathit{A}{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t),$ 4. ${\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}{\mathit{D}}^{(\nu (x,t))}{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)$, 5. ${\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}{\mathit{D}}^{({\nu }_i(x,t))}{\displaystyle {\mathsf{\Phi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t),i=0,1,\dots ,m.$
Stage 4.	Define $R_N(x,t)$ as in Equation (67).
Stage 5.	List $R_N(x_i,t_j)=0,i,j=0,1,\dots ,N$, defined in Equation (68).
Stage 6.	Use Mathematica’s built-in numerical solver to solve the system obtained in [Output 5].
Stage 6.	Calculate $y_N(x,t)$ defined in Equation (62) (Homogeneous IBCs).
Stage 7.	Calculate $q(x,t)$ and $y_N(x,t)$ defined in Equation (75) (Non-homogeneous IBCs).

Algorithm 2 GSJCOPMM algorithm to solve (1) subject to DBCs.
Stage 1.	Given $\widehat{\alpha },\widehat{\beta },\ell ,\mathcal{T},N,\nu (x,t),{\nu }_i(x,t)$ and $f_j,i=1,2,\dots ,m,j=1,2,3,4$.
Stage 2.	Define the basis ${\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x)$, the matrices $\mathit{A},\mathit{H},{\mathit{\epsilon }}_{\mathcal{T},N}(x,t),{\displaystyle {\mathit{\xi }}_{\ell ,N}^{(m)}}(t),{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)$, and calculate the elements of matrices  ${\mathit{H}}^2,{\displaystyle {\mathit{\xi }}_{\mathcal{T},N}^{(1)}}(t),{\displaystyle {\mathit{\xi }}_{\ell ,N}^{(2)}}(x)$,  ${\widehat{\mathit{D}}}^{(\nu (x,t))}$, and ${\widehat{\mathit{D}}}^{({\nu }_i(x,t))},i=1,2,\dots ,m$.
Stage 3.	Calculate the matrices: 1. ${\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}{\displaystyle {\mathsf{\Psi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)$, 2. ${\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}(H{\displaystyle {\mathsf{\Psi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\displaystyle {\mathit{\xi }}_{\mathcal{T},N}^{(1)}}(t))$, 3. $(H^2{\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)+{\displaystyle {\mathit{\xi }}_{\ell ,N}^{(2)}}(x))\mathit{A}{\displaystyle {\mathsf{\Psi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t),$ 4. ${\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}({\widehat{\mathit{D}}}^{(\nu (x,t))}{\displaystyle {\mathsf{\Psi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\mathit{\epsilon }}_{\mathcal{T},N}(x,t))$, 5. ${\displaystyle {\mathsf{\Psi }}_{\ell ,N}^{(\widehat{\alpha },\widehat{\beta })}}(x)\mathit{A}({\widehat{\mathit{D}}}^{({\nu }_i(x,t))}{\displaystyle {\mathsf{\Psi }}_{\mathcal{T},N}^{(\widehat{\alpha },\widehat{\beta })}}(t)+{\mathit{\epsilon }}_{\mathcal{T},N}(x,t)),i=0,1,\dots ,m.$
Stage 4.	Define $R_N(x,t)$ as in Equation (67).
Stage 5.	List $R_N(x_i,t_j)=0,i,j=0,1,\dots ,N$, defined in Equation (68).
Stage 6.	Use Mathematica’s built-in numerical solver to solve the system obtained in [Output 5].
Stage 6.	Calculate $y_N(x,t)$ defined in Equation (62) (Homogeneous DBCs).
Stage 7.	Calculate $q(x,t)$ and $y_N(x,t)$ defined in Equation (75) (Non-homogeneous DBCs).

7. Convergence and Error Analysis

Here, we look at the suggested method’s convergence and error estimations. The space ${\mathcal{S}}_{\mathcal{N}}$, defined as follows, is our primary area of interest,

$${\mathcal{S}}_{\mathcal{N}}=\left\{\begin{array}{cc}Span\{{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x){\displaystyle {\varphi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t):i,j=0,1,\dots ,N\},\hfill & \mathrm{for}\mathrm{IBCs},\hfill \\ Span\{{\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x){\displaystyle {\psi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t):i,j=0,1,\dots ,N\},\hfill & \mathrm{for}\mathrm{DBCs}.\hfill \end{array}\right.$$

Additionally, the error between $y(x,t)$ and its approximation $y_N(x,t)$ can be defined by

$$E_N(x,t)=\left|y(x,t)-y_N(x,t)\right|.$$

(76)

The numerical scheme’s error is examined in the paper via the use of the $L_{\infty }$ norm error estimation

$$\parallel E_N{\parallel }_{\infty }=\parallel y-y_N{\parallel }_{\infty }=\underset{(x,t)\in I}{max}|y(x,t)-y_N(x,t)|,I=[0,\ell ]\times [0,\mathcal{T}].$$

(77)

In the following, Theorem 5 discusses the error estimate when the solution satisfies IBCs, while Theorem 6 discusses it when DBCs are considered.

Theorem 5.

Assume that $y(x,t)=t^{2}x(\ell -x)\upsilon (x,t)$ and that $y_N(x,t)$ has the expression (62) and represents the best possible approximation (BPA) for $y(x,t)$ out of ${\mathcal{S}}_{\mathcal{N}}$. Then,

$$\parallel E_N{\parallel }_{\infty }\le \frac{1}{4}{(\ell \mathcal{T})}^2{W}_{q,N}(\ell ,\mathcal{T}),q=max\{\widehat{\alpha },\widehat{\beta },-1/2\}<N+1,$$

(78)

where

$$W_{q,N}(\ell ,\mathcal{T})=K_1\frac{\ell }{2^{\lambda }}{\left(\frac{e\ell }{4}\right)}^N{(N+1)}^{q-N-1}+K_2\frac{\mathcal{T}}{2^{\lambda }}{\left(\frac{e\mathcal{T}}{4}\right)}^N{(N+1)}^{q-N-1}+K_3\frac{\ell \mathcal{T}}{2^{2\lambda }}{\left(\frac{e^2\ell \mathcal{T}}{16}\right)}^N{(N+1)}^{2(q-N-1)},$$

(79)

where the constants $K_i,i=1,2,3,$ are defined as follows:

$$K_1=\underset{(x,t)\in I}{max}|{\displaystyle \frac{{\partial }^{N+1}\upsilon (x,t)}{\partial x^{N+1}}}|,K_2=\underset{(x,t)\in I}{max}|{\displaystyle \frac{{\partial }^{N+1}\upsilon (x,t)}{\partial t^{N+1}}}|,K_3=\underset{(x,t)\in I}{max}|{\displaystyle \frac{{\partial }^{2N+2}\upsilon (x,t)}{\partial x^{N+1}\partial t^{N+1}}}|.$$

(80)

Proof. 

Let ${\upsilon }_N(x,t)$ be the interpolating polynomial for $\upsilon (x,t)$ at the points $(x_i,t_j),i,j=0,1,\dots ,N,$ where $x_i,(0\le i\le N)$ and $t_j,(0\le j\le N)$ are the roots of ${\displaystyle {\mathcal{J}}_{\ell ,N+1}^{(\widehat{\alpha },\widehat{\beta })}}(x)$ and ${\displaystyle {\mathcal{J}}_{\mathcal{T},N+1}^{(\widehat{\alpha },\widehat{\beta })}}(t)$, respectively, such that $N>q-1$. Then, the function $\upsilon (x,t)$ can be written as [55]:

$$\upsilon (x,t)={\upsilon }_N(x,t)+{\displaystyle \frac{{\partial }^{N+1}\upsilon ({\eta }_x,t)}{\partial x^{N+1}(N+1)!}}{\mathcal{Q}}_1(x)+{\displaystyle \frac{{\partial }^{N+1}\upsilon (x,{\eta }_t)}{\partial t^{N+1}(N+1)!}}{\mathcal{Q}}_2(t)-{\displaystyle \frac{{\partial }^{2N+2}\upsilon (\eta {\prime }_x,\eta {\prime }_t)}{\partial x^{N+1}\partial t^{N+1}{((N+1)!)}^2}}{\mathcal{Q}}_1(x){\mathcal{Q}}_2(t),$$

(81)

where ${\mathcal{Q}}_1(x)={\displaystyle {\prod }_{i=0}^N}(x-x_i)$, ${\mathcal{Q}}_2(t)={\displaystyle {\prod }_{j=0}^N}(t-t_j)$, ${\eta }_x,\eta {\prime }_x\in [0,\ell ]$, and ${\eta }_t,\eta {\prime }_t\in [0,\mathcal{T}]$.

This is to acquire that:

$$\begin{array}{cc}\hfill \parallel \upsilon -{\upsilon }_N{\parallel }_{\infty }\le & {\displaystyle \frac{K_1{\ell }^{N+1}}{(N+1)!{\tilde{c}}_N}}\parallel {\displaystyle {\mathcal{J}}_{\ell ,N+1}^{(\widehat{\alpha },\widehat{\beta })}}{(x)\parallel }_{\infty }+{\displaystyle \frac{K_2{\mathcal{T}}^{N+1}}{(N+1)!{\tilde{c}}_N}}{\parallel {\displaystyle {\mathcal{J}}_{\mathcal{T},N+1}^{(\widehat{\alpha },\widehat{\beta })}}(t)\parallel }_{\infty }\hfill \\ & +{\displaystyle \frac{K_3{(\ell \mathcal{T})}^{N+1}}{{((N+1)!)}^2{({\tilde{c}}_N)}^2}}\parallel {\displaystyle {\mathcal{J}}_{\ell ,N+1}^{(\widehat{\alpha },\widehat{\beta })}}{(x)\parallel }_{\infty }{\parallel {\displaystyle {\mathcal{J}}_{\mathcal{T},N+1}^{(\widehat{\alpha },\widehat{\beta })}}(t)\parallel }_{\infty },\hfill \end{array}$$

(82)

where ${\tilde{c}}_N={\ell }^{N+1}{\displaystyle c_{N+1}^{N+1}}={\displaystyle \frac{\Gamma (2N+\lambda +2)}{(N+1)!\Gamma (N+\lambda +1)}}$, and ${\displaystyle c_{N+1}^{N+1}}$ is the leading coefficient of ${\displaystyle {\mathcal{J}}_{\ell ,N+1}^{(\widehat{\alpha },\widehat{\beta })}}(x)$.

Using the expression [52] (formula (7.32.2)), we derive:

$$\parallel {\displaystyle {\mathcal{J}}_{\ell ,N+1}^{(\widehat{\alpha },\widehat{\beta })}}{\parallel }_{\infty }\simeq {(N+1)}^q,$$

(83)

and thus the inequality (82) takes the form:

$$\begin{array}{cc}\hfill \parallel \upsilon -{\upsilon }_N{\parallel }_{\infty }\le & K_1\frac{{\ell }^{N+1}\Gamma (N+\lambda +1){(N+1)}^q}{\Gamma (2N+\lambda +2)}+K_2\frac{{\mathcal{T}}^{N+1}\Gamma (N+\lambda +1){(N+1)}^q}{\Gamma (2N+\lambda +2)}\hfill \\ & +K_3{(\ell \mathcal{T})}^{N+1}\frac{{\Gamma }^2(N+\lambda +1){(N+1)}^{2q}}{{\Gamma }^2(2N+\lambda +2)}.\hfill \end{array}$$

(84)

By utilizing results (see [56] (pp. 232–233)),

$$\Gamma (m+\lambda )=\mathcal{O}(m^{\lambda -1}m!),(2m)!={\displaystyle \frac{1}{\sqrt{\pi }}}{4}^{m}m!\Gamma (m+1/2),m!=\mathcal{O}\left(\sqrt{2\pi m}{\left({\displaystyle \frac{m}{e}}\right)}^m\right),$$

(85)

the inequality (84) takes the form:

$$\parallel \upsilon -{\upsilon }_N{\parallel }_{\infty }\le W_{q,N}(\ell ,\mathcal{T}),$$

(86)

where

$$W_{q,N}(\ell ,\mathcal{T})=K_1\frac{\ell }{2^{\lambda }}{\left(\frac{e\ell }{4}\right)}^N{(N+1)}^{q-N-1}+K_2\frac{\mathcal{T}}{2^{\lambda }}{\left(\frac{e\mathcal{T}}{4}\right)}^N{(N+1)}^{q-N-1}+K_3\frac{\ell \mathcal{T}}{2^{2\lambda }}{\left(\frac{e^2\ell \mathcal{T}}{16}\right)}^N{(N+1)}^{2(q-N-1)}.$$

(87)

Now, consider the approximation $y(x,t)\simeq Y_N(x,t)=t^{2}x(\ell -x){\upsilon }_N(x,t)$; then,

$$\parallel y-Y_N{\parallel }_{\infty }\le \frac{1}{4}{(\ell \mathcal{T})}^2{\parallel u-{\upsilon }_N\parallel }_{\infty }\le \frac{1}{4}{(\ell \mathcal{T})}^2{W}_{q,N}(\ell ,\mathcal{T}).$$

(88)

Since $y_N(x,t)\in {\mathcal{S}}_N$ represents the BPA to $y(x,t)$, then

$$\parallel y-y_N{\parallel }_{\infty }\le {\parallel y-h\parallel }_{\infty },\forall h\in {\mathcal{S}}_N,$$

(89)

and therefore,

$$\parallel y-y_N{\parallel }_{\infty }\le {\parallel y-Y_N\parallel }_{\infty }\le \frac{1}{4}{(\ell \mathcal{T})}^2{W}_{q,N}(\ell ,\mathcal{T}).$$

(90)

   □

Theorem 6.

Assume that $y(x,t)=tx(\ell -x)(\mathcal{T}-t)\upsilon (x,t)$ and that $y_N(x,t)$ has the expression (63) and represents the BPA for $y(x,t)$ out of ${\mathcal{S}}_{\mathcal{N}}$. Then,

$$\parallel E_N{\parallel }_{\infty }\le \frac{1}{16}{(\ell \mathcal{T})}^2{W}_{q,N}(\ell ,\mathcal{T}),q=max\{\widehat{\alpha },\widehat{\beta },-1/2\}<N+1,$$

(91)

where $W_{q,N}(\ell ,\mathcal{T})$ is defined by (79).

Proof. 

Following the same procedures in the proof of Theorem 5, we obtain (91).    □

The next corollary demonstrates how quickly the resulting errors are convergent.

Corollary 3.

For all $N>q-1$, the following estimate holds:

$$\parallel E_N{\parallel }_{\infty }=\mathcal{O}\left({\left(\frac{e^2\ell \mathcal{T}}{16}\right)}^N{N}^{q-N-1}\right).$$

(92)

The stability of error, or the process of estimating the propagation of error, is the focus of the subsequent theorem.

Theorem 7.

Given any two iterative estimates of $y(x,t)$, the result is:

$$|y_{N+1}-y_N|\lesssim \mathcal{O}\left({\left(\frac{e^2\ell \mathcal{T}}{16}\right)}^N{N}^{q-N-1}\right),N>q-1.$$

(93)

Proof. 

We have

$$|y_{N+1}-y_N|=|y_{N+1}-y+y-y_N|\le |y-y_{N+1}|+|y-y_N|\le \parallel E_{N+1}{\parallel }_{\infty }+{\parallel E_N\parallel }_{\infty }.$$

By considering (92), we can obtain (93).    □

Remark 3.

While relative error can be a useful measure in certain situations, the choice to utilize absolute error in our study was driven by considerations of stability, consistency with established literature, practical interpretation, and the characteristics of the problem at hand. We believe that using absolute error allows for a reliable and meaningful assessment of the accuracy of our proposed method in solving MTVO-TFDWEs.

8. Numerical Simulations

In order to show how the approach presented in Section 6 works and how efficient it is, four examples are provided in this section. The assessment is based on MAE between the precise and approximate solutions. We show in Example 1 that, for certain simple cases of the functions $\nu (x,t)$ and ${\nu }_j(x,t),j=1,2,\dots ,m$, we can use $GSJCOPMM$ to find the precise solution to the given numerical problem, whether it involves IBCs or DBCs, and that it has a polynomial solution of degree N. This solution can be found by combining ${\displaystyle {\psi }_{\ell ,i}^{(\widehat{\alpha },\widehat{\beta })}}(x),{\displaystyle {\varphi }_{\mathcal{T},j}^{(\widehat{\alpha },\widehat{\beta })}}(t),i,j=0,1,\dots ,N-2$. Otherwise, some numerical solutions are obtained with high accuracy. Additionally, the choice of examples in our study is motivated by the desire to cover different conditions, compare with existing results, showcase accuracy and efficiency, and demonstrate practical relevance. These examples collectively provide a comprehensive assessment of the performance and applicability of our proposed method for solving MTVO-TFDWEs.

In addition,

Table 1. MAEs of Example 1 using various $\widehat{\alpha },\widehat{\beta }$, and N.

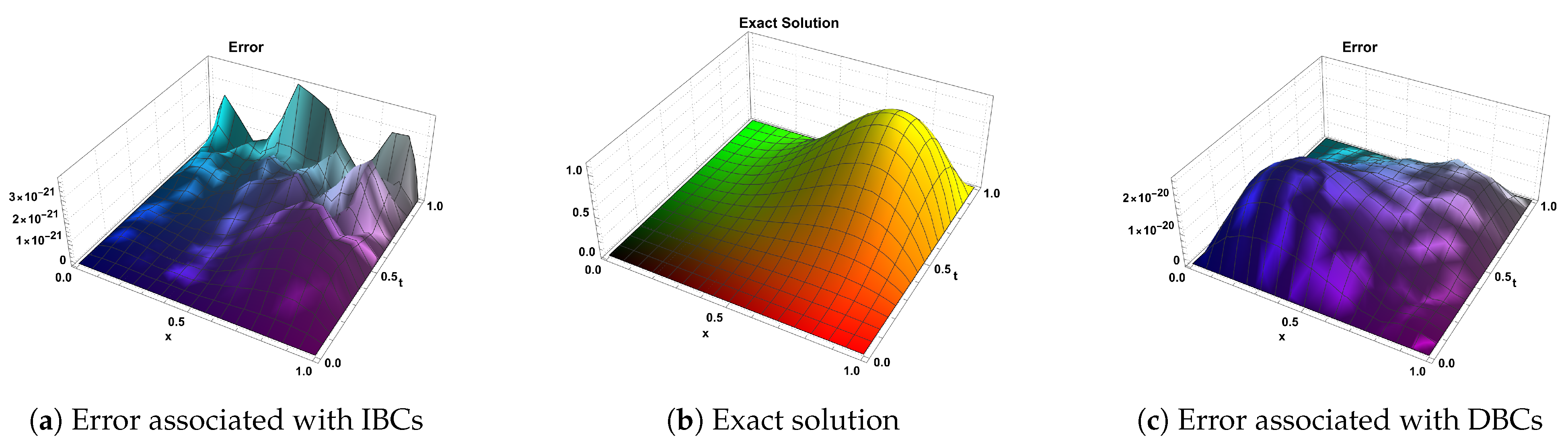
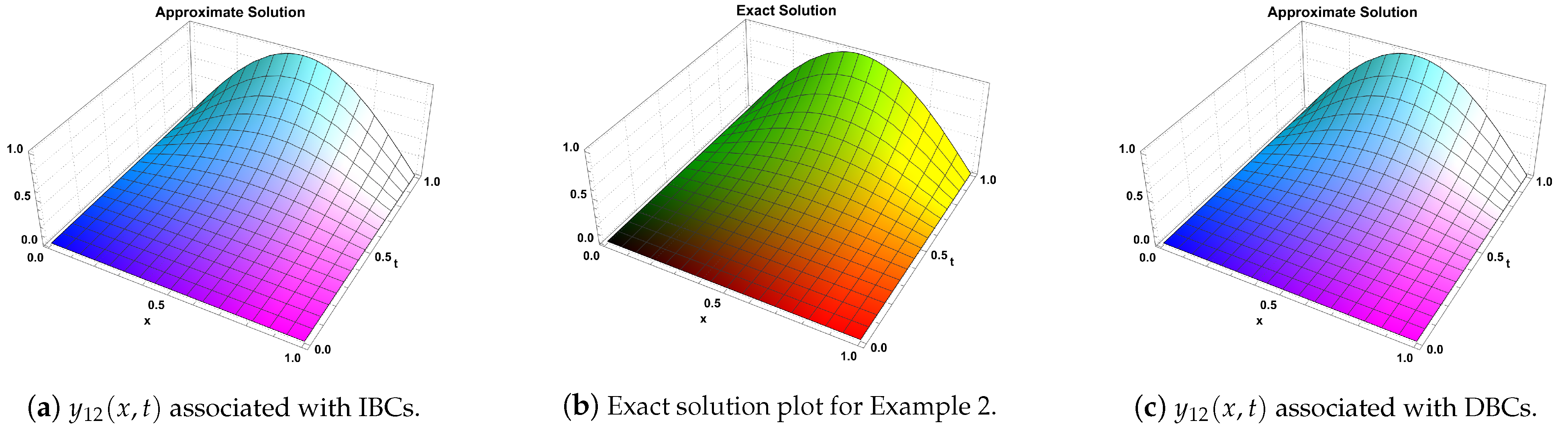
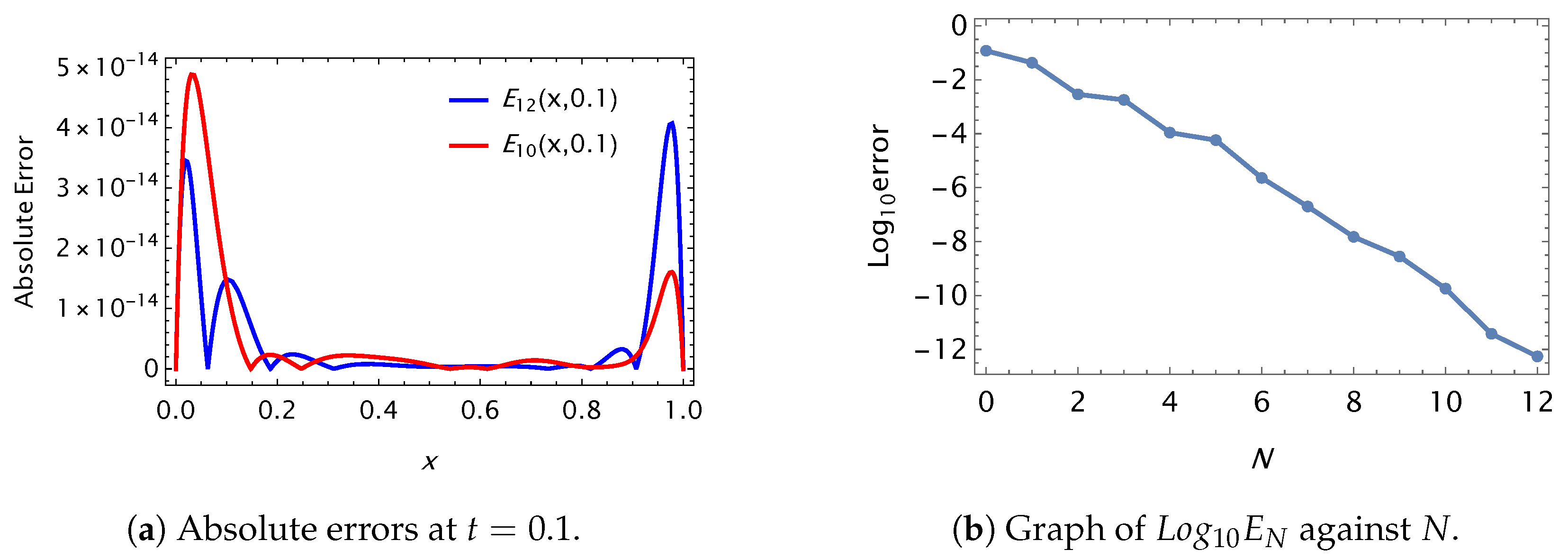
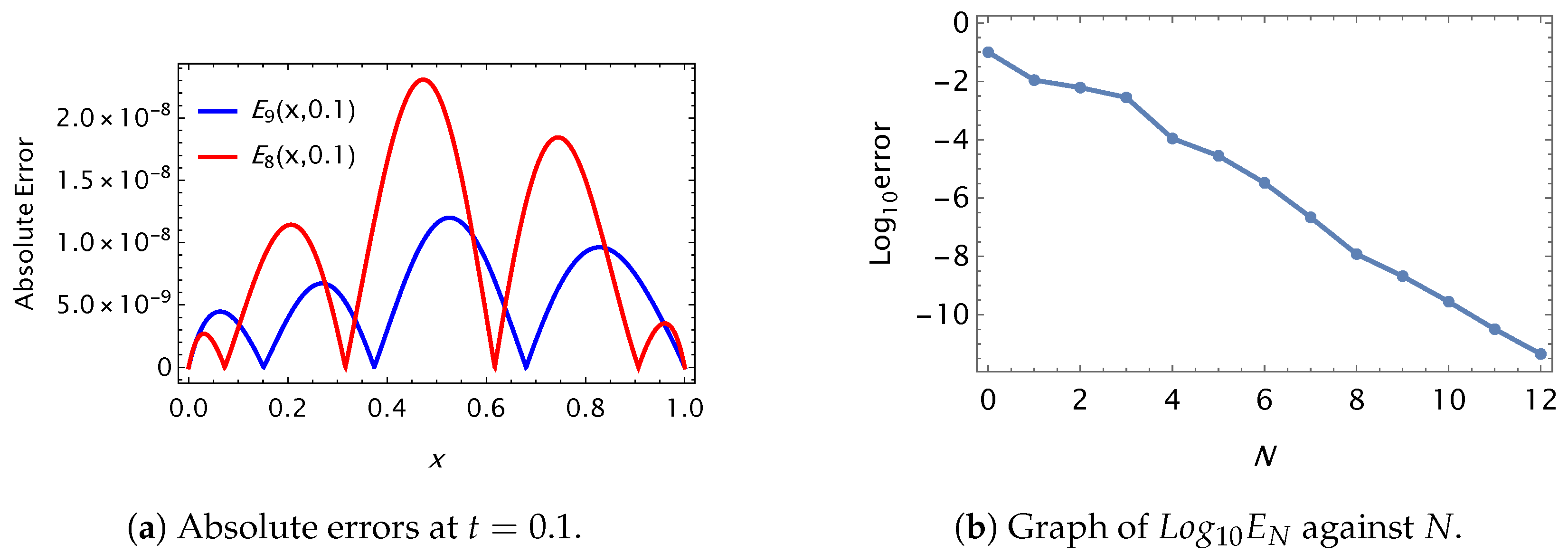
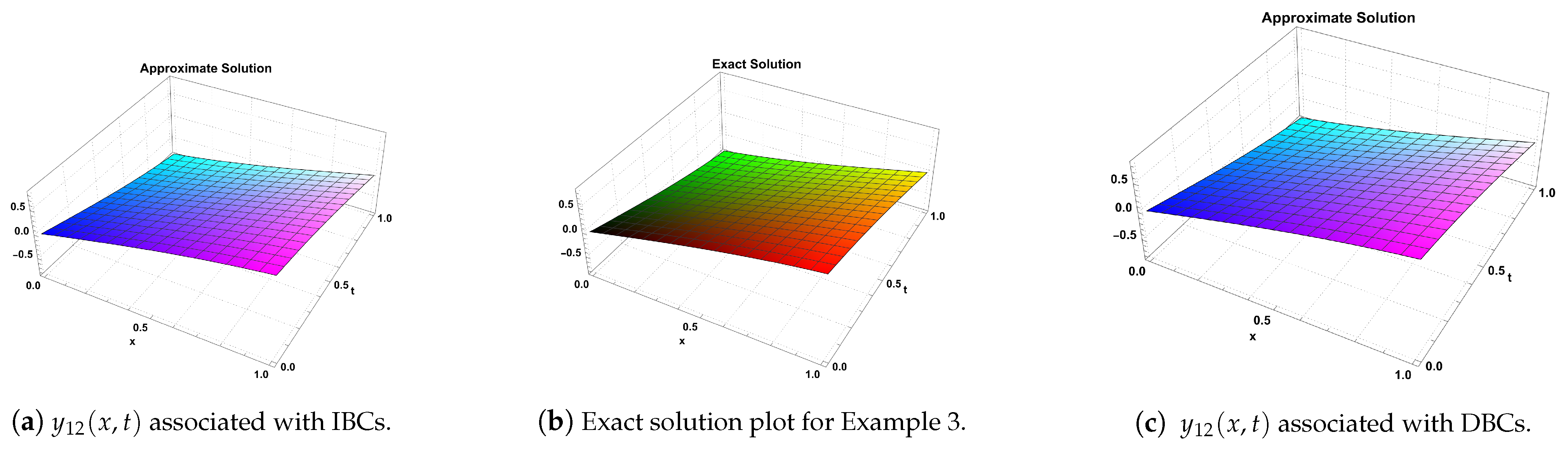
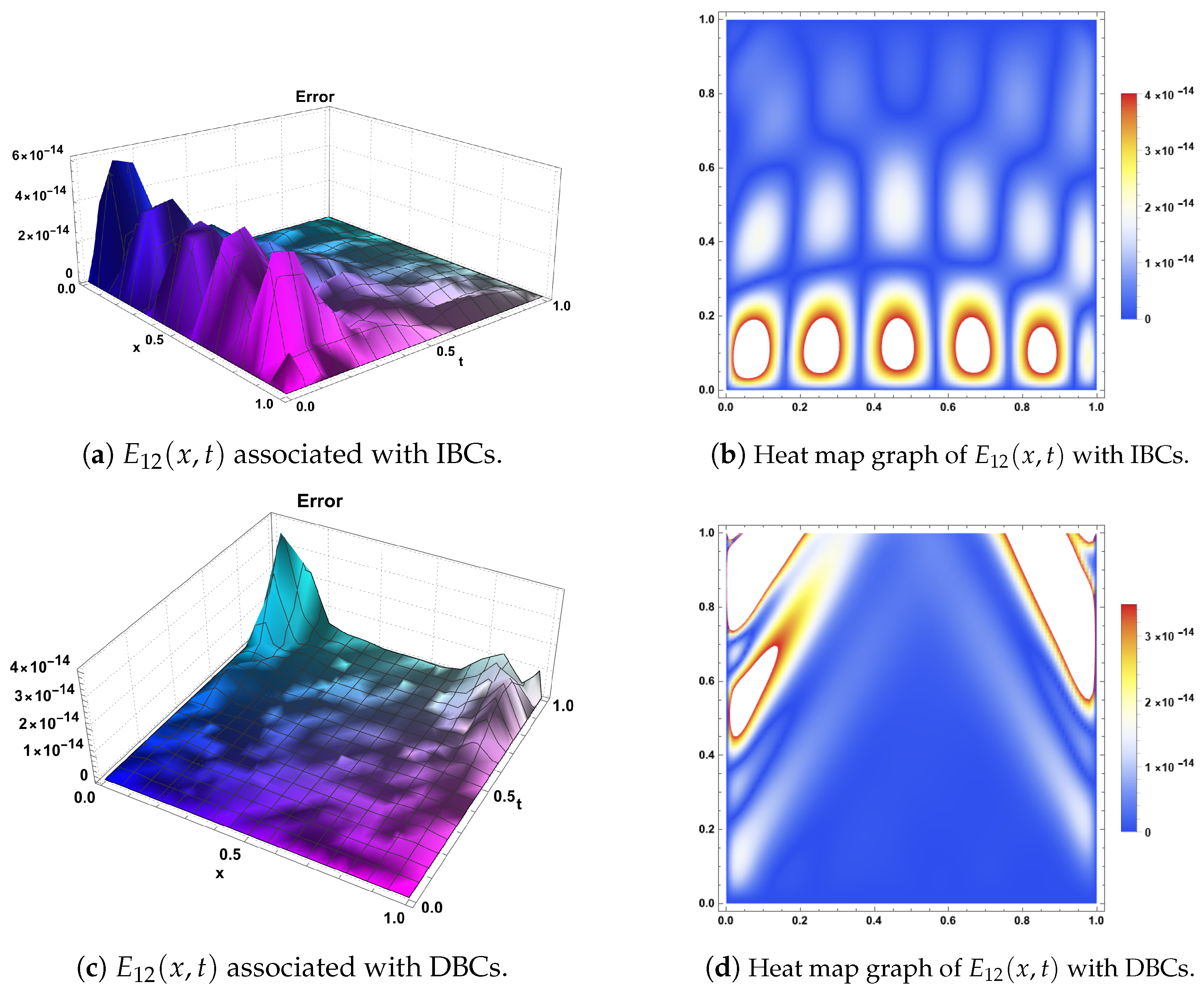
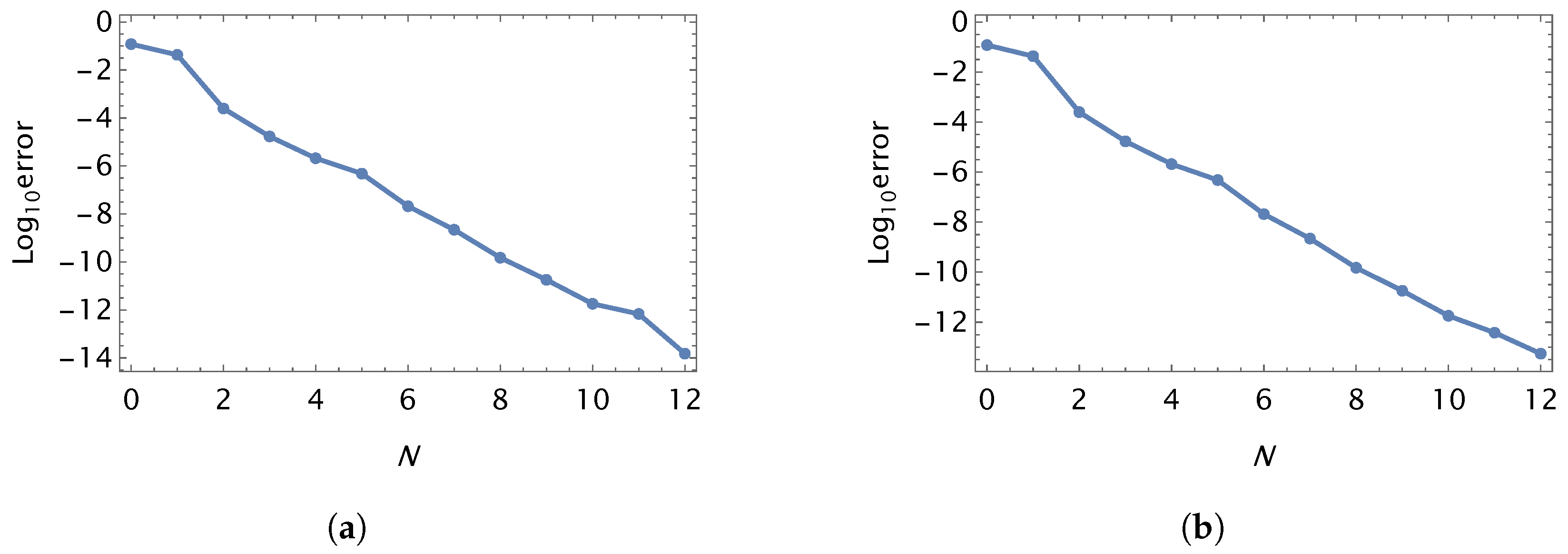
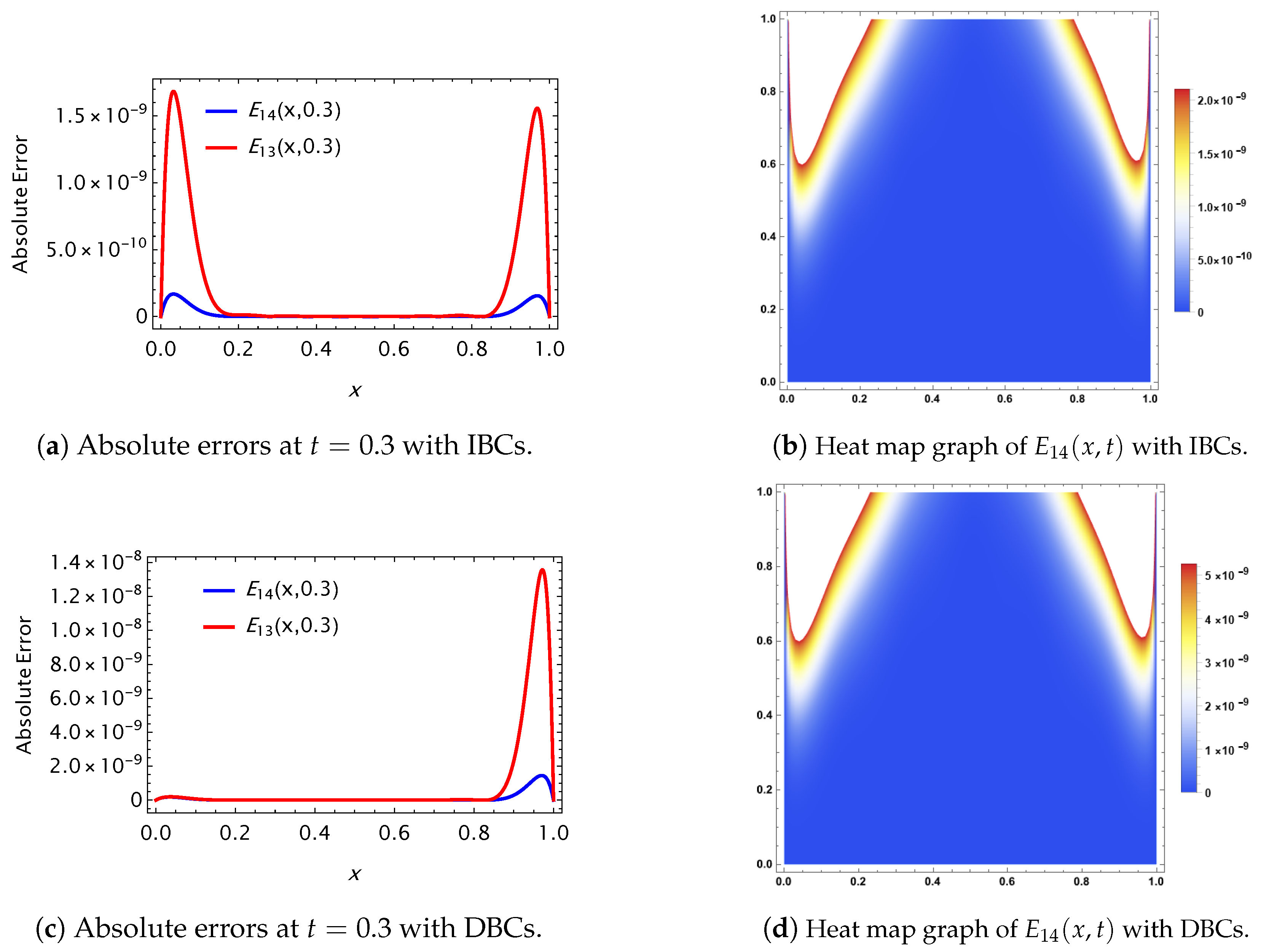
$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\beta }}$	IBCs/DBCs	$\mathit{N}=2$	$\mathit{N}=3$	$\mathit{N}=4$	$\mathit{N}=5$	$\mathit{N}=6$	$\mathit{N}=7$
0	0	IBCs	1.3 × ${10}^{-16}$	2.3 × ${10}^{-17}$	1.9 ×  ${10}^{-18}$	2.4 ×  ${10}^{-19}$	2.7 ×  ${10}^{-20}$	2.4 ×  ${10}^{-21}$
		DBCs	2.6 × ${10}^{-16}$	3.4 ×  ${10}^{-17}$	3.5 ×  ${10}^{-18}$	3.9 ×  ${10}^{-19}$	3.6 ×  ${10}^{-20}$	1.6 ×  ${10}^{-20}$
		CPU time	0.231	0.312	0.401	0.421	0.451	0.515
1/2	1/2	IBCs	2.4 × ${10}^{-16}$	1.3 ×  ${10}^{-17}$	4.1 ×  ${10}^{-18}$	7.2 ×  ${10}^{-19}$	1.8 ×  ${10}^{-20}$	2.5 ×  ${10}^{-21}$
		DBCs	2.7 × ${10}^{-16}$	3.6 ×  ${10}^{-17}$	3.8 ×  ${10}^{-18}$	3.9 ×  ${10}^{-19}$	4.4 ×  ${10}^{-20}$	2.7 ×  ${10}^{-20}$
		CPU time	0.232	0.313	0.403	0.422	0.453	0.517
−1/2	−1/2	IBCs	1.5 × ${10}^{-16}$	2.8 ×  ${10}^{-17}$	4.8 ×  ${10}^{-18}$	1.2 ×  ${10}^{-19}$	1.8 ×  ${10}^{-20}$	2.6 ×  ${10}^{-21}$
		DBCs	1.6 × ${10}^{-16}$	3.6 ×  ${10}^{-17}$	1.9 ×  ${10}^{-18}$	1.9 ×  ${10}^{-19}$	5.4 ×  ${10}^{-20}$	2.1 ×  ${10}^{-20}$
		CPU time	0.221	0.310	0.402	0.422	0.450	0.517
1	0	IBCs	3.3 × ${10}^{-15}$	4.3 ×  ${10}^{-16}$	3.7 ×  ${10}^{-17}$	2.2 ×  ${10}^{-18}$	1.8 ×  ${10}^{-19}$	3.1 ×  ${10}^{-21}$
		DBCs	3.9 × ${10}^{-16}$	3.6 ×  ${10}^{-17}$	2.1 ×  ${10}^{-18}$	1.9 ×  ${10}^{-19}$	2.6 ×  ${10}^{-20}$	2.2 ×  ${10}^{-20}$
		CPU time	0.233	0.314	0.407	0.425	0.458	0.519
0	1	IBCs	4.3 × ${10}^{-15}$	2.3 ×  ${10}^{-16}$	4.5 ×  ${10}^{-17}$	4.4 ×  ${10}^{-18}$	1.7 ×  ${10}^{-19}$	2.9 ×  ${10}^{-21}$
		DBCs	2.9 × ${10}^{-16}$	3.2 ×  ${10}^{-17}$	2.5 ×  ${10}^{-18}$	3.8 ×  ${10}^{-19}$	8.6 ×  ${10}^{-20}$	2.3 ×  ${10}^{-20}$
		CPU time	0.234	0.315	0.407	0.426	0.451	0.519

,

Table 2. MAEs of Example 2 using various $\widehat{\alpha },\widehat{\beta }$, and N.

$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\beta }}$	IBCs/DBCs	$\mathit{N}=0$	$\mathit{N}=1$	$\mathit{N}=2$	$\mathit{N}=5$	$\mathit{N}=8$	$\mathit{N}=12$
0	0	IBCs	1.2 × ${10}^{-1}$	4.3 × ${10}^{-2}$	2.9 ×  ${10}^{-3}$	5.8 ×  ${10}^{-5}$	1.5 ×  ${10}^{-8}$	5.5 ×  ${10}^{-13}$
		DBCs	1.0 × ${10}^{-1}$	1.1 ×  ${10}^{-2}$	6.1 ×  ${10}^{-3}$	4.0 ×  ${10}^{-5}$	1.2 ×  ${10}^{-8}$	4.5 ×  ${10}^{-12}$
		CPU time	0.101	0.122	0.232	0.432	0.521	0.735
1/2	1/2	IBCs	1.3 × ${10}^{-1}$	4.4 ×  ${10}^{-2}$	2.8 ×  ${10}^{-3}$	5.4 ×  ${10}^{-5}$	1.2 ×  ${10}^{-8}$	5.4 ×  ${10}^{-13}$
		DBCs	1.1 × ${10}^{-1}$	1.1 ×  ${10}^{-2}$	5.9 ×  ${10}^{-3}$	4.2 ×  ${10}^{-5}$	1.4 ×  ${10}^{-8}$	4.0 ×  ${10}^{-12}$
		CPU time	0.102	0.123	0.234	0.433	0.525	0.745
−1/2	−1/2	IBCs	1.4 × ${10}^{-1}$	3.3 ×  ${10}^{-2}$	2.1 ×  ${10}^{-3}$	4.9 ×  ${10}^{-5}$	1.3 ×  ${10}^{-8}$	5.7 ×  ${10}^{-13}$
		DBCs	1.2 × ${10}^{-1}$	1.3 ×  ${10}^{-2}$	5.2 ×  ${10}^{-3}$	3.9 ×  ${10}^{-5}$	1.5 ×  ${10}^{-8}$	4.7 ×  ${10}^{-12}$
		CPU time	0.101	0.121	0.231	0.433	0.520	0.732
1	0	IBCs	1.5 × ${10}^{-1}$	3.9 ×  ${10}^{-2}$	3.0 ×  ${10}^{-3}$	6.0 ×  ${10}^{-5}$	2.5 ×  ${10}^{-8}$	4.5 ×  ${10}^{-13}$
		DBCs	1.3 × ${10}^{-1}$	1.4 ×  ${10}^{-2}$	6.2 ×  ${10}^{-3}$	3.3 ×  ${10}^{-5}$	2.0 ×  ${10}^{-8}$	3.5 ×  ${10}^{-12}$
		CPU time	0.104	0.124	0.234	0.435	0.521	0.738
0	1	IBCs	1.7 × ${10}^{-1}$	4.5 ×  ${10}^{-2}$	2.7 ×  ${10}^{-3}$	5.1 ×  ${10}^{-5}$	1.3 ×  ${10}^{-8}$	5.5 ×  ${10}^{-13}$
		DBCs	1.7 × ${10}^{-1}$	1.6 ×  ${10}^{-2}$	6.5 ×  ${10}^{-3}$	4.5 ×  ${10}^{-5}$	1.8 ×  ${10}^{-8}$	4.1 ×  ${10}^{-12}$
		CPU time	0.102	0.125	0.237	0.438	0.529	0.741

,

Table 3. MAEs of Example 3 using various $\widehat{\alpha },\widehat{\beta }$, and N.

$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\beta }}$	IBCs/DBCs	$\mathit{N}=2$	$\mathit{N}=4$	$\mathit{N}=6$	$\mathit{N}=8$	$\mathit{N}=10$	$\mathit{N}=12$
0	0	IBCs	1.4 × ${10}^{-4}$	3.3 × ${10}^{-6}$	2.2 ×  ${10}^{-8}$	4.8 ×  ${10}^{-10}$	2.5 ×  ${10}^{-12}$	4.4 ×  ${10}^{-13}$
		DBCs	1.2 × ${10}^{-4}$	2.1 ×  ${10}^{-6}$	1.1 ×  ${10}^{-8}$	3.2 ×  ${10}^{-10}$	2.3 ×  ${10}^{-12}$	6.8 ×  ${10}^{-14}$
		CPU time	0.231	0.401	0.451	0.521	0.601	0.735
1/2	1/2	IBCs	1.0 × ${10}^{-4}$	2.1 ×  ${10}^{-6}$	2.4 ×  ${10}^{-8}$	4.4 ×  ${10}^{-10}$	2.2 ×  ${10}^{-12}$	5.4 ×  ${10}^{-14}$
		DBCs	1.3 × ${10}^{-4}$	2.1 ×  ${10}^{-6}$	4.9 ×  ${10}^{-8}$	4.3 ×  ${10}^{-10}$	2.1 ×  ${10}^{-12}$	4.2 ×  ${10}^{-14}$
		CPU time	0.233	0.405	0.454	0.525	0.607	0.740
−1/2	−1/2	IBCs	1.5 × ${10}^{-4}$	2.4 ×  ${10}^{-6}$	2.3 ×  ${10}^{-8}$	2.4 ×  ${10}^{-10}$	1.4 ×  ${10}^{-12}$	5.7 ×  ${10}^{-14}$
		DBCs	1.1 × ${10}^{-4}$	1.5 ×  ${10}^{-6}$	4.2 ×  ${10}^{-8}$	2.9 ×  ${10}^{-10}$	3.5 ×  ${10}^{-12}$	2.2 ×  ${10}^{-13}$
		CPU time	0.240	0.410	0.459	0.528	0.610	0.740
1	0	IBCs	1.2 × ${10}^{-4}$	2.3 ×  ${10}^{-6}$	3.1 ×  ${10}^{-8}$	5.0 ×  ${10}^{-10}$	3.5 ×  ${10}^{-12}$	8.2 ×  ${10}^{-14}$
		DBCs	1.3 × ${10}^{-4}$	2.5 ×  ${10}^{-6}$	5.2 ×  ${10}^{-8}$	4.3 ×  ${10}^{-10}$	3.0 ×  ${10}^{-12}$	6.5 ×  ${10}^{-14}$
		CPU time	0.238	0.409	0.458	0.529	0.608	0.739
0	1	IBCs	1.8 × ${10}^{-4}$	2.3 ×  ${10}^{-6}$	2.4 ×  ${10}^{-8}$	5.2 ×  ${10}^{-10}$	2.3 ×  ${10}^{-12}$	4.5 ×  ${10}^{-13}$
		DBCs	1.7 × ${10}^{-4}$	2.5 ×  ${10}^{-6}$	5.5 ×  ${10}^{-8}$	3.5 ×  ${10}^{-10}$	2.8 ×  ${10}^{-12}$	6.1 ×  ${10}^{-14}$
		CPU time	0.237	0.407	0.456	0.527	0.608	0.738

, and

Table 4. MAEs of Example 4 using various $\widehat{\alpha },\widehat{\beta }$, and N.

$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\beta }}$	IBCs/DBCs	$\mathit{N}=2$	$\mathit{N}=4$	$\mathit{N}=6$	$\mathit{N}=8$	$\mathit{N}=10$	$\mathit{N}=14$
1	1	IBCs	1.2 × ${10}^{-2}$	2.3 × ${10}^{-3}$	2.0 ×  ${10}^{-4}$	3.8 ×  ${10}^{-5}$	2.1 ×  ${10}^{-6}$	4.5 ×  ${10}^{-9}$
		DBCs	1.1 × ${10}^{-2}$	3.3 ×  ${10}^{-3}$	2.2 ×  ${10}^{-4}$	4.8 ×  ${10}^{-5}$	3.1 ×  ${10}^{-6}$	2.2 ×  ${10}^{-8}$
		CPU time	0.235	0.402	0.454	0.522	0.604	0.988
3/2	1/2	IBCs	1.3 × ${10}^{-2}$	4.3 ×  ${10}^{-3}$	5.0 ×  ${10}^{-4}$	3.7 ×  ${10}^{-5}$	2.6 ×  ${10}^{-6}$	4.4 ×  ${10}^{-9}$
		DBCs	2.2 × ${10}^{-2}$	3.1 ×  ${10}^{-3}$	2.4 ×  ${10}^{-4}$	3.5 ×  ${10}^{-5}$	2.7 ×  ${10}^{-6}$	4.4 ×  ${10}^{-8}$
		CPU time	0.230	0.317	0.411	0.430	0.460	0.980
1/2	3/2	IBCs	2.2 × ${10}^{-2}$	4.3 ×  ${10}^{-3}$	3.0 ×  ${10}^{-4}$	3.9 ×  ${10}^{-5}$	2.3 ×  ${10}^{-6}$	4.6 ×  ${10}^{-9}$
		DBCs	4.2 × ${10}^{-2}$	3.2 ×  ${10}^{-3}$	1.5 ×  ${10}^{-4}$	5.8 ×  ${10}^{-5}$	2.9 ×  ${10}^{-6}$	4.4 ×  ${10}^{-8}$
		CPU time	0.234	0.319	0.412	0.429	0.459	0.991
2	3	IBCs	3.2 × ${10}^{-2}$	4.3 ×  ${10}^{-3}$	1.0 ×  ${10}^{-4}$	1.8 ×  ${10}^{-5}$	2.2 ×  ${10}^{-6}$	4.6 ×  ${10}^{-9}$
		DBCs	5.2 × ${10}^{-2}$	3.4 ×  ${10}^{-3}$	2.3 ×  ${10}^{-4}$	3.6 ×  ${10}^{-5}$	2.0 ×  ${10}^{-6}$	6.1 ×  ${10}^{-9}$
		CPU time	0.239	0.320	0.413	0.430	0.461	1.001
3	2	IBCs	1.7 × ${10}^{-2}$	2.8 ×  ${10}^{-3}$	2.5 ×  ${10}^{-4}$	2.8 ×  ${10}^{-5}$	2.4 ×  ${10}^{-6}$	4.7 ×  ${10}^{-9}$
		DBCs	2.3 × ${10}^{-2}$	4.3 ×  ${10}^{-3}$	2.5 ×  ${10}^{-4}$	3.9 ×  ${10}^{-5}$	2.8 ×  ${10}^{-6}$	4.6 ×  ${10}^{-9}$
		CPU time	0.238	0.319	0.412	0.428	0.458	0.998

display the calculated errors that were obtained to produce numerical solutions $y_N(x,t)$ using $GSJCOPMM$ with $N=0,1,\dots ,$ 14. In these tables, excellent computational results are obtained. The comparisons between $GSJCOPMM$ and other techniques in [57,58] are presented in

Table 5. The method’s comparisons [57,58] and $GSJCOPMM$ in Example 2 with IBCs and DBCs.

	$\mathit{GSJCOPMM}$ (IBCs)	$\mathit{GSJCOPMM}$ (DBCs)	[57] (IBCs)	[58] (DBCs)
$(\mathit{x},\mathit{t})$	$(\widehat{\mathit{\alpha }}=\widehat{\mathit{\beta }}=\mathbf{1},\mathit{N}=\mathbf{10})$	$(\widehat{\mathit{\alpha }}=\widehat{\mathit{\beta }}=\mathbf{1},\mathit{N}=\mathbf{8})$	$(\mathit{k}=\mathbf{1},\mathit{M}=\mathbf{10})$	$(\mathit{N}=\mathit{M}=\mathbf{8})$
(0.1, 0.1)	1.47 × ${10}^{-14}$	3.15 × ${10}^{-9}$	3.05 × ${10}^{-4}$	1.69 ×  ${10}^{-7}$
(0.2, 0.2)	4.34 × ${10}^{-15}$	1.09 ×  ${10}^{-8}$	8.35 ×  ${10}^{-6}$	1.12 ×  ${10}^{-7}$
(0.3, 0.3)	2.55 × ${10}^{-15}$	4.39 ×  ${10}^{-9}$	2.35 ×  ${10}^{-7}$	1.97 ×  ${10}^{-8}$
(0.4, 0.4)	5.41 × ${10}^{-16}$	1.48 ×  ${10}^{-8}$	5.40 ×  ${10}^{-7}$	1.33 ×  ${10}^{-7}$
(0.5, 0.5)	2.08 × ${10}^{-16}$	8.08 ×  ${10}^{-9}$	6.60 ×  ${10}^{-8}$	1.38 ×  ${10}^{-8}$
(0.6, 0.6)	4.88 × ${10}^{-15}$	3.43 ×  ${10}^{-9}$	1.53 ×  ${10}^{-7}$	1.36 ×  ${10}^{-7}$
(0.7, 0.7)	4.78 × ${10}^{-13}$	2.28 ×  ${10}^{-9}$	3.73 ×  ${10}^{-8}$	1.04 ×  ${10}^{-7}$
(0.8, 0.8)	8.71 × ${10}^{-12}$	1.70 ×  ${10}^{-9}$	1.06 ×  ${10}^{-7}$	1.90 ×  ${10}^{-6}$
(0.9, 0.9)	5.22 × ${10}^{-11}$	3.71 ×  ${10}^{-9}$	6.65 ×  ${10}^{-8}$	4.68 ×  ${10}^{-5}$

and

Table 6. The method’s comparisons [57,58] and $GSJCOPMM$ in Example 3 with DBCs.

	$\mathit{GSJCOPMM}$	$\mathit{GSJCOPMM}$	[58]	[57]	[57]
$(\mathit{x},\mathit{t})$	$(\widehat{\mathit{\alpha }}=\widehat{\mathit{\beta }}=\mathbf{1},\mathbf{N}=\mathbf{10})$	$(\widehat{\mathit{\alpha }}=\widehat{\mathit{\beta }}=\mathbf{1},\mathit{N}=\mathbf{7})$	$(\mathit{M}=\mathit{N}=\mathbf{7})$	$(\mathit{k}=\mathbf{1},\mathit{M}=\mathbf{7})$	$(\mathit{k}=\mathbf{1},\mathit{M}=\mathbf{10})$
(0.1, 0.1)	1.39 × ${10}^{-14}$	1.1 × ${10}^{-13}$	1.29 ×  ${10}^{-13}$	5.62 ×  ${10}^{-8}$	1.04 ×  ${10}^{-12}$
(0.2, 0.2)	3.66 × ${10}^{-15}$	6.2 ×  ${10}^{-13}$	3.41 ×  ${10}^{-12}$	1.87 ×  ${10}^{-8}$	8.61 ×  ${10}^{-12}$
(0.3, 0.3)	2.07 × ${10}^{-15}$	7.5 ×  ${10}^{-13}$	2.37 ×  ${10}^{-12}$	1.34 ×  ${10}^{-7}$	1.11 ×  ${10}^{-12}$
(0.4, 0.4)	1.60 × ${10}^{-15}$	1.6 ×  ${10}^{-12}$	4.27 ×  ${10}^{-11}$	3.25 ×  ${10}^{-7}$	6.39 ×  ${10}^{-13}$
(0.5, 0.5)	2.58 × ${10}^{-15}$	2.6 ×  ${10}^{-12}$	9.46 ×  ${10}^{-11}$	2.57 ×  ${10}^{-7}$	2.06 ×  ${10}^{-12}$
(0.6, 0.6)	4.64 × ${10}^{-15}$	3.3 ×  ${10}^{-12}$	1.14 ×  ${10}^{-10}$	1.66 ×  ${10}^{-7}$	5.52 ×  ${10}^{-12}$
(0.7, 0.7)	2.07 × ${10}^{-14}$	4.6 ×  ${10}^{-12}$	3.26 ×  ${10}^{-11}$	8.95 ×  ${10}^{-8}$	3.11 ×  ${10}^{-12}$
(0.8, 0.8)	2.39 × ${10}^{-14}$	1.7 ×  ${10}^{-10}$	1.93 ×  ${10}^{-9}$	3.78 ×  ${10}^{-8}$	8.14 ×  ${10}^{-13}$
(0.9, 0.9)	3.60 × ${10}^{-13}$	1.2 ×  ${10}^{-9}$	1.32 ×  ${10}^{-8}$	3.34 ×  ${10}^{-8}$	1.89 ×  ${10}^{-12}$

. The tables show that, compared to the other methods, $GSJCOPMM$ gives the most accurate results. Furthermore, as can be seen in Figure 1, Figure 2, Figure 3, Figure 4a, Figure 5a, Figure 6, Figure 7, Figure 8a, Figure 9a, and Figure 10, the precise and approximate solutions in Examples 1–4 have a high level of agreement. The absolute and log errors in Figure 4b, Figure 5b, and Figure 9 serve to illustrate the convergence and stability of the solutions to the given Problems 2 and 3 when applying $GSJCOPMM$ and using different $N,\widehat{\alpha },$ and $\widehat{\beta }$. The choice of parameter combinations enables us to fine-tune our method, which leads to the most accurate results.

Problem  1.

Consider the following MTVO-TFDE equation [57,58]:

$${\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}y(x,t)+{\displaystyle {{}_0{}^c\mathcal{D}}_t^{{\nu }_1(x,t)}}y(x,t)+y_t(x,t)=y_{xx}(x,t)+g(x,t),(x,t)\in [0,1]\times [0,1],$$

(94)

subject to IBCs:

$$y(x,0)=0,y_t(x,0)=0,y(0,t)=0,y(1,t)=0,$$

(95)

or DBCs:

$$y(x,0)=0,y(x,1)=0,y(0,t)=0,y(1,t)=0,$$

(96)

where $g(x,t)$ is selected such that the solution to (94) is $y(x,t)=100x^3{t}^3(1-x)(1-t)$.

The application of $GSJCOPMM$ to obtain approximated solutions with the two cases of IBCs (95) and DBCs (96) using $N=2,\dots ,7,\nu (x,t)=2-0.3e^{-xt}$ and ${\nu }_1(x,t)=2-0.6e^{-xt}$ gives acceptable accuracy, as shown in Table 1. Figure 1a,c demonstrates that the obtained solutions achieve an accuracy of ${10}^{-21}$ at $N=7$, aligning with the exact solution depicted in Figure 1b.

Remark 4.

It is worth noting that, although the precise solution to (94) is a polynomial, the obtained approximate solutions did not give this precise solution; this is because of the complexity form of the two functions $\nu (x,t),{\nu }_1(x,t)$. However, in other special cases, for instance, $\nu (x,t)=xt,{\nu }_1(x,t)=2xt$, for all available values of $\widehat{\alpha }$ and $\widehat{\beta }$, the precise solution is obtained using $N=2$, where the expansion coefficients $c_{i,j}=0,i,j=0,1,2$, have the form:

$$\begin{array}{ccc}{c}_{0,0}=\frac{100\left(\widehat{\alpha }{\widehat{\beta }}^3+4\widehat{\alpha }{\widehat{\beta }}^2+5\widehat{\alpha }\widehat{\beta }+2\widehat{\alpha }+{\widehat{\beta }}^3+4{\widehat{\beta }}^2+5\widehat{\beta }+2\right)}{{(\widehat{\alpha }+\widehat{\beta }+2)}^2{(\widehat{\alpha }+\widehat{\beta }+3)}^2},\hfill & c_{0,1}=\frac{200\left(\widehat{\alpha }{\widehat{\beta }}^2+3\widehat{\alpha }\widehat{\beta }+2\widehat{\alpha }+{\widehat{\beta }}^2+3\widehat{\beta }+2\right)}{{(\widehat{\alpha }+\widehat{\beta }+2)}^2(\widehat{\alpha }+\widehat{\beta }+3)(\widehat{\alpha }+\widehat{\beta }+4)},\hfill & c_{0,2}=\frac{200(\widehat{\alpha }\widehat{\beta }+\widehat{\alpha }+\widehat{\beta }+1)}{(\widehat{\alpha }+\widehat{\beta }+2){(\widehat{\alpha }+\widehat{\beta }+3)}^2(\widehat{\alpha }+\widehat{\beta }+4)},\hfill \\ c_{1,0}=-\frac{100\left(-\widehat{\alpha }{\widehat{\beta }}^2-3\widehat{\alpha }\widehat{\beta }-2\widehat{\alpha }+{\widehat{\beta }}^3+3{\widehat{\beta }}^2+2\widehat{\beta }\right)}{{(\widehat{\alpha }+\widehat{\beta }+2)}^2(\widehat{\alpha }+\widehat{\beta }+3)(\widehat{\alpha }+\widehat{\beta }+4)},\hfill & c_{1,1}=-\frac{200(\widehat{\beta }+2)(\widehat{\beta }-\widehat{\alpha })}{{(\widehat{\alpha }+\widehat{\beta }+2)}^2{(\widehat{\alpha }+\widehat{\beta }+4)}^2},\hfill & c_{1,2}=-\frac{200(\widehat{\beta }-\widehat{\alpha })}{(\widehat{\alpha }+\widehat{\beta }+2)(\widehat{\alpha }+\widehat{\beta }+3){(\widehat{\alpha }+\widehat{\beta }+4)}^2},\hfill \\ c_{2,0}=-\frac{200\left({\widehat{\beta }}^2+3\widehat{\beta }+2\right)}{(\widehat{\alpha }+\widehat{\beta }+2){(\widehat{\alpha }+\widehat{\beta }+3)}^2(\widehat{\alpha }+\widehat{\beta }+4)},\hfill & c_{2,1}=-\frac{400(\widehat{\beta }+2)}{(\widehat{\alpha }+\widehat{\beta }+2)(\widehat{\alpha }+\widehat{\beta }+3){(\widehat{\alpha }+\widehat{\beta }+4)}^2},\hfill & c_{2,2}=-\frac{400}{{(\widehat{\alpha }+\widehat{\beta }+3)}^2{(\widehat{\alpha }+\widehat{\beta }+4)}^2}.\hfill \end{array}$$

Remark 5.

Although errors smaller than ${10}^{-16}$ may not have direct practical significance, increasing the value of N can still meaningfully improve accuracy in numerical computations. The choice of N depends on the specific requirements and desired level of accuracy for the problem under consideration. We emphasize that the relative improvement in accuracy should be considered when evaluating the meaningfulness of different values of N.

Problem  2.

Consider the following MTVO-TFDE equation [57,58]:

$$\left({\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}+{\displaystyle \sum _{j=1}^4}\frac{1}{j+1}{\displaystyle {{}_0{}^c\mathcal{D}}_t^{{\nu }_j(x,t)}}\right)y(x,t)+y_t(x,t)=\frac{1}{3}{y}_{xx}(x,t)+g(x,t),(x,t)\in [0,1]\times [0,1],$$

(97)

subject to IBCs:

$$y(x,0)=0,y_t(x,0)=0,y(0,t)=0,y(1,t)=0,$$

(98)

or DBCs:

$$y(x,0)=0,y(x,1)=sin(\pi x),y(0,t)=0,y(1,t)=0,$$

(99)

where $g(x,t)$ is selected such that the solution to (97) is $y(x,t)=t^{3}sin(\pi x)$.

The application of $GSJCOPMM$ to obtain approximated solutions to (97), subject to IBCs (98) or DBCs (99), respectively, using $N=0,1,2,5,8,12,\nu (x,t)=2-0.3e^{-xt}$ and ${\nu }_j(x,t)=2-(0.1)(j+3)e^{-xt},j=1,2,3,4$, gives acceptable accuracy, as shown in Table 2. Figure 3a,c demonstrates that the obtained solutions achieve an accuracy of ${10}^{-13}$ at $N=12$, aligning with the approximate and exact solutions depicted in Figure 2. Additionally, we may obtain valuable insights into the developments gained by applying $GSJCOPMM$ from the heat map graphs displayed in Figure 3b,d and supported by the error graphs in Figure 4a and Figure 5a.

Problem  3.

Consider the following MTVO-TFDE equation [57,58]:

$$\left({\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}+{\displaystyle \sum _{j=1}^5}\frac{1}{j+1}{\displaystyle {{}_0{}^c\mathcal{D}}_t^{{\nu }_j(x,t)}}\right)y(x,t)+\frac{1}{2}{y}_t(x,t)=\frac{1}{3}{y}_{xx}(x,t)+g(x,t),(x,t)\in [0,1]\times [0,1],$$

(100)

subject to IBCs:

$$y(x,0)=sin(x),y_t(x,0)=-cos(x),y(0,t)=-sin(t),y(1,t)=sin(1-t),$$

(101)

or DBCs:

$$y(x,0)=sin(x),y(x,1)=sin(x-1),y(0,t)=-sin(t),y(1,t)=sin(1-t),$$

(102)

where $g(x,t)$ is selected such that the solution to (100) is $y(x,t)=sin(x-t)$.

The application of $GSJCOPMM$ to obtain approximated solutions to (100) subject to IBCs (101) or DBCs (102), respectively, using $N=2,4,6,8,10,12,\nu (x,t)=1.8+0.2sin(xt)$ and ${\nu }_j(x,t)=1.8-(0.1)j+0.2sin(xt),j=1,2,3,4,5$, gives acceptable accuracy for the solutions obtained, as shown in Table 3 and Figure 7a,c. These solutions reach an agreement of an accuracy of ${10}^{-14}$ at $N=12$, aligning with the approximate and exact solutions depicted in Figure 6. Again, the heat map graphs displayed in Figure 7b,d and the error graphs in Figure 8a and Figure 9a confirm the effectiveness of $GSJCOPMM$.

Remark 6.

In view of the presented CPU time (in seconds), our approach has efficient performance. The calculations show that the memory consumption was excellent. For example, the calculated CPU time using $N=10$ is 6% slower than $N=7$ and, moreover, requires increasing by 20% the memory consumption of RAM compared to the $N=7$ calculation. The numerical examples and comparisons provided in our paper highlight the superior accuracy and efficiency of our algorithm, solidifying its potential for solving MTVO-TFDEs effectively. When we compared the resource use of our method to that described in [57,58], we saw that those papers did not provide CPU time and memory usage. However, based on our analysis, our approach demonstrates better performance compared to the referenced methods.

Problem  4.

Consider the following MTVO-TFDE equation:

$$\left({\displaystyle {{}_0{}^c\mathcal{D}}_t^{\nu (x,t)}}+{\displaystyle \sum _{j=1}^2}{\displaystyle {{}_0{}^c\mathcal{D}}_t^{{\nu }_j(x,t)}}\right)y(x,t)+y_t(x,t)=y_{xx}(x,t)+g(x,t),(x,t)\in [0,1]\times [0,1],$$

(103)

subject to IBCs:

$$y(x,0)=E_{\frac{1}{2},0}(x)+1,y_t(x,0)=\frac{2}{\sqrt{\pi }},y(0,t)=e^{t^2}(1+erf(t)),y(1,t)=e^{t^2}(1+erf(t))+E_{\frac{1}{2},0}(1),$$

(104)

or DBCs:

$$y(x,0)=E_{\frac{1}{2},0}(x)+1,y(x,1)=(1+erf(1))e+E_{\frac{1}{2},0}(x),y(0,t)=e^{t^2}(1+erf(t)),y(1,t)=e^{t^2}(1+erf(t))+E_{\frac{1}{2},0}(1),$$

(105)

where $g(x,t)$ is selected such that the solution of (103) is

$$y(x,t)=E_{\frac{1}{2},1}(t)+E_{\frac{1}{2},0}(x),$$

(106)

and where the functions

$$erf(x)=\frac{2}{\sqrt{\pi }}{\int }_0^x{e}^{-t^2}dt\mathit{and}{E}_{\alpha ,\beta }(x)=\sum _{k=0}^{\infty }\frac{x^k}{\Gamma (k\alpha +\beta )}$$

(107)

are the Gaussian error function and the generalized Mitta–Leffler function, respectively. The application of $GSJCOPMM$ to obtain approximated solutions to (103) subject to IBCs (104) or DBCs (105), respectively, using $N=2,4,6,8,10,14,\nu (x,t)=1+xt$ and ${\nu }_1(x,t)=2-xt,{\nu }_2(x,t)=\frac{3}{2}-\frac{1}{4}xt$, gives acceptable accuracy, as shown in Table 4, and error graphs as shown in Figure 10. These solutions reach an agreement of an accuracy of ${10}^{-9}$ at $N=14$.

9. Conclusions

This study presents a generalized form of shifted JPs that fulfill homogeneous IBCs or DBCs. Then, by making use of the OMs derived in Section 4 and Section 5 with the SCM, an approximation algorithm for the given MTVO-TFDWE is established. Three examples, including MTVO-TFDWE (1), were tested using the suggested technique, $GSJCOPMM$, to prove its high accuracy and efficiency. The examples were subjected to either the IBCs (2) or the DBCs (3). It would be great to see our results generalized to other kinds of initial and boundary conditions. Studying the system’s behavior in different settings would provide interesting insights and make our conclusions even more applicable. Additionally, the theoretical results obtained in this study can be developed to deal with more complex versions of MTVO-TFDWEs, such as multi-dimensional multi-term Caputo’s time-fractional mixed sub-diffusion and diffusion-wave equations. Additionally, incorporating adaptive strategies and parallel computing techniques could further enhance the efficiency and scalability of the algorithm. Overall, this research contributes to the advancement of numerical methods for MTVO-TFDWEs and opens up avenues for exploring their applications in various fields.