The Finite Volume Element Method for Time Fractional Generalized Burgers’ Equation

Abstract

In this paper, we use the finite volume element method (FVEM) to approximate a one-dimensional, time fractional generalized Burgers’ equation. We construct the fully discrete finite volume element scheme for this equation by approximating the time fractional derivative term by the $L1$ formula and approximating the spatial terms using FVEM. The convergence of the scheme is proven. Finally, numerical examples are provided to confirm the scheme’s validity.

1. Introduction

One of the most well-known nonlinear model equations in the field of fluid dynamics is Burgers’ equation. It is obtained from the Navier-Stokes model. These kinds of equations have been studied in the literature using a variety of methods [1,2,3]. Burgers’ equations have been applied in many different areas, including wave propagation, nonlinear acoustics, fluid mechanics and gas dynamics [4,5,6]. Compared to integer derivatives, fractional-order derivatives often have greater advantages in terms of describing physical processes with memory and genetic properties. Therefore, fractional differential equations are widely used in engineering, environmental science, energy development, physics and many other fields [7,8,9]. In particular, fractional Burgers’ equation is widely used in weak shockwave transmission, compressible turbulence and fluid systems [10,11,12,13,14,15,16,17].

In this article, we consider the time fractional generalized Burgers’ equation:

$$(1-q)u_t+q{\beta }_1{}_0^C{D}_t^{\alpha }u-\gamma {\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}+{\beta }_2{u}^p{\displaystyle \frac{\partial u}{\partial x}}=f(x,t),x\in (0,1),t\in \left(0,T\right],$$

(1)

with the following boundary conditions

$$u(0,t)=u(1,t)=0,t\in \left(0,T\right],$$

(2)

and the following initial condition

$$u(x,0)=g(x),x\in (0,1),$$

(3)

where $T\in (0,\infty )$, $q\in (0,1)$, ${\beta }_1,{\beta }_2$ and $\gamma$ are constants, and p is a positive integer. The symbol ${}_0^C{D}_t^{\alpha }$ of order $\alpha$ is the Caputo fractional derivative operator defined by

$${}_0^C{D}_t^{\alpha }u(x,t)={\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\int }_0^t{\displaystyle \frac{\partial u(x,s)}{\partial s}}{\displaystyle \frac{1}{{(t-s)}^{\alpha }}}ds,0<\alpha <1,$$

where $\Gamma (·)$ denotes the usual Gamma function. In the time fractional generalized Burgers’ equation, u is the velocity of the turbulent motion. The first term is the normal change in velocity with respect to time, while the second term is a sub-diffusion term that describes the change in velocity. The second-order derivative shows the classical diffusion term, which describes how u spreads out over space. The last term on the left-hand side represents nonlinear advection. The right side ($f(x,t)=F(x,t)/\rho$) is a forcing term, where $F(x,t)$ is body force and $\rho$ is density. This equation considers the presence of both normal and sub-diffusion phenomena in the fluid, with q representing the proportion of these two phenomena.

From a physical perspective, the time fractional generalized Burgers’ equation can be considered a model of how the chemical substance diffuses across a one-dimensional medium, such a liquid or gas. The SI units of x, u, t, $F(x,t)$ and $\rho$ are m, m/s, s, N/m³ and kg/m³, respectively. The diffusion coefficient ($\gamma$) controls the rate at which the material spreads out, and its unit is m²/s. The parameter ${\beta }_1$ represents the sub-diffusion coefficient with SI ($1/s^{1-\alpha }$), and ${\beta }_2$ represents the advection rate with SI (${(m/s)}^{1-p}$). They depend on the properties of the material. The temporal memory effect (the substance’s past diffusion history impacting its present behavior) in the diffusion process is characterized by the $\alpha$ parameter. In mathematics, dimensionless processing is usually carried out.

In recent years, an increasing number of scholars at home and abroad have carried out numerical research on time fractional Burgers’ equations (TFBEs). Li et al. [18,19] proposed the linear implicit finite difference approach for analysis of a generalized TFBE. Esen et al. [20,21,22] studied this type of problem by means of the finite element method. Zhang and Guo [23] suggested a novel similarity transformation based on the Lie symmetry approach that transforms the TFBE into a fractional ordinary differential equation. Kurt et al. [24] recently discovered the Hopf–Cole transform exact solution to the TFBE, and they obtained an analytical solution using the homotopy analysis method. Cao et al. [25] proposed an approach formed by merging the finite difference method for temporal variables and the discontinuous Galerkin scheme for spatial variables to deal with a two-dimensional TFBE. Liu and Zhang [26] solved this kind of equation using a novel approximation technique named the approximate analytical method.

The finite volume element method (FVEM) is a significant class of numerical methods used to solve differential equations. With a finite partitioning set of volume, this approach discretizes the differential equation using a volume-integral formulation, which is a discrete approximation of the control equation in an integral form. In 2000, Li et al. [27] proposed the use of the FVEM to solve various differential equations. Wang [28] proposed a mixed FVEM to solve biharmonic equations that is based on rectangular partition. Zhang et al. [29] studied a fully discrete two-grid FVEM for a nonlinear parabolic problem. Burgers’ equation in one dimension can be solved using a high-order finite volume compact technique, as proposed by Guo et al. [30]. An FVEM for estimation of the solution to a two-dimensional Burgers’ equation was proposed by Yang [31]. The FVEM is also widely used in the field of fractional diffusion equations [32,33,34,35,36,37]. Wang et al. [38] investigated the transverse vibration of a fractional viscoelastic beam using the mixed FVEM. To the best of our knowledge, the FVEM has not been used to investigate the time fractional generalized Burgers’ equation, despite the fact that this method has been used for many other Burgers’ equations.

Many scholars have investigated the solutions of different kinds of time fractional partial differential equations in the hopes of obtaining effective calculation methods. It is also envisaged that these theoretical analysis and computational approaches may be expanded to sophisticated time fractional models for the solution of additional practical problems. A focus of our studies is the appropriate handling of the nonlinear convection and diffusion factors that are present in various fluid dynamics situations. Here, we provide a theoretical analysis of the time fractional generalized Burgers’ equation, which contains time fractional derivatives and nonlinear terms, by using FVEM. Using flexible grids, the FVEM benefits from both the accuracy of the finite element methods and the simplicity of the finite difference methods. In this sense, we have advanced existing knowledge.

The remainder of this article is structured as follows. In Section 2, we construct the fully discrete scheme. In Section 3, some lemmas required for the theoretical analysis are presented. In Section 4, a convergence analysis of the FVE scheme is provided. Finally, numerical results are presented in Section 5 to confirm our theoretical analysis.

2. Fully Discrete FVE Scheme

Let $T_h:0=x_0<x_1<x_2<\cdots <x_N=1$ be the primal partition of the interval [0, 1] and $I_i=[x_i,x_{i+1}],i=0,1,\cdots ,N-1$ be the corresponding element intervals. We denote the length of $I_i$ as $h_i=x_{i+1}-x_i$; therefore, $h=\underset{0\le i\le N-1}{\max }{h}_i$. The corresponding dual partition is $T_h^{*}:0=x_0<x_{\frac{1}{2}}<x_1<x_{\frac{3}{2}}\cdots <x_{N-\frac{1}{2}}<x_N=1$, where $x_{i+\frac{1}{2}}={\displaystyle \frac{x_i+x_{i+1}}{2}},i=0,1,\cdots ,N-1$. The dual elements are $I_0^{*}=[x_0,x_{\frac{1}{2}}],I_i^{*}=[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}](i=1,2,\cdots ,N-1)$ and $I_N^{*}=[x_{N-\frac{1}{2}},x_N]$.

The finite element spaces are defined as

$$\begin{array}{cc}\hfill & U_h=\left\{u_h\in C(0,1):u_h{|}_{I_i}\in P_1,i=0,1,\cdots ,N-1\right\},\hfill \\ \hfill & V_h=\left\{v_h\in L^2(0,1):v_h{|}_{I_i^{*}}\in P_0,i=0,1,\cdots ,N-1\right\},\hfill \\ \hfill & U_{0h}=\left\{u_h\in U_h:u_h(0)=u_h(1)=0\right\},\hfill \\ \hfill & V_{0h}=\left\{v_h\in V_h:v_h(0)=v_h(1)=0\right\},\hfill \end{array}$$

where $U_h$ is the linear finite element space according to primal subdivision $T_h$, and $V_h$ denotes the constant function space corresponding to dual subdivision $T_h^{*}$. $P_l(l=0,1)$ represents the set of polynomials whose degree is no more than l.

The interpolation operator (${\Pi }_h^{*}:U_{0h}\to V_{0h}$) is expressed as

$${\Pi }_h^{*}{\varphi }_h=\sum _{i=1}^{N-1}{\varphi }_i{\phi }_i(x),\forall {\varphi }_h\in U_{0h},$$

where ${\varphi }_i={\varphi }_h(x_i)$ and ${\phi }_i(x)$ are the basis functions of $V_{0h}$, i.e.,

$${\phi }_i(x)=\left\{\begin{array}{cc}\hfill 1,x\in I_i^{*},& \\ \hfill & i=1,2,\cdots ,N-1.\hfill \\ \hfill 0,x\notin I_i^{*}& .\hfill \end{array}\right.$$

Any $v_h\in V_{0h}$ has the following form:

$$v_h=\sum _{i=1}^{N-1}{v}_i{\phi }_i,$$

where $v_i=v_h(x_i)$. Using any $v_h\in V_{0h}$ to multiply Equation (1) and integrating it on [0, 1], we can obtain

$$(1-q)(u_t,v_h)+q{\beta }_1{(}_0^C{D}_t^{\alpha }u,v_h)+a(u,v_h)+{\beta }_2(u^p{\displaystyle \frac{\partial u}{\partial x}},v_h)=(f,v_h),$$

(4)

where the bilinear form is

$$a(u,v_h)=-\gamma \sum _{i=1}^{N-1}{v}_i[u_x(x_{i+\frac{1}{2}},t)-u_x(x_{i-\frac{1}{2}},t)].$$

Using the operator ${\Pi }_h^{*}$, (4) can also be expressed as

$$\begin{array}{cc}\hfill & (1-q)(u_t,{\Pi }_h^{*}{\varphi }_h)+q{\beta }_1{(}_0^C{D}_t^{\alpha }u,{\Pi }_h^{*}{\varphi }_h)+a(u,{\Pi }_h^{*}{\varphi }_h)+{\beta }_2(u^p{\displaystyle \frac{\partial u}{\partial x}},{\Pi }_h^{*}{\varphi }_h)\hfill \\ & =(f,{\Pi }_h^{*}{\varphi }_h),\forall {\varphi }_h\in U_h,\hfill \end{array}$$

(5)

The semi-discrete FVE scheme of problems (1)–(3) is summarized as follow. For any $t\in [0,T]$, find $u_h(·,t)\in U_{0h}$ such that

$$\left\{\begin{array}{cc}\hfill & (1-q)(u_{ht},{\Pi }_h^{*}{\varphi }_h)+q{\beta }_1{(}_0^C{D}_t^{\alpha }{u}_h,{\Pi }_h^{*}{\varphi }_h)+a(u_h,{\Pi }_h^{*}{\varphi }_h)+{\beta }_2(u_h^p{\displaystyle \frac{\partial u_h}{\partial x}},{\Pi }_h^{*}{\varphi }_h)\hfill \\ & =(f,{\Pi }_h^{*}{\varphi }_h),\forall {\varphi }_h\in U_{0h},\hfill \\ \hfill & u_h(x,0)=g_h(x),x\in (0,1),\hfill \end{array}\right.$$

(6)

where $g_h(x)$ takes the elliptic projection of $g(x)$.

Then, the subdivision of time interval [0, T] is expressed as $0=t_0<t_1<t_2<\cdots <t_M=T$, where $t_n=n\tau ,\tau =T/M$. The backward difference quotient (${\partial }_t{u}_h(x,t_n)=(u_h(x,t_n))-u_h(x,t_{n-1}))/\tau$) is used to approximate $u_{ht}$. Then, we provide several lemmas related to the Caputo derivative.

Lemma 1 

([39]). For $0<\alpha <1,a_l^{(\alpha )}={(l+1)}^{1-\alpha }-l^{1-\alpha },l=0,1,2,\cdots$, one has

$$\begin{array}{cc}\hfill & (\mathrm{i})1=a_0^{\alpha }>a_1^{\alpha }>a_2^{\alpha }>\cdots >a_l^{\alpha }>0;a_l^{\alpha }\to 0,l\to \infty ;\hfill \\ \hfill & (\mathrm{ii})(1-\alpha )l^{-\alpha }<a_{l-1}^{\alpha }<(1-\alpha ){(l-1)}^{-\alpha },l\ge 1.\hfill \end{array}$$

Lemma 2 

([39]). For any function ($v(t)$), assume that $v_{tt}\in C(0,T)$. For the Caputo derivative of order $\alpha (0<\alpha <1)$, one has

$$\begin{array}{cc}\hfill {}_0^C{D}_t^{\alpha }{v}^n& ={\displaystyle \frac{{\tau }^{-\alpha }}{\Gamma (2-\alpha )}}[a_0^{(\alpha )}{v}^n-\sum _{k=1}^{n-1}(a_{n-k-1}^{(\alpha )}-a_{n-k}^{(\alpha )})v^k-a_{n-1}^{(\alpha )}{v}^0]+R_n\hfill \\ \hfill & ={\displaystyle \frac{{\tau }^{-\alpha }}{\Gamma (2-\alpha )}}\sum _{k=1}^n{a}_{n-k-1}^{(\alpha )}(v^k-v^{k-1})+R_n,\hfill \end{array}$$

where $v^n=v(t_n)$, and

$$\left|R_n\right|\le {\displaystyle \frac{1}{2\Gamma (1-\alpha )}}[{\displaystyle \frac{1}{4}}+{\displaystyle \frac{\alpha }{(1-\alpha )(2-\alpha )}}]\underset{t_0\le t\le t_n}{\max }\left|v_{tt}\right|{\tau }^{2-\alpha }.$$

We define $r={\displaystyle \frac{{\tau }^{-\alpha }}{\Gamma (2-\alpha )}}$, $D_{\tau }^{\alpha }{v}^n=r[a_0^{(\alpha )}{v}^n-{\displaystyle \sum _{k=1}^{n-1}}(a_{n-k-1}^{(\alpha )}-a_{n-k}^{(\alpha )})v^k-a_{n-1}^{(\alpha )}{v}^0]$. Then, the fully discrete FVE scheme involves fining $u_h^n\in U_{0h}(n=0,1,\cdots ,M)$, such that

$$\left\{\begin{array}{cc}\hfill & (a)(1-q)({\partial }_t{u}_h^n,{\Pi }_h^{*}{\varphi }_h)+q{\beta }_1(D_{\tau }^{\alpha }{u}_h^n,{\Pi }_h^{*}{\varphi }_h)+a(u_h^n,{\Pi }_h^{*}{\varphi }_h)+{\beta }_2({(u_h^{n-1})}^p{\displaystyle \frac{\partial u_h^n}{\partial x}},{\Pi }_h^{*}{\varphi }_h)\hfill \\ & =(f^n,{\Pi }_h^{*}{\varphi }_h),\forall {\varphi }_h\in U_{0h},\hfill \\ \hfill & (b)u_h^0=g_h,x\in (0,1).\hfill \end{array}\right.$$

(7)

3. Some Lemmas

In this section, we provide several necessary lemmas. First, we introduce the elliptic projection operator ($P_h:H^2(\Omega )\bigcap H_0^1(\Omega )\to U_{0h}$), which is defined as

$$a(P_{h}u,v_h)=a(u,v_h),\forall v_h\in V_{0h}.$$

Lemma 3 

([27]). If $u\in H_0^1(\Omega )\cap H^2(\Omega )$, then

$$\parallel u-P_h{u\parallel }_1\le Ch{\left|u\right|}_2.$$

If $u\in W^{3,p}(\Omega )$, then

$$\parallel u-P_{h}u\parallel \le C{h}^2{\left|u\right|}_{3,p},(p>1).$$

Lemma 4 

([27,40]). For the operator ${\Pi }_h^{*}$, we have

$$\begin{array}{cc}\hfill & (\mathrm{i})(u_h,{\Pi }_h^{*}{w}_h)=(w_h,{\Pi }_h^{*}{u}_h),\forall u_h,w_h\in U_h,\hfill \\ \hfill & (\mathrm{ii})(u_h,{\Pi }_h^{*}{u}_h)\ge 0,\forall u_h\in U_h,\hfill \\ \hfill & (\mathrm{iii})|(u_h,{\Pi }_h^{*}{w}_h)|\le C\parallel u_h\parallel \parallel w_h\parallel ,\forall u_h,w_h\in U_h,\hfill \end{array}$$

where C is a positive constant. We set $\left|\right||u_h\left|\right||={(u_h,{\Pi }_h^{*}{u}_h)}^{\frac{1}{2}}$; then, $\left|\right||·|\left|\right|$ is equivalent to $\parallel ·\parallel$ on $U_h$.

Lemma 5 

([27]). There exist positive constants ($\beta ,C$) such that

$$a(u_h,{\Pi }_h^{*}{u}_h)\ge \beta {\left|u_h\right|}_1^2,\forall u_h\in U_h,$$

$$|a(u_h,{\Pi }_h^{*}{w}_h)|\le C\parallel u_h{\parallel }_1{\parallel w_h\parallel }_1,\forall u_h,w_h\in U_h.$$

If we define $\left|\right||u_h{\left|\right||}_1={[a(u_h,{\Pi }_h^{*}{u}_h)]}^{\frac{1}{2}}$, then $\left|\right||·{\left|\right||}_1$ and ${\parallel ·\parallel }_1$ are equivalent on $U_h$.

Lemma 6 

([27]). Let $\left\{z_k\right\},\left\{g_k\right\}$ be two non-negative sequences. If

$$z_k\le K+\sum _{i=1}^k{g}_i{z}_i,k\ge 0,$$

it holds that

$$z_k\le K·\exp (\sum _{i=1}^k{g}_i),k\ge 0,$$

where K is a non-negative constant.

4. Convergence Analysis

The error estimate for the fully discrete FVE scheme (7) is discussed in this section.

Theorem 1. 

Assume that u and $u_h^n(n=1,2,\cdots ,N)$ are the solutions to problems (1)–(3) and finite volume element format (7), respectively. If u satisfies the required regularity condition, the following error inequality holds:

$$\parallel u^n-u_h^n\parallel \le C(\tau +h),$$

where $u^n=u(x,t_n)$, and $C\ge 0$ is a constant independent of the two mesh parameters (τ and h).

Proof. 

Let

$${\rho }^n=u^n-P_h{u}^n,{\eta }^n=P_h{u}^n-u_h^n;$$

then,

$$u^n-u_h^n={\rho }^n+{\eta }^n.$$

(8)

According to Lemma 3,

$$\parallel {\rho }^n\parallel =\parallel u^n-P_h{u}^n\parallel \le C{h}^2\parallel u^n{\parallel }_{3,p}\le C{h}^2[\parallel u^0{\parallel }_{3,p}+{\int }_0^{t_n}\parallel u_t{\parallel }_{3,p}dt].$$

(9)

By subtracting (7) from (5), we have the error equation:

$$\begin{array}{c}(1-q)(u_t^n-{\partial }_t{u}_h^n,{\Pi }_h^{*}{\varphi }_h)+q{\beta }_1{(}_0^C{D}_t^{\alpha }{u}^n-D_{\tau }^{\alpha }{u}_h^n,{\Pi }_h^{*}{\varphi }_h)+a(u^n-u_h^n,{\Pi }_h^{*}{\varphi }_h)\hfill \\ +{\beta }_2({(u_h^n)}^p{\displaystyle \frac{\partial u_h^n}{\partial x}},{\Pi }_h^{*}{\varphi }_h)-{\beta }_2({(u^{n-1})}^p{\displaystyle \frac{\partial u^n}{\partial x}},{\Pi }_h^{*}{\varphi }_h)=0,\forall {\varphi }_h\in U_{0h}.\hfill \end{array}$$

(10)

Taking ${\varphi }_h={\eta }^n$ in the error Equation (10), the error equation becomes

$$\begin{array}{c}(1-q)({\partial }_t{\eta }^n,{\Pi }_h^{*}{\eta }^n)+a({\eta }^n,{\Pi }_h^{*}{\eta }^n)+q{\beta }_{1}r({\eta }^n,{\Pi }_h^{*}{\eta }^n)\hfill \\ =q{\beta }_{1}r\sum _{k=1}^{n-1}(a_{n-k-1}^{(\alpha )}-a_{n-k}^{(\alpha )})({\eta }^k,{\Pi }_h^{*}{\eta }^n)+q{\beta }_{1}r{a}_{n-1}^{(\alpha )}({\eta }^0,{\Pi }_h^{*}{\eta }^n)-(1-q)(u_t^n-{\partial }_t{P}_h{u}^n,{\Pi }_h^{*}{\eta }^n)\hfill \\ +q{\beta }_1(D_{\tau }^{\alpha }{P}_h{u}^n{-}_0^C{D}_t^{\alpha }{u}^n,{\Pi }_h^{*}{\eta }^n)+{\beta }_2[({(u^n)}^p{\displaystyle \frac{\partial u^n}{\partial x}},{\Pi }_h^{*}{\eta }^n)-({(u_h^{n-1})}^p{\displaystyle \frac{\partial u_h^n}{\partial x}},{\Pi }_h^{*}{\eta }^n)].\hfill \end{array}$$

(11)

Noticing the fact that

$$\begin{array}{cc}\hfill ({\partial }_t{\eta }^n,{\Pi }_h^{*}{\eta }^n)& ={\displaystyle \frac{1}{\tau }}({\eta }^n-{\eta }^{n-1},{\Pi }_h^{*}{\eta }^n)\hfill \\ \hfill & ={\displaystyle \frac{1}{2\tau }}[({\eta }^n,{\Pi }_h^{*}{\eta }^n)-({\eta }^{n-1},{\Pi }_h^{*}{\eta }^{n-1})+({\eta }^n-{\eta }^{n-1},{\Pi }_h^{*}({\eta }^n-{\eta }^{n-1}))]\hfill \\ \hfill & ={\displaystyle \frac{1}{2\tau }}(|\left|\right|{\eta }^n{\left|\right||}^2-\left|\right||{\eta }^{n-1}{\left|\right||}^2+\left|\right||{\eta }^n-{\eta }^{n-1}{\left|\right||}^2)\hfill \\ \hfill & \ge {\displaystyle \frac{1}{2\tau }}(|\left|\right|{\eta }^n{\left|\right||}^2-\left|\right||{\eta }^{n-1}{\left|\right||}^2)\hfill \end{array}$$

and using Lemmas 4 and 5, the left side of Equation (11) is bounded: as follows

$$\begin{array}{cc}\hfill & (1-q)({\partial }_t{\eta }^n,{\Pi }_h^{*}{\eta }^n)+a({\eta }^n,{\Pi }_h^{*}{\eta }^n)+q{\beta }_{1}r({\eta }^n,{\Pi }_h^{*}{\eta }^n)\hfill \\ \hfill & \ge {\displaystyle \frac{1-q}{2\tau }}(|\left|\right|{\eta }^n{\left|\right||}^2-\left|\right||{\eta }^{n-1}{\left|\right||}^2)+|\left|\right|{\eta }^n{\left|\right||}_1^2+q{\beta }_{1}r\left|\right||{\eta }^n{\left|\right||}^2.\hfill \end{array}$$

(12)

The terms on the right side of (11) are denoted as $T_1,T_2,T_3,T_4$ and $T_5$, respectively. Using Hölder inequality and Schwarz inequality,

$$\begin{array}{cc}\hfill & |T_1|=qr\sum _{k=1}^{n-1}(a_{n-k-1}^{(\alpha )}-a_{n-k}^{(\alpha )})|{\beta }_1({\eta }^k,{\Pi }_h^{*}{\eta }^n)|\hfill \\ \hfill & \le Cqr\sum _{k=1}^{n-1}(a_{n-k-1}^{(\alpha )}-a_{n-k}^{(\alpha )})\left|\right||{\eta }^k\left|\right|\left|\right|\left|\right|{\eta }^n\left|\right||\hfill \\ \hfill & \le Cqr\sum _{k=1}^{n-1}(a_{n-k-1}^{(\alpha )}-a_{n-k}^{(\alpha )})\left|\right||{\eta }^k{\left|\right||}^2+Cqr(1-a_{n-1}^{(\alpha )})\left|\right||{\eta }^n{\left|\right||}^2.\hfill \end{array}$$

Noticing $P_h{u}^0=u_h^0$, so ${\eta }^0=0$, then,

$$\begin{array}{c}\hfill |T_2|=qr{a}_{n-1}^{(\alpha )}|{\beta }_1({\eta }^0,{\Pi }_h^{*}{\eta }^n)|=0.\end{array}$$

We denote

$$\begin{array}{cc}\hfill {\xi }^n& =u_t^n-{\partial }_t{u}^n+{\partial }_t{u}^n-{\partial }_t{P}_h{u}^n\hfill \\ \hfill & ={\xi }_1^n+{\xi }_2^n,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\parallel {\xi }_1^n\parallel }^2& ={\int }_{\Omega }{({\displaystyle \frac{1}{\tau }}{\int }_{t_{n-1}}^{t_n}(t-t_{n-1})u_{tt}d\tau )}^{2}dx\hfill \\ \hfill & \le \tau {\int }_{t_{n-1}}^{t_n}{\parallel u_{tt}\parallel }^{2}d\tau ,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\parallel {\xi }_2^n\parallel }^2& ={\int }_{\Omega }{(-{\displaystyle \frac{1}{\tau }}{\int }_{t_{n-1}}^{t_n}(P_h-I)u_{t}d\tau )}^{2}dx\hfill \\ \hfill & \le {\displaystyle \frac{1}{\tau }}{\int }_{t_{n-1}}^{t_n}{\parallel u_t-P_h{u}_t\parallel }^{2}d\tau \hfill \\ \hfill & \le {\displaystyle \frac{C{h}^2}{\tau }}{\int }_{t_{n-1}}^{t_n}{\left|u_t\right|}_2^{2}d\tau .\hfill \end{array}$$

Using Hölder inequality, Schwarz inequality and the above estimates for ${\xi }_1^n$ and ${\xi }_2^n$, we have

$$\begin{array}{cc}\hfill |T_3|& =(1-q)|(u_t^n-{\partial }_t{P}_h{u}^n,{\Pi }_h^{*}{\eta }^n)|\hfill \\ \hfill & =(1-q)|({\xi }^n,{\Pi }_h^{*}{\eta }^n)|\hfill \\ \hfill & \le C(1-q)\left|\right||{\xi }^n{\left|\right||}^2+C(1-q)\left|\right||{\eta }^n{\left|\right||}^2\hfill \\ \hfill & \le C(1-q)\tau {\int }_{t_{n-1}}^{t_n}{\parallel u_{tt}\parallel }^{2}d\tau +{\displaystyle \frac{C(1-q)h^2}{\tau }}{\int }_{t_{n-1}}^{t_n}{\left|u_t\right|}_2^{2}d\tau +C(1-q)\left|\right||{\eta }^n{\left|\right||}^2.\hfill \end{array}$$

We denote

$$\begin{array}{cc}\hfill & {ϵ}^n=D_{\tau }^{\alpha }{P}_h{u}^n{-}_0^C{D}_t^{\alpha }{u}^n\hfill \\ \hfill & =D_{\tau }^{\alpha }{P}_h{u}^n-D_{\tau }^{\alpha }{u}^n+D_{\tau }^{\alpha }{u}^n{-}_0^C{D}_t^{\alpha }{u}^n\hfill \\ \hfill & ={ϵ}_1^n+{ϵ}_2^n.\hfill \end{array}$$

According to Lemmas 2 and 3, we have

$$\begin{array}{cc}\hfill {\parallel {ϵ}_1^n\parallel }^2& =({\int }_{\Omega }{\left|{ϵ}_1^n\right|}^{2}dx)\hfill \\ \hfill & \le C{(n\tau )}^{2-2\alpha }\underset{0\le t\le t_n}{max}{\parallel (P_h-I)u_t\parallel }^2\hfill \\ \hfill & \le C{h}^4{(n\tau )}^{2-2\alpha }\underset{0\le t\le t_n}{max}{\parallel u_t\parallel }_{3,p}^2,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \parallel {ϵ}_2^n\parallel & =({\int }_{\Omega }{\left|{ϵ}_2^n\right|}^{2}dx)\hfill \\ \hfill & \le C{\tau }^{4-2\alpha }\underset{0\le t\le t_n}{max}{\parallel u_{tt}\parallel }^2.\hfill \end{array}$$

Using the above inequalities, we have

$$\begin{array}{cc}\hfill |T_4|& =q|{\beta }_1(D_{\tau }^{\alpha }{P}_h{u}^n{-}_0^C{D}_t^{\alpha }{u}^n,{\Pi }_h^{*}{\eta }^n)|\hfill \\ \hfill & =q|{\beta }_1({ϵ}^n,{\Pi }_h^{*}{\eta }^n)|\hfill \\ \hfill & \le Cq\left|\right||{ϵ}^n{\left|\right||}^2+Cq\left|\right||{\eta }^n{\left|\right||}^2\hfill \\ \hfill & \le Cq{h}^4{(n\tau )}^{2-2\alpha }\underset{0\le t\le t_n}{max}{\parallel u_t\parallel }_{3,p}^2+Cq{\tau }^{4-2\alpha }\underset{0\le t\le t_n}{max}{\parallel u_{tt}\parallel }^2+Cq\left|\right||{\eta }^n{\left|\right||}^2\hfill \\ \hfill & \le Cq{h}^4{T}^{2-2\alpha }\underset{0\le t\le t_n}{max}{\parallel u_t\parallel }_{3,p}^2+Cq{\tau }^{4-2\alpha }\underset{0\le t\le t_n}{max}{\parallel u_{tt}\parallel }^2+Cq\left|\right||{\eta }^n{\left|\right||}^2.\hfill \end{array}$$

Then, we estimate $|T_5|$.

$$\begin{array}{cc}\hfill T_5=& {\beta }_2[({(u^n)}^p{\displaystyle \frac{\partial u^n}{\partial x}},{\Pi }_h^{*}{\eta }^n)-({(u_h^{n-1})}^p{\displaystyle \frac{\partial u_h^n}{\partial x}},{\Pi }_h^{*}{\eta }^n)]\hfill \\ \hfill =& {\beta }_2[({(u^n)}^p{\displaystyle \frac{\partial (u^n-P_h{u}^n)}{\partial x}},{\Pi }_h^{*}{\eta }^n)+(({(u^n)}^p-{(u_h^{n-1})}^p){\displaystyle \frac{\partial P_h{u}^n}{\partial x}},{\Pi }_h^{*}{\eta }^n)\hfill \\ & +({(u_h^{n-1})}^p{\displaystyle \frac{\partial (P_h{u}^n-u_h^n)}{\partial x}},{\Pi }_h^{*}{\eta }^n)]\hfill \\ \hfill =& {\beta }_2[({(u^n)}^p{\displaystyle \frac{\partial {\rho }^n}{\partial x}},{\Pi }_h^{*}{\eta }^n)+(({(u^n)}^p-{(u_h^{n-1})}^p){\displaystyle \frac{\partial P_h{u}^n}{\partial x}},{\Pi }_h^{*}{\eta }^n)+({(u_h^{n-1})}^p{\displaystyle \frac{\partial {\eta }^n}{\partial x}},{\Pi }_h^{*}{\eta }^n)]\hfill \\ \hfill =& T_{51}+T_{52}+T_{53}.\hfill \end{array}$$

According to Lemma 3,

$$\begin{array}{c}\hfill \parallel {\rho }^n{\parallel }_1\le Ch\parallel u^n{\parallel }_2\le Ch[\parallel u^0{\parallel }_2+{\int }_0^{t_n}\parallel u_t{\parallel }_{2}dt].\end{array}$$

Using Hölder inequality and Schwarz inequality, we can obtain

$$\begin{array}{cc}\hfill \left|T_{51}\right|& =\left|{\beta }_2({(u^n)}^p{\displaystyle \frac{\partial {\rho }^n}{\partial x}},{\Pi }_h^{*}{\eta }^n)\right|\hfill \\ \hfill & \le C\left|\right||{\displaystyle \frac{\partial {\rho }^n}{\partial x}}\left|\right|\left|\right|\left|\right|{\eta }^n\left|\right||\hfill \\ \hfill & \le C\left|\right||{\rho }^n{\left|\right||}_1^2+C\left|\right||{\eta }^n{\left|\right||}^2\hfill \\ \hfill & \le C{h}^2[\parallel u^0{\parallel }_2+{\int }_0^{t_n}\parallel u_t{\parallel }_2{dt]}^2+C\left|\right||{\eta }^n{\left|\right||}^2.\hfill \end{array}$$

Therefore, we can make the following inductive hypothesis:

$$\parallel u_h^{n-1}{\parallel }_{\infty }\le K,1\le n\le N,$$

(13)

where $K=\underset{n\tau \le T}{\max }{\parallel u^n\parallel }_{\infty }+1$.

Then, we estimate $|T_{52}|$.

As

$$\begin{array}{cc}\hfill \parallel u^n-u_h^{n-1}\parallel & =\parallel u^n-u^{n-1}+u^{n-1}-u_h^{n-1}\parallel \hfill \\ \hfill & \le \parallel u^n-u^{n-1}\parallel +\parallel {\rho }^{n-1}\parallel +\parallel {\eta }^{n-1}\parallel \hfill \\ \hfill & ={(\tau {\int }_{t_{n-1}}^{t_n}{\parallel u_t\parallel }^{2}d\tau )}^{\frac{1}{2}}+\parallel {\rho }^{n-1}\parallel +\parallel {\eta }^{n-1}\parallel ,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \parallel {(u^n)}^{p-1}+{(u^n)}^{p-2}{u}_h^{n-1}+\cdots +u^n{(u_h^{n-1})}^{p-2}+{(u_h^{n-1})}^{p-1}\parallel \hfill \\ \hfill & \le C+CK+C{K}^2+\cdots +C{K}^{P-2}+K^{P-1}\hfill \\ \hfill & =C{\displaystyle \frac{1-K^p}{1-K}},\hfill \end{array}$$

we have

$$\begin{array}{cc}\hfill & \parallel {(u^n)}^p-{(u_h^{n-1})}^p\parallel \hfill \\ \hfill =& \parallel (u^n-u_h^{n-1})({(u^n)}^{p-1}+{(u^n)}^{p-2}{u}_h^{n-1}+\cdots +u^n{(u_h^{n-1})}^{p-2}+{(u_h^{n-1})}^{p-1})\parallel \hfill \\ \hfill \le & C{\displaystyle \frac{1-K^p}{1-K}}[{(\tau {\int }_{t_{n-1}}^{t_n}{\parallel u_t\parallel }^{2}dt)}^{\frac{1}{2}}+\parallel {\rho }^{n-1}\parallel +\parallel {\eta }^{n-1}\parallel ].\hfill \end{array}$$

Using Lemma 4, Hölder inequality and Schwarz inequality, we can obtain

$$\begin{array}{cc}\hfill \left|T_{52}\right|& =|{\beta }_2({(u^n)}^p-{(u_h^{n-1})}^p{\displaystyle \frac{\partial P_h{u}^n}{\partial x}},{\Pi }_h^{*}{\eta }^n)|\hfill \\ \hfill & \le C\parallel {(u^n)}^p-{(u_h^{n-1})}^p\parallel \left|\right||{\eta }^n\left|\right||\hfill \\ \hfill & \le C{\displaystyle \frac{1-K^p}{1-K}}[{(\tau {\int }_{t_{n-1}}^{t_n}{\parallel u_t\parallel }^{2}dt)}^{\frac{1}{2}}+\parallel {\rho }^{n-1}\parallel +\parallel {\eta }^{n-1}\parallel ]\left|\right||{\eta }^n\left|\right||\hfill \\ \hfill & \le C{\displaystyle \frac{1-K^p}{1-K}}\tau {\int }_{t_{n-1}}^{t_n}{\parallel u_t\parallel }^{2}dt+C{\displaystyle \frac{1-K^p}{1-K}}{h}^2[{\parallel u^0\parallel }_{3,p}+{\int }_0^{t_n}\parallel u_t{{\parallel }_{3,p}dt]}^2\hfill \\ & +C{\displaystyle \frac{1-K^p}{1-K}}{\parallel {\eta }^{n-1}\parallel }^2+C{\displaystyle \frac{1-K^p}{1-K}}\left|\right||{\eta }^n{\left|\right||}^2.\hfill \end{array}$$

According to our induction hypothesis, Hölder inequality and $\epsilon$-inequality, we have

$$\begin{array}{cc}\hfill \left|T_{53}\right|& =\left|{\beta }_2({(u_h^{n-1})}^p{\displaystyle \frac{\partial {\eta }^n}{\partial x}},{\Pi }_h^{*}{\eta }^n)\right|\hfill \\ \hfill & \le C\left|\right||{\eta }^n{\left|\right||}_1\left|\right||{\eta }^n\left|\right||\hfill \\ \hfill & \le \epsilon \left|\right||{\eta }^n{\left|\right||}_1^2+{\displaystyle \frac{C}{4\epsilon }}\left|\right||{\eta }^n{\left|\right||}^2.\hfill \end{array}$$

Substituting the above estimates of $T_{51},T_{52}$ and $T_{53}$ into $T_5$, we have

$$\begin{array}{cc}\hfill |T_5|& \le C{h}^2[\parallel u^0{\parallel }_2+{\int }_0^{t_n}\parallel u_t{{\parallel }_{2}dt]}^2+C{\displaystyle \frac{1-K^p}{1-K}}\tau {\int }_0^T{\parallel u_t\parallel }^{2}dt\hfill \\ & +C{\displaystyle \frac{1-K^p}{1-K}}{h}^2[\parallel u^0{\parallel }_{3,p}+{\int }_0^{t_n}\parallel u_t{\parallel }_{3,p}{dt]}^2+C{\displaystyle \frac{1-K^p}{1-K}}{\parallel {\eta }^{n-1}\parallel }^2+C{\displaystyle \frac{1-K^p}{1-K}}\left|\right||{\eta }^n{\left|\right||}^2\hfill \\ & +C\left|\right||{\eta }^n{\left|\right||}^2+\epsilon \left|\right||{\eta }^n{\left|\right||}_1^2+{\displaystyle \frac{C}{4\epsilon }}\left|\right||{\eta }^n{\left|\right||}^2.\hfill \end{array}$$

Combining estimates of $T_1,T_2,T_3,T_4,T_5$ and (12), we can obtain

$$\begin{array}{c}{\displaystyle \frac{1-q}{2\tau }}(|\left|\right|{\eta }^n{\left|\right||}^2-\left|\right||{\eta }^{n-1}{\left|\right||}^2)+|\left|\right|{\eta }^n{\left|\right||}_1^2+{\beta }_{1}qr\left|\right||{\eta }^n{\left|\right||}^2\hfill \\ \le Cqr\sum _{k=1}^{n-1}(a_{n-k-1}^{(\alpha )}-a_{n-k}^{(\alpha )})\left|\right||{\eta }^k{\left|\right||}^2+Cqr(1-a_{n-1}^{(\alpha )})\left|\right||{\eta }^n{\left|\right||}^2\hfill \\ +C(1-q)\tau {\int }_{t_{n-1}}^{t_n}{\parallel u_{tt}\parallel }^{2}dt+{\displaystyle \frac{C(1-q)h^2}{\tau }}{\int }_{t_{n-1}}^{t_n}{\left|u_t\right|}_2^{2}dt+Cq{h}^4{T}^{2-2\alpha }\underset{0\le t\le t_n}{max}{\parallel u_t\parallel }_{3,p}^2\hfill \\ +Cq{\tau }^{4-2\alpha }\underset{0\le t\le t_n}{max}{\parallel u_{tt}\parallel }^2+C{h}^2[\parallel u^0{\parallel }_2+{\int }_0^{t_n}\parallel u_t{{\parallel }_{2}dt]}^2+C{\displaystyle \frac{1-K^p}{1-K}}\tau {\int }_{t_{n-1}}^{t_n}{\parallel u_t\parallel }^{2}dt\hfill \\ +C{\displaystyle \frac{1-K^p}{1-K}}{h}^2[\parallel u^0{\parallel }_{3,p}+{\int }_0^{t_n}\parallel u_t{\parallel }_{3,p}{dt]}^2+C{\displaystyle \frac{1-K^p}{1-K}}{\parallel {\eta }^{n-1}\parallel }^2+C{\displaystyle \frac{1-K^p}{1-K}}\left|\right||{\eta }^n{\left|\right||}^2\hfill \\ +C\left|\right||{\eta }^n{\left|\right||}^2+\epsilon \left|\right||{\eta }^n{\left|\right||}_1^2+{\displaystyle \frac{C}{4\epsilon }}\left|\right||{\eta }^n{\left|\right||}^2.\hfill \end{array}$$

(14)

Let $\epsilon =1$, $\tilde{C}=C{\displaystyle \frac{1-K^p}{1-K}}$, and multiply both sides of inequality (14) by ${\displaystyle \frac{2\tau }{1-q}}$; then, (14) is equivalent to

$$\begin{array}{c}\left|\right||{\eta }^n{\left|\right||}^2\le {\displaystyle \frac{Cq{\tau }^{1-\alpha }}{1-q}}\sum _{k=1}^{n-1}(a_{n-k-1}^{(\alpha )}-a_{n-k}^{(\alpha )})\left|\right||{\eta }^k{\left|\right||}^2+(1+\tilde{C}{\displaystyle \frac{\tau }{1-q}})\left|\right||{\eta }^{n-1}{\left|\right||}^2\hfill \\ +{\displaystyle \frac{Cq\tau }{1-q}}\left|\right||{\eta }^n{\left|\right||}^2+\tilde{C}{\displaystyle \frac{\tau }{1-q}}\left|\right||{\eta }^n{\left|\right||}^2+{\displaystyle \frac{C\tau }{1-q}}\left|\right||{\eta }^n{\left|\right||}^2\hfill \\ +{\displaystyle \frac{Cq{\tau }^{1-\alpha }}{(1-q)\Gamma (2-\alpha )}}(1-a_{n-1}^{(\alpha )})\left|\right||{\eta }^n{\left|\right||}^2+C{\tau }^2{\int }_0^T{\parallel u_{tt}\parallel }^{2}dt+C{h}^2{\int }_0^T{\left|u_t\right|}_2^{2}dt\hfill \\ +{\displaystyle \frac{Cq{h}^4{T}^{3-2\alpha }}{1-q}}\underset{0\le t\le t_n}{max}{\parallel u_t\parallel }_{3,p}^2+{\displaystyle \frac{Cq{\tau }^{5-2\alpha }}{1-q}}\underset{0\le t\le t_n}{max}{\parallel u_{tt}\parallel }^2+{\displaystyle \frac{C\tau h^2}{1-q}}[\parallel u^0{\parallel }_2+{\int }_0^T\parallel u_t{{\parallel }_{2}dt]}^2\hfill \\ +\tilde{C}{\displaystyle \frac{{\tau }^2}{1-q}}{\int }_{t^{n-1}}^{t^n}\parallel u_t\parallel dt+\tilde{C}{\displaystyle \frac{\tau h^2}{1-q}}[\parallel u^0{\parallel }_{3,p}+{\int }_0^T\parallel u_t{{\parallel }_{3,p}dt]}^2.\hfill \end{array}$$

(15)

Using Lemma 1, we know that

$$\sum _{k=1}^{n-1}(a_{n-k-1}^{(\alpha )}-a_{n-k}^{(\alpha )})=1-a_{n-1}^{(\alpha )}\ge 0.$$

Applying Lemma 6, we have

$$\begin{array}{c}\hfill \parallel {\eta }^n{\parallel }^2\le C_1({\tau }^2+h^2)·\exp C_2,\end{array}$$

(16)

where

$$\begin{array}{cc}\hfill C_1=& \max \{C{\int }_0^T{\parallel u_{tt}\parallel }^{2}dt,C{\int }_0^T{\left|u_t\right|}_2^{2}dt,{\displaystyle \frac{Cq{h}^2{T}^{3-2\alpha }}{1-q}}\underset{0\le t\le t_n}{max}{\parallel u_t\parallel }_{3,p}^2,\hfill \\ & {\displaystyle \frac{Cq{T}^{3-2\alpha }}{1-q}}\underset{0\le t\le t_n}{max}{\parallel u_{tt}\parallel }^2,{\displaystyle \frac{CT}{1-q}}[\parallel u^0{\parallel }_2+{\int }_0^T\parallel u_t{{\parallel }_{2}dt]}^2,{\displaystyle \frac{\tilde{C}}{1-q}}{\int }_0^T\parallel u_t\parallel d\tau ,\hfill \\ & {\displaystyle \frac{\tilde{C}T}{1-q}}{\int }_0^T\parallel u_t{\parallel }_{3,p}^{2}dt\},\hfill \end{array}$$

$$\begin{array}{cc}\hfill C_2=& 1+{\displaystyle \frac{Cq{\tau }^{1-\alpha }}{1-q}}(1-a_{n-1}^{(\alpha )})+{\displaystyle \frac{Cq{\tau }^{1-\alpha }}{(1-q)\Gamma (2-\alpha )}}(1-a_{n-1}^{(\alpha )})+{\displaystyle \frac{Cq\tau }{1-q}}\hfill \\ & +{\displaystyle \frac{C\tau }{1-q}}+2\tilde{C}{\displaystyle \frac{\tau }{1-q}}.\hfill \end{array}$$

Then, we prove the induction hypothesis (13) is true. When $i=0$, this is obviously true. Suppose that the conclusion holds if $i=n-1$. Therefore, when $i=n$, according to the estimate (16), we have $\parallel {\eta }^n\parallel \le \widehat{C}(\tau +h)$. Restricting $\tau =O(h)$ and using the inverse estimate, we obtain

$$\begin{array}{cc}\hfill \parallel u_h^n{\parallel }_{\infty }& \le \parallel P_h{u}^n{\parallel }_{\infty }+{\parallel {\eta }^n\parallel }_{\infty }\hfill \\ \hfill & \le \parallel u^n{\parallel }_{\infty }+\widehat{C}{h}^{-\frac{1}{2}}\parallel {\eta }^n\parallel \hfill \\ & \le \parallel u^n{\parallel }_{\infty }+\widehat{C}{h}^{-\frac{1}{2}}(h+\tau )\hfill \\ \hfill & \le \parallel u^n{\parallel }_{\infty }+1\hfill \\ \hfill & \le K,\hfill \end{array}$$

for sufficiently small h, where $\widehat{C}={\displaystyle \frac{1}{2}}{C}_1^{\frac{1}{2}}·\exp C_2$. Therefore, induction hypothesis (13) is valid for any n. Finally, according to the triangle inequality, we can obtain

$$\begin{array}{c}\hfill \parallel u^n-u_h^n\parallel \le \parallel {\rho }^n\parallel +\parallel {\eta }^n\parallel \le C{h}^2[\parallel u^0{\parallel }_{3,p}+{\int }_0^{t_n}\parallel u_t{\parallel }_{3,p}dt]+\widehat{C}(\tau +h).\end{array}$$

The theorem is proven. □

5. Numerical Examples

In this section, we present two numerical examples to gain insights into the theoretical results established in previous sections. The effectiveness and accuracy order of the FVE scheme are shown by numerical results.

Example 1. 

Let the parameters $q=\gamma ={\displaystyle \frac{1}{2}}$, ${\beta }_1={\beta }_2=1$ and $p=3$ in problem (1) be defined as:

$${\displaystyle \frac{1}{2}}{u}_t+{\displaystyle \frac{1}{2}}{}_0^C{D}_t^{\alpha }u-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}+u^3{\displaystyle \frac{\partial u}{\partial x}}=f(x,t),x\in (0,1),t\in \left(0,1\right],$$

with the following boundary conditions:

$$u(0,t)=u(1,t)=0,t\in \left(0,1\right],$$

and the following initial condition:

$$u(x,0)=g(x),x\in (0,1).$$

We set $f(x,t)=({\displaystyle \frac{\Gamma (5)}{2\Gamma (5-\alpha )}}{t}^{4-\alpha }+2t^3+{\displaystyle \frac{1}{2}}{\pi }^2{t}^4)sin(\pi x)+\pi t^{16}si{n}^3(\pi x)cos(\pi x)$; then, we can deduce the exact solution for $u(x,t)=t^{4}sin(\pi x)$. The spatial step is fixed by $h=0.001$. The time-step length is set as $\tau =1/10,1/20,1/40,1/80$. We present the error and temporal convergence order in

Table 1. $L^2$-norm errors and temporal convergence order of the FVEM.

		$\mathit{\alpha }=0.7$		$\mathit{\alpha }=0.3$
	$\mathsf{\tau }$	$\parallel \mathit{u} - {\mathit{u}}_{\mathit{h}}\parallel$	Order	$\parallel \mathit{u} - {\mathit{u}}_{\mathit{h}}\parallel$	Order
	1/10	0.0374	-	0.0311	-
	1/20	0.0185	1.0155	0.0158	0.9770
	1/40	0.0090	1.0395	0.0079	1.0000
	1/80	0.0044	1.0324	0.0040	0.9819

. The $L^2$-norm error between the exact solution (u) and the numerical solution ($u_h$) is defined as $e(h,\tau )=\sqrt{h{\displaystyle \sum _{i=1}^{m-1}}{[u_i^n-u_h(x_i,t_n)]}^2}$. The result is consistent with the theoretical result reported in Theorem 1, which shows that the convergence order in time is approximately one.

Next, we set the time step as $\tau ={\displaystyle \frac{1}{M}}$ and the spatial step as $h={\displaystyle \frac{1}{N}}$. In order to show the capability of our method, when $M=N^2$, we present the spatial convergence orders and errors obtained by the FVEM in

Table 2. $L^2$-norm errors and spatial convergence order of the FVEM.

		$\mathit{\alpha }=0.7$		$\mathit{\alpha }=0.3$
	h	$\parallel \mathit{u} - {\mathit{u}}_{\mathit{h}}\parallel$	Order	$\parallel \mathit{u} - {\mathit{u}}_{\mathit{h}}\parallel$	Order
	1/8	0.0121	-	0.0113	-
	1/16	0.0029	2.0609	0.0028	2.0128
	1/32	$7.2541\times {10}^{-4}$	1.9992	$7.0135\times {10}^{-4}$	1.9972
	1/64	$4.2090\times {10}^{-4}$	2.0162	$1.7525\times {10}^{-4}$	2.0007

and those obtained by the finite difference method in

Table 3. $L^2$-norm errors and spatial convergence order of the finite-difference method.

		$\mathit{\alpha }=0.7$		$\mathit{\alpha }=0.3$
	h	$\parallel \mathit{u} - {\mathit{u}}_{\mathit{h}}\parallel$	Order	$\parallel \mathit{u} - {\mathit{u}}_{\mathit{h}}\parallel$	Order
	1/8	0.0299	-	0.0300	-
	1/16	0.0109	1.4558	0.0107	1.0310
	1/32	0.0039	1.4828	0.0038	1.0352
	1/64	0.0014	1.4780	0.0013	1.0726

. Table 2 shows that the spatial convergence orders are higher than the theoretical analysis, while Table 3 shows that the finite difference method is less accurate than the FVEM, which proves the effectiveness of the FVEM.

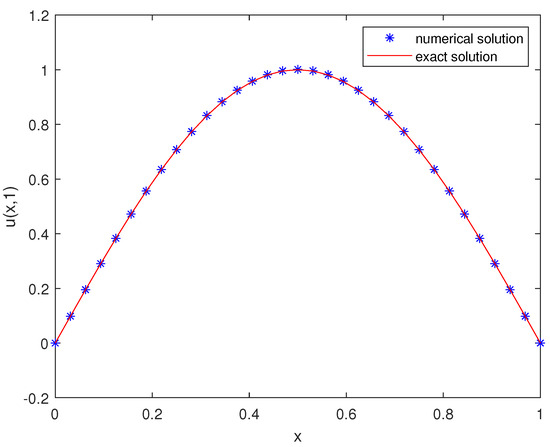
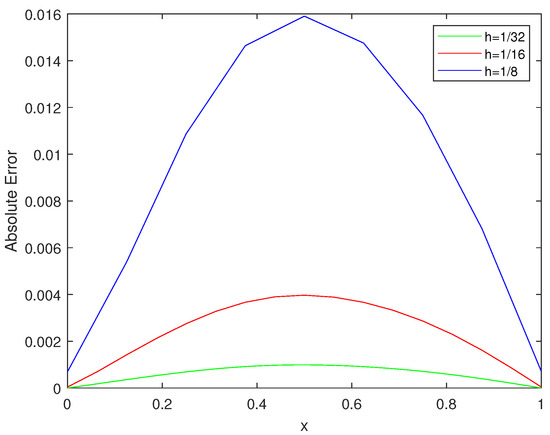
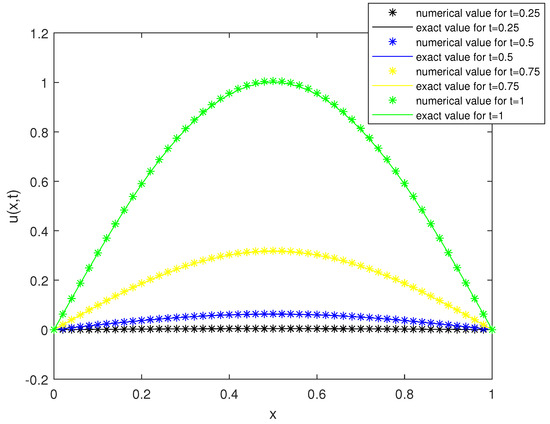
Functional images of the exact solution (u) and the numerical solution ($u_h$) for $\alpha =0.7$ are presented in Figure 1, and surface plots are provided in Figure 2, Figure 3 and Figure 4. As can be seen, there is good agreement between the exact solution and the numerical solution. Figure 5 describes the behavior of absolute errors at t = 1 for h = 1/8, 1/16 and 1/32 and for $\alpha =0.3$. This shows that error decreases as the number of nodes is increased. Figure 6 shows a comparison of approximated and exact values for h = 0.02, $\tau =1/80$ and $\alpha =0.3$ at time levels t = 0.25, 0.5, 0.75 and t = 1.

Example 2. 

In this example, a generalized time fractional Burgers’ equation with an unknown exact solution is considered:

$${\displaystyle \frac{1}{2}}{u}_t+{\displaystyle \frac{1}{2}}{}_0^C{D}_t^{\alpha }u-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}+u^2{\displaystyle \frac{\partial u}{\partial x}}=0,x\in (0,1),t\in \left(0,T\right],$$

with following boundary conditions:

$$u(0,t)=u(1,t)=0,t\in \left(0,T\right],$$

and the following initial condition:

$$u(x,0)=sin(\pi x),x\in (0,1),$$

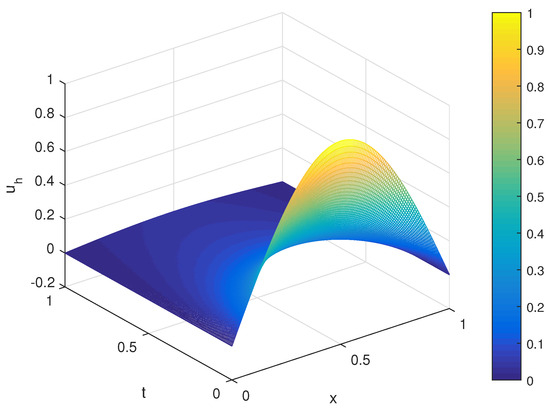
where $T=1$. In this example, the exact solution is not known beforehand, so we take the numerical solution with h = $1/150$ as the reference solution to calculate the error and convergence rate. The experimental rates of convergence associated with the mesh size (h) can be calculated using the formula log($e_i/e_{i+1}$)/log($h_i/h_{i+1}$), where $e_i$ and $e_{i+1}$ are the relative errors corresponding to mesh of sizes $h_i$ and $h_{i+1}$, respectively. In

Table 4. Numerical results for $\alpha =0.2$ and $\alpha =0.8$.

		$\mathit{\alpha }=0.2$		$\mathit{\alpha }=0.8$
	h	$\parallel \mathit{u} - {\mathit{u}}_{\mathit{h}}\parallel$	Order	$\parallel \mathit{u} - {\mathit{u}}_{\mathbf{h}}\parallel$	Order
	1/25	$1.4567\times {10}^{-4}$	-	$5.8463\times {10}^{-4}$	-
	1/30	$1.2661\times {10}^{-4}$	0.7693	$5.0481\times {10}^{-4}$	0.8220
	1/50	$8.0646\times {10}^{-5}$	0.8829	$3.1350\times {10}^{-4}$	0.9325
	1/75	$4.9139\times {10}^{-5}$	1.2218	$1.8788\times {10}^{-4}$	1.2626

, we present the numerical results for $\alpha =0.2$ and $0.8$. As shown in the table, the format is convergent with one order of accuracy. Surface plots of the reference solution (u) and the numerical solution ($u_h$) for $\alpha =0.8$ are presented in Figure 7 and Figure 8, respectively. As evidenced by the table and figures, these results are consistent with the results of our theoretical analysis.

6. Conclusions

In this paper, a fully discrete finite volume element scheme for time fractional generalized Burgers’ equations is presented. The convergence of the numerical method is proven herein. In order to verify our theoretical results, two numerical results are presented.

While several approaches exist to address these kinds of issues, the FVEM demonstrates the following benefits: (i) Its accuracy is higher than that of finite difference methods and almost equal to that of finite element methods, while the computational cost is less than that of finite element methods. (ii) The mass conservation law is upheld, which is generally preferable for calculations involving fluids and subterranean fluids, among other things. (iii) The space smoothness requirement is less compared to that of the finite-element method.

However, prior research suggests that it is possible to loosen the smoothness condition of the fractional-order issue solution. To enhance the application of the FVEM, in the future, we will investigate a case of non-smooth data. Furthermore, to increase the method’s accuracy, the time derivatives can also be discretized using different techniques.