Stability Analysis of Finite Time for a Class of Nonlinear Time-Delay Fractional-Order Systems
Abstract
:1. Introduction
2. Preliminaries
- S1
- iff ;
- S2
- for all ;
- S3
- for all .
- (a)
- converges to a fixed point of Φ;
- (b)
- is the unique fixed point of Φ in ;
- (c)
- If , then .
- (i)
- g is continuous, , and for all such thatwhere is a continuous function and is the Euclidean norm.
- (ii)
- For all , is a continuous function, and there exist such that
3. Main Results
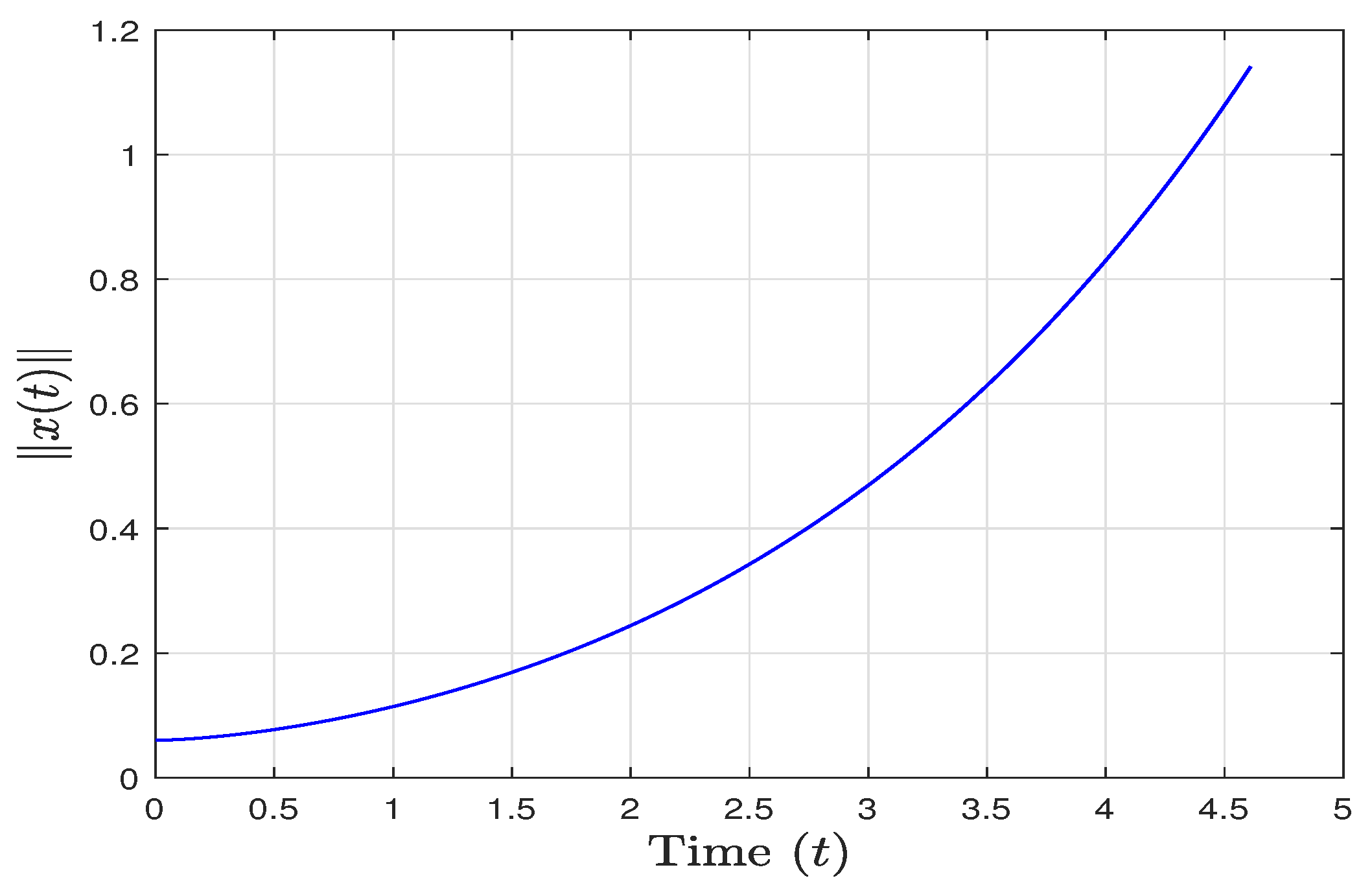
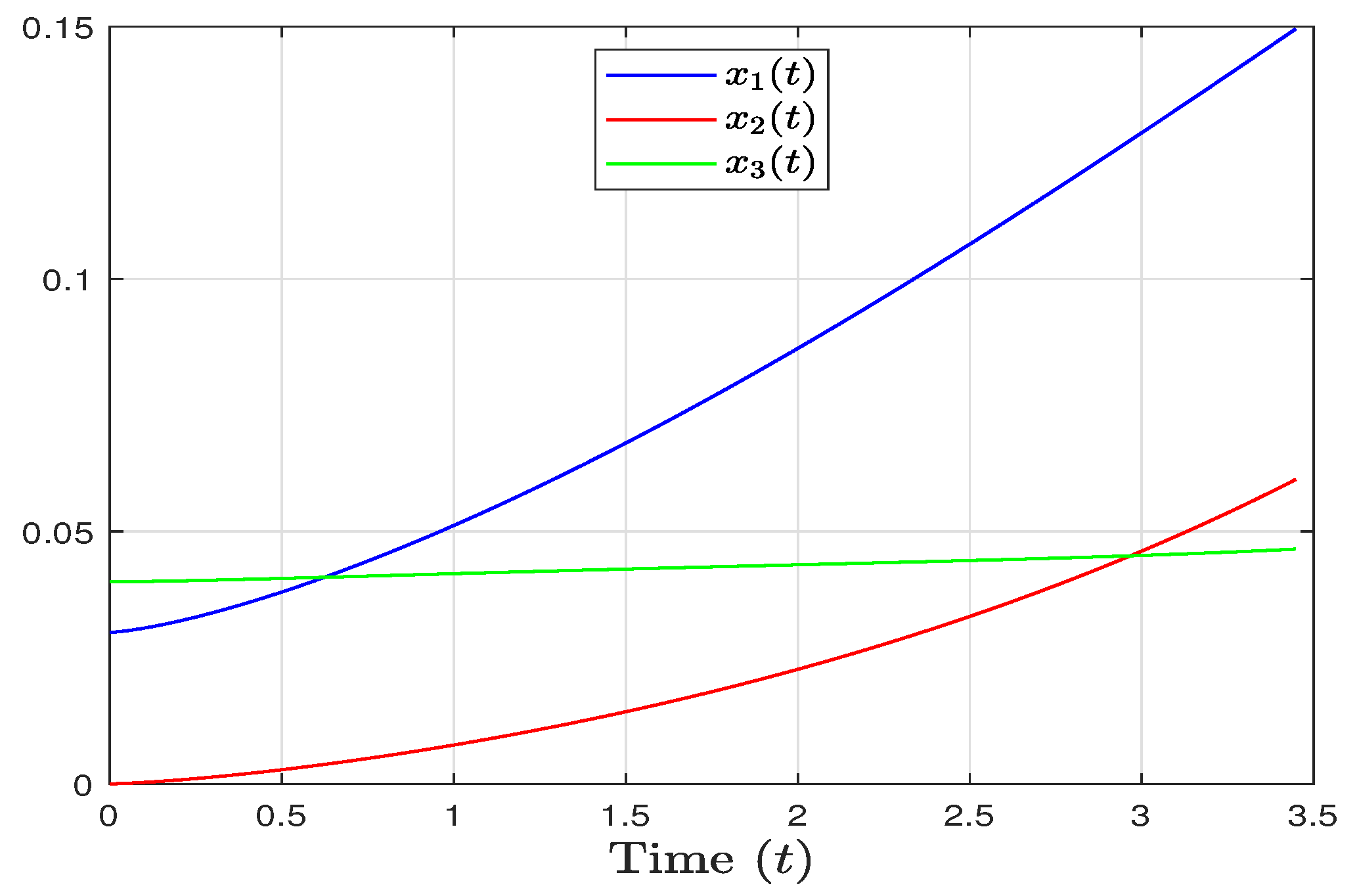
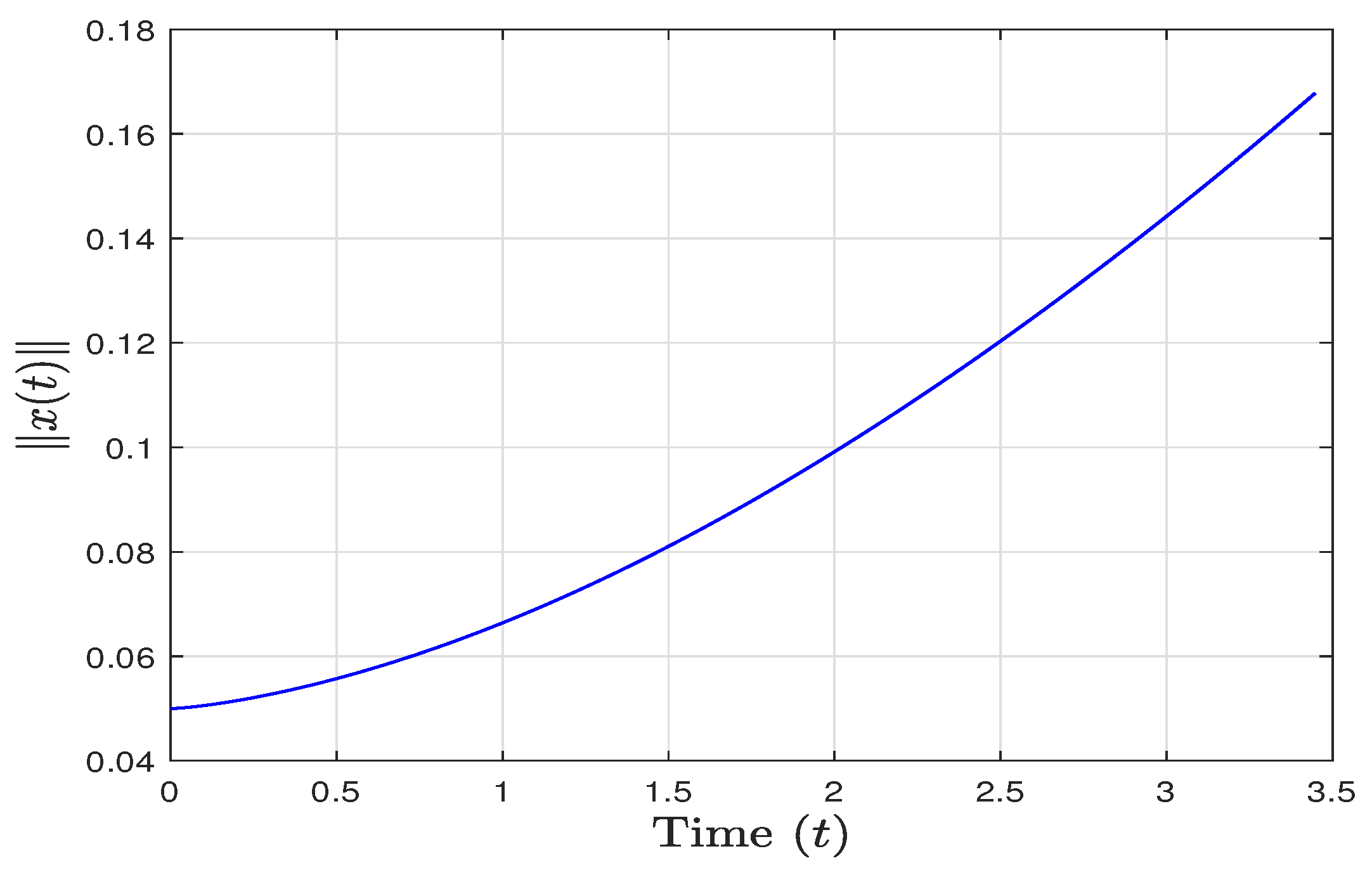
4. Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 9781849963350. [Google Scholar]
- Wu, Z. Multiple asymptotic stability of fractional-order quaternion-valued neural networks with time-varying delays. Neurocomputing 2021, 448, 301–312. [Google Scholar] [CrossRef]
- Naifar, O.; Nagy, A.M.; Ben Makhlouf, A.; Kharrat, M.; Hammami, M.A. Finite-time stability of linear fractional-order time-delay systems. Int. J. Robust Nonlinear Control 2019, 29, 180–187. [Google Scholar] [CrossRef]
- Thanh, N.T.; Phat, V.N.; Niamsup, T. New finite-time stability analysis of singular fractional differential equations with time-varying delay. Fract. Calc. Appl. Anal. 2020, 23, 504–519. [Google Scholar] [CrossRef]
- Etlili, D.; Khedher, A.; Errachdi, A. A Proposed High-Gain Observer for a Class of Nonlinear Fractional-Order Systems. Math. Probl. Eng. 2021, 2021, 7844544. [Google Scholar] [CrossRef]
- Peng, R.; Jiang, C.; Guo, R. Stabilization of a Class of Fractional Order Systems With Both Uncertainty and Disturbance. IEEE Access 2021, 9, 42697–42706. [Google Scholar] [CrossRef]
- Zhang, H.; Yan, Y.; Ming, Z.; Wang, Y. Cooperative fault diagnosis of fuzzy fractional order time-varying multi-agent system with directed networks. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1447–1451. [Google Scholar] [CrossRef]
- Thanh, N.T.; Phat, V.N. Improved Approach for Finite-Time Stability of Nonlinear Fractional-Order Systems With Interval Time-Varying Delay. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1356–1360. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, J.; Hu, J.; Mei, J. New results on finite-time stability for fractional-order neural networks with proportional delay. Neurocomputing 2021, 442, 327–336. [Google Scholar] [CrossRef]
- Chen, L.; He, Y.; Wu, R.; Chai, Y.; Yin, L. Robust finite time stability of fractional-order linear delayed systems with nonlinear perturbations. Int. J. Control. Autom. Syst. 2014, 12, 697–702. [Google Scholar] [CrossRef]
- Wang, F.; Chen, D.; Zhang, X.; Wu, Y. Finite-time stability of a class of nonlinear fractional-order system with the discrete time delay. Int. J. Syst. Sci. 2017, 48, 984–993. [Google Scholar] [CrossRef]
- Ben Makhlouf, A. A Novel Finite Time Stability Analysis of Nonlinear Fractional-Order Time Delay Systems: A Fixed Point Approach. Asian J. Control 2022, 24, 3580–3587. [Google Scholar] [CrossRef]
- Ben Makhlouf, A.; Baleanu, D. Finite Time Stability of Fractional Order Systems of Neutral Type. Fractal Fract. 2022, 6, 289. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Tuan, H.T.; Trinh, H.; Lam, J. Positivity and stability of mixed fractional-order systems with unbounded delays: Necessary and sufficient conditions. Int. J. Robust. Nonlinear Control 2020, 31, 37–50. [Google Scholar] [CrossRef]
- Tuan, H.T.; Trinh, H. A Qualitative theory of time delay nonlinear fractional-order systems. Siam J. Control Optim. 2020, 58, 1491–1518. [Google Scholar] [CrossRef]
- Diaz, J.B.; Margolis, B. A fixed point theorem of the alternative, for contractions on a generalized complete metric space. Bull. Am. Math. Soc. 1968, 74, 305–309. [Google Scholar] [CrossRef]
- Difonzo, F.V.; Przybyłowicz, P.; Wu, Y. Existence, uniqueness and approximation of solutions to Carathéodory delay differential equations. J. Comput. Appl. Math. 2023, 436, 115411. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical Solution of Fractional Differential Equations: A Survey and a Software Tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Garrappa, R.; Popolizio, M. Generalized exponential time differencing methods for fractional order problems. Comput. Math. Appl. 2011, 62, 876–890. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Makhlouf, A.; Mchiri, L.; Rhaima, M. Stability Analysis of Finite Time for a Class of Nonlinear Time-Delay Fractional-Order Systems. Fractal Fract. 2024, 8, 4. https://doi.org/10.3390/fractalfract8010004
Ben Makhlouf A, Mchiri L, Rhaima M. Stability Analysis of Finite Time for a Class of Nonlinear Time-Delay Fractional-Order Systems. Fractal and Fractional. 2024; 8(1):4. https://doi.org/10.3390/fractalfract8010004
Chicago/Turabian StyleBen Makhlouf, Abdellatif, Lassaad Mchiri, and Mohamed Rhaima. 2024. "Stability Analysis of Finite Time for a Class of Nonlinear Time-Delay Fractional-Order Systems" Fractal and Fractional 8, no. 1: 4. https://doi.org/10.3390/fractalfract8010004
APA StyleBen Makhlouf, A., Mchiri, L., & Rhaima, M. (2024). Stability Analysis of Finite Time for a Class of Nonlinear Time-Delay Fractional-Order Systems. Fractal and Fractional, 8(1), 4. https://doi.org/10.3390/fractalfract8010004





