1. Introduction
The inception of the first fixed-point result dates back approximately a century. The technique of successive approximation for solving differential equations was initially formalized by S. Banach [
1], who subsequently characterized it as a concept rooted in contraction mapping. The Banach hypothesis was not only articulated in a clear and straightforward manner but was also exemplified by illustrating the methodology to reach the desired fixed point. Fixed-point theory holds significant relevance across various qualitative sciences, capturing the fascination of researchers due to its simplicity in converting equations from diverse research domains into fixed-point problems. Numerous authors have expanded and generalized Banach’s fixed-point result in various directions, as documented in [
2]. Notably, Eshaghi Gordji, Ramezani, De la Sen, and Cho [
3] recently introduced the concept of an orthogonal set and put forth fixed-point results within the context of
O-MS (orthogonal metric spaces).
In 2012, Wardowski [
4] introduced a novel category of
F-contractions, accompanied by the establishment of several fixed-point theorems. Mahendra Singh, Y., Khan, M. S., and Kang, S. M. [
5] pioneered the concept of
–
F–convex contraction mappings using an admissible map and subsequently validated their proposition with the proof of various fixed-point theorems. In the year 2020, Sawangsup, Sintunavarat, and Cho [
6] introduced the innovative concept of an orthogonal
F–contraction map, providing proofs for fixed-point results within the orthogonal CMS (complete metric space). The exploration of orthogonal contractive-type maps has been a subject of study by various authors, yielding significant outcomes, as documented in [
7,
8,
9,
10,
11,
12,
13].
In this paper, we adapt the notion of –F–convex contraction maps to orthogonal sets, presenting several fixed-point results applicable to –F–convex contraction mappings within the framework of orthogonal complete metric spaces. Additionally, we leverage our primary findings to determine the existence and uniqueness of solutions for fractional integro-differential equations.
2. Preliminaries
In this section, we review fundamental concepts that are employed in this paper. Throughout this paper, we denote the non-empty set, the non-negative real numbers, and the positive integer set by , , and , respectively.
First of all, we note the Wardowski [
4] notion of a control function established in 2012.
Definition 1 ([
4]).
Let be a map with the subsequent conditions:- (F1)
F is strictly increasing;
- (F2)
For every sequence of , we have - (F3)
ℑ denotes the family of all F functions that fulfills the conditions .
Later, in 2018, Mahendra Singh, Khan, and Kang [
5] introduced the concepts of the
–convex contraction via admissible mapping as follows. Let
be a mapping on a metric space
. We denote
Definition 2 ([
5]).
A self mapping on Ψ is said to be an α––convex contraction, if there exists two functions , and such thatfor all , where . Now, the definition of the
O-set (or orthogonal-set), orthogonal sequence, ⊩-preserving, some premises, and examples of an orthogonal set were initiated by Gordji et al. [
3], as follows:
Definition 3 ([
3]).
Let and be a binary relation. If ⊩ fulfills the consecutive condition:then is called an O-set. This element does not have to be unique. For example:
Example 1 ([
3]).
Let and define it by if . Then, by setting or , is an O-set. Definition 4 ([
3]).
Let be an O-set. A sequence is called an orthogonal sequence (briefly, O-sequence) if Definition 5 ([
3]).
Let be an O-set. A function is said to be ⊩-preserving if whenever . Now, we give the notions of O-MS, orthogonal complete (briefly, O-complete), orthogonally continuous, orthogonally -admissible, and orthogonally -admissible.
Definition 6 ([
3]).
The tripled is said to be an O-metric space if is an O-set and is a metric space. Definition 7 ([
3]).
Let be a O-metric space. Then,A map is called orthogonal continuous (⊩-continuous) in if for each O-sequence in Ψ with as , we have as . Also, is called ⊩-continuous on Ψ if is ⊩-continuous in each .
If every Cauchy O-sequence is convergent, then Ψ is called O-complete.
Definition 8 ([
14]).
Let be an O-set and d be a metric on Ψ, and be two functions. We say that is orthogonally α-admissible whenever and Example 2 ([
14]).
Let . Define ⊩ on Ψ by iff . Define and by if and if and . Then, is orthogonally α-admissible. Let be a map on . We denote .
Definition 9. Let be an orthogonally α-admissible map. Then, is called orthogonally -admissible, if for each , we have , . If , we say that is vacuously -admissible.
3. Main Results
Inspired by the
-
F-convex contraction map concepts defined by Mahendra Singh, Khan, and Kang [
5], here we introduce a new orthogonal
–
F–convex contraction mapping and prove some fixed point results in an orthogonal complete metric space (CMS) for this contractive mapping.
Let
be a map on a
O-MS
. Now
Definition 10. A self mapping on Ψ is said to be a –α–F–convex contraction, if there exists two functions , and such that. Theorem 1. Let be an O-CMS and an orthogonal element and be an –α-F–convex contraction mapping such that:
- (i)
is ⊩-preserving;
- (ii)
is orthogonal α-admissible;
- (iii)
∃ and .
Define a sequence in Ψ by , then , whenever or for .
Proof. By condition (iii) in Theorem 1, ∃
,
and
. Let
Consider is an O-sequence in .
If for any , then is a fixed point of .
Assume that
,
. Then,
Since
is ⊩-preserving, then
is an
O-sequence in
. Now, setting
. Condition (ii) in Theorem 1, we get
From (
2), taking
and
, we obtain
By the Definition 1,
,
, by (
3) and (
4), we have
If
, then (
5) gives
Since
and Definition 1,
, we conclude that
Again, from (
2) taking with
and
, we obtain
Using (
3) and (
6), we get
If
, then we obtain
Therefore,
. Proceeding this, one can prove inductively that
is a strictly non-increasing sequence in
. Therefore,
and hence
Similarly, we have
proceeding that, we get
whenever
or
for
. □
Theorem 2. Let be a O-CMS and an orthogonal element , and be an –α-F–convex contraction mapping such that:
- (i)
is ⊩-preserving;
- (ii)
is orthogonally α-admissible;
- (iii)
∃ and ;
- (iv)
is orthogonally continuous, or orthogonally orbitally continuous on Ψ.
Then, has a fixed point in Ψ. Furthermore, if is orthogonally -admissible, then has a unique fixed point . Moreover, for any , if , then .
Proof. By condition (iii) in Theorem 2, ∃
, ∋
and
. Let
Consider is an O-sequence in .
If
for any
, then
is a fixed point of
. Assume that
,
. Then
Since
is ⊩-preserving, then
is an
O-sequence in
. Now, setting
. From condition (ii) in Theorem 2, we obtain
From (
2), taking
and
, where
, we obtain
By Definition 1,
and
are orthogonally
-admissible, and by (
3), we derive
If
, then we get
Which is a contradiction. Hence,
From Theorem 1, we obtain
whenever,
or
for
. From (
6), we obtain
Using
, we derive
From
, ∃
, ∋
Also, by (
7), we have
where
or
for
.
As
in (
11) along with (
9) and (
10), we derive
Now, we have two cases arise.
Case 1: If
is even and
, then
Case 2: If
is odd and
, then
For all
, we derive
Suppose
is orthogonally continuous, then
Hence, has a fixed point, that is, .
Let be orthogonally orbitally continuous on , then as . Since is O-complete, we have . Therefore, .
Now, let
be orthogonally
-admissible, then
, we get
. Using (
2) and (
3), we derive
Since
and using the Definition 1, we obtain
Therefore, has a unique fixed point in . □
Corollary 1. Let be O-CMS and an orthogonal element and be a function. Suppose that is self mapping, such that
- (i)
for all with and where ;
- (ii)
is ⊩-preserving;
- (iii)
is orthogonally α-admissible;
- (iv)
∃ and ;
- (v)
is orthogonally orbitally continuous or, orthogonally continuous on Ψ.
Then, has a fixed point in Ψ. Furthermore, if is orthogonally -admissible, then has a unique fixed point . Moreover, for every if , then .
Proof. Setting
. Obviously,
. From (
16), we derive
which implies that
∀
with
where
. Therefore,
is
-
-
F-convex contraction mapping with
. Thus, all of the hypotheses of Theorem 2 are fulfilled. Therefore,
has a unique fixed point in
. □
Example 3. Let with usual metric Suppose iff . Clearly, is O-CMS. Define and by and Then, is orthogonally α-admissible and orthogonally -admissible. Clearly, is ⊩-preserving and orthogonally continuous. Setting . Then, with , we obtainwhere . Then Therefore, is –α–F–convex contraction mapping with . Hence, all the conditions of Theorem 2 are fulfilled and so has a unique fixed point .
4. Application to Fractional Integro-Differential Equation
We consider a Cauchy problem involving a fractional integro-differential equation with a non-local condition given by
where
denotes the Caputo fractional derivative of order
ℓ,
,
are jointly continuous,
is continuous. Here,
denotes the Banach space
of all continuous maps from
with a topology of uniform convergence with the norm denoted by
, and
, see [
15].
Let
be endowed with the metric
defined as
. Define orthogonality ⊩ on
K by
Then,
is O-CMS. Clearly, a solution of (
17) is a fixed point
where
is the Gamma function.
Theorem 3. Suppose that is a orthogonal CMS equipped with metric with and be an orthogonal continuous operator on K defined by
∀
and satisfying the following inequality Then, the Cauchy problem (17) has a unique solution provided by . Proof. We define
by
. Therefore,
is orthogonally
-admissible and orthogonally
-admissible. Now, we prove that
is ⊩-preserving. For every
with
and
, we have
Then,
is ⊩-preserving. Now, we claim that
is a
–
–
F–convex contraction on
K. Let
with
. Suppose that
. Then,
Since
, therefore,
,
∀
,
which implies that
Hence, all the conditions of Corollary 1 are fulfilled and so has a unique solution. □
Example 4. Consider an integro-differential equation with a fractional derivativesubject to Proof. For each
with
and
, we have
The exact solution of the above equation is
Here,
is an orthogonal continuous function on
where
. We calculated value of this equation, it is called the approximate solution:
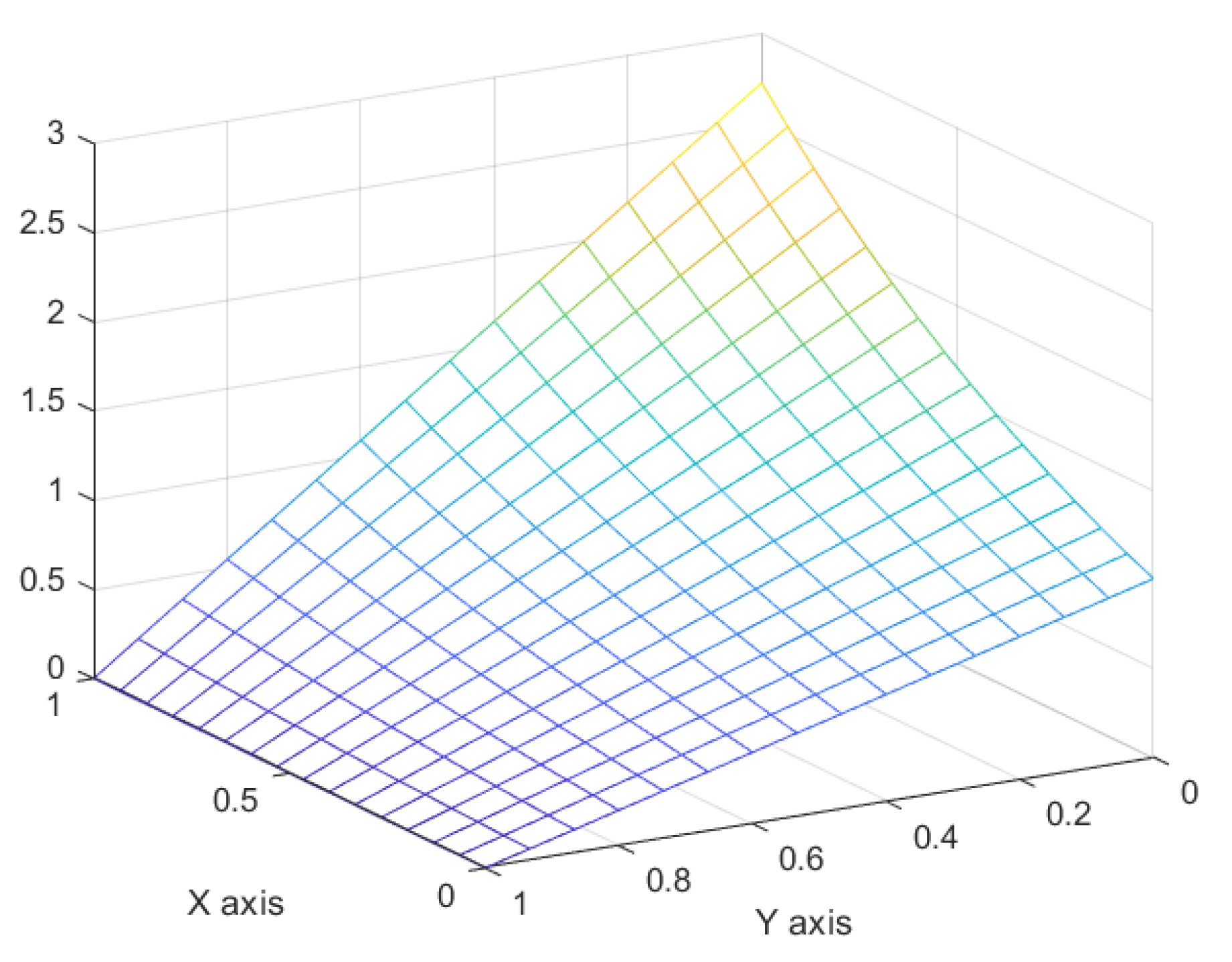
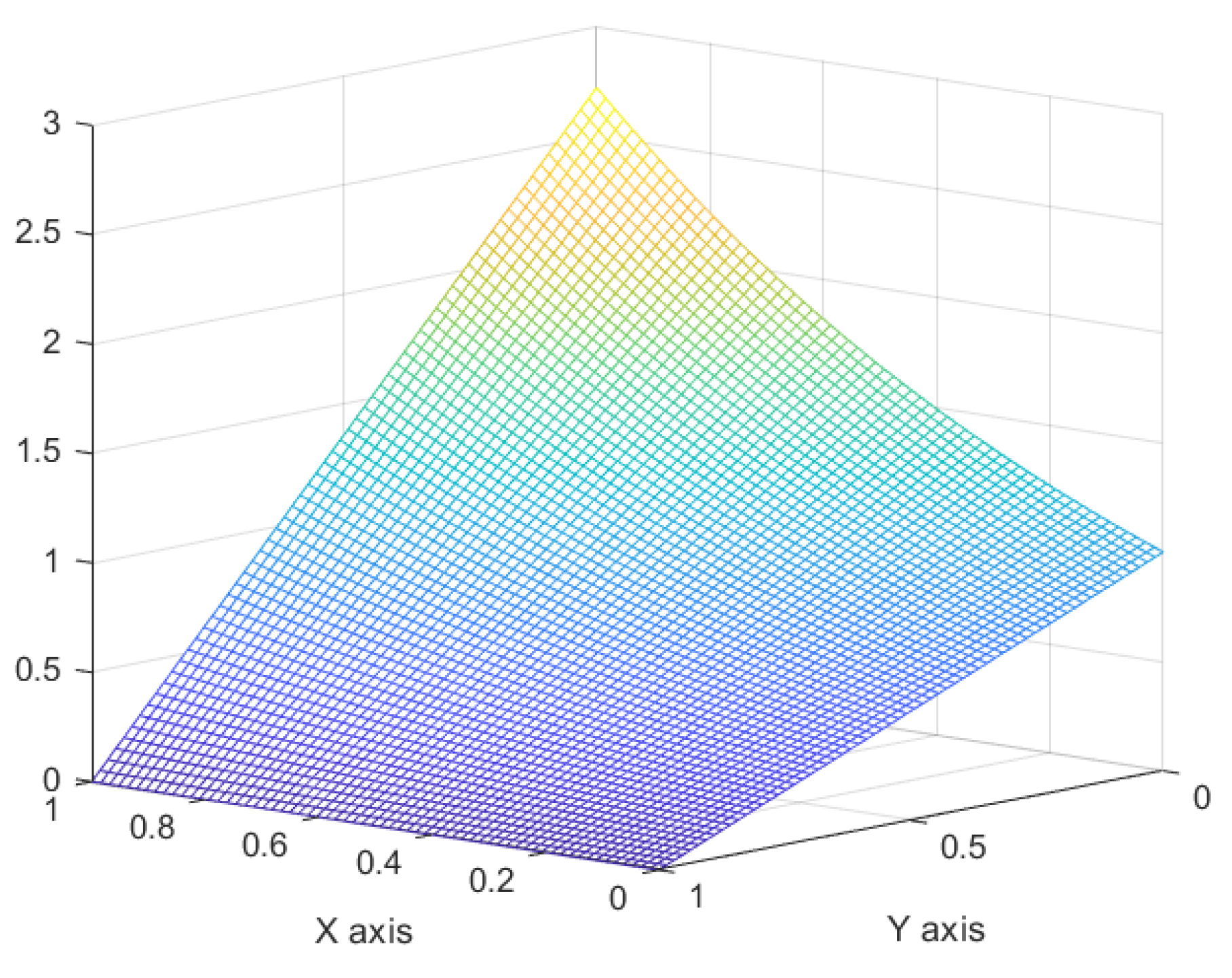
Table 1 shows a comparison of the exact and approximate solutions. For the graph of the convergence between an approximate
and the exact solution with h = 0.1, see
Figure 1. □
5. Application to Nonlinear Partial Volterra Integro-Differential Equation
An application of nonlinear partial Volterra integro-differential equation for a two-dimension with desired order:
where
is an orthogonal continuous in
with
,
is a known function, and
is the calculated function.
Following the approximate solution
, for all
. Consider the mesh nodes on the square as follows:
The two-dimensional function
is approximated with a two-dimensional Haar wavelet on
as follows:
By (
21), (
22) and (
24) in (
23), we get the linear equation
with
.
Unknown coefficients of
are achieved using Theorem 2 in [
16].
Theorem 4. Suppose a function of two variables δ and ξ is approximated by the Haar wavelet approximate given as Suppose that is known at collocation points , and F is orthogonal continuous. Then, the approximate solution of at any other point is as follows:where First, the Kernel of (21) is orthogonal continuous and the Haar wavelet of the two-dimensional approximate solution is as follows: From the above, by (21), we obtain By the Haar wavelet properties, in the following equation, we get Now, collocation points are applied in Equation (27), to get. The values satisfying Theorem 1 and applied in Equation (28) reach the following equations.
where . Equation (28) is a nonlinear system solved by either Broyden or Newton methods. The solution of the system gives at the collocation points. Theorem 4 may be used to determine the value of at points other than collocation sites. One of the methods for partial differential equations can be used to solve the equation Example 5. Consider the following partial integro-differential equation:where The exact solution of this problem is And is orthogonal continuous on , and supplementary conditions are 6. Conclusions
In this paper, we introduced the new orthogonal concept of –F–convex contraction mappings on O-CMS and proved some related fixed-point results. We have discussed a numerical experiment for approximating the fixed-point results. Finally, we obtained a simple and efficient solution for the fractional integro-differential equation by using the fixed-point technique in the setting of O-CMS.
Author Contributions
Conceptualization, A.J.G., B.R. and G.M.; writing—original draft preparation, A.J.G., B.R., G.M., O.E. and R.G.; writing—review and editing, O.E. and R.G.; validation, G.M. and O.E.; formal analysis, G.M. and O.E.; investigation, A.J.G., G.M. and O.E.; visualization, A.J.G. and B.R.; funding acquisition, R.G. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through project number PSAU/2023/01/25637.
Data Availability Statement
No data were used to support this work.
Acknowledgments
We thank the editor for their kind support. The authors are thankful to the learned reviewers for their valuable comments.
Conflicts of Interest
The authors declare that they have no competing interest.
References
- Banach, S. Sur les operations dans les ensembles abstraits et leurs applications aux equations integrales. Fundam. Math. 1992, 3, 133–181. [Google Scholar] [CrossRef]
- Cho, Y.J. Survey on metric fixed point theory and applications. In Advances in Real and Complex Ananlysis with Applications; Ruzhansky, M., Cho, Y.J., Agarwal, P., Ares, I., Eds.; Trends in Mathematics; Springer Nature: Singapore, 2017; pp. 183–241. [Google Scholar]
- Gordji, M.E.; Ramezani, M.; De La Sen, M.; Cho, Y.J. On orthogonal sets and Banach fixed point theorem. Fixed Point Theory 2017, 18, 569–578. [Google Scholar] [CrossRef]
- Wardowski, D. Fixed points of a new type of contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2012, 1, 1–6. [Google Scholar] [CrossRef]
- Mahendra Singh, Y.; Khan, M.S.; Kang, S.M. F-convex contraction via admissible mapping and related fixed point theorems with an application. Mathematics 2018, 6, 105. [Google Scholar] [CrossRef]
- Sawangsup, K.; Sintunavarat, W.; Cho, Y.J. Fixed point theorems for orthogonal F-contraction mappings on O-complete metric spaces. J. Fixed Point Theory Appl. 2020, 22, 10. [Google Scholar] [CrossRef]
- Eshaghi, M.; Habibi, H. Fixed point theory in ϵ-connected orthogonal metric space. Shand Commun. Math. Anal. (SCMA) 2019, 16, 35–46. [Google Scholar]
- Gungor, N.B.; Turkoglu, D. Fixed point theorems on orthogonal metric spaces via altering distance functions. AIP Conf. Proc. 2019, 2183, 040011. [Google Scholar]
- Yamaod, O.; Sintunavarat, W. On new orthogonal contractions in b-metric spaces. Int. J. Pure Math. 2018, 5, 37–40. [Google Scholar]
- Sawangsup, K.; Sintunavarat, W. Fixed point results for orthogonal Z-contraction mappings in O-complete metric space. Int. J. Appl. Phys. Math. 2020, 10, 33–40. [Google Scholar] [CrossRef]
- Senapati, T.; Dey, L.K.; Damjanović, B.; Chanda, A. New fixed results in orthogonal metric spaces with an Application. Kragujev. J. Math. 2018, 42, 505–516. [Google Scholar] [CrossRef]
- Gunaseelan, M.; Arul Joseph, G.; Mishra, L.N.; Mishra, V.N. Fixed point theorem for orthogonal F-suzuki contraction mapping on a O-complete metric space with an application. Malaya J. Mat. 2021, 1, 369–377. [Google Scholar]
- Beg, I.; Gunaseelan, M.; Arul Joseph, G. Fixed point of orthogonal F-suzuki contraction mapping on a O-complete b-metric space with an application. J. Funct. Spaces 2021, 2021, 6692112. [Google Scholar] [CrossRef]
- Maryam, R. Orthogonal metric space and convex contractions. Int. J. Nonlinear Anal. Appl. 2015, 6, 127–132. [Google Scholar]
- Bashir, A.; Sivasundaram, S. Some existence results for fractional integro-differential equations with nonlinear conditions. Commun. Appl. Anal. 2018, 12, 107–112. [Google Scholar]
- Aziz, I.; Siraj-ul-Islam; Khan, F. A new method based on Haar wavelet for the numerical solution of two-dimensional nonlinear integral equation. J. Comput. Appl. Math. 2014, 272, 70–80. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).