Impulsive Controllers Design for the Practical Stability Analysis of Gene Regulatory Networks with Distributed Delays

Abstract

This paper studies gene regulatory networks (GRNs) with distributed delays. The essential concept of practical stability of the genes is introduced. We investigate the problems of practical stability and global practical exponential stability of the GRN model under an impulsive control. New practical stability criteria are proposed by designing appropriate impulsive controllers via the Lyapunov functions approach. In the design of the impulsive controller, we consider the effect of impulsive perturbations at fixed times and distributed delays on the stability of the considered GRNs. Several numerical examples are also presented to justify the proposed criteria.

1. Introduction

Genetic regulatory networks (GRNs) are very important classes of biological neural networks that are used to model the complex dynamics and interactions between genes (mRNA), proteins, and small molecules in the molecular level operating of organisms. Due to the importance of such neural network models, the investigations of their qualitative properties has attracted the attention of many experts in applied mathematics, biology, neuroscience, control science, and cybernetics. Most of the researchers used different classes of differential equations as models of genetic regulatory systems [1,2,3,4,5,6,7].

Due to the fact that delay effects cannot be neglected in the qualitative analysis of GRNs, the delayed models are also intensively studied in the existing literature, including some very recent publications [8,9,10,11,12,13]. However, since the concentrations of genes and proteins depend on the properties of the regulatory function over a specified range of previous time, then it is more adequate to consider distributed and unbounded delays in GRNs. We can point out that, the research on such models is very rare [14,15]. For example, in Ref. [14] the authors proposed a robust stability analysis for the following GRN with distributed delay

$$\left\{\begin{array}{c}{\displaystyle {\dot{m}}_{\iota }=-a_{\iota }{m}_{\iota }\left(t\right)+\sum _{o=1}^N{b}_{\iota o}{\int }_{-\infty }^t{k}_o(t-h)f_0\left(p_o\left(h\right)\right)dh+J_{\iota }}\hfill \\ \\ {\displaystyle {\dot{p}}_{\iota }=-c_{\iota }{p}_{\iota }\left(t\right)+d_{\iota }{\int }_{-\infty }^t{k}_{\iota }(t-h)m_{\iota }\left(h\right)dh,}\hfill \end{array}\right.$$

(1)

where $\iota =1,2,\dots ,N$, $m_{\iota }\left(t\right)$, and $p_{\iota }\left(t\right)$ denote the gene expression level of the $\iota$-th mRNA node and $\iota$-th protein at time t, respectively, $a_{\iota }$ and $c_{\iota }$ are positive real constants that represent the degradation rates, the translation rates are represented by the positive real constants $d_{\iota }$, and $f_o$ are the regulatory functions which are of the Hill form

$${\displaystyle f_o\left(\omega \right)=\frac{{(\omega /{\beta }_o)}^{H_o}}{1+{(\omega /{\beta }_o)}^{H_o}},\iota ,o=1,2,\dots ,N,}$$

in which ${\beta }_o$ are real positive constants, $H_o$ represent the Hill coefficients, and the connecting parameters are the constants $b_{\iota o}$, given as

$$b_{\iota o}=\left\{\begin{array}{c}{\displaystyle {\alpha }_{\iota o},\mathrm{if}o\mathrm{is}\mathrm{an}\mathrm{activator}\mathrm{of}\mathrm{gene}\iota }\hfill \\ {\displaystyle -{\alpha }_{\iota o},\mathrm{if}o\mathrm{is}\mathrm{a}\mathrm{repressor}\mathrm{of}\mathrm{gene}\iota }\hfill \\ {\displaystyle 0,\mathrm{if}\mathrm{there}\mathrm{is}\mathrm{no}\mathrm{link}\mathrm{between}\mathrm{the}\mathrm{node}o}\hfill \\ \mathrm{and}\mathrm{the}\mathrm{gene}\iota ,\hfill \end{array}\right.$$

the basal level of the repressor of gene $\iota$ is denoted as $J_{\iota }$ and $J_{\iota }={\sum }_{o\in I_{\iota }}{\alpha }_{\iota o}$, $I_{\iota }$ is the collection of all the o, which are repressors of the gene $\iota$, and $k_o$ is the delay kernel.

In addition, impulsive perturbations can affect the qualitative behavior in GRNs. In fact, GRN systems are very often subjected to short-term environmental changes at some instants that affect the mRNA molecules and proteins concentrations. Hence, it is natural to include impulsive conditions in the GRN models, and to study their effect on the behavior and properties of the impulsively generalized models. It already well acclaimed that the impulsive differential equations are used as a best formalism to describe processes with abrupt changes during their evolution [16,17,18].

Using the theory of impulsive differential equations, several impulsive GRNs have been proposed and their dynamical properties have been studied. For example, in Ref. [19] the authors applied the method of Lyapunov functions to study the finite-time stability of GRNs with impulsive effects. The paper [20] offered a methodology for analyzing the asymptotic stability of a genetic network under impulsive control. Using the Lyapunov method and linear matrix inequalities, the authors in Ref. [21] investigated the asymptotic stability of delayed stochastic GRNs with impulses. Ref. [22] studied the asymptotic stability of GRNs under impulse control using the direct Lyapunov method. In Ref. [23] an impulsive control law for fractional-order neural GRNs has been proposed and the Mittag–Leffler stability behavior was investigated under the designed impulsive controller. The existence of almost periodic solutions to impulsive fractional GRN models with reaction-diffusion terms is investigated in Ref. [24].

In addition, to avoid unwanted behavior of the states, different control methodologies are applied to some classes of GRNs [25,26]. The type of control strategy called impulsive control, in which the control signals are input into a system only at some time instants, has been efficiently used in population control, ecosystem control, neuronal dynamics control, and other fields [27,28,29,30,31,32]. The advantages in using impulsive controllers in stability and stabilization of systems are also very well known [33,34].

As the authors of Ref. [20] pointed out, the stability behavior of genetic networks is essential in the understanding of the living organism at both molecular and cellular levels. That is why the stability properties of the proposed impulsive models of GRNs are the most investigated qualitative properties. However, in all existing papers, the results on asymptotic and finite-time stability properties are established [10,19,20,21,22,23].

However, from the applied point of view, another extended stability concept is more appropriate. In numerous phenomena, where the model is asymptotically stable or finite-time stable, but is useless in practice, the concept of practical stability is suitable [35]. In such cases the trajectories of the model oscillate sufficiently close to a state of interest. The practical stability notion is used by numerous researchers in the study of applied models and interesting results have been obtained in Refs. [36,37,38,39,40,41,42,43,44,45,46,47,48]. However, despite the superiority of this concept it is not yet introduced to GRNs, and the aim of this paper is to fill the gap.

In this paper, prompted by the above analysis, we design an impulsive control strategy to a GRN model with distributed delay. We propose the practical stability concept to the model and adapt the definitions of practical stability and global practical exponential stability. Then, we apply the Lyapunov methodology to analyze the practically stable behavior of the system under the impulsive control. Indeed, the direct method of Lyapunov is a very powerful mechanism in the study of the qualitative properties of applied mathematical models, including GRNs [19,21,22,23]. The main contributions of our paper are:

(1)

Distributed delays are considered in our GRN model, which makes it more adequate to a real system;

(2)

We introduce the extended notion of practical stability to the GRN system which is justifiable due to some economic and social factors and is applicable when the classical strategies do not allow a mathematically ideal stable behavior;

(3)

An appropriate impulsive control scheme is designed for the practically stable behavior of the genes which allows control signals to be applied only at some fixed time instants;

(4)

By the use of the Lyapunov function methodology and inequality techniques several new sufficient practical stability criteria based on the impulsive control law are provided;

(5)

Numerical examples are presented to demonstrate the strength of the derived criteria.

The content of the paper is constructed according to the following plan. In Section 2 the impulsive control model of GRNs is introduced and some preliminary results are reported. The notion of practical stability is adapted for the proposed model. Some fundamentals related to the Lyapunov method are also presented. In Section 3, the Lyapunov technique is applied to establish the main impulsive control results on the practical stability. Different criteria are proposed using different metrics. Several numerical examples are discussed in Section 4.

2. The Impulsive GRN Model—Preliminaries

Before we propose the impulsive GRN model, we will define some notations. The state space for the system featuring in the present research is ${\mathbb{R}}^N\times {\mathbb{R}}^N$, where ${\mathbb{R}}^N$ is the Euclidean N-dimensional space. We will use the norm of an $m={(m_1,m_2,\dots ,m_N)}^T\in {\mathbb{R}}^N$ defined by ${\displaystyle ||m||=\sum _{\iota =1}^N|m_{\iota }|}$.

Let the impulsive instants ${\tau }_1,{\tau }_2,\dots$ such that $0<{\tau }_1<{\tau }_2<\dots$ and ${\lim }_{l\to \infty }{\tau }_l=\infty$. We propose the following impulsive control GRN model with distributed delays:

$$\left\{\begin{array}{c}{\displaystyle {\dot{\overline{m}}}_{\iota }=-a_{\iota }{\overline{m}}_{\iota }\left(t\right)+\sum _{o=1}^N{b}_{\iota o}{\int }_{-\infty }^t{k}_o(t-h)f_o\left({\overline{p}}_o\left(h\right)\right)dh+J_{\iota },t\ne {\tau }_l,}\hfill \\ {\displaystyle {\dot{\overline{p}}}_{\iota }=-c_{\iota }{\overline{p}}_{\iota }\left(t\right)+d_{\iota }{\int }_{-\infty }^t{k}_{\iota }(t-h){\overline{m}}_{\iota }\left(h\right)dh,t\ne {\tau }_l,}\hfill \\ \\ {\overline{m}}_{\iota }\left({\tau }_l^{+}\right)={\overline{m}}_{\iota }\left({\tau }_l\right)+M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right),\hfill \\ {\overline{p}}_{\iota }\left({\tau }_l^{+}\right)={\overline{p}}_{\iota }\left({\tau }_l\right)+P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right),\hfill \end{array}\right.$$

(2)

where $t\ge 0$, $\iota =1,2,\dots ,N$, ${\overline{m}}_{\iota }\left({\tau }_l\right)={\overline{m}}_{\iota }\left({\tau }_l^{-}\right)$ and ${\overline{p}}_{\iota }\left({\tau }_l\right)={\overline{p}}_{\iota }\left({\tau }_l^{-}\right)$ denote the gene expression level of $\iota$-th mRNA molecule and $\iota$-th protein at time ${\tau }_l$ before the impulsive controller to be applied, respectively, and ${\overline{m}}_{\iota }\left({\tau }_l^{+}\right)$ and ${\overline{p}}_{\iota }\left({\tau }_l^{+}\right)$ denote the concentration of the $\iota$-th mRNA molecule and $\iota$-th protein, respectively at ${\tau }_l^{+}$, i.e., after the application of the impulsive control law at ${\tau }_l$, the impulsive functions $M_{\iota l}$ and $P_{\iota l}$ represent the abrupt variations in ${\overline{m}}_{\iota }\left(t\right)$ and ${\overline{p}}_{\iota }\left(t\right)$, respectively, at ${\tau }_l$, i.e., $\Delta \left({\overline{m}}_{\iota }\left({\tau }_l\right)\right)={\overline{m}}_{\iota }\left({\tau }_l^{+}\right)-{\overline{m}}_{\iota }\left({\tau }_l\right)=M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right)$ and $\Delta \left({\overline{p}}_{\iota }\left({\tau }_l\right)\right)={\overline{p}}_{\iota }\left({\tau }_l^{+}\right)-{\overline{p}}_{\iota }\left({\tau }_l\right)=P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right)$, $\iota =1,2,\dots ,N,l=1,2,\dots$.

For the model (2), we introduce a class of initial functions $\mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N],$ which are bounded, piecewise continuous on $(-\infty ,0]$ with points of jump discontinuities at which the one-sided limits exist and the functions are continuous from the left. We will denote the norm of a function $\overline{\varphi }\in \mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N]$ that corresponds to the norm $||·||$ by

$$||\overline{\varphi }{||}_{\infty }=\underset{\upsilon \in (-\infty ,0]}{\sup }||\overline{\varphi }\left(\upsilon \right)||.$$

Let $\overline{\varphi },\overline{\phi }\in \mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N]$. The initial conditions for the model (2) are of the type

$$\left\{\begin{array}{c}{\overline{m}}_{\iota }(\upsilon ;0,\overline{\varphi })={\overline{\varphi }}_{\iota }\left(\upsilon \right),-\infty <\upsilon \le 0,\hfill \\ {\overline{p}}_{\iota }(\upsilon ;0,\overline{\phi })={\overline{\phi }}_{\iota }\left(\upsilon \right),-\infty <\upsilon \le 0,\hfill \\ {\overline{m}}_{\iota }(0^{+};0,\overline{\varphi })={\overline{\varphi }}_{\iota }\left(0\right),{\overline{p}}_{\iota }(0^{+};0,\overline{\phi })={\overline{\phi }}_{\iota }\left(0\right),\hfill \end{array}\right.$$

(3)

$\iota =1,2,\dots ,N,$ where $m_{\iota }(0^{+};0,\overline{\varphi })$ and $p_{\iota }(0^{+};0,\overline{\phi })$ are the right-hand side limits at $t=0$.

The following assumptions for the introduced impulsive control GRN will be essential in our analysis:

A1.

For all $o=1,2,\dots ,N$ and any $w,\overline{w}\in \mathbb{R}$, $w\ne \overline{w}$ there exist constants $f_o^L$ such that the activation functions $f_o$ are bounded and satisfy

$$0\le \frac{f_o\left(w\right)-f_o\left(\overline{w}\right)}{w-\overline{w}}\le f_o^L.$$

A2.

The following inequality holds for the nonnegative continuous delay kernel functions defined on $\mathbb{R}$

$${\int }_{-\infty }^t{k}_o\left(h\right)dh\le {\kappa }_o$$

for some positive constants ${\kappa }_o$ and all $o=1,2,\dots ,N$.

A3.

The functions $M_{\iota l}$ and $P_{\iota l}$ are continuous on $\mathbb{R}$, $\iota =1,2,\dots ,N$, $l=1,2,\dots .$

The main goal of this paper is to derive practical stability criteria for the impulsive control GRN model (2). To do this, we will adopt the following definition from [18,35].

Definition 1.

The impulsive control GRN model (2) is:

(a) 

$(\eta ,H)$-practically stable, if given $(\eta ,H)$ with $0<\eta <H$, we have $||\overline{\varphi }{||}_{\infty }+||\overline{\phi }{||}_{\infty }\le \eta$ implies $||\overline{m}\left(t\right)||+||\overline{p}\left(t\right)||\le H,t\ge 0$;

(b) 

globally practically exponentially stable, if for all $\overline{\varphi },\overline{\phi }\in \mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N]$ there exist constants $\mu \ge 0$, $\mathrm{\Theta }>0$ and $H>0$ such that

$$||\overline{m}\left(t\right)||+||\overline{p}\left(t\right)||\le \mathrm{\Theta }(||\overline{\varphi }{||}_{\infty }+||\overline{\phi }{||}_{\infty })e^{-\mu t}+H$$

for $t\ge 0$.

Remark 1.

Definition 1(a) shows that the notions of practical stability and Lyapunov stability are different. The Lyapunov stability of a systems does not imply its practical stability and vice versa. In addition, as we can see from part (b) of Definition 1, in some cases for $H=0$ the global practical exponential stability may imply global exponential stability [47].

Let $\varphi ,\phi \in \mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N]$ be initial functions corresponding to the state vectors $m,p\in {\mathbb{R}}^N$ of the GRN system (1), and denote

$${\varphi }_{\iota }^m\left(\xi \right)={\overline{\varphi }}_{\iota }\left(\xi \right)-{\varphi }_{\iota }\left(\xi \right),\xi \in (-\infty ,0],$$

$${\phi }_{\iota }^p\left(\xi \right)={\overline{\phi }}_{\iota }\left(\xi \right)-{\phi }_{\iota }\left(\xi \right),\xi \in (-\infty ,0],$$

$${\tilde{m}}_{\iota }\left(t\right)={\overline{m}}_{\iota }\left(t\right)-m_{\iota }\left(t\right),t\ge 0,$$

$${\tilde{p}}_{\iota }\left(t\right)={\overline{p}}_i\left(t\right)-p_{\iota }\left(t\right),t\ge 0,$$

$\iota =1,2,\dots ,N.$

The impulsive controllers in (2) will be defined as

$$\begin{array}{c}{M}_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right)=U_{\iota l}^m({\overline{m}}_{\iota }\left({\tau }_l\right)-m_{\iota }\left({\tau }_l\right)),\hfill \\ P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right)=U_{\iota l}^p({\overline{p}}_{\iota }\left({\tau }_l\right)-p_{\iota }\left({\tau }_l\right)),\hfill \\ \iota =1,2,\dots ,N,l=1,2,\dots ,\hfill \end{array}$$

(4)

where $U_{\iota l}^m$ and $U_{\iota l}^p$ are well defined functions to guarantee the existence of solutions of the model (2) and the corresponding error system.

Then, the error system is

$$\left\{\begin{array}{c}{\displaystyle {\dot{\tilde{m}}}_{\iota }\left(t\right)=-a_{\iota }{\tilde{m}}_{\iota }\left(t\right)+\sum _{o=1}^N{b}_{\iota o}{\int }_{-\infty }^t{k}_o(t-h)g_o\left({\tilde{p}}_o\left(h\right)\right)dh,t\ne {\tau }_l,}\hfill \\ {\displaystyle {\dot{\tilde{p}}}_i\left(t\right)=-c_i{\tilde{p}}_i\left(t\right)+d_{\iota }{\int }_{-\infty }^t{k}_{\iota }(t-h){\tilde{m}}_{\iota }\left(h\right)dh,t\ne {\tau }_l,}\hfill \\ \\ {\tilde{m}}_{\iota }\left({\tau }_l^{+}\right)={\tilde{m}}_{\iota }\left({\tau }_l\right)+U_{\iota l}^m\left({\tilde{m}}_{\iota }\left({\tau }_l\right)\right),\hfill \\ {\tilde{p}}_{\iota }\left({\tau }_l^{+}\right)={\tilde{p}}_{\iota }\left({\tau }_l\right)+U_{\iota l}^p\left({\tilde{p}}_{\iota }\left({\tau }_l\right)\right),\hfill \end{array}\right.$$

(5)

where $g_o\left({\tilde{p}}_o\left(t\right)\right)=f_o({\tilde{p}}_o\left(t\right)+p_o\left(t\right))-f_o\left(p_o\left(t\right)\right)$, $t\ge 0$, $U_{\iota l}^m\left(0\right)=0$, $U_{\iota l}^p\left(0\right)=0$, $\iota ,o=1,2,\dots ,N$, $l=1,2,\dots$.

Remark 2.

As defined by Definition 1, the practical stability concepts for the impulsive control GRN system (2) can also be applied in the study of the practical synchronization between the GRN model (1) and the impulsive control model (2) or to practical stability of the solution ${(\tilde{m}\left(t\right)+m\left(t\right),\tilde{p}\left(t\right)+p\left(t\right))}^T$ of the error system (5). Hence, the impulses can be used to practically stabilize the behavior of the GRN model (1).

Since we will study an impulsive control system, we will use the method of piecewise continuous Lyapunov functions $L:[0,\infty )\times {\mathbb{R}}^{2N}\to [0,\infty )$ in our practical stability analysis [17,18,23].

Let ${{\rm Y}}_l=({\tau }_{l-1},{\tau }_l)\times {\mathbb{R}}^{2N},l=1,2,\dots ,$${\tau }_0=0$, ${\displaystyle {\rm Y}=\bigcup _{l=1}^{\infty }{{\rm Y}}_l}$.

Definition 2.

A function $L:[0,\infty )\times {\mathbb{R}}^{2N}\to [0,\infty )$ belongs to the class ${\mathcal{L}}_0$ if it satisfies the following conditions:

1. 

The function L is continuous on ${\displaystyle \bigcup _{l=1}^{\infty }{{\rm Y}}_l}$ and $L(t,0,0)=0$ for $t\ge 0$;

2. 

On each of the sets ${{\rm Y}}_l$ the function L is locally Lipschitz continuous on the variables $(m,p)$;

3. 

There exist the finite limits

$$L({\tau }_l^{-},m,p)=\underset{\genfrac{}{}{0pt}{}{t\to {\tau }_l}{t<{\tau }_l}}{\lim }L(t,m,p),L({\tau }_l^{+},m,p)=\underset{\genfrac{}{}{0pt}{}{t\to {\tau }_l}{t>{\tau }_l}}{\lim }L(t,m,p)$$

and

$$L({\tau }_l^{-},m,p)=L({\tau }_l,m,p)$$

for each $l=1,2,\dots$.

For the upper right-hand Dini derivatives of the Lyapunov functions of the class ${\mathcal{L}}_0$ with respect to the system (2) we will use the following definition.

Definition 3.

Given a function $L\in {\mathcal{L}}_0$. For $\overline{\varphi },\overline{\phi }\in \mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N]$ the upper right-hand derivative of L with respect to the system (2) is defined by

$$D_{\left(2\right)}^{+}L(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right))$$

$${\displaystyle =\underset{s\to 0^{+}}{\lim }\sup \frac{1}{s}[L(t+s,\overline{m}(t+s;0,\overline{\varphi }),\overline{p}(t+s;0,\overline{\phi }))-L(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right))],}$$

where ${(\overline{m}(t;0,\overline{\varphi }),\overline{p}(t;0,\overline{\phi }))}^T$ is the state of (2) with $\overline{\varphi },\overline{\phi }\in \mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N]$.

The following result from Ref. [18] will also be used.

Lemma 1.

Assume that the Lyapunov function $L\in {\mathcal{L}}_0$ is such that for $\overline{\varphi },\overline{\phi }\in \mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N]$ and $t\ge 0$:

(i) 

$L(t^{+},\overline{\varphi }\left(0\right)+\Delta \left(\overline{\varphi }\right),\overline{\phi }\left(0\right)+\Delta \left(\overline{\phi }\right))\le L(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right)),t={\tau }_l,l=1,2,\dots$;

(ii) 

For $\mu ,\rho \ge 0$, the inequality

$$D_{\left(2\right)}^{+}L(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right))\le -\mu L(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right))+\rho ,t\ne {\tau }_l$$

is satisfied whenever

$$L(t+\upsilon ,\overline{\varphi }\left(\upsilon \right),\overline{\phi }\left(\upsilon \right))\le L(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right)),-\infty <\upsilon \le 0.$$

(6)

Then,

$${\displaystyle L(t,\overline{m}(t;0,\overline{\varphi }),\overline{p}(t;0,\overline{\phi }))\le \underset{-\infty <\upsilon \le 0}{\sup }L(0,\overline{\varphi }\left(\upsilon \right),\overline{\phi }\left(\upsilon \right))e^{-\mu t}+{\rho }_1,t\ge 0,}$$

where ${\rho }_1={\sup }_{t\ge 0}\rho t{e}^{-\mu t}$.

Remark 3.

Lemma 1 and related comparison lemmas with the Razumikhin condition (6) are widely used in the investigation of the stability properties of different classes of delayed differential systems [14,18,27,29,32,35].

3. Main Practical Stability Results

In this section we will prove practical stability criteria for the impulsive control GRN system (2) using the Lyapunov approach.

We will begin with a $(\eta ,H)$-practical stability result.

Theorem 1.

Assume that $0<\eta <H$, conditions A1–A3 hold, and the parameters and the impulsive control functions of the impulsive GRN (2) satisfy:

(i) 

$$\underset{1\le \iota \le N}{\min }\{a_{\iota },c_{\iota }\}-\underset{1\le \iota \le N}{\max }\{d_{\iota }{\kappa }_{\iota },\sum _{o=1}^N|b_{o\iota }|{\kappa }_{\iota }{f}_{\iota }^L\}>0;$$

(ii) 

$$J_{\iota }=0,\iota =1,2,\dots ,N;$$

(iii) 

$$U_{\iota l}^m({\overline{m}}_{\iota }\left({\tau }_l\right)-m_{\iota }\left({\tau }_l\right))=-{\gamma }_{\iota l}^m{\overline{m}}_{\iota }\left({\tau }_l\right),0<{\gamma }_{\iota l}^m<2,$$

$$U_{\iota l}^p({\overline{p}}_{\iota }\left({\tau }_l\right)-p_{\iota }\left({\tau }_l\right))=-{\gamma }_{\iota l}^p{\overline{p}}_{\iota }\left({\tau }_l\right),0<{\gamma }_{\iota l}^p<2,$$

$\iota =1,2,\dots ,N,l=1,2,\dots .$

Then, the impulsive control GRN (2) is $(\eta ,H)$-practically stable.

Proof. 

For $0<\eta <H$ and $\overline{\varphi },\overline{\phi }\in \mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N]$ let suppose $||\overline{\varphi }{||}_{\infty }+||\overline{\phi }{||}_{\infty }\le \eta$.

Based on the designed impulsive control system (2) and the practical stability concept, we consider a Lyapunov function defined as

$$\begin{array}{c}{\displaystyle L_1(t,\overline{m},\overline{p})=||\overline{m}\left(t\right)||+||\overline{p}\left(t\right)||=\sum _{\iota =1}^N|{\overline{m}}_{\iota }\left(t\right)|+\sum _{\iota =1}^n|{\overline{p}}_{\iota }\left(t\right)|.}\hfill \end{array}$$

(7)

Using A3 and condition (iii) of Theorem 1, at the impulsive control instants $t={\tau }_l$, $l=1,2,\dots$, we have:

$${\displaystyle L_1({\tau }_l^{+},\overline{m}\left({\tau }_l^{+}\right),\overline{p}\left({\tau }_l^{+}\right))}$$

$$=\sum _{\iota =1}^N|{\overline{m}}_{\iota }\left({\tau }_l\right)+M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right)|+\sum _{\iota =1}^N|{\overline{p}}_{\iota }\left({\tau }_l\right)+P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right)|$$

$${\displaystyle \le \sum _{\iota =1}^N|1-{\gamma }_{\iota l}^m||{\overline{m}}_{\iota }\left({\tau }_l\right)|+\sum _{\iota =1}^N|1-{\gamma }_{\iota l}^p||{\overline{p}}_{\iota }\left({\tau }_l\right)|}$$

$${\displaystyle <\sum _{\iota =1}^N|{\overline{m}}_{\iota }\left({\tau }_l\right)|+\sum _{\iota =1}^N|{\overline{p}}_{\iota }\left({\tau }_l\right)|=L_1({\tau }_l,\overline{m}\left({\tau }_l\right),\overline{p}\left({\tau }_l\right)),}$$

or

$$L_1(t^{+},\overline{\varphi }\left(0\right)+\Delta \left(\overline{\varphi }\right),\overline{\phi }\left(0\right)+\Delta \left(\overline{\phi }\right))\le L_1(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right)),t={\tau }_l,l=1,2,\dots .$$

(8)

From A1, A2, and conditions (i), (ii) of Theorem 1, we obtain:

$${\dot{L}}_1(t,\overline{m}\left(t\right),\overline{p}\left(t\right))$$

$${\displaystyle \le \sum _{\iota =1}^N\left[-a_{\iota }|{\overline{m}}_{\iota }\left(t\right)|+\sum _{o=1}^N|b_{ij}|f_o^L{\kappa }_o\underset{-\infty <\upsilon \le 0}{\sup }|{\overline{p}}_o\left(\upsilon \right)|\right]}$$

$$+\sum _{\iota =1}^N\left[-c_{\iota }|{\overline{p}}_{\iota }\left(t\right)|+d_{\iota }{\kappa }_{\iota }\underset{-\infty <\upsilon \le 0}{\sup }|{\overline{m}}_{\iota }\left(\upsilon \right)|\right]$$

$$\le -\underset{1\le \iota \le N}{\min }\{a_{\iota },c_{\iota }\}{L}_1(t,\overline{m}\left(t\right),\overline{p}\left(t\right))$$

(9)

$$+\underset{1\le \iota \le N}{\max }\{d_{\iota }{\kappa }_{\iota },\sum _{o=1}^N|b_{o\iota }|{\kappa }_{\iota }{f}_{\iota }^L\}\underset{-\infty <\upsilon \le 0}{\sup }{L}_1(t+\upsilon ,\overline{m}\left(\upsilon \right),\overline{p}\left(\upsilon \right))$$

or for $\overline{\varphi },\overline{\phi }\in \mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N]$ such that $L_1(t+\upsilon ,\overline{\varphi }\left(\upsilon \right),\overline{\phi }\left(\upsilon \right))\le L_1(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right)),-\infty <\upsilon \le 0,$ the inequality

$$D_{\left(2\right)}^{+}{L}_1(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right))\le 0,t\ne {\tau }_l$$

(10)

is satisfied.

Then, from (8) and (10), according to Lemma 1 for $\mu =\rho =0$, we have

$${\displaystyle L_1(t,\overline{m}(t;0,\overline{\varphi }),\overline{p}(t;0,\overline{\phi }))\le \underset{-\infty <\upsilon \le 0}{\sup }{L}_1(0,\overline{\varphi }\left(\upsilon \right),\overline{\phi }\left(\upsilon \right)),t\ge 0.}$$

Therefore, for $t\ge 0$

$$||\overline{m}\left(t\right)||+||\overline{p}\left(t\right)||\le ||\overline{\varphi }{||}_{\infty }+||\overline{\phi }{||}_{\infty }\le \eta <H$$

and the impulsive control GRN (2) is $(\eta ,H)$-practically stable. □

In the next, we will propose criteria for the global practical exponential stability of the impulsive control GRN system (2).

Theorem 2.

Assume that $H>0$, conditions A1–A3 and (iii) of Theorem 1 hold, and conditions (i) and (ii) in Theorem 1 are replaced by:

$\left(i^{*}\right)$

∃$\mu >0$ such that

$$\underset{1\le \iota \le N}{\min }\{a_{\iota },c_{\iota }\}-\underset{1\le \iota \le N}{\max }\{d_{\iota }{\kappa }_{\iota },\sum _{o=1}^N|b_{o\iota }|{\kappa }_{\iota }{f}_{\iota }^L\}\ge \mu ;$$

$\left(i{i}^{*}\right)$

∃$\rho \ge 0$ such that

$$\sum _{\iota =1}^N|J_i|<\rho ,\underset{t\ge 0}{\sup }\rho t{e}^{-\mu t}=H,$$

then the impulsive control GRN (2) is globally practically exponentially stable.

Proof. 

Let $H>0$. Consider again the Lyapunov function $L_1(t,\overline{m},\overline{p})$ defined by (7).

From A1, A2, and conditions $\left(i^{*}\right)$, $\left(i{i}^{*}\right)$ of Theorem 2, we have that for $t\ne {\tau }_l$, $\overline{\varphi },\overline{\phi }\in \mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N]$ such that $L_1(t+\upsilon ,\overline{\varphi }\left(\upsilon \right),\overline{\phi }\left(\upsilon \right))\le L_1(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right)),-\infty <\upsilon \le 0,$ the inequality

$$D_{\left(2\right)}^{+}{L}_1(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right))\le -\mu L_1(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right))+\rho$$

(11)

is satisfied.

Then, from (8), (11) and Lemma 1, we obtain

$$L_1(t,\overline{m}(t;0,\overline{\varphi }),\overline{p}(t;0,\overline{\phi }))$$

$${\displaystyle \le \underset{-\infty <\upsilon \le 0}{\sup }{L}_1(0,\overline{\varphi }\left(\upsilon \right),\overline{\phi }\left(\upsilon \right))e^{-\mu t}+H,t\ge 0.}$$

Therefore, for any $\mathrm{\Theta }\ge 1$, we have

$$||\overline{m}\left(t\right)||+||\overline{p}\left(t\right)||\le \mathrm{\Theta }(||\overline{\varphi }{||}_{\infty }+||\overline{\phi }{||}_{\infty })e^{-\mu t}+H$$

for $t\ge 0$, which proves the global practical exponential stability of the impulsive control GRN system (2). □

Remark 4.

Due to its advantages, the practical stability notion has been studied for numerous applied systems [36,37,38,39,41,42,45,46,48]. The recent results on practical stability of neural network models is a further evidence of its remarkable importance for such models [40,43,44,47]. The problem of applying it to GRN models deserves our attention, which was realized in Theorems 1 and 2.

Remark 5.

In addition, since the practical stability concept is useful in many biological systems when the dynamic of the model is contained within particular bounds, the presented result can be extended to different biological systems.

In Theorems 1 and 2 we used the norm of $(m,p)={(m_1,m_2,\dots ,m_N,p_1,p_2,\dots ,p_N)}^T\in {\mathbb{R}}^{2N}$ defined by

$${||(m,p)||}_1=||m||+||p||=\sum _{\iota =1}^N|m_{\iota }|+\sum _{\iota =1}^N|p_{\iota }|.$$

In the next result in order to provide global practical exponential stability of the impulsive control GRN system (2) we will consider the norm of a vector $(m,p)\in {\mathbb{R}}^{2N}$ given as

$${||(m,p)||}_2=\sqrt{{\displaystyle \sum _{\iota =1}^N|m_{\iota }{|}^2+\sum _{\iota =1}^N{|p_{\iota }|}^2}}.$$

Theorem 3.

Assume that $H>0$, conditions A1–A3, (ii), (iii) of Theorem 1 hold, and the parameters of the impulsive controlled GRN (2) satisfy:

$$\begin{array}{c}\underset{1\le \iota \le N}{\min }\{2a_{\iota }-\sum _{o=1}^N|b_{\iota o}|{\kappa }_o{f}_o^L,2c_{\iota }-d_{\iota }{\kappa }_{\iota }\}\hfill \\ \\ -\underset{1\le \iota \le N}{\max }\{d_{\iota }{\kappa }_{\iota },\sum _{o=1}^N|b_{ji}|{\kappa }_{\iota }{f}_{\iota }^L\}\ge \mu >0.\hfill \end{array}$$

(12)

Then, the impulsive control GRN (2) is globally practically exponentially stable.

Proof. 

For $\overline{\varphi },\overline{\phi }\in \mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N]$ we define

$$||(\overline{\varphi },\overline{\phi }){||}_{2\infty }=\underset{\upsilon \in (-\infty ,0]}{\sup }||(\overline{\varphi }\left(\upsilon \right),\overline{\phi }\left(\upsilon \right)){||}_2$$

and the Lyapunov function

$${\displaystyle L_2(t,\overline{m},\overline{p})=\sum _{\iota =1}^N|{\overline{m}}_{\iota }\left(t\right){|}^2+\sum _{\iota =1}^n{|{\overline{p}}_{\iota }\left(t\right)|}^2.}$$

(13)

Using A3 and condition (iii) of Theorem 1, at the impulsive control instants $t={\tau }_l$, $l=1,2,\dots$, we have:

$${\displaystyle L_2({\tau }_l^{+},\overline{m}\left({\tau }_l^{+}\right),\overline{p}\left({\tau }_l^{+}\right))}$$

$$=\sum _{\iota =1}^N|{\overline{m}}_{\iota }\left({\tau }_l\right)+M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right){|}^2+\sum _{\iota =1}^N{|{\overline{p}}_{\iota }\left({\tau }_l\right)+P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right)|}^2$$

$${\displaystyle \le \sum _{\iota =1}^N|1-{\gamma }_{\iota l}^m{|}^2|{\overline{m}}_{\iota }\left({\tau }_l\right){|}^2+\sum _{\iota =1}^N|1-{\gamma }_{\iota l}^p{|}^2{|{\overline{p}}_{\iota }\left({\tau }_l\right)|}^2}$$

$${\displaystyle <\sum _{\iota =1}^N|{\overline{m}}_{\iota }\left({\tau }_l\right){|}^2+\sum _{\iota =1}^N{|{\overline{p}}_{\iota }\left({\tau }_l\right)|}^2=L_2({\tau }_l,\overline{m}\left({\tau }_l\right),\overline{p}\left({\tau }_l\right)),}$$

or

$$L_2(t^{+},\overline{\varphi }\left(0\right)+\Delta \left(\overline{\varphi }\right),\overline{\phi }\left(0\right)+\Delta \left(\overline{\phi }\right))$$

$$\le L_2(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right)),t={\tau }_l,l=1,2,\dots .$$

(14)

From A1, A2, and condition (ii) of Theorem 1, we get:

$${\dot{L}}_2(t,\overline{m}\left(t\right),\overline{p}\left(t\right))$$

$${\displaystyle \le \sum _{\iota =1}^N\left[-2a_{\iota }|{\overline{m}}_{\iota }{\left(t\right)|}^2+2\sum _{o=1}^N|b_{\iota o}|f_o^L{\kappa }_o\underset{-\infty <\upsilon \le 0}{\sup }|{\overline{p}}_o\left(\upsilon \right)||{\overline{m}}_{\iota }\left(t\right)|\right]}$$

$$+\sum _{\iota =1}^N\left[-2c_{\iota }|{\overline{p}}_{\iota }{\left(t\right)|}^2+2d_{\iota }{\kappa }_{\iota }\underset{-\infty <\upsilon \le 0}{\sup }|{\overline{m}}_{\iota }\left(\upsilon \right)||{\overline{p}}_{\iota }\left(t\right)|\right]$$

$${\displaystyle \le \sum _{\iota =1}^N\left[-2a_{\iota }|{\overline{m}}_{\iota }{\left(t\right)|}^2+\sum _{o=1}^N|b_{\iota o}|f_o^L{\kappa }_o(\underset{-\infty <\upsilon \le 0}{\sup }|{\overline{p}}_o{\left(\upsilon \right)|}^2+|{\overline{m}}_{\iota }\left(t\right){|}^2)\right]}$$

$$+\sum _{\iota =1}^N\left[-2c_{\iota }|{\overline{p}}_{\iota }{\left(t\right)|}^2+d_{\iota }{\kappa }_{\iota }(\underset{-\infty <\upsilon \le 0}{\sup }|{\overline{m}}_{\iota }{\left(\upsilon \right)|}^2+|{\overline{p}}_{\iota }\left(t\right){|}^2)\right]$$

$$\le -\underset{1\le \iota \le N}{\min }\{2a_{\iota }-\sum _{o=1}^N|b_{\iota o}|{\kappa }_o{f}_o^L,2c_{\iota }-d_{\iota }{\kappa }_{\iota }\}{L}_2(t,\overline{m}\left(t\right),\overline{p}\left(t\right))$$

$$+\underset{1\le \iota \le N}{\max }\{d_{\iota }{\kappa }_{\iota },\sum _{o=1}^N|b_{o\iota }|{\kappa }_{\iota }{f}_{\iota }^L\}\underset{-\infty <\upsilon \le 0}{\sup }{L}_2(t+\upsilon ,\overline{m}\left(\upsilon \right),\overline{p}\left(\upsilon \right)).$$

Condition (12) implies that the inequality

$$D_{\left(2\right)}^{+}{L}_2(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right))\le -\mu L_2(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right)),t\ne {\tau }_l$$

(15)

is valid if $L_2(t+\upsilon ,\overline{\varphi }\left(\upsilon \right),\overline{\phi }\left(\upsilon \right))\le L_2(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right)),-\infty <\upsilon \le 0.$

Then, from (14), (16), and Lemma 1, we obtain

$$L_2(t,\overline{m}(t;0,\overline{\varphi }),\overline{p}(t;0,\overline{\phi }))$$

$${\displaystyle \le \underset{-\infty <\upsilon \le 0}{\sup }{L}_2(0,\overline{\varphi }\left(\upsilon \right),\overline{\phi }\left(\upsilon \right))e^{-\mu t},t\ge 0.}$$

Therefore, for any $\mathrm{\Theta }\ge 1$, we have

$$||(\overline{m}\left(t\right),\overline{p}\left(t\right)){||}_2^2\le \mathrm{\Theta }||(\overline{\varphi },\overline{\phi }){||}_{2\infty }^2{e}^{-\mu t}$$

for $t\ge 0$.

So, for any $H>0$

$$||(\overline{m}\left(t\right),\overline{p}\left(t\right)){||}_2\le \sqrt{\mathrm{\Theta }}||(\overline{\varphi },\overline{\phi }){||}_{2\infty }{e}^{-\frac{\mu }{2}t}+H,t\ge 0,$$

which proves the global practical exponential stability of the impulsive control GRN system (2). The proof is completed. □

For the last result we will use the following lemma.

Lemma 2

(Young’s Inequality [49]). For $a>0$, $b>0$, $q>1$, $\frac{1}{q}+\frac{1}{r}=1$ the following inequality

$$ab\le \frac{1}{q}{a}^q+\frac{1}{r}{b}^r$$

holds.

Theorem 4.

Assume that $0<\eta <H$, conditions A1–A3, (ii), abd (iii) of Theorem 1 hold, and there exist real positive constants ${\eta }_{\iota }$, ${\theta }_{\iota o}$, $\iota ,o=1,2,\dots ,N$, and μ such that the parameters of the impulsive controlled GRN (2) satisfy:

$$\begin{array}{c}{\displaystyle \underset{1\le \iota \le N}{\min }\{q{a}_i-\sum _{o=1}^N(q-1)|b_{\iota o}{|}^{\frac{q{\theta }_{\iota o}}{q-1}}{\kappa }_o{f}_o^L,q{c}_{\iota }-(q-1)d_{\iota }^{\frac{q{\eta }_{\iota }}{q-1}}{\kappa }_{\iota }\}}\hfill \\ \\ {\displaystyle -\underset{1\le \iota \le N}{\max }\{{\kappa }_{\iota }{d}_{\iota }^{q(1-{\eta }_{\iota })},\sum _{o=1}^N|b_{o\iota }{|}^{q(1-{\theta }_{o\iota })}{\kappa }_{\iota }{f}_{\iota }^L\}\ge \mu .}\hfill \end{array}$$

(16)

Then, the impulsive control GRN (2) is globally practically exponentially stable.

Proof. 

Let $\overline{\varphi },\overline{\phi }\in \mathcal{PCB}[(-\infty ,0],{\mathbb{R}}^N]$ and define the norm

$$||(\overline{\varphi },\overline{\phi }){||}_{q\infty }=\underset{\upsilon \in (-\infty ,0]}{\sup }||(\overline{\varphi }\left(\upsilon \right),\overline{\phi }\left(\upsilon \right)){||}_q,$$

where

$$||(\overline{m},\overline{p}){||}_q={\left\{{\displaystyle \sum _{\iota =1}^N|{\overline{m}}_{\iota }{|}^q+\sum _{\iota =1}^N{|{\overline{p}}_{\iota }|}^q}\right\}}^{1/q},q\le 1.$$

Consider the Lyapunov-type function

$${\displaystyle L_q(t,\overline{m},\overline{p})=\sum _{\iota =1}^N|{\overline{m}}_{\iota }\left(t\right){|}^q+\sum _{\iota =1}^N{|{\overline{p}}_{\iota }\left(t\right)|}^q.}$$

(17)

Using A3 and condition (iii) of Theorem 1, at the impulsive control instants $t={\tau }_l$, $l=1,2,\dots$, we have:

$${\displaystyle L_q({\tau }_l^{+},\overline{m}\left({\tau }_l^{+}\right),\overline{p}\left({\tau }_l^{+}\right))}$$

$$=\sum _{\iota =1}^N|{\overline{m}}_{\iota }\left({\tau }_l\right)+M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right){|}^q+\sum _{\iota =1}^N{|{\overline{p}}_{\iota }\left({\tau }_l\right)+P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right)|}^q$$

$${\displaystyle \le \sum _{\iota =1}^N|1-{\gamma }_{\iota l}^m{|}^q|{\overline{m}}_{\iota }\left({\tau }_l\right){|}^q+\sum _{\iota =1}^N|1-{\gamma }_{\iota l}^p{|}^q{|{\overline{p}}_{\iota }\left({\tau }_l\right)|}^q}$$

$${\displaystyle <\sum _{\iota =1}^N|{\overline{m}}_{\iota }\left({\tau }_l\right){|}^q+\sum _{\iota =1}^N{|{\overline{p}}_{\iota }\left({\tau }_l\right)|}^q=L_q({\tau }_l,\overline{m}\left({\tau }_l\right),\overline{p}\left({\tau }_l\right)),}$$

or

$$L_q(t^{+},\overline{\varphi }\left(0\right)+\Delta \left(\overline{\varphi }\right),\overline{\phi }\left(0\right)+\Delta \left(\overline{\phi }\right))$$

$$\le L_q(t,\overline{\varphi }\left(0\right),\overline{\phi }\left(0\right)),t={\tau }_l,l=1,2,\dots .$$

(18)

Let $t\ge 0$, $t\ne {\tau }_l$, $l=1,2,\dots$. After the application of A1, A2, and condition (ii) of Theorem 1, we get:

$${\dot{L}}_q(t,\overline{m}\left(t\right),\overline{p}\left(t\right))$$

$${\displaystyle \le \sum _{\iota =1}^{N}q\left[-a_{\iota }|{\overline{m}}_{\iota }{\left(t\right)|}^q+\sum _{o=1}^n|b_{\iota o}|f_o^L{\kappa }_o\underset{-\infty <\upsilon \le 0}{\sup }|{\overline{p}}_o\left(\upsilon \right)||{\overline{m}}_{\iota }{\left(t\right)|}^{q-1}\right]}$$

$$+\sum _{\iota =1}^{N}q\left[-c_{\iota }|{\overline{p}}_{\iota }{\left(t\right)|}^q+d_{\iota }{\kappa }_{\iota }\underset{-\infty <\upsilon \le 0}{\sup }|{\overline{m}}_{\iota }\left(\upsilon \right)||{\overline{p}}_{\iota }{\left(t\right)|}^{q-1}\right]$$

$${\displaystyle =\sum _{\iota =1}^{N}q[-a_{\iota }|{\overline{m}}_{\iota }{\left(t\right)|}^q-c_{\iota }{|{\overline{p}}_{\iota }\left(t\right)|}^q}$$

$$+\sum _{o=1}^n|b_{\iota o}{|}^{1-{\theta }_{\iota o}}{f}_o^L{\kappa }_o\underset{-\infty <\upsilon \le 0}{\sup }|{\overline{p}}_o\left(\upsilon \right)|{\left(|b_{\iota o}{|}^{\frac{{\theta }_{\iota o}}{q-1}}|{\overline{m}}_{\iota }\left(t\right)|\right)}^{q-1}$$

$$+d_{\iota }^{1-{\eta }_{\iota }}{\kappa }_{\iota }\underset{-\infty <\upsilon \le 0}{\sup }|{\overline{m}}_{\iota }\left(\upsilon \right)|{\left(d_{\iota }^{\frac{{\eta }_{\iota }}{q-1}}|{\overline{p}}_{\iota }\left(t\right)|\right)}^{q-1}].$$

For $a=|b_{\iota o}{|}^{1-{\theta }_{\iota o}}{\sup }_{-\infty <\upsilon \le 0}|{\overline{p}}_o\left(\upsilon \right)|$ and $b={\left(|b_{\iota o}{|}^{\frac{{\theta }_{\iota o}}{q-1}}|{\overline{m}}_{\iota }\left(t\right)|\right)}^{q-1}$ we have from Lemma 2

$$|b_{\iota o}{|}^{1-{\theta }_{\iota o}}\underset{-\infty <\upsilon \le 0}{\sup }|{\overline{p}}_o\left(\upsilon \right)|{\left(|b_{\iota o}{|}^{\frac{{\theta }_{\iota o}}{q-1}}|{\overline{m}}_{\iota }\left(t\right)|\right)}^{q-1}$$

$$\le \frac{1}{q}|b_{\iota o}{|}^{q(1-{\theta }_{\iota o})}\underset{-\infty <\upsilon \le 0}{\sup }{|{\overline{p}}_o\left(\upsilon \right)|}^q$$

(19)

$$+\frac{q-1}{q}|b_{\iota o}{|}^{\frac{q{\theta }_{\iota o}}{q-1}}{|{\overline{m}}_{\iota }\left(t\right)|}^q.$$

Analogously, for $a=d_{\iota }^{1-{\eta }_{\iota }}{\sup }_{-\infty <\upsilon \le 0}|{\overline{m}}_{\iota }\left(\upsilon \right)|$ and $b={\left(d_{\iota }^{\frac{{\eta }_{\iota }}{q-1}}|{\overline{p}}_{\iota }\left(t\right)|\right)}^{q-1}$, Lemma 2 implies

$$d_{\iota }^{1-{\eta }_{\iota }}\underset{-\infty <\upsilon \le 0}{\sup }|{\overline{m}}_{\iota }\left(\upsilon \right)|{\left(d_{\iota }^{\frac{{\eta }_{\iota }}{q-1}}|{\overline{p}}_{\iota }\left(t\right)|\right)}^{q-1}$$

$$\le \frac{1}{q}{d}_{\iota }^{q(1-{\eta }_{\iota })}\underset{-\infty <\upsilon \le 0}{\sup }{|{\overline{m}}_{\iota }\left(\upsilon \right)|}^q$$

(20)

$$+\frac{q-1}{q}{d}_{\iota }^{\frac{q{\eta }_{\iota }}{q-1}}{|{\overline{p}}_{\iota }\left(t\right)|}^q.$$

Using (19) and (20), we get:

$${\displaystyle {\dot{L}}_q(t,\overline{m}\left(t\right),\overline{p}\left(t\right))\le \sum _{\iota =1}^{N}q[-a_{\iota }|{\overline{m}}_{\iota }{\left(t\right)|}^q-c_{\iota }{|{\overline{p}}_{\iota }\left(t\right)|}^q}$$

$$+\sum _{o=1}^N{f}_o^L{\kappa }_o\frac{1}{q}|b_{\iota o}{|}^{q(1-{\theta }_{\iota o})}\underset{-\infty <\upsilon \le 0}{\sup }{|{\overline{p}}_o\left(\upsilon \right)|}^q$$

$$+\sum _{o=1}^N{f}_o^L{\kappa }_o\frac{q-1}{q}|b_{\iota o}{|}^{\frac{q{\theta }_{\iota o}}{q-1}}|{\overline{m}}_{\iota }{\left(t\right)|}^q+{\kappa }_{\iota }\frac{1}{q}{d}_{\iota }^{q(1-{\eta }_{\iota })}\underset{-\infty <\upsilon \le 0}{\sup }{|{\overline{m}}_{\iota }\left(\upsilon \right)|}^q$$

$$+{\kappa }_{\iota }\frac{q-1}{q}{d}_{\iota }^{\frac{q{\eta }_{\iota }}{q-1}}{|{\overline{p}}_{\iota }\left(t\right)|}^q]$$

$${\displaystyle =\sum _{\iota =1}^N[-a_{\iota }q|{\overline{m}}_{\iota }{\left(t\right)|}^q-c_{\iota }q|{\overline{p}}_{\iota }{\left(t\right)|}^q+\sum _{o=1}^N{f}_o^L{\kappa }_o|b_{\iota o}{|}^{q(1-{\theta }_{\iota o})}\underset{-\infty <\upsilon \le 0}{\sup }{|{\overline{p}}_o\left(\upsilon \right)|}^q}$$

$$+\sum _{o=1}^N{f}_o^L{\kappa }_o(q-1)|b_{\iota o}{|}^{\frac{q{\theta }_{\iota o}}{q-1}}|{\overline{m}}_{\iota }{\left(t\right)|}^q+{\kappa }_{\iota }{d}_{\iota }^{q(1-{\eta }_{\iota })}\underset{-\infty <\upsilon \le 0}{\sup }{|{\overline{m}}_{\iota }\left(\upsilon \right)|}^q$$

$$+{\kappa }_{\iota }(q-1)d_{\iota }^{\frac{q{\eta }_{\iota }}{q-1}}{|{\overline{p}}_{\iota }\left(t\right)|}^q].$$

The rest of the proof repeats the steps in the proof of Theorem 3 using condition (16) and the norm ${||(m,p)||}_q$ of $(m,p)={(m_1,m_2,\dots ,m_N,p_1,p_2,\dots ,p_N)}^T\in {\mathbb{R}}^{2N}$. □

Remark 6.

Theorem 4 generalizes Theorems 2 and 3. For $q=1$ we can easily obtain Theorem 2, and for $q=2$ Theorem 3 follows as a corollary.

Remark 7.

The obtained practical stability results generalize and complement the results in Ref. [14] to the impulsive control case applying the practical stability notion. The results are new and offer an impulsive control strategy to the model (1) that can be reached in a setting time and greatly improve the functionality in real application. The main advantages of the impulsive control strategy lie in the fact that it is applied only in some discrete times ${\tau }_l$ and can reduce the amount of transmitted information drastically [27,28,29,30,31,32,33,34]. The controllers have effects on sudden changes of the states of (1) at the instances ${\tau }_l$. The functions $U_{\iota l}^m$ and $U_{\iota l}^p$ characterize the control gains of synchronizing impulses. Hence, we designed an impulsive control law under which the model (2) is practically synchronized onto model (1).

Remark 8.

The asymptotic stability and finite-time stability concepts have been applied by few authors to some classes of GRNs with impulsive effects [19,20,21,22,23]. Different from all existing stability results we offer practical stability results for an impulsive GRN. The presented results can be considered as an extension and complement of the results in Refs. [19,20,21,22,23] and some others. The practical stability concept [35] is inspired by numerous applications [36,37,38,40,41,42,43,44,46,47,48] and can be successfully used when the nodes of a GRN model oscillate close to a state, in which the behavior is still acceptable, but not necessarily mathematically stable.

Remark 9.

Note that, the practical stability definition is with respect to the region containing the origin [35]. However, it can be applied to any other equilibrium after a corresponding translation of this state to the origin. Hence, if the stability analysis is developed for the equilibrium at the origin, then without loss of generality, it can be universally used for other equilibria of the model.

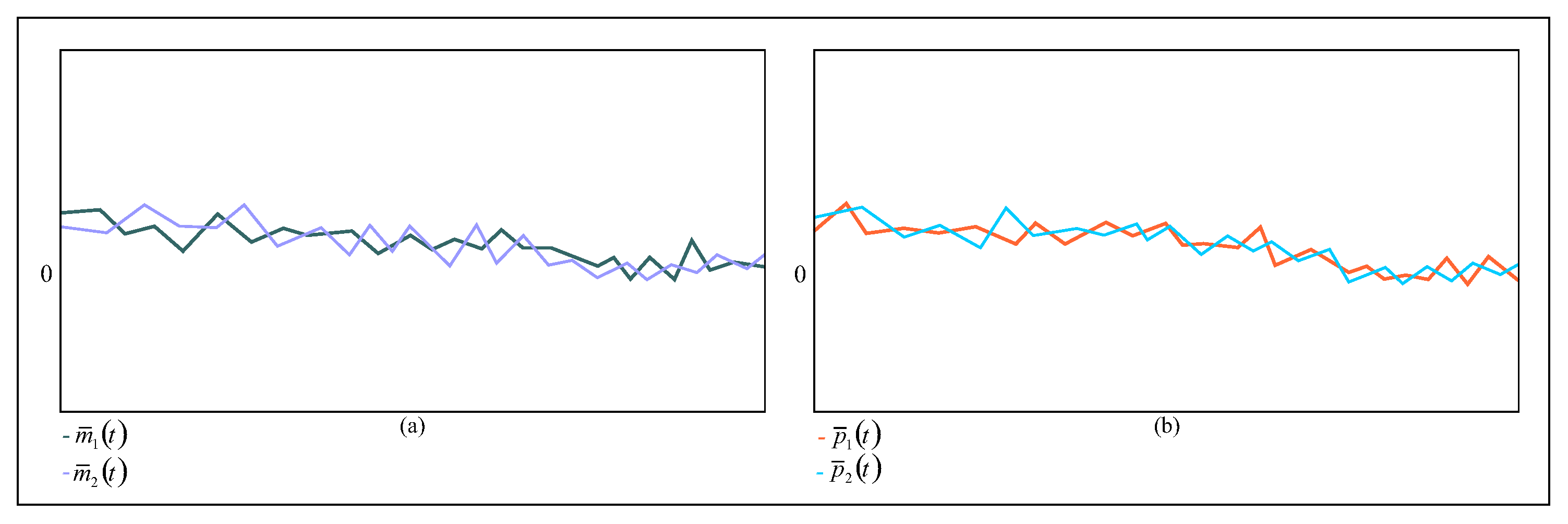
4. Numerical Examples

4.1. Example 1

In this example, we consider the following GRN model as a drive system

$$\left\{\begin{array}{c}{\dot{m}}_{\iota }=-a_{\iota }{m}_{\iota }\left(t\right)\hfill \\ {\displaystyle +\sum _{o=1}^2{b}_{\iota o}{\int }_{-\infty }^t{k}_o(t-h)f_o\left(p_o\left(h\right)\right)dh+J_{\iota }}\hfill \\ {\displaystyle {\dot{p}}_{\iota }=-c_{\iota }{p}_{\iota }\left(t\right)+d_{\iota }{\int }_{-\infty }^t{k}_{\iota }(t-h)m_{\iota }\left(h\right)dh,}\hfill \end{array}\right.$$

(21)

where $\iota =1,2$, $a_1=a_2=0.5$, $J_1=J_2=0$, $c_1=c_2=2.5$, $d_1=0.4$, $d_2=0.3$, $f_o\left(p_o\right)=\frac{p_o^2}{1+p_o^2}$, $k_o\left(h\right)=e^{-h}$, $o=1,2,$

$$b_{ij}=\left(\begin{array}{cc}{b}_{11}\hfill & \hfill b_{12}\\ b_{21}\hfill & \hfill b_{22}\end{array}\right)=\left(\begin{array}{cc}0.3\hfill & \hfill -0.3\\ -0.01\hfill & \hfill 0.1\end{array}\right).$$

The impulsively controlled GRN model is

$$\left\{\begin{array}{c}{\displaystyle {\dot{\overline{m}}}_{\iota }=-a_{\iota }{\overline{m}}_{\iota }\left(t\right)+\sum _{o=1}^2{b}_{\iota o}{\int }_{-\infty }^t{k}_o(t-h)f_o\left({\overline{p}}_o\left(h\right)\right)dh+J_{\iota },t\ne {\tau }_l,}\hfill \\ {\displaystyle {\dot{\overline{p}}}_{\iota }=-c_{\iota }{\overline{p}}_{\iota }\left(t\right)+d_{\iota }{\int }_{-\infty }^t{k}_{\iota }(t-h){\overline{m}}_{\iota }\left(h\right)dh,t\ne {\tau }_l,}\hfill \\ \\ {\overline{m}}_{\iota }\left({\tau }_l^{+}\right)={\overline{m}}_{\iota }\left({\tau }_l\right)+M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right),\hfill \\ {\overline{p}}_{\iota }\left({\tau }_l^{+}\right)={\overline{p}}_{\iota }\left({\tau }_l\right)+P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right),\hfill \end{array}\right.$$

(22)

where $0<{\tau }_1<{\tau }_2<\dots <{\tau }_l<{\tau }_{l+1}<\dots ,$${\tau }_l\to \infty$ as $l\to \infty ,$ the impulsive functions are $M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right)=-\frac{1}{5}{\overline{m}}_{\iota }\left({\tau }_l\right)$, $P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right)=-\frac{1}{4}{\overline{p}}_{\iota }\left({\tau }_l\right)$, $\iota =1,2$, $l=1,2,\dots$.

We can check, that

$$f_{\iota }^L=1,{\kappa }_{\iota }=1,\iota =1,2$$

and

$$\underset{1\le \iota \le 2}{\min }\{a_{\iota },c_{\iota }\}-\underset{1\le \iota \le 2}{\max }\{d_{\iota }{\kappa }_{\iota },\sum _{o=1}^2|b_{o\iota }|{\kappa }_{\iota }{f}_{\iota }^L\}=0.5-0.4>0.$$

Hence, by Theorem 1, we can conclude that for $0<\eta <H$ such that $||\overline{\varphi }{||}_{\infty }+||\overline{\phi }{||}_{\infty }\le \eta$, the impulsive control GRN model (22) is $(\eta ,H)$-practically stable. The practically stable behavior of the genes is shown in Figure 1.

4.2. Example 2

Consider system (21) as a drive system with $J_1=J_2=0.3$. The corresponding impulsive control GRN model is

$$\left\{\begin{array}{c}{\displaystyle {\dot{\overline{m}}}_{\iota }=-a_{\iota }{\overline{m}}_{\iota }\left(t\right)+\sum _{o=1}^2{b}_{\iota o}{\int }_{-\infty }^t{k}_o(t-h)f_o\left({\overline{p}}_o\left(h\right)\right)dh+J_{\iota },t\ne {\tau }_l,}\hfill \\ {\displaystyle {\dot{\overline{p}}}_{\iota }=-c_{\iota }{\overline{p}}_{\iota }\left(t\right)+d_{\iota }{\int }_{-\infty }^t{k}_{\iota }(t-h){\overline{m}}_{\iota }\left(h\right)dh,t\ne {\tau }_l,}\hfill \\ \\ {\overline{m}}_{\iota }\left({\tau }_l^{+}\right)={\overline{m}}_{\iota }\left({\tau }_l\right)+M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right),\hfill \\ {\overline{p}}_{\iota }\left({\tau }_l^{+}\right)={\overline{p}}_{\iota }\left({\tau }_l\right)+P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right),\hfill \end{array}\right.$$

(23)

where $0<{\tau }_1<{\tau }_2<\dots <{\tau }_l<{\tau }_{l+1}<\dots ,$${\tau }_l\to \infty$ as $l\to \infty ,$ the impulsive functions are $M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right)=-\frac{2}{7}{\overline{m}}_{\iota }\left({\tau }_l\right)$, $P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right)=-\frac{1}{5}{\overline{p}}_{\iota }\left({\tau }_l\right)$, $\iota =1,2$, $l=1,2,\dots$.

For the parameters of the impulsive GRN (23) condition (iii) of Theorem 1 is satisfied. In addition, conditions of Theorem 2 are also met for $0\le \mu \le 0.1$ and $\rho >0.6$.

Hence, Theorem 2 guarantees that for $H={\sup }_{t\ge 0}=\rho t{e}^{-\mu t}>0$, $\rho >0.6$, the impulsive control GRN model (23) is globally practically exponentially stable. The global practically exponentially stable behavior of the genes is shown on Figure 2. Thus, if the impulsive control functions $M_{\iota l}$ and $P_{\iota l}$ are chosen accordingly, the global practically exponentially stable behavior of the driven system (21) can be efficiently controlled.

Note that condition (12) of Theorem 3 is not valid for the model (23) since

$$\begin{array}{c}{\min }_{1\le \iota \le 2}\{2a_{\iota }-\sum _{o=1}^2|b_{\iota o}|{\kappa }_o{f}_o^L,2c_{\iota }-d_{\iota }{\kappa }_{\iota }\}\hfill \\ \\ -{\max }_{1\le \iota \le 2}\{d_{\iota }{\kappa }_{\iota },\sum _{o=1}^2|b_{o\iota }|{\kappa }_{\iota }{f}_{\iota }^L\}=0.4-0.4=0.\hfill \end{array}$$

4.3. Example 3

Consider the GRN model (21) as a drive system with the following parameters $a_1=a_2=2$, $J_1=J_2=0$, $c_1=c_2=0.6$, $d_1=0.2$, $d_2=0.1$, $f_o\left(p_o\right)=\frac{p_o^2}{1+p_o^2}$, $k_o\left(h\right)=e^{-h}$, $o=1,2,$ ${\displaystyle b_{ij}=\left(\begin{array}{cc}{b}_{11}\hfill & \hfill b_{12}\\ b_{21}\hfill & \hfill b_{22}\end{array}\right)=\left(\begin{array}{cc}0.5\hfill & \hfill -0.4\\ -0.3\hfill & \hfill 0.4\end{array}\right).}$

Keeping the parameters in the continuous part, the response system is given by

$$\left\{\begin{array}{c}{\displaystyle {\dot{\overline{m}}}_{\iota }=-a_{\iota }{\overline{m}}_{\iota }\left(t\right)+\sum _{o=1}^2{b}_{\iota o}{\int }_{-\infty }^t{k}_o(t-h)f_o\left({\overline{p}}_o\left(h\right)\right)dh+J_{\iota },t\ne {\tau }_l,}\hfill \\ {\displaystyle {\dot{\overline{p}}}_{\iota }=-c_{\iota }{\overline{p}}_{\iota }\left(t\right)+d_{\iota }{\int }_{-\infty }^t{k}_{\iota }(t-h){\overline{m}}_{\iota }\left(h\right)dh,t\ne {\tau }_l,}\hfill \\ \\ {\overline{m}}_{\iota }\left({\tau }_l^{+}\right)={\overline{m}}_{\iota }\left({\tau }_l\right)+M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right),\hfill \\ {\overline{p}}_{\iota }\left({\tau }_l^{+}\right)={\overline{p}}_{\iota }\left({\tau }_l\right)+P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right),\hfill \end{array}\right.$$

(24)

where $0<{\tau }_1<{\tau }_2<\dots <{\tau }_l<{\tau }_{l+1}<\dots ,$${\tau }_l\to \infty$ as $l\to \infty ,$ the impulsive functions are $M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right)=-\frac{1}{5}{\overline{m}}_{\iota }\left({\tau }_l\right)$, $P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right)=-\frac{1}{3}{\overline{p}}_{\iota }\left({\tau }_l\right)$, $\iota =1,2$, $l=1,2,\dots$.

We can check that for system (24) condition (12) of Theorem 3 is valid for $f_{\iota }^L=1$, ${\kappa }_{\iota }=1$, $\iota =1,2$ and ${\min }_{1\le \iota \le 2}\{2a_{\iota }-{\sum }_{o=1}^2|b_{\iota o}|{\kappa }_o{f}_o^L,2c_{\iota }-d_{\iota }{\kappa }_{\iota }\}=1$, ${\max }_{1\le \iota \le 2}\{d_{\iota }{\kappa }_{\iota },{\sum }_{o=1}^2|b_{o\iota }|$${\kappa }_{\iota }{f}_{\iota }^L\}=0.8$, or for $0\le \mu \le 0.2$, and condition $\left(i^{*}\right)$ of Theorem 2 is not satisfied.

In this case, according to Theorem 3, we can conclude that the impulsive control GRN model (24) is globally practically exponentially stable for $0<\eta <H$.

4.4. Example 4

We again consider the GRN model (21) as a drive system with the following parameters $a_1=a_2=1$, $J_1=J_2=0$, $c_1=c_2=2$, $d_1=0.9$, $d_2=0.8$, $f_o\left(p_o\right)=\frac{p_o^2}{1+p_o^2}$, $k_o\left(h\right)=e^{-h}$, $o=1,2,$ ${\displaystyle b_{ij}=\left(\begin{array}{cc}{b}_{11}\hfill & \hfill b_{12}\\ b_{21}\hfill & \hfill b_{22}\end{array}\right)=\left(\begin{array}{cc}0.2\hfill & \hfill 0.4\\ -0.2\hfill & \hfill 0.3\end{array}\right).}$

The response system with the same values of the parameters in the continuous part is given by

$$\left\{\begin{array}{c}{\displaystyle {\dot{\overline{m}}}_{\iota }=-a_{\iota }{\overline{m}}_{\iota }\left(t\right)+\sum _{o=1}^2{b}_{\iota o}{\int }_{-\infty }^t{k}_o(t-h)f_o\left({\overline{p}}_o\left(h\right)\right)dh+J_{\iota },t\ne {\tau }_l,}\hfill \\ {\displaystyle {\dot{\overline{p}}}_{\iota }=-c_{\iota }{\overline{p}}_{\iota }\left(t\right)+d_{\iota }{\int }_{-\infty }^t{k}_{\iota }(t-h){\overline{m}}_{\iota }\left(h\right)dh,t\ne {\tau }_l,}\hfill \\ \\ {\overline{m}}_{\iota }\left({\tau }_l^{+}\right)={\overline{m}}_{\iota }\left({\tau }_l\right)+M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right),\hfill \\ {\overline{p}}_{\iota }\left({\tau }_l^{+}\right)={\overline{p}}_{\iota }\left({\tau }_l\right)+P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right),\hfill \end{array}\right.$$

(25)

where $0<{\tau }_1<{\tau }_2<\dots <{\tau }_l<{\tau }_{l+1}<\dots ,$${\tau }_l\to \infty$ as $l\to \infty ,$ the impulsive functions are $M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right)=-\frac{1}{3}{\overline{m}}_{\iota }\left({\tau }_l\right)$, $P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right)=-\frac{1}{2}{\overline{p}}_{\iota }\left({\tau }_l\right)$, $\iota =1,2$, $l=1,2,\dots$.

We can check that for system (25) we have $f_{\iota }^L=1,{\kappa }_{\iota }=1,\iota =1,2$. In addition, condition $\left(i^{*}\right)$ of Theorem 2 is satisfied for ${\min }_{1\le \iota \le 2}\{a_{\iota },c_{\iota }\}=1$, ${\max }_{1\le \iota \le 2}\{d_{\iota }{\kappa }_{\iota },{\sum }_{o=1}^2|b_{o\iota }|{\kappa }_{\iota }{f}_{\iota }^L\}=0.9$ (or $0\le \mu \le 0.1$), and condition (12) of Theorem 3 is satisfied for ${\min }_{1\le \iota \le 2}\{2a_{\iota }-{\sum }_{o=1}^2|b_{\iota o}|{\kappa }_o{f}_o^L,2c_{\iota }-d_{\iota }{\kappa }_{\iota }\}=1.4$, ${\max }_{1\le \iota \le 2}\{d_{\iota }{\kappa }_{\iota },{\sum }_{o=1}^2|b_{o\iota }|{\kappa }_{\iota }{f}_{\iota }^L\}=0.9$ (or for $0\le \mu \le 0.5$).

In this case, using both Theorems 2 and 3, we can conclude that the impulsive control GRN model (25) is globally practically exponentially stable.

4.5. Example 5

Consider the GRN model (21) as a drive system with the following parameters $a_1=a_2=1.1.3$, $J_1=J_2=0$, $c_1=c_2=2$, $d_1=d_2=1.1$, $f_o\left(p_o\right)=\frac{p_o^2}{1+p_o^2}$, $k_o\left(h\right)=e^{-h}$, $o=1,2,$ ${\displaystyle b_{ij}=\left(\begin{array}{cc}{b}_{11}\hfill & \hfill b_{12}\\ b_{21}\hfill & \hfill b_{22}\end{array}\right)=\left(\begin{array}{cc}1\hfill & \hfill 0.2\\ 0.3\hfill & \hfill 0.2\end{array}\right).}$

The response system with the same values of the parameters in the continuous part is given by

$$\left\{\begin{array}{c}{\displaystyle {\dot{\overline{m}}}_{\iota }=-a_{\iota }{\overline{m}}_{\iota }\left(t\right)+\sum _{o=1}^2{b}_{\iota o}{\int }_{-\infty }^t{k}_o(t-h)f_o\left({\overline{p}}_o\left(h\right)\right)dh+J_{\iota },t\ne {\tau }_l,}\hfill \\ {\displaystyle {\dot{\overline{p}}}_{\iota }=-c_{\iota }{\overline{p}}_{\iota }\left(t\right)+d_{\iota }{\int }_{-\infty }^t{k}_{\iota }(t-h){\overline{m}}_{\iota }\left(h\right)dh,t\ne {\tau }_l,}\hfill \\ \\ {\overline{m}}_{\iota }\left({\tau }_l^{+}\right)={\overline{m}}_{\iota }\left({\tau }_l\right)+M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right),\hfill \\ {\overline{p}}_{\iota }\left({\tau }_l^{+}\right)={\overline{p}}_{\iota }\left({\tau }_l\right)+P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right),\hfill \end{array}\right.$$

(26)

where $0<{\tau }_1<{\tau }_2<\dots <{\tau }_l<{\tau }_{l+1}<\dots ,$${\tau }_l\to \infty$ as $l\to \infty ,$ the impulsive functions are $M_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right)=-\frac{2}{5}{\overline{m}}_{\iota }\left({\tau }_l\right)$, $P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right)=-\frac{1}{4}{\overline{p}}_{\iota }\left({\tau }_l\right)$, $\iota =1,2$, $l=1,2,\dots$.

We can check that for system (26) we have $f_{\iota }^L=1,{\kappa }_{\iota }=1,\iota =1,2$.

Additionally,

$$\underset{1\le \iota \le 2}{\min }\{a_{\iota },c_{\iota }\}=1.2<\underset{1\le \iota \le 2}{\max }\{d_{\iota }{\kappa }_{\iota },\sum _{o=1}^2|b_{o\iota }|{\kappa }_{\iota }{f}_{\iota }^L\}=1.3,$$

and

$$\underset{1\le \iota \le 2}{\min }\{2a_{\iota }-\sum _{o=1}^2|b_{\iota o}|{\kappa }_o{f}_o^L,2c_{\iota }-d_{\iota }{\kappa }_{\iota }\}=1.3$$

$$=\underset{1\le \iota \le 2}{\max }\{d_{\iota }{\kappa }_{\iota },\sum _{o=1}^2|b_{o\iota }|{\kappa }_{\iota }{f}_{\iota }^L\}=1.3.$$

Hence, condition $\left(i^{*}\right)$ of Theorem 2 and condition (12) of Theorem 3 do not hold.

However, if we consider $q=3$, ${\eta }_{\iota }={\theta }_{\iota o}=2/3$, $\iota ,o=1,2$, we have

$$\underset{1\le \iota \le 2}{\min }\{3a_{\iota }-\sum _{o=1}^{2}2|b_{\iota o}|{\kappa }_o{f}_o^L,3c_{\iota }-2d_{\iota }{\kappa }_{\iota }\}=1.4$$

$$>\underset{1\le \iota \le 2}{\max }\{d_{\iota }{\kappa }_{\iota },\sum _{o=1}^2|b_{o\iota }|{\kappa }_{\iota }{f}_{\iota }^L\}=1.3.$$

Hence, by Theorem 4, we can conclude that the impulsive control GRN model (26) is globally practically exponentially stable.

In addition, if in the impulsive control system, we consider impulsive functions given by

$$\begin{array}{c}{M}_{\iota l}\left({\overline{m}}_{\iota }\left({\tau }_l\right)\right)=-\frac{2}{5}{\overline{m}}_{\iota }\left({\tau }_l\right),\hfill \\ P_{\iota l}\left({\overline{p}}_{\iota }\left({\tau }_l\right)\right)=\frac{1}{4}{\overline{p}}_{\iota }\left({\tau }_l\right),\iota =1,2,l=1,2,\dots ,\hfill \end{array}$$

(27)

then we cannot make any conclusion by Theorem 4 for the practical stable behavior of system (26). The trajectories of the genes are demonstrated on Figure 3. We can see that the impulses cannot practically control the trajectories of ${\overline{p}}_1\left(t\right)$ and ${\overline{p}}_2\left(t\right)$.

Remark 10.

By Example 5 we demonstrate how the impulses can affect the practical stability properties of the model and how they can be efficiently applied to design suitable impulsive control strategies.

5. Conclusions

In this paper, an impulsive control stability analysis is conducted for the states of a GRNs with distributed delays. The extended notion of practical stability is introduced and new criteria that guarantee practical stability and global exponential practical stability of the proposed impulsive control model are established. Using the Lyapunov function methodology the effectiveness of impulses on the practical stability behavior are considered. A number of examples is presented to illustrate the proposed results and the use of different criteria. The suggested results and technique can be also applied to a fractional-order version of the model, which is a subject of our future research.