Distinctive Shape Functions of Fractional Differential Quadrature for Solving Two-Dimensional Space Fractional Diffusion Problems

Abstract

The aim of this study is to utilize a differential quadrature method with various kernels, such as Lagrange interpolation and discrete singular convolution, to tackle problems related to the Riesz fractional diffusion equation and the Riesz fractional advection–dispersion equation. The governing equation for convection and diffusion depends on both spatial and transient factors. By using the block marching technique, we transform these equations into an algebraic system using differential quadrature methods and the Caputo-type fractional operator. Next, we develop a MATLAB program that generates code capable of solving the fractional convection–diffusion equation in (1+2) dimensions for each shape function. Our goal is to ensure that our methods are reliable, accurate, efficient, and capable of convergence. To achieve this, we conduct two experiments, comparing the numerical and graphical results with both analytical and numerical solutions. Additionally, we evaluate the accuracy of our findings using the L_∞ error. Our tests show that the differential quadrature method, which relies mainly on the discrete singular convolution shape function, is a highly effective numerical approach for fractional convective diffusion problems. It offers superior accuracy, faster convergence, and greater reliability than other techniques. Furthermore, we study the impact of fractional order derivatives, velocity, and positive diffusion parameters on the results.

1. Introduction

Many researchers have been drawn to the study and use of fractional differential equations in recent decades. Classical differential equations are generalized by fractional order differential equations to explain complex problems such as viscoelasticity, biological engineering, fluid mechanics, engineering, stream through porous media [1,2], fractional operators [3], mathematical physics, and other fields. These equations are classified into three kinds based on the presence of fractional order derivatives in space, time, or space–time [4]. Currently, several various techniques are applied to solve fractional diffusion problems such as the Laplace, Mellin, and Fourier transforms. Mirza et al. [5] solved the time-fractionalized advection–diffusion equation by exploiting the Atangana–Baleanu fractional derivative operator. Khan et al. [6] performed a new modification of the Adomian decomposition method to solve the fractional convection–diffusion equation. Attar et al. [7] proposed an analytical method called Akbari–Ganji’s technique for solving nonlinear fractional differential equations. Shah et al. [8] presented fractional-order diffusion equations via the Natural transform decomposition method.

Solving the fractional convection–diffusion equation numerically is a difficult task, especially for high-dimensional cases, due to the fractional derivative characteristic of the space fractional derivative differential operator. Various numerical methods have been proposed for approximating one-dimensional fractional convection–diffusion equations, including the finite difference method [9], Galerkin method [10], collocation method [11], homotopy analysis transform method [12], and finite volume element method [13]. Ding et al. [14] suggested an improved matrix transform numerical approach to solve the one-dimensional space fractional advection–dispersion model, and an analytical solution was obtained using the Padé approximation. Recently, a shifted Grünwald–Letnikov difference operator for space and a Crank–Nicolson scheme for time were used to solve the space fractional convection–diffusion equation with variable coefficients, which achieved second-order convergence in both time and space with extrapolation [15]. Liu et al. [16] developed a radial basis functions finite difference (RBF-FD) for solving the time fractional convection–diffusion equation. Saadeh [17] implemented a space finite volume and finite difference approaches to solve the fractional convection–diffusion equation.

To handle two-dimensional space fractional diffusion problems, numerical approaches such as the Galerkin finite element [18], the alternating direction implicit (ADI) [19], the Kronecker product splitting [20], and the finite volume approaches [21] are utilized. Zhuang et al. [22] investigated the implicit difference approach of a time fractional diffusion equation. Pingyang et al. [23] investigated the explicit and implicit difference methods for time–space fractional reaction–diffusion equations, as well as their stability and convergence. Povstenko [24] and Zhang et al. [25] used the integral transform approach to achieve analytical findings for the time fractional diffusion-wave equation with a source term in cylindrical dimensions. The Jacobi collocation technique was employed to solve a particular case of the fractional advection–diffusion equation with a nonlinear source term by Parvizi et al. [11]. Bu et al. [26] introduced a finite element multi-grid technique for multi-term time fractional advection diffusion equations. Povstenko et al. [27] reported two approximation conclusions in two distinct modifications of the space–time-fractional advection–diffusion equation. The Laplace and Fourier transforms were used to get the basic solutions, as well as the numerical results. Mohyud-Din Email et al. [28] discovered a fully implicit finite difference approach for the time fractional advection diffusion equation based on extended cubic B-splines. In Marin et al. [29], they dealt with the mixed initial boundary value problem for a dipolar structure in the context of thermo elastic theory as well as Hölder-type stability. It is commonly understood that fractional operators are nonlocal, and hence, independent of the numerical methods utilized. To achieve an acceptable computing cost, the Toeplitz or Toeplitz times-diagonal structure was used and explored [30]. Tuan et al. [31] utilized a finite difference discretization with Caputo derivative sense to solve a two-dimensional space fractional diffusion equation. Devshali and Arora [32] introduced the differential transform method and the differential quadrature technique to solve the fractional diffusion equation in two dimensions. Jannelli and Speciale [33] applied Lie symmetries and an implicit classical numerical method with the Caputo definition of fractional derivative to solve a two-dimensional time-fractional–diffusion–reaction equation. Zureigat et al. [34] offered two compact finite difference schemes with a fuzzy Caputo generalized Hukuhara derivative to obtain a certain solution for fractional convection–diffusion equation. Mustafa et al. [35,36] solved fractional-order chaotic systems with the Sinc shape function and analyzed drug diffusion via a thin membrane using the differential quadrature approach.

In our framework, we solve the fractional order differential equation in both time and space via a differential quadrature approach with distinct shape function and Caputo definition fractional derivative. The distinct shape functions are Lagrange interpolation function [37,38], Delta Lagrange kernel, and Regularized Shannon kernel [39], which have been effectively used in the (1+2) dimensional fractional convection–diffusion equation when paired with the block marching approach. Additionally, we design a MATLAB code for each approach to obtain a numerical solution for three problems to be examined. When compared to earlier analytical [40,41] and numerical [13,42,43] methodologies, the derived numerical results attain excellent efficiency and accuracy. Furthermore, we present some parametric studies to highlight the reliability of our methods with the influence of fractional order derivative, the velocity, and positive diffusion parameters on the results.

The organization of this work is as follows: The formulation of the problems used to explain the proposed schemes is detailed in Section 2. A detailed explanation of these methods can be found in Section 3. Section 4 presents the overall performance of the methods via three types of fractional partial differential problems. The findings obtained are also discussed in the same section before Section 5 summarizes the main conclusions.

2. Formulation of the Problem

To explain our idea, we consider three types of fractional partial differential equations on a finite domain that model advection and diffusion processes:

2.1. The One-Dimensional Riesz Space Fractional Advection Equation

In this section, we consider the following Riesz fractional advection equation:

$$\frac{\partial \upsilon \left(x,t\right)}{\partial t}=-C_x\frac{{\partial }^{\beta }\upsilon \left(x,t\right)}{\partial {\left|x\right|}^{\beta }}, 0<t<T; 0<x<L$$

(1)

where $1>\beta >2$ and refers to a Riesz space fractional derivatives [44]. $\upsilon \left(x,t\right)$ is the solute concentration [45], $“x”$represents the x-direction, and $“t”$ represents time. The expression $“C_x\ge 0”$ represents the coefficient for the velocity parameter.

Subject to the initial and boundary conditions are taken as follows [42]:

$$\upsilon \left(x,0\right)=x^2\left(\pi -x\right) \mathrm{at} 0<x\le \pi$$

(2)

$$\upsilon \left(0,t\right)=\upsilon \left(\pi ,t\right)=0 \mathrm{at} 0<t\le T$$

(3)

Additionally, the exact solution is given in reference [42]:

$$\upsilon \left(x,t\right)={\displaystyle \sum _{n=1}^{\infty }\left[\frac{8}{n^3}{\left(-1\right)}^{n+1}-\frac{4}{n^3}\right]}\cdot \sin \left(nx\right)\cdot \exp \left(-{\left(n^2\right)}^{\beta /2}{C}_x.t\right)$$

(4)

2.2. The One-Dimensional Riesz Space Fractional Advection–Dispersion Equation

In this section, we consider the following one-dimensional Riesz space fractional advection–dispersion:

$$\frac{\partial \upsilon \left(x,t\right)}{\partial t}=-C_x\frac{{\partial }^{\alpha }\upsilon \left(x,t\right)}{\partial {\left|x\right|}^{\alpha }}+d_x\frac{{\partial }^{\beta }\upsilon \left(x,t\right)}{\partial {\left|x\right|}^{\beta }}, 0<t<T; 0<x<L$$

(5)

where $C_{ x}\ge 0 \mathrm{and} d_x>0$ express the velocity parameter and positive diffusion coefficients, respectively; $0<\alpha <1 \mathrm{and} 1<\beta <2$ are the Riesz space fractional order derivatives, defined a follows:

$$\frac{{\partial }^{\alpha }\upsilon \left(x,t\right)}{\partial {\left|x\right|}^{\alpha }}=-\frac{1}{2}(\sec \frac{\pi }{2}\alpha ) ({}_{0}D{}_x^{\alpha }+{}_{x}D{}_L^{\alpha }) \upsilon \left(x,t\right), \alpha \ne 1$$

(6)

$$\frac{{\partial }^{\beta }\upsilon \left(x,t\right)}{\partial {\left|x\right|}^{\beta }}=-\frac{1}{2}(\sec \frac{\pi }{2}\beta ) ({}_{0}D{}_x^{\beta }+{}_{x}D{}_L^{\beta }) \upsilon \left(x,t\right), \beta \ne 1$$

(7)

where

$${}_{0}D{}_x^{\alpha }\upsilon (x,t)=\frac{1}{\mathsf{\Gamma }(1-\alpha )} \frac{\partial }{\partial x} {\displaystyle \underset{0}{\overset{x}{\int }}{(x-\eta )}^{-\alpha } \upsilon (\eta ,t) d\eta , }$$

$${}_{x}D{}_L^{\alpha }\upsilon (x,t)=\frac{-1}{\mathsf{\Gamma }(1-\alpha )} \frac{\partial }{\partial x} {\displaystyle \underset{x}{\overset{L}{\int }}{(\eta -x)}^{-\alpha } \upsilon (\eta ,t) d\eta , }$$

$${}_{0}D{}_x^{\beta }\upsilon (x,t)=\frac{1}{\mathsf{\Gamma }(2-\beta )} \frac{{\partial }^2}{\partial x^2} {\displaystyle \underset{0}{\overset{x}{\int }}{(x-\eta )}^{1-\beta } \upsilon (\eta ,t) d\eta , }$$

$${}_{x}D{}_L^{\beta }\upsilon (x,t)=\frac{1}{\mathsf{\Gamma }(2-\beta )} \frac{{\partial }^2}{\partial x^2} {\displaystyle \underset{x}{\overset{L}{\int }}{(\eta -x)}^{1-\beta } \upsilon (\eta ,t) d\eta , }$$

${}_{0}D{}_x^{\alpha }\left({}_{0}D{}_x^{\beta }\right)$ and ${}_{x}D{}_L^{\alpha }\left({}_{x}D{}_L^{\beta }\right)$ are defined as the left- and right-side Riemann–Liouville derivatives.

The one-dimensional Riesz space fractional advection–dispersion Equation (5) has a physical meaning [46]. Physical considerations of a fractional advection–dispersion transport model restrict$0<\alpha <1, 1<\beta <2$, and we assume $d_x>0$ and $C_x⩾0$ so that the flow is from left to right. The physical meaning of applying homogeneous Dirichlet boundary conditions is that the boundary is placed sufficiently far away from an evolving plume that no significant concentrations reach it [47]. When $\alpha =1$ and $\beta =2$, Equation (5) simplifies to the classical advection–dispersion equation. However, this paper exclusively focuses on fractional cases. Specifically, when $d_x=0$, Equation (5) transforms into the Riesz fractional advection equation as Equation (1) [48]; on the other hand, when$d_x\ne 0$, we obtain the Riesz fractional advection–dispersion equation [46] as Equation (5).

Subject to the initial and boundary conditions, they are given as follows [42]:

$$\upsilon \left(x,0\right)=x^2\left(\pi -x\right) \mathrm{at} 0<x\le \pi$$

(8)

$${\left.\upsilon \left(x,t\right)\right|}_{\mathrm{at} x=0,\pi }=0 \mathrm{at} 0<t\le T 1<\alpha , \beta <2$$

(9)

In addition, the exact solution is offered in reference [42]:

$$\upsilon \left(x,t\right)={\displaystyle \sum _{n=1}^{\infty }\left[\frac{8}{n^3}{\left(-1\right)}^{n+1}-\frac{4}{n^3}\right]}\cdot \sin \left(nx\right)\cdot \exp \left(-{\left(n^2\right)}^{\beta /2}{C}_x\cdot t-{\left(n^2\right)}^{\alpha /2}{d}_x\cdot t\right),$$

(10)

2.3. The 2-D Fractional Diffusion Equation with Source Term [42]

Let us take a bounded domain as $\mathsf{\Omega }=\left[0,L_x\right]\times \left[0,L_y\right], {\mathsf{\Omega }}_t=\left[0,T\right]$ for our discretization of the problem. The aim is to find the numerical approximation of the 2-D fractional diffusion problem with zero Dirichlet boundary conditions over the finite domain $\mathsf{\Omega }\times {\mathsf{\Omega }}_t$.

$$\frac{\partial \upsilon \left(x,y,t\right)}{\partial t}=d_x\frac{{\partial }^{\beta }\upsilon \left(x,t\right)}{\partial {\left|x\right|}^{\beta }}+d_y\frac{{\partial }^{\gamma }\upsilon \left(x,y,t\right)}{\partial {\left|y\right|}^{\gamma }}+P\left(x,y,t\right), \left(x,y,t\right)\in \mathsf{\Omega }\times {\mathsf{\Omega }}_t$$

(11)

where $1<\beta , \gamma <2$ are fractional order derivatives, and $d_x \mathrm{and} d_y$ express the diffusion coefficients. With the source term:

$$\begin{array}{cc}P\left(x,y,t\right)& =\beta {\left(t+1\right)}^{\beta -1}{x}^2{\left(1-x\right)}^2\gamma {\left(t+1\right)}^{\gamma -1}{y}^2{\left(1-y\right)}^2\hfill \\ & +\frac{d_x{\left(t+1\right)}^{\beta }}{2\cos \frac{\pi \beta }{2}}\left[\frac{2}{\mathsf{\Gamma }\left(3-\beta \right)}\left(x^{2-\beta }+{\left(1-x\right)}^{2-\beta }\right)-\frac{12}{\mathsf{\Gamma }\left(4-\beta \right)}\right.\hfill \\ & \left(x^{3-\beta }+{\left(1-x\right)}^{3-\beta }\right)+\left.\frac{24}{\mathsf{\Gamma }\left(5-\beta \right)}\left(x^{4-\beta }+{\left(1-x\right)}^{4-\beta }\right)\right]y^2{\left(1-y\right)}^2\hfill \\ & +\frac{d_y{\left(t+1\right)}^{\gamma }}{2\cos \frac{\pi \gamma }{2}}\left[\frac{2}{\mathsf{\Gamma }\left(3-\gamma \right)}\left(y^{2-\gamma }+{\left(1-y\right)}^{2-\gamma }\right)-\frac{12}{\mathsf{\Gamma }\left(4-\gamma \right)}\right.\hfill \\ & \left(y^{3-\gamma }+{\left(1-y\right)}^{3-\gamma }\right)+\left.\frac{24}{\mathsf{\Gamma }\left(5-\gamma \right)}\left(y^{4-\gamma }+{\left(1-y\right)}^{4-\gamma }\right)\right]x^2{\left(1-x\right)}^2\hfill \end{array}$$

(12)

Subject to the initial and boundary conditions, they are given as follows [42]:

$$\upsilon \left(x,y,0\right)=x^2{\left(1-x\right)}^2{y}^2{\left(1-y\right)}^2, 0<x\le 1, 0<y\le 1,$$

(13)

$${\left.\upsilon \left(x,y,t\right)\right|}_{\partial \mathsf{\Omega }}=0 \mathrm{at} 0<t\le T 1<\beta , \gamma <2,$$

(14)

3. Method of Solution

Here, we seek to solve the fractional order differential equation in both time and space using a differential quadrature approach with distinct shape functions. These shape functions with block marching are used to solve (1+2) dimensions fractional convection–diffusion problems.

Firstly, we start with the definition of a fractional derivative, where there exist many definitions, and the most accepted Caputo’s definition is considered in this work.

3.1. Caputo’s Fractional Derivative

Caputo proposed Caputo’s fractional derivative, a novel definition of a fractional derivative based on the Riemann–Liouville Fractional Derivative [49]. Also, Weilbeer [50] showed this definition as follows:

Let $\lambda \in R^{+}$, and if $“\kappa ”$ is a positive integer, then $\kappa -1<\lambda <\kappa$. The Riemann–Liouville Fractional Derivative of a function $\upsilon \left(t\right)$ with order$\lambda$, expressing $\left(\beta ,\gamma \right)$, is defined as follows:

$$D_a^{\lambda }\upsilon (t)=\frac{1}{\mathsf{\Gamma }(\kappa -\lambda )} \frac{d^{\kappa }}{d{t}^{\kappa }} {\displaystyle \underset{a}{\overset{t}{\int }}{(t-x)}^{\kappa -\lambda -1} {\upsilon }^{\kappa }(x) dx, }$$

(15)

Caputo’s Fractional Derivative of order $\lambda$ is defined as follows:

$$D_a^{\lambda }\upsilon (t)=\left\{\begin{array}{l}\frac{1}{\mathsf{\Gamma }(\kappa -\lambda )}{\displaystyle \underset{a}{\overset{t}{\int }}{(t-x)}^{\kappa -\lambda -1} {\upsilon }^{\kappa }(x) dx, \kappa -1<\lambda <\kappa }\\ \frac{d^{\kappa }\upsilon }{d{t}^k} \kappa =\lambda \end{array}\right.$$

(16)

where $D_a^{\lambda }\upsilon \left(t\right)$ is the fractional derivative of $\upsilon \left(t\right)$, and $“a”$ is the integration lower limit.

For $\lambda =\kappa$, the classical definition of integer order derivative is obtained.

Secondly, we introduce the definition of differential quadrature method with the following different shape functions:

3.2. Lagrange Interpolation Polynomial (PDQM)

According to this shape function, the functional values for any unknown $“\upsilon ”$ at a definite number of grid points $“N”$ can be expressed as follows [37,38]:

$$\upsilon (t_i)={\displaystyle \sum _{j=1}^N\frac{{\displaystyle \prod _{k=1}^N(t_i-t_k)}}{(t_i-t_j){\displaystyle \prod _{j=1,j\ne k}^N(t_j-t_k)}}\upsilon (t_j)} , (i=1:N),$$

(17)

Thus, the different derivatives of this unknown $“\upsilon ”$ can be determined as follows:

$$\frac{{\partial }^n\upsilon }{\partial t^n}\left|\begin{array}{c}\\ t=t_i\end{array}\right.={\displaystyle \sum _{j=1}^N{\Re }_{ij}^{(n)}}\upsilon (t_j) (i=1:N),$$

(18)

where ${\Re }_{ij}^{\left(n\right)}$ is the weighting coefficient for the nth derivative. But the key to the accuracy of DQM is in determining the weighting coefficients. Therefore, they are different based on the shape function.

Consequently, the weighting coefficients ${\Re }_{ij}^{\left(1\right)}$for the first derivative and${\Re }_{ij}^{\left(2\right)}$ for the second derivative can be found by differentiating Equation (17):

$${\Re }_{ij}^{(1)}= \left\{\begin{array}{c}\frac{1}{(t_i-t_j)}{\displaystyle \prod _{\begin{array}{l}k=1,\\ k\ne i,j\end{array}}^N\frac{(t_i-t_k)}{(t_j-t_k)}} i\ne j\\ \\ -{\displaystyle \sum _{\begin{array}{l}j=1,\\ j\ne i\end{array}}^N{\Re }_{ij}^{(1)}} i=j\end{array}\right. , {\Re }_{ij}^{(2)}= \left[{\Re }_{ij}^{(1)}\right]\left[{\Re }_{ij}^{(1)}\right],$$

(19)

3.3. Discrete Singular Convolution (DSCDQM)

The singular convolution can be written as follows [51,52]:

$$g\left(t\right)=\left(F\times \eta \right)\left(t\right)={{\displaystyle \int }}_{-\infty }^{\infty }F\left(t-s\right) \eta \left(s\right)ds$$

(20)

where $F\left(t-s\right)$and $\eta \left(t\right)$ are a singular kernel and a test function space element, respectively.

The shape function in this type depends on the choice of kernel type. But this shape function has numerous kernels, so we will use two of them to describe the functional values of the unknown $“\upsilon ”$ and its derivatives at a certain number of grid points $“N”$, as follows:

Kernel (1)—the shape function of Delta Lagrange Kernel (DSCDQM-DLK) is described as follows:

$$\upsilon (t_i)={\displaystyle \sum _{j=-M}^M\frac{1}{(t_i-t_j)} \times \frac{{\displaystyle \prod _{k=-M}^M (t_i-t_k)}}{{\displaystyle \prod _{j=-M, k\ne i,j}^M (t_j-t_k)}} \times \upsilon (t_j)}, (i=-N:N), M\ge 1$$

(21)

$$\frac{{\partial }^n\upsilon }{\partial t^n}\left|\begin{array}{c}\\ t=t_i\end{array}\right.={\displaystyle \sum _{j=1}^N{\Re }_{ij}^{(n)}}\upsilon (t_j) \left(i=-N:N\right)$$

(22)

Consequently, ${\Re }_{ij}^{\left(1\right)}$ and ${\Re }_{ij}^{\left(2\right)}$ can be given by differentiating Equation (18) as follows [39,52,53,54]:

$${\mathfrak{R}}_{ij}^{\left(1\right)}= \left\{\begin{array}{c}\frac{1}{(t_i-t_j)}{\displaystyle \prod _{\begin{array}{c}k=-M, \hfill \\ k\ne i,j\hfill \end{array}}^M}\frac{(t_i-t_k)}{(t_j-t_k)} i\ne j\\ \\ -{\displaystyle \sum _{\begin{array}{c}j=-M,\hfill \\ j\ne i\hfill \end{array}}^M}{\mathfrak{R}}_{ij}^{\left(1\right)} i=j\end{array}\right. , {\mathfrak{R}}_{ij}^{\left(2\right)}= \left\{\begin{array}{c}2\left({\mathfrak{R}}_{ij}^{\left(1\right)}{\mathfrak{R}}_{ij}^{\left(1\right)}-\frac{{\mathfrak{R}}_{ij}^{\left(1\right)}}{(t_i-t_j)}\right) i\ne j\\ \\ -{\displaystyle \sum _{\begin{array}{c}j=-M,\hfill \\ j\ne i\hfill \end{array}}^M}{\mathfrak{R}}_{ij}^{\left(2\right)} i=j\end{array}\right. ,$$

(23)

Also, in kernel (2), the shape function of the Regularized Shannon kernel (DSCDQM-RSK) is introduced as follows:

$$\upsilon (t_i)={\displaystyle \sum _{j=-M}^M〈\frac{\sin \left[\frac{\pi (t_i-t_j)}{\Delta }\right]}{\frac{\pi (t_i-t_j)}{\Delta }} \exp (\frac{-{(t_i-t_j)}^2}{2{\sigma }^2})〉 \upsilon (x_j)}, (i=-N:N),\sigma =(\tau \times \Delta ) >0$$

(24)

where $\sigma , \tau , \mathrm{and} \mathsf{\Delta }$ represent the Regularized Shannon factor, the computational parameter, and the step size, respectively.

$$\frac{{\partial }^n\upsilon }{\partial t^n}\left|\begin{array}{c}\\ t=t_i\end{array}\right.={\displaystyle \sum _{j=1}^N{\Re }_{ij}^{(n)}}\upsilon (t_j) \left(i=-N:N\right)$$

(25)

Consequently, ${\Re }_{ij}^{\left(1\right)}$ and ${\Re }_{ij}^{\left(2\right)}$ can be determined by differentiating Equation (21) as follows [55]:

$${\Re }_{ij}^{(1)}=\left\{\begin{array}{c}\frac{{(-1)}^{i-j}}{\Delta (i-j)}\exp (-{\Delta }^2(\frac{{(i-j)}^2}{2{\sigma }^2})), i\ne j\\ \\ 0 i=j\end{array}\right. ,{\Re }_{ij}^{(2)}=\left\{\begin{array}{c}(\frac{2{(-1)}^{i-j+1}}{{\Delta }^2{(i-j)}^2}+\frac{1}{{\sigma }^2})\exp (-{\Delta }^2(\frac{{(i-j)}^2}{2{\sigma }^2})), i\ne j\\ \\ -\frac{1}{{\sigma }^2}-\frac{{\pi }^2}{3{\Delta }^2} i=j\end{array}\right.$$

(26)

This debate has revealed that the kernel type, regular grid points$“N”$, and bandwidth $\left(2M+1\right)$ play an important role in obtaining convergence and accuracy solutions.

Third, we apply the DQM with three kernels in Caputo’s Fractional Derivative to determine the weighting coefficients ${\Re }_{ij}^{\alpha }$ for $\alpha =\lambda \in \left(0,1\right)$ and ${\Re }_{ij}^{\beta ,\gamma }$for $\beta ,\gamma =\lambda \in \left(1,2\right)$, as follows:

a. Caputo’s Fractional Derivative of order $\alpha =\lambda \in \left(0,1\right)$ is offered as follows:

$$D_{}^{\alpha }\upsilon (t)=\left\{\begin{array}{l}\frac{1}{\mathsf{\Gamma }(1-\alpha )}{\displaystyle \underset{a}{\overset{t}{\int }}{(t-x)}^{-\alpha } {\upsilon }^{\prime }(x) dx}= {\displaystyle \sum _{j=1}^N{\Re }_{ij}^{\alpha } \upsilon (t_j},x), 0<\alpha <1 \\ {\displaystyle \sum _{j=1}^N{\Re }_{ij}^{(1)} \upsilon (t_j},x) \alpha =1\end{array}\right.$$

(27)

b. Caputo’s Fractional Derivative of order $\beta ,\gamma =\lambda \in \left(1,2\right)$ is explained as follows:

$$D_{}^{\beta ,\gamma }\upsilon (t)=\left\{\begin{array}{l}\frac{1}{\mathsf{\Gamma }(2-\beta ,\gamma )}{\displaystyle \underset{a}{\overset{t}{\int }}{(t-x)}^{1-\beta ,\gamma } {\upsilon }^{″}(x) dx}= {\displaystyle \sum _{j=1}^N{\Re }_{ij}^{\beta ,\gamma } \upsilon (t_j},x), 1<\beta ,\gamma <2 \\ {\displaystyle \sum _{j=1}^N{\Re }_{ij}^{(2)} \upsilon (t_j},x) \beta ,\gamma =2\end{array}\right.$$

(28)

Then, the weighting coefficients are computed as follows:

$${\Re }_{ij}^{\alpha }=A^{1-\alpha } {\Re }_{ij}^{(1)}-\frac{{\Re }_{1,j}^{(1)}}{\mathsf{\Gamma }(2-\alpha )} {(t-a)}^{1-\alpha }, A_{ij}={\Re }_{ij}^{(1)}-{\Re }_{1j}^{(1)}$$

(29)

$${\Re }_{ij}^{\beta ,\gamma }=B^{2-\beta ,\gamma } {\Re }_{ij}^{(2)}-\frac{{\Re }_{1,j}^{(2)}}{\mathsf{\Gamma }(3-\beta ,\gamma )} {(t-a)}^{2-\beta ,\gamma }, B_{ij}={\gamma }_{ij}={\Re }_{ij}^{(2)}-{\Re }_{1j}^{(2)}$$

(30)

where $A_{ij}$ and $B_{ij}$ are fractional weighting coefficients for $\alpha \in \left(0,1\right)$ and$\beta ,\gamma \in \left(1,2\right)$, respectively.

Equations (29) and (30) can be proved as follows:

For $\alpha \in \left(0,1\right)$let

$$J^{\alpha }\upsilon \left(t\right)=\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\underset{a}{\overset{t}{{\displaystyle \int }}}{\left(t-x\right)}^{\alpha -1}\upsilon \left(x\right)dx$$

Then,

$$\begin{array}{l}{\upsilon }^{\prime }(a)= d \upsilon (a), d={\Re }_{1j}^1, \\ J^{\alpha }{\upsilon }^{\prime }(a)=d J^{\alpha }\upsilon (a)=d \frac{\upsilon (a)}{\mathsf{\Gamma }(\alpha )}{\displaystyle \underset{a}{\overset{t}{\int }}{(t-x)}^{\alpha -1} dx=}\frac{\upsilon (a)}{\mathsf{\Gamma }(\alpha +1)}d {(t-a)}^{\alpha },\end{array}$$

(31)

Cconsequently,

$$J_a^{1-\alpha }{\upsilon }^{\prime }(a)=\frac{\upsilon (a)}{\mathsf{\Gamma }(2-\alpha )}d {(t-a)}^{1-\alpha },$$

(32)

Also,

$${\displaystyle \underset{a}{\overset{t}{\int }}\upsilon (t)dt=}{\displaystyle \sum _{j=1}^{N_x}({\Re }_{ij}^1-{\Re }_{1j}^1)\upsilon (t_j},x), A_{ij}={\Re }_{ij}^1-{\Re }_{1j}^1$$

(33)

Then,

$$\begin{array}{l}{J}^1\upsilon (t)={\displaystyle \underset{a}{\overset{t}{\int }}\upsilon (x) dx=A }\upsilon (t) \Rightarrow \\ J^2\upsilon (t)= {\displaystyle \underset{a}{\overset{t}{\int }}{\displaystyle \underset{a}{\overset{t}{\int }}\upsilon (x)} dx={\displaystyle \underset{a}{\overset{t}{\int }}(t-x)\upsilon (x) dx=A^2\upsilon (t)} }\end{array}$$

(34)

Further,

$$J^{\alpha }\upsilon (t)=A^{\alpha }\upsilon (t) \Rightarrow J^{1-\alpha }{\upsilon }^{\prime }(t)=A^{1-\alpha }{\Re }_{ij}^1\upsilon (t)$$

(35)

Similarly, for $\beta ,\gamma \in \left(1,2\right)$.

Finally, to deal with time-dependent equations in the three problems and transform the governing equations to algebraic equations, we use the block marching method. This method provides more accuracy for DQM with three kernels. Therefore, we explain this technique as follows:

3.4. Block Marching Technique with Differential Quadrature Discretization

The governing Equations (1), (5), and (11) for the three problems are (1+2)-dimensional (x,y) and time-dependent (t) equations. The time-dependent models are solved using the block marching approach [56]. This approach divides the semi-infinite domain into numerous time intervals $\left(\delta t^1,\delta t^2,\delta t^3,\dots \right)$in the t-direction. Each block consists of one interval$\delta t$, with the x-direction domain ranging from 0 to L_x and y-direction domain ranging from 0 to L_y.

The grid point distribution is equal for all blocks, and these weighting coefficients are applied to all blocks by producing $\delta t^1=\delta t^2=\delta t^3=\cdots$. The following mesh sizes are utilized in the $x$ and $t$directions in the nth block [57]:

$$x_i=\frac{1}{2}{L}_x\left(1-\cos \left(\frac{\pi \left(i-1\right)}{N-1}\right)\right), (i=1:N)$$

(36)

$$y_j=\frac{1}{2}{L}_y\left(1-\cos \left(\frac{\pi \left(j-1\right)}{M-1}\right)\right), (j=1:M)$$

(37)

$$t_k=\delta t\left[(ℝ-1)+\frac{1}{2}\left(1-\cos \left(\frac{\pi \left(k-1\right)}{L-1}\right)\right)\right], (k=1:L)$$

(38)

where $ℝ$ is the number of blocks, N and M denote the x and y—mesh width, and L denotes the block’s time level.

4. Numerical Results

In this section of our paper, the developed DQ techniques are examined on three test problems and demonstrate the accuracy and efficiency of the presented approaches. The developed techniques such as PDQM [37,38], DSCDQM-DLK, DSCDQM-RSK [51,52,58], and block marching with notion of Caputo are used for studying fractional order differential equations in both time and space for (1+2) dimensions fractional convection–diffusion equations. We carried out our calculations by creating MATLAB code for each method. The primary objective of our paper is to evaluate the performance, validity, efficiency, and accuracy of the developed techniques. We confirm this by comparing the computed results with existing numerical solutions [13,42,43,59] and analytical solutions [40,41,44]. To assess the convergence and accuracy of the developed methods, we use the error computation method outlined in [13,42,43,59]:

$$L_{\infty }^{} \mathrm{Error}=\underset{1 \le i \le N}{\max }\left|{\upsilon }_{\mathrm{numerical}}(x_i,t_l)-{\upsilon }_{\mathrm{exact}}(x_i,t_l)\right|$$

(39)

Problem 4.1.

The one-dimensional Riesz space fractional advection equation after substituting Equations (27) and (28) in (1):

$${\displaystyle \sum _{j=1}^L{\Re }_{ij}^{(1)}\upsilon \left(x,t_j\right)}=-C_x{\displaystyle \sum _{j=1}^N{\Re }_{ij}^{\beta }\upsilon \left(x_j,t\right)}$$

(40)

Also, to deal with the boundary and initial conditions (3,4), this was conducted through adapting the governing equations.

Now, we start to demonstrate the obtained results to know the reliability, stability, convergence, and performance of DQM based on three types of kernels and block marching with Caputo sense as follows:

Table 1. Computation of $L_{\infty }$ error norms in [0, 1] via uniform and non-uniform PDQM for problem (4.1) at different grid points (N), times (T), and number of blocks$\left(ℝ\right)$.$\beta =1.85, C_x=2, L=8$.

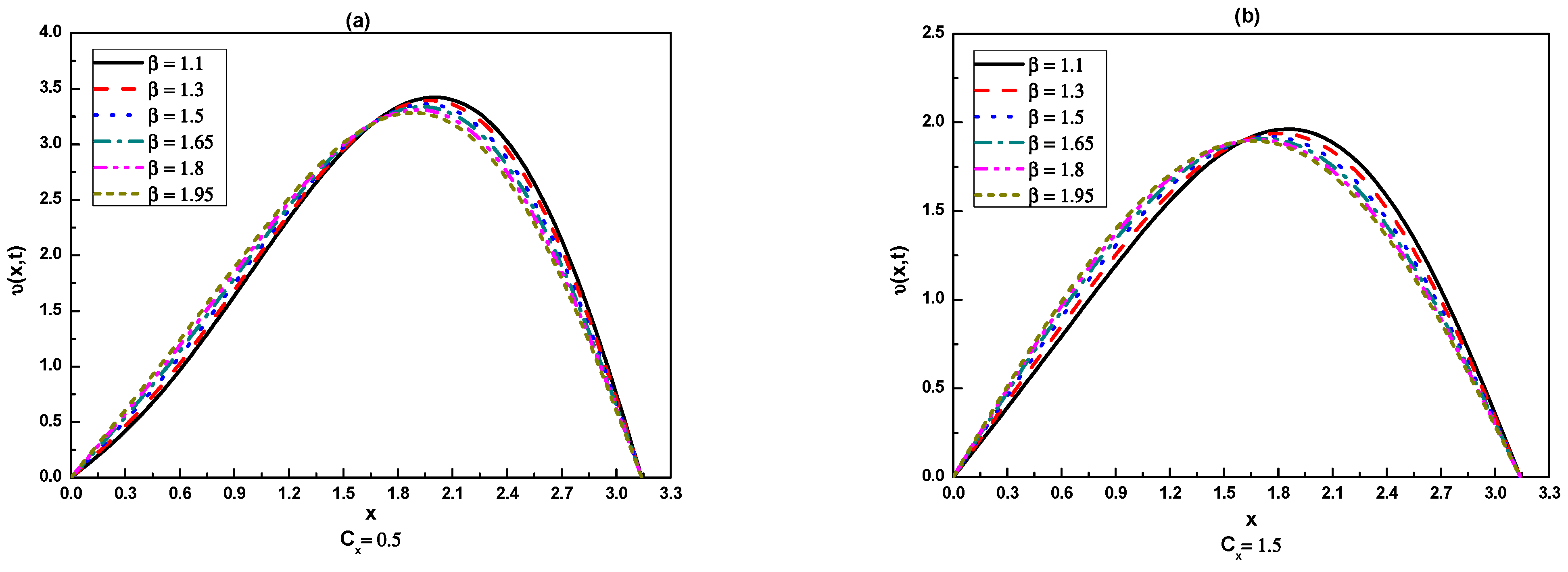
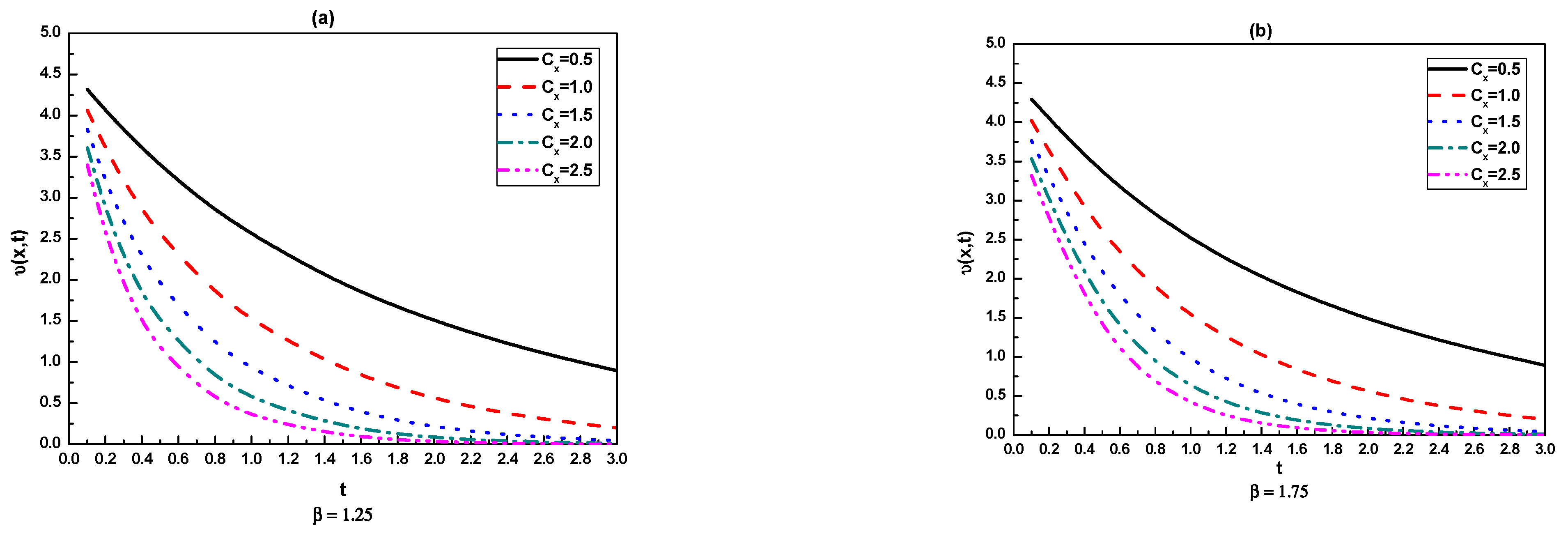
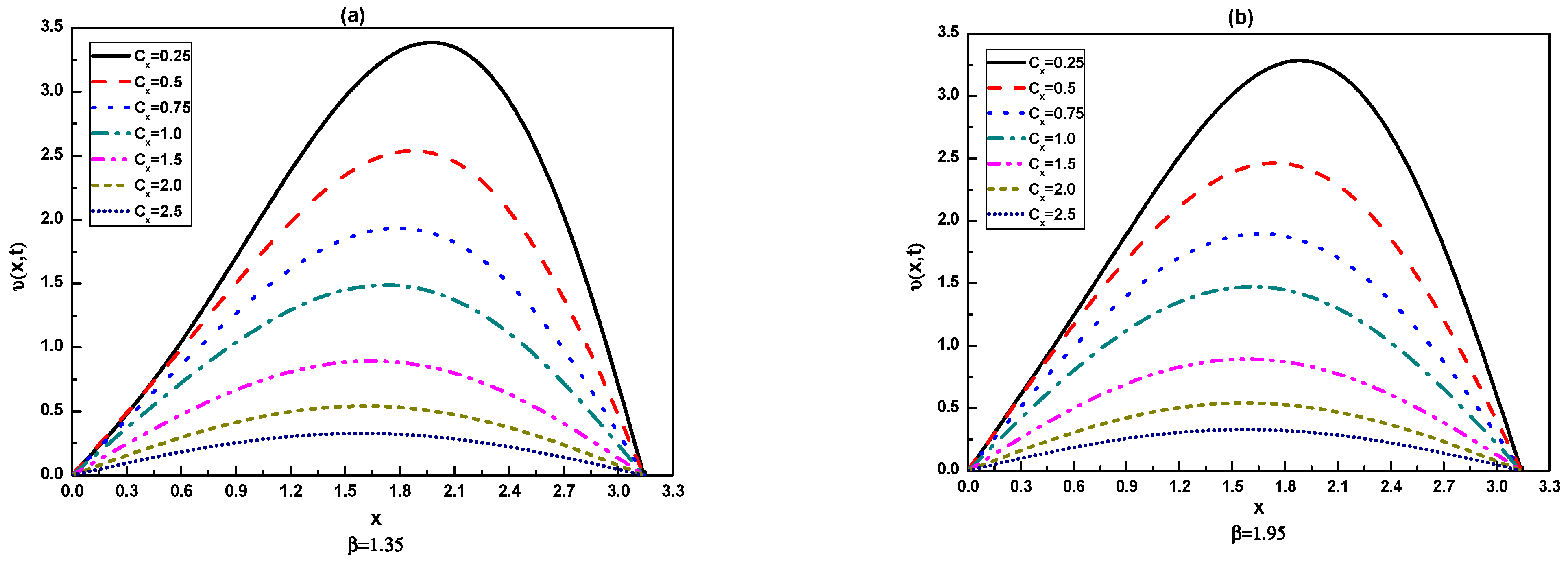
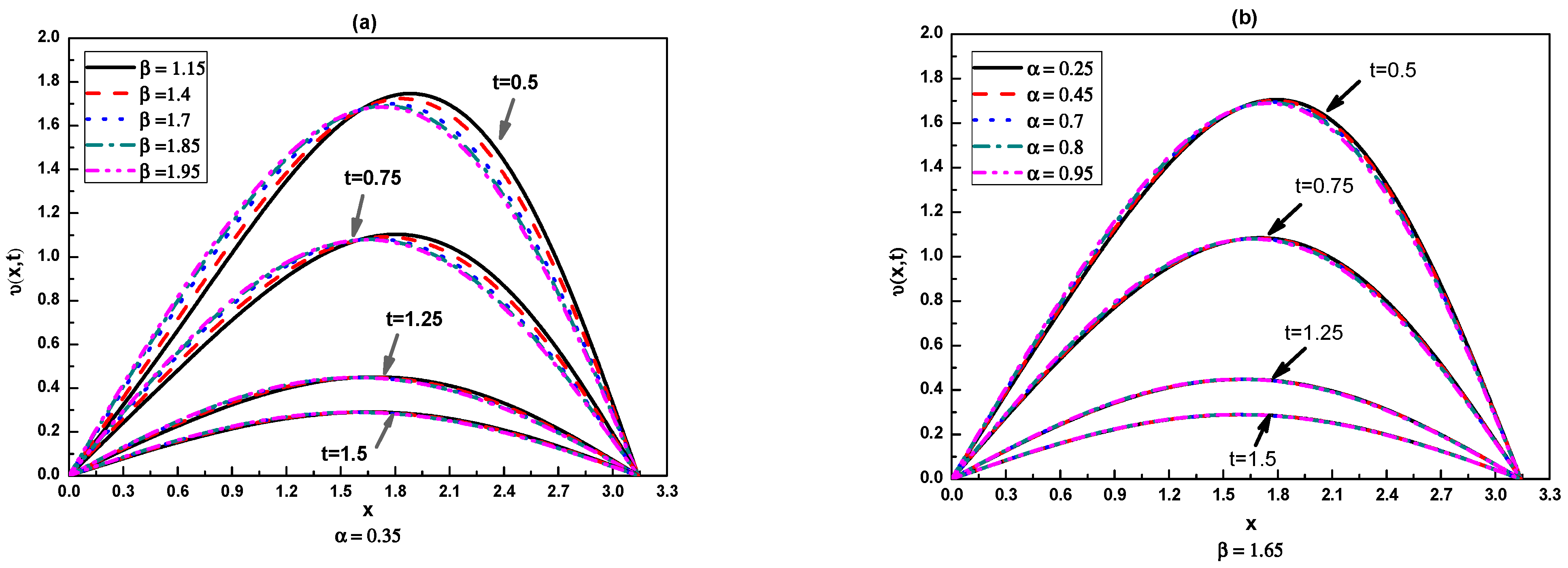
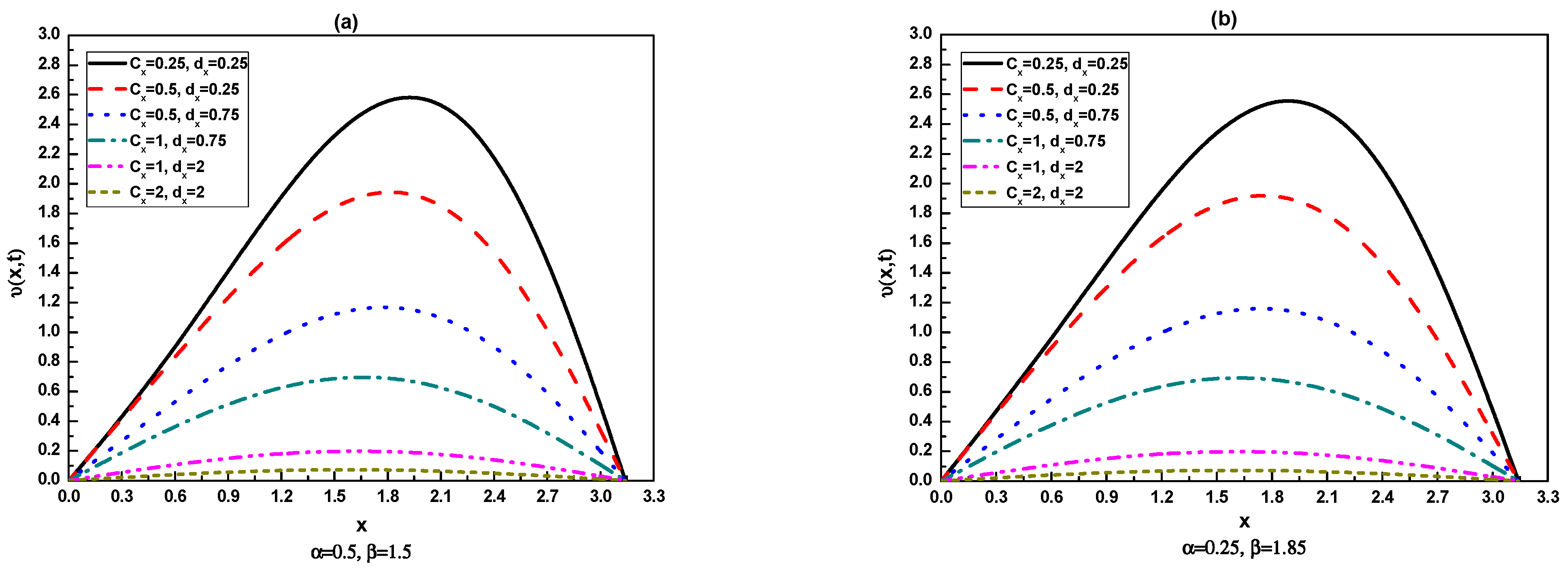
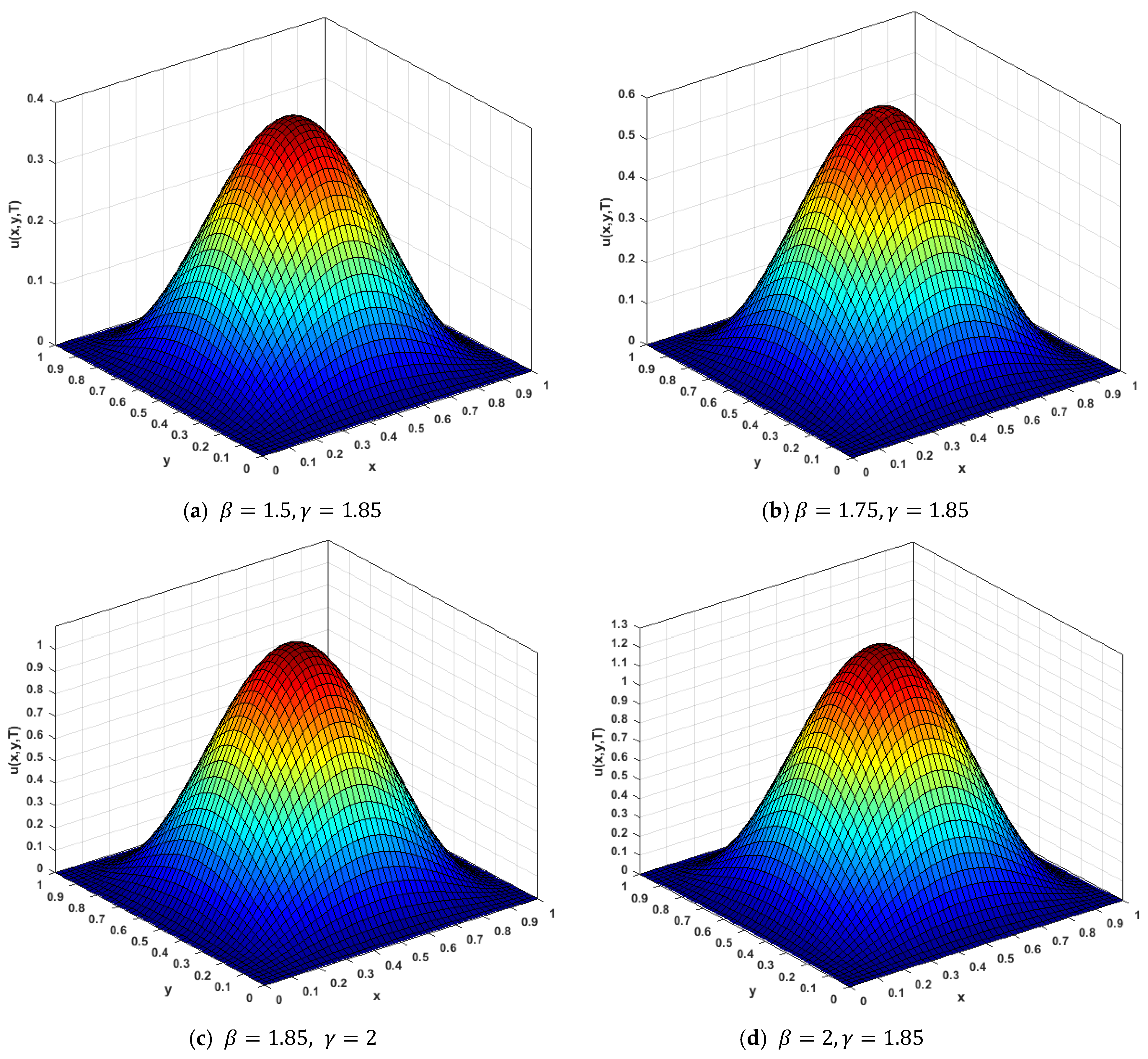
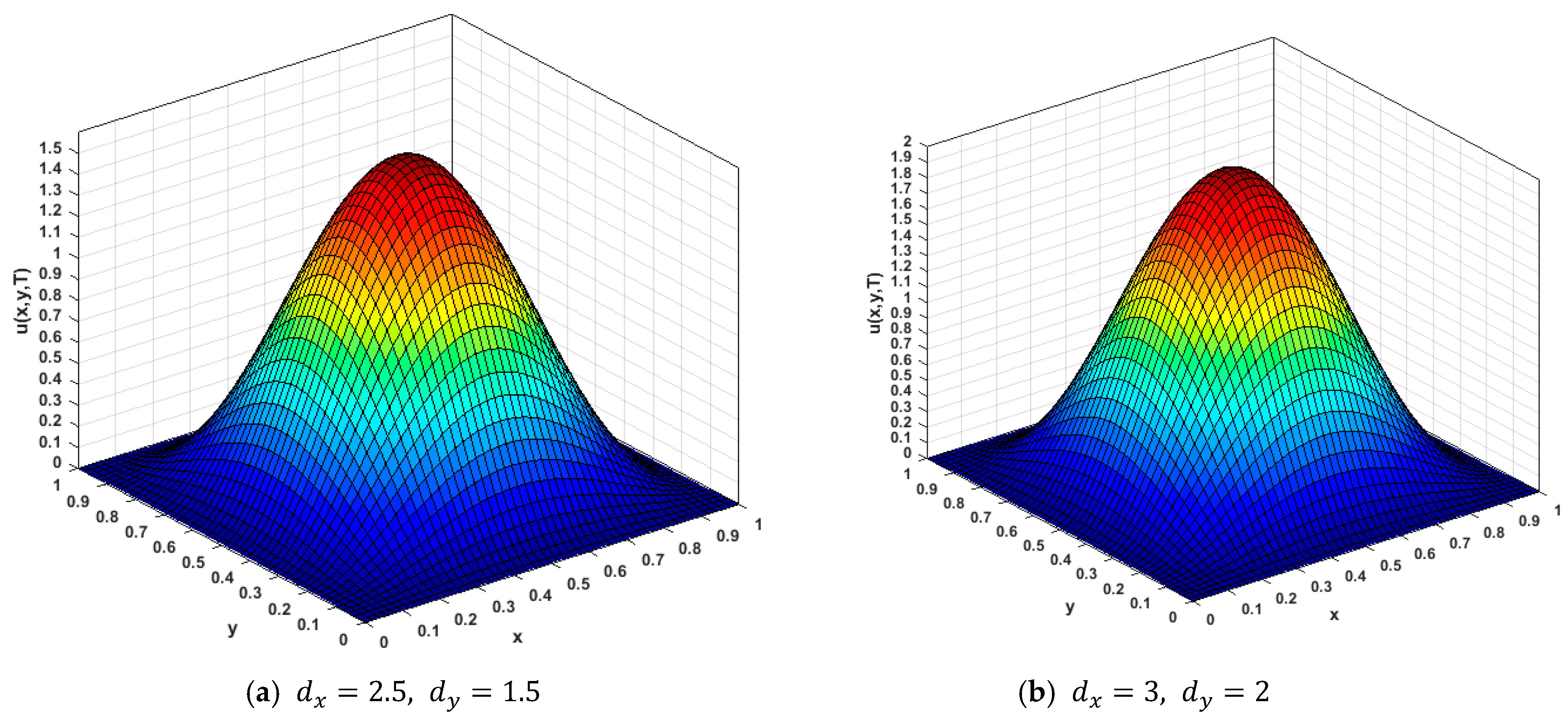
T	$\mathbf{ℝ}$	${\mathit{N}}_{\mathit{x}}\times {\mathit{N}}_{\mathit{t}}$	Uniform	CPU (s)	Non-Uniform	CPU (s)
1	3	4 × 4	0.0020	0.04	0.0009	0.03
		7 × 7	8.1287 × 10−5	0.05	7.4412 × 10−5	0.04
		11 × 11	3.5473 × 10−5	0.08	2.2825 × 10−5	0.07
		15 × 15	1.9741 × 10−5	0.11	6.3590 × 10−6	0.1
		20 × 20	7.1438 × 10−6	0.14	5.0111 × 10−6	0.12
		30 × 30	7.0035 × 10−6	0.16	5.0023 × 10−6	0.15
2	5	4 × 4	0.00859	0.05	0.00687	0.04
		7 × 7	1.8517 × 10−4	0.06	0.5667 × 10−4	0.05
		11 × 11	8.2024 × 10−5	0.11	4.3356 × 10−5	0.11
		15 × 15	4.8793 × 10−5	0.15	2.4123 × 10−5	0.14
		20 × 20	0.9991 × 10−5	0.16	7.0087 × 10−6	0.16
		30 × 30	9.0028 × 10−6	0.18	1.0885 × 10−6	0.17
3	7	4 × 4	0.0587	0.065	0.0098	0.06
		7 × 7	0.00247	0.07	0.00082	0.068
		11 × 11	9.2018 × 10−4	0.12	5.4402 × 10−4	0.11
		15 × 15	5.0011 × 10−4	0.16	1.9321 × 10−4	0.15
		20 × 20	9.0023 × 10−5	0.17	4.0185 × 10−5	0.165
		30 × 30	7.1616 × 10−5	0.20	2.8874 × 10−5	0.19
Earlier numerical solutions [13,42,43,59]		10 × 10	2.217 × 10−2
		20 × 20	5.759 × 10−3
		40 × 40	1.481 × 10−3
		80 × 80	3.727 × 10−4

shows the effect of applying uniform and non-uniform PDQM on computation of solute concentration $\upsilon \left(x,t\right)$ at $\beta =1.85, C_x=2, L=8$. It is noticed that the $L_{\infty }$ error is decreasing when the grid points are increasing, that is, the PDQM is stability in the x-direction, as well as the computed results via non-uniform grids are higher agree with earlier numerical solutions [13,42,43,59] than uniform ones. Also, $L_{\infty }$ error (1.0885 × 10⁻⁶) and performance time (0.17 s) for non-uniform PDQM achieved the least. Therefore, the computed results’ validity, efficiency, and accuracy to earlier numerical solutions via non-uniform PDQM are better than uniform PDQM. Increasing number of grids (30 × 30) leads to more accuracy at any number of blocks$\left(ℝ\right)$, but 3-blocks with 8-levels give the fewest CPU time. Furthermore, non-uniform PDQM with $N_x\times N_t=30\times 30$, $ℝ=3$, $L=8$ is better than uniform PDQM.

Table 2. Numerical results of solute concentration $\upsilon \left(x,t\right)$via DSCDQM-DLK and DSCDQM-RSK for problem (4.1) at different regularized Shannon factor $\left(\sigma =\tau \times \Delta \right)$, grid points (N), and bandwidth (2M+1). $\beta =1.85, C_x=0.5, L=8, ℝ=3 blocks, \delta t=0.5, T=1$.

${\mathit{N}}_{\mathit{x}}\times {\mathit{N}}_{\mathit{t}}$	2M+1	DSCDQM-DLK	DSCDQM-RSK
			$\mathit{\sigma }=1.2\times \mathbf{\Delta }$	$\mathit{\sigma }=1.3\times \mathbf{\Delta }$	$\mathit{\sigma }=1.45\times \mathbf{\Delta }$	$\mathit{\sigma }=1.5\times \mathbf{\Delta }$
7 × 7	3	5.0055	8.3321	5.0714	4.6247	4.5932
	5	4.8790	8.3198	5.0678	4.6005	4.5714
	7	4.6211	8.3025	5.0652	4.5932	4.5602
	9	4.5929	8.2577	5.0400	4.5929	4.5600
	11	4.5929	8.2577	5.0400	4.5929	4.5600
9 × 9	3	4.9657	8.2470	5.0666	4.6211	4.5928
	5	4.8001	8.2231	5.0641	4.5937	4.5710
	7	4.6111	8.2133	5.0352	4.5930	4.5599
	9	4.5929	8.2055	5.0344	4.5929	4.5599
	11	4.5929	8.2055	5.0344	4.5929	4.5599
11 × 11	3	4.9611	8.2466	5.0660	4.6209	4.5925
	5	4.7974	8.2225	5.0638	4.5932	4.5605
	7	4.6000	8.2055	5.0343	4.5929	4.5599
	9	4.5929	8.2055	5.0344	4.5929	4.5599
	11	4.5929	8.2055	5.0344	4.5929	4.5599
Earlier numerical solutions [13,42,43,59] $N_x\times N_t=100\times 100$		4.5929
Exact [40,41,44]		4.5929

and

Table 3. Numerical results of solute concentration $\upsilon \left(x,t\right)$via DSCDQM-DLK and DSCDQM-RSK for problem (4.1) at different regularized Shannon factor $\left(\sigma =\tau \times \Delta \right)$, grid points (N), and bandwidth (2M+1).$\beta =1.85, C_x=0.5, L=12, ℝ=3 blocks, \delta t=0.1, T=1$.

${\mathit{N}}_{\mathit{x}}\times {\mathit{N}}_{\mathit{t}}$	2M+1	DSCDQM-DLK		DSCDQM-RSK
				$\mathit{\sigma }=1.2\times \mathbf{\Delta }$	$\mathit{\sigma }=1.3\times \mathbf{\Delta }$	$\mathit{\sigma }=1.45\times \mathbf{\Delta }$	$\mathit{\sigma }=1.5\times \mathbf{\Delta }$
7 × 7	3	4.8322		8.1111	5.0512	4.6200	4.5911
	5	4.7595		8.0923	5.0439	4.5935	4.5706
	7	4.6101		8.0899	5.0399	4.5931	4.5592
	9	4.5929		8.0033	5.0296	4.5929	4.5588
	11	4.5929		8.0033	5.0296	4.5929	4.5288
9 × 9	3	4.8225		8.1109	5.0510	4.6199	4.5910
	5	4.7577		8.0915	5.0435	4.5931	4.5705
	7	4.6099		8.0885	5.0395	4.5930	4.5590
	9	4.5929		8.0033	5.0296	4.5929	4.5588
	11	4.5929		8.0033	5.0296	4.5929	4.5288
11 × 11	3	4.8200		8.1107	5.0508	4.6180	4.5908
	5	4.7510		8.0908	5.0433	4.5930	4.5702
	7	4.6000		8.0033	5.0390	4.5929	4.5588
	9	4.5929		8.0033	5.0296	4.5929	4.5588
	11	4.5929		8.0033	5.0296	4.5929	4.5288
Earlier numerical solutions [13,42,43,59] $N_x\times N_t=100\times 100$			4.5929
Exact [40,41,44]			4.5929

investigate the effect of values on the accuracy of DSCDQM-RSK and DSCDQM-DLK such as regularized Shannon factor$\left(\sigma \right)$, computational parameter$\left(\tau \right)$, and step size (Δ). Table 2 explains that DSCDQM-RSK is more accurate than DSCDQM-DLK for computing the solute concentration $\upsilon \left(x,t\right)$, compared with earlier numerical [13,42,43,59] and exact [40,41,44] solutions. Also, the bandwidth $\left(2M+1=7\right)$ and$\left(\sigma =1.45\times \Delta \right)$ are the most suitable choices for numerical results for problem (4.1), which achieve more efficient results. In addition, Table 2 and Table 3 exhibit that increasing the time levels (L) and decreasing the step size $\left(\delta t\right)$ for each block $\left(\delta t=0.1, L=12\right)$ lead to more efficiency at a lower bandwidth.

Table 4. Computation of $L_{\infty }$ error norms in [0, 1] via DSCDQM-DLK and DSCDQM-RSK for problem (4.1) at different grid points (N), times (T), and number of blocks $\left(ℝ\right)$. $\beta =1.85, C_x=2, L=8, \sigma =1.45\times \Delta$.

T	$\mathbf{ℝ}$	${\mathit{N}}_{\mathit{x}}\times {\mathit{N}}_{\mathit{t}}$	DSCDQM-DLK	CPU (s)	DSCDQM-RSK	CPU (s)
1	3	4 × 4	4.2547 × 10−4	0.03	4.0005 × 10−4	0.03
		7 × 7	3.00591 × 10−4	0.04	2.8741 × 10−4	0.03
		11 × 11	9.5479 × 10−5	0.07	9.0214 × 10−5	0.06
		15 × 15	9.01125 × 10−5	0.9	9.8881 × 10−6	0.08
		20 × 20	9.7841 × 10−6	0.10	8.9125 × 10−6	0.09
		30 × 30	7.8747 × 10−6	0.13	7.0012 × 10−6	0.12
2	5	4 × 4	0.0087	0.04	0.0032	0.04
		7 × 7	3.2147 × 10−4	0.05	2.1313 × 10−4	0.06
		11 × 11	1.0054 × 10−4	0.10	0.9881 × 10−4	0.09
		15 × 15	2.1524 × 10−5	0.13	1.9651 × 10−5	0.11
		20 × 20	0.3942 × 10−5	0.14	0.2089 × 10−5	0.13
		30 × 30	9.3530 × 10−6	0.16	8.91248 × 10−6	0.16
3	7	4 × 4	0.0974	0.06	0.0441	0.05
		7 × 7	0.0009	0.07	9.9874 × 10−4	0.07
		11 × 11	3.2525 × 10−4	0.11	2.9745 × 10−4	0.10
		15 × 15	9.0114 × 10−5	0.14	8.7815 × 10−5	0.12
		20 × 20	8.6478 × 10−5	0.15	8.0345 × 10−5	0.14
		30 × 30	9.0014 × 10−6	0.18	7.9992 × 10−6	0.17
Earlier numerical solutions [13,42,43,59]		10 × 10	2.217 × 10−2
		20 × 20	5.759 × 10−3
		40 × 40	1.481 × 10−3
		80 × 80	3.727 × 10−4

presents a comparison between DSCDQM-DLK and DSCDQM-RSK at different grid points (N), times (T), and number of blocks$\left(ℝ\right)$. The computed results proved that DSCDQM-RSK is the most efficient method compared with DSCDQM-DLK and PDQM. This preference belongs to low CPU time (0.12 s), $L_{\infty }$ error (7.0012 × 10⁻⁶).

Using the previously obtained conditions for$L=12, ℝ=3 blocks, \delta t=0.1, \sigma =1.45\times \Delta$ at $\beta =1.9,$ the numerical results of solute concentration $\upsilon \left(x,t\right)$and $L_{\infty }$ error norms via DSCDQM-DLK and DSCDQM-RSK at different values of velocity parameter coefficient ($C_x$) and time (T) are illustrated in

Table 5. Numerical results of solute concentration $\upsilon \left(x,t\right)$ and $L_{\infty }$ error norms via DSCDQM-DLK and DSCDQM-RSK for problem (4.1) at different grid points (N) and times (T).$\beta =1.9, L=12, ℝ=3 blocks, \delta t=0.1, \sigma =1.45\times \Delta$.

${\mathit{C}}_{\mathit{x}}$	T	DSCDQM-DLK	DSCDQM-RSK	Exact [40,41,44]	${\mathit{L}}_{\mathit{\infty }}$ Error Norms
0.5	1	2.466317	2.466317	2.466317	10−6
	1.5	1.890399	1.890398	1.890398	10−6
	2	1.471863	1.471863	1.471863	10−6
	2.5	1.146013	1.1460129	1.1460129	10−7
	3	0.8925198	0.8925198	0.8925198	10−7
1	1	1.471863	1.471863	1.471863	10−6
	1.5	0.89252	0.892519	0.892519	10−6
	2	0.541341	0.541341	0.541341	10−6
	2.5	0.32834	0.3283399	0.3283399	10−7
	3	0.1991483	0.1991482	0.1991482	10−7
1.5	1	0.89252	0.892519	0.892519	10−6
	1.5	0.421597	0.421596	0.421596	10−6
	2	0.1991482	0.1991482	0.199148	10−6
	2.5	0.094071	0.0940709	0.09407098	10−7
	3	0.044436	0.0444359	0.04443598	10−7
2	1	0.541341	0.541341	0.541341	10−6
	1.5	0.1991483	0.1991482	0.1991482	10−6
	2	0.0732626	0.0732625	0.0732625	10−6
	2.5	0.026952	0.0269517	0.0269517	10−7
	3	0.009915	0.00991500	0.00991500	10−7

. The results realized that increasing the values of the velocity parameter coefficient and time lead to more matching with exact values [40,41,44], with high accuracy with $L_{\infty }={10}^{-7}$.

Now, we can use DSCDQM-RSK with the previous best conditions to introduce detailed parametric studies for problem (4.1).

Figure 1 shows the variance of solute concentration with different fractions $\beta \in \left(1,2\right)$ and velocity parameter coefficients ($C_x$). Also, this figure demonstrates that when the value of ($C_x$) increases, the solute concentration decreases, but it increases with increasing fraction power $\beta$ up to $\left(x\approx 1.75\right)$, then decreases.

Figure 2 and Figure 3 show the relation between solute concentration, time and Riesz space at different fractions of $\beta \in \left(1,2\right)$, and velocity parameter coefficients ($C_x$). It is remarkable that from these figures, the solute concentration is inversely proportional to time and directly proportional to space up to $\left(x\approx 1.75\right)$.

Problem 4.2.

The one-dimensional Riesz space fractional advection–dispersion equation after substituting Equations (25) and (26) in (5):

$${\displaystyle \sum _{j=1}^L{\Re }_{ij}^{(1)}\upsilon \left(x,t_j\right)}=-C_x{\displaystyle \sum _{j=1}^N{\Re }_{ij}^{\alpha }\upsilon \left(x_j,t\right)}+d_x{\displaystyle \sum _{j=1}^N{\Re }_{ij}^{\beta }\upsilon \left(x_j,t\right)}$$

(41)

This equation is subjected to the boundary and initial conditions (8,9). Therefore, we deal with these conditions by adapting the governing equations.

In problem (4.2), we have solved this problem via DQM based on three types of kernels and block marching with Caputo sense. Therefore, we focus on determining the values whose influence is on the accuracy and convergence of the calculated results as uniform and non-uniform grid points, number of blocks, regularized Shannon factor$\left(\sigma \right)$, computational parameter $\left(\tau \right)$, and step size $\left(\Delta \right)$. The values of these parameters are recorded in

Table 6. Computation of $L_{\infty }$ error norms in [0, 1] via uniform and non-uniform PDQM for problem (4.2) at different grid points (N), times (T), and number of blocks$\left(ℝ\right)$.$\alpha =1, \beta =1.25, C_x=2, d_x=2, L=8$.

T	$\mathbf{ℝ}$	${\mathit{N}}_{\mathit{x}}\times {\mathit{N}}_{\mathit{t}}$	Uniform	CPU (s)	Non-Uniform	CPU (s)
1	3	4 × 4	0.0035	0.05	0.0011	0.04
		7 × 7	3.9743 × 10−4	0.06	1.8222 × 10−4	0.05
		11 × 11	1.7810 × 10−4	0.12	5.2824 × 10−5	0.10
		15 × 15	1.0461 × 10−4	0.15	2.3020 × 10−5	0.12
		20 × 20	6.4410 × 10−5	0.17	1.0636 × 10−5	0.13
		30 × 30	3.3502 × 10−5	0.19	3.7374 × 10−6	0.18
2	5	4 × 4	0.0871	0.05	0.0197	0.05
		7 × 7	5.5308 × 10−4	0.07	3.7420 × 10−4	0.06
		11 × 11	4.0382 × 10−4	0.13	1.2287 × 10−4	0.12
		15 × 15	2.4131 × 10−4	0.16	5.4123 × 10−5	0.15
		20 × 20	1.5008 × 10−4	0.18	2.5138 × 10−5	0.17
		30 × 30	7.8785 × 10−4	0.20	8.8650 × 10−6	0.19
3	7	4 × 4	0.9243	0.078	0.1893	0.06
		7 × 7	0.0085	0.089	4.8959 × 10−4	0.08
		11 × 11	6.3737 × 10−4	0.14	1.9956 × 10−4	0.11
		15 × 15	3.8886 × 10−4	0.17	8.8831 × 10−5	0.16
		20 × 20	2.4417 × 10−4	0.20	4.1470 × 10−5	0.19
		30 × 30	1.2855 × 10−4	0.22	1.4676 × 10−5	0.21
Earlier numerical solutions [13,42,43,59]		10 × 10	1.70 × 10−2
		20 × 20	4.4 × 10−3
		40 × 40	1.1 × 10−3
		80 × 80	2.7919 × 10−4
		160 × 160	6.9932 × 10−4

,

Table 7. Numerical results of solute concentration $\upsilon \left(x,t\right)$via DSCDQM-DLK and DSCDQM-RSK for problem (4.2) at different regularized Shannon factor $\left(\sigma =\tau \times \Delta \right)$, grid points (N), and bandwidth (2M+1).$\alpha =0.75, \beta =1.85, C_x=0.5, d_x=1.5, ℝ=3 blocks, \delta t=0.5, L=8, T=1$.

${\mathit{N}}_{\mathit{x}}\times {\mathit{N}}_{\mathit{t}}$	2M+1		DSCDQM-DLK	DSCDQM-RSK
				$\mathit{\sigma }=1.0\times \mathbf{\Delta }$	$\mathit{\sigma }=1.25\times \mathbf{\Delta }$	$\mathit{\sigma }=1.3\times \mathbf{\Delta }$	$\mathit{\sigma }=1.35\times \mathbf{\Delta }$
7 × 7	3		1.364173	7.369612	1.49798649	0.59077	0.6206803
	5		0.855820	5.031103	1.22468775	0.55218	0.6065857
	7		0.6120001	4.324652	0.94795129	0.544277	0.601601
	9		0.5489179	2.588603	0.77950301	0.5432457	0.5976476
	11		0.54315976	2.573993	0.77520586	0.5431598	0.593952
9 × 9	3		0.7522591	5.3551083	1.31063075	0.5710912	0.6148362
	5		0.6465491	4.8875784	1.20578029	0.5515822	0.602117
	7		0.5586295	3.869154	0.88263461	0.5440192	0.5930067
	9		0.54401919	2.0033313	0.73653151	0.5431598	0.585358
	11		0.54315976	2.0033313	0.73653151	0.5431598	0.585358
11 × 11	3		0.6885753	4.0367427	1.13874475	0.5520119	0.6004837
	5		0.63236859	3.0483982	1.05022346	0.5446208	0.5882798
	7		0.58793606	2.5714146	0.85951594	0.5438473	0.576935
	9		0.54324570	1.7059686	0.67637141	0.5431598	0.5689426
	11		0.54315976	1.7059686	0.67637141	0.5431598	0.5689426
Earlier numerical solutions [13,42,43,59] $N_x\times N_t=100\times 100$		0.54316
Exact [40,41,44]		0.54316

and

Table 8. Numerical results of solute concentration $\upsilon \left(x,t\right)$via DSCDQM-DLK and DSCDQM-RSK for problem (4.2) at different regularized Shannon factor $\left(\sigma =\tau \times \Delta \right)$, grid points (N), and bandwidth (2M+1). $\alpha =0.75, \beta =1.85, C_x=0.5, d_x=1.5, ℝ=3 blocks, \delta t=0.1, L=12, T=1$.

${\mathit{N}}_{\mathit{x}}\times {\mathit{N}}_{\mathit{t}}$	2M+1	DSCDQM-DLK	DSCDQM-RSK
			$\mathit{\sigma }=1.0\times \mathbf{\Delta }$	$\mathit{\sigma }=1.25\times \mathbf{\Delta }$	$\mathit{\sigma }=1.3\times \mathbf{\Delta }$	$\mathit{\sigma }=1.35\times \mathbf{\Delta }$
7 × 7	3	0.81388021	3.4265474	0.93420041	0.5566528	0.6196490
	5	0.57238038	2.6719679	0.90669865	0.5511525	0.6013432
	7	0.54917577	2.60837	0.86200829	0.5435895	0.5957569
	9	0.54315976	2.5739929	0.77520586	0.5431598	0.5939521
	11	0.54315976	2.5739929	0.77520586	0.5431598	0.5939521
9 × 9	3	0.69957602	3.1291846	0.8508357	0.5517541	0.5962725
	5	0.54745691	2.1202138	0.82934995	0.5508946	0.5930067
	7	0.54487862	2.0643509	0.76317384	0.5433316	0.5854437
	9	0.54315976	2.0033313	0.73653151	0.5431598	0.5853578
	11	0.54315976	2.0033313	0.73653151	0.5431598	0.5853578
11 × 11	3	0.60417929	3.0956669	0.76747099	0.5508946	0.5778807
	5	0.54573805	2.0153634	0.75114182	0.5442770	0.5757322
	7	0.54315976	1.7472212	0.68668457	0.5431598	0.5692005
	9	0.54315976	1.7059686	0.67637141	0.5431598	0.5689427
	11	0.54315976	1.7059686	0.67637141	0.5431598	0.5689427
Earlier numerical solutions [13,42,43,59] $N_x\times N_t=100\times 100$		0.54316
Exact [40,41,44]		0.54316

.

In Table 6, it is found that the computed results for solute concentration $\upsilon \left(x,t\right)$ at $\alpha =1, \beta =1.25, C_x=2, d_x=2, L=8$ by PDQM with non-uniform grids are higher in agreement with earlier numerical solutions [13,42,43,59] than uniform ones at $N_x\times N_t=30\times 30$,$ℝ=3, L=8, L_{\infty }$ error (3.7374 × 10⁻⁶) and performance time (0.18 s).

Also, Table 7 and Table 8 produce the best values for bandwidth $\left(2M+1=9\right)$, and$\sigma =1.3\times \Delta$ that achieves DSCDQM-RSK is more accurate than DSCDQM-DLK for computing the solute concentration $\upsilon \left(x,t\right)$, compared with earlier numerical [13,42,43,59] and exact [40,41,44] solutions. And these tables explain that increasing the time levels (L) and decreasing the step size $\left(\delta t\right)$ for each block$\left(\delta t=0.1, L=12\right)$ lead to more efficiency at a lower bandwidth.

In addition,

Table 9. Computation of $L_{\infty }$ error norms in [0, 1] via DSCDQM-DLK and DSCDQM-RSK for problem (4.2) at different grid points (N), times (T), and number of blocks $\left(ℝ\right)$.$\alpha =1, \beta =1.25, C_x=2, d_x=2, L=8, \sigma =1.3\times \Delta$.

T	$\left(\mathbf{ℝ}\right)$	${\mathit{N}}_{\mathit{x}}\times {\mathit{N}}_{\mathit{t}}$	DSCDQM-DLK	CPU (s)	DSCDQM-RSK	CPU (s)
1	3	4 × 4	4.8206 × 10−4	0.035	5.1248 × 10−4	0.03
		7 × 7	3.0167 × 10−4	0.05	2.5357 × 10−4	0.036
		11 × 11	1.5084 × 10−4	0.08	1.3345 × 10−4	0.065
		15 × 15	9.3066 × 10−5	0.10	8.4774 × 10−5	0.09
		20 × 20	5.9753 × 10−5	0.11	5.5136 × 10−5	0.097
		30 × 30	3.1624 × 10−5	0.15	3.0054 × 10−5	0.13
2	5	4 × 4	0.0144	0.042	0.0036	0.038
		7 × 7	6.9981 × 10−4	0.055	5.6238 × 10−4	0.062
		11 × 11	3.4394 × 10−4	0.10	3.0571 × 10−4	0.093
		15 × 15	2.1524 × 10−4	0.13	1.9651 × 10−4	0.11
		20 × 20	1.3942 × 10−4	0.15	1.2879 × 10−4	0.135
		30 × 30	7.3970 × 10−5	0.17	7.0371 × 10−5	0.16
3	7	4 × 4	0.2326	0.063	0.0578	0.055
		7 × 7	0.0027	0.072	6.5842 × 10−4	0.068
		11 × 11	5.4871 × 10−4	0.105	4.8945 × 10−4	0.09
		15 × 15	3.4771 × 10−4	0.12	3.1815 × 10−4	0.11
		20 × 20	2.2711 × 10−4	0.14	2.1005 × 10−4	0.13
		30 × 30	1.2252 × 10−4	0.16	1.1680 × 10−4	0.155
Earlier numerical solutions [13,42,43,59]		10 × 10	1.75 × 10−2
		20 × 20	4.5 × 10−3
		40 × 40	1.1 × 10−3
		80 × 80	2.8337 × 10−4
		160 × 160	7.0902 × 10−5

demonstrates that DSCDQM-RSK is the most efficient method compared with DSCDQM-DLK and PDQM, which recorded low CPU time (0.13 s), $L_{\infty }$ error (3.0054 × 10⁻⁵).

Moreover, from all results in Table 6, Table 7, Table 8 and Table 9, it is noted that the computed results are more accurate and converge at$ℝ=3 blocks, \delta t=0.1, L=12, \sigma =1.3\times \Delta$and $\alpha =0.5, \beta =1.9$ via DSCDQM-RSK. Then, in

Table 10. Numerical results of solute concentration$\upsilon \left(x,t\right)$and $L_{\infty }$ error norms via PDQM, DSCDQM-DLK, and DSCDQM-RSK for problem (4.2) at different grid points (N) and times (T). $\alpha =0.5, \beta =1.9, L=12, \sigma =1.3\times \Delta , ℝ=3 blocks, \delta t=0.1$.

(${\mathit{C}}_{\mathit{x}}, {\mathit{d}}_{\mathit{x}}$)	T	DSCDQM-DLK	DSCDQM-RSK	Exact [40,41,44]	${\mathit{L}}_{\mathit{\infty }}$ Error Norms
(0.5, 1)	1	0.892502	0.892501	0.892501	10−6
	1.5	0.421598	0.421597	0.4215967	10−6
	2	0.1991484	0.1991483	0.1991483	10−6
	2.5	0.094072	0.09407098	0.094071	10−7
	3	0.044437	0.044436	0.044436	10−7
(1, 1.5)	1	0.328342	0.3283398	0.3283398	10−6
	1.5	0.0940714	0.094071	0.094071	10−6
	2	0.0269518	0.02695179	0.02695179	10−6
	2.5	0.0077219	0.0077218	0.0077218	10−7
	3	0.0022124	0.0022123	0.0022123	10−7
(1.5, 2)	1	0.1207896	0.1207895	0.1207895	10−6
	1.5	0.0209900	0.0209900	0.0209900	10−6
	2	0.003647528	0.003647527	0.003647527	10−6
	2.5	0.00063385	0.000633845	0.000633845	10−7
	3	0.000110147	0.000110146	0.000110146	10−7
(2, 2.5)	1	0.044436	0.04443599	0.04443599	10−6
	1.5	0.00468353	0.00468352	0.00468352	10−6
	2	0.0004936392	0.0004936392	0.000493639	10−6
	2.5	5.20291906 × 10−5	5.20291906 × 10−5	5.20291906 × 10−5	10−7
	3	5.4838363 × 10−6	5.4838363 × 10−46	5.4838363 × 10−6	10−7

, we present the numerical results of solute concentration $\upsilon \left(x,t\right)$ and $L_{\infty }$ error norms via DSCDQM-DLK and DSCDQM-RSK at the different values of the velocity parameter coefficient ($C_x, d_x$) and time (T). The results proved that increasing the values of ($C_x, d_x$) and time lead to more matching with exact values [40,41,44], with high accuracy with $L_{\infty }={10}^{-7}$

Finally, we introduce the parametric studies for problem (4.2) via DSCDQM-RSK to show the flexibility and reliability of this method.

Figure 4 explains the effects of fractions$\beta \in \left(1,2\right)$ and $\alpha \in \left(0,1\right)$ on the solute concentration. This figure indicates that when the fraction (α) increased, the solute concentration decreases. But it increases with increasing the fraction power (β) up to x ≈ 1.75, then decreases.

Also, Figure 5 exhibits the influence of the solute concentration with change in the time and fractions of $\beta \in \left(1,2\right)$ and $\alpha \in \left(0,1\right)$. The solute concentration is directly proportional to $\left(\alpha ,\beta \right)$ up to $x\approx 1.75$, then decreases and is inversely proportional to time.

And Figure 6 displays the relation between solute concentration and different $C_x$ and $d_x$ at different fractions of $\beta \in \left(1,2\right)$ and $\alpha \in \left(0,1\right)$. The solute concentration is inversely proportional to different coefficients ($C_x$ and $d_x$).

Problem 4.3.

The 2-D fractional diffusion equation with source term after substituting Equations (27) and (28) in (11):

$${\displaystyle \sum _{k=1}^L{\Re }_{i,j,k}^{(1)}\upsilon \left(x,y,t_k\right)}=d_x{\displaystyle \sum _{k=1}^N{\Re }_{i,j,k}^{\beta }\upsilon \left(x_k,y,t\right)}+d_y{\displaystyle \sum _{k=1}^M{\Re }_{i,j,k}^{\gamma }\upsilon \left(x,y_k,t\right)}$$

(42)

This equation is subjected to the boundary and initial conditions (13,14). Therefore, we deal with these conditions by adapting the governing equations.

In problem (4.3), we have solved this problem via DSCDQM-RSK$\left(L=12, ℝ=3 blocks, \delta t=0.1,\sigma =1.3\times \Delta \right)$ and block marching with Caputo sense. The following formula is used to determine the order of convergence in both space and time for a 2-D fractional diffusion equation:

$$\mathrm{Order} \mathrm{of} \mathrm{Convergence} \left(\mathrm{ROC}\right)=\log {}_2 \left(\frac{{‖E\left({\Delta }_x,{\Delta }_y,{\Delta }_t\right)‖}_{\infty }}{{‖E\left({\Delta }_x/2,{\Delta }_y/2,{\Delta }_t/2\right)‖}_{\infty }}\right)$$

(43)

where $\Vert E{\left({\Delta }_x,{\Delta }_y,{\Delta }_t\right)\Vert }_{\infty }$ is the maximum error for a two-dimensional space fractional problem.

Table 11. Convergence order and maximum error via DSCDQM-RSK for problem (4.3) at different step size$\left({\Delta }_x,{\Delta }_y,{\Delta }_t\right)$ and fractional orders for $\left(T=1, L=12, ℝ=3 blocks, \sigma =1.3\times \Delta , \delta t=0.1, \mathrm{and} d_x=d_y=2\right)$.

	${\mathbf{\Delta }}_{\mathit{x}}={\mathbf{\Delta }}_{\mathit{y}}={\mathbf{\Delta }}_{\mathit{t}}$	$\mathit{\gamma }=1.5$		$\mathit{\gamma }=1.95$		CPU (s)
		$\Vert \mathit{E}{\left({\mathbf{\Delta }}_{\mathit{x}},{\mathbf{\Delta }}_{\mathit{y}},{\mathbf{\Delta }}_{\mathit{t}}\right)\Vert }_{\mathit{\infty }}$	Order	$\Vert \mathit{E}{\left({\mathbf{\Delta }}_{\mathit{x}},{\mathbf{\Delta }}_{\mathit{y}},{\mathbf{\Delta }}_{\mathit{t}}\right)\Vert }_{\mathit{\infty }}$	Order
$\beta =1.85$	0.5	2.05 × 10−3	---	1.6 × 10−3	---	0.05
	0.1	2.59 × 10−4	2.0193	4.05 × 10−4	1.98207	0.07
	0.05	6.56 × 10−5	1.9812	9.62 × 10−5	2.0738	0.09
	0.025	1.57 × 10−5	2.0629	2.35 × 10−5	2.0333	0.15
Earlier numerical solutions [13,42,43,59]	0.1	2.57 × 10−2	---	1.56 × 10−2	---	---
	0.05	5.5 × 10−3	2.2243	3.2 × 10−3	2.2854	---
	0.025	7.41 × 10−4	2.4894	7.97 × 10−4	2.0056	---
	0.0125	1.66 × 10−4	2.1565	1.9977 × 10−4	1.9961	---

shows the stability and convergence of DSCDQM-RSK for solving a two-dimensional space fractional problem. Also, the performance time of this method is calculated to ensure that DSCDQM-RSK is an effective method for such problems.

Figure 7 and Figure 8 demonstrate the effects of fractions $\beta ,\gamma \in \left(1,2\right)$ on the solute concentration $\upsilon \left(x,y,t\right)$. These figures show that this method is flexible when altering the fraction order $\left(\beta \mathrm{or} \gamma \right)$, which raises the solute concentration when they increase. According to Figure 8, when fractional orders are equal$\beta =\gamma =2$, the diffusion coefficients have a significant impact on the solute concentration results, and their effect increases as they increase.

5. Conclusions

This work presents effective numerical techniques for solving fractional advection and advection–dispersion equations in (1+2) dimensional Riesz space. The developed methods utilize unique shape functions, including Lagrange interpolation polynomial, delta Lagrange, and Regularized Shannon kernels, within the framework of the differential quadrature method (DQM). Additionally, the Caputo type is applied to treat the fractional differential operators. Also, to achieve more accurate and efficient results we used the block marching technique to deal with time dependency. Therefore, a MATLAB program was used to design code for solving three tested problems.

According to the presented techniques, we solved the considered problems in which the numerical evidence confirmed the earlier established numerical [13,42,43,44,59,60] and exact [40,41,44] solutions. Further, we confirmed that the convergence of the offered techniques by calculating L_∞ error norms. Therefore, the results computed via our methods are much more accurate, stable, and efficient. The best values of parameters, which control our methods, are$L=12, ℝ=3 blocks, \delta t=0.1$, mesh size > (7 × 7), and $\sigma =1.45\times \Delta$for problem (1) and$\sigma =1.3\times \Delta$for problems (2–3), and these values were achieved at $L_{\infty }={10}^{-7}$ and computation time = 0.036 s.

Furthermore, we investigated the effect of the velocity parameter, positive diffusion coefficients, and fractional order derivative at different locations and times on the solute concentration. The solute concentration is directly proportional to (α, β) up to (x ≈ 1.75), then decreases and is inversely proportional to time. Also, the solute concentration is inversely proportional to different coefficients (C_x and d_x). If the fractional orders are the same, the diffusion coefficients will strongly influence the solute concentration results, and the impact will become greater as the coefficients increase. Additionally, it has been discovered that the suggested methods possess a distinct ability to solve fractional partial differential equations with both initial and boundary conditions. As a result, there is optimism that these techniques can be employed to tackle other nonlinear fractional problems that arise in a variety of fields within applied science.