Quasi-Cauchy Regression Modeling for Fractiles Based on Data Supported in the Unit Interval
Abstract
:1. Introduction
2. Fractile Regression for Data in the Unit Interval
2.1. Prelude to Fractile Regression
2.2. Conditions Necessary for the Link Function
2.3. Choice of the Link Function
2.4. Interpretation
2.5. Simulation Study
- Step 1: Select an appropriate link function that satisfies the conditions mentioned in Section 2.2.
- Step 3: Use the expression for given in (8) to ascertain the impact of changing one unit of the covariate on the response variable.
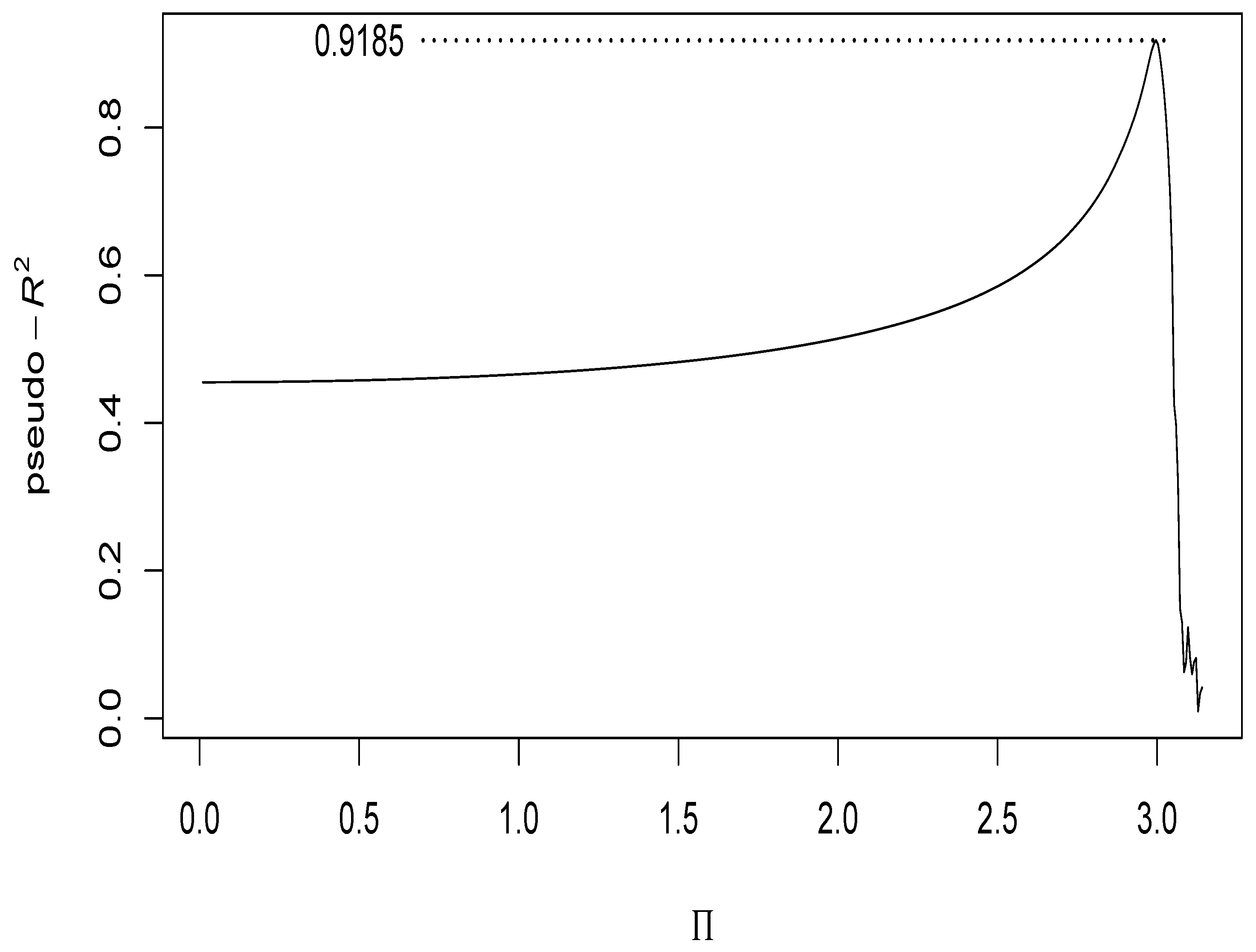
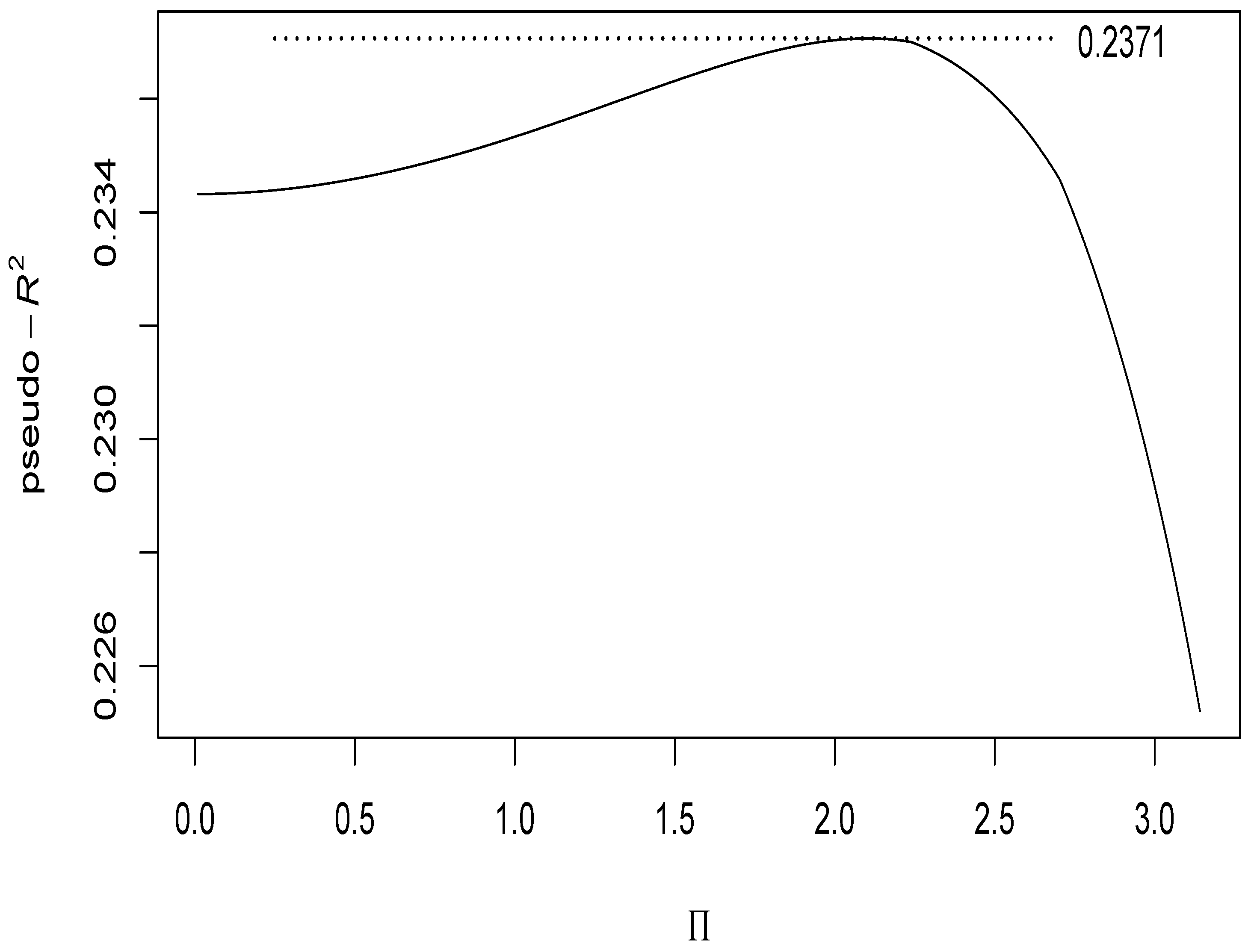
2.6. Choosing the Value for
3. Applications
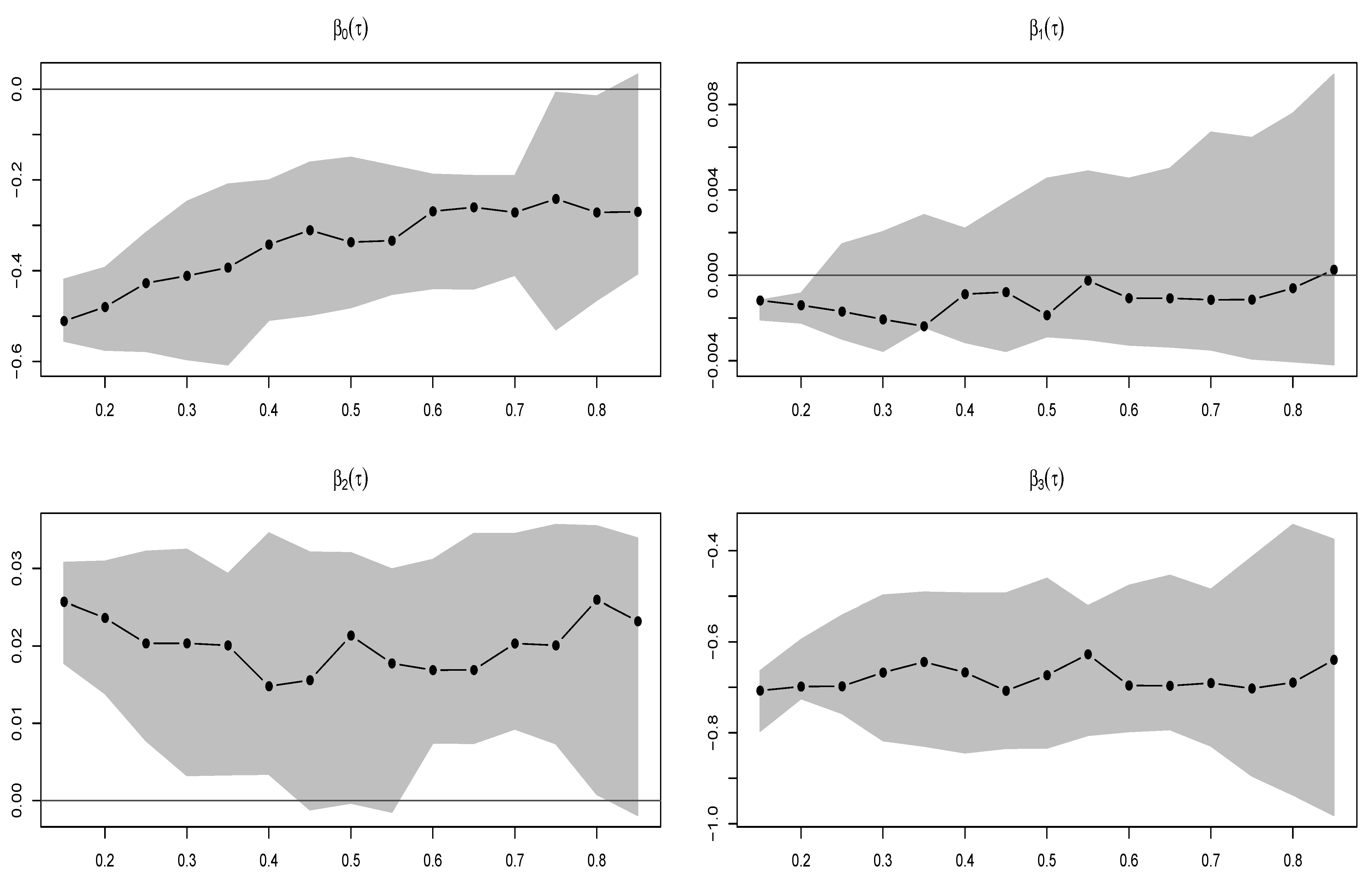
3.1. Application 1
3.2. Application 2
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; Wiley: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; Wiley: New York, NY, USA, 1995; Volume 2. [Google Scholar]
- Kotz, S.; Leiva, V.; Sanhueza, A. Two new mixture models related to the inverse Gaussian distribution. Methodol. Comput. Appl. Probab. 2010, 12, 199–212. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.; Dey, S. The unit-Birnbaum-Saunders distribution with applications. Chil. J. Stat. 2018, 9, 47–57. [Google Scholar]
- Shahin, A.I.; Almotairi, S. A deep learning BiLSTM encoding-decoding model for COVID-19 pandemic spread forecasting. Fractal Fract. 2021, 5, 175. [Google Scholar] [CrossRef]
- Ribeiro, T.F.; Cordeiro, G.M.; Peña-Ramírez, F.A.; Guerra, R.R. A new quantile regression for the COVID-19 mortality rates in the United States. Comput. Appl. Math. 2022, 40, 255. [Google Scholar] [CrossRef]
- Mazucheli, M.; Alves, B.; Menezes, A.F.B.; Leiva, V. An overview on parametric quantile regression models and their computational implementation with applications to biomedical problems including COVID-19 data. Comput. Methods Programs Biomed. 2022, 221, 106816. [Google Scholar] [CrossRef]
- Li, S.; Chen, J.; Li, B. Estimation and testing of random effects semiparametric regression model with separable space-time filters. Fractal Fract. 2022, 6, 735. [Google Scholar] [CrossRef]
- Jiang, J. Linear and Generalized Linear Mixed Models and Their Applications; Springer: New York, NY, USA, 2006. [Google Scholar]
- Leiva, V.; Rojas, E.; Galea, M.; Sanhueza, A. Diagnostics in Birnbaum-Saunders accelerated life models with an application to fatigue data. Appl. Stoch. Model. Bus. Ind. 2014, 30, 115–131. [Google Scholar] [CrossRef]
- Ramalho, E.A.; Ramalho, J.J.; Murteira, J.M. Alternative estimating and testing empirical strategies for fractional regression models. J. Econ. Surv. 2011, 25, 19–68. [Google Scholar] [CrossRef]
- Papke, L.E.; Wooldridge, J. Econometric methods for fractional response variables with an application to 401(k) plan participation rates. J. Appl. Econom. 1996, 11, 619–632. [Google Scholar] [CrossRef]
- Ferrari, S.; Cribari-Neto, F. Beta regression for modelling rates and proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Smithson, M.; Verkuilen, J. A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables. Psychol. Methods 2006, 11, 54–71. [Google Scholar] [CrossRef] [PubMed]
- Mazucheli, J.; Menezes, A.F.B.; Chakraborty, S. On the one parameter unit-Lindley distribution and its associated regression model for proportion data. J. Appl. Stat. 2019, 46, 700–714. [Google Scholar] [CrossRef]
- Altun, E.; El-Morshedy, M.; Eliwa, M. A new regression model for bounded response variable: An alternative to the beta and unit-Lindley regression models. PLoS ONE 2021, 16, e0245627. [Google Scholar] [CrossRef] [PubMed]
- Ospina, R.; Ferrari, S.L. A general class of zero-or-one inflated beta regression models. Comput. Stat. Data Anal. 2012, 56, 1609–1623. [Google Scholar] [CrossRef]
- Korkmaz, M.; Chesneau, C. On the unit Burr-XII distribution with the quantile regression modeling and applications. Comput. Appl. Math. 2021, 40, 29. [Google Scholar] [CrossRef]
- Korkmaz, M.; Korkmaz, Z.S. The unit log-log distribution: A new distribution with alternative quantile regression modeling and educational measurements applications. J. Appl. Stat. 2023, 50, 889–908. [Google Scholar] [CrossRef]
- Leiva, V.; Mazucheli, J.; Alves, B. A novel regression model for fractiles: Formulation, computational aspects, and applications to medical data. Fractal Fract. 2023, 7, 169. [Google Scholar] [CrossRef]
- Korkmaz, M.; Leiva, V.; Martin, C. The continuous Bernoulli distribution: Mathematical characterization, fractile regression, computational simulations, and applications. Fractal Fract. 2023, 7, 386. [Google Scholar] [CrossRef]
- Saulo, H.; Vila, R.; Bittencourt, V.; Leao, J.; Leiva, V.; Christakos, G. On a new extreme value distribution: Characterization, parametric quantile regression, and application to extreme air pollution events. Stoch. Environ. Res. Risk Assess. 2023, 37, 1119–1136. [Google Scholar] [CrossRef]
- Saulo, H.; Vila, R.; Borges, G.; Bourguignon, M.; Leiva, V.; Marchant, C. Modeling income data via new quantile regressions: Formulation, computation, and application. Mathematics 2023, 11, 448. [Google Scholar] [CrossRef]
- Bottai, M.; Cai, B.; McKeown, R.E. Logistic quantile regression for bounded outcomes. Stat. Med. 2010, 29, 309–317. [Google Scholar] [CrossRef] [PubMed]
- Lindsey, J.K. Applying Generalized Linear Models; Springer: New York, NY, USA, 2000. [Google Scholar]
- Koenker, R.; Bassett, G. Regression quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Koenker, R. Quantile Regression; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Bonat, W.H.; Lopes, J.E.; Shimakura, S.E.; Ribeiro, P.J., Jr. Likelihood analysis for a class of simplex mixed models. Chil. J. Stat. 2018, 9, 3–17. [Google Scholar]
- dos Santos, A.R.P.; de Faria, R.Q.; Amorim, D.J.; Giandoni, V.C.R.; da Silva, E.A.A.; Sartori, M.M.P. Cauchy, Cauchy-Santos-Sartori-Faria, logit, and probit functions for estimating seed longevity in soybean. Agron. J. 2019, 111, 2929–2939. [Google Scholar] [CrossRef]
- Shoemaker, A.C. Effects of misspecification of the link function in models for binomial data. J. Stat. Plan. Inference 1984, 33, 213–231. [Google Scholar]
- Koenker, R. Quantreg: Quantile Regression. R Package Version 5.86. 2021. Available online: https://CRAN.R-project.org/package=quantreg (accessed on 13 July 2023).
- Cox, D.R.; Hinkley, D.V. Theoretical Statistics; CRC Press: Boca-Raton, FL, USA, 1979. [Google Scholar]
- Griffiths, W.; Hill, C.; Judge, R.; Griffiths, G.G.W.; Hill, R.C.; Judge, G.G. Learning and Practicing Econometrics; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Cribari-Neto, F.; Zeileis, A. Beta regression in R. J. Stat. Softw. 2010, 34, 1–24. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: www.r-project.org (accessed on 18 August 2023).
- Korosteleva, O. Advanced Regression Models with SAS and R; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
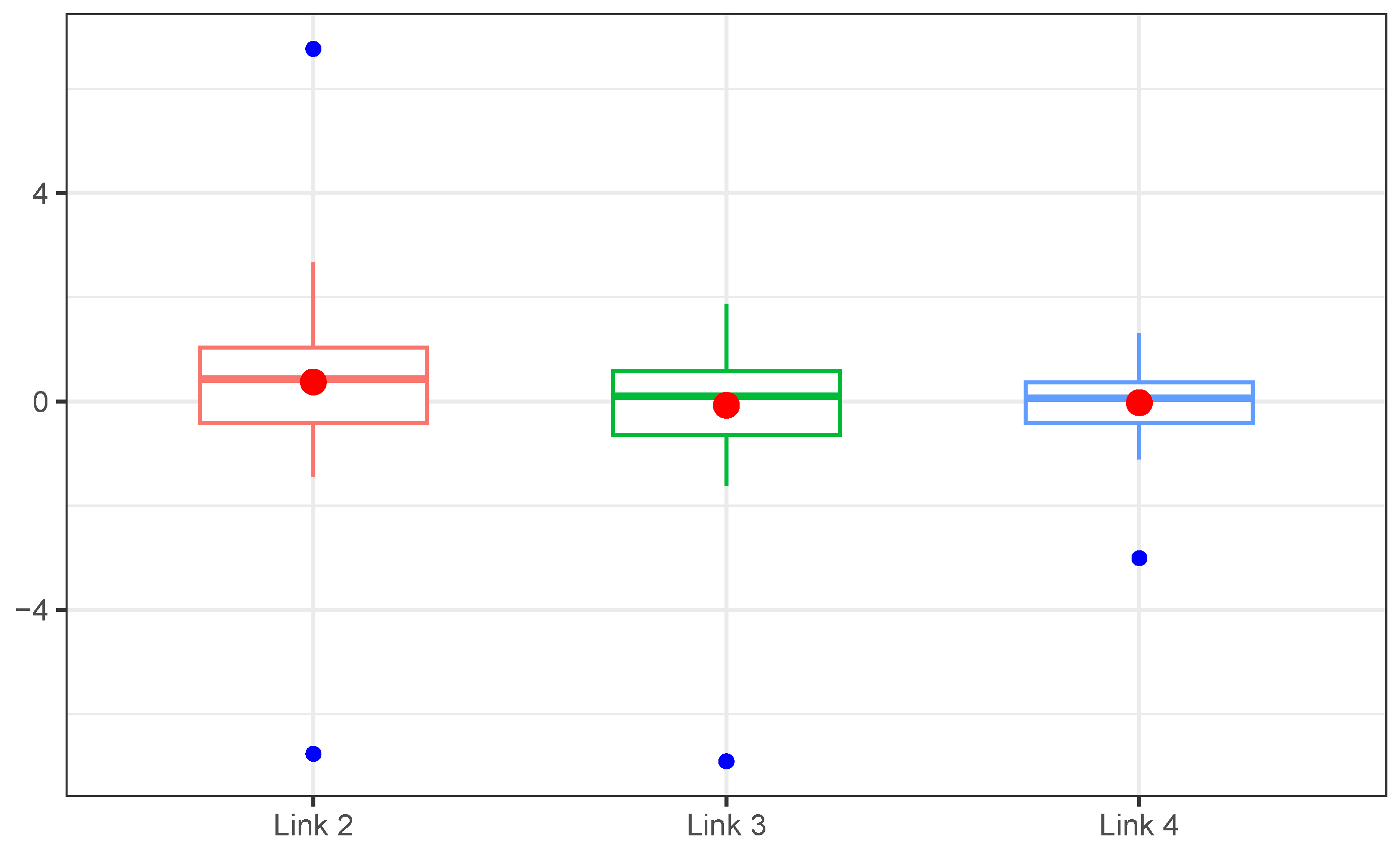


| Link | Minimum | Quartile 1 | Median | Mean | Quartile 3 | Maximum |
|---|---|---|---|---|---|---|
| Identity | ||||||
| Logit | ||||||
| Logit | ||||||
| Cauchy |
| 1.5000 | |||||||
|---|---|---|---|---|---|---|---|
| M() | |||||||
| B() | |||||||
| MSE() | |||||||
| M() | |||||||
| B() | |||||||
| MSE() | |||||||
| M() | |||||||
| B() | |||||||
| MSE() | |||||||
| M() | |||||||
| B() | |||||||
| MSE() | |||||||
| M() | |||||||
| B() | |||||||
| MSE() | |||||||
| Parameter | M1 | M2 | M3 | |||
|---|---|---|---|---|---|---|
| Estimate | E | Estimate | E | Estimate | E | |
| 0.1349 | 0.0150 | −0.6143 * | −0.1293 | −0.3250 * | −0.1285 | |
| (0.5075) | (0.2632) | (0.1408) | ||||
| −0.0181 * | −0.0020 | −0.0094 * | −0.0020 | −0.0050 * | −0.0020 | |
| (0.0077) | (0.0039) | (0.0021) | ||||
| 0.1762 | 0.0197 | 0.0889 | 0.0187 | 0.0473 * | 0.0187 | |
| (0.1108) | (0.0557) | (0.0296) | ||||
| Pseudo- | 0.1701 | 0.2353 | 0.2371 | |||
| Parameter | M4 | M5 | M6 | |||
|---|---|---|---|---|---|---|
| Estimate | E | Estimate | E | Estimate | E | |
| 0.4948 | 0.0538 | −0.6968 * | −0.0924 | −0.3370 * | −0.1811 | |
| (0.3048) | (0.2074) | (0.0715) | ||||
| −0.0079 | −0.0009 | −0.0116 * | −0.0015 | −0.0019 | −0.0010 | |
| (0.0119) | (0.0061) | (0.0015) | ||||
| 0.1101 * | 0.0120 | 0.0731 * | 0.0097 | 0.0213 * | 0.0115 | |
| (0.0359) | (0.0237) | (0.0067) | ||||
| −3.7126 * | −0.4038 | −2.9549 * | −0.3918 | −0.6733 * | −0.3617 | |
| (0.4492) | (0.3347) | (0.0752) | ||||
| Pseudo- | 0.3091 | 0.3036 | 0.4396 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Oliveira, J.S.C.; Ospina, R.; Leiva, V.; Figueroa-Zúñiga, J.; Castro, C. Quasi-Cauchy Regression Modeling for Fractiles Based on Data Supported in the Unit Interval. Fractal Fract. 2023, 7, 667. https://doi.org/10.3390/fractalfract7090667
de Oliveira JSC, Ospina R, Leiva V, Figueroa-Zúñiga J, Castro C. Quasi-Cauchy Regression Modeling for Fractiles Based on Data Supported in the Unit Interval. Fractal and Fractional. 2023; 7(9):667. https://doi.org/10.3390/fractalfract7090667
Chicago/Turabian Stylede Oliveira, José Sérgio Casé, Raydonal Ospina, Víctor Leiva, Jorge Figueroa-Zúñiga, and Cecilia Castro. 2023. "Quasi-Cauchy Regression Modeling for Fractiles Based on Data Supported in the Unit Interval" Fractal and Fractional 7, no. 9: 667. https://doi.org/10.3390/fractalfract7090667
APA Stylede Oliveira, J. S. C., Ospina, R., Leiva, V., Figueroa-Zúñiga, J., & Castro, C. (2023). Quasi-Cauchy Regression Modeling for Fractiles Based on Data Supported in the Unit Interval. Fractal and Fractional, 7(9), 667. https://doi.org/10.3390/fractalfract7090667










