Abstract
Lagrangian dispersion of fluid particle pairs refers to the study of how individual fluid particles disperse and move in a fluid flow, providing insights to understand transport phenomena in various environments, from laminar to turbulent conditions. Here, we explore this phenomenon in synthetic velocity and magnetic fields generated through a reduced-order model of the magnetohydrodynamic equations, which is able to mimic both a laminar and a turbulent environment. In the case of laminar conditions, we find that the average square distance between particle pairs increases linearly with time, implying a dispersion pattern similar to Brownian motion at all time steps. On the other hand, under turbulent conditions, surprisingly enough we observe a Richardson scaling, indicating a super-ballistic dispersion pattern, which aligns with the expected scaling properties for a turbulent environment. Additionally, our study reveals that the magnetic field plays an organizing role. Lastly, we explore a purely hydrodynamic case without magnetic field effects, showing that, even in a turbulent environment, the behavior remains Brownian-like, highlighting the crucial role of the magnetic field in generating the Richardson scaling observed in our model.
1. Introduction
Magnetohydrodynamic (MHD) turbulence is a fascinating and complex phenomenon that occurs both in astrophysical and laboratory plasma environments where magnetic fields and fluid flows actively interact [1,2]. Understanding MHD turbulence is crucial for unraveling the behavior of various cosmic objects, such as stars, accretion disks, and galaxies, as well as for advancing the field of fusion energy, e.g., [3,4,5,6]. The study of MHD turbulence combines theoretical, computational, and experimental approaches. Numerical simulations based on MHD equations provide valuable insights into the complex interplay between fluid motions and magnetic fields, e.g., [7,8,9]. Experimental investigations in laboratory devices, such as magnetized plasma devices or liquid metal experiments, offer the opportunity to probe the intricate dynamics of MHD turbulence under controlled conditions, e.g., [10,11]. Theoretical models and analytical techniques, including statistical theories and spectral analysis, provide frameworks to understand the fundamental aspects of MHD turbulence and predict its behavior in different regimes, e.g., [2,12,13,14,15,16]. Despite the significant progress that has been made in advancing our understanding of MHD turbulence in recent years, many challenges remain, such as the role of turbulence in energizing/accelerating neutral and charged particles, which is important for many applications, e.g., [17,18].
Turbulence is usually described in the Eulerian framework, i.e., from the point of view of a still observer, and in a statistical way, i.e., by searching for high-order statistics of fluctuations at a given scale, e.g., [19,20,21]. The scaling of fluctuations accounts for spatial intermittency in the turbulence cascade, which implies, statistically, non-Gaussian tails for the probability distributions of both velocity and magnetic field increments, leading to abrupt energizations/accelerations of particles. Similar considerations can be drawn for Lagrangian turbulence, e.g., [22,23], where a universal form can be retrieved for a locally averaged energy transfer rate along particle trajectories. Nevertheless, the Lagrangian statistic is still intermittent, thus questioning how it affects the dispersion of particles [24].
Due to the inherent complexity and multi-scale behavior of turbulence, it is widely approached from a reduced-order modeling point of view, such as that for cascade models, which provides a valuable and relatively simple framework for understanding the energy transfer processes and the emergence of different scales in fluid and MHD turbulence [25,26,27,28,29]. These models describe the transfer of energy from large-scale structures to smaller scales through a series of cascades, capturing the essential dynamics of MHD turbulence, ultimately determining the distribution of energy and the formation of coherent structures in the turbulent flow. Cascade models can be seen as a low-order description of the MHD equations following some prescribed rules on the coupling between the different scales, generally relying on the so-called triad interactions [25,29]. An even more simplified low-order model, known as poor man’s MHD equations, has been recently derived by Alberti et al. [13]. It captures the essential behavior of magnetohydrodynamics in a reduced form and can be used as a simplified model to study certain aspects of MHD systems while neglecting certain complexities. Despite its simplifications, the PMMHD model is able to preserve the total energy in the ideal MHD approximation to recover all fixed points of the usual MHD equations, to reproduce a kinematic dynamo action, and to show a Kolmogorov-like spectral scaling, as expected for turbulent plasmas [2,13].
In this paper, we exploit Lagrangian particle dispersion in synthetic velocity and magnetic fields generated via the PMMHD model under both laminar and turbulent conditions. We show that under laminar conditions the average square distance between particle pairs behaves linearly in time, thus suggesting a Brownian-like dispersion for all time steps. Conversely, under turbulent conditions, a Richardson scaling, corresponding to a super-ballistic dispersion, is observed, in agreement with the scaling properties expected for a turbulent environment. Indeed, the observed scaling is observed along the inertial sub-range of turbulence reproduced by the PMMHD model. We also show that the magnetic field is much more efficient in dispersing particle pairs with respect to the velocity one in a turbulent environment, while no differences are found for a laminar one. However, stronger anisotropies are generated by the velocity field with respect to the magnetic one, thus suggesting an ordering role of the magnetic field. Finally, by exploiting a purely hydrodynamic case (with no magnetic field effects) we show that, also for a turbulent environment, a Brownian-like behavior is observed, thus pointing out a key role of the magnetic field in generating a Richardson scaling. This paper is organized as follows. Section 2 describes the suitable theoretical framework for Lagrangian dispersion, while Section 3 briefly recaps the PMMHD model. Then, in Section 4, we present our Lagrangian model setup to inspect the dispersion of particles in laminar and turbulent fields generated via the PMMHD model under three different scenarios: velocity dispersion (Section 5), alfvénic dispersion (Section 6), and purely hydrodynamic dispersion (Section 7). Finally, we summarize our results and possible future outlooks in Section 8.
2. Lagrangian Dispersion of Particle Pairs
Particle pair separation in a turbulent environment is a classical issue of fluid flows [30], which is important not only from a theoretical point of view, but even for practical issues [31]. In MHD turbulence, this is not yet well-established, in particular the existence of a Richardson law. Numerical simulations have been widely used to describe pair dispersion properties [32], although it is interesting to use turbulent environments AND not direct numerical simulations to verify the robustness of the classical laws for pair dispersion. This is particularly true for MHD turbulence, where anisotropy cannot be ruled out.
The main variable we can investigate [30] is the concentration of a cloud of particles at the time t, so that we can define a continuous function as the relative number of particle pairs whose coordinates differ by an amount
normalized in a way that the integral over all pairs of is equal to one. The dispersive process can then be fully described through the probability that, given , the averaged concentration at the time , we recover the concentration at a time t, namely
However, the determination of the probability requires the estimate of the quantity , which could be quite difficult from experiments or numerical simulations. As an alternative, we can estimate the components of the relative dispersion tensor . Given a cloud of N particles which move dispersively within a fluctuating environment, for every pair of particles, , identified at time t by the coordinates and , we calculate the relative distance along each direction, thus defining the dispersion tensor as
where brackets means average over all particle pairs. In an isotropic situation where every direction plays the same role, then the out-of-diagonal elements of the tensor are, in principle, identically zero and the trace of the tensor represents the average radius of the cloud of particles at the time t, being . In this case, we can define an effective eddy diffusivity for the cloud.
Assuming that the eddy diffusivity must depend solely on the average energy dissipation rate and on the length scale ℓ, it immediately follows that the eddy diffusivity is related to the trace of the dispersion tensor through the celebrated Richardson fourth-third law [33,34]
By defining an eddy diffusivity equation , it follows that particle pairs separate in time following a super-ballistic law
where g is a constant. Both fundamental laws (4) and (5) have been verified in fluid flows and numerical simulations [23,24,31,34]. As an important consequence, since is obviously related to the turbulent velocity fluctuations across eddies at that scale , it follows that scaling property (4) requires a turbulent environment with a Kolmogorov scaling saying the Richardson pair dispersion law is valid in the inertial sub-range of turbulence.
The Richardson law is an asymptotic property of dispersion within the inertial sub-range of turbulence, where particles lost memory of their infinitesimal initial separation [34]. This is a rough approximation, as shown in some recent papers [35,36,37]. We can introduce a revised version of the model by conjecturing instead that the eddy-diffusivity must depend on the initial pair average separation, say, , on the average dissipation rate , and explicitly on time, so that the eddy diffusivity can assume a more generic form
Dimensional arguments lead to and , where is arbitrary. By assuming a quadratic dependence of the eddy diffusivity on time, say, , we recover the Richardson’s law. However, according to the considerations by Elsinga et al. [37], if we assume a linear dependence on time, it follows that
which means a ballistic separation of particle pairs
This corresponds to the Batchelor’s law of particle pair dispersion, and is valid for times less than, say, , the eddy-turnover-time at the scale . On the contrary, the Richardson law is valid in the intermediate range of times , with being the large-scale eddy-turnover-time [37], or the time needed for the particle to loose memory of the initial conditions. As particles separate enough, say, for , they decorrelate, so that they must evolve without any correlation and the eddy diffusivity must be constant, say, , thus obtaining a Brownian-like Taylor’s dispersion
3. The Poor Man’s Magnetohydrodynamic (PMMHD) Model
In the low-frequency approximation, fluctuations in plasmas are usually described in an incompressible framework via the MHD equations, which read as
with and being the velocity and magnetic fields, respectively, and the sound and Alfvén speeds, and the kinematic viscosity and magnetic diffusivity, respectively, and we assumed, for simplicity, a unitary mass density . Equation (10) describes the collective motion of a plasma in a single-fluid approximation (ions are inertial, electrons are at rest) and Equation (11) is the induction equation derived from the Maxwell–Faraday law, while Equation (12) is the incompressibility condition for both fields.
Equations (10) and (11) can be projected over a divergence-free space, without loss of generality, by using the Leray operator that allows us to neglect the term . Then, by using dimensionless variables and by adopting a Galerkin truncation retaining a single fixed wavevector [38], Alberti et al. [13] derived the poor man’s magnetohydrodynamic (PMMHD) model
where (non-)dotted variables refer to the value at the time ().
Equations (13) and (14) constitute a six-dimensional autonomous dynamical system with 12 bifurcation parameters, , , and , which can be linked with physically-based quantities. Specifically,
with L being the integral scale and the Taylor scale, respectively [13], while and are the fluid and magnetic Reynolds numbers, respectively [1]. Thus, and are related to the nature of the considered plasma, allowing us to describe a laminar environment when or a turbulent one when [13]. Furthermore,
with [13], represents the directional derivatives of the field components, or, equivalently, is related to field gradients that define the topological space properties [13,38]. They also represent the off-diagonal term of the third-order coupling tensor
with the Einstein notation assumed
Thus, determines the symmetric and/or asymmetric nature of the field gradients, namely that they define the geometry of the system.
Despite its reduced-order representation, it has been shown [13] that the PMMHD model
- preserves MHD invariants in the ideal approximation (), namely the energy and the helicity;
- admits all fixed points, namely the fluid (), the alfvénic (), and the static Taylor force-free ( and );
- presents a dissipative behavior with a signature of chaos (i.e., sensitive dependence on initial conditions while preserving the statistics of both fields);
- displays a Kolmogorov-like spectral scaling under turbulent conditions over an inertial sub-range.
4. Lagrangian Formulation of the PMMHD Model
We built-up a Lagrangian model for investigating the dispersion of fluid particle pairs in a velocity and/or magnetic field, generated via the PMMHD model. Note that both velocity and magnetic variables play the same role, being the velocity of alfvénic fluctuations along a given direction. By defining as the particle coordinate at the time and as its coordinate at a further time , we can write the difference of the coordinates of two different particles, say, the n-th and the m-th, along a given direction
The trajectory of each particle evolves according to the equation
where is one of the field along a given coordinate, say, , so that the differences in coordinates depends on the field we are investigating, say, . The dispersive properties of particle pairs are then contained in the time evolution of the relative dispersion tensor (see also Equation (3))
where the average is over a large amount of particle pairs at time . The relative dispersion tensor takes into account the possible advection of both kind of fluctuations, say, velocity and alfvénic, along the three different directions. For example, the chaotic advection of purely velocity elements is described by
while for purely alfvénic elements, we have
which both play a privileged role with respect to mixed elements
In the simplest case of isotropic dynamics, the off-diagonal elements are identically zero. In this case, the advection is measured by the square distances between elements, say,
assuming summation over repeated indices. The anisotropic advection can instead be measured through the anisotropy angles
namely in the case of purely isotropic advection.
Our Lagrangian model consists of solving Equation (21) for particles starting from the same initial position, randomly selected, within a circle of radius , e.g., when flowing in a plasma environment described by the PMMHD model in Equations (13) and (14). In this way, we can investigate the separation between particle pairs along time, thus allowing a proper evaluation of the dispersion tensor and to investigate their statistics under different environmental conditions, as the bifurcation parameters , , and are varied. In particular, we explore the dispersion of particles in a laminar () and a turbulent () plasma environment. This corresponds to Reynolds numbers between and , assuming that the ratio between the integral scale L and the Taylor scale is of the order of or greater, as in natural plasmas [2]. We investigate both symmetric () and asymmetric field gradients () generated via the PMMHD model under three different scenarios: velocity dispersion (Section 5), magnetic dispersion (Section 6), and purely hydrodynamic dispersion (Section 7).
5. Fluid Velocity Dispersion
The first case we study is the fluid velocity dispersion, i.e., , of particles. Figure 1 reports the phase-space dynamics of the diagonal and off-diagonal elements of the dispersion tensor under the different conditions.
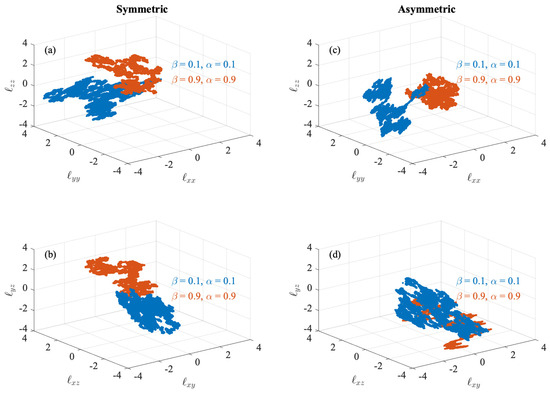
Figure 1.
The phase-space dynamics of the diagonal (a) and off-diagonal (b) elements of the velocity dispersion tensor under the effect of symmetric field gradients . (c,d) The same for the asymmetric field gradients. Blue and orange points refer to laminar and turbulent plasma environments, respectively. Axes are reported in units of standard deviations for clarity.
We cannot observe a distinctive phase-space dynamic between the different conditions, which seem to be all characterized by a Brownian-like coverage of the phase-space [39]. However, it seems that particles move along outward and inward trajectories that becomes very irregular for long times. Furthermore, there are also no distinctive features between the diagonal and off-diagonal separations, thus suggesting the existence of a chaotic nature [39]. We further inspect the statistics of the dispersion tensor by looking at the average square distances between elements as a function of the time steps under the different conditions. The results are reported in Figure 2.
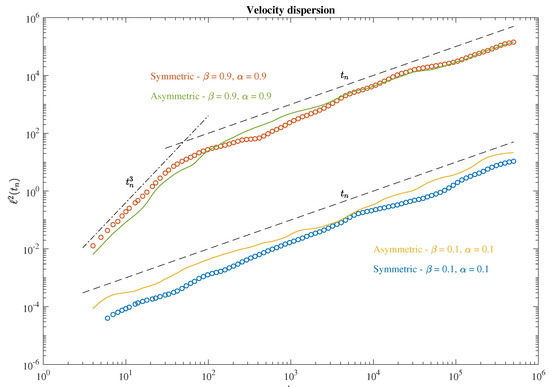
Figure 2.
The average square distances between elements for the velocity dispersion as a function of the time steps. Dots refer to the symmetric field gradients, while lines refer to asymmetric field gradients. Orange and green correspond to turbulent conditions, while yellow and blue to laminar ones. The dashed-dotted line marks the Richardson scaling , while the dashed line refers to the Brownian scaling .
Here, a distinctive feature clearly emerges between laminar and turbulent plasmas. While the former are characterized by an uncorrelated path at all times, the latter are instead characterized by a Richardson scaling for short times, which transits towards a Brownian-like dispersion for long times. This behavior clearly reflects the existence of a spectral break separation in the Fourier PSD behavior, as previously reported by Alberti et al. [13] for turbulent conditions, being absent for laminar ones [13]. Indeed, an intermediate range of frequency is observed with a Kolmogorov-like spectral slope , followed by an behavior of large frequencies. The position of the scaling break for is consistent with the location of the previously observed spectral break. This means that, despite its simplifications, the Lagrangian turbulence developed with a PMMHD model is in agreement with theoretical expectations from the Lagrangian counterpart of the Kolmogorov theory of turbulence, saying that the Richardson law can only be recovered and valid if an inertial sub-range of scales is observed [23,24]. As a further step, we investigated the anisotropic nature of the advection by looking at the anisotropy angles under the different conditions, as reported in Figure 3.
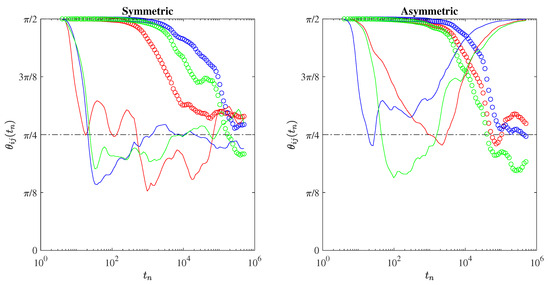
Figure 3.
The anisotropy angles as a function of the time steps. Dots refer to laminar conditions, while lines refer to turbulent ones. Red, green, and blue lines/symbols refer to , , and , respectively. The dashed-dotted horizontal lines mark the purely isotropic advection condition .
The results look really intriguing. We clearly highlight that, after an initial transient activity, the chaotic advection of Lagrangian particles under turbulent conditions with symmetric field gradients becomes purely isotropic (apart from some transient fluctuations), faster (∼10) than the observed break (∼) associated with the Richardson scaling. Conversely, under asymmetric field gradients, it again becomes highly anisotropic for long times (), which cannot be attributed to transient activity. This seems to underline that singularities in the field gradients along different directions can play a key role in destroying isotropy. Furthermore, when looking at laminar conditions, the anisotropy angles behave in an almost similar way both for symmetric and asymmetric field gradients, thus suggesting that the loss of memory processes is the key driver of Lagrangian dispersion in non-turbulent environments. Our findings clearly highlight, with a simple model, a key property of turbulence, i.e., the mixing of chaotic trajectories [23].
6. Alfvénic Dispersion
The second case we study is the alfvénic dispersion, i.e., , of particles. Figure 4 reports the phase-space dynamics of the diagonal and off-diagonal elements of the dispersion tensor under the different conditions.
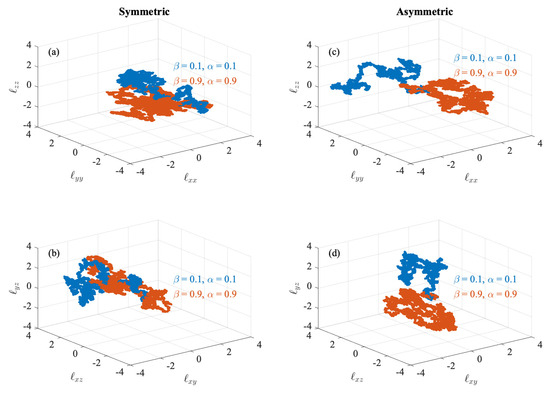
Figure 4.
The phase-space dynamics of the diagonal (a) and off-diagonal (b) elements of the alfvénic dispersion tensor under the effect of symmetric field gradients . (c,d) The same for the asymmetric field gradients. Blue and orange points refer to laminar and turbulent plasma environments, respectively. Axes are reported in units of standard deviations for clarity.
As for fluid velocity dispersion, there are no distinctive phase-space dynamics between the different conditions, which seem to all be characterized by a Brownian-like coverage of the phase-space [39]. However, more elongated structures are found for the symmetric case with respect to the asymmetric one, almost independent on the diagonal and off-diagonal separations. This seems to suggest that the magnetic field can play a role in ordering trajectories within a chaotic environment. We then inspect the statistics of the alfvénic dispersion tensor by looking at the average square distances between elements as a function of the time steps under the different conditions. The results are reported in Figure 5.
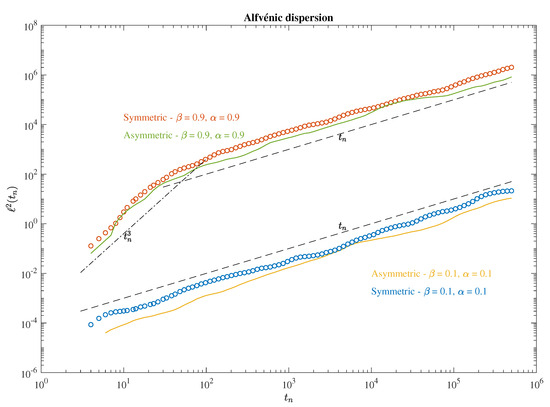
Figure 5.
The average square distances between elements for the alfvénic dispersion as a function of the time steps. Dots refer to the symmetric field gradients, while lines refer to asymmetric field gradients. Orange and green correspond to turbulent conditions, while yellow and blue to laminar ones. The dashed-dotted line marks the Richardson scaling , while the dashed line refers to the Brownian scaling .
Again, here, a distinctive feature emerges between laminar and turbulent plasmas, independently of the topological properties of field gradients. Indeed, laminar conditions lead to a Brownian-like scaling for all times, while turbulent ones produce a short-term Richardson scaling and a long-term Brownian-like dispersion. This is, as for fluid dispersion, the Lagrangian counterpart of the Kolmogorov theory of turbulence, implying that the Richardson law exists if an inertial sub-range of scales is observed [23,24]. We further inspect the anisotropic nature of the advection by looking at the anisotropy angles under the different conditions, as reported in Figure 6.
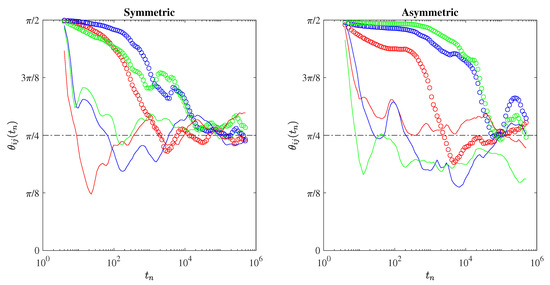
Figure 6.
The anisotropy angles as a function of the time steps. Dots refer to laminar conditions, while lines refer to turbulent ones. Red, green, and blue lines/symbols refer to , , and , respectively. The dashed-dotted horizontal lines mark the purely isotropic advection condition .
The results again look surprising. Indeed, we almost observe a similar behavior as fluid dispersion for laminar conditions, although it seems that isotropy is now recovered in a shorter time than that depicted for the fluid dispersion. Thus, the magnetic field also seems to produce faster isotropization of Lagrangian trajectories for laminar environments. In a similar way to fluid dispersion, after an initial transient activity, the chaotic advection of Lagrangian particles under turbulent conditions with symmetric field gradients becomes purely isotropic (apart from some transient fluctuations), faster (∼10) than the observed break (∼) associated with the Richardson scaling. The main difference with respect to the fluid dispersion is that, under asymmetric field gradients, the highly anisotropic behavior previously observed for long times () disappears. Thus, the magnetic field seems to be able to suppress the role of singularities in the field gradients along different directions and to restore isotropy. This confirms our initial thoughts on the ordering role of the magnetic field.
7. Hydrodynamic Dispersion
The last case we study is the hydrodynamic dispersion, i.e., and , of particles, which the PMMHD model reduces to
Figure 7 reports the phase-space dynamics of the diagonal and off-diagonal elements of the dispersion tensor under the different conditions.
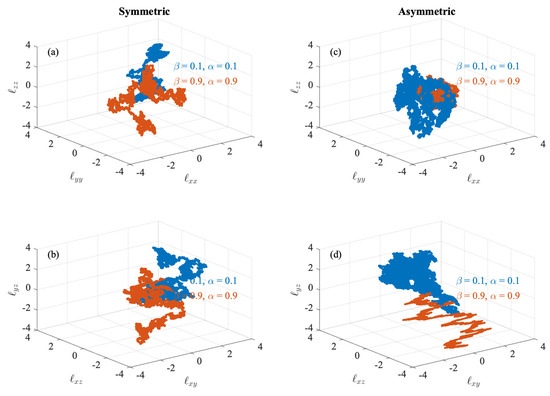
Figure 7.
The phase-space dynamics of the diagonal (a) and off-diagonal (b) elements of the hydrodynamic dispersion tensor under the effect of symmetric field gradients . (c,d) The same for the asymmetric field gradients. Blue and orange points refer to laminar and turbulent plasma environments, respectively. Axes are reported in units of standard deviations for clarity.
As for previous cases, we cannot highlight any distinctive feature of the phase-space dynamics between the different conditions. We then inspect the statistics of the hydrodynamic dispersion tensor by looking at the average square distances between elements as a function of the time steps under the different conditions. The results are reported in Figure 8.
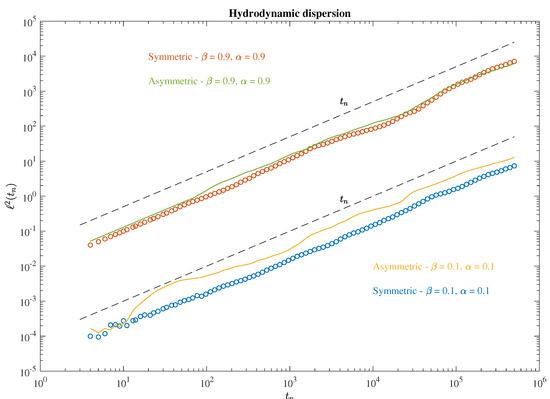
Figure 8.
The average square distances between elements for the hydrodynamic dispersion as a function of the time steps. Dots refer to the symmetric field gradients, while lines refer to asymmetric field gradients. Orange and green correspond to turbulent conditions, while yellow and blue to laminar ones. The dashed lines refer to the Brownian scaling .
For all conditions, the Richardson scaling disappears, with the presence of a Brownian-like scaling for all times. This result clearly suggests that the Lagrangian counterpart of the Kolmogorov theory of turbulence, implying that the Richardson law exists if an inertial sub-range of scales is observed, could no longer be valid for MHD turbulence, now requiring an additional condition. This condition is the existence of a magnetic field. However, this can be related to the reduced-order nature of the PMMHD model in the case . Indeed, by looking at Equation (29), it is easy to observe that it admits two different fixed points: one is the trivial solution (), and the other is [13]. The latter condition relates the equilibrium solution with the parametrization of the spatial gradients along perpendicular directions to the considered component, thus modifying the scaling for pair separation and likely destroying the correlations induced by the energy cascade. This could explain the missing of the Richardson scaling in the absence of a magnetic field in our moodel, which is not usually observed in numerical simulations of pure fluid flows retaining more spatial modes, e.g., [34]. By further inspecting the anisotropic nature (see Figure 9), we recover similar results as for the fluid case.
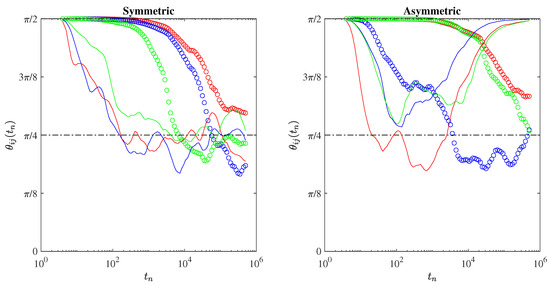
Figure 9.
The anisotropy angles as a function of the time steps. Dots refer to laminar conditions, while lines refer to turbulent ones. Red, green, and blue lines/symbols refer to , , and , respectively. The dashed-dotted horizontal lines mark the purely isotropic advection condition .
This means that, after an initial transient activity, the chaotic advection of Lagrangian particles under turbulent conditions with symmetric field gradients and/or for laminar plasmas becomes purely isotropic . Conversely, under asymmetric field gradients, it becomes again highly anisotropic for long times (), which cannot be attributed to transient activity. This seems to underline again that the lack of a magnetic field allows singularities in the field gradients along different directions to play a key role in destroying isotropy. Furthermore, when looking at laminar conditions under asymmetric field gradients, we observe a shorter time for recovering isotropic conditions for the separation that can be attributed to the different lower value of for this setup with respect to and .
8. Summary and Conclusions
In this research, we investigate the dispersion of Lagrangian particles in synthetic velocity and magnetic fields created using the PMMHD model, considering both laminar and turbulent conditions. Our findings demonstrate distinct behaviors for each case.
Under laminar conditions, we observe that the average square distance between particle pairs shows a linear dependence on time, indicating Brownian-like dispersion throughout all time steps. Conversely, turbulent conditions exhibit a Richardson scaling pattern, resulting in super-ballistic dispersion. This scaling aligns with the anticipated properties for a turbulent environment and is particularly evident within the inertial sub-range of turbulence, as reproduced by the PMMHD model.
Furthermore, we find that in a turbulent environment, the magnetic field proves significantly more effective in dispersing particle pairs compared with the velocity field. However, in a laminar setting, no such differences are detected. Additionally, the velocity field generates stronger anisotropies than the magnetic field, suggesting an ordering influence of the magnetic field.
Finally, through an investigation of a purely hydrodynamic scenario where magnetic field effects are absent, we show that even in turbulent conditions, a Brownian-like behavior is observed. This indicates the crucial role of the magnetic field in generating the Richardson scaling observed in reduced-order models of turbulent environments. However, this can be related to a link between the equilibrium solution and the parameterization of the spatial gradients that could modify the scaling for pair separation and likely destroy the correlations induced by the energy cascade. This could be the explanation for the missing of the Richardson scaling in the absence of a magnetic field, which is not usually observed in numerical simulations retaining more spatial modes, e.g., [34]. However, this aspect is a claim for specific future investigations.
Our results are well in agreement with those reported by Carbone et al. [40] through a five-mode reduced-order model of two-dimensional MHD equations. Indeed, they have shown that in the presence of magnetic fluctuations, Lagrangian dispersion closely follows the standard Richardson description, while when magnetic fluctuations are excluded from the model, the Richardson regime is not observed and a Brownian-like behavior is observed [40]. Furthermore, they also reported a significant role of the intrinsic large-scale anisotropy of the model in affecting the direction of Lagrangian pair separation. Furthermore, we also recover similar results with those obtained using direct numerical simulations of anisotropic MHD turbulence [32], who reported scalings for relative Lagrangian dispersion in agreement with the Richardson prediction over the inertial sub-range and with a Brownian-like behavior for longer times. These aspects clearly highlight that, despite our drastic truncation of the MHD equations, our PMMHD model is able to reproduce similar results obtained via intermediate-to-high-complexity models, thus making it highly appropriate for utilization in scenarios where one needs synthetic turbulent fields with authentic characteristics, such as when conducting intricate investigations (e.g., sub-grid-scale models for MHD simulations). Clearly, our "one-scale" approach can open a novel framework for investigating the role of the ergodic nature of the synthetic field derived via the PMMHD model, which preserves temporal scaling properties (e.g., Kolmogorov-like spectra, Richardson dispersion), although neglecting the multiple spatial scale nature of turbulent fields, thus being a promising outstanding (and additional) challenge in turbulence.
Author Contributions
Conceptualization, T.A. and V.C.; methodology, T.A.; software, T.A.; formal analysis, T.A.; investigation, V.C.; writing—original draft preparation, T.A. and V.C.; writing—review and editing, T.A. and V.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No data were created for this study.
Acknowledgments
We would like to sincerely acknowledge all the many collaborators, friends, and colleagues with whom we have interacted on the contents reported in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Biskamp, D. Magnetohydrodynamic Turbulence; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Bruno, R.; Carbone, V. Turbulence in the Solar Wind; Springer: Berlin/Heidelberg, Germany, 2016; Volume 928. [Google Scholar]
- Canuto, V.M.; Christensen-Dalsgaard, J. TURBULENCE IN ASTROPHYSICS: Stars. Annu. Rev. Fluid Mech. 1998, 30, 167–198. [Google Scholar] [CrossRef]
- Hersant, F.; Dubrulle, B.; Huré, J.M. Turbulence in circumstellar disks. Astron. Astrophys. 2005, 429, 531–542. [Google Scholar] [CrossRef]
- Brandenburg, A.; Nordlund, A. Astrophysical turbulence. Rep. Prog. Phys. 2011, 74, 046901. [Google Scholar] [CrossRef]
- McKee, C.; Stone, J. Turbulence in the heavens. Nat. Astron. 2021, 5, 342–343. [Google Scholar] [CrossRef]
- Valentini, F.; Servidio, S.; Perrone, D.; Califano, F.; Matthaeus, W.H.; Veltri, P. Hybrid Vlasov-Maxwell simulations of two-dimensional turbulence in plasmas. Phys. Plasmas 2014, 21, 082307. [Google Scholar] [CrossRef]
- Oughton, S.; Matthaeus, W.H.; Wan, M.; Parashar, T. Variance anisotropy in compressible 3-D MHD. J. Geophys. Res. (Space Phys.) 2016, 121, 5041–5054. [Google Scholar] [CrossRef]
- Pezzi, O.; Parashar, T.N.; Servidio, S.; Valentini, F.; Vásconez, C.L.; Yang, Y.; Malara, F.; Matthaeus, W.H.; Veltri, P. Revisiting a Classic: The Parker-Moffatt Problem. Astrophys. J. 2017, 834, 166. [Google Scholar] [CrossRef]
- Piron, L.; Bonfiglio, D.; Piovesan, P.; Zaniol, B.; Auriemma, F.; Carraro, L.; Chacón, L.; Marrelli, L.; Valisa, M.; Veranda, M.; et al. 3D magnetic fields and plasma rotation in RFX-mod tokamak plasmas. Nucl. Fusion 2013, 53, 113022. [Google Scholar] [CrossRef]
- Poli, F.M. Integrated Tokamak modeling: When physics informs engineering and research planning. Phys. Plasmas 2018, 25, 055602. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Matthaeus, W.H.; Parashar, T.N. Single-mode nonlinear Langevin emulation of magnetohydrodynamic turbulence. Phys. Rev. E 2018, 97, 053211. [Google Scholar] [CrossRef]
- Alberti, T.; Consolini, G.; Carbone, V. A discrete dynamical system: The poor man’s magnetohydrodynamic (PMMHD) equations. Chaos 2019, 29, 103107. [Google Scholar] [CrossRef] [PubMed]
- Alexandrova, O.; Jagarlamudi, V.K.; Hellinger, P.; Maksimovic, M.; Shprits, Y.; Mangeney, A. Spectrum of kinetic plasma turbulence at 0.3-0.9 astronomical units from the Sun. Phys. Rev. E 2021, 103, 063202. [Google Scholar] [CrossRef] [PubMed]
- Carbone, V.; Lepreti, F.; Vecchio, A.; Alberti, T.; Chiappetta, F. On the origin of high-frequency magnetic fluctuations in the interplanetary medium: A Brownian-like approach. Front. Phys. 2021, 9, 18. [Google Scholar] [CrossRef]
- Carbone, V.; Telloni, D.; Lepreti, F.; Vecchio, A. High-frequency Magnetic Fluctuations in Space Plasmas and the Role of Electron Landau Damping. Astrophys. J. Lett. 2022, 924, L26. [Google Scholar] [CrossRef]
- Cho, J.; Lazarian, A. Particle Acceleration by Magnetohydrodynamic Turbulence. Astrophys. J. 2006, 638, 811. [Google Scholar] [CrossRef]
- Lemoine, M. Particle acceleration in strong MHD turbulence. Phys. Rev. D 2021, 104, 063020. [Google Scholar] [CrossRef]
- Kolmogorov, A. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Akad. Nauk SSSR Dokl. 1941, 30, 301–305. [Google Scholar]
- Iroshnikov, P.S. Turbulence of a Conducting Fluid in a Strong Magnetic Field. Sov. Ast. 1964, 7, 566. [Google Scholar]
- Kraichnan, R.H. Inertial-Range Spectrum of Hydromagnetic Turbulence. Phys. Fluids 1965, 8, 1385–1387. [Google Scholar] [CrossRef]
- Borgas, M.S. The Multifractal Lagrangian Nature of Turbulence. Philos. Trans. R. Soc. Lond. Ser. A 1993, 342, 379–411. [Google Scholar] [CrossRef]
- Benzi, R.; Biferale, L.; Calzavarini, E.; Lohse, D.; Toschi, F. Velocity-gradient statistics along particle trajectories in turbulent flows: The refined similarity hypothesis in the Lagrangian frame. Phys. Rev. E 2009, 80, 066318. [Google Scholar] [CrossRef]
- Bentkamp, L.; Lalescu, C.C.; Wilczek, M. Persistent accelerations disentangle Lagrangian turbulence. Nat. Commun. 2019, 10, 3550. [Google Scholar] [CrossRef] [PubMed]
- Carbone, V. Cascade model for intermittency in fully developed magnetohydrodynamic turbulence. Phys. Rev. Lett. 1993, 71, 1546–1548. [Google Scholar] [CrossRef] [PubMed]
- Chillà, F.; Peinke, J.; Castaing, B. Multiplicative Process in Turbulent Velocity Statistics: A Simplified Analysis. J. Phys. II 1996, 6, 455–460. [Google Scholar] [CrossRef]
- Dubrulle, B. Intermittency in fully developed turbulence: Log-Poisson statistics and generalized scale covariance. Phys. Rev. Lett. 1994, 73, 959–962. [Google Scholar] [CrossRef] [PubMed]
- Laval, J.P.; Dubrulle, B. A LES-Langevin model for turbulence. Eur. Phys. J. B 2006, 49, 471–481. [Google Scholar] [CrossRef][Green Version]
- Schertzer, D.; Lovejoy, S. Generalised scale invariance in turbulent phenomena. PhysicoChemical Hydrodyn. 1985, 6, 623–635. [Google Scholar]
- Monin, A.S.; Yaglom, A.M.; Ablow, C.M. Statistical Fluid Mechanics: The Mechanics of Turbulence. Am. J. Phys. 1977, 45, 1010. [Google Scholar] [CrossRef]
- Toschi, F.; Bodenschatz, E. Lagrangian Properties of Particles in Turbulence. Annu. Rev. Fluid Mech. 2009, 41, 375–404. [Google Scholar] [CrossRef]
- Pratt, J.; Busse, A.; Müller, W.C. Reynolds number dependence of Lagrangian dispersion in direct numerical simulations of anisotropic magnetohydrodynamic turbulence. J. Fluid Mech. 2022, 944, A36. [Google Scholar] [CrossRef]
- Richardson, L.F. Atmospheric diffusion shown on a distance-neighbour graph. Proc. R. Soc. London. Ser. A Contain. Pap. A Math. Phys. Character 1926, 110, 709–737. [Google Scholar]
- Salazar, J.P.L.C.; Collins, L.R. Two-Particle Dispersion in Isotropic Turbulent Flows. Annu. Rev. Fluid Mech. 2009, 41, 405–432. [Google Scholar] [CrossRef]
- Thalabard, S.; Krstulovic, G.; Bec, J. Turbulent pair dispersion as a continuous-time random walk. J. Fluid Mech. 2014, 755, R4. [Google Scholar] [CrossRef]
- Bourgoin, M. Turbulent pair dispersion as a ballistic cascade phenomenology. J. Fluid Mech. 2015, 772, 678–704. [Google Scholar] [CrossRef]
- Elsinga, G.; Ishihara, T.; Hunt, J. Non-local dispersion and the reassessment of Richardson’s t3-scaling law. J. Fluid Mech. 2022, 932, A17. [Google Scholar] [CrossRef]
- McDonough, J.M. Three-dimensional poor man’s Navier-Stokes equation: A discrete dynamical system exhibiting k-5/3 inertial subrange energy scaling. Phys. Rev. E 2009, 79, 065302. [Google Scholar] [CrossRef]
- Wang, L.P.; Maxey, M.R.; Burton, T.D.; Stock, D.E. Chaotic dynamics of particle dispersion in fluids. Phys. Fluids A Fluid Dyn. 1992, 4, 1789–1804. [Google Scholar] [CrossRef][Green Version]
- Carbone, F.; Telloni, D.; Zank, G.; Sorriso-Valvo, L. Chaotic advection and particle pairs diffusion in a low-dimensional truncation of two-dimensional magnetohydrodynamics. EPL Europhys. Lett. 2022, 138, 53001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).