1. Introduction
The concepts and theories of plate tectonics are considered to have undergone the most significant advances in earth sciences in the 20th century and have become the dominant theory for explaining many geological processes and events such as geodynamics, the formation and distribution of resources and energy, and geological hazards such as volcanic eruptions and earthquakes [
1]. Classical calculus, such as differential equations and physics of Newton’s theory, has been extensively applied to describe the motion of the plates including mantle convection, plate subduction, heat flow, and ocean floor morphology at the mid-ocean ridges, as well as basin formation during the whole Wilson circle of plate tectonics [
2,
3]. However, it has been pointed out that these types of models are less successful in fitting energy and mass distributions due to fractality and the singularity caused by extreme geological events (e.g., earthquakes, magmatic activities including volcanic eruptions, and mineralization) that occurred during the multiplicative cascade plate tectonics and in response to self-organized criticality (SOC) or phase transitions (PTs) [
4].
Since the fractal geometries no longer hold the fundamental properties of the Lebesgue additive property required for ordinary calculus, new calculus has to be developed based on fractal geometries. In applied mathematics and mathematical analysis, a special type of derivatives and integrals, termed fractional calculus (FC), is used to calculate fractional order derivatives and integrals of a function. It has received increasing attention due to its potential applications in many fields involving complex and nonlinear systems [
5,
6]. For example, FC has been applied to modeling anomalous heat conduction and diffusion [
7,
8,
9]. However, this branch of mathematics has not been extensively utilized in earth sciences. One of the challenges of applying FC to a practical problem is associating both the geometrical and physical properties of a system that corresponds to the fractional order of FC. Further research is needed to show how these operations can represent physical properties such as the density of fractal geometries. Therefore, the current research focuses on constructing fractal density with FC. It will first introduce the Hausdorff and Fractal calculus, developed in the context of FC, which can associate functions with geometries with fractal dimensions [
6,
10]. A case study will also show how to apply singularity analysis based on the fractal density concept and calculations to characterize seismic frequency–depth clusters at the convergent plate boundaries of the Tethys collision zone and the Pacific subduction zone [
10,
11].
2. Frequency–Depth Clusters of Earthquakes at the Converging Plate Boundaries
Earthquakes are typical extreme geological events, usually occurring on sudden shifts in the Earth’s crust or shifting plate boundaries. Earthquakes can release abnormal amounts of energy in a short period, which can cause severe damage. Therefore, earthquakes are a major topic in geological and geophysical research, attracting widespread attention from geoscientists in various fields. While many studies focus on actual detailed earthquake mechanics based on rock strike–slip friction laws [
12,
13], numerous studies have been devoted to linking the global and regional distribution of earthquakes in terms of space (including depth) and time to the tectonic setting and lithospheric rheology [
14]. For example, it was reported that 76% of earthquakes dissipate about 60% of the total energy in the first ~50 km in depth [
15]. Deeper earthquakes (>300 km) mostly occur in the western subduction zone of the Pacific plate, while deep earthquakes on the eastern boundary of the Pacific plate are rare [
16]. Furthermore, the earthquakes in the Pacific plates’ southern and western subduction zones are deeper than those in the northeastern zones [
17]. This may be because the subduction slabs along West Pacific plate boundaries are generally colder and older than those in the East Pacific plate boundaries [
18,
19,
20]. Studies on the association of the distribution of dehydration events with earthquakes indicate a nonlinear correlation between the maximum depth of earthquakes and the slab’s temperature, with fewer deep earthquakes in young subduction zones [
16]. The Gutenberg–Richter (GR) power law model has been widely used to analyze earthquake frequency–size distribution. Many authors have investigated the spatial and temporal variability of the b-value of the GR power law model. For example, Gibowicz [
21] analyzed the frequency–magnitude, depth, and time relations for earthquakes in an island arc and found that the exponent b-value of the GR power law model (1956) increases linearly with depth from 1.0 for shallow earthquakes to 1.4 for those at a depth of 120 km and then decreases to 0.75 at 300–350 km. The analysis of the frequency–magnitude distributions of earthquakes of magnitudes (M ≥ 5) that occurred in different tectonic settings indicated that the exponent b-value of the GR power law model systematically increases from mid-ocean ridges through subduction to collision zones [
22]. Compared with the study of earthquake frequency–magnitude using the GR power law model, relatively few studies focus on the statistical studies of the distribution of earthquake depth. In a recent study on earthquake depth, Hauksson and Meier [
23] explored how earthquake depth histograms (EDHs) are related to crustal strength, lithology, and crust temperature. However, there is no physical proof of an association between the shape of the yield strength envelope (YSE) and EDHs. There has been a substantial interest in studying earthquakes’ distribution around Moho’s depth. For example, when compared with the locations of large earthquakes (M ≥ 9) with lengths of trenches of subduction zones and speed of subduction [
24], “supraslab” earthquake clusters were seen at depths of 25 to 50 km, with most of these clusters occurring below the depth of the forearc Moho [
14]. These clusters are interpreted to represent seismicity in seamounts detached from the Pacific plate during slab descent [
14]. Studies also indicated that earthquakes with magnitudes greater than 5.0 worldwide recorded from January 1991 to 31 December 1996 are generally shallow, with depths less than 70 km [
17]. The author’s earlier research on the distribution of earthquakes along the subduction zones of Pacific plates indicated that earthquakes are clustered around 34–44 km, and the depth distribution of earthquakes can be described by power law function with singularity [
25]. There is a lack of systemic and comparative studies about the nonlinear decay of clusters of earthquakes around the Moho and their associations with global plate tectonics. The seismic depth distribution on the converging plate boundaries in the Pacific Rim and the Tethys Belt will be further discussed and compared.
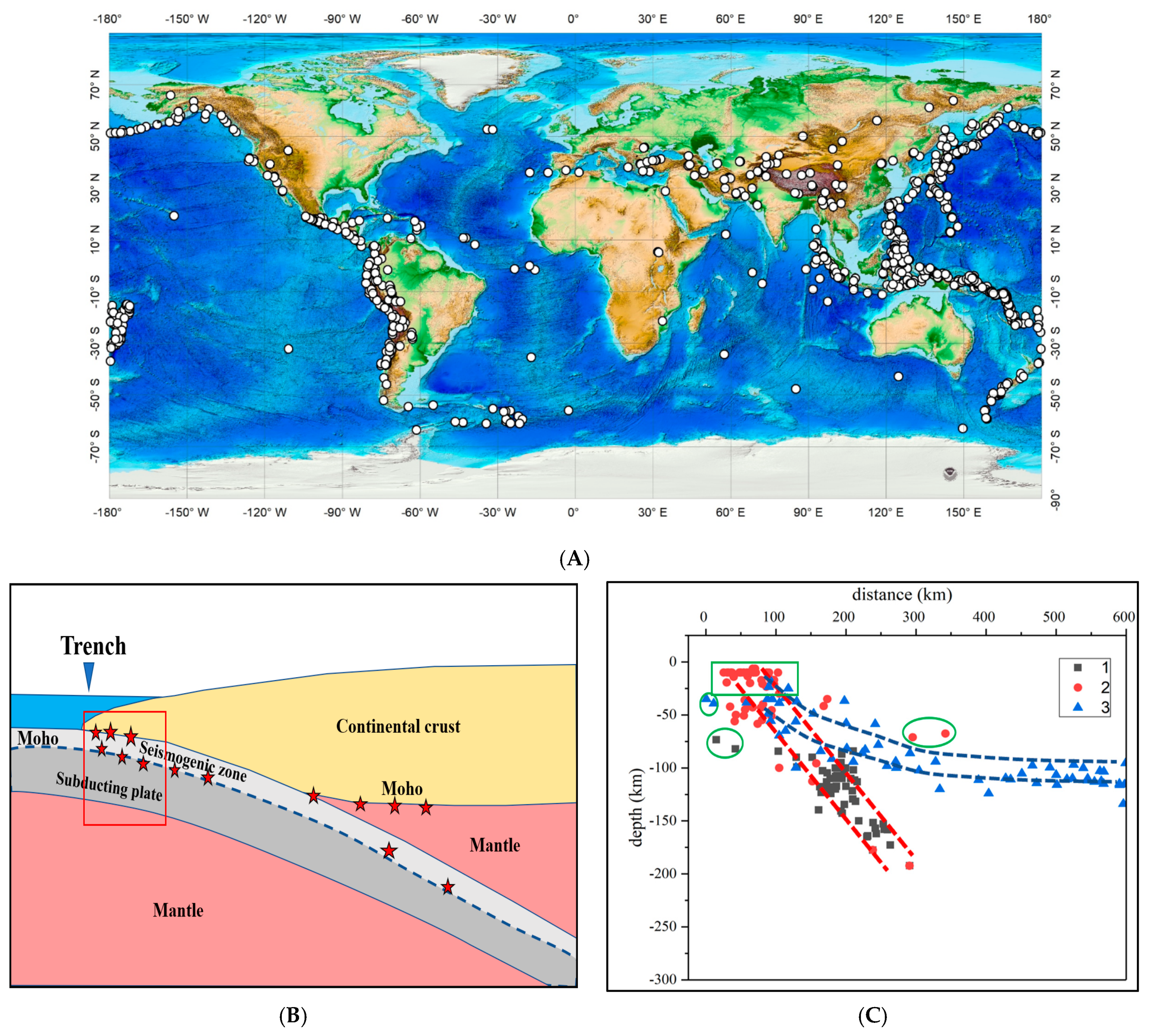
4. Datasets of Shallow Earthquakes
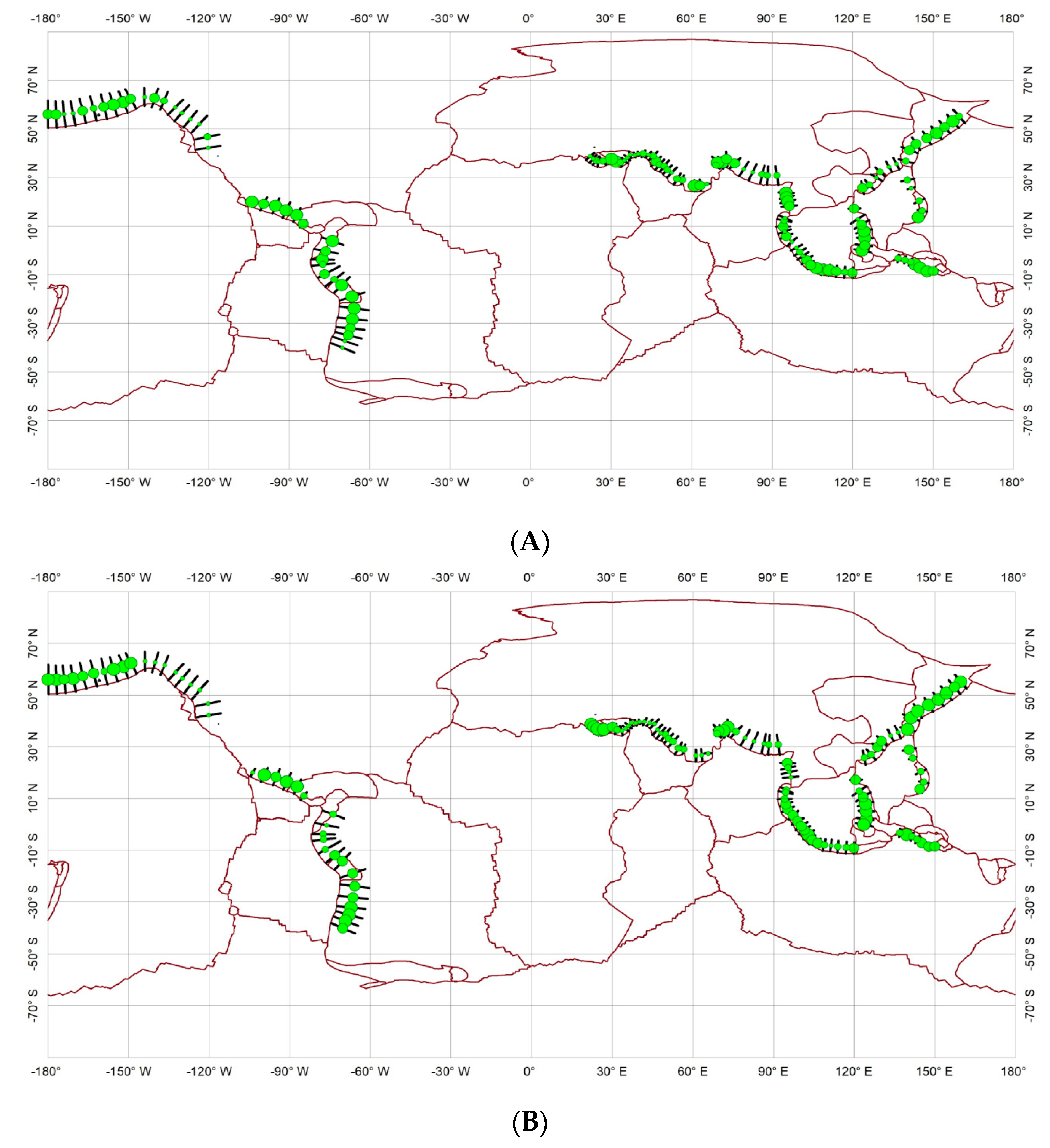
The earthquakes to be analyzed are those that occurred in the lower crust and upper mantle around the Moho and with moment magnitude (Mw) 3 or above at the boundary of the Pacific and Tethys convergent plates, as shown in
Figure 2A–C. The data were downloaded from the USGS website under the section of the USGS Earthquake Hazards Program (
https://earthquake.usgs.gov/earthquakes/map/ (accessed on 1 February 2019)). The datasets include the occurrence time, locations, depths, moment magnitudes (magnitude to be used in the rest of the paper), updated time, error of depths, error of magnitudes, nearest seismic recording station, and the distance to the nearest station. A total of 130 different sections were drawn, with lengths at about 300 km, perpendicular to plate boundaries within subduction or collision regions. The locations of the sections are indicated by the bars in
Figure 3. A buffer zone with a width of 100 km on either side of these profiles was chosen to select a subset of earthquakes whose epicenters were located within each buffer zone around the 130 profiles. The lengths of the profiles were chosen after several trials to ensure most datasets contained adequate earthquakes (a few dozen to hundreds of earthquakes with magnitudes 3 or above) for statistical analysis. Since this study focuses on the frequency–depth distributions of sallow earthquakes in the low crust and upper mantle crossing the Moho transition zones, earthquakes with magnitudes 3 or above and located close to the subduction slabs at depths ranging from 30 km to 100 km were chosen. Profound peaks of frequency distributions are observed at 33 km in most datasets. Considering the depth of shallow earthquakes being set at a “normal” depth of 33 km, when available seismic data poorly constrained depths, only those earthquakes with depths ranging from 34 km to 94 km were analyzed. Further to reduce the potential effect of inaccuracy of earthquake depth data caused by the “false” depth assigned to 33 km without available seismic information, in the analysis, only those earthquakes that can be projected along the “slabs” sketched by the clusters of earthquakes were considered. A few earthquakes projected far apart from the slabs in each profile (examples seen in
Figure 2C) were excluded manually from the analysis. In addition, the earthquakes were also filtered using a threshold of error of depth (<10 km). This threshold was chosen taking into account that the grouping depth for further analysis will be in units of 10 km depth.
To some extent, these treatments can eliminate the effect of earthquakes with arbitrary depths or large errors. Further error assessments were also conducted to show how the depth errors affect the results. Peaks starting from 34 km instead of 33 km can be considered a truncated treatment, which will be further discussed in the remaining section. The earthquakes were further grouped according to 10 km depth bins starting from 34 km downward. The interval with a depth greater than or equal to 34 km and less than 44 km can be regarded as the second bin, assuming the first bin is from 23 km to 34 km. The data of the first bin were not used given the issue mentioned earlier and were thus treated as “missing data” or “unknown data”. Therefore, the distance between the center of the second bin and the center of the first bin is 10 km. Subsequently, the distances between the centers of further bins are in multiple increments of 10 km. Several options can be randomly taken to partition the data with the first bin containing a depth of 33 km. The first bin can be excluded from further mathematical model calibration by treating it as “missing data” or “unknown data”. Several choices of origins of centers of the first bin and bin widths were experimented with. Given the fact that the obtained results by adding this randomness in choosing parameters are similar, only the results obtained by the 10 km bin with the first bin from 23 km to 34 km excluded will be presented. As far as partition parameters are concerned, in terms of consistency for all datasets, the results should be comparable.
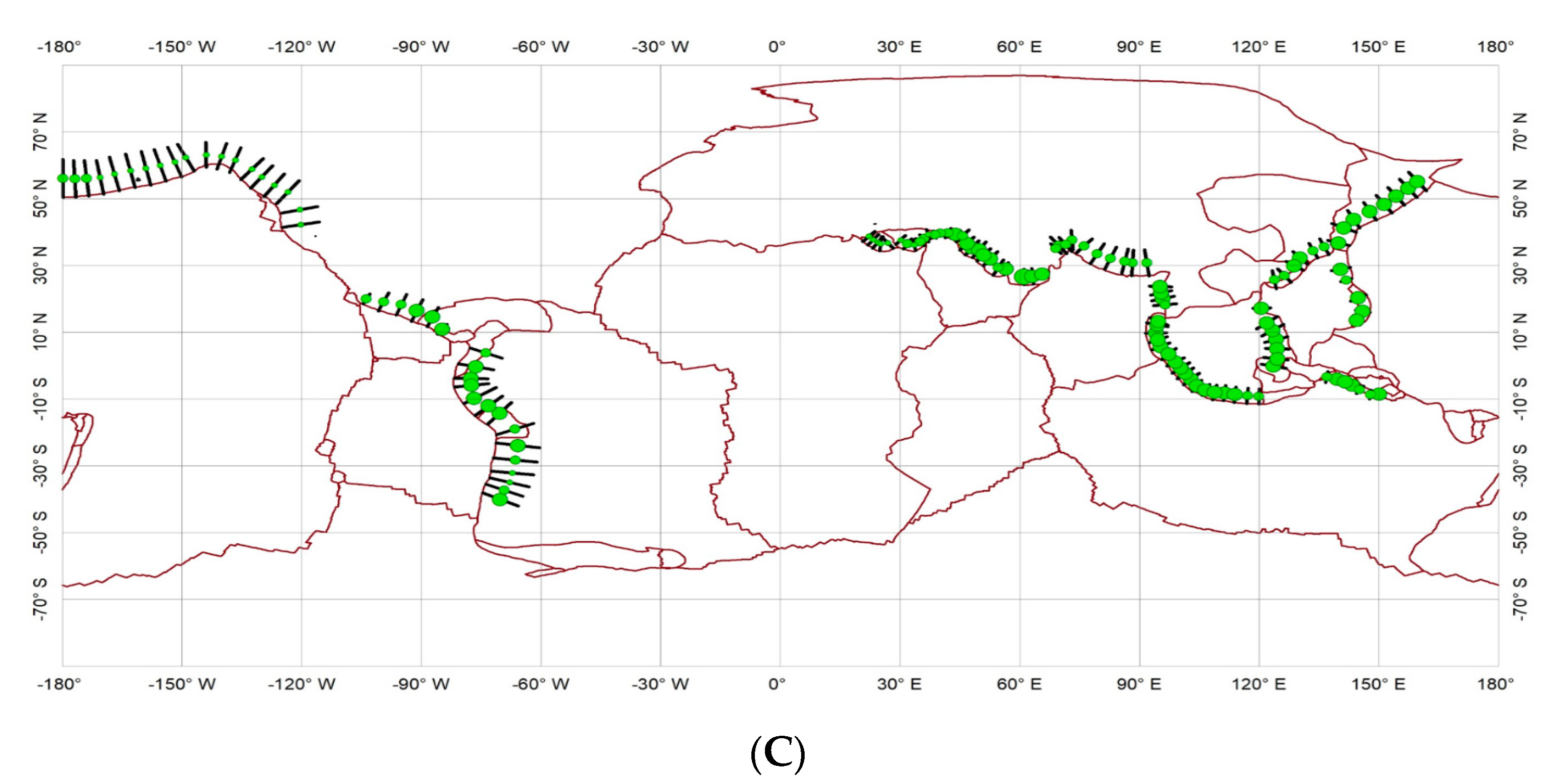
Figure 3.
Characteristics of distributions of earthquakes in a buffer area of 100 km around profiles perpendicular to the trench: (A) average depth of earthquakes; (B) number of earthquakes; and (C) the average magnitude of earthquakes. Folded lines represent the boundaries of plates and the short dark blue colored lines for profiles drawn perpendicular to the trench. The dots in the middle of the profile show the average earthquakes with size proportional to average depth, the number of earthquakes, and average magnitudes, respectively.
Figure 3.
Characteristics of distributions of earthquakes in a buffer area of 100 km around profiles perpendicular to the trench: (A) average depth of earthquakes; (B) number of earthquakes; and (C) the average magnitude of earthquakes. Folded lines represent the boundaries of plates and the short dark blue colored lines for profiles drawn perpendicular to the trench. The dots in the middle of the profile show the average earthquakes with size proportional to average depth, the number of earthquakes, and average magnitudes, respectively.
5. Results
The basic statistics of earthquakes, including the average depth of earthquakes, the number of earthquakes, and the average magnitudes of earthquakes, in all 130 datasets are given in
Table S1 in Supplementary Materials and also shown in
Figure 3A–C. The spatial distributions in
Figure 3 show that, compared with the Pacific plate’s southeastern boundary, earthquakes on the Pacific plate’s northeastern boundary are generally smaller and shallower. Except for earthquakes near the junctions of plate boundaries, earthquakes on the western Tethys plate converging boundaries are generally smaller and shallower than those on the eastern Tethys plate boundaries. To test whether the earthquakes in each dataset follow the Gutenberg–Richter law, the frequency–magnitudes of earthquakes in several selected sections were calculated and plotted in
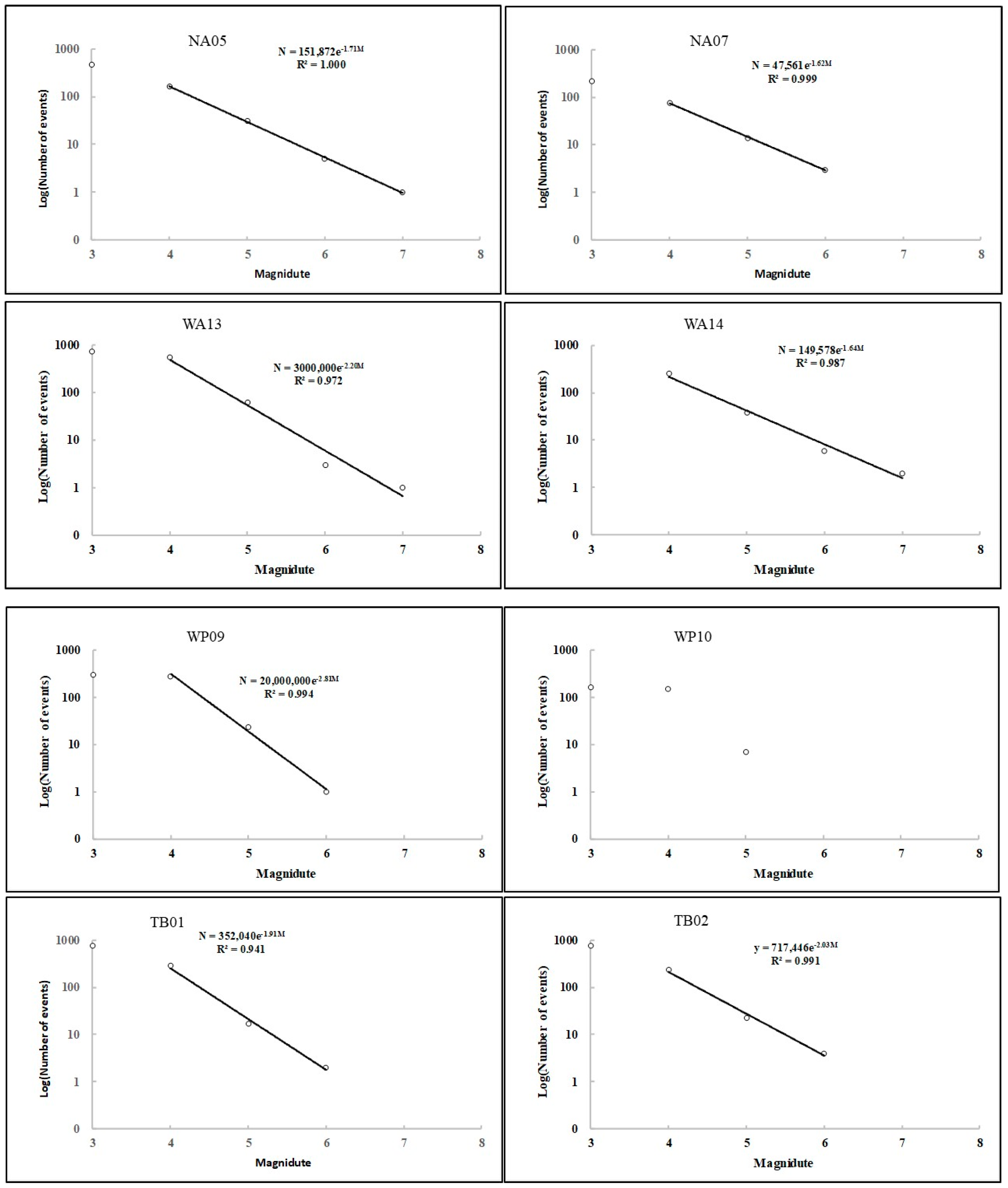
Figure 4. It was found that some datasets include earthquakes of magnitudes 3 to 7 and others only magnitudes 3–6, without 7. The frequency–magnitudes of the datasets with magnitudes 4–7 can generally be fitted using a GR power law relationship. However, the fittings to datasets with only three magnitudes 4–6 may not have statistical significance.
Instead of frequency–magnitude relationships, the frequency–depth distribution of earthquakes is now explored. For example, the results of the average density of frequency–depth distributions for earthquakes with depths between 34 and 94 km are calculated according to Equation (26a). The results from several selected profiles are shown in
Figure 5 (graphs of frequency–depth distributions for the complete list of datasets are given in
Supplementary Materials Figures S1–S4). These graphs show profound truncated frequency peaks at 34–44 km. The frequency density decreases rapidly from the peak at 34–44 km downward over 60 km (from 34 to 94 km).
Figure 4.
Distribution of frequency–magnitude of earthquakes with magnitudes equal to or greater than 3 from around the Moho with depths ranging from 34 km to 94 km. The GR power law functions (log(N) = a – bM) were fitted to the observed data using least squares. Labels on the graphs indicate the location of the datasets; for example, NA05 and NA07 are datasets 05 and 07 from the North American and Pacific subduction zone; SA indicates the South American and Pacific subduction zone; WP indicates the West Pacific subduction zones; and TB indicates the Tethys Belt.
Figure 4.
Distribution of frequency–magnitude of earthquakes with magnitudes equal to or greater than 3 from around the Moho with depths ranging from 34 km to 94 km. The GR power law functions (log(N) = a – bM) were fitted to the observed data using least squares. Labels on the graphs indicate the location of the datasets; for example, NA05 and NA07 are datasets 05 and 07 from the North American and Pacific subduction zone; SA indicates the South American and Pacific subduction zone; WP indicates the West Pacific subduction zones; and TB indicates the Tethys Belt.
Figure 5.
Distribution of frequency–depth density of earthquakes with magnitudes equal to or greater than 3 from around the Moho with depths ranging from 34 km to 94 km. The decay curves were calculated with earthquakes with about 5–15% of earthquakes excluded by the threshold of the error of depth <10 km. The frequency density of earthquakes was calculated using Equation (26a). Three types of functions (linear, log-linear, and log–log-linear functions) were fitted to the observed data using least squares. Labels on the graphs indicate the location of the datasets; for example, NA05 and NA07 are datasets 05 and 07 from the North American and Pacific subduction zone; SA indicates the South American and Pacific subduction zone; WP indicates the West Pacific subduction zones; and TB is the Tethys Belt.
Figure 5.
Distribution of frequency–depth density of earthquakes with magnitudes equal to or greater than 3 from around the Moho with depths ranging from 34 km to 94 km. The decay curves were calculated with earthquakes with about 5–15% of earthquakes excluded by the threshold of the error of depth <10 km. The frequency density of earthquakes was calculated using Equation (26a). Three types of functions (linear, log-linear, and log–log-linear functions) were fitted to the observed data using least squares. Labels on the graphs indicate the location of the datasets; for example, NA05 and NA07 are datasets 05 and 07 from the North American and Pacific subduction zone; SA indicates the South American and Pacific subduction zone; WP indicates the West Pacific subduction zones; and TB is the Tethys Belt.
Most datasets show a general decay trend in mean earthquake number density as the depth increases from 34 km down to 94 km in 10 km bins. The LS method fitted three types of functions to these data trends. The results of parameters calculated from these LS-fitted functions for all datasets are given in
Table S1 in Supplementary Materials. The decay curves in
Figure 5 are LS fittings to the data with linear, log-linear (logarithmic), and double log-linear (power law) functions. The likelihoods of fittings are also calculated as coefficients of determination for the LS fittings, and the results are shown in
Table S1 in Supplementary Materials. The maximum coefficients of determination were based on determining the function types for the LS fittings. Most of the LS fittings involved in the datasets are statistically significant with R
2 > 0.9, and the corresponding Student’s
t-value > 6.3 (use of 6 points of value for fitting). This means that the datasets can be grouped into three classes according to the types of functions fitted to the data using the LS method. These three decay functions show variable degrees of nonlinearity (linear function, logarithmic function, and power law function) (
Figure 6). Before these results are further discussed in the next section, an error assessment should be given to determine how depth errors may affect the results. In addition to the results in
Figure 5 that show the decay curves calculated with earthquakes with about 5–15% of earthquakes excluded by the threshold of the error of depth < 10 km, the results are recalculated with all earthquakes from each dataset for comparison. The results for the six datasets used in
Figure 5 without filtering of depth errors are given in
Supplementary Materials Figure S5, and they indicate that the error filtering of the datasets may slightly affect the values of the estimates of the parameters involved in the LS fittings. Still, it does not change the types of decay functions.
Figure S6 in Supplementary Materials shows the distributions of earthquake magnitudes vs. the depth calculated from the datasets as used in
Figure 5. The results do not show correlations between magnitudes and depths of earthquakes.
6. Discussion
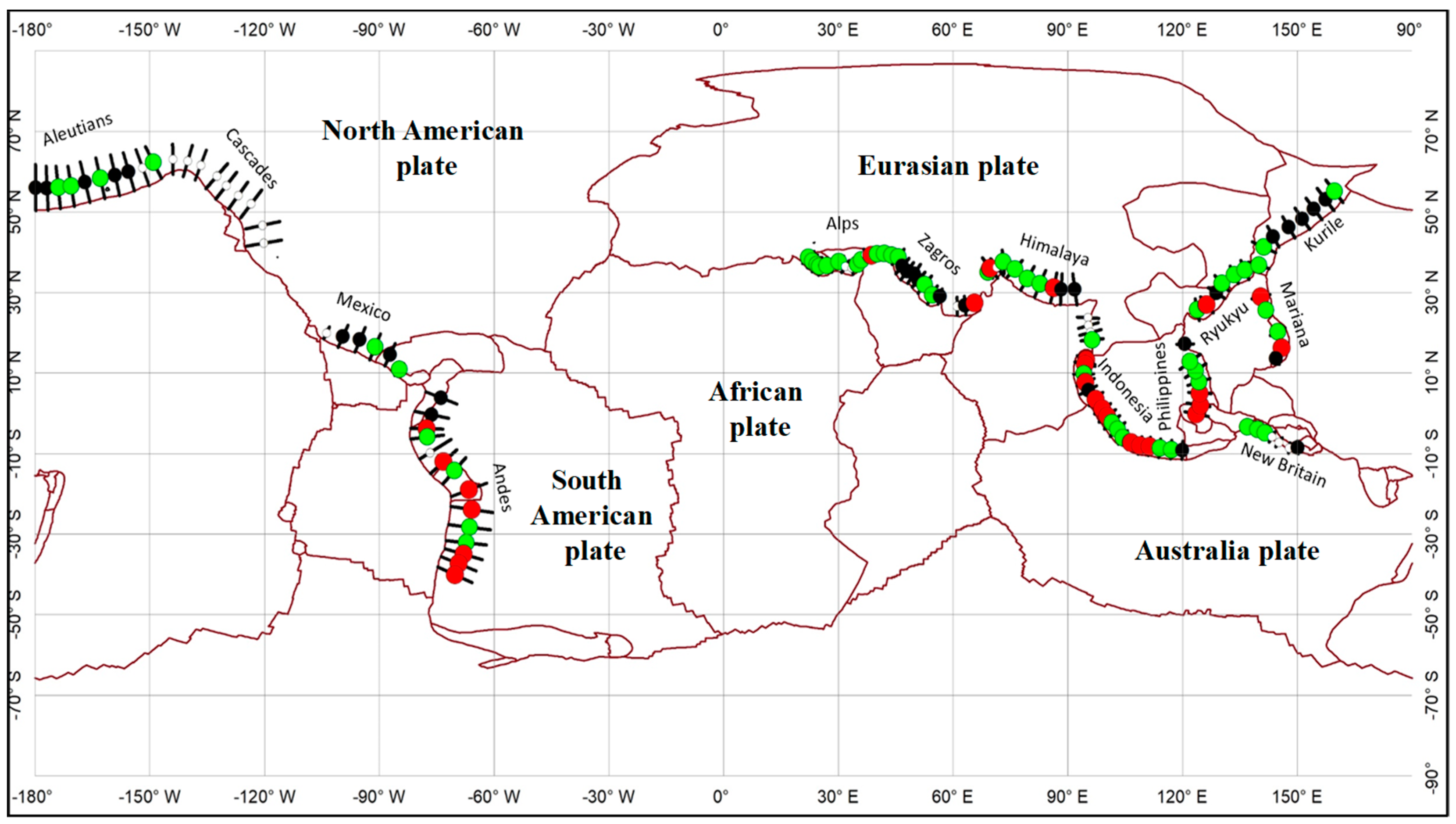
The spatial distributions of earthquakes classified by the three types of frequency–magnitude relationships (linear, log-linear, and double log-linear) show that the datasets can be roughly divided into two main groups based on their geographic locations separated by 10° N latitudes (
Figure 7). The results from earthquakes north of 10° N generally correspond to a linear and log-linear relationship (black and green dots in
Figure 7). In contrast, those south of 10° N correspond to a double log-linear relationship (red dots). In addition, linear attenuation relationships are observed from earthquakes in areas such as the Aleutian Islands, Mexico, and the Kuril Islands in the Pacific subduction zone beneath the North American continent. The logarithmic relationships are observed from earthquakes in the mid-low latitude (10° N–40° N) including the areas in Tethys collision zones (Alps, Himalaya) and West Pacific zone (northern Philippines and Ryukyu) underneath Eurasian continents, respectively. Power law relationships are mainly observed from earthquakes in areas in mid-low latitude (10° N–40° S) underneath the South American continents and Eurasian continents, for example, in mid-southeastern Tethys (Indonesia), Southeast Pacific zones (Andes) and Southwest Pacific subduction zones (southern Philippines), respectively. These three types of “linear” relations of the anomalous seismic frequency–depth distribution at depths of 34–44 km downward imply that, from north latitude to south latitude, from the North Pacific subduction zone to the Tethys collision zone, and to the South Pacific subduction zone, the attenuation of the seismic clusters is from linear, to log-linear, to double log-linear.
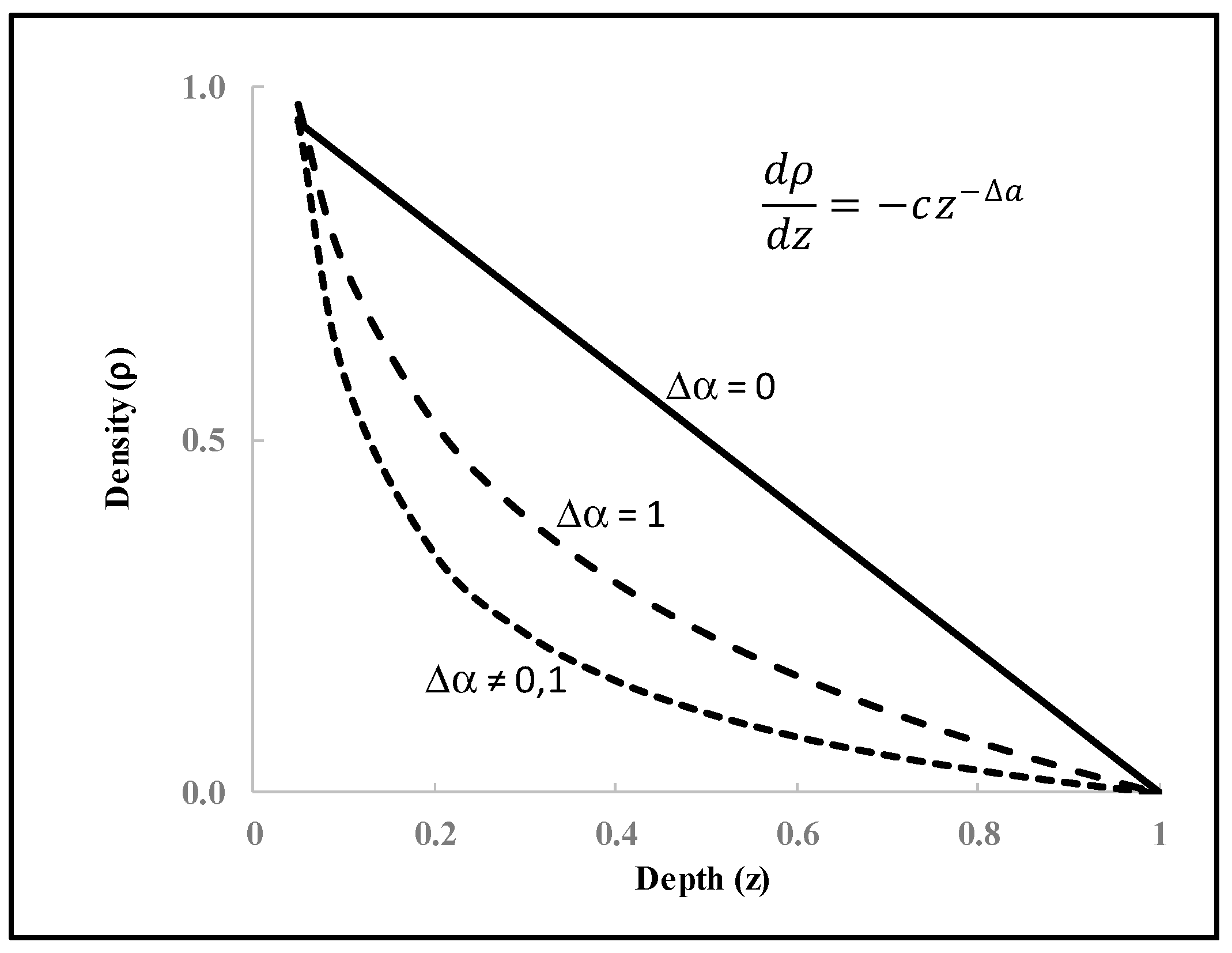
To further explore the property of the density (
ρ), the following differential equation can be used to uniformly represent all three situations with a variable index:
The above relationship shows that the rate of density change depends on the depth z from the peak following a power law relation, which gives three special solutions with three values of exponent (
Figure 6):
If Δα = 0, then z + c0, where c and c0 are constant values. This shows that the density decays linearly with the scale of measurement z;
If Δα = 1, then . This shows that the density scales log-linearly with the scale of measurement;
If Δα ≠ 0, 1, then . This shows that the density scales double log-linearly with the scale of measurement.
The above three cases show that the nonlinearity of the density of the frequency–depth cluster of earthquakes described with the power law function (27) increases with the value of the power law exponent Δα (=0, 1, and others), from a linear relationship to a log-linear relationship to a double log-linear relationship. Recognizing these differences in decay rate may provide insight into the nonlinearity of the seismic system. Geometrically, the exponent value (Δα) indicates the ratio of the change in density against the change in scale or depth. In the first situation of the linear relationship between density and scale, the factor of c determines the density change rate with the scale change. In the second situation of the log-linear relationship between the density and scale, c determines the ratio of the change rate of the density over the log-transformed scale; and in the third situation of the double log-linear relationship between the density and scale, 1 − ∆α (or α) determines the change rate of log-transformed density over the log-transformed scale.
The above discussions also indicate that the frequency–depth cluster distributions of these three groups of earthquakes can be uniformly described with power law functions, which have different degrees of nonlinearity and are quantified by the index values ∆α (0, 1, and others). In addition to the findings reported in the literature indicating that the distributions of earthquake depths may be related to the physical properties of plates, such as temperature and age, this finding further shows that the attenuation of the peak of shallow seismic frequency–depth distribution around the cluster at about 34–44 km may be related to the aggregation of plates and the continental covers. These results, therefore, provide new insights into the characterization of earthquakes in Tethys and the Pacific converging boundaries. Of course, the specific correlation and mechanism corresponding to these three groups of earthquakes need further investigation, which is out of the scope of the current paper.
Variable frequency–depth distributions of crustal earthquakes and lithological compositions are often integrated to characterize crust deformation about variations in tectonic style [
38,
39]. For example, a linearly increasing number of earthquakes with depth, followed by a sharp, exponential decrease, has been reported for long, leading to the detection of similar shapes of curves for seismicity distribution and yielding rheological profiles (e.g., [
40,
41]). Albaric et al. [
42] suggested that seismicity peaks and cut-off depths correlate, respectively, with the upper and lower bounds of the brittle–ductile transitions (semi-brittle fields) within the continental crust. The author’s earlier work [
6] related the nonlinear distribution of frequency–depth earthquakes to the nonlinear property of rheology in phase transition zones. With the identification of the three linear (linear, log-linear, and double log-linear) decay trends of earthquake frequency–depth cluster at 34–44 km, further study is needed to investigate the impact of these nonlinear patterns with relation to lithosphere rheology around the Moho transition zones.
The mechanical behavior of the Moho as a transition zone with discontinuity of lithosphere separating the crust and the mantle is not only characterized by remarkable changes in seismic wave velocity and lithosphere density but also closely associated with the formation and distribution of earthquakes and other extreme events [
43,
44,
45]. For example, Bird [
46] noted that a thrust sheet might readily form through the delamination of the lithosphere at the Moho, as the strength of the upper mantle is far greater than that of the lower crust. Based on field observations of rock deformation, Andersen et al. [
44] reported that large Alpine subduction earthquakes might have occurred along the subducting plate’s Moho. A recent study reported a triggering mechanism for earthquakes around the Moho in southern Tibet [
47]. There are several factors that Moho transition zones could correspond to the aggregation of earthquakes. These factors include, but are not limited to, changes in density, temperature, pressure, and water fugacity. During the subduction and collision of plates, the solid phase lithosphere can be partially melted to facilitate magma formation and cause strain rate change in the lithosphere, promoting intermediate and deep earthquakes [
48]. Both thermal weakening and fluid overpressure weakening can cause active deformation in crustal seismic belts [
49,
50]. The stress generated by volume change reactions may cause fracturing and potentially trigger earthquakes [
50]. It has been substantially studied that an earthquake alters the shear and normal stress on surrounding faults, which causes aftershocks and clusters of earthquakes both spatially and temporally [
51]. Phase transition, self-organized criticality, and multiplicative cascade processes are commonly considered to be mechanisms that generate power law distributions of mass or energy density [
52]; the power law density differential equation observed from the earthquake data may imply that the Moho as a phase transition zone may be responsible for the clustering of earthquakes around 34–44 km. However, more studies are required to explain what causes the nonlinearity of the clustering distribution of earthquakes around the Moho.
7. Conclusions
According to the properties of the fractal density and the relevant fractal calculus operations defined by the author in this paper based on fractals/multifractals, these concepts can be regarded as extensions of the ordinary physical mass density and calculus defined on regular geometries. Fractal density refers to density defined on fractal geometries with fractal dimensions, so fractal derivatives with fractal dimensions must describe it. In this case, the ordinary density becomes a scale-dependent parameter following a power law relations of scale with two factors, namely fractal density and the exponent or singularity index (∆α), showing the difference between the fractal and the Euclidean dimension. The fractal density reduces to the ordinary density when the fractal dimension becomes the regular Euclidean dimension.
The three types of functions (linear, log-linear, and double log-linear) derived from the fractal density concept fit well the seismic frequency–depth cluster data from all 130 sections perpendicular to plate boundaries within subduction around Pacific plates or in Tethys plates collision zones. These three functions are unified as solutions of a power law differential equation with different exponents 0, 1, or otherwise, characterizing the density decay rate of the seismic frequency–depth cluster. This study attempts to study the frequency–depth cluster distribution of earthquakes from the perspective of fractal density. The nonlinear decay rates represented by these three functions may provide insight into characterizing the clustering of earthquakes in subduction or collision zones.
It should be noted that the precision of the seismic depth data used in this paper varies, so the interpretation of the results should be subject to some degree of uncertainty. More accurate data from earthquakes in the broader area and at other depths should be used in the future to validate the methods and results presented in the current study. One of the questions worthy of further research is the association between the rheological properties of the lithosphere around the Moho and the nonlinearity of the clustering of earthquakes.