Fractal Operators and Fractional-Order Mechanics of Bone

Abstract

In recent years, the concept of physical fractal space has been abstracted from muscle/ligament fibers, nerve fibers and blood flows. In the physical fractal space, bio-fractal mechanics may be set up. Surprisingly, the concepts and methods developed in the above bio-fractal mechanics are of universalities, i.e., the physical fractal spaces, fractal operators and fractional-order mechanics universally exist in various biological systems such as bones. This paper will focus on the bones in which the physical fractal space is abstracted, the fractal operators are derived and the fractional-order mechanics is established.

1. Introduction

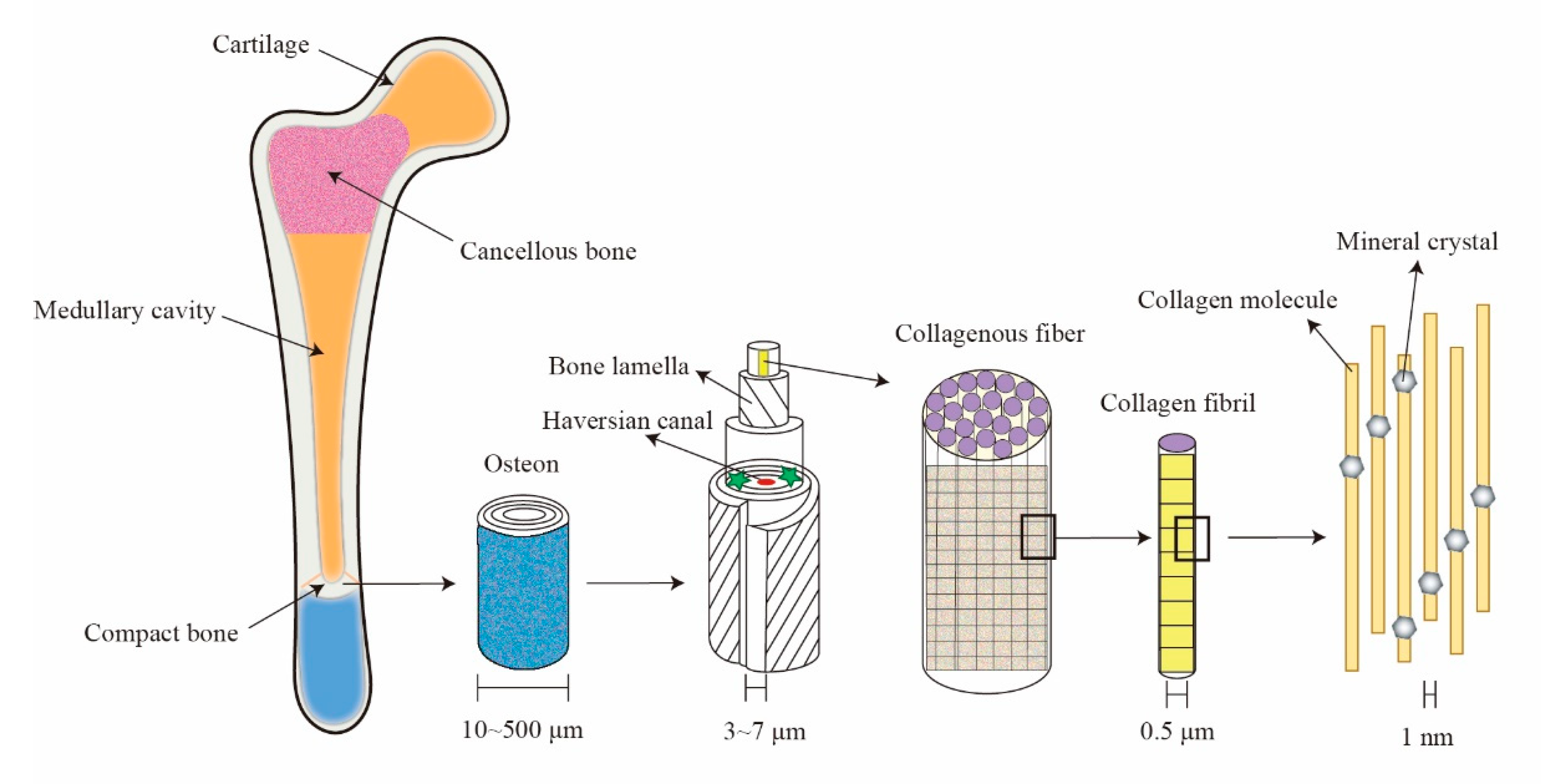
Natural biological composites have excellent mechanical properties, including hard bones, teeth, spider silk, shells and soft tendons, etc. Such biological structures are usually composed of materials with poor mechanical properties at the macro scale. However, through natural optimization from nano to macro scales, they often have very ingenious microstructures. As a typical bio-composite, bone has extremely significant physiological functions in the human body, such as supporting the body, protecting internal organs, hematopoiesis and movement. At the micro scale, mineral crystals with low toughness are interlaced in a collagen matrix with low modulus, which forms the nano-composite structure of bone. After functional self-assembly at different levels, a real bone with high elastic modulus and fracture toughness is formed at the macro scale [1], as shown in Figure 1.

In recent years, we have abstracted the concept of physical fractals from tendon/ligament fibers [2] and nerve fibers [3]. In this fractal space, we reveal the relations between biomaterial fractal space and fractional-order mechanics. Interestingly, the mechanics of biological fibers can be characterized by fractal operators with fractional orders [4]. This progress displays amazing commonness in biological fibers. We may further ask the following question: can the above commonalities be generalized to bone mechanics? This article is dedicated to finding the answer.

At the macro scale, bone is mainly composed of compact bone and cancellous bone. Cancellous bone is located on the inner side and at either end of long bones. Its geometric characteristics are irregular porous structure. In the past, people have tried to establish the porous fractal microstructure of cancellous bone [5].

On the other hand, compact bone is usually located in the outer area of bone, with high hardness. It is mainly composed of osteon (with the shape of 20–30 concentric circular plates) [6]. An organic fiber matrix accounts for about 35% of the weight in dried bone, 95% of which is collagen fiber. Inorganic mineral composition accounts for 65% of the weight in dried bone and the main component is hydroxy calcium phosphate crystal. This composite structure with a hard phase and soft phase not only has high stiffness, but also excellent fracture toughness [7]. Collagen fibers play a structural role as a grid, orient in certain directions and provide certain resistance to compressive load along the long axis of bones. Compact bone has many fractal characteristics, such as multi-scale fiber characteristics, typical micro–nano structure, multi-level self-similarity, etc.

Surprisingly, physical fractal space and fractal operators with fractional orders exist in compact bones, which means that fractional mechanics may also exist in compact bones. This paper will focus on the bones in which the physical fractal space is abstracted, the fractal operators are derived and the fractional-order mechanics is established.

2. Multi-Level Self-Similar Structure of Bone

A fractal cell is a physical and mechanical concept abstracted from biological fibers, which has universal significance in organisms [8,9]. It has previously been confirmed that muscles/ligaments and nerves all possess multi-level self-similar structures [8]. We expanded real biological fibers from the finite order to the infinite order so as to obtain the physical fractal structures [9]. In other words, tissues, organs and systems with multi-level fiber characteristics in organisms can always be studied as chain-like structures. Based on the abstraction of self-similarity, fractal cells have fractional-dimension space and fractional-order time characteristics.

Fratzl studied the multi-level structures of tendons, bones and other biomaterials and explained their multi-scale deformation mechanisms through experiments [10]. Tendons are composed of parallel tendons arranged in bundles and tendon bundles are composed of parallel collagen fiber bundles, embedded in a matrix rich in proteoglycans. From microfibers to fibers, geometric characteristics of self-similarity are observed.

Similar to the multi-level structure of tendons, the hierarchical structures of bones are sequentially as follows: compact bone (macro)—osteon (micro)—bone lamella (sub-micro)–mineralized collagen fiber (nano)–mineralized collagen fibril structure and nano-composite structure (sub-nano), as shown in Figure 1. On the nano scale, Jager and Fratzl observed the arrangement of hydroxyapatite in the collagen matrix [11]. Based on this, Ji and Gao proposed a TSC (tensile shear chain) model, and its load transfer path can be simplified into a tandem spring model containing stretched minerals and sheared proteins [12,13].

Compact bone has the characteristics of multi-scale fibers, and from chain-like fibers, we can abstract the fractal structure.

3. Mechanical Exploration of Bone

Bone has excellent mechanical properties. Bone is a typical bio-composite composed of hard substances (“as hard and brittle as chalk”) and soft substances (“as soft as human skin”), but it has high hardness equivalent to minerals and high fracture toughness equivalent to proteins at the same time. What kind of structures are used to achieve such fantastic physical functions? Researchers have carried out a series of mechanical explorations.

Wolff believes the structural change of bone is a dynamic adaptation process to cope with the dynamic characteristics of load [14]. Wolff’s law enables us to have a qualitative understanding of bone. Its importance lies in revealing that the compliance change process of bone structure with mechanical environment is not the result of natural selection. Therefore, the excellent performance of bone is the result of long-term mechanical action and structural optimization.

Frost further enriches and develops Wolff’s theory [15]. He observes and describes the process of activation, absorption and formation in compact bone and cancellous bone. Frost believes the adaptive structural change of bone tissue is a negative feedback system in which strain is input signal and mineral content and structure of bone are output signals. Frost tries to establish a relation between strain (mechanical quantity) and bone mineral density (physical quantity), but does not abstract the structure in mechanical way.

Gao proposes a mechanical model of tension shear chain (TSC) [12,13] showing the chained load transfer method. This chained load transfer model effectively localizes the deformation and stress of minerals. Researchers have further developed the TSC model. Liu and Zhang extend the TSC model to three-dimensional [16,17]. Liu’s research shows [18] that when the modulus ratio of a two-phase material is about 1000 and slenderness ratio of minerals is 30, the stiffness of a composite can be increased to the same level as minerals, and even be close to minerals.

Cell biology and molecular biology taking bone cell mechanics as a representative greatly expands the research methods of bone mechanics, combining with different theoretical systems such as experiments, statistical mechanics, and biochemical reaction dynamics [19,20].

4. “Geometric Fractals” and “Physical Fractals” in Bone

In the TSC model, Gao proposes the concept of “fractal bone” [21], in which each level is similar to the nano-composite structure. It should be noted that “fractal bone” is essentially “geometric fractal”. The equivalent modulus $E$ of the entire nano-composite structure is affected by spatial geometry, as shown in Formula (1), where $\phi$ is the volume fraction of minerals, ${\mu }_{\mathrm{p}}$ is the shear modulus of collagen and $E_{\mathrm{m}}$ and $\rho$ are the Young’s modulus and slenderness ratio of minerals, respectively. $E_{\mathrm{m}}$ and ${\mu }_{\mathrm{p}}$ are the material constants. The equivalent modulus of structure mainly depends on geometric quantities (slenderness ratio of minerals $\rho$, volume fraction $\phi$, spatial arrangement and orientation, etc.).

$$\frac{1}{E}=\frac{4\left(1-\phi \right)}{{\mu }_{\mathrm{p}}{\phi }^2{\rho }^2}+\frac{1}{\phi E_{\mathrm{m}}}.$$

(1)

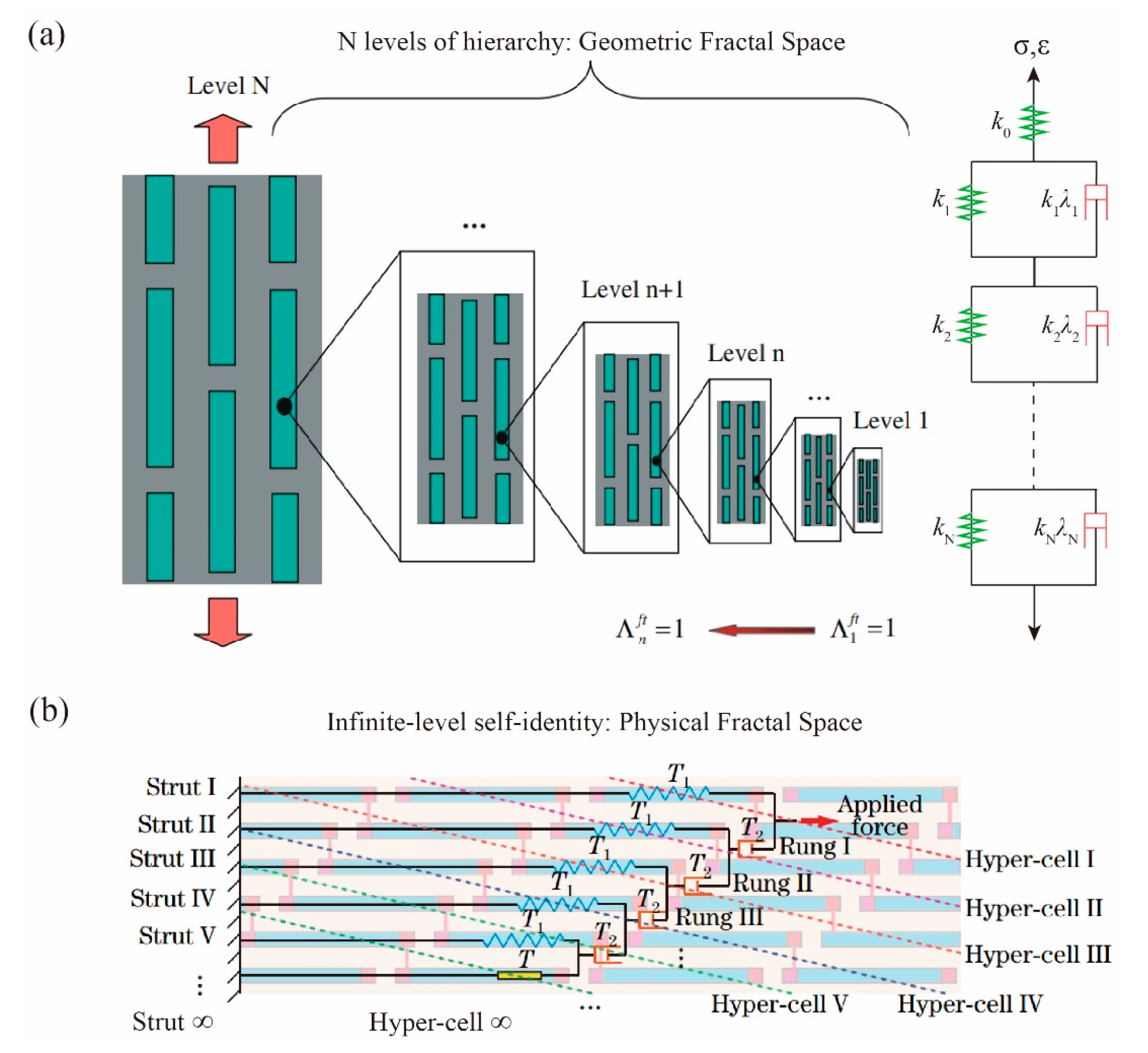
Unlike “geometric fractal”, we previously introduced “physical fractal” [9], as shown in Figure 2. This article will abstract the physical fractal of bone.

It has previously been highlighted that the structural composition of bone is extremely complex, and different scales correspond to certain functions and properties, which increases the difficulty of mechanical abstraction. In the TSC model, proteins between the short edges of adjacent mineral crystals mainly undergo tensile deformation and transfer minimal and negligible loads. The size, proportion, orientation and arrangement of hydroxyapatite are related to the overall mechanical properties of bone. As the structural hierarchy of the biosystem continues to increase, the “geometric fractal” model becomes more complex in computation. When the fractal hierarchy approaches infinity, traditional bone mechanics models will also become infinitely complex in computation. At this point, the “physical fractal” model provides a new computational method for characterizing the mechanical properties of organisms.

The mechanical design based on fractal theory can bear more cases of complex load. According to the multi-level self-similar structure and strengthening mechanism of bone, we can distinguish “geometric fractal” from “physical fractal” bone, that is, the difference in spatial form: the former is geometric space and the latter is functional space. We note that the viscoelastic response in Gao’s “geometric fractal space” is still based on the description of quasilinear viscoelastic constitutive, and the constitutive equations are all in the form of integer-order calculus, as shown in Figure 2a. When we study “physical fractal space”, the dynamic response of physical components in the fractal tree of self-identical components is characterized by the operator algebraic equation, which usually has the property of non-integer order, as shown in Figure 2b. In addition, the physical component can also be fractional. Starting from the micro-nano self-similar structure of bone, the functional fractal structure is abstracted, and then the internal correlation between fractional-dimension space and fractional-order time can be established. It is expected that the generalized physical fractal model can correspond to actual biological function, which is a process from function to the functional application of biological structure.

5. Fractal Operators and Fractional-Order Mechanics of Bone

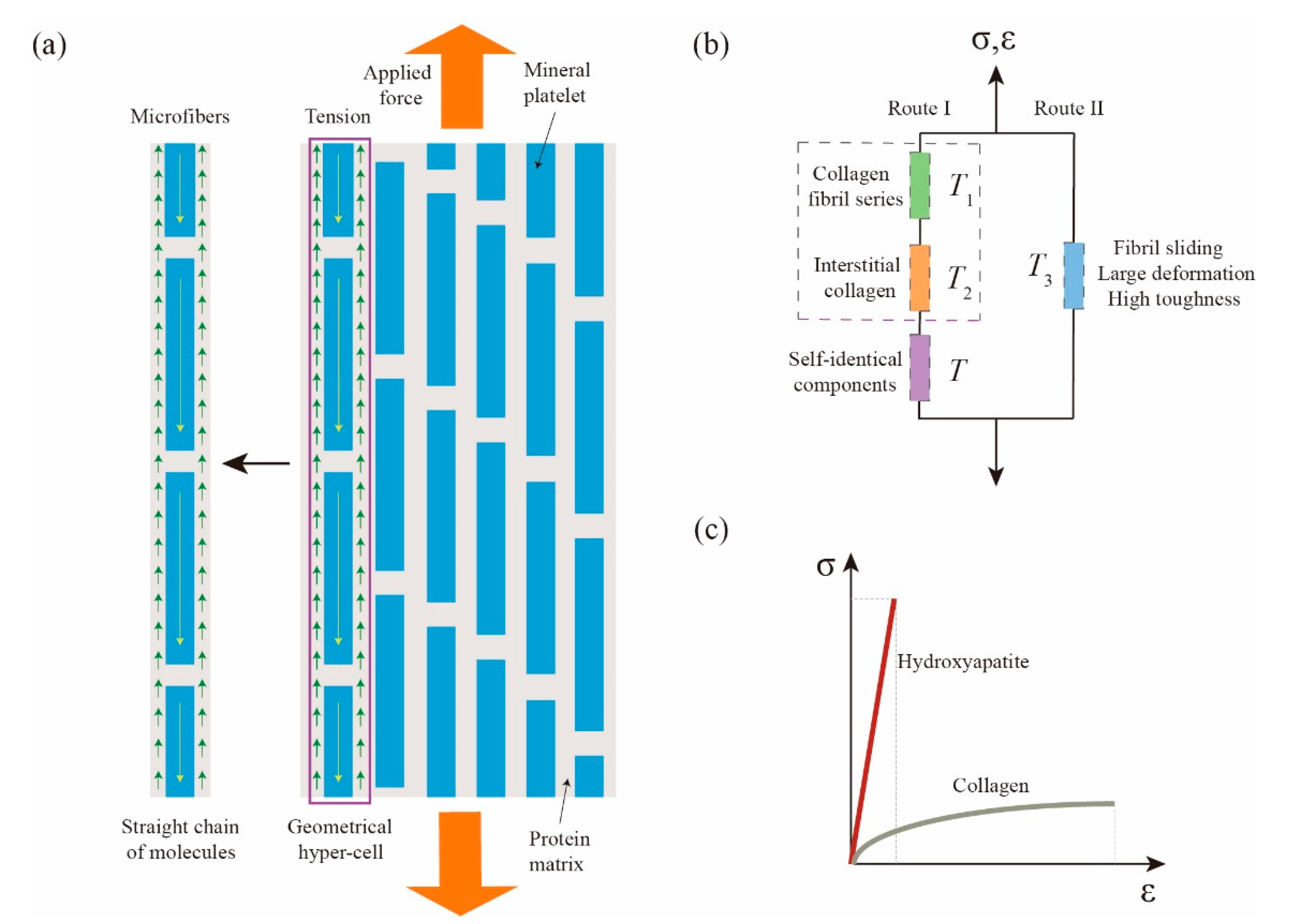
In this section, we will abstract the physical fractal space and fractal cell of compact bone. Unlike conventional methods, our selected research object is a microfiber, as shown in Figure 3a, wherein hydroxyapatite is equivalent to a spring with the operator $T_1$, the protein between hydroxyapatite is equivalent to a spring with the operator $T_2$ and the surrounding protein matrix is equivalent to fractional rubber (dashpot) with the operator $T_3$.

The reasons for the above abstraction are as follows: the stiffness $K_1$ of a single hydroxyapatite is usually 10 times the bone’s macro modulus [12]. Therefore, it is necessary to concatenate a spring $T_2$ (the stiffness $K_1$ of hydroxyapatite is usually 1000 times collagen’s $K_2$ [21]) connected with $T_1$. The introduction of $T_2$ effectively reduces the global stiffness (from 1000 $K_2$ to 1.001 $K_2$). Since parallel connection always increases the stiffness, when the fractional-order rubber (dashpot) model $T_3$ is paralleled, the fractal tree of self-identical components abstracted from the straight chain can be extended to infinite, as shown in Figure 3b. At the same time, its physical process can also be explained clearly. Hydroxyapatite has high stiffness, but the allowable deformation is very small. After $T_2$ is connected in series, the large deformation can be borne by $T_2$. Meanwhile, the stiffness of the branched system is reduced, so the parallel rubber (dashpot) $T_3$ with fractional-order characteristics can be accumulated step by step to infinity, thus matching the macro mechanical properties of bone. It can be seen from Figure 3 c that the rigidity of hydroxyapatite is high, corresponding to a high slope in the stress—strain curve. The tensile strength of collagen is close to that of hydroxyapatite, which also explains the fact that the allowable deformation of collagen substrate is relatively large under the same or similar strength and the load can be transferred well through shear deformation.

The establishment of a physical fractal cell in compact bone is closely related to its multi-level self-similar structure and strengthening mechanism. Here, we summarize the essential differences between the TSC model and “physical fractal “model: (1) the TSC model is “geometric fractal”, which can not break through the classic spatial form of Euclidean geometry. The final mechanical quantity is related to the geometric form of hard and soft phases, that is, starting from the geometry of biomaterials, which corresponds to the function of bone by changing geometric parameters. Our model is “physical fractal” [9], that is, starting from the function of physical components, we can adjust mechanical properties of components, which corresponds to the physical function of bone. This property gives the credit to the concept of “fractal cell” and “physical fractal space”. (2) The viscoelastic response of the TSC model is still based on the description of the quasilinear viscoelastic constitutive. Instead, we can introduce fractional-order physical components to build the fractal operators and fractional-order mechanics of bone.

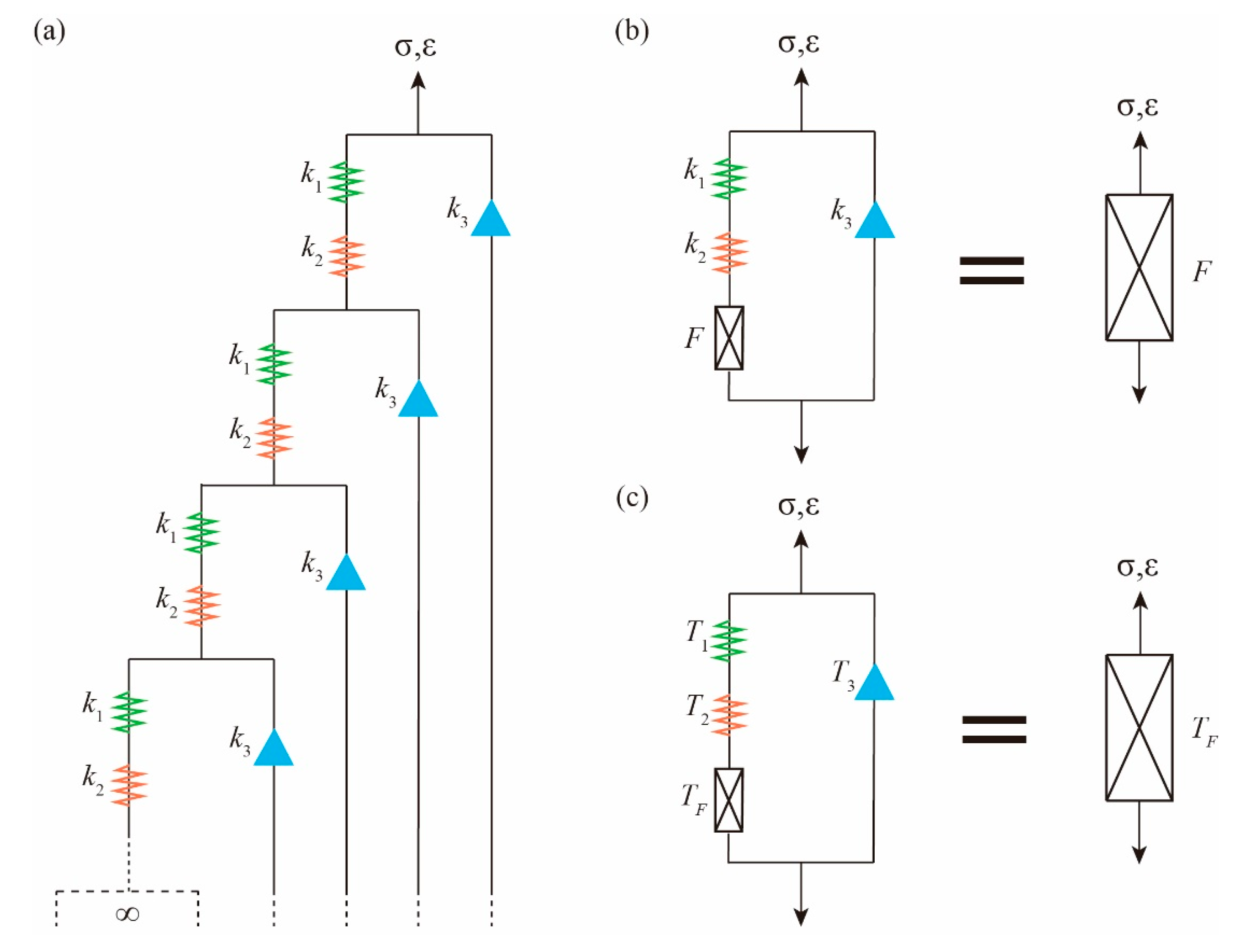
According to the transmission path of force and deformation along the straight chain, we can abstract the fractal tree with self-identical components. If the series of multi-level structure tends to infinity, the fractal tree with self-identical components becomes special, as shown in Figure 4a. Locally, the adjacent structure of the fractal tree is congruent. On the whole, multi-level structure possesses perfect self-identity, which is a special form of regular fractal self-similarity. The least-repeated substructure in the physical fractal space is called the fractal cell. It should be noted that there is no infinite structure in organisms, so there cannot be an infinite number of collagen molecules in the straight chain. The infinite order is just an idealized limit state. In scientific exploration, this is a simplified way that we often use.

At this point, we can say that physical fractal space and fractal cell exist in compact bone. In other words, chain-shaped fibers with multi-level self-similar structures in organisms can always be abstracted to the fractal cell and physical fractal space.

The fractal tree of components composed of $T_1$, $T_2$ and $T_3$ can be equivalent to a fractal component $F$ with operator $T$ as a whole. From the primary branch to the secondary structure, another fractal element $F$ can be seen. Therefore, the whole fractal tree is equivalent to the following simple structure: $T_1$ and $T_2$ of the first level are connected in series with the fractal element $F$, and then connected in parallel with $T_3$. The equivalent structure is the fractal cell, as shown in Figure 4b. In other words, the fractal cell is necessarily equivalent to the fractal component $F$. As shown in Figure 4b, “=” means that the intrinsic invariance in “physical fractal space” is the equivalence of the fractal cell and fractal tree [9].

The mechanical response of physical components can be characterized by operators. If the stress on a general element is $\sigma$, with the strain $\epsilon$ and modulus $G$, respectively, then we have the following:

$$\sigma =T\epsilon .$$

(2)

For elastic element $k$, we have the following:

$$T=T_k=G.$$

(3)

For viscous elements $\mu$, we have the following:

$$T=T_{\mu }=G\lambda p.$$

(4)

where $\lambda$ is the relaxation time constant and $p$ is the classic time differential operator, expressed as follows:

$$p=\frac{\mathrm{d}}{\mathrm{d}t}.$$

(5)

For the physical components with fractional order, such as the Abel dashpot [22,23,24], their viscous force $F^d$ and strain ${\epsilon }^d$ satisfy the relation of the fractional derivative, and their fractional order is expressed on the time differential operator:

$$F^d={\lambda }^{\alpha }\frac{{\mathrm{d}}^{\alpha }{\epsilon }^d}{\mathrm{d}{t}^{\alpha }}.$$

(6)

In the literature, the Abel dashpot model has been used to describe the rheological properties of various biomaterials, such as single-protein molecules [25], arteries [26], etc. However, most of the works simply replaced the linear dashpot component with the Abel dashpot in the spring—dashpot model, which cannot reveal the inherent relationship between the mechanical function of biomaterials and their micro and nanostructures. In addition, fractional-order equations with such “short-memory” characteristics can also be used to develop the time-fractional damage model of an abdominal aortic aneurysm [27] and derive the Noether’s theorem of the generalized Birkhoff equations [28].

For fractal cell $F$, we have the following:

$$T=T_F.$$

(7)

At this time, the fractal operator $T_F$ is an unknown operator to be solved. It has been proven [9]: in Figure 4b, if the component is replaced with the corresponding operator, the invariance described by the “=” sign is still valid, as shown in Figure 4c. The invariance of the operator fractal space provides an algebraic equation for the fractal operator $T_F$ below:

$$\frac{1}{\frac{1}{T_1}+\frac{1}{T_2}+\frac{1}{T_F}}+T_3=T_F.$$

(8)

In mechanics, the right-hand side of Equation (8) can be regarded as the stiffness of the fractal component and the left-hand side can be regarded as the stiffness of the fractal cell. It is further deduced that

$$\left(T_1+T_2\right)T_F^2-\left(T_1+T_2\right)T_3{T}_F-T_1{T}_2{T}_3=0.$$

(9)

Equation (9) is the algebraic equation for the fractal operator $T_F$. This is a quadratic equation with a radical solution:

$$T_F=\frac{T_3\pm \sqrt{T_3^2+4\frac{T_1{T}_2{T}_3}{\left(T_1+T_2\right)}}}{2}.$$

(10)

So far, the fractal operator $T_F$ of compact bone is determined, as shown in Equation (10).

According to the experimental results in the literature [12,13], the elastic modulus of bone is 10–20 GPa, the elastic modulus of hydroxyapatite is 50–100 GPa, the elastic modulus of collagen is 50–100 MPa and the relaxation time constant $\lambda$ is in the range of 200–4000 s. Therefore, we take the modulus $G_1$ of the elastic component $T_1$ characterizing hydroxyapatite (hard phase) as 100 GPa, the modulus $G_3$ of the viscous component $T_3$ characterizing collagen (soft phase) as 50 MPa and the relaxation time $\lambda$ as 1000 s. 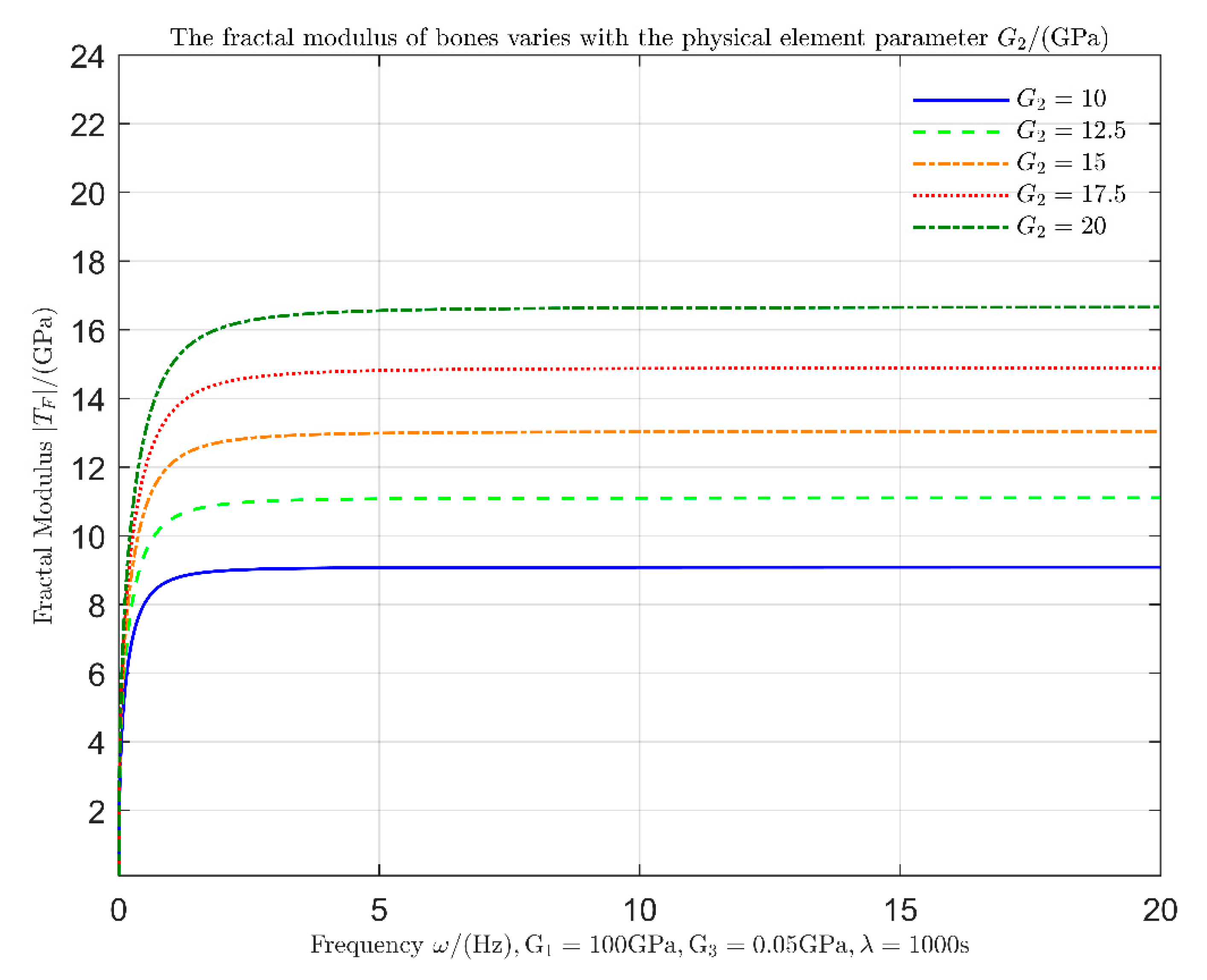Changing the modulus $G_2$ of the protein $T_2$ between hydroxyapatite, transferring the fractal operator $T_F$ to the frequency domain for analysis and bringing in the above physical parameters of real bone, the fractal modulus is shown in Figure 5.

It can be seen that when the elastic modulus $G_2$ of physical component $T_2$ is taken as 10 GPa, 12.5 GPa, 15 GPa, 17.5 GPa and 20 GPa, the fractal modulus of bone converges to 9.09 GPa, 11.11 GPa, 13.04 GPa, 14.89 GPa and 16.67 GPa. The above results are in good agreement with the experimental data of bone [29,30,31], which also brings new mechanical inspiration to biological fractal design. By selecting the basic components of organisms, the idea of fractalization can be effectively utilized to study the mechanical properties of biological materials. In other words, multifunctional fractal operators can be effectively designed by regulating the intrinsic properties of physical components. Once the operator is controllable, the fundamental mechanical equations of biomaterials possess designability. It should be noted that the physical components used here are relatively basic spring–dashpot components, which can also be selected according to the actual biological structure of various types of fractional-order components.

Similarly, biological materials such as shell [32] and nacre [33] also have a multi-level geometric fractal self-assembly pattern with alternating soft–hard phases. Lin et al. used the strain gradient viscoelastic theory and found the equivalent modulus is more accurate than the TSC model [34]. Meanwhile, Lin noted that the effective modulus predicted by the traditional tension shear chain model is much smaller than the experimental results [35,36]. This is because the TSC model does not include significant microstructural effects at the micro—nanoscales. Likewise, our proposed physical fractal mechanics model of bones effectively predicts the modulus of bones, which reveals the multiscale effects of bone mechanics. It is worth noting that the proposed fractal model not only reflects the multi-level geometric fractal structure of bones, but also describes the physical fractal properties of biomaterials.

Moreover, this kind of physical fractal model is not only valid in the mechanics of bones. According to the structural characteristics of shells, we can also use the physical fractal operator to describe their physical function more accurately. In conclusion, the fractal operators of bones in the physical fractal space provide a new way to characterize the mechanical properties of biomaterials.

6. Properties of Fractal Operator

The fractal operator $T_F$ satisfies the algebraic equation, which is derived from the invariance of physical fractal space.

As confirmed in previous research [8], the highest power $n$ in the algebraic equation of a fractal operator depends on the topological invariant of the fractal cell, that is, the bifurcation number. The tree-like fractal space of dense bone has a two-branch topology, so n equals 2. This leads to the fractal operator $T_F$ presenting a 1/2 order in appearance. Of course, the final order of the radical $\sqrt{\left(\cdot \right)}$ depends not only on the 1/2 order of the $\sqrt{ }$ sign, but also on the order of the operator $\left(\cdot \right)$ in the root sign.

Compared to the fractal operator in previous articles [2,3], the fractal operator $T_F$ of compact bone is of more general form. When $T_1$ or $T_2$ is equal to zero, $T_F$ may degenerate to Guo’s model [2,3] and can reflect the long-term viscoelastic response in ligaments/tendons and other biological fibers.

The introduction of $T_2$ strengthens the designability of the fractal operator $T_F$ and broadens the application scope of the above physical fractal space. The designability of the fractal cell essentially reflects biodiversity.

In Equation (10), only when $T_2$ tends to infinity does the overall stiffness converge to a finite value. This is because $T_1$ is connected in series with $T_2$, which effectively disperses the stiffness of this branch, powerfully explaining how the excellent mechanical property in organisms comes from multi-scale soft and hard fusion. In other words, $T_F$ is jointly determined by the operators of physical components, and the collaboration between components and the topological structure of the fractal tree plays a central role.

Multi-level self-similar structures are universal in organisms, and the mechanical behavior of soft and hard material/structure integrated design is not unique to bone, but widely exists in biological materials such as shells [32], nacre [33] and so on. It is worth mentioning that the abstraction of entire biomechanics inspires the manufacturing process of new materials: only using hydroxyapatite of continuous arrangement cannot reflect the high toughness of bone, and it is a more natural way to fill the gap with collagen. This multi-level self-assembly mode can give rise to excellent properties of two-phase materials at the same time, and the idea of fractalization shows its power again. We are quite convinced the fractal cell is a highly creative concept in the physical fractal space, and there is a deep internal correlation between fractional-order time and fractional-dimension space. Different from the traditional geometric fractal mode, physical components in the physical fractal space directly determine the properties of the fractal operator $T_F$. Once the operator is controllable, the fundamental mechanical equations of biomaterials possess designability.

In short, the designability of the fractal operator $T_F$ may improve the manufacturing vitality of artificial materials. The fractal operator $T_F$ offers a novel approach to calculate the fractional-order mechanical properties of extremely high-level biological fractal structures, which cannot be achieved using traditional bone mechanics models.

7. Conclusions

In tendons/ligaments, fractal operators exist universally. Now, we can say that in compact bone, fractal operators also exist universally. Such a conclusion is derived from the structural and functional features of natural biological materials, rather than subjective intuition.

The mechanics of bone is indeed of a 1/2 order fractional order. In fact, once the physical fractal space with two-branched topology is abstracted, the fractal operator with 1/2 order may be ascertained, and the 1/2 order bone mechanics may be assured.

The essential difference between “geometric fractal” and “physical fractal” is the space form: the former is geometric space, and the latter is functional space. The mechanical (functional) quantity of “geometric fractal” is determined by geometry, and the mechanical quantity of “physical fractal” is determined by the properties of physical elements (fractal operator $T_F$ can be regarded as some algebraic combination of component operators). “Physical fractal” corresponds to actual functions.

Physical fractal is an interesting spatial form in which fractional mechanics is controlled by fractal operators. This proposition possesses universal applicability in biomechanics.