Global Stability of Fractional Order HIV/AIDS Epidemic Model under Caputo Operator and Its Computational Modeling
Abstract
1. Introduction
2. Structure of the Model
3. Deterministic System (1) and Its Analysis
3.1. Positivity of Solutions
3.2. The Invariant Region
3.3. The Disease-Free State and Derivation of
3.4. Global Stability Analysis of
3.5. Existence of the Endemic Equilibrium
3.6. Global Stability of the Endemic Equilibrium
4. Formulation of Fractional Model
Fundamental Results
5. Qualitative Analysis of the Assume Model
Stability Results for Model
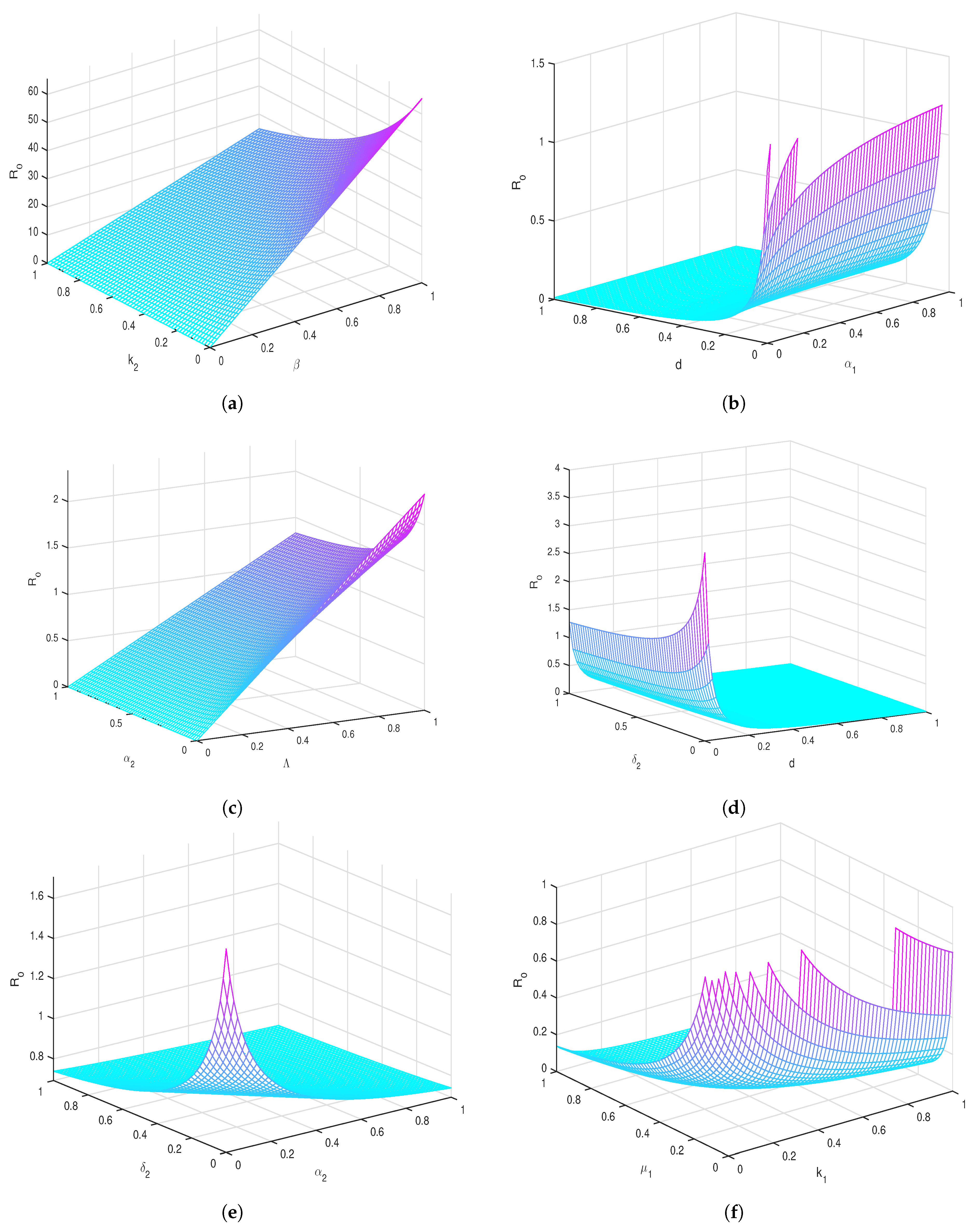
6. Sensitivity Analysis
Sensitivity Indexes for with Respect to Each Parameter
7. Numerical Scheme and Simulations
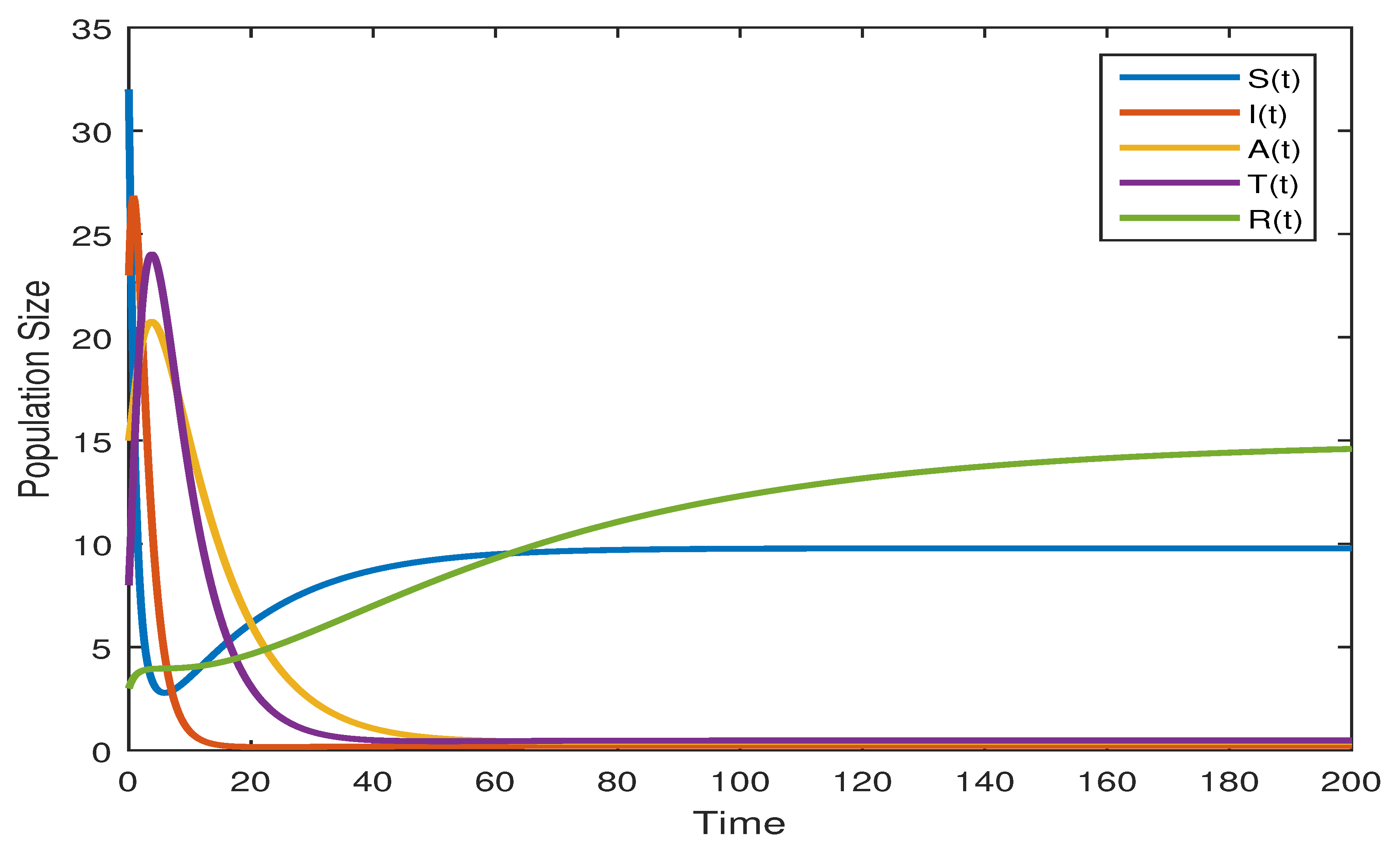
7.1. Numerical Analysis of the Deterministic Model (1) by RK4 Method
7.2. Numerical Scheme for Model (31)
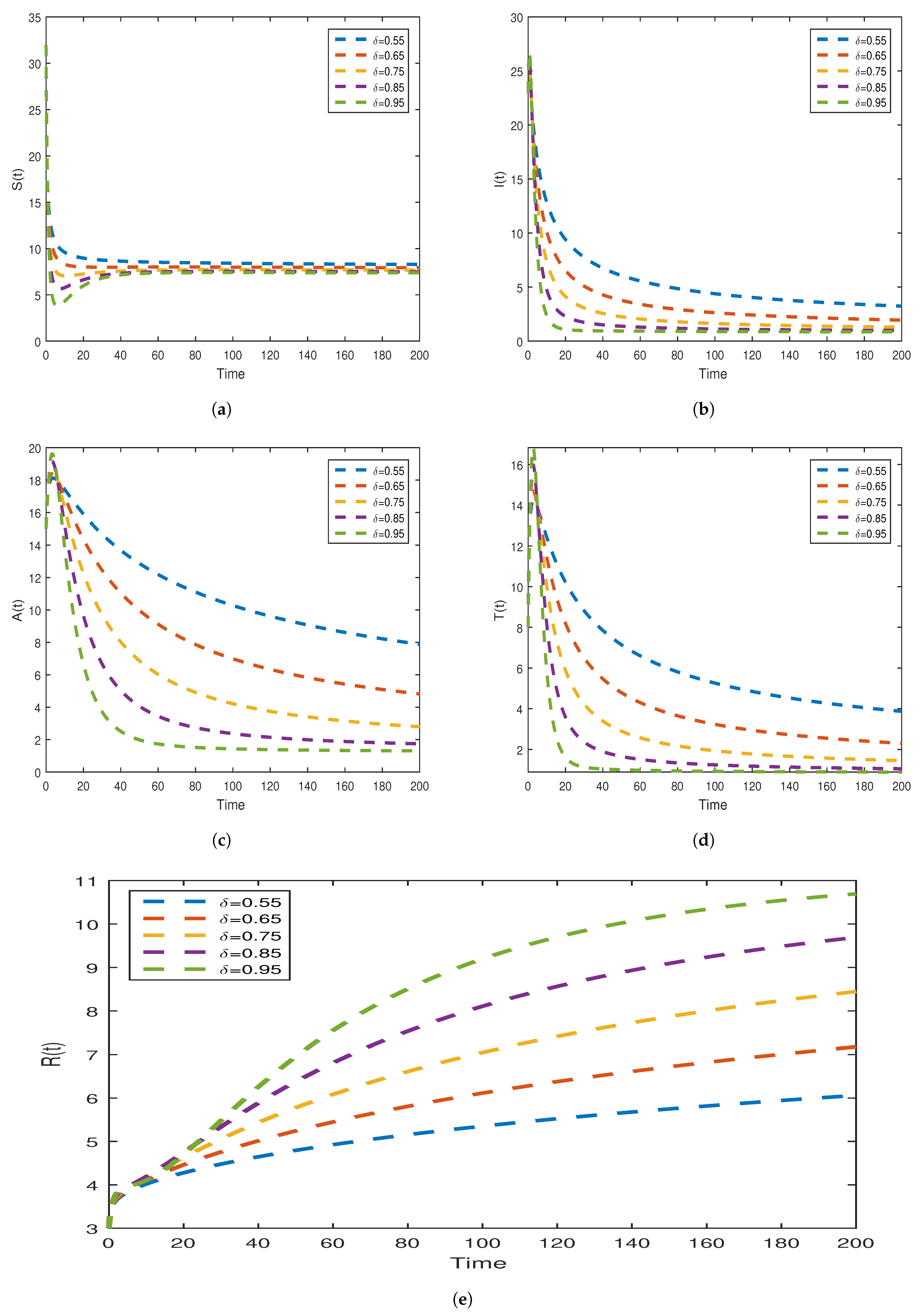
7.2.1. Numerical Scheme via Newton’s Polynomial for Model (31)
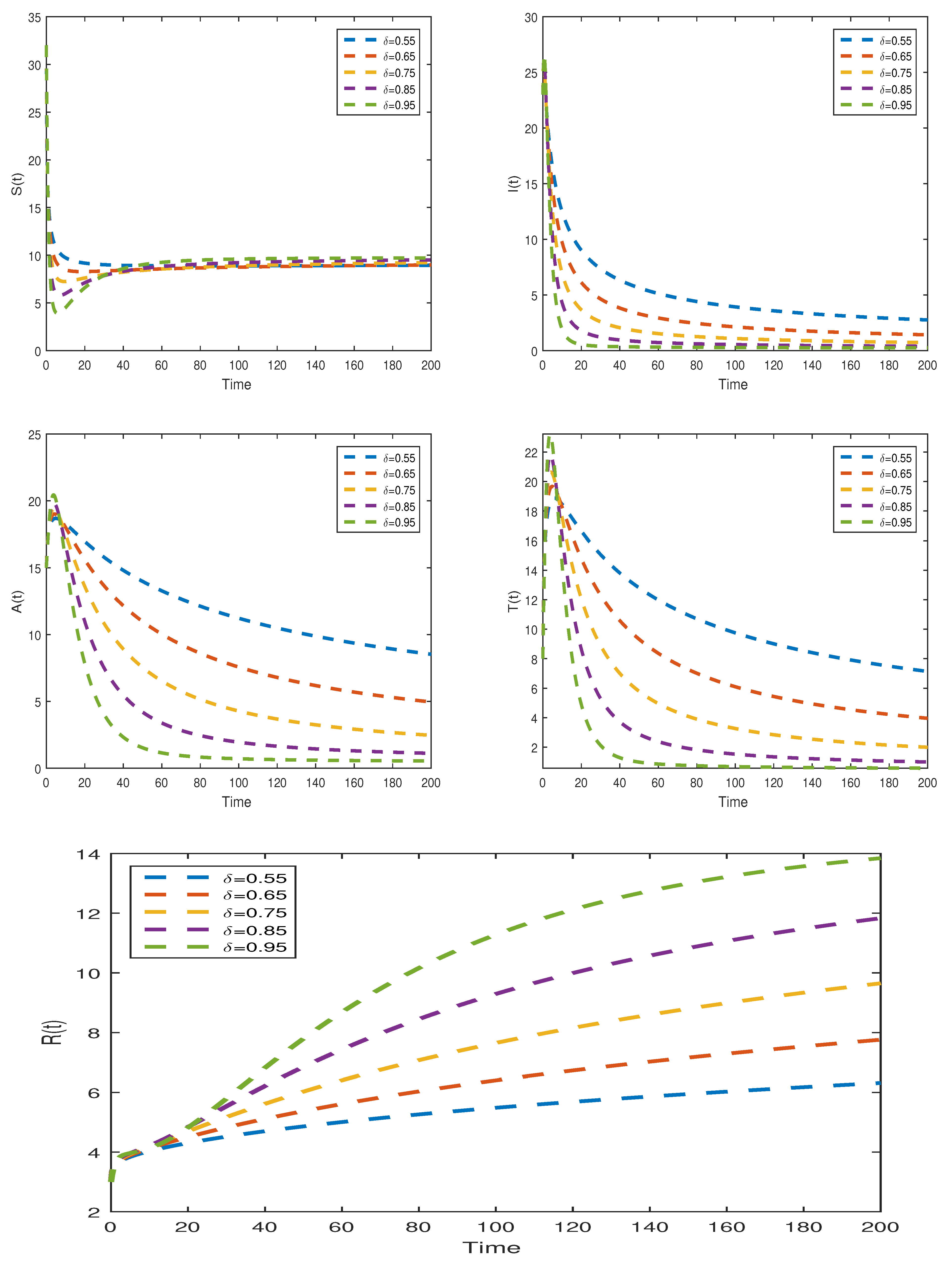
7.2.2. Numerical Scheme via Toufik–Atangana Method for Model (31)
- : Represents the value of the variable of interest at time step .
- : Denotes the functional dependence of the problem, involving the variable of interest and its derivative.
- : Signifies the fractional order of the derivative in the Caputo sense.
- : Refers to the Gamma function evaluated at .
- : Represents the discretized time step r.
- h: Stands for the step size between consecutive time points.
- and : These are the values of the variable of interest at time steps and , respectively.
- and : These terms are used in the context of the time step index for the summations.
- : Denotes the Gamma function evaluated at .
- The term is a part of the approximation process within the numerical scheme.
7.2.3. Application of Toufik–Atangana Numerical Method for Caputo Model Using (33)
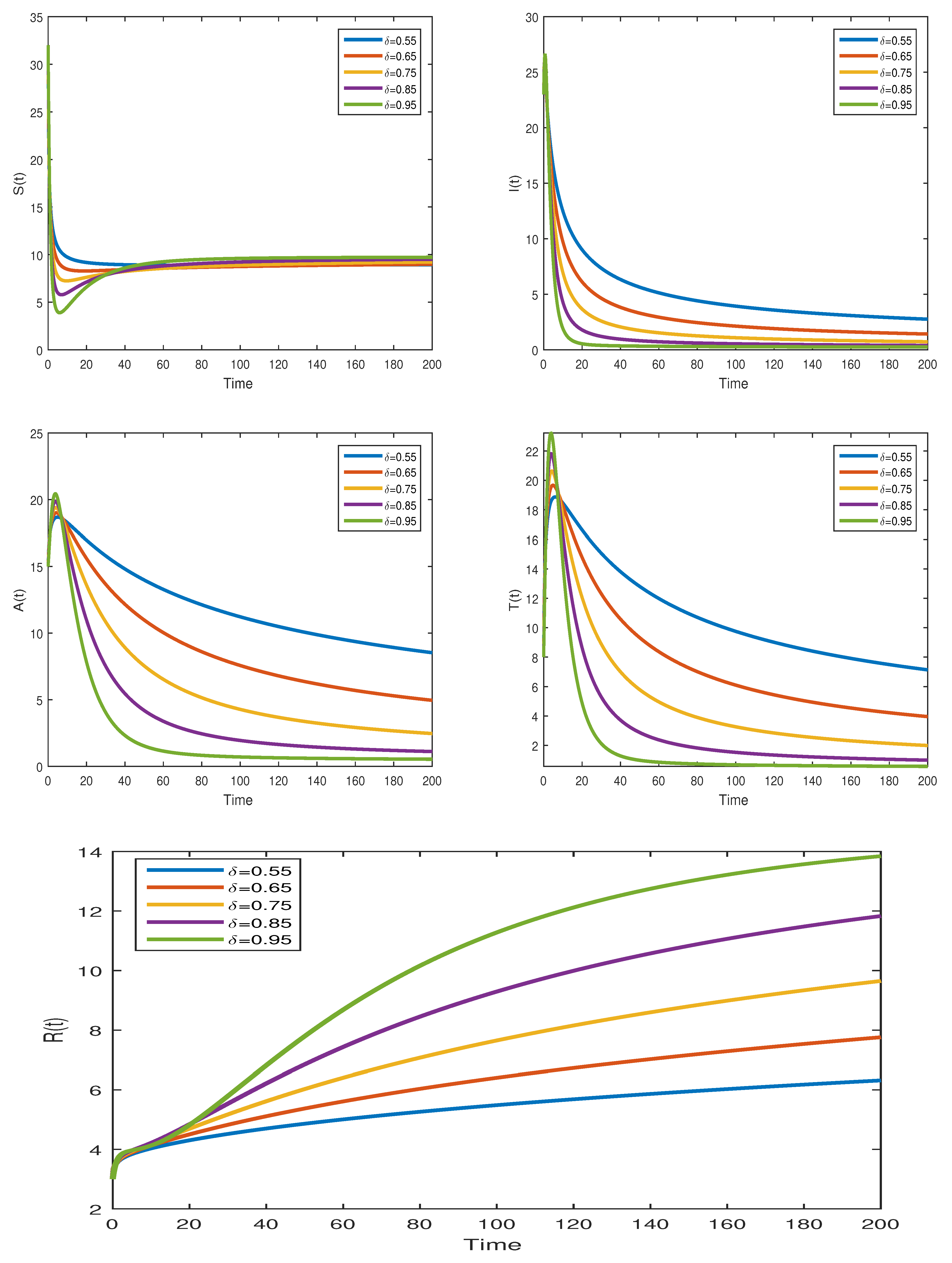
7.2.4. Graphical Results Model (31)
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Palella, F.J.; Delaney, K.M. Declining morbidity and mortality among patients with advanced human immunodeficiency virus infection. N. Engl. J. Med. 1998, 339, 405–406. [Google Scholar] [CrossRef] [PubMed]
- Kandwal, R.; Garg, P.K.; Garg, R.D. Health GIS and HIV/AIDS studies; perspective and retrospective. J. Biomed. Inf. 2009, 42, 748–755. [Google Scholar] [CrossRef] [PubMed]
- Lou, J.; Lou, Y.; Wu, J. Threshold virus dynamics with impulsive antiretroviral drug effects. J. Math. Biol. 2012, 65, 623–652. [Google Scholar] [CrossRef] [PubMed]
- Chibaya, S.; Kgosimore, M. Mathematical analysis of drug resistance in vertical transmission of HIV/AIDS. Open J. Epidemiol. 2013, 3, 139–148. [Google Scholar] [CrossRef]
- Naresh, R.; Tripathi, A.; Omar, S. Modelling the spread of AIDS epidemic with vertical transmission. Appl. Math. Comput. 2006, 178, 262–272. [Google Scholar] [CrossRef]
- Waziri, A.S.; Makinde, O.D. Mathematical modelling of HIV/AIDS dynamics with treatment and vertical transmission. J. Appl. Math. 2012, 2, 77–89. [Google Scholar] [CrossRef]
- Naresh, R.; Sharma, D. An HIV/AIDS model with vertical transmission and time delay. World J. Model. Simul. 2011, 7, 230–240. [Google Scholar]
- Walensky, R.P.; Paltiel, A.D. The survival benefits of AIDS treatment in the united states. Infect. Dis. Soc. Am. 2006, 194, 11–19. [Google Scholar] [CrossRef]
- Yusuf, T.; Benyah, F. Optimal strategy for controlling the spread of HIV/AIDS disease: A case study of South Africa. J. Biol. Dyn. 2012, 6, 475–494. [Google Scholar] [CrossRef]
- Huo, H.F.; Feng, L.X. Global stability for an HIV/AIDS epidemic model with different latent stages and treatment. Appl. Math. Model. 2012, 37, 1480–1489. [Google Scholar] [CrossRef]
- Meng, X.; Chen, L.; Cheng, H. Two profitless delays for the SEIRS epidemic disease model with nonlinear incidence and pulse vaccination. Appl. Math. Comput. 2007, 186, 516–529. [Google Scholar] [CrossRef]
- Hsieh, Y.H.; Chen, C.H. Modelling the social dynamics of a sex industry: Its implications for spread of HIV/AIDS. Bull. Math. Biol. 2004, 66, 143. [Google Scholar] [CrossRef] [PubMed]
- Diallo, O.; Kone, Y.; Pousin, J. A model of spatial spread of an infection with applications to HIV/AIDS in mali. Appl. Math. 2012, 3, 1877–1881. [Google Scholar] [CrossRef]
- Sharomi, O.; Podder, C.N. Modelling the transmission dynamics and control of the novel 2009 swine influenza (h1n1) pandemic. Bull. Math. Biol. 2011, 73, 515–548. [Google Scholar] [CrossRef]
- Taneco-Hernández, M.A.; Vargas-De-León, C. Stability and Lyapunov functions for systems with Atangana–Baleanu Caputo derivative: An HIV/AIDS epidemic model. Chaos Solitons Fractals 2020, 132, 109586. [Google Scholar] [CrossRef]
- Ali, Z.; Rabiei, F.; Shah, K.; Khodadadi, T. Fractal-fractional order dynamical behavior of an HIV/AIDS epidemic mathematical model. Eur. Phys. J. Plus 2021, 136, 36. [Google Scholar] [CrossRef]
- Jan, A.; Srivastava, H.M.; Khan, A.; Mohammed, P.O.; Jan, R.; Hamed, Y.S. In Vivo HIV Dynamics, Modeling the Interaction of HIV and Immune System via Non-Integer Derivatives. Fractal Fract. 2023, 7, 361. [Google Scholar] [CrossRef]
- Almoneef, A.A.; Barakat, M.A.; Hyder, A.A. Analysis of the Fractional HIV Model under Proportional Hadamard-Caputo Operators. Fractal Fract. 2023, 7, 220. [Google Scholar] [CrossRef]
- Algahtani, O.J.J. Comparing the Atangana-Baleanu and Caputo-Fabrizio derivative with fractional order: Allen Cahn model. Chaos Solitons Fractals 2016, 89, 552–559. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Hilfer, R. Mathematical and physical interpretations of fractional derivatives and integrals. Handb. Fract. Calc. Appl. 2019, 1, 47–85. [Google Scholar]
- van den Driessche, P. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Gautam, R. Reproduction numbers for infections with free-living pathogens growing in the environment. J. Biol. Dyn. 2012, 6, 923–940. [Google Scholar]
- Cheng, Y.; Wang, J.; Yang, X. On the global stability of a generalized cholera epidemiological model. J. Biol. Dyn. 2012, 6, 1088–1104. [Google Scholar] [CrossRef] [PubMed]
- Li, G.H.; Jin, Z. Global stability of a SEIR epidemic model with infectious force in latent, infected and immune period. Chaos Solitons Fractals 2005, 25, 1177–1184. [Google Scholar] [CrossRef]
- LaSalle, J.P. The stability of dynamical systems. In Regional Conference Series in Applied Mathmatics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1976; Volume 25. [Google Scholar]
- Huo, H.F.; Feng, L.X. Global stability of an epidemic model with incomplete treatment and vaccination. Discret. Dyn. Nat. Soc. 2012, 14, 530267. [Google Scholar] [CrossRef]
- Naresh, R.; Tripathi, A.; Sharma, D. Modelling and analysis of the spread of AIDS epidemic with immigration of HIV infectives. Math. Comput. Model. 2009, 49, 880–892. [Google Scholar] [CrossRef]
- Yang, X.; Wu, L.; Zhang, H. A space-time spectral order sinc-collocation method for the fourth-order nonlocal heat model arising in viscoelasticity. Appl. Math. Comput. 2023, 2023457, 128192. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Wang, W.; Zhang, H. A Predictor–Corrector Compact Difference Scheme for a Nonlinear Fractional Differential Equation. Fractal Fract. 2023, 7, 521. [Google Scholar] [CrossRef]
- Zhang, H.; Han, X. Quasi-wavelet method for time-dependent fractional partial differential equation. Int. J. Comput. Math. 2013, 90, 2491–2507. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.I. New Numerical Scheme with Newton Polynomial: Theory, Methods, and Applications; Academic Press: New York, NY, USA, 2021. [Google Scholar]
- Atangana, A.; İğret Araz, S. Mathematical model of COVID-19 spread in Turkey and South Africa: Theory, methods, and applications. Adv. Differ. Equ. 2020, 2020, 659. [Google Scholar] [CrossRef]
- Zarin, R.; Khan, A.; Kumar, P. Fractional-order dynamics of Chagas-HIV epidemic model with different fractional operators. AIMS Math. 2022, 7, 18897–18924. [Google Scholar] [CrossRef]
- İğret Araz, S. Analysis of a Covid-19 model: Optimal control, stability and simulations. Alex. Eng. J. 2021, 60, 647–658. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Jleli, M. A numerical analysis for fractional model of the spread of pests in tea plants. Numer. Methods Partial. Differ. Equ. 2022, 38, 540–565. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Samet, B.; Dutta, H. A study on fractional host–parasitoid population dynamical model to describe insect species. Numer. Methods Partial. Differ. Equ. 2021, 37, 1673–1692. [Google Scholar] [CrossRef]


| Parameters | The Physical Interpretation | Value | Date Source |
|---|---|---|---|
| The rate at which people are entering into the susceptible class | 0.55 year−1 | [10] | |
| d | Natural mortality rate | 0.0196 year−1 | [9] |
| Transmitting coefficient of the disease phase | 0.03 year−1 | Estimate | |
| The rate at which people moves form class I to T | 0.35 year−1 | Estimate | |
| Denotes the fraction of people with fail treatment | Variable | ||
| Denotes the fraction of people with full treatment | Variable | ||
| The rate at which people moves form class A to I | 0.15 year−1 | Estimate | |
| AIDS-induced mortality rate | 0.0909 year−1 | [9] | |
| Percentage of vulnerable people who modified their behaviors | 0.03 year−1 | [9] | |
| Mortality rate in the treatment compartment due to the infection | 0.0667 year−1 | [9] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, A.; Ali, R.; Ahmad, I.; Awwad, F.A.; Ismail, E.A.A. Global Stability of Fractional Order HIV/AIDS Epidemic Model under Caputo Operator and Its Computational Modeling. Fractal Fract. 2023, 7, 643. https://doi.org/10.3390/fractalfract7090643
Ahmad A, Ali R, Ahmad I, Awwad FA, Ismail EAA. Global Stability of Fractional Order HIV/AIDS Epidemic Model under Caputo Operator and Its Computational Modeling. Fractal and Fractional. 2023; 7(9):643. https://doi.org/10.3390/fractalfract7090643
Chicago/Turabian StyleAhmad, Ashfaq, Rashid Ali, Ijaz Ahmad, Fuad A. Awwad, and Emad A. A. Ismail. 2023. "Global Stability of Fractional Order HIV/AIDS Epidemic Model under Caputo Operator and Its Computational Modeling" Fractal and Fractional 7, no. 9: 643. https://doi.org/10.3390/fractalfract7090643
APA StyleAhmad, A., Ali, R., Ahmad, I., Awwad, F. A., & Ismail, E. A. A. (2023). Global Stability of Fractional Order HIV/AIDS Epidemic Model under Caputo Operator and Its Computational Modeling. Fractal and Fractional, 7(9), 643. https://doi.org/10.3390/fractalfract7090643






