Abstract
We propose a framework for fitting multivariable fractional polynomial models as special
cases of Bayesian generalized nonlinear models, applying an adapted version of the genetically
modified mode jumping Markov chain Monte Carlo algorithm. The universality of the Bayesian
generalized nonlinear models allows us to employ a Bayesian version of fractional polynomials in
any supervised learning task, including regression, classification, and time-to-event data analysis.
We show through a simulation study that our novel approach performs similarly to the classical
frequentist multivariable fractional polynomials approach in terms of variable selection, identification
of the true functional forms, and prediction ability, while naturally providing, in contrast to its
frequentist version, a coherent inference framework. Real-data examples provide further evidence in
favor of our approach and show its flexibility.
1. Introduction
Linear regression models are arguably among the most popular tools in statistics, especially their generalized versions (GLM). As the name suggests, they model a (function of a) response variable with a linear function of the predictors. While imposing a linear structure has many advantages, including the reduction in the variance, often it may not adequately reflect the functional form of the association of a predictor with the response and may lead to nonlinear structures of the residuals, which indicates a violation of the model assumptions and inappropriateness of the standard asymptotic inference procedures. For example, mis-specifying a truly nonlinear functional form of the predictor–response relationship as linear may result in biased estimates of the regression coefficients, a non-constant variance, and finally in a wrong interpretation of the modeling results. Heteroscedasticity can still be a problem in Bayesian linear regression models. The reason is that the posterior distributions of the regression coefficients depend on the likelihood, which in turn depends on the residuals. Residuals with non-constant variance may affect the shape of the likelihood and lead to incorrect posteriors for the regression coefficients.
Nonlinearities in the predictor–response relationship can be adequately captured by flexible modeling approaches such as splines, often used within the framework of (generalized) additive models. Although powerful and effective, these approaches have the strong drawback of making the model interpretation hard. Roughly speaking, these methods do not supply regression coefficients that can be easily interpreted. For this reason, it is often convenient to transform the predictors with specific global functions, for example, by taking the logarithm or the square root, and then assuming a linear relationship of the transformed predictor with the response variable. In a linear model, the corresponding regression coefficient will then have the familiar interpretation of “expected difference in the response variable for a unit difference of the—now transformed—predictor”. Following this way of thinking, Royston and Altman [1] introduced the fractional polynomial approach. The basic idea is to select a transformation of a predictor x from a set of eight possible functions (), which is then used as an independent variable in the linear model. This set corresponds to a set of powers of polynomials for the Box–Tidwell transformation, where [2].
Many refinements have been considered, including combinations of these functions’ fractional polynomials of order d (see Royston and Altman [1]), a multivariable approach [3], a modification to account for interactions [4,5], and others. In particular, the fractional polynomials of order d, hereafter , allow multiple transformations of the predictor such that, for a simple linear model,
where belong to . By convention, the case that for any indicates a repeated power with transformations and . While in theory fractional polynomials of any order d are possible, in practice only fractional polynomials of order 1 or 2 have typically been used ([5], Ch 5.9).
Multivariable fractional polynomials are the natural extension of the procedure to multivariable regression problems. In this case, each predictor receives a specific transformation among those allowed by the order of the fractional polynomial. While conceptually straightforward, this modification complicates the fitting procedure due to the high complexity of the model space. Sauerbrei and Royston [3] proposed a sort of back-fitting algorithm to fit multivariable fractional polynomial (MFP) models. Herein, all variables are first ordered based on the significance of their linear effect (increasing p-values for the hypothesis of no effect). Then, variable by variable, a function selection procedure (FSP) based on a closed testing procedure with likelihood ratio tests is used to decide whether the variable must be included or can be omitted and if it should be included with the best-fitting second-order fractional polynomial, with the best-fitting first-order fractional polynomial, or without transformation. The FSP is performed for all predictors, keeping the remaining fixed (as transformed in the previous step) for a pre-specified number of rounds or until there are no differences with the results of the previous cycle.
Limited to Gaussian linear regression, Sabanés Bové and Held [6] implemented an approach to MFP under the Bayesian paradigm. Based on hyper-g priors [7], their procedure explores the model space by MCMC and provides a framework in which inferential results are not affected, for example, by the repeated implementation of likelihood-ratio tests. The restriction to Gaussian linear regression problems highly limits the applicability of this procedure. Moreover, while computationally attractive, the MCMC algorithm may struggle to efficiently explore the complicated model space induced by highly correlated predictors.
To address these drawbacks, here, we propose a novel approach based on the characterization of the fractional polynomial models as special cases of Bayesian generalized nonlinear models ([8], BGNLM) and the implementation of a fitting algorithm based on the genetically modified mode jumping MCMC (GMJMCMC) algorithm of Hubin et al. [9]. Bayesian generalized nonlinear models provide a very general framework that allows us a straightforward implementation of MFP beyond the linear Gaussian regression case, including, but not limited to, generalized linear models, generalized linear mixed models, Cox regression, and models with interactions. In addition, GMJMCMC enables searching through the model space to find the set of models with substanital probability mass. GMJMCMC is an extension of the mode jumping MCMC, which is an MCMC variant designed to better explore the posterior distributions, particularly useful when the posterior distribution is complex and has multiple modes. Mode jumping struggles when the dimensionality increases, which can be an issue in the case of fractional polynomials, as one needs to explore models (in the case of the first-order fractional polynomials described above) as compared to for the linear models. The GMJMCMC algorithm resolves these limitations by creating a genetic evolution of sets of features controlled by the genetic component, where simple mode jumping MCMCs can be run. In this work, therefore, we provide a powerful tool for fitting fractional polynomials in various applications.
Thus, the main contributions and innovations of this paper include building a novel Bayesian framework for fitting fractional polynomials using the genetically modified mode jumping Markov chain Monte Carlo (GMJMCMC) algorithm. Further, our priors ensure theoretically consistent model selection. The approach is validated through a comprehensive simulation study, demonstrating its reliable model selection consistency and good predictive performance of the method in three real-data examples, including regression, classification, and survival tasks. The inclusion of interactions in the fractional polynomial model enhances its interpretability and captures complex relationships between predictors and the response. The versatility of our framework allows for generalization to different types of responses and predictors from the exponential family, making it applicable to a wide range of real-world problems. Overall, our work provides a robust and interpretable Bayesian method for fitting fractional polynomials with strong predictive ability in various data analysis tasks.
The rest of the paper is organized as follows. Section 2 describes the multivariable Bayesian fractional polynomial models in the framework of BGNLM, including the fitting algorithm based on GMJMCMC. In Section 3, the performance of our procedure is evaluated via simulations, while three applications to real data are reported in Section 4, where we show our approach applied to regression, classification, and time-to-event data problems. Finally, some remarks conclude the paper in Section 5.
2. Methods
2.1. Bayesian Generalized Nonlinear Models
Consider the situation with a response variable Y and a J-dimensional random vector of input predictors . Bayesian fractional polynomial models can be seen as special cases of Bayesian generalized nonlinear models [8],
where denotes the parametric distribution of Y belonging to the exponential family with mean and dispersion parameter . The function h is a link function, and are unknown parameters, and is an indicator variable that specifies whether the (possibly nonlinear) transformation of predictors , and its set of inner parameters , is included in the model.
Equation (1) provides a very general framework, that contains as special cases models that span from the linear Gaussian regression to neural networks. Following Hubin et al. [8], if the set of nonlinear functions contains , which is the sigmoid function, then BGNLM covers numerous possible neural networks with the sigmoid activation function. BGNLM also includes decision trees, intervals, and higher-dimensional regions through multiplications of simple decision rules represented by the nonlinear function . Multivariate adaptive regression splines can be incorporated using piece-wise linear functions and . Logic regressions, among others, are also easily included within the BGNLM framework. Moreover, BGNLM allows for combinations of different types of features, resulting in complex predictors such as . With the appropriate choice of nonlinear functions, highly interpretable models can be built. For example, in Hubin et al. [8], the authors show that BGNLM can recover Kepler’s third law in the closed form. However, when nonlinear functions are not chosen carefully for a given application, a complicated black-box solution may arise. Furthermore, the cardinality of the model space of BGNLM grows super-exponentially with respect to the depth of the features, which slows the inference down significantly. Both of these issues do not arise in Bayesian fractional polynomials, which are a special case of BGNLM that we study in this paper.
Bayesian Fractional Polynomials
For the purpose of this paper, it is convenient to constrain the framework to only allow univariate transformations , , of the predictors, and regression on the mean, :
Note that the vector fully characterizes a model, as it defines which predictors are included in the model and after which transformation . This vector allows us to perform model comparison and selection using standard Bayesian approaches, including the median probability model [10], Bayes factors [11], or log posterior marginal probabilities.
It is now sufficient to define priors on M and on the related (read given M) coefficients and to complete the procedure. Let us start by defining the prior for M,
where and , . Here, is the total number of terms included in the model, which can be bounded by q to favor sparse models, and are prior penalties on the individual terms. Furthermore, are (common for each predictor) prior indicators which restrict the number of terms per predictor to be simultaneously included into the model. d controls the order of the fractional polynomials, with only allowing for one polynomial term per predictor, i.e., the classical definition of a fractional polynomial model. At the same time, allows softer versions of prior penalties and, thus, more flexibility in modeling a fractional polynomial regression. Thus, q and d are defining prior constraints on the models. If M and are two models satisfying the constraints induced by d and q but differing in one component, say in M and in , then
showing that larger models are penalized more. This result easily generalizes to the comparison of more different models and provides the basic intuition behind the chosen prior.
As a fully Bayesian approach, BGNLM also requires priors on the parameters. Here, we follow Hubin et al. [9] and use the common improper prior [12,13] to the unknown dispersion parameter , and simple Jeffreys priors [14,15] on the regression parameters, where is the observed information for the model M.
The Jeffreys prior is known to have attractive properties of being objective and scale invariant [15]. Moreover, when using the Jeffreys prior, the marginal likelihood of a model can be approximated accurately using the Laplace approximation. In the case of a Gaussian model, if we choose the aforementioned priors for the dispersion parameter and the coefficients, the Laplace approximation becomes exact [16]. This results in a marginal likelihood of the simple form
where refers to the maximum likelihood estimates of all parameters involved and n is the sample size. On the log scale, this corresponds exactly to the BIC model selection criterion [17] when using a uniform model prior.
2.2. Consistency of Model Selection under Our Priors
In this section, we shall show model selection consistency under our priors. Assume , where is an arbitrary positive and finite scalar. This is a special case of what is called BIC-type penalization of complexity in Hubin et al. [8] that we shall also use in the experimental sections. Let be the maximum likelihood estimate (MLE) of the parameters in model . Define as the sum of the standard BIC penalty [18] and our prior penalty (excluding ) for . Define to be a negative log posterior (up to a constant) of under Laplace approximations, i.e., as
where is the log-likelihood of the data given the MLE of the parameters in model . Then, . Assuming the true model is in the set of candidate models and does not coincide with the null model, in the following proposition we show that as , the probability of selecting the true model among the candidate models goes to one. The regularity conditions are very standard for the model selection literature, the only important thing to keep in mind in practice is that in the case of nonidentifiable predictors, i.e., a binary , which is collinear with say , the true model is assumed to include but not in order to be selected by our PIC criterion. Furthermore, it is worth mentioning that in practice there is no true model generating the data, unless we have a simulated or fully human-created phenomenon.
Proposition 1.
Let with . Let be the unique parsimonious true model living on our model space which has and . Further, let be the set of candidate models on that satisfy constraints induced by q and d. Then, the PIC criterion from Equation (5) is consistent in selecting among .
Proof.
The proof consists of 3 standard steps for proving model selection consistency: I. We take a limit in probability of the PIC criterion for the true model and the alternative model. II. We take a limiting difference of the PICs of these models. III. We resolve ties to guarantee consistency in all cases.
- I.
- Let be the event that the PIC selects the true model , i.e.: We want to show that as . By the law of large numbers and the continuous mapping theorem, we have where plim is the limit in the probability operator and denotes the expectation under the true model . Therefore, we haveSimilarly, where denotes the expectation under model .
- II.
- Taking the limiting difference between and , we havewhere and . In other words, we show that
- III.
- Above, and we have two cases to check: 1. if , then is a nested model of and hence by the uniqueness and parsimony of the true model. 2. For , it is sufficient that , and is always finite by the construction of our priors and the fact that and . Thus, we have shown that the PIC criterion is consistent in selecting the true model as the sample size increases.
□
2.3. Bayesian Fractional Polynomial Models as Bayesian Generalized Nonlinear Models
In order to recover our fractional polynomial models, we just need to specify the appropriate set of transformations and parameters in the prior on M defined in Equation (3). The parameters of the latter, in particular, control both the order of the fractional polynomials and the model selection mechanism.
2.3.1. Set of Transformations:
As per the definition of fractional polynomials, the following transformations of each predictor are allowed: the identity, ; 7 simple functions , , ; and 8 functions specifying repeated powers , , , , . If we want to fit fractional polynomials of order 1, then , while for fractional polynomials of order 2, . In this framework, it is straightforward to increase the order of the fractional polynomials by adding further interaction terms, but according to (Royston and Sauerbrei [5], Ch. 5.9) they are not used in practice, and we do not consider them here.
2.3.2. Order of the Fractional Polynomials:
The order of the fractional polynomials is controlled by the value of the parameter d in the prior (3), as d is the maximum number of transformations that are allowed for each explanatory variable. So, only allows for one polynomial term per variable, while allows more flexibility in modeling a fractional polynomial regression up to the desired order. Note that in the case , additional modifications of the prior on M are necessary if one wants to exclude combinations in without the corresponding term in . This can be easily achieved by forcing the model priors including such transformations to be 0.
2.3.3. Model Selection:
In MFP models, there are two sources of complexity to take into account when performing a model selection procedure: the number of regression parameters and the degree of the transformations. Following a paradigm of parsimony, one would ideally consider including variables only if they are related to the response and transforming the variables only if needed. In the framework of BGNLM, there are two separate (sets of) parameters to control the two sources: the parameter q sets an upper bound to the number of active components of the models (i.e., the predictors and their transformations), while the , , set a cost to include individual predictors and can, therefore, be used to penalize harder more complex transformations. The penalty to add a linear term (the transformation belonging to ) is set to be much lower than that for adding a transformation (those in and ). Fractional polynomials of order 2 are naturally penalized more as they require 2 terms, i.e., the penalty on the log scale has the form .
Further, in this work, we follow Sabanés Bové and Held [6] and use the median probability rule [10] to select a set of important predictors. This means we select , which is in practice robust to model mis-specifications.
2.4. Model Fitting via the Genetically Modified Mode Jumping MCMC
In fractional polynomial regression models with the mean parameter linked to the data through Equation (2), the model space can become prohibitively large even with only moderate values of the number of candidate predictors J. The strong correlation among predictors (especially that between different transformations of the same variable), moreover, can lead to many local minima in the posterior distribution, in which a standard fitting algorithm such as the classical MCMC may become stuck with a higher probability. To address these issues, we implement the genetically modified mode jumping MCMC algorithm proposed by Hubin et al. [9] to fit Bayesian fractional polynomial models.
The key idea behind GMJMCMC is to iteratively apply a mode jumping MCMC algorithm [19] to smaller sets of model components of size . This reduces the number of models in the model space to . A sequence of so-called populations is generated. Each population is a set of s transformations and forms a separate search space for exploration through mode jumping MCMC iterations. The populations dynamically evolve allowing GMJMCMC to explore different parts of the total model space.
The generation of the new population given works as follows: some components with low posterior probability from the current population are removed, and then replaced by new components generated through mutation, multiplication, modification, or projection operators. The probabilities for each operator are defined as , , , and , respectively, and must add up to 1. Since fractional polynomials are a specific case of BGNLM with only modification transformations allowed, in this context the algorithm is simplified by setting and . The algorithm is summarized in Algorithm 1 and accompanied by diagramns in Figure 1 for easier understanding of the steps of GMJMCMC.
| Algorithm 1 GMJMCMC |
|
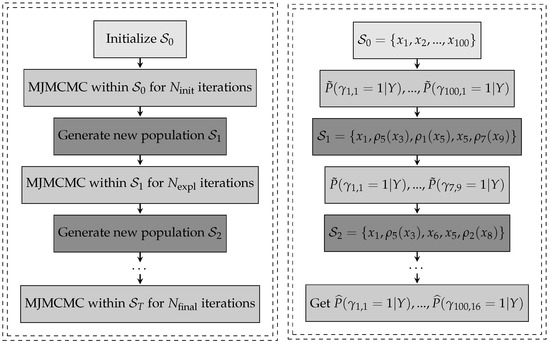
Figure 1.
Left panel: Visulaization of Algorithm 1 and Right panel: Illustration of its work .
For a complete description of the mode jumping MCMC, including its theoretical properties, we refer the reader to Hubin and Storvik [19]. For further details on the GMJMCMC, see Hubin et al. [9], while results on its asymptotic exploration of the space of nonlinear models are available in Hubin et al. [8].
2.5. Using the Output of GMJMCMC to Compute the Marginals of Interest
The posterior probability of a model M given the observed data Y can be expressed as the product of the prior probability of the model and the marginal likelihood of the data given the model divided by the sum of the same expression over all possible models in the model space , which is infeasible to explore. To approximate this, the GMJMCMC algorithm explores for a set of good models (either all models visited by GMJMCMC or models from the last population can serve as ), and the resulting approximation for the posterior probability of a model M given the data Y is denoted as
The marginal inclusion probabilities for a specific effect , denoted as , can then be calculated as the sum of the approximated posterior probabilities over all models in that include this effect, i.e.,
Further, the marginal posterior of any other quantity of interest can be approximated as
This allows us to make predictions based on the output of GMJMCMC.
2.6. Extensions of the Model
The description of the Bayesian fractional polynomial models seen so far only covers the GLM setting (see Formula (2)), but our approach can be easily extended to many other cases. Due to their particular practical relevance, here we cover the cases of generalized linear mixed models, the Cox regression model, and models with interactions.
2.6.1. Latent Gaussian Models
It is straightforward to extend our approach to generalized linear mixed models by incorporating both polynomial terms and latent Gaussian variables. These variables can be used to model correlations between observations in space and time, as well as over-dispersion. Basically, we just need to substitute the function h in Equation (2) with
where are latent Gaussian variables with covariance matrices . These variables allow us to model different correlation structures between individual observations. The matrices typically depend only on a few parameters , so that in practice we have .
The model prior of Equation (3) needs to be generalized to handle inclusion indicators of the latent Gaussian variables and becomes:
where are prior inclusion penalties for the corresponding latent Gaussian variables.
The parameter priors are adjusted as follows:
We can choose any type of hyperparameters of priors that are compatible with the integrated nested Laplace approximations (INLA) [20]. This allows us to efficiently compute the marginal likelihoods of individual models using the INLA approach [21]. For a detailed example of how to use latent Gaussian variables in our context applied to epigenetic data, see Section 5.3.2 in Hubin et al. [8]. In the context of BFP, one would only be limited to the functions in the set .
Additionally, any other extensions with computable marginal likelihoods are possible within our framework, as the availability of the marginal likelihood is sufficient to run our inference algorithm described in Section 2.4.
2.6.2. Cox Regression Model
Our approach can also be used to analyze time-to-event data, for example by using the Cox regression model. Here, the adaptation of the formula in Equation (2) is not straightforward, as the Cox regression model works with hazards and not densities,
where is the so-called baseline hazard function, i.e., that function that models the part of the hazard that does not depend on the predictors (including the intercept, we will not have a parameter here). An additional complication in the analysis of time-to-event data is the presence of censored observations, i.e., those statistical units for which the outcome is only partly observed (the typical case of censoring occurs when the event of interest is known to happen after some observed time, but not exactly when). For our model fitting procedure, however, we just need the (partial) likelihood of the Cox model:
where includes all the observations at risk at the time , and consider
In the case of a partial likelihood in the form of Equation (9), there is a useful approximation of the marginal likelihood provided by Raftery et al. [22]. Here, we used their results. The priors on the model and the parameter, instead, are the same as those in Section 2.3.
2.6.3. Fractional Polynomials with Flexible Interactions
As a specific case of BGNLM, our BGNLM_FP can easily be generalized to handle interactions up to a given order I between the polynomial terms of different predictors, which results in the following generalization of our model:
Now, an extended vector fully characterizes a model with the order of interactions up to I. It then defines which predictors , which transformations , and which interactions between them are included in the model. Finally, we generalize the priors from Equation (3) by means of setting and defining as follows:
The parameter priors here remain the same as those defined in Section 2.3. The inference is enabled by assigning a non-zero value to the tuning parameter in the GMJMCMC algorithm.
3. Simulation Studies
3.1. Aims
The primary goal of the simulation study is to evaluate numerically the consistency of our novel algorithm and contrast its performances with those of current implementations of multivariable fractional polynomials. In particular, we want to assess its ability to recover the true data-generating process when increasing the signal-to-noise ratio, or, at least, selecting the relevant variables.
3.2. Data-Generating Mechanism
We take advantage of the ART study [5], an existing simulation design essentially created to assess fractional polynomial models. Based on a large breast cancer data set [23], the ART study provides a realistic framework when it concerns the distribution of the predictors and their correlation structure; see Tables 10.1 and 10.3 in Royston and Sauerbrei [5] for the details. More specifically, the ART study consists of six continuous (, , , , , ) and four categorical explanatory variables, in particular an ordered three-level (), an unordered three-level () and two binary ( and ) variables. For a detailed description of the univariate distributions of the variables and their correlation structure, we refer to chapter 10 in Royston and Sauerbrei [5]. The response is computed through the model
where denotes the second level of (the first being used as a baseline) and . The instances used in the original simulation study are available at http://biom131.imbi.uni-freiburg.de/biom/Royston-Sauerbrei-book/Multivariable_Model-building/downloads/datasets/ART.zip (accessed on 3 August 2023) and directly used here. In total, the dataset has observations.
While the original study is interesting to evaluate the FP approach in a likely situation, it does not allow us to fully investigate the properties of our algorithm, since the term is not feasible in the settings of fractional polynomials and prevents us evaluating how often the algorithm selects the true model.
In order to study the properties of our priors and algorithm, we propose a modification of the existing study. We change the original model by including an FP(−1) effect for (instead of , such that the true model belongs to the set of the possible models) and by modifying the effect of from linear to an FP2(−0.5, −0.5), to make the search for the true model more challenging. The new response generating mechanism now follows
where again denotes the second level of and is a small positive real number used to avoid problems with the support of a logarithm function. As in the original formulation ([5], chapter 10), the true regression coefficients are all set equal to 1. Finally, and we run 16 different scenarios with a sample size of and allowing us to quantify the consistency of model selection for the compared approaches when increasing the signal-to-noise ratios (that, under the Gaussian distribution, is mathematically equivalent to increasing the sample size). For the corresponding values of , see Figure 2.
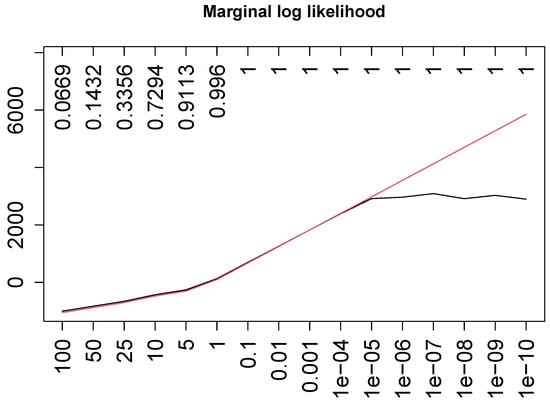
Figure 2.
Best log marginal posteriors found with GMJMCMC (black) and those of a data-generative model (red). Upper axis report of the true model.
3.3. Estimands and Targets
The targets of interest in this simulation study are the sets of predictors selected by a method and their functional form.
For each method, we consider the selected predictors and transformations that the respective method declared to be (with respect to the criterion used in the method) optimal for the dataset. For the Bayesian approaches, a predictor is classified as selected if the (estimated) marginal inclusion probability is larger than 0.5. This corresponds to the median probability model of Barbieri et al. [10].
3.4. Methods
Our novel model, hereafter BGNLM_FP, was fitted using the GMJMCMC algorithm using the EMJMCMC package available at http://aliaksah.github.io/EMJMCMC2016/ (accessed on 3 August 2023). The simulations for each were run on 32 parallel threads times. Each thread was run for 20,000 iterations with a mutation rate of 250 and the last mutation at iteration 15,000. The population size of the GMJMCMC algorithm was set to 20. For the detection of the functional forms, the median probability rule [10] was used. For all simulation scenarios, we specified the following values of the hyperparameters of the model priors: and . Further, was chosen to be for , for , and for . No additional fine-tuning was performed to specify our tuning and hyperparameters. The final script is available on GitHub https://github.com/aliaksah/EMJMCMC2016/blob/master/supplementaries/BFP/simulations.R (accessed on 3 August 2023).
For comparison, the frequentist version of multivariate fractional polynomials (MFPs) was fitted using the R package mfp [24]. We allowed for fractional polynomials of maximal order 2 and used a significance level .
The current Bayesian version of fractional polynomials by Sabanés Bové and Held [6] was fitted using the R package bfp [25], with “flat” (BFP_F), “sparse” (BFP_S), and “dependent” (BFP_D) priors. We used the default value of 4 as the hyperparameter for the hyper-g prior and the option “sampling” to explore the posterior model space. In this case, as well, the median probability rule was used to detect the functional form.
3.5. Performance Metrics
We distinguish between functional (strict) and predictor (soft) levels. In the former, we are interested in how often the model selects the true functional form (and how often a wrong one); in the latter, in how often the model selects a relevant variable (no matter in which form) and how often it incorrectly selects an irrelevant variable. This distinction of levels is useful because the difference between functional forms may be quite small (consider, for example, the logarithmic and the square root transformation) and, therefore, the impact of selecting a wrong functional form on predictions may be low.
Specifically, we compute:
- true positive rate (TPR), defined as the relative frequency of selection of truly relevant effects (often addressed as power in variable selection studies);
- false discovery rate (FDR), measuring the relative frequency of selection of irrelevant variables among all selections.
Both TPR and FDR are computed at the functional and predictor levels. At the former level, a find is considered a “true positive” only if the model includes the true predictor with the correct transformation. At the latter level, instead, we consider it sufficient to select a relevant predictor (so even if the model includes the variable with an incorrect transformation). Similarly, for the FDR, a “false positive” is any functional form that is not included in the model generative function (functional level) or a variable that is not included at all (variable level).
3.6. Results
In Figure 3, top row, we see that the TPR grows, both at the functional (left panel) and at the predictor level (right panel), for all approaches when the signal-to-noise ratio increases. At the functional level, our approach (BGNLM_FP) and MFP uniformly outperform the current Bayesian approaches when there is enough signal (from on), while BFP with a data-dependent prior (BFP_D) works the best for low signal-to-noise data. Note, moreover, that BGNLM_FP has a better performance than MFP in almost all scenarios, with the single exception of . At the variable level, all approaches have a comparable TPR, with the notable exception of BFP_F on the low signal-to-noise ratios. In fact, in these cases, BFP with a flat prior selects all variables with a linear effect, which raises some doubts about the choice of this prior in this context. Obviously, as a consequence, the FDR for BFP_F at the variable level (Figure 3, bottom right panel) is worse than all the others.
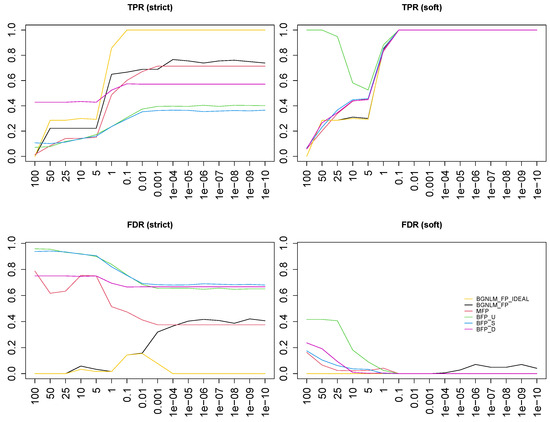
Figure 3.
TPR and FDR at the functional and predictor level for various methods: BGNLM_FP (black), MFP (red), BFP_F (green), BFP_S (blue), BFP_D (purple), and BGNLM_FP_IDEAL (yellow).
At both the functional and variable levels, we see the FDR decreasing with larger signal-to-noise for both MFP and BFP (bottom line of Figure 3, left and right panels, respectively). While noticeably smaller than that of the competitors in almost all cases, a bit surprisingly, the FDR of BGNLM_FP becomes larger for a stronger signal. This counter-intuitive behavior is most probably related to the strong correlation between the true functional forms and other FP transformations. Even GMJMCMC seems to be stuck in some local extrema for lower noise levels, which under the same number of iterations do not allow it to reach the close neighborhood of the true model. When we force the search path to also include the true model (BGNLM_FP_IDEAL), in contrast, the median probability model correctly identifies it as the best option (see the yellow line in the left panels of Figure 3): for noise levels smaller or equal to , the TPR is 1 and the FDR is 0, showing in practice the consistency in model selection under our family of priors. Furthermore, the problem with FPR is almost negligible at the variable level (right panels of Figure 3).
Figure 2 displays this BGNLM_FP’s behavior through the maximum value of the posterior. The GMJMCMC algorithm, whose search for the best model reaches the largest possible value (that of the true model, red in the figure) at lower signal-to-noise ratios, at certain points settles for a “good enough” value and does not reach anymore the largest one given the same number of iterations. This can be explained by the fact that with a larger signal the correlation between the response and almost right fractional polynomials increases, leading to stronger local extrema from which it becomes harder to escape.
To better appreciate the performance of all approaches on a single dimension, we also report in Figure 4 the TPR for the variable . The left panel shows the TPR at the variable level: the task of identifying as relevant seems pretty easy as all reasonable (remember that BFP_F includes all variables) approaches start to include it when is between and 1. Even giving an unfair advantage in the case of BGNLM_FP_IDEAL does not change much, as the same process happens at almost the same signal-to-noise ratio level.
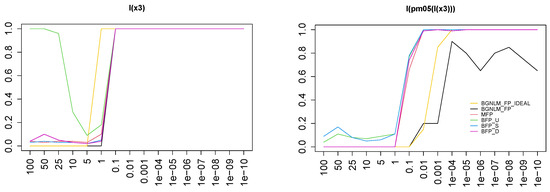
Figure 4.
Left panel: TPR for variable for different methods. Right panel: TPR for functional form FP1(, −0.5) across methods (colors same as in Figure 3).
More interestingly, MFP and all the BFP models seem to almost always include as FP1(−0.5), meaning that they identify the first-order part of the transformation. BGNLM_FP does not have the same behavior, and even at the largest signal-to-noise ratio sometimes sticks to the correlated form (most probably FP1(-1); see the right panel of Figure 4). None of the approaches (except for the artificial BGNLM_BFP_IDEAL), anyhow, manage to identify the correct FP2(−0.5, −0.5) form (data not shown), no matter how large the signal-to-noise ratio is. Only the version of BGNLM_FP_IDEAL with the right model forced into the search path achieves it, starting at and fully happening from . This can be inferred by contrasting the right plot of Figure 4 and the top left panel of Figure 3.
4. Real-Data Applications
In this section, we contrast our approach with many competitors in real-data examples with responses of different natures, namely, a continuous response, a binary response, and a time-to-event response. Note that the Bayesian approaches considered here are based on sampling from the posterior, and, therefore, contain a stochastic component. For these algorithms, we perform 100 runs and report the median, the minimum, and the maximum result. As a consequence, we can also evaluate their stability. All scripts are available on GitHub https://github.com/aliaksah/EMJMCMC2016/tree/master/supplementaries/BFP (accessed on 3 August 2023).
4.1. Regression Task on the Abalone Shell Dataset
The Abalone dataset, publicly available at https://archive.ics.uci.edu/ml/datasets/Abalone (accessed on 3 August 2023), has served as a reference dataset for prediction models for more than two decades. The goal is to predict the age of the abalone from physical measurements such as gender, length, diameter, height, whole weight, peeled weight, the weight of internal organs, and the shell. The response variable, age in years, is obtained by adding 1.5 to the number of rings. There are a total of 4177 observations in this dataset, of which 3177 were used for training and the remaining 1000 for testing. To compare all approaches, we use the following metrics: root mean square error (RMSE); mean absolute error (MAE); and Pearson’s correlation between observed and predicted response (CORR), also defined in Hubin et al. [8].
In our case, 1000 was the test sample size. In addition to the aforementioned approaches, here we also include the original BGNLM (see Equation (1)) from Hubin et al. [8] and a version with only linear terms BGLM (see Equation (2), with ).
For BGNLM_FP, GMJMCMC was run on 32 parallel threads for each of the 100 seeds. Each thread was run until 10,000 unique models were visited, with a mutation rate of 250 and the last mutation at iteration 10,000. The population size of the GMJMCMC algorithm was set to 15. For all runs, we used the following hyperparameters for the model priors: and . Further, was chosen to be for , for , and for .
The best performance (see Table 1) is obtained with the general BGNLM approach. This is probably not surprising as the relationship between response and explanatory variables seems complex (see also Table 2) and BGNLM is the most flexible approach, which contains all the other models as special cases. Notably, this result seems to show that the GMJMCMC algorithm is effective in exploring the huge model space. On the other hand, the performance of BGLM, ranking the worst in all the three metrics considered, shows the importance of including nonlinear effects in the model when analyzing this dataset.

Table 1.
Abalone shell dataset: prediction performances for different models based on RMSE, MAE, and CORR. Median measures (with minimum and maximum in parentheses) are displayed for methods with variable outcomes. Models are sorted by median RMSE.

Table 2.
Abalone shell dataset, BGNLM_FP: frequency of selection of explanatory variables and nonlinear transformations with posterior inclusion probability above 0.1 in more than 10 out of 100 simulation runs (in brackets, the “power” of the transformation). Frequency indicates the number of simulations selecting the given feature.
Between these two extremes lie all the FP implementations. Our proposed approach BGNLM_FP seems slightly better than MFP and BFP_D but worse than the other two implementations of BFP (BFP_F and BFP_S), which, in this case, have exactly the same performances. Nonetheless, no matter which metrics we consider, the differences among all FP-based approaches are very small. Additionally, results for other less related statistical learning baselines are added to Appendix A of the paper. They confirm the overall robustness and good performance of the Bayesian nonlinear method for this task.
Table 2 provides insight into the variable selection for our approach. This helps us to identify nonlinear effects and give us a hint of each variable’s importance for the prediction task. The frequency of inclusion shows that all nine explanatory variables were selected in all 100 simulation runs, meaning that each variable is relevant, at least with a linear effect. In addition, many nonlinear effects had a posterior probability larger than 0.1 (see the right column of Table 2). In particular, the variables WholeWeight, ShuckedWeights, Height, Length, and VisceraWeights seem to have an effect between quadratic and cubic, while ShellWeight seems to have a logarithmic effect, as the logarithmic transformation is selected 58% of the time (third row of Table 2), against around 20% for other transformations (quadratic 21%, cubic 16%, and 13%). The presence of these nonlinear polynomials in the model indicates that the relationship between the explanatory variables and the response (abalone age) is most probably nonlinear and highlights the importance of using methods such as BGNLM_FP to predict the outcome.
4.2. Classification Task on the Wisconsin Breast Cancer Dataset
This example uses breast cancer data with 357 benign and 212 malignant tissue observations, which were obtained from digitized fine needle aspiration images of a breast mass. The data can be found at the website https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic) (accessed on 3 August 2023). Each cell nucleus is described by 10 characteristics, including radius, texture, perimeter, area, smoothness, compactness, concavity, points of concavity, symmetry, and fractal dimension. For each variable, the mean, standard error, and mean of the top three values per image were calculated, resulting in 30 explanatory variables per image. The study used a randomly selected quarter of the images as the training dataset, and the rest of the images were used as the test set.
As in the previous example, we compare the performance of the BGNLM_FP to that of other methods, namely, MFP, BGNLM, and its linear version BGLM. As BFP is not available for classification tasks, it could not be included in the comparison. BGNLM_FP uses Bernoulli observations and a logit link function, and the variance parameter is fixed at . Forecasts are made using , where represents the response variable in the test set. The model averaging approach is used for prediction, where marginal probabilities are calculated using the Laplace approximation.
For BGNLM_FP, GMJMCMC was run on 32 parallel threads for each of the 100 seeds. Each thread was run until unique models were visited, with a mutation rate every 250 iterations and the last mutation at iteration . The population size of the GMJMCMC algorithm was set to 45. For all runs, we used the following hyperparameters for the model priors: and . was chosen to be as follows: for , for , and for . To evaluate the performance of the models we computed the following metrics: prediction accuracy (ACC), false positive rate (FPR), and false negative rate (FNR). The choice of these metrics is in line with that of Hubin et al. [8], and allows direct comparison with the results therein. Detailed definitions of the metrics are also available in Hubin et al. [8].
Table 3 presents the results for each metric. We can see that BGNLM_FP performs better than MFP both in terms of prediction accuracy and false negative rate, while it is slightly worse than MFP when it concerns the false positive rate. Both FP-based models, however, perform worse than both BGNLM and its linear version BGLM. The very good performance of the latter, almost as good as the former in terms of accuracy and FNR, and even slightly better in terms of FPR, seems to suggest that nonlinearities are not very important for this classification problem. This also explains why there is not much advantage in using an FP-based method. Both the frequentist approach and our proposed procedures tend to only select linear effects, as can be seen (for BGNLM_FP) from Table 4, where all the effects selected in more than 10 (out of 100) runs are reported. The same happens for BGNLM (see [8], Table 4): even the most general model only selects mostly linear effects. The reason why BGNLM and BGLM have better results in this example is most probably related to better use of the priors (see the Discussion for more on this point). Furthermore, additional baselines, reported in Appendix B of the paper, confirm our main conclusions of the linear relationship between the covariates and the responses and of the high robustness of the proposed BFP approach.

Table 3.
Breast cancer dataset: prediction performances for different models based on ACC, FNR, and FPR. Median measures (with minimum and maximum in parentheses) are displayed for methods with variable outcomes. The models are sorted according to median ACC.

Table 4.
Breast cancer dataset, BGNLM_FP: frequency of selection of the explanatory variables with a posterior inclusion probability above 0.1 in more than 10 out of 100 simulation runs.
4.3. Time-to-Event Analysis on the German Breast Cancer Study Group Dataset
As an example outside the GLM context, we consider a dataset with a time-to-event response. In particular, the German Breast Cancer Study Group dataset contains data from 686 patients with primary node-positive breast cancer enrolled in a study from July 1984 to December 1989. Out of the 686 patients, 299 experience the event of interest (death or cancer recurrence), while the remaining 387 are censored observations. The data are publicly available at https://www.uniklinik-freiburg.de/fileadmin/mediapool/08_institute/biometrie-statistik/Dateien/Studium_und_Lehre/Lehrbuecher/Multivariable_Model-building/gbsg_br_ca.zip (accessed on 3 August 2023) and contain information about eight variables: five continuous (age, tumor size, number of positive nodes, progesterone status, and estrogen status), two binary (menopausal status and hormonal treatment) and one ordinal variable with three stages (tumor grade). The training set contains about two-thirds of the observations (457), with the remaining one-third forming the test set. The observations are randomly split, but the proportion of censored observations is forced to be the same in the two sets.
As in the previous examples, here we compare our approach BGNLM_FP with a few competitors, namely, the general BGNLM, its linear version BGLM, the classical MFP, and a linear version of the latter as well. All approaches are based on the partial likelihood of Equation (9), so all approaches provide a Cox model, with the latter model being the simple Cox regression model. Furthermore, in this case, BFP is not used as it is only developed for Gaussian responses.
For BGNLM_FP, GMJMCMC was run on 32 parallel threads for each of the 100 seeds. Each thread was run for 20,000 iterations, with a mutation rate of 250 and the last mutation at iteration 15,000. The population size of the GMJMCMC algorithm was set to 15. For all runs, we had the same hyperparameters of the model priors as in all of the other examples: and . Further, was chosen to be for , for , and for .
To evaluate the performance of the models, here we compute the standard metrics: integrated Brier score (IBS) and concordance index (C-index). Both IBS and C-index are defined and computed following the notation from pec [26].
Table 5 reports the results of this experiment. This dataset was used by Royston and Sauerbrei [5] to illustrate the fractional polynomials, so probably not surprisingly the two FP-based approaches have the best performance. Both MFP and our proposed BGNLM_FP are better than the competitors, especially those based on linear effects. It is known, indeed, that the effect of the variable nodes is not linear ([5], Section 3.6.2), and our approach finds this nonlinearity 100% of the time (see Table 6). A bit more surprisingly, BGNLM does not perform so well in this example, but this is most probably related to the fact that the extreme simplicity of a good model (at least the one found by BGNLM_FP only contains two explanatory variables, one of them even with a simple linear effect) does not justify the use of complex machinery.

Table 5.
German Breast Cancer Study Group dataset: prediction performance for different models based on IBS and C-index. Median measures (with minimum and maximum in parentheses) are displayed for methods with variable outcomes. Models are sorted by median IBS.

Table 6.
German Breast Cancer Study Group dataset, BGNLM_FP: frequency of selection of the variables/nonlinear transformations with a posterior inclusion probability above 0.1 in more than 10 out of 100 simulation runs.
4.4. Including Interaction Terms into the Models
As discussed in Section 2.6.3, our approach makes it straightforward to add interaction terms in the Bayesian fractional polynomial models. Mathematically, we need to go back to Formula (1) and also consider bivariate transformation, while algorithmically we need to enable multiplication operators in the GMJMCMC algorithm. In this section, we report the results obtained by BGNLM_FP with interactions. We keep all other tuning parameters of GMJMCMC unchanged, except for allowing multiplications. Furthermore, all hyperparameters of the models are unchanged, except for setting and .
4.4.1. Abalone Data
As we can see in Table 7, allowing interactions into the model enhances the performance of the BGNLM_FP model on the abalone shell age dataset. Adding the interactions is not sufficient to reach the performances of the general BGNLM, but it considerably reduces the gap.

Table 7.
Abalone shell dataset: results for the BGNLM_FP model when allowing for interactions. The results for BGNLM and BGNLM_FP are reported from Table 1 for comparison.
4.4.2. Breast Cancer Classification Data
As expected from the results of Table 3, in the case of the breast cancer classification dataset, in which BGLM already performs better than BGNLM_FP, incorporating interaction terms into the FP model does not produce any substantial advantage (see Table 8). This does not come as a surprise, as nonlinearities do not seem to play a credible role in the prediction model.

Table 8.
Breast cancer dataset: results for the BGNLM_FP model when allowing for interactions. The results for BGNLM and BGNLM_FP are reported from Table 3 for comparison.
4.4.3. German Breast Cancer Study Group Data
Finally, Table 9 shows the results of the model with interactions for the time-to-event data analysis. There is no advantage in allowing for interactions here as well. This is a typical case of the advantage related to the bias-variance trade-off when using simpler models for prediction tasks. We can notice from its IBS values that the model with interactions can have the best performance (0.1597), but the performance varies so much (as bad as 0.1660) that the median is worse than for the simpler model (that without interactions). Note, moreover, that Table 6 seems to suggest that there are only two relevant variables, so it is not likely to detect relevant interactions.

Table 9.
German Breast Cancer Study Group dataset: results for the BGNLM_FP model when allowing for interactions. The results for BGNLM and BGNLM_FP are reported from Table 3 for comparison.
5. Discussion
In this paper, we studied how BGNLM fitted by GMJMCMC introduced by Hubin et al. [8] can deal with fractional polynomials. It can be seen as an opportunity of fitting a BGNLM that can handle nonlinearities without any loss in model interpretability, and, more importantly, as a convenient implementation of a fractional polynomial model that assures a coherent inferential framework, without losing (if not gaining) anything in terms of prediction ability. The broad generality of the BGNLM framework, moreover, allows adding complexity with a minimum effort, as we show for the inclusion of interaction terms.
Note that the current implementation is based on a direct adaptation of the priors defined in Hubin et al. [8]. Further investigations on the choice of the priors will certainly be beneficial and further improve the performance of BGNLM_FP, as we already noticed in the simulation study in Section 3. For example, a better balance between the penalty for the different fractional polynomial forms can be implemented. Our real-data experiments never showed evidence in favor of a fractional polynomial of order 2. This may be related to the implausibility of an FP(2) transformation, especially in a prediction context where simplicity is often awarded, but it may also indicate that we penalized these terms too much.
One drawback with the Bayesian versions of the fractional polynomial models is the computational costs of fitting them. This is not specific to our approach, it also concerns the current BFP implementation of Sabanés Bové and Held [6] and can become an issue in the case of very large datasets. Currently, we distribute the computational workload across multiple processors to achieve convergence to descent regions in the model space. In the future, subsampling the data could allow for a reduction in computational cost when computing the marginal likelihoods. This will allow the use of the Bayesian fractional polynomial approach in big data problems as well. Furthermore, in the case of large datasets, Laplace approximations of the marginal likelihoods become very accurate, making this approach even more appealing. To make the computations efficient, stochastic gradient descent (SGD) can be used to compute the Laplace approximations, which also guarantees convergence [27] of MJMCMC in the class of Bayesian GLMs. Therefore, incorporating data subsampling and using SGD to compute the Laplace approximations may be a promising future direction in inference on Bayesian fractional polynomials under the setting of a large n.
Another challenge is selecting appropriate values for the tuning parameters of GMJMCMC. The tuning parameters in GMJMCMC control the proposal distributions, population size, frequencies of genetic operators, and other characteristics of the Markov chain. Their values can significantly affect the convergence and mixing properties of the algorithm. To deal with this challenge, one may perform extensive tuning of the algorithm, which involves testing a range of values for the tuning parameters and evaluating the performance of the algorithm using problem-specific diagnostic tools such as power (TPR)-FDR in simulations or RMSE for regression prediction tasks. A detailed discussion of setting the tuning parameters in GMJMCMC is given in the "Rejoinder to the Discussion" in Hubin et al. [9]. In the future, it may also be interesting to develop adaptive tuning methods that automatically adjust the tuning parameters based on the performance of the algorithm as it is running.
GMJMCMC is a Markov chain Monte Carlo algorithm that is designed to explore the space of models with non-zero posterior probabilities. However, as with any MCMC algorithm, there is a risk that the chain may not converge to the desired target distribution in a finite time. This means in our settings that the set of models with non-zero posterior probabilities may not be fully explored in a single run of the algorithm. One consequence of this is that the estimates obtained from GMJMCMC may vary from run to run, since different runs may explore different parts of the model space. Even if the algorithm is run for a long time, there is still a positive probability that it may miss some of the models with non-zero posterior probabilities. Variance in the estimated posterior in turn induces variance in the predictions if the latter is of interest. To mitigate this issue, it is recommended to run the algorithm multiple times, using as many of the available resources as one can and check for convergence of the estimates. Additionally, it may be helpful to use informative model priors or other techniques to help guide the algorithm toward the most relevant parts of the model space.
Even though there are still a few challenges and limitations in the current state of Bayesian fractional polynomials, these models have potential applications in a variety of areas where uncertainty handling, explainability, and nonlinear relationships are essential. These include but are not limited to fields such as pharmacology, epidemiology, finance, and engineering. In pharmacology, for example, fractional polynomials can be used to model the dose–response relationship between a drug and a patient’s response, taking into account the nonlinear and complex relationships between the variables. In finance, fractional polynomials can be used to model the relationship between financial variables such as stock prices, interest rates, and exchange rates, and to quantify the uncertainty associated with these relationships. Similarly, in engineering, fractional polynomials can be used to model the relationship between variables such as stress, strain, and material properties, providing a way to make predictions while taking into account nonlinear relationships and the associated uncertainty. In all of these cases, Bayesian fractional polynomials offer a flexible and robust way to handle uncertainty and model nonlinear relationships, making them a useful tool for a wide range of applications in the future. Given the important role that uncertainty handling, explainability, and nonlinear relationships play in various applications, we hope that the novel Bayesian fractional polynomial inference algorithm presented in this paper, as well as the suggested extensions to various practical settings such as survival analysis and GLM, will allow these often overlooked models to be more widely used in the future.
Author Contributions
Conceptualization, A.H. and R.D.B.; Methodology, A.H. and R.D.B.; Software, A.H.; Validation, G.H.; Formal analysis, R.D.B.; Investigation, A.H. and G.H.; Data curation, R.D.B.; Writing—original draft, A.H. and R.D.B.; Writing—review & editing, A.H., G.H. and R.D.B.; Visualization, A.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
ART study: http://biom131.imbi.uni-freiburg.de/biom/Royston-Sauerbrei-book/Multivariable_Model-building/downloads/datasets/ART.zip (accessed on 3 August 2023); Abalone data: https://archive.ics.uci.edu/ml/datasets/Abalone (accessed on 3 August 2023); Wisconsin breast cancer data: https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic) (accessed on 3 August 2023); German breast cancer data: https://www.uniklinik-freiburg.de/fileadmin/mediapool/08_institute/biometrie-statistik/Dateien/Studium_und_Lehre/Lehrbuecher/Multivariable_Model-building/gbsg_br_ca.zip (accessed on 3 August 2023); code available at https://github.com/aliaksah/EMJMCMC2016/tree/master/supplementaries/BFP (accessed on 3 August 2023).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Additional Baselines for the Regression Task
For additional baseline methods on the abalone age regression task, we reproduced the analysis from the supplementary script https://github.com/aliaksah/EMJMCMC2016/tree/master/supplementaries/BGNLM/abalone%20age (accessed on 3 August 2023) of Hubin et al. [8]. The results are summarized in Table A1. Here, RIDGE stands for ridge regression, GR for linear regression, LASSO for lasso regression, RFOREST for random forest, DEEPNETS for artificial neural networks [28] for all five models, and VARBAYES is the variational inference for linear regression from Carbonetto and Stephens [29]. Finally, LXGBOOST stands for linear extreme gradient boosting and TXGBOOST for tree-based extreme gradient boosting [30]. These results confirm that linear algorithms such as RIDGE and LASSO perform more poorly compared to some nonlinear methods. Hence, nonlinear relationships between the features and target are important in this data. The results for deep learning algorithms are, however, relatively diverse, with some deep learning models performing very well, while others perform poorly, which is often the case in neural networks, which tend to converge to different local extrema of the parameter space in different runs. Hence, more regularization may be needed to smooth the penalized likelihood. We observe here both superior and more robust performance of the Bayesian nonlinear methods suggested in this paper.

Table A1.
Abalone shell dataset: additional baseline results.
Table A1.
Abalone shell dataset: additional baseline results.
| Algorithm | RMSE | MAE | CORR |
|---|---|---|---|
| RFOREST | 2.0352 (2.0020, 2.0757) | 1.4924 (1.4650, 1.5259) | 0.7633 (0.7530, 0.7712) |
| LASSO | 2.0765 (-,-) | 1.5386 (-,-) | 0.7514 (-,-) |
| VARBAYES | 2.0779 (-,-) | 1.5401 (-,-) | 0.7516 (-,-) |
| GR | 2.0801 (-,-) | 1.5401 (-,-) | 0.7500 (-,-) |
| LXGBOOST | 2.0880 (2.0879, 2.0880) | 1.5429 (1.5429, 1.5429) | 0.7479 (0.7479, 0.7479) |
| TXGBOOST | 2.0881 (2.0623, 2.1117) | 1.5236 (1.4981, 1.5438) | 0.7526 (0.7461, 0.7590) |
| RIDGE | 2.1340 (-,-) | 1.5649 (-,-) | 0.7347 (-,-) |
| DEEPNETS | 2.1466 (1.9820, 3.5107) | 1.5418 (1.3812, 3.1872) | 0.7616 (0.6925, 0.7856) |
Appendix B. Additional Baselines for the Classification Task
For the classification task, we also reproduced the baselines from Hubin et al. [8]; scripts at https://github.com/aliaksah/EMJMCMC2016/tree/master/supplementaries/BGNLM/breast%20cancer (accessed on 3 August 2023). The results in Table A2 show the performance comparison of the rest of the models for the breast cancer classification task. The metrics used are, as previously, accuracy (ACC), false positive rate (FPR), and false negative rate (FNR). The linear methods, RIDGE, LR (logistic regression) [28] and LASSO, have higher median accuracy compared to the nonlinear methods, LXGBOOST, TXGBOOST, RFOREST, and NBAYES (naive Bayes) [31]. This confirms the results from the main paper, that linear methods perform better on this particular dataset. Among these baselines, RIDGE has the highest median accuracy of 0.9742, followed by regularized DEEPNETS with 0.9695. The highly nonlinear methods have lower accuracy, with the highest being TXGBOOST with 0.9531 and the lowest being RFOREST with 0.9343 on average. These results confirm that linear relationships between features and the target are more important in this dataset, and nonlinear methods may overfit the data and find irrelevant nonlinearities. Thus, we confirm the robust good performance of the Bayesian nonlinear methods suggested in this paper.

Table A2.
Breast cancer dataset: additional baseline results.
Table A2.
Breast cancer dataset: additional baseline results.
| Model | ACC | FNR | FPR |
|---|---|---|---|
| RIDGE | 0.9742 (-,-) | 0.0592 (-,-) | 0.0037 (-,-) |
| DEEPNETS | 0.9695 (0.9225, 0.9789) | 0.0674 (0.0305, 0.1167) | 0.0074 (0.0000, 0.0949) |
| LR | 0.9671 (-,-) | 0.0479 (-,-) | 0.0220 (-,-) |
| LASSO | 0.9577 (-,-) | 0.0756 (-,-) | 0.0184 (-,-) |
| LXGBOOST | 0.9554 (0.9554, 0.9554) | 0.0809 (0.0809, 0.0809) | 0.0184 (0.0184, 0.0184) |
| TXGBOOST | 0.9531 (0.9484, 0.9601) | 0.0647 (0.0536, 0.0756) | 0.0326 (0.0291, 0.0361) |
| RFOREST | 0.9343 (0.9038, 0.9624) | 0.0914 (0.0422, 0.1675) | 0.0361 (0.0000, 0.1010) |
| NBAYES | 0.9272 (-,-) | 0.0305 (-,-) | 0.0887 (-,-) |
References
- Royston, P.; Altman, D.G. Regression using fractional polynomials of continuous covariates: Parsimonious parametric modelling. J. R. Stat. Soc. Ser. 1994, 43, 429–453. [Google Scholar] [CrossRef]
- Box, G.E.; Tidwell, P.W. Transformation of the independent variables. Technometrics 1962, 4, 531–550. [Google Scholar] [CrossRef]
- Sauerbrei, W.; Royston, P. Building multivariable prognostic and diagnostic models: Transformation of the predictors by using fractional polynomials. J. R. Stat. Soc. Ser. (Stat. Soc.) 1999, 162, 71–94. [Google Scholar] [CrossRef]
- Royston, P.; Sauerbrei, W. A new measure of prognostic separation in survival data. Stat. Med. 2004, 23, 723–748. [Google Scholar] [CrossRef] [PubMed]
- Royston, P.; Sauerbrei, W. Multivariable Model-Building: A Pragmatic Approach to Regression Anaylsis Based on Fractional Polynomials for Modelling Continuous Variables; Wiley: Chichester, UK, 2008. [Google Scholar]
- Sabanés Bové, D.; Held, L. Bayesian fractional polynomials. Stat. Comput. 2011, 21, 309–324. [Google Scholar] [CrossRef]
- Liang, F.; Paulo, R.; Molina, G.; Clyde, M.A.; Berger, J.O. Mixtures of g priors for Bayesian variable selection. J. Am. Stat. Assoc. 2008, 103, 410–423. [Google Scholar] [CrossRef]
- Hubin, A.; Storvik, G.; Frommlet, F. Flexible Bayesian Nonlinear Model Configuration. J. Artif. Intell. Res. 2021, 72, 901–942. [Google Scholar] [CrossRef]
- Hubin, A.; Storvik, G.; Frommlet, F. A novel algorithmic approach to Bayesian logic regression (with discussion). Bayesian Anal. 2020, 15, 263–333. [Google Scholar] [CrossRef]
- Barbieri, M.M.; Berger, J.O. Optimal predictive model selection. Ann. Stat. 2004, 32, 870–897. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Li, Y.; Clyde, M.A. Mixtures of g-priors in generalized linear models. J. Am. Stat. Assoc. 2018, 113, 1828–1845. [Google Scholar] [CrossRef]
- Bayarri, M.J.; Berger, J.O.; Forte, A.; García-Donato, G. Criteria for Bayesian model choice with application to variable selection. Ann. Stat. 2012, 40, 1550–1577. [Google Scholar] [CrossRef]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. 1946, 186, 453–461. [Google Scholar]
- Gelman, A.; Stern, H.S.; Carlin, J.B.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Raftery, A.E.; Madigan, D.; Hoeting, J.A. Bayesian model averaging for linear regression models. J. Am. Stat. Assoc. 1997, 92, 179–191. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Claeskens, G.; Hjort, N.L. Model Selection and Model Averaging; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Hubin, A.; Storvik, G. Mode jumping MCMC for Bayesian variable selection in GLMM. Comput. Stat. Data Anal. 2018, 127, 281–297. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Sosciety 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Hubin, A.; Storvik, G. Estimating the marginal likelihood with Integrated nested Laplace approximation (INLA). arXiv 2016, arXiv:1611.01450v1. [Google Scholar]
- Raftery, A.E.; Painter, I.S.; Volinsky, C.T. BMA: An R package for Bayesian model averaging. Newsl. Proj. Vol. 2005, 5, 2–8. [Google Scholar]
- Schmoor, C.; Olschewski, M.; Schumacher, M. Randomized and non-randomized patients in clinical trials: Experiences with comprehensive cohort studies. Stat. Med. 1996, 15, 263–271. [Google Scholar] [CrossRef]
- Heinze, G.; Ambler, G.; Benner, A. mfp: Multivariable Fractional Polynomials, R Package Version 1.5.2.2; R Foundation for Statistical Computing: Vienna, Austria, 2022. Available online: https://cran.r-project.org/web/packages/mfp/mfp.pdf(accessed on 14 July 2023).
- Sabanés Bové, D.; Gravestock, I.; Davies, R.; Moshier, S.; Ambler, G.; Benner, A. Bfp: Bayesian Fractional Polynomials, R Package Version Version 0.0.46; R Foundation for Statistical Computing: Vienna, Austria, 2022. Available online: https://cran.r-project.org/web/packages/bfp/bfp.pdf(accessed on 14 July 2023).
- Gerds, T.A. Pec: Prediction Error Curves for Risk Prediction Models in Survival Analysis, R Package Version 2022.05.04; R Foundation for Statistical Computing: Vienna, Austria, 2022. Available online: https://cran.r-project.org/web/packages/pec/pec.pdf(accessed on 14 July 2023).
- Lachmann, J.; Storvik, G.; Frommlet, F.; Hubin, A. A subsampling approach for Bayesian model selection. Int. J. Approx. Reason. 2022, 151, 33–63. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Carbonetto, P.; Stephens, M. Scalable variational inference for Bayesian variable selection in regression, and its accuracy in genetic association studies. Bayesian Anal. 2012, 7, 73–108. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Murphy, K.P. Naive Bayes Classifiers; University of British Columbia: Vancouver, BC, USA, 2006; Volume 18, pp. 1–8. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).