The Improved Stochastic Fractional Order Gradient Descent Algorithm
Abstract
:1. Introduction
2. Materials and Methods
3. Main Results
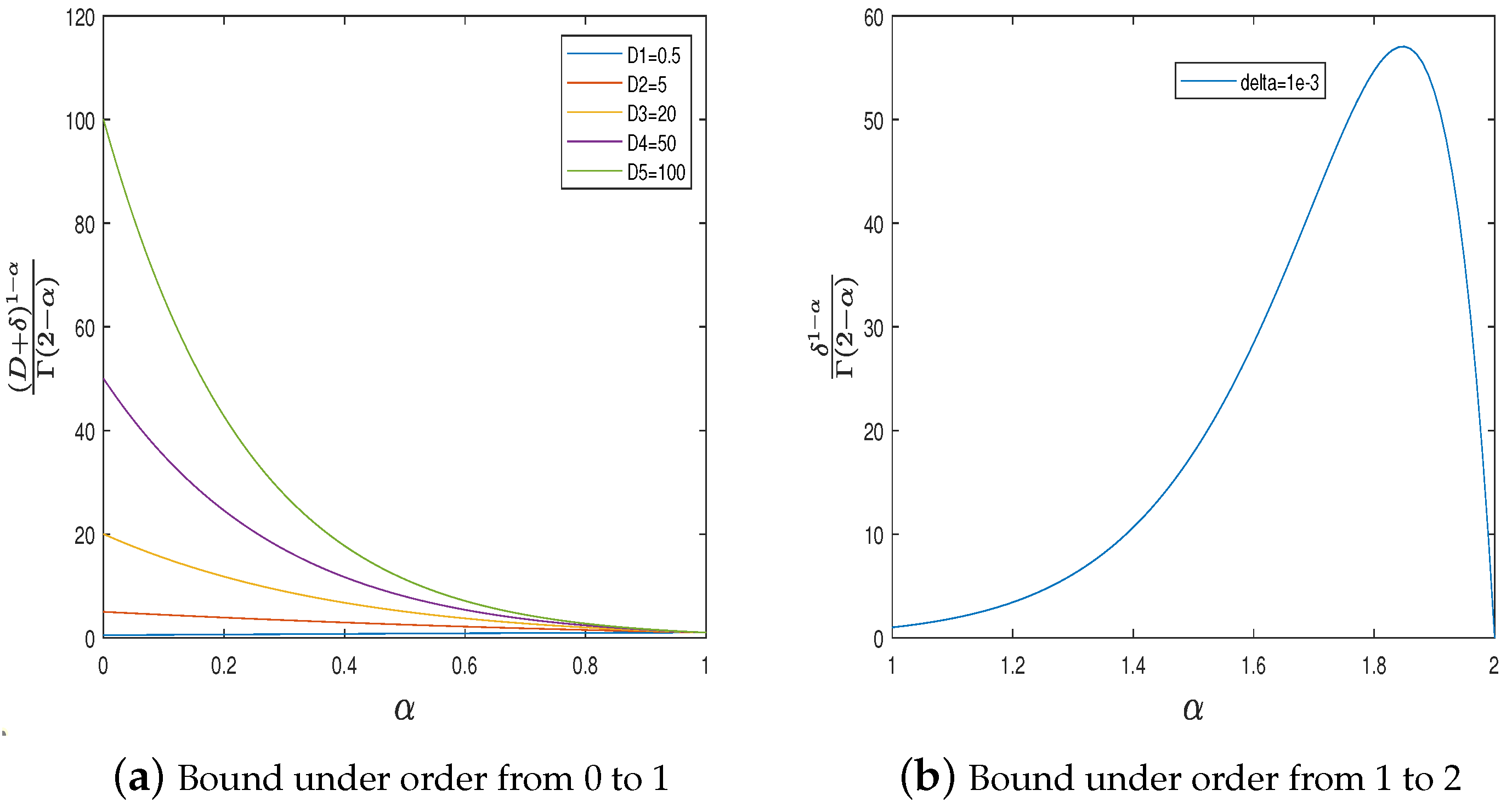
3.1. Standard SGD with Fractional Order Gradient
| Algorithm 1 SGD with fractional order. |
|
3.2. Adagrad Algorithm with Fractional Order
| Algorithm 2 Adagrad with fractional order. |
|
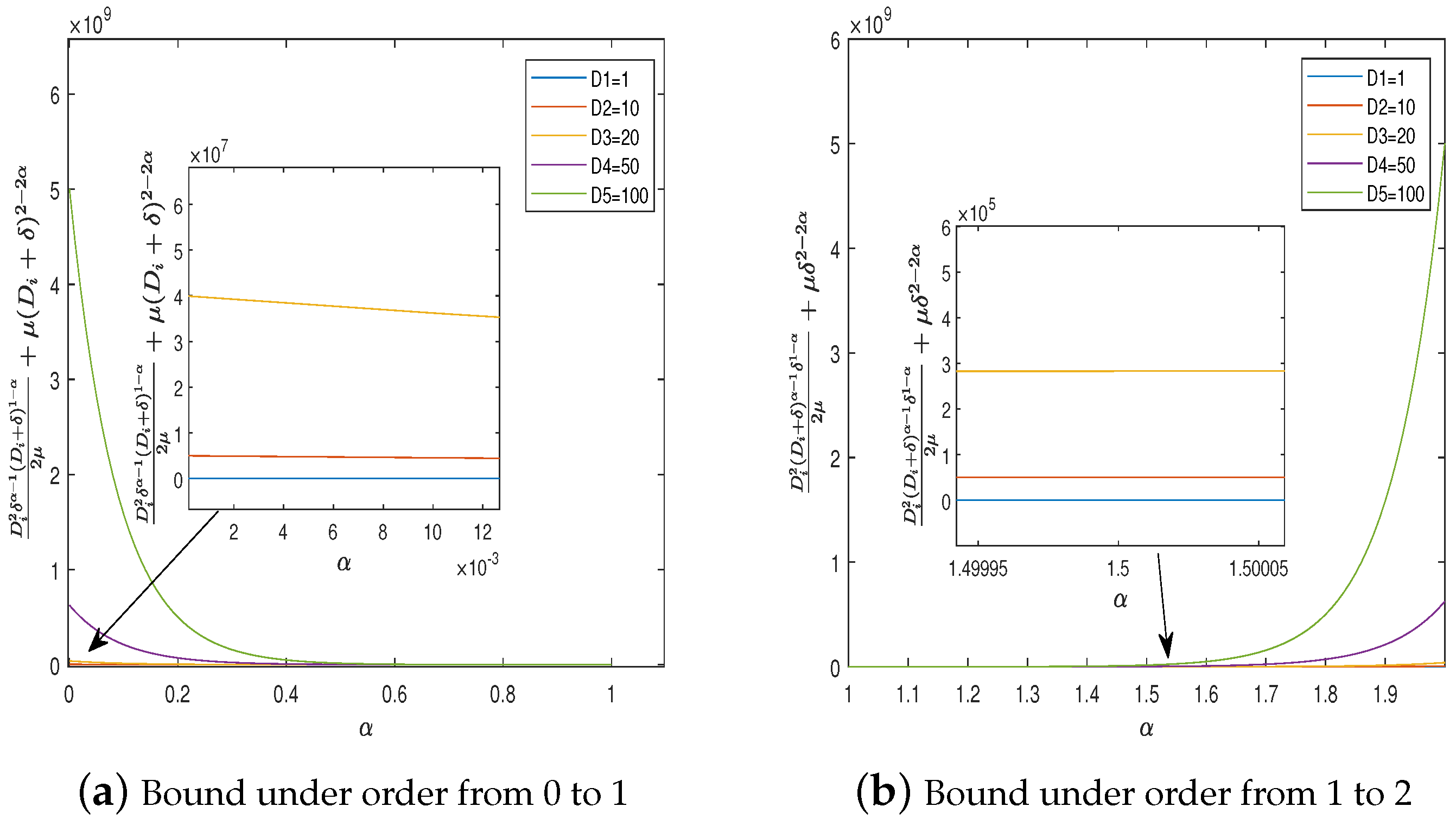
3.3. SGD with Momentum and Fractional Order Gradient
| Algorithm 3 mSGD with fractional order |
|
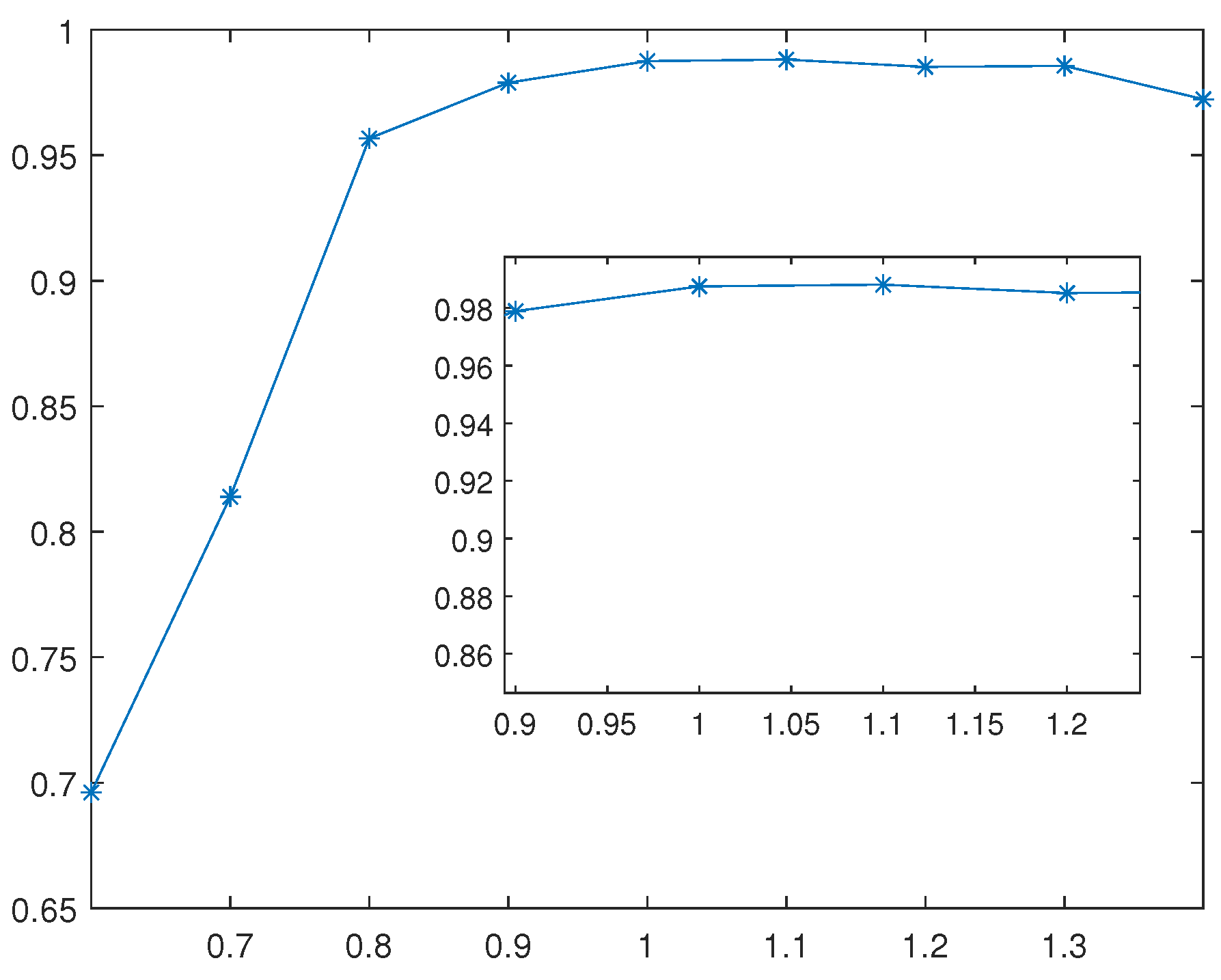
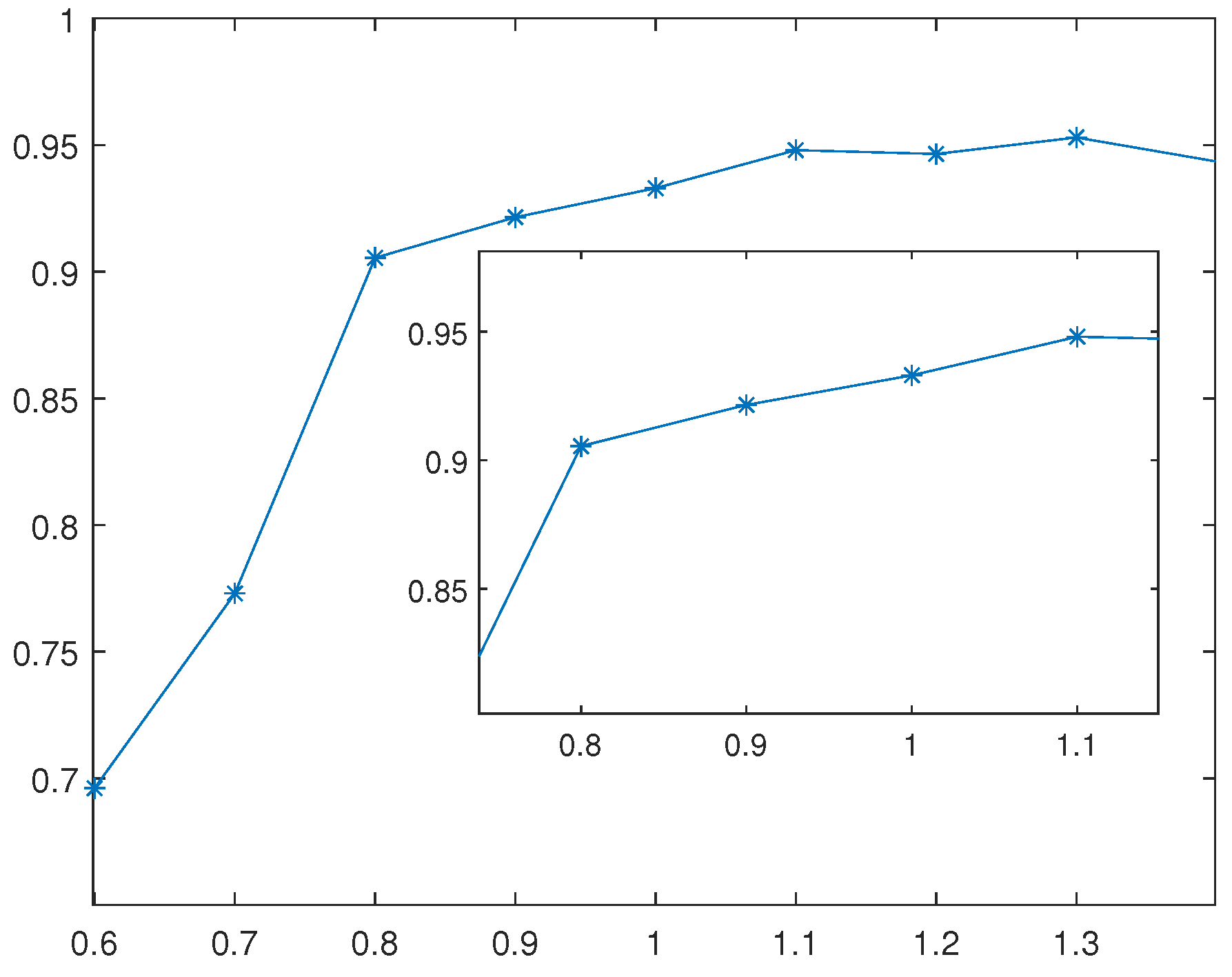
4. Simulations
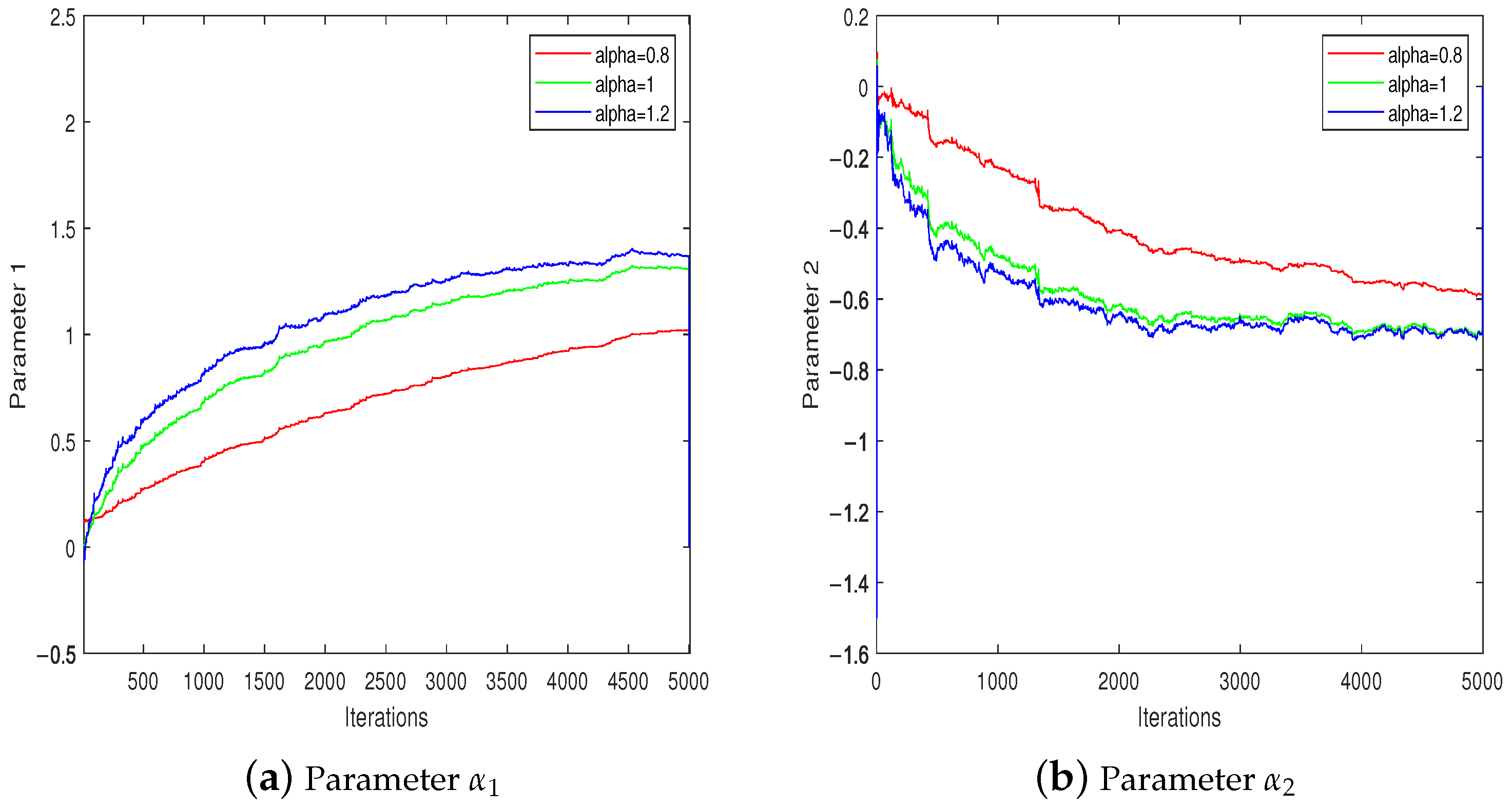
4.1. Example 1
4.2. Example 2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SGD | Stochastic Gradient Descent |
| FOGD | Fractional Order Gradient Descent |
References
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Bottou, L.; Bousquet, O. The tradeoffs of large scale learning. Adv. Neural Inf. Process. Syst. 2007, 20, 1–8. [Google Scholar]
- Bottou, L.; Curtis, F.E.; Nocedal, J. Optimization methods for large-scale machine learning. SIAM Rev. 2018, 60, 223–311. [Google Scholar] [CrossRef]
- Dean, J.; Corrado, G.; Monga, R.; Chen, K.; Devin, M.; Mao, M.; Ranzato, M.; Senior, A.; Tucker, P.; Yang, K.; et al. Large scale distributed deep networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1223–1231. [Google Scholar]
- Zinkevich, M. Online convex programming and generalized infinitesimal gradient ascent. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 928–936. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Zeiler, M.D. Adadelta: An adaptive learning rate method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Lei, Y.; Hu, T.; Li, G.; Tang, K. Stochastic gradient descent for nonconvex learning without bounded gradient assumptions. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 4394–4400. [Google Scholar] [CrossRef]
- Wei, Y.; Kang, Y.; Yin, W.; Wang, Y. Generalization of the gradient method with fractional order gradient direction. J. Frankl. Inst. 2020, 357, 2514–2532. [Google Scholar] [CrossRef]
- Shin, Y.; Darbon, J.; Karniadakis, G.E. Accelerating gradient descent and Adam via fractional gradients. Neural Netw. 2023, 161, 185–201. [Google Scholar] [CrossRef]
- Yin, C.; Chen, Y.; Zhong, S.m. Fractional-order sliding mode based extremum seeking control of a class of nonlinear systems. Automatica 2014, 50, 3173–3181. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, Q.; Wei, Y.; Wang, Y. Study on fractional order gradient methods. Appl. Math. Comput. 2017, 314, 310–321. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, Y.; Wang, Y.; Chen, Y. Fractional order gradient methods for a general class of convex functions. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; IEEE: Manhattan, NY, USA, 2018; pp. 3763–3767. [Google Scholar]
- Liu, J.; Zhai, R.; Liu, Y.; Li, W.; Wang, B.; Huang, L. A quasi fractional order gradient descent method with adaptive stepsize and its application in system identification. Appl. Math. Comput. 2021, 393, 125797. [Google Scholar] [CrossRef]
- Xue, H.; Shao, Z.; Sun, H. Data classification based on fractional order gradient descent with momentum for RBF neural network. Netw. Comput. Neural Syst. 2020, 31, 166–185. [Google Scholar] [CrossRef]
- Mei, J.J.; Dong, Y.; Huang, T.Z. Simultaneous image fusion and denoising by using fractional-order gradient information. J. Comput. Appl. Math. 2019, 351, 212–227. [Google Scholar] [CrossRef]
- Zhang, H.; Mo, L. A Novel LMS Algorithm with Double Fractional Order. Circuits Syst. Signal Process. 2023, 42, 1236–1260. [Google Scholar] [CrossRef]
- Wang, J.; Wen, Y.; Gou, Y.; Ye, Z.; Chen, H. Fractional-order gradient descent learning of BP neural networks with Caputo derivative. Neural Netw. 2017, 89, 19–30. [Google Scholar] [CrossRef]
- Sheng, D.; Wei, Y.; Chen, Y.; Wang, Y. Convolutional neural networks with fractional order gradient method. Neurocomputing 2020, 408, 42–50. [Google Scholar] [CrossRef]
- Lacoste-Julien, S.; Schmidt, M.; Bach, F. A simpler approach to obtaining an O (1/t) convergence rate for the projected stochastic subgradient method. arXiv 2012, arXiv:1212.2002. [Google Scholar]
- Shalev-Shwartz, S.; Singer, Y.; Srebro, N. Pegasos: Primal estimated sub-gradient solver for svm. In Proceedings of the 24th International Conference on Machine Learning, New York, NY, USA, 20–24 June 2007; pp. 807–814. [Google Scholar]
- Chen, X.; Wu, S.Z.; Hong, M. Understanding gradient clipping in private SGD: A geometric perspective. Adv. Neural Inf. Process. Syst. 2020, 33, 13773–13782. [Google Scholar]
- Yu, Z.; Sun, G.; Lv, J. A fractional-order momentum optimization approach of deep neural networks. Neural Comput. Appl. 2022, 34, 7091–7111. [Google Scholar] [CrossRef]



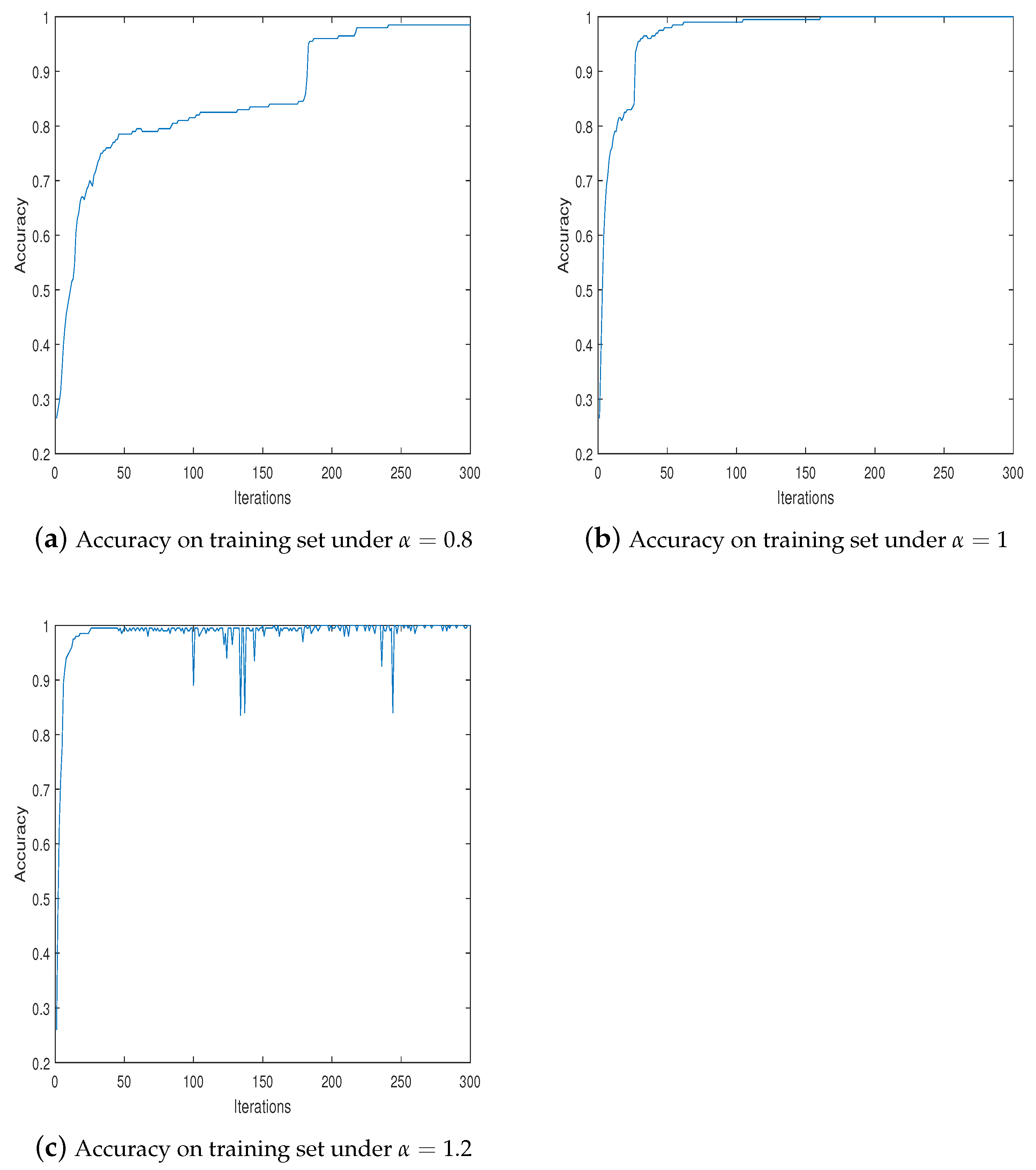
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Mo, L.; Hu, Y.; Long, F. The Improved Stochastic Fractional Order Gradient Descent Algorithm. Fractal Fract. 2023, 7, 631. https://doi.org/10.3390/fractalfract7080631
Yang Y, Mo L, Hu Y, Long F. The Improved Stochastic Fractional Order Gradient Descent Algorithm. Fractal and Fractional. 2023; 7(8):631. https://doi.org/10.3390/fractalfract7080631
Chicago/Turabian StyleYang, Yang, Lipo Mo, Yusen Hu, and Fei Long. 2023. "The Improved Stochastic Fractional Order Gradient Descent Algorithm" Fractal and Fractional 7, no. 8: 631. https://doi.org/10.3390/fractalfract7080631
APA StyleYang, Y., Mo, L., Hu, Y., & Long, F. (2023). The Improved Stochastic Fractional Order Gradient Descent Algorithm. Fractal and Fractional, 7(8), 631. https://doi.org/10.3390/fractalfract7080631




