Optimal Control for Neutral Stochastic Integrodifferential Equations with Infinite Delay Driven by Poisson Jumps and Rosenblatt Process

Abstract

In this paper, we investigate the optimal control problems for a class of neutral stochastic integrodifferential equations (NSIDEs) with infinite delay driven by Poisson jumps and the Rosenblat process in Hilbert space involving concrete-fading memory-phase space, in which we define the advanced phase space for infinite delay for the stochastic process. First, we introduce conditions that ensure the existence and uniqueness of mild solutions using stochastic analysis theory, successive approximation, and Grimmer’s resolvent operator theory. Next, we prove exponential stability, which includes mean square exponential stability, and this especially includes the exponential stability of solutions and their maps. Following that, we discuss the existence requirements of an optimal pair of systems governed by stochastic partial integrodifferential equations with infinite delay. Then, we explore examples that illustrate the potential of the main result, mainly in the heat equation, filter system, traffic signal light systems, and the biological processes in the human body. We conclude with a numerical simulation of the system studied. This work is a unique combination of the theory with practical examples and a numerical simulation.

1. Introduction

Since arbitrary fluctuations and noise are common and predictable in both natural and artificial systems, stochastic models should be studied rather than deterministic ones. Stochastic differential equations incorporate uncertainty into the mathematical representation of a specific occurrence of stochastic differential equations (SDEs). Due to their use in modeling numerous phenomena in physics, population dynamics, ecology, medicine, biology, engineering, and other areas of research, SDEs in both infinite and finite dimensions have garnered a lot of attention in recent years. For excellent information for learning about stochastic differential equations and their applications, see [1,2,3,4,5].

Since SDEs with delay are suitable for simulating physical systems with delay, such as those found in medicine, economics, epidemiology, biology, and chemistry, research on SDEs with delay has attracted a lot of attention over the past few decades; see [1,6,7,8] for a brief overview. Numerous writers have looked at the existence, uniqueness, controllability, and stability of the qualitative and quantitative characteristics of SDEs with delay solutions (see [9,10,11,12,13,14] and references therein). Researchers have been examining the existence and asymptotic behavior of some mild solutions to SDEs in Hilbert spaces using a semigroup approach [11], comparison theorem [15], Razumikhin-type theorem [16], analytic technique [17], Banach fixed point principle [18], etc.

In the literature, neutral stochastic partial differential equations (SPDEs) have been used to simulate a variety of dynamical systems [13,19,20]. Some of these equations have delayed state derivatives, which are different from SPDEs with delays that rely on the past and the present states. We merely recommend to see more information on this theory and its applications [14,21,22]. Recently, SIDEs have drawn a lot of interest with an emphasis on qualitative characteristics like optimality conditions, regularity, control issues, periodicity, and stability; we refer readers to [10,12,18]. Instead of using the continuous semigroup operators, the resolvent operator theory has been implemented as the system contains an integral term (see [23] for further details). However, the majority of academics that study exponential stability have focused only on infinite delays; see [9,18]. The solutions that are continuously dependent on the initial value have been the focus of this study. Authors in [21,22,24] discussed asymptotic and exponential stability of stochastic systems with infinite delay using the phase space given by Hale and Kato [25]. Notable is the paucity of research on the subject of defining the stochastic time delay systems involving exponential stability ([13,14,20,26]).

On the other hand, we consider the stationary Gaussian sequence ${\left({\xi }_n\right)}_{n\in \mathbb{Z}}$ with variance and mean zero whose correlation function is $\mathrm{R}\left(n\right):=\mathbb{E}\left({\xi }_0{\xi }_n\right)=n^{\frac{2\mathrm{H}-2}{\mathrm{k}}}L\left(n\right)$, with $\mathrm{H}\in \left(\frac{1}{2},1\right)$. Let f be a Hermite polynomial with rank k Let L be a slowly varying function at infinity. Also, if f admits the following expansion in Hermite polynomials

$$\begin{array}{ccc}\hfill f\left(x\right)& =& \sum _{j\ge 0}{c}_j{\mathrm{H}}_j\left(x\right),c_j=\frac{1}{j!}\mathbb{E}\left(f\left({\xi }_0\mathrm{H}\left({\xi }_0\right)\right)\right),\hfill \end{array}$$

where $\mathrm{k}=\min \left\{j|c_j\ne 0\right\}\ge 1$ and ${\mathrm{H}}_j\left(x\right)$ represent the Hermite polynomial of degree j defined as ${\mathrm{H}}_j\left(x\right)={(-1)}^j{e}^{\frac{x^2}{2}}\frac{d_j}{d{x}_j}{e}^{-\frac{x^2}{2}}$, then by virtue of the Non-Central Limit Theorem, this series $\frac{1}{n^{\mathrm{H}}}{\sum }_{\left[nt\right]}^{j=1}g\left({\xi }_j\right)$ converges in the form of distribution in finite-dimension as $n\to \infty .$

$$\begin{array}{ccc}\hfill {\mathbb{Z}}_{\mathrm{H}}^{\mathrm{k}}\left(t\right)& =& c(\mathrm{H},\mathrm{k}){\int }_{{\mathbb{R}}^{\mathrm{k}}}{\int }_0^t\left(\prod _{j=1}^{\mathrm{k}}{(s-y_j)}_{+}^{-\left(\frac{1}{2}+\frac{1-\mathrm{H}}{\mathrm{k}}\right)}\right)dsd\mathbb{B}\left(y_1\right)\dots d\mathbb{B}\left(y_{\mathrm{k}}\right).\hfill \end{array}$$

(1)

Here, $c(\mathrm{H},\mathrm{k})$ is a positive normalization constant that depends on $\mathrm{H}$ and $\mathrm{k},$ and the multiple integral in Equation (1) is of Wiener–It$\widehat{o}$-type integral of order $\mathrm{k}$ with respect to the standard Brownian motion ${\left(\mathbb{B}\left(y_k\right)\right)}_{k\in \mathbb{R}}$. For $c>0$, this process ${\left({\mathbb{Z}}_{\mathrm{H}}^{\mathrm{k}}\left(t\right)\right)}_{t\ge 0}$ is called the Hermite process and is self-similar to the $\left({\mathbb{Z}}_{\mathrm{H}}^{\mathrm{k}}\left(ct\right)\right)=\left(c^{\mathrm{H}}{\mathbb{Z}}_{\mathrm{H}}^{\mathrm{k}}\left(t\right)\right)$ and it has stationary increments [27].

When $\mathrm{k}=1$, the Hermite process (1) is the fractional Brownian motion (fBm) with Hurst parameter $\mathrm{H}\in \left(\frac{1}{2},1\right)$ [28]. If $k=2$, then the process (1) is called the Rosenblatt process, which occurs from the Non-Central Limit Theorem (see [29,30] and references therein). Self-similar processes with long-range dependence are important in practice and are employed in many areas, including finance, turbulence, internal traffic, hydrology, and econometrics, to mention a few [31,32]. The self-similar Rosenblatt process, which has stationary increments, seems to be the upper bound for long-range dependent stationary series, which is not a Gaussian process. Due to its significance in numerous fields of science and engineering, the fBm is undoubtedly the Hermite process in the class that has received the most research [12,33,34]. However, one can apply the Rosenblatt process in actual circumstances when the model’s assumption of Gaussianity is implausible. However, in contrast to the fBm, the study of the Rosenblatt process has received little attention due to its non-Gaussianity trait and complexity of its dependence structures. The study of SDEs using the Rosenblatt technique looks interesting. Because a subset of the class of self-decomposition distributions following the multivariate Rosenblatt distribution belongs to the Thorin class, it is possible to take advantage of this characteristic. Maejima and Tudor [27] showed that further properties of the Rosenblatt distribution can be discovered. Ramkumar et al. [35] recently used semigroup theory and the successive approximation method to study higher-order neutral SDEs driven by the Rosenblatt process in Hilbert space and Poisson jumps. One might consult the papers [12,14,34,36] and their references for more information on the Rosenblatt procedure. In system engineering, the optimal control issues arise frequently. The primary objective of optimum control is to identify the ideal values of the control variables for the dynamic system that maximize or minimize a specified performance index in an open-loop control. Because dynamic systems are nonlinear, finding the optimal control is a challenging and open-ended endeavor. In biomedicine, optimal control is frequently used to simulate cancer chemotherapy, and it has also recently been used in medicine and epidemiological models [37,38]. Rajivganthi and Muthukumar [39] examined the properties of Poisson jumps with fractional stochastic evolution equations and virtually automorphic solutions, as well as their optimal control. Wang et al. [40] studied the best possible control that is achieved for delayed SDEs powered by fBms. Very recently, Ramkumar et al. [41] investigated the existence of mild solutions and optimal controls for a class of fractional neutral SDEs driven by fBm and Poisson jumps in Hilbert spaces. Only a few authors have studied the optimal control results of stochastic differential/integrodifferential equations in infinite dimensional spaces (see [42,43] and references therein). Section 7 is devoted to the practical applications. We discuss the stochastic heat equation, the filter system, the traffic signal light systems, and the biological reaction on a human body to justify the practical applications of the theory studied.

More precisely, Boufoussi et al. [44] studied the global existence and uniqueness result of the mild solution for stochastic functional differential equations in Hilbert space driven by a fractional Brownian motion of the form

$$\begin{array}{ccc}\hfill d\mathrm{x}\left(t\right)& =& \left[A\mathrm{x}\left(t\right)+\mathfrak{f}\left({\mathrm{x}}_t\right)\right]dt+\sigma \left({\mathrm{x}}_t\right)d{B}^{\mathrm{H}}\left(t\right),t\ge 0,\hfill \\ \hfill \mathrm{x}\left(t\right)& =& \eta \left(t\right),t\in [-r,0].\hfill \end{array}$$

Next, Hajji et al. [45] extended the study of [44] and concerned themselves with the existence and uniqueness of mild solutions for a class of neutral functional stochastic differential equations described in the form

$$\begin{array}{ccc}\hfill d\left[\mathrm{x}\left(t\right)+g(t,\mathrm{x}(\rho \left(t\right)\left)\right)\right]& =& \left[\mathfrak{A}\mathrm{x}\left(t\right)+\mathfrak{f}(t,\mathrm{x}(\rho \left(t\right)\left)\right)\right]dt+\sigma \left(t\right)d{B}_Q^{\mathrm{H}}\left(t\right),t\in [0,T],\hfill \\ \hfill \mathrm{t}& =& \phi \left(t\right),-r\le t\le 0.\hfill \end{array}$$

We extended the system studied by Hajji et al. [45] with numerous applications. Also, previous authors have not discussed the numerical simulation to justify their theory.

Considering the following neutral SIDEs with infinite delay driven by Poisson jumps and the Rosenblatt process given on the entire probability space $(\mathsf{\Omega },\Im ,\mathbb{P})$ is motivated by the explanation above:

$$\begin{array}{ccc}\hfill d\left[\mathrm{x}\left(t\right)+{\mathfrak{f}}_1(t,{\mathrm{x}}_t)\right]& =& \mathfrak{A}\left[\mathrm{x}\left(t\right)+{\mathfrak{f}}_1(t,{\mathrm{x}}_t)\right]dt+\mathfrak{f}(t,{\mathrm{x}}_t)dt+{\int }_0^t\mathsf{{\rm Y}}(t-s)\left[\mathrm{x}\left(s\right)+{\mathfrak{f}}_1(s,{\mathrm{x}}_s)\right]dsdt\hfill \\ & +& \sigma (t,{\mathrm{x}}_t)d{\mathbb{Z}}_{\mathrm{H}}\left(t\right)+{\int }_{\mathrm{Z}}\mathfrak{h}(t,{\mathrm{x}}_t,z)\tilde{N}(dt,dz),t\ge 0.\hfill \\ \hfill {\mathrm{x}}_0(·)& =& \varphi \in {\mathfrak{C}}_{\zeta };\hfill \end{array}$$

(2)

where $\varphi$ is ${\Im }_0$-measurable, and the next section provides more information on the concrete fading memory-phase space ${\mathfrak{C}}_{\zeta }$. $\mathsf{{\rm Y}}\left(t\right)$ is given as a closed linear operator. Also, a closed linear operator $\mathfrak{A}:\mathfrak{D}\left(\mathfrak{A}\right)\subset \mathbb{H}\to \mathbb{H}$ is defined on a separable Hilbert space $\mathbb{H}$ such that $\mathfrak{D}\left(\mathfrak{A}\right)\subset \mathfrak{D}\left(\mathsf{{\rm Y}}\right(t\left)\right)$. Assume that $\mathbb{B}$ is another real separable Hilbert space. ${\mathfrak{f}}_1,\mathfrak{f}:[0,+\infty )\times {\mathfrak{C}}_{\zeta }\to \mathbb{H}$, $\sigma :[0,+\infty )\times {\mathfrak{C}}_{\zeta }\to {\mathcal{L}}_2^0(\mathbb{B},\mathbb{H})$, $\mathfrak{h}:[0,+\infty )\times {\mathfrak{C}}_{\zeta }\times \mathrm{Z}\to \mathbb{H}$ are appropriate functions; we see that function ${\mathrm{x}}_t:\{(-\infty ,0]\to \mathbb{H},t\ge 0$, such that ${\mathrm{x}}_t\left(\theta \right)=\mathrm{x}(t+\theta )\}$ takes the value from the phase space ${\mathfrak{C}}_{\zeta }$. Let $(\mathsf{\Omega },\Im ,\mathbb{P})$ be the complete probability space. Assume that the Poisson counting measure $N(dt,dz)$ induced by the Poisson point process $\mathrm{p}(·)$ in the measurable space $(\mathrm{Z},\mathcal{B}(\mathrm{Z}\left)\right)$. $\tilde{N}(dt,dz)=N(dt,dz)-\varphi \left(dz\right)dt$ is the compensated martingale measure. ${\mathbb{Z}}_{\mathrm{H}}\left(t\right)$ is a $\mathbb{B}$-valued Rosenblatt process with parameter $\mathrm{H}\in \left(\frac{1}{2},1\right)$. The space of all continuous functions $\mathfrak{C}\left(\right(-\infty ,0],\mathbb{H})$ is endowed with the norm given as

$$∥\mathsf{\Phi }∥=\underset{-\infty <\theta \le 0}{\sup }∥\mathsf{\Phi }\left(\theta \right)∥.$$

We present the abstract phase space ${\mathfrak{C}}_{\zeta }$. Assume that ${\zeta }_t:(-\infty ,0]\to (0,\infty )$ is a continuous function with $l={\int }_{-\infty }^0\zeta \left(s\right)ds<\infty$. Assume the fading memory ${\mathfrak{C}}_{\zeta }$ for $\zeta >0$, defined as ${\mathfrak{C}}_{\zeta }:=\{\mathsf{\Phi }\in \mathfrak{C}((-\infty ,0],\mathbb{H})$: ${\left(\mathbf{E}{∥\mathsf{\Phi }∥}^2\right)}^{1/2}$, is a bounded and measurable function on $[-\delta ,0]$ for any $\delta >0$ and ${\int }_{-\infty }^0\zeta \left(t\right){\sup }_{t\le \delta \le 0}{\left(\mathbf{E}{∥\mathsf{\Phi }\left(s\right)∥}^2\right)}^{1/2}dt<\infty ;{\lim }_{\delta \to -\infty }{e}^{\zeta \delta }\mathsf{\Phi }\left(\delta \right)$ exists in $\mathbb{H}\}$.

This space (${\mathfrak{C}}_{\zeta },{\parallel ·\parallel }_{\zeta }$) represents a Banach space with the norm

$${∥\mathsf{\Phi }∥}_{{\mathfrak{C}}_{\zeta }}={\int }_{-\infty }^0\zeta \left(s\right)\underset{-\infty <\delta \le 0}{\sup }∥\mathsf{\Phi }\left(\delta \right)∥ds,\forall \mathsf{\Phi }\in {\mathfrak{C}}_{\zeta }.$$

The following lemma of phase spaces is essential for the infinite delay system.

Lemma 1.

Suppose $z\in {\mathfrak{C}}_{\zeta }$, then $\forall t\in [0,T]$, $z_t\in {\mathfrak{C}}_{\zeta }$. Moreover,

$$\begin{array}{ccc}\hfill l{\left(\mathbf{E}\left({∥z\left(t\right)∥}^2\right)\right)}^{\frac{1}{2}}& \le & l\underset{0\le s\le t}{\sup }{\left(\mathbf{E}{∥z\left(s\right)∥}^2\right)}^{\frac{1}{2}}+{∥z_0∥}_{{\mathfrak{C}}_{\zeta }},z_t\in {\mathfrak{C}}_{\zeta },\hfill \end{array}$$

where $l={\int }_{-\infty }^0\zeta \left(s\right)ds<\infty$.

Proof. 

It is simple to see that $z_t$ is bounded and measurable on $[-a,0]$ for $a>0$ for any $t\in [0,a]$,

$$\begin{array}{ccc}\hfill \parallel z_t{\parallel }_{{\mathfrak{C}}_{\zeta }}& =& {\int }_{-\infty }^0\zeta \left(s\right)\underset{\delta \in [s,0]}{\sup }\mathbf{E}\left|\right|z_t\left(\delta \right)\left|\right|ds\hfill \\ & =& {\int }_{-\infty }^{-t}\zeta \left(s\right)\underset{\delta \in [s,0]}{\sup }\mathbf{E}\left|\right|z(t+\delta )\left|\right|ds+{\int }_{-t}^0\zeta \left(s\right)\underset{\delta \in [s,0]}{\sup }\mathbf{E}\left|\right|z(t+\delta )\left|\right|ds\hfill \\ & =& {\int }_{-\infty }^{-t}\zeta \left(s\right)\underset{{\delta }_1\in [t+s,t]}{\sup }\mathbf{E}\left|\right|z\left({\delta }_1\right)\left|\right|ds+{\int }_{-t}^0\zeta \left(s\right)\underset{{\delta }_1\in [t+s,t]}{\sup }\mathbf{E}\left|\right|z\left({\delta }_1\right)\left|\right|ds\hfill \\ & \le & {\int }_{-\infty }^{-t}\zeta \left(s\right)\left[\underset{{\delta }_1\in [t+s,0]}{\sup }\mathbf{E}\left|\right|z\left({\delta }_1\right)\left|\right|+\underset{{\delta }_1\in [0,t]}{\sup }\left(\mathbf{E}\right||z\left({\delta }_1\right){\left|\right|}^2{)}^{1/2}\right]ds\hfill \\ & +& {\int }_{-t}^0\zeta \left(s\right)\underset{{\delta }_1\in [0,t]}{\sup }\left(\mathbf{E}\right||z\left({\delta }_1\right){\left|\right|}^2{)}^{1/2}ds\hfill \\ & =& {\int }_{-\infty }^{-t}\zeta \left(s\right)\underset{{\delta }_1\in [t+s,0]}{\sup }\mathbf{E}\left|\right|z\left({\delta }_1\right)\left|\right|ds+{\int }_{-\infty }^{0}b\left(s\right)ds.\underset{s\in [0,t]}{\sup }\left(\mathbf{E}\right||z\left(s\right){\left|\right|}^2{)}^{1/2}\hfill \\ & \le & {\int }_{-\infty }^{-t}\zeta \left(s\right)\underset{{\delta }_1\in [s,0]}{\sup }\mathbf{E}\left|\right|z\left({\delta }_1\right)\left|\right|ds+l\underset{s\in [0,t]}{\sup }\left(\mathbf{E}\right||z\left(s\right){\left|\right|}^2{)}^{1/2}\hfill \\ & \le & {\int }_{-\infty }^0\zeta \left(s\right)\underset{{\delta }_1\in [s,0]}{\sup }\mathbf{E}\left|\right|z\left({\delta }_1\right)\left|\right|ds+l\underset{s\in [0,t]}{\sup }\left(\mathbf{E}\right||z\left(s\right){\left|\right|}^2{)}^{1/2}\hfill \\ & =& {\int }_{-\infty }^0\zeta \left(s\right)\underset{{\delta }_1\in [s,0]}{\sup }\left|\right|z_0\left({\delta }_1\right)\left|\right|ds+l\underset{s\in [0,t]}{\sup }\left(\mathbf{E}\right||z\left(s\right){\left|\right|}^2{)}^{1/2}\hfill \\ & =& l\underset{s\in [0,t]}{\sup }{\left(\mathbf{E}\right|\left|z\left(s\right)\right||}^2{)}^{1/2}+{\parallel z_0\parallel }_{{\mathfrak{C}}_{\zeta }}.\hfill \end{array}$$

Since $\mathsf{\Phi }\in {\mathfrak{C}}_{\zeta }$, then $z_t\in {\mathfrak{C}}_{\zeta }$,

$$\parallel z_t{\parallel }_{{\mathfrak{C}}_{\zeta }}={\int }_{-\infty }^0\zeta \left(s\right)\underset{\delta \in [s,0]}{\sup }\left|\right|z_t\left(\delta \right)\left|\right|ds\ge \left|\right|z_t\left(\delta \right)\left|\right|{\int }_{-\infty }^0\zeta \left(s\right)ds\mathbf{E}\left|\right|z\left(t\right)\left|\right|.$$

The proof is complete. □

The phase space ${\mathfrak{C}}_{\zeta }$ defined above satisfies all the conditions of phase space given by Hall and Kato [25].

According to the author’s understanding, this research is the first to examine neutral SIDEs with infinite latency driven by Poisson jumps and the Rosenblatt process, as well as their existence and exponential stability. This paper’s key contribution is to identify prerequisites that guarantee:

(i)

The existence, uniqueness, and exponential stability of the solutions and their maps of system 2, including mean square exponential stability and nearly certain exponential stability, are explored.

(ii)

We demonstrate the outcome via stochastic methods and Grimmer’s [23] resolvent operator theory. It is important to note that system 2 was explored with a finite delay by Diop et al. [18]. They studied the existence of mild solutions with exponential stability. Due to this, our method can be viewed as an extension of the conclusion of [18] for the case of infinite delay.

(iii)

The literature does not address the best controls for neutral SIDEs with infinite delay of system (35), and this fact drives us to create the current work on this subject by both extending the existing controls and creating new ones.

(iv)

Lastly, to demonstrate the established idea, we came up with three alternative cases.

This manuscript is organized as follows: In Section 2 There are some notations and preliminary remarks. Section 3 represents the existence and uniqueness of mild solutions for neutral SIDEs with infinite delay. Section 4 ensures the conditions assuring mean square moment exponential stability of the solution $\mathrm{z}\left(t\right)$ and almost surely exponential stability of the solution $\mathrm{z}\left(t\right)$ is studied in Section 5. Section 6 displays the outcomes for optimal pairs of systems governed by the stochastic control system (35). Section 7 contains four examples to illustrate the theory. To illustrate the efficiency of the theoretical result, we study the numerical simulation in Section 8.

2. Preliminary Remarks

Let $\mathbb{H}$ and $\mathbb{K}$ be two real separable Hilbert spaces and represent the norm operator in $\mathbb{H}$, $\mathbb{K}$. The space $\mathcal{L}(\mathbb{K},\mathbb{H})$ from $\mathbb{K}$ to $\mathbb{H}$ consists of bounded linear operators endowed with $∥·∥$, and system 2 is attired with a normal filtration ${\left\{{\Im }_t\right\}}_{t\ge 0}$.

Rosenblatt Process: The basic properties of the Rosenblatt process and Wiener integral are given below. Let $\left\{{\mathbb{Z}}_{\mathrm{A}\left(t\right)},t\in [0,\mathrm{T}]\right\}$ be a one-dimensional Rosenblatt process with parameter $\mathrm{A}\in \left(\frac{1}{2},1\right)$ on $[0,\mathrm{T}]$, with $\mathrm{T}$ being an arbitrary fixed horizon representing the following equation [30]:

$$\begin{array}{ccc}\hfill {\mathbb{Z}}_{\mathrm{A}}\left(t\right)& =& d\left(\mathrm{A}\right){\int }_0^t{\int }_0^t\left[{\int }_{y_1\vee y_2}^t\frac{\partial {\mathrm{B}}^{{\mathrm{A}}^{{}^{\prime }}}}{\partial \mathrm{x}}(\mathrm{x},y_1)\frac{\partial {\mathrm{B}}^{{\mathrm{A}}^{{}^{\prime }}}}{\partial \mathrm{x}}(\mathrm{x},y_2)\right]d\mathbb{B}\left(y_1\right)d\mathbb{B}\left(y_2\right),\mathrm{for}A>\frac{1}{2},\hfill \end{array}$$

with ${\mathrm{B}}^{\mathrm{A}}(t,s)$ given by

$${\mathrm{B}}^{\mathrm{A}}=c_{\mathrm{A}}{s}^{\frac{1}{2}-\mathrm{A}}{\int }_s^t{(\mathrm{x}-s)}^{\mathrm{A}-\frac{3}{2}}{\mathrm{x}}^{\mathrm{A}-\frac{1}{2}}d\mathrm{x},\mathrm{for}t>s,$$

where $c_{\mathrm{A}}=\sqrt{\frac{\mathrm{A}(2\mathrm{A}-1)}{\beta (2-2\mathrm{A},\mathrm{A}-\frac{1}{2})}}$, ${\mathrm{B}}^{\mathrm{A}}(t,s)=0$ when $t\le s$, $\left\{\mathbb{B}\left(t\right),t\in [0,T]\right\}$ is a standard Brownian motion, ${\mathrm{A}}^{{}^{\prime }}=\frac{\mathrm{A}+1}{2}$ and $d\left(\mathrm{A}\right)=\frac{1}{\mathrm{A}+1}\sqrt{\frac{\mathrm{A}}{2(2\mathrm{A}-1)}}$ is a normalizing constant and $\beta (·,·)$ is the Beta function. The covariance function of the Rosenblatt process $\left\{{\mathbb{Z}}_{\mathrm{A}\left(t\right)},t\in [0,T]\right\}$ is

$$\mathbb{E}\left({\mathbb{Z}}_{\mathrm{A}}\left(t\right){\mathbb{Z}}_{\mathrm{A}}\left(s\right)\right)=\frac{1}{2}\left(s^{2\mathrm{A}}+t^{2\mathrm{A}}-{\left|s-t\right|}^{2\mathrm{A}}\right).$$

The Wiener integral can be constructed with respect to the Rosenblatt process due to its covariance structure. For more background information for this section, the reader is referred to [29,30].

Poisson Process: For $t\ge 0$, $\mathrm{p}\left(t\right)$ is a $\mathbb{B}$-valued, $\sigma$-finite stationary, and the ${\Im }_t$-adapted Poisson point process has values in measurable space $(\mathrm{Z},\mathcal{B})$ and an intensity measure of $\sigma$-finite $v\left(dz\right)$. We define $N(ds,dz)$ as the Poisson counting measure. $\mathrm{p}(·)$ induces the Poisson counting measure and the compensatory martingale is provided by

$$\tilde{N}(ds,dz)=N(ds,dz)-v\left(dz\right)ds.$$

Definition 1.

A resolvent operator $\mathcal{R}\left(t\right)\in \mathcal{L}\left(\mathbb{X}\right)$, $t\ge 0$ is a bounded linear operator-valued function for Equation (2) if $\mathcal{R}\left(t\right)$ attains the following:

(i) 

$\mathcal{R}\left(0\right)=I$, $∥\mathcal{R}\left(t\right)∥\le \mathrm{N}{e}^{\alpha t}\forall$$t\ge 0$, $\mathrm{N}\ge 1$, $\alpha \in R$.

For $\alpha >0$, $\mathcal{R}\left(t\right)$ is exponentially stable.

(ii) 

The function $t\in \mathcal{R}\left(t\right)x$ is strongly continuous for each $t\ge 0$ and for $x\in \mathbb{X}$, $\mathrm{x}$ in $\mathbb{Y}$, $\mathcal{R}(·)\mathrm{x}\in {\mathfrak{C}}^1([0,+\infty );\mathbb{X})\bigcap \mathfrak{C}([0,+\infty );\mathbb{Y})$ and satisfies

$$\begin{array}{ccc}\hfill d\mathcal{R}\left(t\right)\mathrm{x}& =& \left(\mathfrak{A}\mathcal{R}\left(t\right)\mathrm{x}+{\int }_0^t\mathsf{{\rm Y}}(t-s)\mathcal{R}\left(s\right)\mathrm{x}ds\right)dt\hfill \\ & =& \left(\mathcal{R}\left(t\right)\mathfrak{A}\mathrm{x}+{\int }_0^t\mathcal{R}(t-s)\mathsf{{\rm Y}}\left(s\right)\mathrm{x}ds\right)dt.\hfill \end{array}$$

The existence of solutions for Equation (3) is ensured by the following two criteria, which are adopted from Grimmer [23].

(A1)

The operator $\mathfrak{A}$ is an infinitesimal generator of a ${\mathfrak{C}}_0$-semigroup on $\mathbb{X}$.

(A2)

For all $t\ge 0$, $\mathsf{{\rm Y}}\left(t\right)$ denotes a closed, continuous linear operator from $\mathfrak{D}\left(\mathfrak{A}\right)$ to $\mathbb{X}$, and $\mathsf{{\rm Y}}\left(t\right)$ belongs to $\mathcal{L}(\mathbb{Y},\mathbb{X})$. For any $y\in \mathbb{Y}$, the map $t\to \mathsf{{\rm Y}}\left(t\right)y$ is bounded, differentiable, and its derivative $d\mathsf{{\rm Y}}\left(t\right)y/dt$ is bounded and uniformly continuous on $[0,\infty )$.

Remark 1.

The existence and uniqueness of $\mathcal{R}\left(t\right)$ is guaranteed by (A1) and (A2).

Consider the following deterministic integrodifferential equation:

$$\begin{array}{ccc}\hfill d\mathrm{u}\left(t\right)& =& \left(\mathfrak{A}\mathrm{u}\left(t\right)+{\int }_0^t\mathsf{{\rm Y}}(t-s)\mathrm{u}\left(s\right)ds+\mathrm{a}\left(t\right)\right)dt,t\ge 0,\hfill \\ \hfill \mathrm{u}\left(0\right)& =& {\mathrm{u}}_0\in \mathbb{X}\hfill \end{array}$$

(3)

and $\mathrm{a}\left(t\right):[0,+\infty )\to \mathbb{X}$ is a continuous function.

Lemma 2.

Let assumptions (A1) and (A2) hold good. If $\mathrm{u}$ is a strict solution of (3), i.e., $\mathrm{u}\in {\mathfrak{C}}^1([0,+\infty );\mathbb{X})\bigcap \mathfrak{C}([0,+\infty );\mathbb{Y})$, then

$$\begin{array}{ccc}\hfill \mathrm{u}\left(t\right)& =& \mathcal{R}\left(t\right){\mathrm{u}}_0+{\int }_0^t\mathcal{R}(t-s)\mathrm{a}\left(s\right)ds,t\ge 0.\hfill \end{array}$$

(4)

Lemma 3.

If $\mathsf{\Psi }:[0,T]\to {\mathcal{L}}_2^0(\mathbb{B},\mathbb{A})$ satisfies ${\int }_0^T{∥\mathsf{\Psi }\left(s\right)∥}_{{\mathcal{L}}_2^0}^{2}ds<\infty$ then system (1) is well defined as an $\mathbb{H}$-valued random variable, and

$$\mathbb{E}{∥{\int }_0^t\mathsf{\Psi }\left(s\right)d{\mathbb{Z}}_{\mathrm{A}}\left(s\right)∥}^2<{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}-1}{\int }_0^t{∥\mathsf{\Psi }\left(s\right)∥}_{{\mathcal{L}}_2^0}^{2}ds.$$

Definition 2.

A mild solution of Equation (2) is an $\mathbb{H}$-valued process $\left\{\mathrm{z}\left(t\right),0\le t\le T\right\}$ satisfying the following:

(i) 

$\mathrm{z}\left(t\right)$ is ${\Im }_t$-adapted and ${\int }_0^T{∥\mathrm{z}\left(t\right)∥}^{2}dt<\infty$ almost surely.

(ii) 

$\mathrm{z}\left(t\right)$ is continuous for $t\in [0,T]$ and satisfies

$$\begin{array}{ccc}\hfill \mathrm{z}\left(t\right)& =& \mathcal{R}\left(t\right)\left[\varphi \left(0\right)+{\mathfrak{g}}_1(0,\varphi )\right]-{\mathfrak{g}}_1(t,{\mathrm{z}}_t)+{\int }_0^t\mathcal{R}(t-s)\mathfrak{g}(s,{\mathrm{z}}_s)ds\hfill \\ & +& {\int }_0^t\mathcal{R}(t-s)\sigma (s,{\mathrm{z}}_s)d{\mathbb{Z}}_{\mathrm{A}}\left(s\right)+{\int }_0^t{\int }_{\mathrm{Z}}\mathcal{R}(t-s)\mathfrak{h}(s,{\mathrm{z}}_s,z)\tilde{N}(ds,dz),\hfill \end{array}$$

(5)

with ${\mathrm{z}}_0(·)=\varphi \in {\mathfrak{C}}_{\zeta }$.

The following presumptions are useful to accomplish the main objective.

(H1)

$\mathcal{R}(·)$ is exponentially stable; that is, there exist two constants $\varphi >0$ and $\mathrm{M}\ge 1$∋

$$∥\mathcal{R}\left(t\right)∥\le \mathrm{M}{e}^{-\varphi t},t\ge 0.$$

(H2)

∃ a real number ${\mathrm{B}}_0>0$∋ ${∥{\mathfrak{f}}_1(t,\mathrm{x})-{\mathfrak{f}}_1(t,\mathrm{y})∥}^2\le {\mathrm{B}}_0{∥\mathrm{x}-\mathrm{y}∥}_{{\mathfrak{C}}_{\zeta }}^2;\mathrm{x},\mathrm{y}\in {\mathfrak{C}}_{\zeta },t\ge 0.$

(H3)

∃ a real number ${\mathrm{B}}_1>0$, such that

$$\begin{array}{c}\hfill \left(i\right){∥\mathfrak{f}(t,\mathrm{x})-\mathfrak{f}(t,\mathrm{y})∥}^2\bigvee {∥\sigma (t,\mathrm{x})-\sigma (t,\mathrm{y})∥}^2\le {\mathrm{B}}_1{∥\mathrm{x}-\mathrm{y}∥}_{{\mathfrak{C}}_{\zeta }}^2,\\ \hfill \left(ii\right){\int }_{\mathrm{Z}}{∥\mathfrak{h}(t,\mathrm{x},z)-\mathfrak{h}(t,\mathrm{y},z)∥}^{2}v\left(dz\right)dt\bigvee \\ \hfill {\left({\int }_{\mathrm{Z}}{∥\mathfrak{h}(t,\mathrm{x},z)-\mathfrak{h}(t,\mathrm{y},z)∥}^{4}v\left(dz\right)dt\right)}^{\frac{1}{2}}\le {\mathrm{B}}_1{∥\mathrm{x}-\mathrm{y}∥}_{{\mathfrak{C}}_{\zeta }}^2,\mathrm{x},\mathrm{y}\in {\mathfrak{C}}_{\zeta },t\ge 0.\\ \hfill \left(iii\right){\left({\int }_{\mathrm{Z}}{∥\mathfrak{h}(t,\mathrm{x},z)-\mathfrak{h}(t,\mathrm{y},z)∥}^{2}v\left(dz\right)dt\right)}^{\frac{1}{2}}\le {\mathrm{B}}_1{∥\mathrm{x}-\mathrm{y}∥}_{{\mathfrak{C}}_{\zeta }}^2,\mathrm{x},\mathrm{y}\in {\mathfrak{C}}_{\zeta }.\end{array}$$

Obviously, ${\mathfrak{f}}_1(t,0)\equiv \mathfrak{f}(t,0)\equiv \sigma (t,0)\equiv \mathfrak{h}(t,0,z)\equiv 0$.

Remark 2.

To ensure that the stochastic system has a zero equilibrium solution, the condition ${\mathfrak{f}}_1(t,0)=\mathfrak{f}(t,0)=\sigma (t,0)=\mathfrak{h}(t,0,z)=0$ is taken into consideration (2). If this supposition is incorrect, it is always possible to convert the equilibrium solution for (2) into the zero equilibrium solution of another system.

3. Existence and Uniqueness

First, we ensure sufficiency for the existence and uniqueness of the solution for (2). The sequential approximation method and numerous stochastic analytic methods are used to accomplish this. However, in order to deal with infinite delay, we must create some novel strategies. In the sections that follow, we replace $\mathbb{X}$ for the Hilbert space $\mathbb{H}$ in (A1) and (A2). We now offer the primary finding listed below.

Theorem 1.

Let assumptions (A1), (A2), (H2), and (H3) hold good with ${\mathrm{B}}_0<\frac{1}{10}$. Then, system (2) has a unique mild solution.

Proof. 

We use the successive approximation technique to Equation (5).

For $t\le 0,{\mathrm{x}}^n\left(t\right)=\varphi \left(t\right),n\in \mathbb{N}$, and for $0\le t\le T$,

$$\begin{array}{ccc}\hfill & & {\mathrm{x}}^n\left(t\right)=\mathcal{R}\left(t\right)\left[\varphi \left(0\right)+{\mathfrak{f}}_1(0,\varphi )\right]-{\mathfrak{f}}_1(t,{\mathrm{x}}_t^n)+{\int }_0^t\mathcal{R}(t-s)\mathfrak{f}(s,{\mathrm{x}}_s^{n-1})ds\hfill \\ & +& {\int }_0^t\mathcal{R}(t-s)\sigma (s,{\mathrm{x}}_s^{n-1})d{\mathbb{Z}}_{\mathrm{A}}\left(s\right)+{\int }_0^t{\int }_{\mathrm{Z}}\mathcal{R}(t-s)\mathfrak{h}(s,{\mathrm{x}}_s^{n-1},z)\tilde{N}(ds,dz);\hfill \end{array}$$

(6)

and

$$\begin{array}{ccc}\hfill {\mathrm{x}}^0\left(t\right)& =& \mathcal{R}\left(t\right)\varphi \left(0\right),0\le t\le T,n\ge 1.\hfill \end{array}$$

Let

$${\mathrm{M}}_{\mathrm{T}}=\underset{0\le t\le T}{\sup }{∥\mathcal{R}\left(t\right)∥}_{\mathcal{L}\left(\mathbb{A}\right)}.$$

i.e., ${\mathrm{M}}_{\mathrm{T}}$ is uniformly bounded.

The proof now follows the steps below:

Step 1: $\left\{{\mathrm{x}}^n\left(t\right)\right\}$, $n\ge 0$ is bounded.

Using (6)

$$\mathbb{E}{∥{\mathrm{x}}^n\left(t\right)∥}^2=\mathbb{E}{∥\varphi \left(t\right)∥}_{{\mathfrak{C}}_{\zeta }}^2<\infty ,t\in (-\infty ,0],$$

we obtain that

$$\mathbb{E}\underset{0\le s\le t}{\sup }∥{\mathrm{x}}^0\left(t\right)∥\le {\mathrm{M}}_{\mathrm{T}}^2\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2<\infty ,t\in [0,T].$$

Then, for any $n\ge 1$, we have,

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\mathrm{x}}^n\left(t\right)∥}^2& =& \mathbb{E}\parallel \mathcal{R}\left(t\right)\left[\varphi \left(0\right)+{\mathfrak{f}}_1(0,\varphi )\right]-{\mathfrak{f}}_1(t,{\mathrm{x}}_t^n)+{\int }_0^t\mathcal{R}(t-s)\mathfrak{f}(s,{\mathrm{x}}_s^{n-1})ds\hfill \\ & +& {\int }_0^t\mathcal{R}(t-s)\sigma (s,{\mathrm{x}}_s^{n-1})d{\mathbb{Z}}_{\mathrm{A}}\left(s\right)+{\int }_0^t{\int }_{\mathrm{Z}}\mathcal{R}(t-s)\mathfrak{h}(s,{\mathrm{x}}_s^{n-1},z)\tilde{N}(ds,dz){\parallel }^2\hfill \\ \hfill \mathbb{E}{∥{\mathrm{x}}^n\left(t\right)∥}^2& =& 5\sum _{i=1}^5{\Delta }_i.\hfill \end{array}$$

(7)

From assumption (H2), we obtain

$$\begin{array}{ccc}\hfill {\Delta }_1& =& \mathbb{E}\underset{0\le s\le t}{\sup }{∥\mathcal{R}\left(t\right)\left[\varphi \left(0\right)+{\mathfrak{f}}_1(0,\varphi )\right]∥}^2,\hfill \\ & \le & 2{\mathrm{M}}_{\mathrm{T}}^2\left(1+{\mathrm{B}}_0\right)\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2,\hfill \end{array}$$

(8)

and

$$\begin{array}{ccc}\hfill {\Delta }_2& =& \mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathfrak{f}}_1(s,{\mathrm{x}}_s^n)∥}^2,\hfill \\ & \le & {\mathrm{B}}_0\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}_s^n∥}_{{\mathfrak{C}}_{\zeta }}^2.\hfill \end{array}$$

(9)

Next, combining (H3) and Hölder’s inequality yields

$$\begin{array}{ccc}\hfill {\Delta }_3& =& {\mathrm{M}}_{\mathrm{T}}^2\mathbb{E}\underset{0\le s\le t}{\sup }{\left({\int }_0^t∥\mathfrak{f}(s,{\mathrm{x}}_s^{n-1})∥ds\right)}^2,\hfill \\ & \le & {\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1{\int }_0^t\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}_s^{n-1}∥}_{{\mathfrak{C}}_{\zeta }}^2.\hfill \end{array}$$

(10)

Now, using Lemma 2, and (H3), we obtain

$$\begin{array}{ccc}\hfill {\Delta }_4& =& {\mathrm{M}}_{\mathrm{T}}^2\mathbb{E}\underset{0\le s\le t}{\sup }{\left({\int }_0^t∥\sigma (s,{\mathrm{x}}_s^{n-1})∥d{\mathbb{Z}}_{\mathrm{A}}\left(s\right)\right)}^2,\hfill \\ & \le & {\mathrm{M}}_{\mathrm{T}}^2{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}{\int }_0^t\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}_s^{n-1}∥}^{2}ds.\hfill \\ \hfill \end{array}$$

(11)

Finally, with (H3), Lemma 2, and Hölder’s inequality, we obtain

$$\begin{array}{ccc}\hfill {\Delta }_5& =& {\mathrm{M}}_{\mathrm{T}}^2\{\mathbb{E}{\int }_0^t{\int }_{\mathrm{Z}}{∥\mathfrak{h}(s,{\mathrm{x}}_s^{n-1},z)∥}^{2}v\left(dz\right)ds\hfill \\ & +& \mathbb{E}{\left({\int }_0^t{\int }_{\mathrm{Z}}{∥\mathfrak{h}(s,{\mathrm{x}}_s^{n-1},z)∥}^{4}v\left(dz\right)ds\right)}^{\frac{1}{2}}\}\hfill \\ & \le & 3{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1\mathrm{T}{\int }_0^t\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}_s^{n-1}∥}^{2}ds.\hfill \end{array}$$

(12)

Substituting (8) and (9) into (7), we obtain

$$\begin{array}{ccc}\hfill \mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}^n\left(s\right)∥}^2& \le & 10{\mathrm{M}}_{\mathrm{T}}^2\left(1+{\mathrm{B}}_0\right)\mathbb{E}{∥\varphi ∥}^2+5{\mathrm{B}}_0\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}_s^n∥}^2\hfill \\ & +& {\mathfrak{Q}}_1{\int }_0^t\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}_s^{n-1}∥}^{2}ds,\hfill \end{array}$$

(13)

where ${\mathfrak{Q}}_1=5{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1\left[2t+2{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}+3\right]$.

By using the definition of the norm ${∥·∥}_{{\mathfrak{C}}_{\zeta }}$, we can write

$$\begin{array}{ccc}\hfill \mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}^n\left(s\right)∥}^2& \le & {\mathfrak{Q}}_2+\frac{{\mathfrak{Q}}_1}{1-5{\mathrm{B}}_0}{\int }_0^t\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}^{n-1}\left(s\right)∥}^{2}ds,\hfill \end{array}$$

(14)

where ${\mathfrak{Q}}_2=\left[10{\mathrm{M}}_{\mathrm{T}}^2\left(1+{\mathrm{B}}_0\right)+5{\mathrm{B}}_0+{\mathfrak{Q}}_1\mathrm{T}\right]$.

Therefore,

$$\begin{array}{c}\hfill \underset{1\le n\le k}{\max }\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}^n\left(s\right)∥}^2\le {\mathfrak{Q}}_2+{\mathfrak{Q}}_3{\int }_0^t\underset{1\le n\le k}{\max }\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}^{n-1}\left(s\right)∥}^{2}ds,k\ge 1,\end{array}$$

(15)

where ${\mathfrak{Q}}_3=\frac{{\mathfrak{Q}}_1}{1-5{\mathrm{B}}_0}$. Besides that, we have

$$\begin{array}{ccc}\hfill \underset{1\le n\le k}{\max }\mathbb{E}{∥{\mathrm{x}}^{n-1}\left(s\right)∥}^2& \le & \mathbb{E}{∥{\mathrm{x}}^0\left(\mathrm{s}\right)∥}^2+\underset{1\le n\le k}{\max }\mathbb{E}{∥{\mathrm{x}}^n\left(s\right)∥}^2\hfill \\ & \le & {\mathrm{M}}_{\mathrm{T}}^2\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+\underset{1\le n\le k}{\max }\mathbb{E}{∥{\mathrm{x}}^n\left(s\right)∥}^2.\hfill \end{array}$$

It follows that

$$\begin{array}{ccc}\hfill \underset{1\le n\le k}{\max }\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}^n\left(s\right)∥}^2& \le & {\mathfrak{Q}}_2+{\mathfrak{Q}}_3{\mathrm{M}}_{\mathrm{T}}^2\mathrm{T}\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+{\mathfrak{Q}}_3{\int }_0^t\underset{1\le n\le k}{\max }\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}^n\left(s\right)∥}^{2}ds,\hfill \\ & \le & {\mathfrak{Q}}_4+{\mathfrak{Q}}_3{\int }_0^t\underset{1\le n\le k}{\max }\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}^n\left(s\right)∥}^{2}ds,\hfill \end{array}$$

where ${\mathfrak{Q}}_4={\mathfrak{Q}}_2+{\mathfrak{Q}}_3{\mathrm{M}}_{\mathrm{T}}^2\mathrm{T}\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2$.

Using Gronwall’s inequality,

$$\begin{array}{ccc}\hfill \underset{1\le n\le k}{\max }\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}^n\left(s\right)∥}^2& \le & {\mathfrak{Q}}_4{e}^{{\mathfrak{Q}}_{3}t}<\infty .\hfill \end{array}$$

Since k is arbitrary, we have

$$\begin{array}{c}\hfill \mathbb{E}{∥{\mathrm{x}}^n\left(t\right)∥}^2\le {\mathfrak{Q}}_4{e}^{{\mathfrak{Q}}_{3}t}<\infty ,\end{array}$$

which completes the proof.

Step 2: $\left\{{\mathrm{x}}^n,\right\}n\in \mathbb{N}$ is a Cauchy sequence.

The successive approximations are constructed to have ${\mathrm{x}}^n\left(t\right)={\mathrm{x}}^{n-1}$ on $(-\infty ,0]$ for $n\ge 1$. So we now establish

$$\begin{array}{c}\hfill {∥{\mathrm{x}}_t^0∥}_{{\mathfrak{C}}_{\zeta }}^2\le \left(1+{\mathrm{M}}_{\mathrm{T}}^2\right){∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2,t\in [0,T].\end{array}$$

Therefore from (3.1), we have

$$\begin{array}{c}\hfill \mathbb{E}{∥{\mathrm{x}}_t^1-{\mathrm{x}}_t^0∥}^2\le 5\sum _{i=1}^5{\mathsf{\Omega }}_i.\end{array}$$

(16)

By using (H2), we obtain

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_1& \le & \mathbb{E}{∥\mathcal{R}\left(t\right){\mathfrak{f}}_1(0,\varphi )∥}^2,\hfill \\ & \le & {\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_0\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2.\hfill \end{array}$$

(17)

and

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_2& \le & \mathbb{E}{∥{\mathfrak{f}}_1(t,{\mathrm{x}}_t^1)∥}^2\hfill \\ & \le & {\mathrm{B}}_0\mathbb{E}{∥{\mathrm{x}}_t^1∥}_{{\mathfrak{C}}_{\zeta }}^2\hfill \\ & \le & 2{\mathrm{B}}_0\left[\mathbb{E}{∥{\mathrm{x}}_t^1-{\mathrm{x}}_t^0∥}_{{\mathfrak{C}}_{\zeta }}^2+\mathbb{E}{∥{\mathrm{x}}_t^0∥}_{{\mathfrak{C}}_{\zeta }}^2\right]\hfill \\ & \le & 2{\mathrm{B}}_0\mathbb{E}{∥{\mathrm{x}}_t^1-{\mathrm{x}}_t^0∥}_{{\mathfrak{C}}_{\zeta }}^2+2{\mathrm{B}}_0\left(1+{\mathrm{M}}_{\mathrm{T}}^2\right)\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2.\hfill \end{array}$$

(18)

Next, using (H3) and Hölder’s inequality, we obtain

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_3& \le & {\mathrm{M}}_{\mathrm{T}}^2\mathbb{E}{\left({\int }_0^t∥\mathfrak{f}(s,{\mathrm{x}}_s^0)∥ds\right)}^2\hfill \\ & \le & {\mathrm{M}}_{\mathrm{T}}^2{\mathrm{T}}^2{\mathrm{B}}_1\mathbb{E}{\int }_0^t{∥{\mathrm{x}}_s^0∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds\hfill \\ & \le & {\mathrm{M}}_{\mathrm{T}}^2{\mathrm{T}}^2{\mathrm{B}}_1\left(1+{\mathrm{M}}_{\mathrm{T}}^2\right)\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds.\hfill \end{array}$$

(19)

From Lemma 2, we have

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_4& \le & {\mathrm{M}}_{\mathrm{T}}^2\mathrm{T}\mathbb{E}\left({\int }_0^t\sigma (s,{\mathrm{x}}_s^0)d\mathbb{Z}\left(s\right)\right)\hfill \\ & \le & {\mathrm{M}}_{\mathrm{T}}^2\mathrm{T}{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}{\int }_0^T\mathbb{E}{∥{\mathrm{x}}_s^0∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds\hfill \\ & \le & {\mathrm{M}}_{\mathrm{T}}^2\mathrm{T}{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}\left(1+{\mathrm{M}}_{\mathrm{T}}^2\right)\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds.\hfill \end{array}$$

(20)

In a similar way, using (H3), we obtain

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_5& =& {\mathrm{M}}_{\mathrm{T}}^2\{\mathbb{E}{\int }_0^t{\int }_{\mathrm{Z}}{∥\mathfrak{h}(s,{\mathrm{x}}_s^0,z)∥}^{2}v\left(dz\right)ds\hfill \\ & +& \mathbb{E}{\left({\int }_0^t{\int }_{\mathrm{Z}}{∥\mathfrak{h}(s,{\mathrm{x}}_s^0,z)∥}^{4}v\left(dz\right)ds\right)}^{\frac{1}{2}}\}\hfill \\ & \le & 3{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1\mathrm{T}\left(1+{\mathrm{M}}_{\mathrm{T}}^2\right)\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds.\hfill \end{array}$$

(21)

Substituting (17)–(21) into (16), we obtain

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\mathrm{x}}^1\left(t\right)-{\mathrm{x}}^0\left(0\right)∥}^2& \le & 10{\mathrm{B}}_0\mathbb{E}{∥{\mathrm{x}}_t^1-{\mathrm{x}}_t^0∥}_{{\mathfrak{C}}_{\zeta }}^2+5\{{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_0+2{\mathrm{B}}_0\left(1+{\mathrm{M}}_{\mathrm{T}}^2\right)\hfill \\ & +& {\mathrm{M}}_{\mathrm{T}}^2{\mathrm{T}}^2{\mathrm{B}}_1\left(1+{\mathrm{M}}_{\mathrm{T}}^2\right)+{\mathrm{M}}_{\mathrm{T}}^2\mathrm{T}{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}\left(1+{\mathrm{M}}_{\mathrm{T}}^2\right)\hfill \\ & +& 3{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1\mathrm{T}\left(1+{\mathrm{M}}_{\mathrm{T}}^2\right)\}\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2\hfill \\ & \le & {\mathfrak{Q}}_5+10{\mathrm{B}}_0\mathbb{E}{∥{\mathrm{x}}_t^1-{\mathrm{x}}_t^0∥}_{{\mathfrak{C}}_{\zeta }}^2;\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill {\mathfrak{Q}}_5& =& 5\{{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_0+2{\mathrm{B}}_0\left(1+{\mathrm{M}}_{\mathrm{T}}^2\right)\hfill \\ & +& {\mathrm{M}}_{\mathrm{T}}^2{\mathrm{T}}^2{\mathrm{B}}_1\left(1+{\mathrm{M}}_{\mathrm{T}}^2\right)+{\mathrm{M}}_{\mathrm{T}}^2\mathrm{T}{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}\left(1+{\mathrm{M}}_{\mathrm{T}}^2\right)\hfill \\ & +& 3{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1\mathrm{T}\left(1+{\mathrm{M}}_{\mathrm{T}}^2\right)\}\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2.\hfill \end{array}$$

This yields

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\mathrm{x}}^1\left(t\right)-{\mathrm{x}}^0\left(0\right)∥}^2& \le & \underset{0\le s\le t}{\sup }{∥{\mathrm{x}}^1\left(t\right)-{\mathrm{x}}^0\left(t\right)∥}^2.\hfill \end{array}$$

Next, we can deduce

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\mathrm{x}}^1\left(t\right)-{\mathrm{x}}^0\left(0\right)∥}^2& \le & \frac{{\mathfrak{Q}}_5}{1-10{\mathrm{B}}_0}={\mathfrak{Q}}_6.\hfill \end{array}$$

Similarly,

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\mathrm{x}}^2\left(t\right)-{\mathrm{x}}^1\left(t\right)∥}^2& \le & 4\{\mathbb{E}{∥{\mathfrak{f}}_1(t,{\mathrm{x}}_t^2)-{\mathfrak{f}}_1(t,{\mathrm{x}}_t^1)∥}^2+\mathbb{E}{∥{\int }_0^t\mathcal{R}(t-s)[\mathfrak{f}(s,{\mathrm{x}}_s^1)-\mathfrak{f}(s,{\mathrm{x}}_s^0)]ds∥}^2\hfill \\ & +& \mathbb{E}{∥{\int }_0^t\mathcal{R}(t-s)[\sigma (s,{\mathrm{x}}_s^1)-\sigma (s,{\mathrm{x}}_s^0)]d{\mathbb{Z}}_{\mathrm{A}}\left(s\right)∥}^2\hfill \\ & +& \mathbb{E}{∥{\int }_0^t{\int }_{\mathrm{Z}}\mathcal{R}(t-s)[\mathfrak{h}(s,{\mathrm{x}}_s^1,z)-\mathfrak{h}(s,{\mathrm{x}}_s^0,z)]\tilde{N}(ds,dz)∥}^2\}\hfill \\ & \le & 4{\mathrm{B}}_0\mathbb{E}{∥{\mathrm{x}}_t^2-{\mathrm{x}}_t^1∥}_{{\mathfrak{C}}_{\zeta }}^2+4{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1\left\{\mathrm{T}+{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}+3\mathrm{T}\right\}{\int }_0^t\mathbb{E}{∥{\mathrm{x}}_s^1-{\mathrm{x}}_s^0∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds\hfill \\ & \le & 4{\mathrm{B}}_0\mathbb{E}{∥{\mathrm{x}}_t^2-{\mathrm{x}}_t^1∥}_{{\mathfrak{C}}_{\zeta }}^2+4{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1\left\{\mathrm{T}+{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}+3\mathrm{T}\right\}t{\mathfrak{Q}}_6.\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\mathrm{x}}^2\left(s\right)-{\mathrm{x}}^1\left(s\right)∥}^2& \le & \frac{4{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1\left\{\mathrm{T}+{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}+3\mathrm{T}\right\}t}{1-4{\mathrm{B}}_0}{\mathfrak{Q}}_6,\hfill \\ & =& {\mathfrak{Q}}_{6}t{\mathfrak{Q}}_7,\hfill \end{array}$$

where ${\mathfrak{Q}}_7=\frac{4{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1\left\{\mathrm{T}+{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}+3\mathrm{T}\right\}}{1-4{\mathrm{B}}_0}$.

Sequentially, we can prove that

$$\begin{array}{ccc}\hfill \mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}^3\left(s\right)-{\mathrm{x}}^2\left(s\right)∥}^2& \le & \frac{{\left({\mathfrak{Q}}_{7}t\right)}^2}{2!}{\mathfrak{Q}}_6.\hfill \end{array}$$

Using the successive iteration scheme, $\forall n\ge 0$,

$$\begin{array}{ccc}\hfill \mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}^{n+1}\left(s\right)-{\mathrm{x}}^n\left(s\right)∥}^2& \le & \frac{{\left({\mathfrak{Q}}_{7}t\right)}^n}{n!}{\mathfrak{Q}}_6.\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\mathrm{x}}^m\left(t\right)-{\mathrm{x}}^n\left(t\right)∥}^2& \le & {\mathfrak{Q}}_6\sum _{k=n}^{m-1}\frac{{\left({\mathfrak{Q}}_{7}t\right)}^k}{k!}\hfill \\ & \to & 0\mathrm{as}n\to \infty ,m>n\ge 0.\hfill \end{array}$$

This argument proves that $\left\{{\mathrm{x}}^n\left(t\right)\right\},n\ge 0$ is a Cauchy sequence in ${\mathcal{L}}^2(\mathsf{\Omega },\mathbb{H})$.

Step 3: Existence and uniqueness of Equation (2).

We have ${\mathrm{x}}^n\left(t\right)\to \mathrm{x}\left(t\right)$ in ${\mathcal{L}}^2$ as $n\to \infty$. For all $t\in [0,\mathrm{T}]$, the Borel–Cantelli lemma shows that ${\mathrm{x}}^n\left(t\right)$ converge to $\mathrm{x}\left(t\right)$ uniformly as $n\to \infty$, for $t\in (-\infty ,\mathrm{T}]$. We prove the next inequality using (H2) and (H3).

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\mathfrak{f}}_1(t,{\mathrm{x}}_t^n)-{\mathfrak{f}}_1(t,{\mathrm{x}}_t)∥}^2& \le & {\mathrm{B}}_0\mathbb{E}{∥{\mathrm{x}}_t^n-{\mathrm{x}}_t∥}_{{\mathfrak{C}}_{\zeta }}^2\hfill \\ & \le & {\mathrm{B}}_0\mathbb{E}\underset{0\le s\le t}{\sup }{∥{\mathrm{x}}_s^n-{\mathrm{x}}_s∥}^2\to 0,\mathrm{as}n\to \infty .\hfill \end{array}$$

Next,

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\int }_0^t\mathcal{R}(t-s)[\mathfrak{f}(s,{\mathrm{x}}_s^n)-\mathfrak{f}(s,{\mathrm{x}}_s)]ds∥}^2& \le & {\mathrm{M}}_{\mathrm{T}}^2\mathrm{T}{\mathrm{B}}_1{\int }_0^t\mathbb{E}{∥{\mathrm{x}}_s^n-{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds\hfill \\ & \to & 0,\mathrm{as}n\to \infty .\hfill \end{array}$$

Similarly, we have

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\int }_0^t\mathcal{R}(t-s)[\sigma (s,{\mathrm{x}}_s^n)-\sigma (s,{\mathrm{x}}_s)]d\mathbb{Z}\left(s\right)∥}^2& \le & {\mathrm{M}}_{\mathrm{T}}^2\mathrm{T}{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}{\int }_0^t\mathbb{E}{∥{\mathrm{x}}_s^n-{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds\hfill \\ & \to & 0,\mathrm{as}n\to \infty ;\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\int }_0^t\mathcal{R}(t-s)[\mathfrak{h}(s,{\mathrm{x}}_s^n,z)-\mathfrak{h}(s,{\mathrm{x}}_s,z)]\tilde{N}(ds,dz)∥}^2& \le & 3{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1\mathrm{T}{\int }_0^t\mathbb{E}{∥{\mathrm{x}}_s^n-{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds\hfill \\ & \to & 0,\mathrm{as}n\to \infty .\hfill \end{array}$$

Taking the limit as $n\to \infty$ yields,

$$\begin{array}{ccc}\hfill \mathrm{x}\left(t\right)& =& \mathcal{R}\left(t\right)\left[\varphi \left(0\right)+{\mathfrak{f}}_1(0,\varphi )\right]-{\mathfrak{f}}_1(t,{\mathrm{x}}_t)+{\int }_0^t\mathcal{R}(t-s)\mathfrak{f}(s,{\mathrm{x}}_s)ds\hfill \\ & +& {\int }_0^t\mathcal{R}(t-s)\sigma (s,{\mathrm{x}}_s)d{\mathbb{Z}}_{\mathrm{A}}\left(s\right)+{\int }_0^t{\int }_{\mathrm{Z}}\mathcal{R}(t-s)\mathfrak{h}(s,{\mathrm{x}}_s,z)\tilde{N}(ds,dz).\hfill \end{array}$$

Gronwall’s lemma assures the assertion which completes the proof. □

Remark 3.

The existence and uniqueness of the local solution is defined on $(-\infty ,T]$, and that leads us to the global solution on $(-\infty ,+\infty )$.

4. Exponential Stability

Definition 3.

For any initial value $\varphi \in {\mathfrak{C}}_{\zeta }$, the mild solution of 2 is said to be mean square mment exponentially stable if it is ${\Im }_0$-measurable and ∃ two positive real numbers $\alpha >0$ and $\beta >0$ such that

$$\mathbb{E}{∥\mathrm{x}\left(t\right)∥}^2\le \alpha \mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2\exp (-\beta t),\forall t\ge 0.$$

The following theorem contains the major finding of this work.

Theorem 2.

Let us assume that for all conditions of Theorem 1, the following inequalities hold:

$$\begin{array}{c}\hfill 2\mu >\varphi \mathrm{and}\frac{{\mathfrak{Q}}_{10}}{1-5{\mathrm{B}}_0}-\varphi <0.\end{array}$$

(22)

The mild solution $\mathrm{x}\left(t\right)$ of Equation (2) and the solution ${\mathrm{x}}_t$ that maps to Equation (2) are then both mean square moment exponentially stable.

Proof. 

The mean square moment exponential stability of $\mathrm{x}\left(t\right)$: Combining Lemma 3 and (H1)–(H3), we can write

$$\begin{array}{ccc}\hfill \mathbb{E}{∥\mathrm{x}\left(t\right)∥}^2& \le & 5\{\mathbb{E}{∥\mathcal{R}\left(t\right)\left[\varphi \left(0\right)+{\mathfrak{f}}_1(0,\varphi )\right]∥}^2+\mathbb{E}{∥{\mathfrak{f}}_1(t,{\mathrm{x}}_t)∥}^2\hfill \\ & +& \mathbb{E}{∥{\int }_0^t\mathcal{R}(t-s)\mathfrak{f}(s,{\mathrm{x}}_s)ds∥}^2+\mathbb{E}{∥{\int }_0^t\mathcal{R}(t-s)\sigma (s,{\mathrm{x}}_s)d{\mathbb{Z}}_{\mathrm{A}}\left(s\right)∥}^2\hfill \\ & +& \mathbb{E}{∥{\int }_0^t{\int }_{\mathrm{Z}}\mathcal{R}(t-s)\mathfrak{h}(s,{\mathrm{x}}_s,z)\tilde{N}(ds,dz)∥}^2\}\hfill \\ & =& 5\sum _{i=1}^5{\Theta }_i.\hfill \end{array}$$

(23)

Note that

$$\begin{array}{ccc}\hfill {\Theta }_1& =& \mathbb{E}{∥\mathcal{R}\left(t\right)\left[\varphi \left(0\right)+{\mathfrak{f}}_1(0,\varphi )\right]∥}^2\hfill \\ & \le & 2\left\{\mathbb{E}{∥\mathcal{R}\left(t\right)\varphi \left(0\right)∥}^2+\mathbb{E}{∥\mathcal{R}\left(t\right){\mathfrak{f}}_1(0,\varphi )∥}^2\right\}\hfill \\ & \le & 2{\mathrm{M}}^2{e}^{-\varphi t}\left(1+{\mathrm{B}}_0\right)\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2,\hfill \end{array}$$

(24)

and

$$\begin{array}{ccc}\hfill {\Theta }_2& =& \mathbb{E}{∥{\mathfrak{f}}_1(t,{\mathrm{x}}_t)∥}^2\le {\mathrm{B}}_0\mathbb{E}{∥{\mathrm{x}}_t∥}_{{\mathfrak{C}}_{\zeta }}^2.\hfill \end{array}$$

(25)

By Hölder’s inequality,

$$\begin{array}{ccc}\hfill {\Theta }_3& =& \mathbb{E}{∥{\int }_0^t\mathcal{R}(t-s)\mathfrak{f}(s,{\mathrm{x}}_s)ds∥}^2\hfill \\ & \le & {\mathrm{M}}^2{\int }_0^t{e}^{-2\varphi (t-s)}{\int }_0^t{e}^{-\varphi (t-s)}\mathbb{E}{∥{\mathfrak{f}}_1(s,{\mathrm{x}}_s)∥}^{2}ds\hfill \\ & \le & {\mathrm{M}}^2{\int }_0^t{e}^{-\varphi (t-s)}ds{\int }_0^t{e}^{-\varphi (t-s)}\mathbb{E}{∥{\mathfrak{f}}_1(s,{\mathrm{x}}_s)∥}^{2}ds\hfill \\ & \le & {\mathrm{M}}^2\frac{1}{\varphi }{\mathrm{B}}_1{\int }_0^t{e}^{-\varphi (t-s)}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds\hfill \\ & \le & {\mathrm{M}}^2{\varphi }^{-1}{\mathrm{B}}_1{\int }_0^t{e}^{-\varphi (t-s)}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds.\hfill \end{array}$$

(26)

Using Lemma 3 and (H3), we obtain

$$\begin{array}{ccc}\hfill {\Theta }_4& =& \mathbb{E}{∥{\int }_0^t\mathcal{R}(t-s)\sigma (s,{\mathrm{x}}_s)d{\mathbb{Z}}_{\mathrm{A}}\left(s\right)∥}^2\hfill \\ & \le & {\mathrm{M}}^2{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}\frac{1}{\varphi }{\mathrm{B}}_1{\int }_0^t{e}^{-\varphi (t-s)}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds\hfill \\ & \le & {\mathrm{M}}^2{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}{\left(\varphi \right)}^{-1}{\mathrm{B}}_1{\int }_0^t{e}^{-\varphi (t-s)}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds.\hfill \end{array}$$

(27)

Finally, using (H1) and (H3), we obtain

$$\begin{array}{ccc}\hfill {\Theta }_5& =& \mathbb{E}{∥{\int }_0^t{\int }_{\mathrm{Z}}\mathcal{R}(t-s)\mathfrak{h}(s,{\mathrm{x}}_s,z)\tilde{N}(ds,dz)∥}^2\hfill \\ & \le & {\mathrm{M}}^2\{\mathbb{E}{\int }_0^t{e}^{-2\varphi (t-s)}{\int }_{\mathrm{Z}}{∥\mathfrak{h}(s,\mathrm{x}(s),z)∥}^{2}v\left(dz\right)ds\hfill \\ & +& \mathbb{E}{\left({\int }_0^t{\int }_{\mathrm{Z}}{∥\mathfrak{h}(s,\mathrm{x}(s),z)∥}^{2}v\left(dz\right)ds\right)}^{\frac{1}{2}}\}\hfill \\ & \le & 3{\mathrm{M}}^2{\mathrm{B}}_1{\left(\varphi \right)}^{-1}{\int }_0^t{e}^{-\varphi (t-s)}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds.\hfill \end{array}$$

(28)

Substituting (24)–(28) into (23), and using Definition 3, we obtain

$$\begin{array}{ccc}\hfill \mathbb{E}{∥\mathrm{x}\left(t\right)∥}^2& \le & 10{\mathrm{M}}^2{e}^{-\varphi t}\left(1+{\mathrm{B}}_0\right)\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+5{\mathrm{B}}_0\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^2\hfill \\ & +& \left(5{\mathrm{M}}^2{\varphi }^{-1}{\mathrm{B}}_1+{\mathrm{M}}^2{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}{\left(\varphi \right)}^{-1}{\mathrm{B}}_1+5{\mathrm{M}}^2{\mathrm{B}}_1{\left(\varphi \right)}^{-1}\right){\int }_0^t{e}^{-\varphi (t-s)}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds\hfill \\ & \le & 10{\mathrm{M}}^2{e}^{-\varphi t}\left(1+{\mathrm{B}}_0\right)\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+5{\mathrm{B}}_0\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^2\hfill \\ & +& {\mathfrak{Q}}_8{\int }_0^t{e}^{-\varphi (t-s)}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds,\hfill \end{array}$$

(29)

where ${\mathfrak{Q}}_8=5{\mathrm{M}}^2{\varphi }^{-1}{\mathrm{B}}_1+{\mathrm{M}}^2{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}{\left(\varphi \right)}^{-1}{\mathrm{B}}_1+5{\mathrm{M}}^2{\mathrm{B}}_1{\left(\varphi \right)}^{-1}$.

Multiplying both sides of (29) by $e^{\varphi t}$ yields

$$\begin{array}{ccc}\hfill e^{\varphi t}\mathbb{E}{∥\mathrm{x}\left(t\right)∥}^2& \le & 10{\mathrm{M}}^2\left(1+{\mathrm{B}}_0\right)\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+5{\mathrm{B}}_0{e}^{\varphi t}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^2\hfill \\ & +& {\mathfrak{Q}}_8{\int }_0^t{e}^{\varphi s}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds.\hfill \end{array}$$

(30)

For $t>0$, we have

$$\begin{array}{ccc}\hfill e^{\varphi t}\mathbb{E}{∥\mathrm{x}\left(t\right)∥}^2& \le & 10{\mathrm{M}}^2\left(1+{\mathrm{B}}_0\right)\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+5{\mathrm{B}}_0{e}^{\varphi t}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^2\hfill \\ & +& {\mathfrak{Q}}_8{\int }_0^t{e}^{\varphi s}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds,\hfill \end{array}$$

(31)

From Appendix A, pp. 12 of [46], we have the following estimation:

$$\begin{array}{ccc}\hfill \mathbb{E}{e}^{\varphi t}{∥\mathrm{x}\left(t\right)∥}^2& \le & 10{\mathrm{M}}^2\left(1+{\mathrm{B}}_0\right)\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+5{\mathrm{B}}_0\left\{e^{(\varphi -2\mu )t}\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+\mathbb{E}\underset{0\le s\le t}{\sup }{e}^{\varphi s}{∥\mathrm{x}\left(s\right)∥}^2\right\}\hfill \\ & +& {\mathfrak{Q}}_8{\int }_0^t\left[e^{(\varphi -2\mu )s}\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+\mathbb{E}\underset{0\le s\le t}{\sup }{e}^{\varphi s}{∥\mathrm{x}\left(s\right)∥}^2\right]ds.\hfill \end{array}$$

Recall that ${\mathrm{B}}_0<\frac{1}{10}$ and $\varphi -2\mu <0$; hence,

$$\begin{array}{ccc}\hfill \mathbb{E}\underset{0\le s\le t}{\sup }{e}^{\varphi s}{∥\mathrm{x}\left(s\right)∥}^2& \le & \frac{1}{1-5{\mathrm{B}}_0}\left[10{\mathrm{M}}^2\left(1+{\mathrm{B}}_0\right)+5{\mathrm{B}}_0\right]\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2\hfill \\ & +& \frac{{\mathfrak{Q}}_8}{1-5{\mathrm{B}}_0(2\mu -\varphi )}\left[1-e^{(\varphi -2\mu )t}\right]\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+\frac{{\mathfrak{Q}}_8}{1-5{\mathrm{B}}_0}{\int }_0^t\mathbb{E}\underset{0\le s\le t}{\sup }{e}^{\varphi s}{∥\mathrm{x}\left(s\right)∥}^{2}ds\hfill \\ & =& {\mathfrak{Q}}_9+{\mathfrak{Q}}_{10}{\int }_0^t\mathbb{E}\underset{0\le s\le t}{\sup }{e}^{\varphi s}{∥\mathrm{x}\left(s\right)∥}^{2}ds,\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {\mathfrak{Q}}_9=\frac{10{\mathrm{M}}^2(1+{\mathrm{B}}_0)+5{\mathrm{B}}_0+\frac{{\mathfrak{Q}}_8}{2\mu -\varphi }}{1-5{\mathrm{B}}_0}\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2\mathrm{and}{\mathfrak{Q}}_{10}=\frac{{\mathfrak{Q}}_8}{1-5{\mathrm{B}}_0}.\end{array}$$

By virtue of Gronwall’s lemma,

$$\begin{array}{ccc}\hfill \mathbb{E}\underset{0\le s\le t}{\sup }{e}^{\varphi s}{∥\mathrm{x}\left(s\right)∥}^2& \le & {\mathfrak{Q}}_9{e}^{{\mathfrak{Q}}_{10}t},\hfill \end{array}$$

which implies that

$$\begin{array}{ccc}\hfill \mathbb{E}{∥\mathrm{x}\left(t\right)∥}^2& \le & {\mathfrak{Q}}_9{e}^{({\mathfrak{Q}}_{10}-\varphi )t}.\hfill \end{array}$$

The result of the square moment exponential stability of solution $\mathrm{x}\left(t\right)$ is therefore satisfied given the criterion in (22). For any $t\ge 0$, we have

$$\begin{array}{ccc}\hfill {∥{\mathrm{x}}_t∥}_{{\mathfrak{C}}_{\zeta }}^2& \le & e^{-2\mu t}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+\underset{0\le s\le t}{\sup }{∥\mathrm{x}\left(s\right)∥}^2,\hfill \end{array}$$

multiplying both sides by $e^{\varphi t}$,

$$\begin{array}{ccc}\hfill e^{\varphi t}{∥{\mathrm{x}}_t∥}_{{\mathfrak{C}}_{\zeta }}^2& \le & e^{(\varphi -2\mu )t}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+\underset{0\le s\le t}{\sup }{e}^{\varphi s}{∥\mathrm{x}\left(s\right)∥}^2\hfill \\ & \le & {∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+\underset{0\le s\le t}{\sup }{e}^{\varphi s}{∥\mathrm{x}\left(s\right)∥}^2.\hfill \end{array}$$

From (30), we have

$$\begin{array}{ccc}\hfill \mathbb{E}\underset{0\le s\le t}{\sup }{e}^{\varphi s}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^2& \le & {∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+10{\mathrm{M}}^2\left(1+{\mathrm{B}}_0\right)\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+5{\mathrm{B}}_0{e}^{\varphi t}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^2+{\mathfrak{Q}}_8{\int }_0^t{e}^{\varphi s}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds\hfill \\ \hfill (1-5{\mathrm{B}}_0)\mathbb{E}\underset{0\le s\le t}{\sup }{e}^{\varphi s}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^2& \le & \left[1+10{\mathrm{M}}^2\left(1+{\mathrm{B}}_0\right)\right]\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+{\mathfrak{Q}}_8{\int }_0^t{e}^{\varphi s}\mathbb{E}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds\hfill \\ & \le & {\mathfrak{Q}}_{10}\mathbb{E}{∥\varphi ∥}_{{\mathfrak{C}}_{\zeta }}^2+{\mathfrak{Q}}_{11}{\int }_0^t\mathbb{E}\underset{0\le s\le t}{\sup }{e}^{\varphi s}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^{2}ds,\hfill \end{array}$$

where ${\mathfrak{Q}}_{10}=\frac{1+10{\mathrm{M}}^2\left(1+{\mathrm{B}}_0\right)}{1-5{\mathrm{B}}_0}$ and ${\mathfrak{Q}}_{11}=\frac{{\mathfrak{Q}}_8}{1-5{\mathrm{B}}_0}$. Thus, we have

$$\begin{array}{ccc}\hfill \mathbb{E}\underset{0\le s\le t}{\sup }{e}^{\varphi s}{∥{\mathrm{x}}_s∥}_{{\mathfrak{C}}_{\zeta }}^2& \le & {\mathfrak{Q}}_{10}{e}^{({\mathfrak{Q}}_{11}-\varphi )t}.\hfill \end{array}$$

(32)

The inequality in (31) ensures that the square moment of the solution map ${\mathrm{x}}_t$ is exponentially stable.

□

5. Almost Surely Exponential Stability

Definition 4.

If the following inequality is almost certainly guaranteed, the mild solution of (2) is said to be exponentially stable if

$$0>\underset{t\to \infty }{\lim }\sup \frac{1}{t}log∥\mathrm{x}\left(t\right)∥\forall \varphi \in {\mathfrak{C}}_{\zeta }.$$

Theorem 3.

Suppose that in Theorem 2 the prerequisites are all true.

(i) 

${\lim }_{t\to \infty }\sup \frac{1}{t}\log ∥\mathrm{x}\left(t\right)∥\le \frac{({\mathfrak{Q}}_{10}-\varphi )ϵ}{2}$ almost surely,

(ii) 

${\lim }_{t\to \infty }\sup \frac{1}{t}\log ∥{\mathrm{x}}_t∥\le \frac{({\mathfrak{Q}}_{10}-\varphi )ϵ}{2}$ almost surely,

which means that $\mathrm{x}\left(t\right)$ and ${\mathrm{x}}_t$ are almost surely exponentially stable for any $ϵ\in (0,1)$.

Proof. 

Theorem 1 guarantees condition (i) of Theorem 3 $\forall n\ge 0$.

$$\begin{array}{ccc}\hfill \mathbb{E}\underset{n\le t\le n+1}{\sup }{∥\mathrm{x}\left(t\right)∥}^2& \le & {\mathfrak{Q}}_9{e}^{({\mathfrak{Q}}_{10}-\varphi )(n+1)}\hfill \\ & =& {\mathfrak{Q}}_9{e}^{e^{{\mathfrak{Q}}_{10}-\varphi }}.e^{({\mathfrak{Q}}_{10}-\varphi )n}.\hfill \end{array}$$

For any $ϵ\in (0,1)$. Let ${\mathrm{I}}_n$ be the interval $[n,n+1]$.

$${\mathfrak{Q}}_{10}=\frac{{\mathfrak{Q}}_{10}}{1-5{\mathrm{B}}_0}.$$

Since $1-ϵ>0$ and ${\mathfrak{Q}}_{10}-\varphi <0$, by using the Markov inequality, we have

$$\begin{array}{ccc}\hfill \mathbb{P}\left(\underset{t\in {\mathrm{I}}_n}{\sup }{∥\mathrm{x}\left(t\right)∥}^2>e^{({\mathfrak{Q}}_{10}-\varphi )nϵ}\right)& \le & \frac{\mathbb{E}{∥\mathrm{x}\left(t\right)∥}^2}{e^{({\mathfrak{Q}}_{10}-\varphi )nϵ}}\hfill \end{array}$$

(33)

$$\begin{array}{ccc}& \le & {\mathfrak{Q}}_9{e}^{{\mathfrak{Q}}_{10}-\varphi }{e}^{({\mathfrak{Q}}_{10}-\varphi )n(1-ϵ)}.\hfill \end{array}$$

(34)

In Equation (33), the right-hand-side term is bounded by

$$\sum _{n=0}^{\infty }{e}^{(1-ϵ)({\mathfrak{Q}}_{10}-\varphi )n}<\infty .$$

Therefore, the Borel–Cantelli lemma guarantees that ∃ an integer $n_0$ such that $\forall n\ge n_0$,

$$\underset{t\in {\mathrm{I}}_n}{\sup }{∥\mathrm{x}\left(t\right)∥}^2\le e^{({\mathfrak{Q}}_{10}-\varphi )nϵ},\mathrm{almost}\mathrm{surely}.$$

Thus,

$$\frac{1}{t}\log {∥\mathrm{x}\left(t\right)∥}^2\le \frac{1}{n}\left({\mathfrak{Q}}_{10}-\varphi \right)nϵ=({\mathfrak{Q}}_{10}-\varphi )ϵ,t\in {\mathrm{I}}_n,n\ge n_0,$$

yields,

$$\underset{t\to \infty }{\lim }\sup \frac{1}{t}\log ∥\mathrm{x}\left(t\right)∥\le \frac{\left({\mathfrak{Q}}_{10}-\varphi \right)nϵ}{2},\mathrm{almost}\mathrm{surely},$$

which shows that Theorem 3 (i) is satisfied. The argument that proves Theorem 3 (ii) follows an analogous reasoning. To be specific, we can use the assumption that solution map ${\mathrm{x}}_t$ is square moment exponentially stable and reach the same conclusion by using the same logic as before. The details are left out. □

6. Optimal Control

Let control $\mathbf{u}$ be associated with the mild solution ${\mathrm{x}}_{\mathbf{u}}$ of (2). Let $\mathcal{B}$ be the reflexive Banach space where the values of control $\mathbf{u}$ are taken. ${\mathcal{B}}_{\infty }(J,\mathcal{L}(\mathcal{B},\mathbb{A}))$ represents the set of operator valued functions that are uniformly bounded in J and measurable in the strong operator topology. Let ${\mathcal{L}}_{\Im }^2(J,\mathcal{B})$ be the closed subspace of $\mathcal{B}$ containing all measurable and ${\Im }_t$-adapted, $\mathcal{B}$-valued stochastic processes satisfying the condition ${\int }_0^t{∥\mathbf{u}\left(t\right)∥}_{\mathcal{B}}^{2}dt<\infty$ and endowed with the norm

$${∥\mathbf{u}\left(t\right)∥}_{{\mathcal{L}}_{\Im }^2(J,\mathcal{B})}={\left[{\int }_0^t{∥\mathbf{u}\left(t\right)∥}_{\mathcal{B}}^{2}dt\right]}^{\frac{1}{2}}.$$

A nonempty closed bounded convex set $\mathrm{v}(·)$ is a subset of $\mathcal{B}$.

Define ${\mathcal{A}}_{ad}=\left\{\mathbf{u}(·)\in {\mathcal{L}}_{\Im }^2(J,\mathcal{B}):\mathbf{u}\left(t\right)\in {\mathcal{A}}_{ad}a.e,t\in J\right\}$. We preemptively believe the following:

(H4)

$\mathrm{B}\in {\mathcal{B}}_{\infty }(J,\mathcal{L}(\mathcal{B},\mathbb{A}))$.

Using Bolza problem $\tilde{\mathrm{P}}$ (see [39]), we can find an optimal pair $({\mathrm{x}}^0,{\mathbf{u}}^0)\in {\mathfrak{C}}_{\zeta }\times {\mathcal{A}}_{ad}$, such that $l({\mathrm{x}}^0,{\mathbf{u}}^0)\le l({\mathrm{x}}^{\mathbf{u}},\mathbf{u})$, $\forall \mathbf{u}\in {\mathcal{A}}_{ad}$ where the cost functional

$$\begin{array}{ccc}\hfill l({\mathrm{x}}^{\mathbf{u}},\mathbf{u})& =& \mathbb{E}{\int }_0^t\mathcal{J}(t,{\mathrm{x}}_t^{\mathbf{u}},{\mathrm{x}}^{\mathbf{u}}\left(t\right),\mathbf{u}\left(t\right))dt+\mathbb{E}\Theta \left({\mathrm{x}}^{\mathbf{u}}\left(\mathrm{T}\right)\right).\hfill \end{array}$$

(H5)

We introduce the following hypotheses:

(1) The functional $\mathcal{J}:[0,\mathrm{T}]\times {\mathfrak{C}}_{\zeta }\times \mathbb{A}\times \mathcal{B}\to \mathbb{R}\cup \left\{\infty \right\}$ is Borel measurable.

(2) For almost all $t\in [0,\mathrm{T}]$, $\mathcal{J}(t,·,·,·)$ is sequentially lower semi-continuous on ${\mathfrak{C}}_{\zeta }\times \mathbb{A}\times \mathcal{B}$.

(3) For almost all $t\in [0,\mathrm{T}]$, $\mathcal{J}(t,\mathrm{x},{\mathrm{x}}_t,·)$ is convex on $\mathcal{B}$ for each $\mathrm{x}\in {\mathfrak{C}}_{\zeta }$.

(4) For $\mathfrak{j}>0$, ${\mu }_0$ is non-negative, ${\mu }_0\in {\mathcal{L}}^1([0,\mathrm{T}];\mathbb{R})$∋.

$$\begin{array}{ccc}\hfill {\mu }_0\left(t\right)+d\mathbb{E}{∥\mathrm{x}∥}^2+e\mathbb{E}{∥{\mathrm{x}}_t∥}^2+\mathfrak{j}\mathbb{E}{∥\mathbf{u}∥}_{\mathcal{B}}^2& \le & \mathcal{J}(t,\mathrm{x}\left(t\right),{\mathrm{x}}_t,\mathbf{u}\left(t\right));\hfill \end{array}$$

where $d,e\ge 0$ are constants.

Consider the optimal control for neutral SIDEs with infinite delay driven by Poisson jumps and the Rosenblatt process:

$$\begin{array}{ccc}\hfill d\left[\mathrm{x}\left(t\right)+{\mathfrak{f}}_1(t,{\mathrm{x}}_t)\right]& =& \mathfrak{A}\left[\mathrm{x}\left(t\right)+{\mathfrak{f}}_1(t,{\mathrm{x}}_t)\right]dt+\mathfrak{f}(t,{\mathrm{x}}_t)dt+\mathrm{B}\left(t\right)\mathbf{u}\left(t\right)dt\hfill \\ & +& {\int }_0^t\mathsf{{\rm Y}}(t-s)\left[\mathrm{x}\left(s\right)+{\mathfrak{f}}_1(s,{\mathrm{x}}_s)\right]ds+\sigma (t,{\mathrm{x}}_t)d{\mathbb{Z}}_{\mathrm{A}}\left(t\right)\hfill \\ & +& {\int }_{\mathrm{Z}}\mathfrak{h}(t,{\mathrm{x}}_t,z)\tilde{N}(dt,dz),t\in J^{{}^{\prime }}=(0,\mathrm{T}],t\ge 0,J=[0,T].\hfill \\ \hfill u_0(·)& =& \varphi \in {\mathfrak{C}}_{\zeta }.\hfill \end{array}$$

(35)

Theorem 4.

If (H1)–(H5) are satisfied, then there exists a unique mild solution of the system (35) for every $\mathbf{u}\in {\mathcal{A}}_{ad}$ of the form

$$\begin{array}{ccc}\hfill \mathrm{x}\left(t\right)& =& \mathcal{R}\left(t\right)\left[\varphi \left(0\right)+{\mathfrak{f}}_1(0,\varphi )\right]-{\mathfrak{f}}_1(t,{\mathrm{x}}_t)+{\int }_0^t\mathcal{R}(t-s)\mathfrak{f}(s,{\mathrm{x}}_s)ds+{\int }_0^t\mathcal{R}(t-s)\mathrm{B}\left(s\right)\mathbf{u}\left(s\right)ds\hfill \\ & +& {\int }_0^t\mathcal{R}(t-s)\sigma (s,{\mathrm{x}}_s)d{\mathbb{Z}}_{\mathrm{A}}\left(s\right)+{\int }_0^t{\int }_{\mathrm{Z}}\mathcal{R}(t-s)\mathfrak{h}(s,{\mathrm{x}}_s,z)\tilde{N}(ds,dz),t\in J.\hfill \end{array}$$

(36)

Proof. 

This theorem’s proof is comparable to that of Theorem 1, and since the successive approximation approach can be used to demonstrate the solution to system (35), it is removed. □

Theorem 5.

Assume that (H1)–(H5) are fulfilled. Also, Theorems 1 and 4 hold good. Then, the stochastic control problem (35) admits at least one optimal pair.

Proof. 

If $\inf \left\{l\left(\mathbf{u}\right):\mathbf{u}\in {\mathcal{A}}_{ad}\right\}=+\infty$, then there is nothing to prove. Assume that $\inf \left\{l\left(\mathbf{u}\right):\mathbf{u}\in {\mathcal{A}}_{ad}\right\}=ϵ<\infty$. Using $\left(\mathbf{H}\mathbf{5}\right)$, we have $ϵ>-\infty$. By definition of infimum, ∃ a minimizing sequence feasible pair $\left\{({\mathrm{x}}^n,{\mathbf{u}}^n)\right\}\subset {\mathcal{A}}_{ad}\equiv \{(\mathrm{x},\mathbf{u}):{\mathrm{x}}^n$ is a mild solution of system (35) corresponding to ${\mathbf{u}}^n\in {\mathcal{A}}_{ad}\}$ such that $l({\mathrm{x}}^n,{\mathbf{u}}^n)\to ϵ$ as $n\to +\infty$. Since ${\mathbf{u}}^n\in {\mathcal{A}}_{ad}$, ${\left\{{\mathbf{u}}^n\right\}}_{n\ge 1}\subset {\mathcal{L}}_2(J,\mathcal{B})$ is bounded, ∃${\mathbf{u}}^0\in {\mathcal{L}}_2(J,\mathcal{B})$ and a subsequence is extracted from ${\mathbf{u}}^n$ such that ${\mathbf{u}}^n\stackrel{w}{\to }{\mathbf{u}}^0$ in ${\mathcal{L}}_2(J,\mathcal{B})$. Since ${\mathcal{A}}_{ad}$ is closed and convex, the Mazur lemma forces us to conclude that ${\mathbf{u}}^0\in {\mathcal{A}}_{ad}$. Suppose that ${\mathrm{x}}^n$ and ${\mathrm{x}}^0$ are the mild solutions of (35) corresponding to ${\mathbf{u}}^n$ and ${\mathbf{u}}^0$, respectively; i.e.,

$$\begin{array}{c}\hfill {\mathrm{x}}^n\left(t\right)=\left\{\begin{array}{c}\varphi \left(t\right),t\in [-r,0],\hfill \\ \mathcal{R}\left(t\right)\left[\varphi \left(0\right)+{\mathfrak{f}}_1(0,\varphi )\right]-{\mathfrak{f}}_1(t,{\mathrm{x}}_t)+{\int }_0^t\mathcal{R}(t-s)\mathfrak{f}(s,{\mathrm{x}}_s^n)ds+{\int }_0^t\mathcal{R}(t-s)\mathrm{B}\left(s\right){\mathbf{u}}^{\mathbf{n}}\left(s\right)ds\hfill \\ +{\int }_0^t\mathcal{R}(t-s)\sigma (s,{\mathrm{x}}_s^n)d{\mathbb{Z}}_{\mathrm{A}}\left(t\right)+{\int }_0^t{\int }_{\mathrm{Z}}\mathcal{R}(t-s)\mathfrak{h}(s,{\mathrm{x}}_s^n,z)\tilde{N}(dt,dz),t\in J.\hfill \end{array}\right.\end{array}$$

Similarly, corresponding to ${\mathbf{u}}^{\mathbf{0}}$, ∃ a mild solution ${\mathrm{x}}^0$ of (35); that is,

$$\begin{array}{c}\hfill {\mathrm{x}}^0\left(t\right)=\left\{\begin{array}{c}\varphi \left(t\right),t\in [-r,0],\hfill \\ \mathcal{R}\left(t\right)\left[\varphi \left(0\right)+{\mathfrak{f}}_1(0,\varphi )\right]-{\mathfrak{f}}_1(t,{\mathrm{x}}_t)+{\int }_0^t\mathcal{R}(t-s)\mathfrak{f}(s,{\mathrm{x}}_s^0)ds+{\int }_0^t\mathcal{R}(t-s)\mathrm{B}\left(s\right){\mathbf{u}}^{\mathbf{0}}\left(s\right)ds\hfill \\ +{\int }_0^t\mathcal{R}(t-s)\sigma (s,{\mathrm{x}}_s^0)d{\mathbb{Z}}_{\mathrm{A}}\left(t\right)+{\int }_0^t{\int }_{\mathrm{Z}}\mathcal{R}(t-s)\mathfrak{h}(s,{\mathrm{x}}_s^0,z)\tilde{N}(dt,dz),t\in J.\hfill \end{array}\right.\end{array}$$

Using (H1)–(H5) and the Hölder inequality for $t\in J$, we have

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\mathrm{x}}^n\left(t\right)-{\mathrm{x}}^0\left(t\right)∥}^2& \le & 5{\mathrm{B}}_0\mathbb{E}{∥{\mathrm{x}}^n\left(s\right)-{\mathrm{x}}^0\left(s\right)∥}^2+5{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_{1}t{\int }_0^t\left(\mathbb{E}{∥{\mathrm{x}}^n\left(s\right)-{\mathrm{x}}^0\left(s\right)∥}^2\right)ds\hfill \\ & +& 5{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}{\int }_0^t\left(\mathbb{E}{∥{\mathrm{x}}^n\left(s\right)-{\mathrm{x}}^0\left(s\right)∥}^2\right)ds\hfill \\ & +& 10{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1{\int }_0^t\left(\mathbb{E}{∥{\mathrm{x}}^n\left(s\right)-{\mathrm{x}}^0\left(s\right)∥}^2\right)ds+5{\mathrm{M}}_{\mathrm{T}}^{2}t{∥\mathrm{B}\left(s\right){\mathbf{u}}^{\mathbf{n}}\left(s\right)-\mathrm{B}\left(s\right){\mathbf{u}}^{\mathbf{0}}\left(s\right)∥}_{\mathcal{L}(J,\mathcal{B})}^2.\hfill \end{array}$$

By Lemma 4.2 in [41], $\mathrm{B}$ is strongly continuous. Also, by Lebesgue’s dominated convergence theorem, we have

$$\begin{array}{ccc}\hfill {\mathfrak{G}}_1& =& 5{\mathrm{M}}_{\mathrm{T}}^2{\mathrm{B}}_1\left[t+{\mathrm{C}}_{\mathrm{A}}{t}^{2\mathrm{A}}+2\right]{\int }_0^t\left(\mathbb{E}\underset{0\le s\le t}{\sup }∥{\mathrm{x}}_s^n-{\mathrm{x}}_s^0∥\right)ds\to 0\mathrm{as}n\to \infty ,\hfill \\ \hfill {\mathfrak{G}}_2& =& 5{\mathrm{M}}_{\mathrm{T}}^{2}t\mathbb{E}{∥\mathrm{B}\left(s\right){\mathbf{u}}^{\mathbf{n}}\left(s\right)-\mathrm{B}\left(s\right){\mathbf{u}}^{\mathbf{0}}\left(s\right)∥}_{\mathcal{L}(J,\mathcal{B})}^2\to 0\mathrm{as}n\to \infty .\hfill \end{array}$$

For each $t\in J$, ${\mathrm{x}}^n(·)$, ${\mathrm{x}}^0(·)\in \mathbb{A}$, we have

$$\begin{array}{ccc}\hfill \mathbb{E}{∥{\mathrm{x}}^n\left(t\right)-{\mathrm{x}}^0\left(t\right)∥}^2& \le & \frac{{\mathfrak{G}}_1+{\mathfrak{G}}_2}{1-5{\mathrm{B}}_0},5{\mathrm{B}}_0<1.\hfill \end{array}$$

So, let us infer that ${\mathrm{x}}^n\to {\mathrm{x}}^0$ as $n\to \infty$. Finally using Balder’s theorem [41] and (H5), we obtain

$$\begin{array}{ccc}\hfill ϵ=\underset{n\to \infty }{\lim }{\int }_0^t\mathcal{L}(t,{\mathrm{x}}^n\left(t\right),{\mathrm{x}}_t^n,{\mathbf{u}}^{\mathbf{n}}\left(t\right))dt& \ge & {\int }_0^t\mathcal{L}(t,{\mathrm{x}}^0\left(t\right),{\mathrm{x}}_t^0,{\mathbf{u}}^{\mathbf{0}}\left(t\right))dt\hfill \\ & =& l\left({\mathbf{u}}^{\mathbf{0}}\right)\ge ϵ.\hfill \end{array}$$

Hence, the result is followed that l attains its minimum at ${\mathbf{u}}^{\mathbf{0}}\in {\mathcal{A}}_{ad}$. □

Remark 4.

The main idea of the proof here is similar to that of [41].

7. Applications

Example 1: Consider the following neutral SIDEs driven by Poisson jumps and the Rosenblatt process with infinite delay:

$$\begin{array}{cc}\hfill & \frac{\partial }{\partial t}\left[\mathrm{x}(t,\zeta )+e^{\mu \theta \left(t\right)}\widehat{{\mathfrak{f}}_1}(t,\mathrm{x}(t+\theta \left(t\right),\zeta ))\right]\hfill \\ \hfill & =\frac{{\partial }^2}{\partial {\zeta }^2}\left[\mathrm{x}(t,\zeta )+e^{\mu \theta \left(t\right)}\widehat{{\mathfrak{f}}_1}(t,\mathrm{x}(t+\theta \left(t\right),\zeta ))\right]dt+{\int }_0^t\widehat{\mathrm{B}(s,\zeta )\mathbf{u}(s,\zeta )}ds\hfill \\ \hfill & +{\int }_0^{t}b(t-s)\frac{{\partial }^2}{\partial {\zeta }^2}\left[\mathrm{x}(t,\zeta )+e^{\mu \theta \left(t\right)}\widehat{{\mathfrak{f}}_1}(t,\mathrm{x}(t+\theta \left(t\right),\zeta ))\right]dt\hfill \\ \hfill & +{\int }_{-\infty }^0{e}^{2\mu s}\widehat{\mathfrak{f}}(t,s,\mathrm{x}(\mathrm{t}+\mathrm{s},\zeta ))dsdt+e^{\mu \theta \left(t\right)}\sigma (t,\mathrm{x}(t+\theta \left(t\right),\zeta ))d{\mathbb{Z}}_{\mathrm{A}}\left(t\right)\hfill \\ \hfill & +{\int }_{e^{\mu \theta \left(t\right)}}\widehat{\mathfrak{h}}(t,\mathrm{x}(t+\theta \left(t\right),\zeta ),z)\tilde{N}(dt,dz),t\ge 0,\zeta \in [0,\pi ],\hfill \\ \hfill \mathrm{x}(t,0)& =\mathrm{x}(t,\pi )=0,t\ge 0,\hfill \\ \hfill \mathrm{x}(\theta ,\zeta )& ={\mathrm{x}}_0(\theta ,\zeta ),\theta \in (-\infty ,0],\zeta \in [0,\pi ].\hfill \end{array}$$

(37)

Here, ${\mathbb{Z}}_{\mathrm{A}}\left(t\right)$ denotes a Q-Rosenblatt process, $\mathfrak{h}:{\mathbb{R}}^{+}\times \mathbb{R}\to \mathbb{R}$ and ${\mathfrak{f}}_1,\sigma :{\mathbb{R}}^{+}\times \mathbb{R}\to \mathbb{R}$, $\mathfrak{f}:{\mathbb{R}}^{+}\times (-\infty ,0]\times \mathbb{R}\to \mathbb{R}$ are continuous functions, ${\mathrm{x}}_0\in {\mathfrak{C}}_{\zeta }$ and $b\in {\mathfrak{C}}^1({\mathbb{R}}^{+},\mathbb{R})$.

Let $\mathbb{A}={\mathcal{L}}^2(0,\pi )$ with the norm $∥·∥$. Define $\mathfrak{A}:\mathfrak{D}\left(\mathfrak{A}\right)\subset \mathbb{A}\to \mathbb{A}$ by $\mathfrak{A}=\frac{{\partial }^2}{\partial {\zeta }^2}$ with domain $\mathfrak{D}\left(\mathfrak{A}\right)={\mathrm{A}}^2(0,\pi )\cap {\mathrm{A}}_0^1(0,\pi )$. Obviously, $\mathfrak{A}$ generates a strongly continuous semigroup ${\left(\mathfrak{S}\left(t\right)\right)}_{t\ge 0}$ on $\mathbb{A}$. So, (A1) is guaranteed. The operator $\mathsf{{\rm Y}}:\mathfrak{D}\left(\mathfrak{A}\right)\subset \mathbb{A}\to \mathbb{A}$ is $\mathsf{{\rm Y}}\left(t\right)\left(\mathrm{x}\right)=b\left(t\right)\mathfrak{A}\mathrm{x}$.

The resolvent operator ${\left(\mathcal{R}\left(t\right)\right)}_{t\ge 0}$ decays exponentially; i.e.,

$$∥\mathcal{R}\left(t\right)∥\le \mathrm{M}{e}^{-\varphi t}.$$

Let us assume the following:

(i)

$\widehat{{\mathfrak{f}}_1}(t,0)=\widehat{\mathfrak{f}}(t,s,0)=\widehat{\sigma }(t,0)=\widehat{\mathfrak{h}}(t,0,z)=0$; $t\ge 0$, $s\le 0$.

(ii)

There exist real numbers $\widehat{{\mathrm{B}}_0}\in (0,\frac{1}{10})$, $\widehat{{\mathrm{B}}_1}>0$∋

$$\begin{array}{ccc}\hfill \widehat{{\mathrm{B}}_0}{∥{\mathrm{x}}_1-{\mathrm{x}}_2∥}^2& \ge & {∥\widehat{{\mathfrak{f}}_1}(t,{\mathrm{x}}_1)-\widehat{{\mathfrak{f}}_1}(t,{\mathrm{x}}_2)∥}^2.\hfill \\ \hfill \widehat{{\mathrm{B}}_1}{∥{\mathrm{x}}_1-{\mathrm{x}}_2∥}^2& \ge & {∥\widehat{\mathfrak{f}}(t,{\mathrm{x}}_1)-\widehat{\mathfrak{f}}(t,{\mathrm{x}}_2)∥}^2\bigvee {∥\widehat{\sigma }(t,{\mathrm{x}}_1)-\widehat{\sigma }(t,{\mathrm{x}}_2)∥}^2\bigvee {\int }_z{∥\widehat{\mathfrak{h}}(t,{\mathrm{x}}_1)-\widehat{\mathfrak{h}}(t,{\mathrm{x}}_2)∥}^2.\hfill \end{array}$$

(iii)

∃ an integrable function $r:(-\infty ,0]\to [0,+\infty )$ such that

$$\begin{array}{ccc}\hfill {∥\widehat{\mathfrak{f}}(t,s,{\mathrm{x}}_1)-\widehat{\mathfrak{f}}(t,s,{\mathrm{x}}_2)∥}^2& \le & r\left(s\right){∥{\mathrm{x}}_1-{\mathrm{x}}_2∥}^2;{\mathrm{x}}_1,{\mathrm{x}}_2\in \mathbb{R}.\hfill \end{array}$$

For $\varphi \in {\mathfrak{C}}_{\zeta }\to {\mathcal{L}}_2^0(\mathbb{R},\mathbb{A})$, $\zeta \in [0,\pi ]$,

$$\begin{array}{ccc}\hfill {\mathfrak{f}}_1(t,{\varphi }_1)\left(\zeta \right)& =& e^{\mu \theta \left(t\right)}\widehat{{\mathfrak{f}}_1}(t,\mathrm{x}(t+\theta \left(t\right),\zeta ))\hfill \\ \hfill \sigma (t,{\varphi }_1)\left(\zeta \right)& =& e^{\mu \theta \left(t\right)}\widehat{\sigma }(t,\mathrm{x}(t+\theta \left(t\right),\zeta ))\hfill \\ \hfill \mathfrak{h}(t,\mathrm{x}(t+\theta \left(t\right),\zeta ),z)& =& e^{\mu \theta \left(t\right)}\widehat{\mathfrak{h}}(t,\mathrm{x}(t+\theta \left(t\right),\zeta ),z),\hfill \end{array}$$

which involve a variable delay term and the following equation contains a distributed delay term:

$$\begin{array}{ccc}\hfill \mathfrak{f}(t,{\varphi }_1)\left(\zeta \right)& =& {\int }_{-\infty }^0{e}^{2\mu s}\mathfrak{f}(t,s,{\varphi }_1\left(s\right)\left(\zeta \right))ds.\hfill \end{array}$$

Set $\mathrm{x}\left(t\right)\zeta =\mathrm{x}(t,\zeta )$ and $\varphi \left(\theta \right)\left(\zeta \right)={\mathrm{x}}_0(\theta ,\zeta )\forall \theta \in (-\infty ,0]$. Then, (37) represents (2).

Using condition (ii) with the norm ${∥·∥}_{{\mathfrak{C}}_{\zeta }}$ yields

$$\begin{array}{ccc}\hfill \widehat{{\mathrm{B}}_0}{∥{\varphi }_1-{\varphi }_2∥}_{{\mathfrak{C}}_{\zeta }}^2& \ge & {∥{\mathfrak{f}}_1(t,{\varphi }_1)-{\mathfrak{f}}_1(t,{\varphi }_2)∥}^2,\hfill \\ \hfill \widehat{{\mathrm{B}}_1}{∥{\varphi }_1-{\varphi }_2∥}_{{\mathfrak{C}}_{\zeta }}^2& \ge & {∥\widehat{\mathfrak{f}}(t,{\varphi }_1)-\widehat{\mathfrak{f}}(t,{\varphi }_1)∥}^2\bigvee {∥\widehat{\sigma }(t,{\varphi }_1)-\widehat{\sigma }(t,{\varphi }_1)∥}^2\bigvee {\int }_z{∥\widehat{\mathfrak{h}}(t,{\varphi }_1)-\widehat{\mathfrak{h}}(t,{\varphi }_1)∥}^2,\hfill \end{array}$$

using condition (iii) with Hölder’s inequality,

$$\begin{array}{ccc}\hfill \widehat{{\mathrm{B}}_1}{∥{\varphi }_1-{\varphi }_2∥}_{{\mathfrak{C}}_{\zeta }}^2& \ge & {∥{\mathfrak{f}}_1(t,{\varphi }_1)-{\mathfrak{f}}_1(t,{\varphi }_2)∥}^2,t\ge 0\mathrm{and}{\varphi }_1,{\varphi }_2\in {\mathfrak{C}}_{\zeta }.\hfill \end{array}$$

Thus, (37) follows the presumptions of Theorem 1 with ${\mathrm{B}}_0=\widehat{{\mathrm{B}}_0}$ and ${\mathrm{B}}_1=\widehat{{\mathrm{B}}_1}$. Theorems 2 and 3 assure the mild solution of (37) with mean square surely and almost surely exponentially stable operators with the following conditions:

$$5{\mathrm{M}}^2{\mathrm{B}}_1\left(\frac{1}{{\varphi }^2}+\frac{2}{\varphi }\right)<1-5{\mathrm{B}}_0\mathrm{and}\varphi <2\mu .$$

Let us consider the cost functional as

$$l(\mathrm{x},\mathbf{u})\left(\zeta \right)={\int }_0^{\pi }{\int }_0^1\mathbb{E}{∥\mathrm{x}(t,\zeta )∥}^{2}dtd\zeta +{\int }_0^{\pi }{\int }_0^1{∥\mathbf{u}(t,\zeta )∥}^{2}dtd\zeta .$$

Here, $\mathrm{B}\mathbf{u}(t,\zeta )={\int }_0^t\widehat{\mathrm{B}(s,\zeta )\mathbf{u}(s,\zeta )}ds$. Now,

$$\begin{array}{ccc}\hfill {\int }_0^{\pi }{\int }_0^1{∥\mathrm{B}\mathbf{u}(t,\zeta )∥}^{2}dtd\zeta & \le & {\int }_0^{\pi }{\int }_0^t{∥\widehat{\mathrm{B}(s,\zeta )\mathbf{u}(s,\zeta )}ds∥}^{2}dtd\zeta \hfill \\ & \le & {\mathrm{M}}^2{\int }_0^{\pi }{\int }_0^t{\int }_0^1{∥\mathbf{u}(t,\zeta )∥}^{2}dsdtd\zeta \hfill \\ & \le & {\mathrm{M}}^2\times mes\left(\pi \right)\times {∥\mathbf{u}(t,\zeta )∥}_{\mathcal{L}\left(\right[0,1],[0,\pi \left]\right)}^2,\hfill \end{array}$$

where ${\mathrm{M}}^2=\max \left\{{∥\mathrm{B}(t,\zeta )∥}^2:t\in [0,1]\right\}$. Consequently, it may be said that $\mathrm{B}$ is a bounded linear operator in ${\mathcal{L}}^2([0,1],[0,\pi ])$. Additionally, if Theorem 4’s presumptions are met, at least one optimal pair of $\left(\mathrm{x}\right(t,\zeta ),\mathbf{u}(t,\zeta \left)\right)$ exists.

Example 2: Filter System. An advanced filter is a system that applies mathematical operations to a digitized sign that has been examined in order to tone down or enhance some of the prepared signal’s highlights. We represented a filter design for our framework, which is depicted in Figure 1 driven by the strategies studied in [47]. A simple block diagram pattern is shown in Figure 1 to help improve the feasibility of an arrangement with the fewest input sources available.

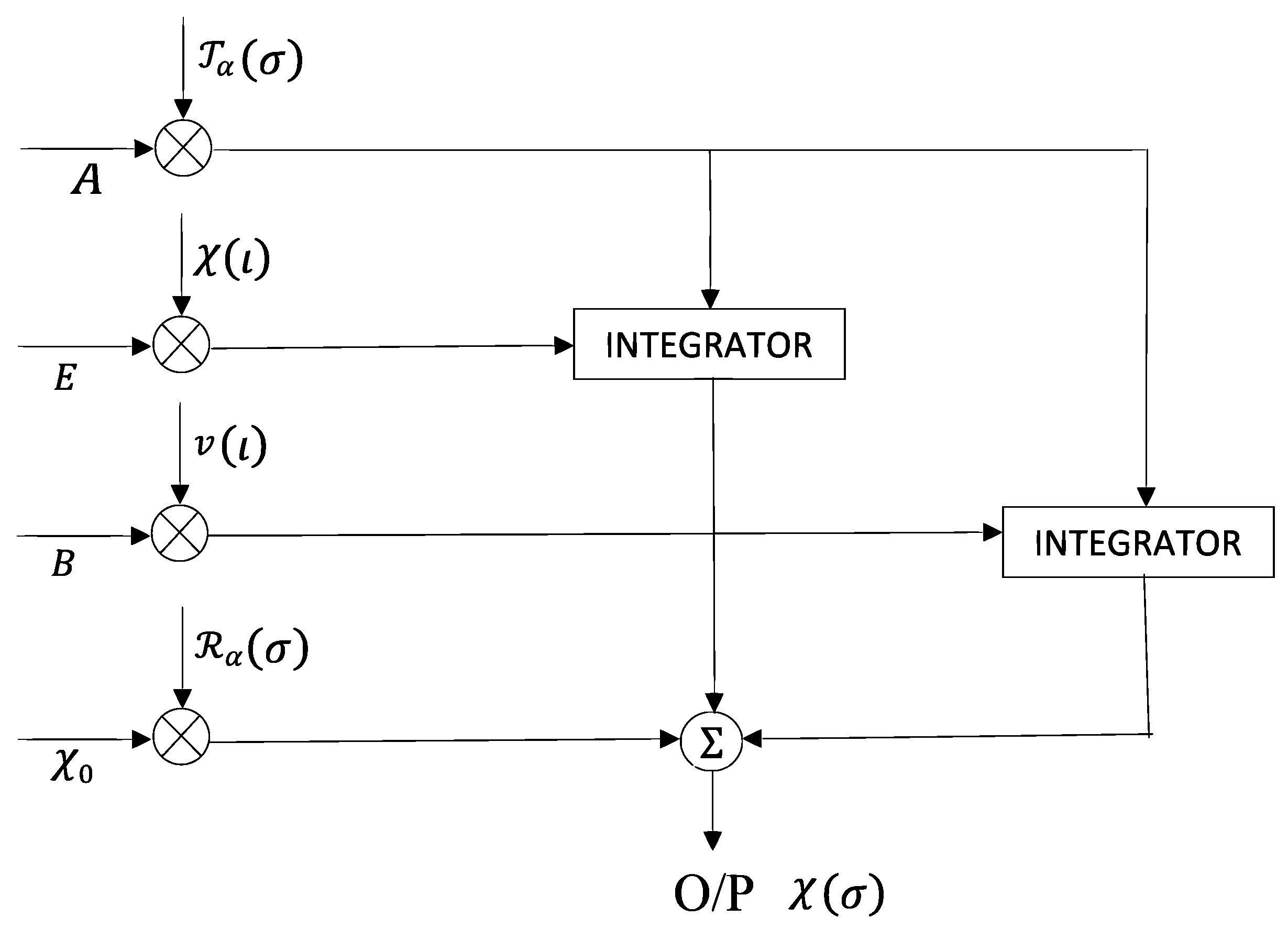
• Modulator Product (MP)-1 acquires the input A, ${\tau }_{\alpha }\left(\sigma \right)$, which represents the output as $A{\tau }_{\alpha }\left(\sigma \right)$.
• (MP)-2 acquires $x\left(\iota \right)$, E, and represents $E(\iota ,\mathrm{x}(\iota \left)\right)$.
• (MP)-3 acquires $v\left(\iota \right)$, B, and represents $Bv\left(\iota \right)$.
• (MP)-4 acquires $x_0$ and ${\mathcal{R}}_{\alpha }\left(\sigma \right)$ at time $\sigma =0$, and represents ${\mathcal{R}}_{\alpha }\left(\sigma \right)x_0$.
• The integral of ${\tau }_{\alpha }\left(\sigma \right)[E(\sigma ,\mathrm{x}\left(\sigma \right))+Bv\left(\sigma \right)]$ is executed by integrators over $\sigma$.
• Inputs ${\tau }_{\alpha }\left(\sigma \right)$ and E are multiplied and come together with an integrator output over $(0,\sigma )$.
• ${\tau }_{\alpha }\left(\sigma \right)$ and B are multiplied and come together over $(0,\sigma )$.

Finally, all integrator signals are sent to a digital network which attains the output $\mathrm{x}\left(t\right)$.

$$\begin{array}{cc}\hfill \mathrm{x}\left(\sigma \right)& ={\mathcal{R}}_{\alpha }\left(\sigma \right){\mathrm{x}}_0+{\int }_0^{\sigma }{\tau }_{\alpha }(\sigma -\iota )E(\iota ,\mathrm{x}\left(\iota \right))d\iota +{\int }_0^{\sigma }{\tau }_{\alpha }(\sigma -\iota )Bv\left(\iota \right)d\iota ,\sigma \in V.\hfill \end{array}$$

Example 3: Traffic Signal Light System. If $(\mathsf{\Omega },\Im ,{\{\Im \mathrm{t}\}}_{t\ge 0},\mathbb{P})$ are complete probability space, then $\{\Im \mathrm{t}\},\mathrm{t}\ge 0$ are natural filters that meet the usual requirement (i.e., they are right continuous and ${\Im }_0$ contains all $\mathbb{P}$-null sets). The family of piecewise right continuous functions $PC([-r,0],{\mathbb{R}}^n)$ is defined as $\varphi$: $[-r,0]\mapsto$${\mathbb{R}}^n$ with respect to $\parallel \varphi \parallel =su{p}_{-r\le u\le 0}\left|\varphi \left(u\right)\right|$, for $r>0$. Let $P{L}_{{\Im }_0}^p([-r,0],{\mathbb{R}}^n)$ denote the family for all ${\Im }_0$-measurable, $PC([-r,0],{\mathbb{R}}^n)$ valued random variables satisfying $su{p}_{-r\le u\le 0}\mathbb{E}{\left|\varphi \left(u\right)\right|}^p<\infty$. Let $\mathbb{E}[.]$ denote the corresponding expectation operator with respect to the probability measure $\mathbb{P}.$ Assume that $B\mathrm{t}=B\left(\mathrm{t}\right)={(B1\left(\mathrm{t}\right),B2\left(\mathrm{t}\right),\dots ,Bm\left(\mathrm{t}\right))}^T$ is an m-dimensional Brownian motion that is specified on the complete probability space. Let $\tau \left(\mathrm{t}\right)$ be a right continuous fBm on the probability space $(\mathsf{\Omega },\Im ,\mathbb{P})$ taking values in a finite state space $S=\{r_1,r_2,...,r_m\}$ with the generator $Q={\left(q_{ij}\right)}_{m\times m}$ given by

$$\mathbb{P}(\tau (t+\Delta \mathrm{t})=r_j|\tau \left(\mathrm{t}\right)=r_i)=\left\{\begin{array}{cc}{q}_{ij}\Delta t+o(\Delta t),& \mathrm{if}i\ne j,\\ 1+q_{ii}\Delta \mathrm{t}+o(\Delta \mathrm{t}),& \mathrm{if}i=j,\end{array}\right.$$

where $\Delta \mathrm{t}>0$. Here, $q_{ij}\ge 0$ is the transition rate from $r_i$ to $r_j$ if $r_i\ne r_j$, while $q_{ii}={\sum }_{j\ne i}{q}_{ij}=-q_i.$ Define ${\xi }_0=0, {\xi }_k=inf\{t>{\xi }_{k-1};\tau \left(t\right)\ne \tau \left({\xi }_{k-1}\right)\}$ and $r\left(n\right)=\tau \left({\xi }_n\right).$ From fBm theory, we know that $\left\{r\right(n),n\in Z\}$ is an fBm. Its transition probability is $r_{ij}^{\left(1\right)}=(1-{\delta }_{ij})\frac{q_{ij}}{q_i}$. Here, we assume that Rossenblatt process $\left\{\tau \right(t),t\ge 0\}$ is independent of the Brownian motion and the fBm.

Electronic Control System: If the volume of the traffic on the route reaches A, the red light is turned on. The green light is on if the vehicle flows below A. With the generator, we define a two-state Rosenblatt chain $\left\{\tau \right(\mathrm{t}),\mathrm{t}\ge 0\}$.

$$Q=\left[\begin{array}{cc}{q}_{11}& q_{12}\\ q_{21}& q_{22}\end{array}\right]$$

{the vehicle flow exceeds A} = {the red light on} = $\{\tau \left(t\right)=r_1\}.$

{the vehicle flow does not exceed A} = {the green light on} = $\{\tau \left(t\right)=r_2\}.$

The electronic control system will receive either the red light or the green light signal. However, the sign transport latency varies depending on the sign brightness. In addition, noise will disturb the electrical control system, making impulsive signals (such as a quick voltage change) inevitable. The electronic control system can be characterized by the following two systems, depending on whether the red light (or the green light) is on:

$$\begin{array}{ccc}\hfill d\mathrm{x}\left(\mathrm{t}\right)& =& f(\mathrm{t},\mathrm{x}\left(\mathrm{t}\right),\mathrm{x}(\mathrm{t}-r_i))d\mathrm{t}+g(\mathrm{t},\mathrm{x}\left(\mathrm{t}\right),\mathrm{x}(\mathrm{t}-r_i))d{B}_{\mathrm{t}},\hfill \\ \hfill \mathrm{x}\left({\mathrm{t}}_k\right)& =& I_k({\mathrm{t}}_k^{-}-r_i,\mathrm{x}({\mathrm{t}}_k^{-}-r_i)),k=1,2,\dots ,\mathrm{t}={\mathrm{t}}_k;\hfill \end{array}$$

where $i=1,2.$ Although the movement of the vehicle is unpredictable, the Rosenblatt chain $\tau \left(\mathrm{t}\right)$ governs the random switching of the electronic control system during the aforementioned two systems.

Example 4: Biological impact of an infinite delay on the human body: After overnight fasting, a patient is called to the hospital for the routine yearly body check-up to measure blood sugar and other diseases caused due to the age factor. Last year, he was diagnozed with the normal lab results, but this time he detected diabetes. The patient was curious to know when exactly the diabetes entered the body with the particular month and date, but the doctor showed insufficiency in answering his question. There is no medical instrument which gives us this information so far. This is the practical example of an infinite time delay problem which we have studied in system (2). During this time, the patient took sweets in his diet very frequently and that resulted in boosting up sugar levels, which is a study of stochastic process.

Remark 5.

Ramkumar et al. [48] studied the river-dam-contamination problem as one of the applications of the stochastic delay system with optimal control. By taking ${\mathfrak{f}}_1=0$, system (35) is converted to [48]. Thus, our system is in the more generalized form.

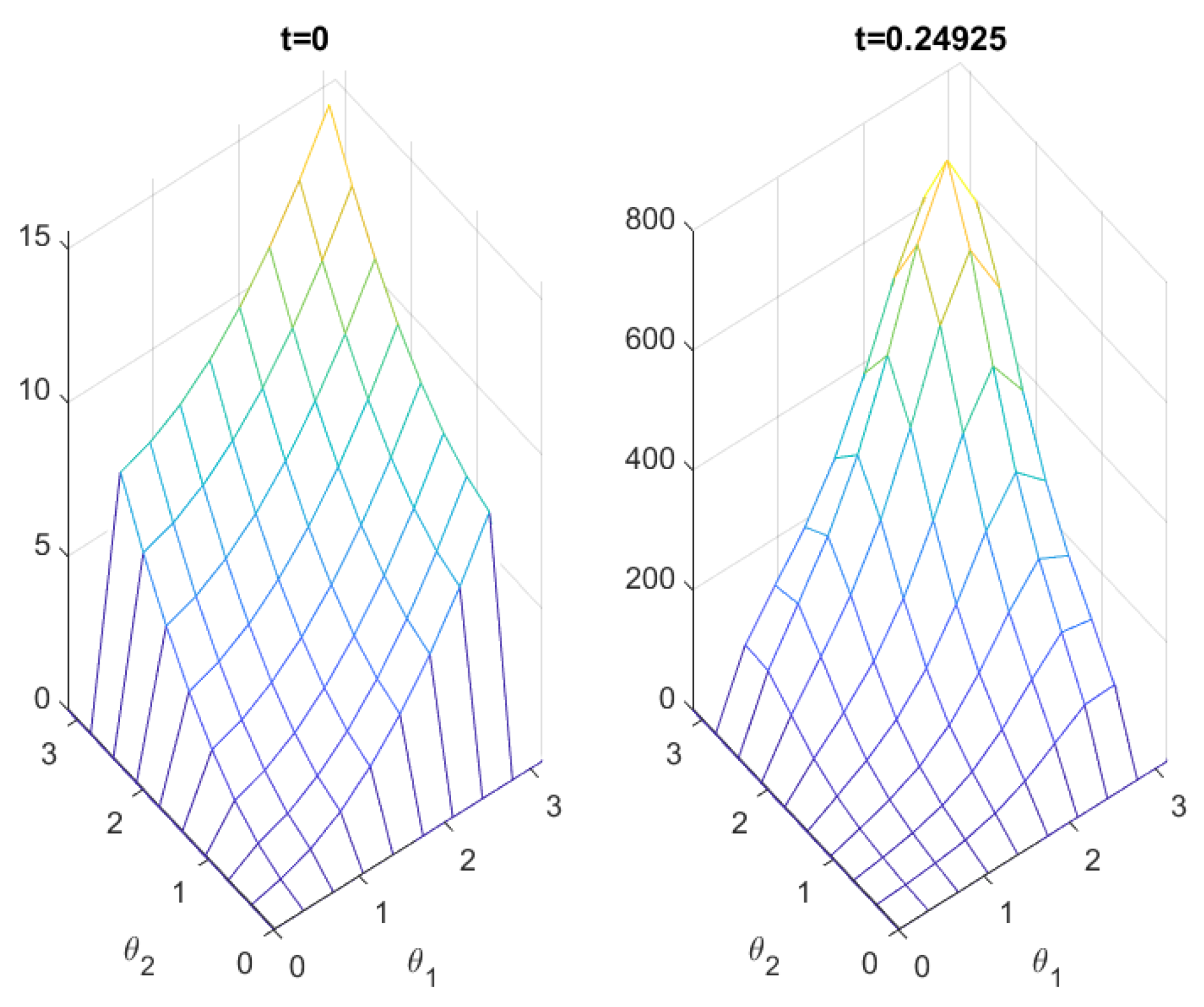
8. Numerical Simulation

In this section, we provide numerical simulations of the application of Equation (38). This example includes several interesting and tricky parts that relate to approximating a numerical solution. If it merely contained a parabolic partial differential equation (PDE), we could solve it using a variety of software packages and the techniques detailed in the cited [38,39] sources. If there was merely a neutral delay term, we could apply the techniques in [40]. All of these elements are represented in this equation along with an integral term.

$$\begin{array}{ccc}\hfill \frac{\partial }{\partial \zeta }\left[\vartheta (\zeta ,\theta )+\frac{{\zeta }^2+e^{\zeta }{\left|\vartheta (\zeta -\phi ,\theta )\right|}^2}{18}\right]& =& \frac{{\partial }^2}{\partial {\theta }^2}\left[\vartheta (\zeta ,\theta )+\frac{{\zeta }^2+e^{\zeta }{\left|\vartheta (\zeta -\phi ,\theta )\right|}^2}{18}\right]\hfill \\ & +& {\int }_0^{\zeta }\tilde{\mathsf{\Lambda }}(\zeta -\zeta )\left[\vartheta (\zeta ,\theta )+\frac{{\zeta }^2+e^{\zeta }{\left|\vartheta (\zeta -\phi ,\theta )\right|}^2}{18}\right]+\mathbf{c}(\zeta ,\theta )\hfill \\ & +& \frac{e^{\zeta }\vartheta (\zeta -\phi ,\theta )/\sqrt{2}+\vartheta (\zeta ,\sin \zeta \left|\vartheta (\zeta ,\theta )\right|)/\sqrt{2}}{9}\hfill \\ & +& \frac{\zeta e^{-\zeta }}{3+e^{\zeta }}\frac{\mathrm{d}{\mathbb{Z}}^{\mathcal{A}}\left(\zeta \right)}{\mathrm{d}\zeta }+{\int }_{e^{\zeta ,\theta \left(t\right)}}\cos \theta \nu \left(\zeta \right)\sqrt{(1-{\eta }^2)}\tilde{N}(dt,dz),\hfill \\ & & \hfill \zeta \in (0,1],\theta \in [0,\pi ],\\ \hfill \vartheta (\zeta ,0)& =& 0,\hfill \\ \hfill \vartheta (\zeta ,\theta )& =& \phi (\zeta ,\theta ),\theta \in [0,\pi ], \zeta \in (-\infty ,0),\eta \in (0,1).\hfill \end{array}$$

(38)

Now we can write

$${\int }_{e^{\zeta ,\theta \left(t\right)}}\cos \theta \nu \left(\zeta \right)\sqrt{(1-{\eta }^2)}\tilde{N}(dt,dz)={\int }_{e^{\zeta ,\theta \left(t\right)}}\cos \theta \nu \left(\zeta \right)\sqrt{(1-{\eta }^2)}\varphi d\zeta d\theta .$$

When $\theta =\frac{\pi }{3},\eta =0.5$ and $\varphi =0.5,$ then by using [49], we have

$${\int }_{e^{\zeta ,\theta \left(t\right)}}\cos \theta \nu \left(\zeta \right)\sqrt{(1-{\eta }^2)}\varphi d\zeta d\theta \le {\left(0.4193\right)}^{2}E{∥\nu ∥}^2=0.1758E{∥\nu ∥}^2,$$

and we know that

$$E{∥\nu ∥}^2\le C.$$

Since (37) with infinite delay and mixed fBm does not yet have an established software suite that can handle all of these components, we created the one using Matlab. The code contains all of the details of the simulation; however, the following are the main methods. The time derivative was made apparent by using a forward finite difference. Each spatial $\theta$ derivative was approximated by a centered difference. The integral term was approximated at each discretization point using the trapezoid rule, which is implemented by the Matlab function trapz.m. Difference derivatives on the mesh were also used to roughly estimate the delayed derivative terms.

The simulations provided (Figure 1 and Figure 2) used the following functions and settings. For each timestep, we used $n=2$ and a total of 400 spatial points, with 20 points in each spatial dimension. We used 5000 timesteps, so $d\iota =0.0002$. The fBm parameter $h=0.7$. The functions are $\varphi (\zeta ,\theta )={\iota }^2+{\sum }_i^n{\theta }_i^2$, $\mathsf{\Lambda }\left(s\right)=\cos \left(s\right)$, and $E{∥\nu ∥}^2\le 0.5$. Figure 2 shows the function at the beginning, when $\iota =0$, and halfway through the experiment. At about the halfway point of the experiment and at the end, Figure 3 shows the simulation.

9. Conclusions

For a class of neutral SIDEs driven by Poisson jumps and Rosenblatt processes utilizing concrete-fading memory-phase space $C\zeta$ defined for the stochastic process, we looked into the optimal control difficulties. Grimmer’s resolvent operator theory, successive approximation, and stochastic analysis theory have all been used to examine the existence and uniqueness of mild solutions. The exponential stability, including mean square exponential stability, is then demonstrated. The best-performing pair of systems demonstrates the solution of exponential stability and their maps and is most likely controlled by stochastic partial integrodifferential equations with infinite delay. In order to support the hypothesis, we created a numerical framework. The code includes all of the simulation information for the Matlab finite difference approach. In this study, theoretical proof and numerical estimates are combined in an original way. The following are the research’s potential future applications:

• The same concept can be expanded utilizing Riemann–Liouville (R-L) and Caputo derivatives for the fractional order/hybrid fractional order system with deviating inputs. Consider the Hilfer fractional system with non-instantaneous impulses and state-dependent delay.
• The new work with the numerical simulation will be the system’s trajectory controllability.
• The Measure of Noncompactness method can be used in place of the technique employed in this paper. Additionally, the same system and several types of fractional order SIDEs can be studied using monotone operator theory.
• The approach of "Integral Contractor with Regularity" can be used to weaken Lipschitz continuity in the nonlinear operators.