Abstract
In this article, we study the fractional SIR epidemic model with the Atangana–Baleanu–Caputo fractional operator. We explore the properties and applicability of the ZZ transformation on the Atangana–Baleanu–Caputo fractional operator as the ZZ transform of the Atangana–Baleanu–Caputo fractional derivative. This study is an application of two power methods. We obtain a special solution with the homotopy perturbation method (HPM) combined with the ZZ transformation scheme; then we present the problem and study the existence of the solution, and also we apply this new method to solving the fractional SIR epidemic with the ABC operator. The solutions show up as infinite series. The behavior of the numerical solutions of this model, represented by series of the evolution in the time fractional epidemic, is compared with the Adomian decomposition method and the Laplace–Adomian decomposition method. The results showed an increase in the number of immunized persons compared to the results obtained via those two methods.
Keywords:
Atangana–Baleanu–Caputo fractional operator; homotopy perturbation method; ZZ integral transform; fractional SIR epidemic model MSC:
26A33; 35A24; 65R10; 35E15
1. Introduction
Fractional calculus plays a fundamental role in modeling many problems in fluid mechanics, acoustics and electromagnetism, as well as studying some phenomena of dynamic systems [1,2,3,4,5]. Fractal calculus is very effective, for example, in dealing with phenomena in hierarchical or porous media [6]. In the study just cited, J-H He touched on the basic concept of the fractal gradient of temperature to reveal the basic properties of calculus and then the fractal velocity and the derivative of the fractal material were introduced to derive the laws of fluid mechanics and thermal conductivity in fractal space. Many studies use different fractional operators to describe certain phenomena in physics, engineering and biology [7,8,9]. For example, in [10], He et al. present the definition of a new fractional derivative by demonstrating its application in explaining the excellent thermal protection of polar bear hair so that the fractal porosity of its internal structure makes the polar bear mathematically adapted to live in the harsh Arctic region. Recently, many classifications of fractional operators have been proposed, for example, Caputo, Riemann–Liouville, Caputo–Fabrizio, Atangana–Baleanu–Caputo fractional operators, to accurately and successfully study and describe complex phenomena in science and engineering [11,12].
In the recent past, definitions of fractional derivatives based on nonsingular kernels, like the Atangana–Baleanu fractional derivative, were also provided. Additionally, some models of dissipative events cannot be fully characterized by a single fractional operator, which highlights the significance of fractional derivatives with nonsingular kernels. Material heterogeneities and some structures or media with varying scales can be depicted using the Atangana–Baleanu operator. The new kernel’s nonlocality enables a better representation of memory within structures and media with various scales. Additionally, we may state that this derivative can play a particular role in the investigation of some materials’ macroscopic behavior in relation to nonlocal exchanges, which are crucial for characterizing a material’s properties. Therefore, the Atangana–Baleanu–Caputo fractional derivative is the most general fractional operator based on the Mittag–Leffler function, which is more suitable for describing real-world complex problems [13].
In [14], the authors take the advantages of the Atangana–Baleanu partial integral operator and the Bessel functions, some differential dependency results were extracted and the work was developed for the case of the analytical functions specified on the open unit disk. The applications of the Atangana–Baleanu fractional integral were considered in recent studies related to geometric function theory to obtain interesting differential subordinations, etc.; see [15,16,17,18].
These complex problems have been studied in the literature, and are divided into linear and nonlinear, as they have aroused the interest of many researchers who study their behavior in terms of solvability, uniqueness and the stability of their solutions, especially nonlinearity [19,20,21]. Due to the complexities of nonlinear phenomena in searching for their solutions by modeling them into ordinary or fractional differential equations, they do not always contain accurate analytical solutions. Because of this difficulty, researchers have focused their attention on developing several numerical methods to find an approximate solution. There are many techniques employed to search for the numerical solution of the linear or nonlinear fractional differential equations, integral equations and the linear or nonlinear systems of fractional differential equations. Since the integral transformations, such as the Laplace transform, Sumudu transform, and so on, could not solve the nonlinear types, we therefore note that many mathematicians have studied the methods of solving nonlinear differential equations or nonlinear fractional differential systems. Among these methods, we cite a more effective method called the homotopy perturbation method (HPM) [22,23] and a modified Laplace transform to solve some nonlinear differential equations such as the case of the ZZ transform. This integral transform generalizes a few well-known transformations that are connected to other well-known transformations. To obtain the natural transformation, divide the ZZ transformation by the adjusted variable. The ZZ transform can be used to address problems without switching to a new frequency domain and to provide new, iterative results since it has the ability to preserve the scale and the unity, and the ZZ transform is useful for solving fractional differential equations with variable coefficients [24,25,26].
Thus, we find that some researchers are working on a combination of analytical or semi-analytical methods with certain integral transformations [27,28,29,30]. The HPM method involves dividing the solution domain into sub-domains and transforming the FPDEs into a set of algebraic equations. These equations are then solved by using other numerical methods. The solution is then transformed back to the original domain and the solution is obtained by combining the solutions from each sub-domain.
The homotopy perturbation method has been coupled with the ZZ transform (HPZZTM) to facilitate the process of solving ordinary differential equations and partial derivatives of integer order or fractional order [31]. This combination has also been applied to solve systems of nonlinear partial differential equations of fractional order. This method combines the advantages of both the HPM and the ZZ Transform methods [23].
The aim of this work is to investigate the properties of the ZZ transformation on the Atangana–Baleanu–Caputo fractional derivative; consequently, we combined it with the homotopy perturbation method and applied this new technique to the linear and nonlinear general fractional differential non-homogeneous equations, especially to the following fractional SIR epidemic model with the Atangana–Baleanu–Caputo fractional operator:
Many studies have been tried to resolve the SIR epidemic model of integer order; in [32], by using the homotopy analysis method; in [33], an exact solution was suggested via the homotopy perturbation method; and the differential transform method in [34]. Recently, A. Qazza and R. Saadeh presented the solution of the fractional SIR epidemic model with a Caputo fractional derivative by using the Laplace residual-power-series method in [35].
This epidemic mathematical model is known as the Susceptible-Infected-Recovered model (SIR) ([36,37]). Concerning the SIR model, it is assumed that in the presence of Infectious Disease A, a fixed population size can be divided into three groups, that is, (), (I) and (R), respectively. Specifically, the compartments used in the McKendrick–Kermack design are defined as follows [38]:
(a) Compartment () (susceptible) includes persons of the total population not yet infected by the disease at time ⊺, or those who are susceptible to the disease. The number of persons in that compartment corresponds to .
(b) Compartment () (infected) is composed of persons who have been infected by the epidemic disease and who may transmit the disease to those in the sensitive category. The number of persons in that compartment corresponds to .
(c) Compartment (ℜ) (recovered) is composed of individuals who have been infected during outbreaks and have fully recovered. The number of persons in that compartment corresponds to . They cannot be infected again and they are unable to pass the disease on to others.
The paper is organized as follows: In Section 2, we present some basic tools in the form of definitions, properties of the fractional calculus and ZZ transform. In Section 3, we introduce the main results of the homotopy perturbation method coupled with the ZZ transform to the general nonlinear fractional differential equations. In Section 4, we apply this method to the fractional SIR epidemic model with the Atangana–Baleanu–Caputo fractional operator. In Section 5, we show the numerical results and discussion. Finally, we conclude our research in the final section.
2. Basic Definitions
Definition 1.
Let , , ; then, the Atangana–Baleanu fractional derivative in the Caputo sense [13,39] is given as:
where the kernel is the Mittag–Leffler function of one parameter and is a normalization function such that [40].
Definition 2.
The fractional integral of order σ of a new fractional derivative is defined by:
Here is the Euler Gamma function.
2.1. Definitions and Properties of the ZZ Transform
We give some basic definitions and properties of the ZZ transform (see [24,25]).
Throughout, set
and suppose that is an integrable function defined on the set .
Definition 3.
Let be a function defined for all . The ZZ transform of is the function defined by
The integral transform (4) exists for all .
2.1.1. Some Properties of the ZZ Transform
Theorem 1.
The ZZ transform of the derivative of is given by
Theorem 2.
The ZZ transform of convolution of functions and
Moreover,
Proof.
We have
Using the ZZ transform and the Leibniz theorem, we obtain
By setting , we obtain
Furthermore, the convolution of the inverse transform is
Hence,
□
2.1.2. ZZ Transform of Several Elementary Functions
In this following table, we will give the transformation of some elementary functions by the ZZ Transform.
| ine 1 | 1 |
| ine ⊺ | |
| ine | , |
| ine |
Lemma 1.
Let and such that ; then,
Proof.
We have
Since , the result is that
□
Corollary 1.
In the same way as in the last Lemma 1, we obtained the ZZ transform of the function as:
and the ZZ transform of the function as:
Theorem 3.
The ZZ transform of the Atangana–Baleanu–Caputo fractional derivative is defined as:
3. Implementation of HPZZTM to the General Nonlinear Fractional Differential Equations
We present the basic idea of the homotopy perturbation ZZ transform method, so we consider the following general nonlinear fractional partial differential non-homogeneous equation
with the initial terms
where R is the differential linear operator, N is the nonlinear operator and is the source terms.
When we apply the ZZ transformation on either side of (15), we obtain
Using this transformation’s differentiating characteristic, we have
Consider the reverse ZZ transformation on each side of (18) and then according to (16), we obtain
where the terms are the non-homogeneous terms and the previously established conditions. Now, we apply the perturbation technique ([22,41]). We express the solution with this technique as a power series in , as shown below
We break down the nonlinear term into
where are the polynomials of He [23], which are calculated with the following formulas
By substituting (20) and (21) into Equation (19), we obtain
This is a coupling of the homotopy perturbation method and the ZZ transform (HPZZTM).
Now, by matching both sides of Equation (23) with respect to the power of , we obtain the following first terms of the solution
Finally, the approximate solution is calculated by
In [42,43], it has been established that this series converges.
4. Study the Epidemic Model with Atangana–Baleanu–Caputo Fractional Derivative
4.1. Presentation of the Problem
The problem of the spread of a disease in a supposed population of constant size during the period of the epidemic is examined in [44].
At time ⊺, suppose the population consists of susceptible population: the population not infected to date and subject to the infection.
represent the infected population: those who have the disease and are still at large.
represents the recovered population: those who have recovered and have therefore become immune.
Suppose there is a constant rate between and which causes the transmission. Then, over time , become infectious, or
If is the isolation rate of the current infected population, then
The number of new isolated population is given by
Now , then the following system determines the progress of the disease:
4.2. The Existence of the Solution
Lemma 2.
The function F is Lipschitz continuous on , with
so there exists a constant and
with being the Manhattan norm.
Proof.
We shall prove that the function F satisfies the Lipschitz condition in the second argument .
and we have
In the same way, we can prove that
Then
where
□
4.3. The Solution by Applying This Approach
In the second, we take the inverse ZZ transform for both sides of (33) and using the initial conditions, we have
Now, we represent the solutions as the following infinite series
and the nonlinear terms as
The first elements of He’s polynomials are provided by
And
Also
5. Numerical Results and Discussion
For the comparison with the results of Biazar [45,46], we consider the following values:
;
Initial population of , who are susceptible;
Initial population of , who are infected;
Initial population of , who are recovered;
Rate of change from susceptible population to infected population;
Rate of change from infected population to recovered population.
The three-term approximations for , and are calculated and presented below.
These results (43) are illustrated in Figure 1; as shown in the graphs, the number of infected persons increases and then is followed by a decrease in the number of susceptible people during the period of the epidemic; during this time of epidemic, the number of people immunized increases compared to the results of the number of immune population obtained via the Adomian decomposition method and the Laplace–Adomian decomposition method (see graphs 1, 2 and 3 of [45] and the graphs 1 and 2 and the table of [46]). Comparing the results obtained via HPZZTM with those obtained via ADM in [45] and L-ADM in [46] shows that the results of the three-term approximations of HPZZTM are the same as the results of the three-term approximations of ADM and L-ADM. Hence, we conclude that this method has proven successful in this epidemic model (Figure 2, Figure 3 and Figure 4).
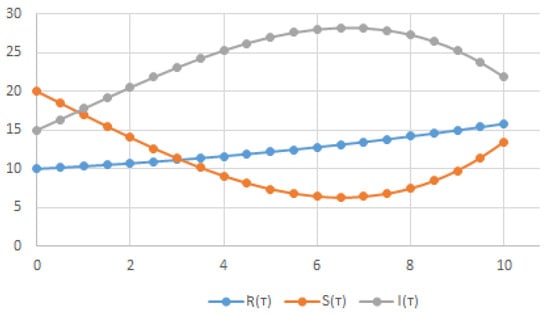
Figure 1.
The three-term approximations for , and .
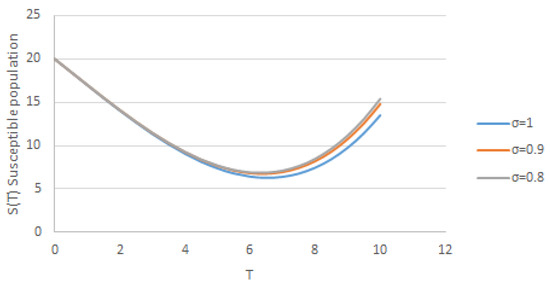
Figure 2.
Nature of solution with respect to time for different values of .
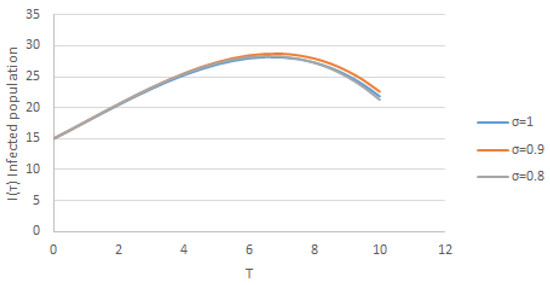
Figure 3.
Nature of solution with respect to time for different values of .
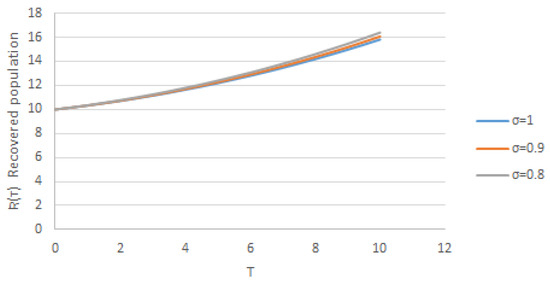
Figure 4.
Nature of solution with respect to time for different values of .
6. Conclusions
The study presented in this paper is an investigation of the properties of the ZZ transform with respect to the Atangana–Baleanu–Caputo fractional operator; additionally, we combined the homotopy perturbation method with the ZZ integral transform, which is called the homotopy perturbation ZZ transform method (HPZZTM). This method was also used to solve the linear and nonlinear general fractional differential non-homogeneous equations, especially the fractional SIR epidemic model with the Atangana–Baleanu–Caputo fractional operator. Therefore, this new method is easy to apply to reach the desired results, as illustrated with the help of the presented model through the results obtained; it was also compared with the Adomian decomposition method and the Laplace–Adomian decomposition method. The HPZZTM method has proven its effectiveness and potential in solving these types of equations and it enabled us to obtain the exact solution in a faster way than the classical methods such as ADM and L-ADM presented in [45,46]; this is what the results showed as the number of immunized persons increased compared to the results obtained via these two methods. The ease of use and the strength of this method in achieving a solution is evidence of its speed in solving the example presented in this work or other linear or nonlinear problems.
Author Contributions
Writing—original draft, L.R., M.H.C. and C.C.; Writing—review & editing, L.R., M.H.C. and C.C. The authors equally contributed to writing this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ray, S.S.; Atangana, A.; Noutchie, S.C.O.; Kurulay, M.; Bildik, N.; Kilicman, A. Fractional Calculus and Its Applications in Applied Mathematics and Other Sciences. Math. Probl. Eng. 2014, 2014, 849395. [Google Scholar] [CrossRef]
- Jacob, J.S.; Priya, J.H.; Karthika, A. Applications of fractional calculus in science and engineering. J. Crit. Rev. 2020, 7, 4385–4394. [Google Scholar]
- Fellah, Z.E.A.; Fellah, M.; Ongwen, N.O.; Ogam, E.; Depollier, C. Acoustics of Fractal Porous Material and Fractional Calculus. Mathematics 2021, 9, 1774. [Google Scholar] [CrossRef]
- Siddique, I.; Mirza, A.M.; Shahzadi, K.; Akbar, M.A.; Jarad, F. Diverse Precise Traveling Wave Solutions Possessing Beta Derivative of the Fractional Differential Equations Arising in Mathematical Physics. J. Funct. Spaces 2022, 2022, 5613708. [Google Scholar] [CrossRef]
- Nadeem, M.; Wahash, H.A. Analysis of Fractional Kundu-Eckhaus and Massive Thirring Equations Using a Hybridization Scheme. J. Funct. Spaces 2023, 2023, 6704537. [Google Scholar] [CrossRef]
- He, J.H. Fractal calculus and its geometrical explanation. Results Phys. 2018, 10, 272–276. [Google Scholar] [CrossRef]
- Baleanu, D.; Mohammadi, H.; Rezapour, S. A fractional differential equation model for the COVID-19 transmission by using the Caputo-Fabrizio derivative. Adv. Differ. Equ. 2020, 2020, 299. [Google Scholar] [CrossRef]
- Amara, A.; Etemad, S.; Rezapour, S. Approximate solutions for a fractional hy-brid initial value problem via the Caputo conformable derivative. Adv. Differ. Equ. 2020, 2020, 608. [Google Scholar] [CrossRef]
- Shah, N.A.; Alyousef, H.A.; El-Tantawy, S.A.; Shah, R.; Chung, J.D. Analytical investigation of fractional-order Korteweg-De-Vries-Type equations under Atan-gana-Baleanu-Caputo operator: Modeling nonlinear waves in a plasma and fluid. Symmetry 2022, 14, 739. [Google Scholar] [CrossRef]
- He, J.H.; Li, Z.B.; Wang, Q.L. A new fractional derivative and its application to explanation of polar bear hairs. J. King Saud Univ. Sci. 2016, 28, 190–192. [Google Scholar] [CrossRef]
- He, J.H.; Elagan, S.K.; Li, Z.B. Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus. Phys. Lett. A 2012, 376, 257–259. [Google Scholar] [CrossRef]
- MAl-Refai, M.; Baleanu, D. On an extension of the operator with Mittag-Leffler kernel. Fractals 2021, 12, 22401296. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non singular kernel: Theory and application to heat transfer model. Ther. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Catas, A.; Lupas, A.A. Some Subordination Results for Atangana–Baleanu Frac-tional Integral Operator Involving Bessel Functions. Symmetry 2022, 14, 358. [Google Scholar] [CrossRef]
- Alqahtani, R.T. Atangana–Baleanu derivative with fractional order applied to the model of groundwater within an unconfined aquifer. J. Nonlinear Sci. Appl. 2016, 9, 3647–3654. [Google Scholar] [CrossRef]
- Syam, M.I.; Al-Refai, M. Fractional differential equations with Atangana–Baleanu fractional derivative: Analysis and applications. Chaos Solitons Fractals X 2 2019, 2, 100013. [Google Scholar] [CrossRef]
- Lupas, A.A.; Catas, A. Applications of the Atangana–Baleanu Fractional Integral Operator. Symmetry 2022, 14, 630. [Google Scholar] [CrossRef]
- Lupas, A.A.; Catas, A. Properties of a Subclass of Analytic Functions Defined by Using an Atangana–Baleanu Fractional Integral Operator. Symmetry 2022, 14, 649. [Google Scholar] [CrossRef]
- Chikh, S.B.; Amara, A.; Etemad, S.; Rezapour, S. On Hyers-Ulam stability of a multi-order boundary value problems via Riemann-Liouville derivatives and integrals. Adv. Differ. Equ. 2020, 2020, 547. [Google Scholar] [CrossRef]
- Rezapour, S.; Imran, A.; Hussain, A.; Martinez, F.; Etemad, S.; Kaabar, M.K.A. Condensing Functions and Approximate Endpoint Criterion for the Existence Analysis of Quantum Integro-Difference FBVPs. Symmetry 2021, 13, 469. [Google Scholar] [CrossRef]
- Mukhtar, M.; Yaqoob, M.; Samraiz, M.; Shabbir, I.; Etemad, S.; De la Sen, M.; Re-zapour, S. Novel Mean-Type Inequalities via Generalized Riemann-Type Fractional Integral for Composite Convex Functions: Some Special Examples. Symmetry 2023, 15, 479. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of homotopy technique and perturbation technique for nonlinear problems. Int. J. Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Meth. Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Zafar, Z.U.A. Application of ZZ Transform Method on Some Fractional Differential Equations. Int. J. Adv. Eng. Glob. Technol. 2016, 4, 1355–1363. [Google Scholar]
- Zafar, Z.U.A. ZZ Transform Method. Int. J. Adv. Eng. Glob. Technol. 2016, 4, 1605–1611. [Google Scholar]
- Areshi, M.; Naeem, M.; Wyal, N. Analytical Investigation of Some Dy-namical Systems by ZZ Transform with Mittag-Leffler Kernel. Complexity 2022, 2022, 7635696. [Google Scholar] [CrossRef]
- Gihan, E.H.A.; Asaad, A.A.; Elagan, S.K.; Mawaheb, E.-A.; AlDien, M.S. Using Laplace transform method for obtaining the exact analytic solutions of some ordinary fractional differential equations. Glob. J. Pure Appl. Math. 2017, 13, 5021–5035. [Google Scholar]
- Watugala, G.K. Sumudu transform: A new integral transform to solve differen-tial equations and control engineering problems. Int. J. Math. Educ. Sci. Technol. 1993, 24, 35–43. [Google Scholar] [CrossRef]
- Maitama, S.; Zhao, W. New Integral Transform: Shehu Transform a Generaliza-tion of Sumudu and Laplace Transform for Solving differential equations. Int. J. Anal. Appl. 2019, 17, 167–190. [Google Scholar]
- Al-Hayani, W. Combined Laplace Transform-Homotopy Perturbation Method for Sine-Gordon Equation. Appl. Math. Inf. Sci. 2016, 10, 1781–1786. [Google Scholar] [CrossRef]
- Riabi, L.; Belghaba, K.; Cherif, M.H.; Ziane, D. Homotopy Perturbation Method Combined with ZZ Transform To Solve some Nonlinear Fractional Differential Equations. Int. J. Anal. Appl. 2019, 17, 406–419. [Google Scholar]
- Khan, H.; Mohapatra, R.N.; Vajravelu, K.; Liao, S.J. The explicit series solution of SIR and SIS epidemic models. Appl. Math. Comput. 2009, 215, 653–669. [Google Scholar] [CrossRef]
- Shabbir, G.; Khan, H.; Sadiq, M.A. A note on exact solution of SIR and SIS epidemic models. arXiv 2010, arXiv:1012.5035. [Google Scholar]
- Abubakar, S.; Akinwande, N.I.; Jimoh, O.R.; Oguntolu, F.A.; Ogwumu, O.D. Approximate solution of SIR infectious disease model using homotopy perturbation kethod (HPM). Pac. J. Sci. Technol. 2013, 14, 163–169. [Google Scholar]
- Qazza, A.; Saadeh, R. On the Analytical Solution of Fractional SIR Epidemic Model. Appl. Comput. Intell. Soft Comput. 2023, 2023, 6973734. [Google Scholar] [CrossRef]
- Ammi, M.R.S.; Tahiri, M.; Torres, D.F.M. Global stability of a Caputo fractional SIRS model with general incidence rate. Math. Comput. Sci. 2021, 15, 91–105. [Google Scholar] [CrossRef]
- Ammia, M.R.S.; Tahirib, M.; Torres, D.F.M. Local existence and uniqueness for a fractional SIRS model with Mittag-Leffler law. Gen. Lett. Math. 2021, 10, 61–71. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A 1927, 115, 700–721. [Google Scholar]
- Atangana, A.; Koca, I. Chaos in a simple nonlinear system with Atangana–Baleanu derivatives with fractional order. Chaos Solitons Fractals 2016, 89, 447–454. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Biazar, J.; Ghazvini, H. Convergence of the homotopy perturbation method for partial differential equations. Nonlinear Anal. 2009, 10, 2633–2640. [Google Scholar] [CrossRef]
- Ayatia, Z.; Biazar, J. On the convergence of Homotopy perturbation method. J. Egypt. Math. Soc. 2015, 23, 424–428. [Google Scholar] [CrossRef]
- Eshkuvatov, Z.K.; Zulkarnain, F.S.; Muminov, Z.; Asri, N.M.; Long, N. Convergence of modified homotopy perturbation method for Fredholm-Volterra integro-differential equation of order m. Malays. J. Fundam. Appl. Sci. 2017, 13, 340–345. [Google Scholar] [CrossRef]
- Jordan, D.W.; Smith, P. Nonlinear Ordinary Differential Equations, 3rd ed.; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Biazar, J. Solution of the epidemic model by Adomian decomposition method. Appl. Math. Comput. 2006, 173, 1101–1106. [Google Scholar] [CrossRef]
- Rida, S.Z.; Arafa, A.A.M.; Gaber, Y.A. Solution of the Fractional Epidemic Model by L-ADM. J. Fract. Calc. Appl. 2016, 7, 189–195. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).