Finite Time Stability Results for Neural Networks Described by Variable-Order Fractional Difference Equations

Abstract

Variable-order fractional discrete calculus is a new and unexplored part of calculus that provides extraordinary capabilities for simulating multidisciplinary processes. Recognizing this incredible potential, the scientific community has been researching variable-order fractional discrete calculus applications to the modeling of engineering and physical systems. This research makes a contribution to the topic by describing and establishing the first generalized discrete fractional variable order Gronwall inequality that we employ to examine the finite time stability of nonlinear Nabla fractional variable-order discrete neural networks. This is followed by a specific version of a generalized variable-order fractional discrete Gronwall inequality described using discrete Mittag–Leffler functions. A specific version of a generalized variable-order fractional discrete Gronwall inequality represented using discrete Mittag–Leffler functions is shown. As an application, utilizing the contracting mapping principle and inequality approaches, sufficient conditions are developed to assure the existence, uniqueness, and finite-time stability of the equilibrium point of the suggested neural networks. Numerical examples, as well as simulations, are provided to show how the key findings can be applied.

1. Introduction

Fractional operators are fundamentally multi-scale because of their differ-integral character. Whereas time fractional operators support memory impacts, space fractional operators may accommodate the impacts of non-locality and scale. In the past decade, a surge in attention to fractional-order operators and their applicability to physical issue modeling has emerged (see [1,2,3,4,5,6,7]). Despite the fact that fractional calculus theory could address many critically important physical problems, it cannot depict important sets of physical events whose order is governed by dependent or independent factors. Variable-order operators are an analytic generalization of fractional operators. The order of integration variables like time, space, or even a distinct external variable can vary constantly in variable order operators. Variable fractional calculus has witnessed an increase in attention and many different applicabilities related to the simulation of scientific and engineering systems throughout the last decade [8,9,10].

Several mathematicians have expressed a strong interest in discrete fractional calculus in the past few years. For the fractional backward or nabla difference, we call your attention to [11,12,13]. However, academics’ interest in discrete variable order fractional calculus, which is the equivalent of variable fractional calculus, has increased in popularity throughout the last several years, despite the fact that few publications have been published [14,15,16,17,18].

Many features of differential and difference equations are investigated using mathematical inequalities. The Gronwall inequality, which is the focus of this paper, has been developed for fractional differential equations [19,20]. Nonetheless, research on the Gronwall inequality for fractional difference equations is uncommon [21,22]. Prior to studying the qualitative features of different forms of differential or difference equations, Many researchers concentrated on the presence and uniqueness of solutions as an essential use of Gronwall inequality. Many recent studies on the existence, uniqueness, and stability of solutions for differential equations with fractional order were published [23,24]. Furthermore, various effective and long-term results concerning the dynamic behavior of solutions for difference equations with fractional order were established [25,26]. However, according to the researchers, there is minimal study on this behavior for variable-order fractional difference equations.

The major issue in many real systems is the system’s behavior over a finite timeframe [27]. The standard Lyapunov approach is inapplicable in this circumstance. As a consequence, the finite-time stability technique is presented. When a system’s initial condition is stated, if the system’s state variable is within a defined constraint in a given time interval, the system is finite-time stable [28]. In comparison to the classic Lyapunov technique, the finite-time stability approach seems to be more realistic and less conservative. There have been several publications on the finite-time stability of difference equations with fractional order. As an example, in [29], a finite-time convergence criteria for Caputo delta difference equations was established applying Gronwall inequality. Other works regarding this type of stability may be found in [30,31].

Neural networks that are characterized by non-integer-order differential operators are a significant class of non-integer-order dynamical systems. Numerous studies have been performed to examine the dynamics of these systems. For instance, in [32], the bifurcation of a fractional-order BAM neural network with mixed time delays was investigated. Additionally, the bifurcation behavior of delayed BAM neural networks with both integer and fractional orders was studied in [33]. Bifurcation dynamics and control mechanisms of tri-neuron bidirectional associative memory neural networks, including delay, were covered in [34]. Furthermore, a new perspective on the bifurcation of fractional-order 4D neural networks with two distinct time delays was explored in [35]. The stability and bifurcation analysis of a fractional predator-prey model with two non-identical delays were examined in [36]. Merging discrete fractional calculus with neural networks has been shown in recent years to improve overall model efficiency. In comparison to traditional discrete neural networks, fractional discrete neural networks efficiently capture the features of neurons, such as memory and heritability, in many systems. Because fractional-order systems have limitless memory, they are extremely effective. It needs to be highlighted as well that the computation capabilities of fractional discrete neural networks enable efficient data processing, stimulus prediction, and phase shift during oscillatory neuron firing. Consequently, the discrete fractional-order version of neural networks has proven an outstanding and strong tool in different computing domains. Several studies have been undertaken with the examination of the dynamics of fractional discrete neural networks, As an example, in [37], a type of semi-linear fractional difference equations was proposed, and the fixed point concept was used to determine some stability criteria, with finite-time stability addressed and contrasted as an application. In [38], certain suitable delay-dependent conditions were inferred to verify the solution’s existence and finite-time stability of a suggested neural network. In [39], a variable-order discrete neural network was described, and two unique theorems on the solution’s existence and Ulam-Hyers stability were demonstrated. In [40], new theorems on the asymptotic stability of variable-order nabla systems and variable-order nabla neural networks were illustrated. For more references, one can refer to [41,42,43,44].

The goal of this study is to advance previously investigated models by providing more in-depth understanding of the various dynamics of variable-order fractional discrete neural networks. The formation of variable-order fractional discrete-time neural networks is followed by the presentation of the first generalized variable-order discrete Gronwall inequality in terms of the Nabla variable-order fractional difference sum operator, followed by the establishment of the necessary and sufficient conditions for its finite-time stability with the help of the noval variable-order discrete Gronwall inequality and the fixed point technique. Following is an outline of the paper in the following order:

• We present a new theorem concerning the Gronwall inequality for generalized variable-order discrete using the Caputo Nabla fractional variable-order operator.
• We introduce novel variable-order fractional discrete neural networks.
• The uniqueness of the solution of the system under consideration was examined with the help of the contracting mapping principle and inequality approaches.
• The stability of variable-order fractional discrete neural networks is addressed, and a finite-time stability approach is used.
• Numerical simulations are illustrated to reflect theoretical conclusions.

The following is how the paper is managed: Section 2 introduces certain definitions and features of fractional variable-order discrete calculus. Section 3 provides a modified variable-order fractional discrete Gronwall inequality that extends and improves on the current ones. Its applications to the uniqueness as well as finite-time stability of variable-order fractional discrete neural networks are discussed in Section 4. Section 5 includes various examples to show how the theoretical findings may be applied. Finally, in Section 6, conclusions are reached.

2. Mathematical Background

This section defines multiple concepts related to fractional as well as variable discrete calculus.

Given ${\mathfrak{r}}_0,\hspace{1em}T\in \mathbb{R}$, We use the designation ${\mathbb{N}}_{{\mathfrak{r}}_0}=\{{\mathfrak{r}}_0,\hspace{1em}{\mathfrak{r}}_0+1,\hspace{1em}{\mathfrak{r}}_0+2,\hspace{1em}\dots \}$ and ${\mathbb{N}}_{{\mathfrak{r}}_0}^T=\{{\mathfrak{r}}_0,\hspace{1em}{\mathfrak{r}}_0+1,\hspace{1em}{\mathfrak{r}}_0+2,\hspace{1em}\dots ,\hspace{1em}T\}.$

Definition 1

([45]). Let $\mathit{\ell }:{\mathbb{N}}_{{\mathfrak{r}}_0+1}\to \mathbb{R}\mathrm{and}0<\delta \le 1$ be provided. The $\delta -$th order is determined by

$${}_{{\mathfrak{r}}_0}{\nabla }_{\mathfrak{r}}^{-\delta }\mathit{\ell }\left(\mathfrak{r}\right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left({\delta }_{}\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{{\delta }_{}-1}}\mathit{\ell }\left(\mathfrak{s}\right),\hspace{1em}\rho \left(\mathfrak{r}\right)=\mathfrak{r}-1,\hspace{1em}\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1},\hspace{1em}$$

(1)

where

$${\mathfrak{r}}^{\overline{\delta }}={\displaystyle \frac{\mathrm{\Gamma }(\mathfrak{r}+\delta )}{\mathrm{\Gamma }\left(\mathfrak{r}\right)}},\hspace{1em}\mathfrak{r},\hspace{1em}\delta \in \mathbb{R},\hspace{1em}$$

(2)

while the gamma function Γ is represented as follows:

$$\mathrm{\Gamma }\left({\delta }_{}\right)={\int }_0^{\infty }{\mathfrak{r}}^{{\delta }_{}-1}{exp}^{-\mathfrak{r}}d\mathfrak{r}.$$

(3)

Definition 2

([45]). Consider $\mathit{\ell }\left(\mathfrak{r}\right)$ determined on ${\mathbb{N}}_{{\mathfrak{r}}_0+1}$ and $0<\delta \le 1$. The Caputo nabla difference is identified by:

$${}_{{\mathfrak{r}}_0}^C{\nabla }^{\delta }\mathit{\ell }\left(\mathfrak{r}\right)={\nabla }_{{\mathfrak{r}}_0}^{-(m-\delta )}{\nabla }^m\mathit{\ell }\left(\mathfrak{r}\right),\hspace{1em}\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1},\hspace{1em}$$

(4)

If $m=1$, then what follows occurs

$${}_{{\mathfrak{r}}_0}^C{\nabla }^{\delta }\mathit{\ell }\left(\mathfrak{r}\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(1-{\delta }_{})}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{-\delta }}\nabla \mathit{\ell }\left(\mathfrak{s}\right),\hspace{1em}\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1},\hspace{1em}$$

(5)

while

$$\nabla \mathit{\ell }\left(\mathfrak{r}\right)=\mathit{\ell }\left(\mathfrak{r}\right)-\mathit{\ell }(\mathfrak{r}-1).$$

(6)

Definition 3

([45]). Given $\mu \in \mathbb{R},\hspace{1em}|\mu |<1$ and $\theta ,\hspace{1em}\beta ,\hspace{1em}\mathfrak{r}\in \mathbb{C},\hspace{1em}$ with $Re\left(\theta \right)>0,\hspace{1em}$ the discrete nabla Mittag–Leffler function is described by:

$$F_{\overline{\theta ,\hspace{1em}v}}(\mu ,\hspace{1em}\mathfrak{r}-{\mathfrak{r}}_0)=\sum _{k=0}^{\infty }{\lambda }^k{\displaystyle \frac{{(\mathfrak{r}-{\mathfrak{r}}_0)}^{\overline{k\theta +v-1}}}{\mathrm{\Gamma }(k\theta +v)}},\hspace{1em}\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0}.$$

(7)

Definition 4

([46]). Consider $0<\delta \left(\mathfrak{r}\right)\le 1$ for each $\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0}$. The left nabla sum of order $\delta \left(\mathfrak{r}\right)$ for $\mathit{\ell }:{\mathbb{N}}_{{\mathfrak{r}}_0}\to \mathbb{R},\hspace{1em}$ is referred to by

$${}_{{\mathfrak{r}}_0}{\nabla }^{-\delta \left(\mathfrak{r}\right)}\mathit{\ell }\left(\mathfrak{r}\right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\delta \right(\mathfrak{r}\left)\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{\delta \left(\mathfrak{r}\right)-1}}\mathit{\ell }\left(\mathfrak{s}\right),\hspace{1em}\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}.$$

(8)

Definition 5

([46]). In the case of $\mathit{\ell }:{\mathbb{N}}_{{\mathfrak{r}}_0+1}\to \mathbb{R}$ and $0<\delta \left(\mathfrak{r}\right)<1$. The Caputo nabla variable-order difference is provided by:

$${}_{{\mathfrak{r}}_0}^C{\nabla }^{\delta \left(\mathfrak{r}\right)}\mathit{\ell }\left(t\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\delta (\mathfrak{r}\left)\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{-\delta \left(\mathfrak{r}\right)}}\nabla \mathit{\ell }\left(\mathfrak{s}\right),\hspace{1em}\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}.$$

(9)

3. A Gronwall Inequality

Recently, Ref. [31] presented a Gronwall inequality related to the Nabla fractional operator for fractional difference equations. Ref. [47] also established a discrete Gronwall inequality for the discrete Atangana Baleanu fractional operator. Inspired by it, in this section, we describe and illustrate a unique variable-order discrete variant of the generalized Gronwall’s inequality.

Theorem 1.

Suppose that $\mathfrak{u}\left(\mathfrak{r}\right)$ and $\mathfrak{v}\left(\mathfrak{r}\right)$ are discrete non-negative, non-decreasing functions, with $0\le \mathfrak{v}\left(\mathfrak{r}\right)\le L<1$. For each $\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}$, $\mathit{\ell }\left(\mathfrak{r}\right)$ is non-negative and fulfills the following

$$\mathit{\ell }\left(\mathfrak{r}\right)\le \mathfrak{u}\left(\mathfrak{r}\right)+\mathfrak{v}\left(\mathfrak{r}\right){\nabla }_{\mathfrak{r}}^{-\delta \left(\mathfrak{r}\right)}\mathit{\ell }\left(\mathfrak{r}\right),\hspace{1em}$$

(10)

then,

$$\mathit{\ell }\left(\mathfrak{r}\right)\le \mathfrak{u}\left(\mathfrak{r}\right)F_{\overline{{\delta }_1}}(K\mathfrak{v}\left(\mathfrak{r}\right),\hspace{1em}\mathfrak{r}-{\mathfrak{r}}_0),\hspace{1em}$$

(11)

where

$${\delta }_1\le \delta \left(\mathfrak{r}\right)\le {\delta }_2,\hspace{1em}S=max\{{(\mathfrak{r}-{\mathfrak{r}}_0)}^{{\delta }_1-1},\hspace{1em}{(\mathfrak{r}-{\mathfrak{r}}_0)}^{{\delta }_2-1}\}\mathit{and}K={\displaystyle \frac{S\mathrm{\Gamma }\left({\delta }_1\right)}{{(\mathfrak{r}-{\mathfrak{r}}_0)}^{\overline{{\delta }_1-1}}\mathrm{\Gamma }\left({\delta }_2\right)}}.$$

Proof. 

According to [40], one can find that for $\mathfrak{T}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}$ we have:

$${\mathfrak{T}}^{\delta \left(\mathfrak{r}\right)-1}={\displaystyle \frac{\mathrm{\Gamma }\left(\mathfrak{T}\delta \right(\mathfrak{r})-1)}{\mathrm{\Gamma }\left(\mathfrak{T}\right)}}\le \left\{\begin{array}{c}{\mathfrak{T}}^{{\delta }_1-1},\hspace{1em}0\le \mathfrak{T}\le 1,\hspace{1em}\hfill \\ {\mathfrak{T}}^{{\delta }_2-1},\hspace{1em}\mathfrak{T}>1.\hfill \end{array}\right.$$

(12)

Given $\mathfrak{T}=\mathfrak{r}-{\mathfrak{r}}_0$ and $S=max\{{\mathfrak{T}}^{{\delta }_1-1},\hspace{1em}{\mathfrak{T}}^{{\delta }_2-1}\}$. Using the characteristic of $\mathrm{\Gamma }\left(\mathfrak{r}\right)$ on $(0,\hspace{1em}1)$, we obtain $\mathrm{\Gamma }\left({\delta }_2\right)\le \mathrm{\Gamma }\left(\delta \left(\mathfrak{r}\right)\right)\le \mathrm{\Gamma }\left({\delta }_1\right)$, that provides along with Definition 4:

$$\begin{array}{cc}\hfill \mathit{\ell }\left(\mathfrak{r}\right)& \le \mathfrak{u}\left(\mathfrak{r}\right)+\mathfrak{v}\left(\mathfrak{r}\right){\displaystyle \frac{1}{\mathrm{\Gamma }\left(\delta \right(\mathfrak{r}\left)\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{\delta \left(\mathfrak{r}\right)-1}}\mathit{\ell }\left(\mathfrak{s}\right),\hspace{1em}\hfill \\ \hfill & \le \mathfrak{u}\left(\mathfrak{r}\right)+\mathfrak{v}\left(\mathfrak{r}\right){\displaystyle \frac{S}{\mathrm{\Gamma }\left({\delta }_2\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{{\displaystyle \frac{(\mathfrak{r}-\rho (\mathfrak{s}\left)\right)}{{\mathfrak{T}}^{\overline{\delta \left(\mathfrak{r}\right)-1}}}}}^{\overline{\delta \left(\mathfrak{r}\right)-1}}\mathit{\ell }\left(\mathfrak{s}\right),\hspace{1em}\hfill \\ \hfill & \le \mathfrak{u}\left(\mathfrak{r}\right)+\mathfrak{v}\left(\mathfrak{r}\right){\displaystyle \frac{S}{\mathrm{\Gamma }\left({\delta }_2\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{\left({\displaystyle \frac{(\mathfrak{r}-\rho (\mathfrak{s}\left)\right)}{\mathfrak{T}}}\right)}^{\overline{{\delta }_1-1}}\mathit{\ell }\left(\mathfrak{s}\right),\hspace{1em}\hfill \\ \hfill & \le \mathfrak{u}\left(\mathfrak{r}\right)+K\mathfrak{v}\left(\mathfrak{r}\right){}_{{\mathfrak{r}}_0}{\nabla }_t^{-{\delta }_1}\mathit{\ell }\left(\mathfrak{r}\right),\hspace{1em}\hfill \end{array}$$

where $K={\displaystyle \frac{S\mathrm{\Gamma }\left({\delta }_1\right)}{{\mathfrak{T}}^{\overline{{\delta }_1-1}}\mathrm{\Gamma }\left({\delta }_2\right)}}$.

Now, let be the operator $\psi \mathit{\ell }\left(\mathfrak{r}\right)=K\mathfrak{v}\left(\mathfrak{r}\right){}_{{\mathfrak{r}}_0}{\nabla }_{\mathfrak{r}}^{-{\delta }_1}\mathit{\ell }\left(\mathfrak{r}\right)$, then,

$$\mathit{\ell }\left(\mathfrak{r}\right)\le \mathfrak{u}\left(\mathfrak{r}\right)+\psi \mathit{\ell }\left(\mathfrak{r}\right),\hspace{1em}$$

(13)

given the monotonicity of operator $\psi$, we obtain

$$\psi \mathit{\ell }\left(\mathfrak{r}\right)\le \psi u\left(\mathfrak{r}\right)+{\psi }^2\mathit{\ell }\left(\mathfrak{r}\right),\hspace{1em}$$

(14)

carrying out with the above process yields:

$$\mathit{\ell }\left(\mathfrak{r}\right)\le \sum _{\mathfrak{p}=0}^{n-1}{\psi }^{\mathfrak{p}}\mathfrak{u}\left(\mathfrak{r}\right)+{\psi }^n\mathit{\ell }\left(\mathfrak{r}\right).$$

(15)

Following that, we will demonstrate that:

$$\begin{array}{cc}\hfill & {\psi }^n\mathit{\ell }\left(\mathfrak{r}\right)\le {\mathfrak{v}}^n\left(\mathfrak{r}\right){}_{{\mathfrak{r}}_0}{\nabla }_t^{-n{\delta }_1}\mathit{\ell }\left(\mathfrak{r}\right),\hspace{1em}\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & \underset{n^{\to }\infty }{lim}{\psi }^n=0.\hfill \end{array}$$

(17)

Indeed, inequality (16) plainly remains true for $n=1$. Using mathematical induction, for $n=\mathfrak{p},\hspace{1em}$ we obtain:

$${\psi }^{\mathfrak{p}}\mathit{\ell }\left(\mathfrak{r}\right)\le {\mathfrak{v}}^{\mathfrak{p}}\left(\mathfrak{r}\right){}_{{\mathfrak{r}}_0}{\nabla }_{\mathfrak{r}}^{-\mathfrak{p}{\delta }_1}\mathit{\ell }\left(\mathfrak{r}\right).$$

(18)

Because $\mathfrak{v}\left(\mathfrak{r}\right)$ is a discrete non-decreasing function on ${\mathbb{N}}_{{\mathfrak{r}}_0+1}$, we obtain

$$\begin{array}{cc}\hfill {\psi }^{\mathfrak{p}+1}\mathit{\ell }\left(\mathfrak{r}\right)& =\psi ({\psi }^{\mathfrak{p}}\mathit{\ell }\left(\mathfrak{r}\right)),\hspace{1em}\hfill \\ \hfill & =K\mathfrak{v}\left(\mathfrak{r}\right){}_{{\mathfrak{r}}_0}{\nabla }_{\mathfrak{r}}^{-{\delta }_1}{\psi }^{\mathfrak{p}}\mathit{\ell }\left(\mathfrak{r}\right)),\hspace{1em}\hfill \\ \hfill & \le K\mathfrak{v}\left(\mathfrak{r}\right){}_{{\mathfrak{r}}_0}{\nabla }_{\mathfrak{r}}^{-{\delta }_1}\left({\mathfrak{v}}^{\mathfrak{p}}\left(\mathfrak{s}\right){}_{{\mathfrak{r}}_0}{\nabla }_{\mathfrak{s}}^{-\mathfrak{p}{\delta }_1}\mathit{\ell }\left(\mathfrak{s}\right)\right),\hspace{1em}\hfill \\ \hfill & =\mathfrak{v}\left(\mathfrak{r}\right){\displaystyle \frac{K}{\mathrm{\Gamma }\left({\delta }_1\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{{\delta }_1-1}}\left({\mathfrak{v}}^{\mathfrak{p}}\left(\mathfrak{s}\right){\displaystyle \frac{1}{\mathrm{\Gamma }\left(\mathfrak{p}{\delta }_1\right)}}\sum _{{\mathfrak{s}}^{\prime }={\mathfrak{r}}_0+1}^{\mathfrak{s}}{(\mathfrak{s}-\rho ({\mathfrak{s}}^{\prime }))}^{\overline{\mathfrak{p}{\delta }_1-1}}\mathit{\ell }({\mathfrak{s}}^{\prime })\right),\hspace{1em}\hfill \\ \hfill & \le K{\mathfrak{v}}^{\mathfrak{p}+1}\left(\mathfrak{r}\right){}_{{\mathfrak{r}}_0}{\nabla }_{\mathfrak{r}}^{-(\mathfrak{p}+1){\delta }_1}\mathit{\ell }\left(\mathfrak{r}\right),\hspace{1em}\hfill \end{array}$$

where the procedure for composing two fractional sums was applied. As a result, we may conclude that the inequality (16) holds for any $n\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}$.

Since $\mathfrak{v}\left(\mathfrak{r}\right)\le L$, we may deduce from inequality (16) that

$$\begin{array}{cc}\hfill {\psi }^n\mathit{\ell }(\mathfrak{r})& \le L^n{\displaystyle \frac{K}{\mathrm{\Gamma }(n{\delta }_1)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho (\mathfrak{s}))}^{\overline{n{\delta }_1-1}}\mathit{\ell }\left(\mathfrak{s}\right),\hspace{1em}\hfill \\ \hfill & \le K{L}^{n}X{\displaystyle \frac{1}{\mathrm{\Gamma }(n{\delta }_1)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho (\mathfrak{s}))}^{\overline{n{\delta }_1-1}},\hspace{1em}\hfill \end{array}$$

$$\begin{array}{cc}\hfill =KX{L}^n& {\displaystyle \frac{{(\mathfrak{r}-{\mathfrak{r}}_0)}^{\overline{n{\delta }_1}}}{\mathrm{\Gamma }(n{\delta }_1+1)}},\hspace{1em}\hfill \end{array}$$

(19)

where $X={max}_{\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}}\{\mathit{\ell }\left(\mathfrak{r}\right)\}.$

As a result, relation (19) is derived. Furthermore, one may deduce that

$${\psi }^n\mathit{\ell }\left(\mathfrak{r}\right)\le K{L}^{n}X{\displaystyle \frac{{(\mathfrak{r}-{\mathfrak{r}}_0)}^{\overline{n{\delta }_1}}}{\mathrm{\Gamma }(n{\delta }_1+1)}}\to 0\mathrm{as}n\to +\infty ,\hspace{1em}\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1,\hspace{1em}}$$

(20)

and we obtain ${lim}_{n\to \infty }{\psi }^n\mathit{\ell }\left(\mathfrak{r}\right)=0$. Therefore:

$$\begin{array}{cc}\hfill \mathit{\ell }\left(\mathfrak{r}\right)& \le \sum _{\mathfrak{p}=0}^{n-1}{\psi }^{\mathfrak{p}}\mathfrak{u}\left(\mathfrak{r}\right)=\mathfrak{u}\left(\mathfrak{r}\right)+\sum _{\mathfrak{p}=1}^{n-1}{\psi }^{\mathfrak{p}}\mathfrak{u}\left(\mathfrak{r}\right)\le \mathfrak{u}\left(\mathfrak{r}\right)+\sum _{\mathfrak{p}=1}^{+\infty }{\psi }^{\mathfrak{p}}\mathfrak{u}\left(\mathfrak{r}\right)\le \mathfrak{u}\left(\mathfrak{r}\right)+\sum _{\mathfrak{p}=1}^{+\infty }{K}^{\mathfrak{p}}{\mathfrak{v}}^{\mathfrak{p}}\left(\mathfrak{r}\right){}_{{\mathfrak{r}}_0}{\nabla }_{\mathfrak{r}}^{-\mathfrak{p}{\delta }_1}u\left(\mathfrak{r}\right).\hfill \end{array}$$

(21)

We may derive from (16) and the hypothesis that $\mathfrak{u}(\mathfrak{r})$ is a non-decreasing function for $\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}^T$ that:

$$\begin{array}{cc}\hfill \mathit{\ell }(\mathfrak{r})& \le \mathfrak{u}(\mathfrak{r})+\sum _{\mathfrak{p}=1}^{+\infty }{K}^{\mathfrak{p}}{\mathfrak{v}}^{\mathfrak{p}}(\mathfrak{r}){}_{{\mathfrak{r}}_0}{\nabla }_{\mathfrak{r}}^{-\mathfrak{p}{\delta }_1}\mathfrak{u}(\mathfrak{r}),\hspace{1em}\hfill \\ \hfill & \le \mathfrak{u}(\mathfrak{r})+\sum _{\mathfrak{p}=1}^{+\infty }{K}^{\mathfrak{p}}{\mathfrak{v}}^{\mathfrak{p}}(\mathfrak{r}){\displaystyle \frac{1}{\mathrm{\Gamma }(\mathfrak{p}{\delta }_1)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho (\mathfrak{s}))}^{\overline{\mathfrak{p}{\delta }_1-1}}\mathfrak{u}(\mathfrak{s}),\hspace{1em}\hfill \\ \hfill & \le \mathfrak{u}(\mathfrak{r})+\sum _{\mathfrak{p}=1}^{+\infty }{K}^{\mathfrak{p}}{\mathfrak{v}}^{\mathfrak{p}}(\mathfrak{r})\mathfrak{u}(\mathfrak{r}){\displaystyle \frac{1}{\mathrm{\Gamma }(\mathfrak{p}{\delta }_1)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho (\mathfrak{s}))}^{\overline{\mathfrak{p}{\delta }_1-1}},\hspace{1em}\hfill \\ \hfill & \le \mathfrak{u}(\mathfrak{r})+\sum _{\mathfrak{p}=1}^{+\infty }{K}^{\mathfrak{p}}{\mathfrak{v}}^{\mathfrak{p}}(\mathfrak{r})\mathfrak{u}(\mathfrak{r}){\displaystyle \frac{{(\mathfrak{r}-{\mathfrak{r}}_0)}^{\overline{p{\delta }_1}}}{\mathrm{\Gamma }(p{\delta }_1+1)}},\hspace{1em}\hfill \\ \hfill & =\mathfrak{u}(\mathfrak{r})\sum _{\mathfrak{p}=0}^{+\infty }{(K\mathfrak{v}(\mathfrak{r}))}^{\mathfrak{p}}{\displaystyle \frac{{(\mathfrak{r}-{\mathfrak{r}}_0)}^{\overline{\mathfrak{p}{\delta }_1}}}{\mathrm{\Gamma }(\mathfrak{p}{\delta }_1+1)}}\hfill \\ \hfill & =\mathfrak{u}(\mathfrak{r})F_{\overline{{\delta }_1}}(K\mathfrak{v}\left(\mathfrak{r}\right),\hspace{1em}\mathfrak{r}-{\mathfrak{r}}_0).\hfill \end{array}$$

As with the usual Gronwall inequality, the importance of (11) rests in the fact that it establishes a bound for $\mathit{\ell }\left(\mathfrak{r}\right)$ in terms of $\mathfrak{u}\left(\mathfrak{r}\right)$, $\mathfrak{v}\left(\mathfrak{r}\right)$, and $\delta \left(\mathfrak{r}\right)$. The proof is completed. □

4. Finite–Time Stability of Nabla Variable-Order Neural Networks

To demonstrate the application of the essential results, we prove the uniqueness and limited time stability of nabla variable-order neural networks using the results from the prior section.

We investigate the variable-order fractional discrete neural network

$${}_{{\mathfrak{r}}_0}^C{\nabla }^{\delta \left(\mathfrak{r}\right)}\mathit{\ell }\left(\mathfrak{r}\right)=-D\mathit{\ell }\left(\mathfrak{r}\right)+Ch(\mathfrak{r},\hspace{1em}\mathit{\ell }\left(\mathfrak{r}\right))+I.$$

(22)

whereas ${}_{{\mathfrak{r}}_0}^C{\nabla }^{\delta \left(\mathfrak{r}\right)}$ is the Caputo nabla operator of order $\delta \left(\mathfrak{r}\right),\hspace{1em}0<\delta \left(\mathfrak{r}\right)<1$, $\mathit{\ell }\left(\mathfrak{r}\right)={({\mathit{\ell }}_1\left(\mathfrak{r}\right),\hspace{1em}{\mathit{\ell }}_2\left(\mathfrak{r}\right),\hspace{1em}\dots ,\hspace{1em}{\mathit{\ell }}_n\left(\mathfrak{r}\right))}^T\in {\mathbb{R}}^n$ represents the state vector, $D=diag(d_1,\hspace{1em}{d}_2,\hspace{1em}\dots ,\hspace{1em}{d}_n)\in {\mathbb{R}}^{n*n}$ denotes the self-feedback connecting weight with $d_i>0$, The connection weight matrix is $C={\left(c_{\mathfrak{i}\mathit{\ell }}\right)}_{n*n}\in {\mathbb{R}}^{n*n}$. $h(\mathfrak{r},\hspace{1em}\mathit{\ell }\left(\mathfrak{r}\right))={(h_1(\mathfrak{r},\hspace{1em}\mathit{\ell }\left(\mathfrak{r}\right)),\hspace{1em}{h}_2(\mathfrak{r},\hspace{1em}\mathit{\ell }\left(\mathfrak{r}\right)),\hspace{1em}\dots ,\hspace{1em}{h}_n(\mathfrak{r},\hspace{1em}\mathit{\ell }\left(\mathfrak{r}\right)))}^T$: $C({\mathbb{N}}_{{\mathfrak{r}}_0+1}\to {\mathbb{R}}^n)$ is the activation function, and $I={(I_1,\hspace{1em}\dots ,\hspace{1em}{I}_n)}^T$ is the vector of external inputs.

Definition 6

([2]). Given positive numbers $\gamma ,\hspace{1em}ϵ$, and for the initial condition ϕ, system (22) is said finite-time stable with regard to $\{\gamma ,\hspace{1em}ϵ,\hspace{1em}T\},\hspace{1em}$$\gamma <ϵ$ if only for

$$\parallel \varphi \parallel \le \gamma ,\hspace{1em}$$

(23)

then,

$$\parallel \mathit{\ell }\left(\mathfrak{r}\right)\parallel \le ϵ,\hspace{1em}t\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}^T.$$

(24)

First, few assumptions are made before proceeding with the investigation of this study.

Hypothesis 1.

Assume that $h(\mathfrak{r},\hspace{1em}\mathit{\ell }(\mathfrak{r}\left)\right)$ is a continuous function that meets the Lypschitz condition with regard to ℓ, i.e.,

$$|h_{\mathfrak{i}}(\mathfrak{r},\hspace{1em}{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right))-h_{\mathfrak{i}}(\mathfrak{r},\hspace{1em}{\mathfrak{y}}_{\mathfrak{i}}\left(\mathfrak{r}\right))|\le l_{\mathfrak{i}}|{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathfrak{y}}_{\mathfrak{i}}\left(\mathfrak{r}\right)|,\hspace{1em}\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}.$$

(25)

Hypothesis 2.

For $d_i,\hspace{1em}$$c_{\mathfrak{i}\mathit{\ell }}$, and $l_{\mathit{\ell }}$, it holds that:

$$0<-\underset{\mathfrak{i}=1,\hspace{1em}\dots ,\hspace{1em}n}{min}{d}_{\mathfrak{i}}+\sum _{\mathfrak{i}=1}^n\underset{\mathit{\ell }=1,\hspace{1em}\dots ,\hspace{1em}n}{max}|c_{\mathfrak{i}\mathit{\ell }}|l_{\mathit{\ell }}\le 1.$$

(26)

Hypothesis 3.

For γ and ϵ defined in Definition 6, it holds that:

$$F_{\overline{{\delta }_1}}\left(-\underset{\mathfrak{i}=1,\hspace{1em}\dots ,\hspace{1em}n}{min}{d}_{\mathfrak{i}}+\sum _{\mathfrak{i}=1}^n\underset{\mathit{\ell }=1,\hspace{1em}\dots ,\hspace{1em}n}{max}|c_{\mathfrak{i}\mathit{\ell }}|l_{\mathit{\ell }},\hspace{1em}\mathfrak{r}-{\mathfrak{r}}_0\right)<{\displaystyle \frac{ϵ}{\gamma }}.$$

(27)

Theorem 2.

Assuming condition $\left(H_1\right)$ holds. If $\mathit{\ell }\left(\mathfrak{r}\right)$ and $\mathfrak{y}\left(\mathfrak{r}\right)$ are distinct solutions for system (22), then, $\mathit{\ell }\left(\mathfrak{r}\right)=\mathfrak{y}\left(\mathfrak{r}\right)$.

Proof. 

Suppose ℓ as well as $\mathfrak{y}$ are distinct solutions of (22), with the same initial conditions. $\omega$ is denoted by $\omega \left(\mathfrak{r}\right)=\mathit{\ell }\left(\mathfrak{r}\right)-\mathfrak{y}\left(\mathfrak{r}\right)$. Thus, for $\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}$ we have:

$$\begin{array}{cc}\hfill {\omega }_{\mathfrak{i}}\left(\mathfrak{r}\right)& ={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\delta \right(\mathfrak{r}\left)\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{\delta \left(\mathfrak{r}\right)-1}}\left(-d_{\mathfrak{i}}{\omega }_{\mathfrak{i}}\left(\mathfrak{s}\right)+\sum _{\mathit{\ell }=1}^n{c}_{\mathfrak{i}\mathit{\ell }}(h_{\mathit{\ell }}(\mathfrak{s},\hspace{1em}{\mathit{\ell }}_j\left(\mathfrak{s}\right))-h_{\mathit{\ell }}(\mathfrak{s},\hspace{1em}{\mathfrak{y}}_{\mathit{\ell }}\left(\mathfrak{s}\right)))\right),\hspace{1em}\mathfrak{i}=1,\hspace{1em}\dots ,\hspace{1em}n.\hfill \end{array}$$

(28)

This implies:

$$\begin{array}{cc}\hfill |{\omega }_{\mathfrak{i}}\left(\mathfrak{r}\right)|& \le {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\delta \right(\mathfrak{r}\left)\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{\delta \left(\mathfrak{r}\right)-1}}\left(d_{\mathfrak{i}}|{\omega }_{\mathfrak{i}}\left(\mathfrak{s}\right)|+\sum _{\mathit{\ell }=1}^n|c_{\mathfrak{i}\mathit{\ell }}||h_{\mathit{\ell }}(\mathfrak{s},\hspace{1em}{\mathit{\ell }}_{\mathit{\ell }}\left(\mathfrak{s}\right))-h_{\mathit{\ell }}(\mathfrak{s},\hspace{1em}{\mathfrak{y}}_{\mathit{\ell }}\left(\mathfrak{s}\right))|\right),\hspace{1em}\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & \le {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\delta \right(\mathfrak{r}\left)\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^t{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{\delta \left(\mathfrak{r}\right)-1}}\left(d_{\mathfrak{i}}|{\omega }_{\mathfrak{i}}\left(\mathfrak{s}\right)|+\sum _{\mathit{\ell }=1}^n|c_{\mathfrak{i}\mathit{\ell }}|l_{\mathit{\ell }}|{\omega }_j\left(\mathfrak{s}\right)|\right).\hfill \end{array}$$

(30)

Which leads us to

$$\begin{array}{cc}\hfill \parallel \omega \left(\mathfrak{r}\right)\parallel & =\sum _{\mathfrak{i}=1}^n|{\omega }_{\mathfrak{i}}\left(\mathfrak{r}\right)|,\hspace{1em}\hfill \\ \hfill & \le {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\delta \right(\mathfrak{r}\left)\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{\delta \left(\mathfrak{r}\right)-1}}\left(\alpha \sum _{\mathfrak{i}=1}^n|{\omega }_{\mathfrak{i}}\left(\mathfrak{s}\right)|+\sum _{\mathfrak{i}=1}^n\sum _{\mathit{\ell }=1}^n|c_{\mathfrak{i}\mathit{\ell }}|l_{\mathit{\ell }}|{\omega }_{\mathit{\ell }}\left(\mathfrak{s}\right)|\right),\hspace{1em}\hfill \\ \hfill & \le {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\delta \right(\mathfrak{r}\left)\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{\delta \left(\mathfrak{r}\right)-1}}\left(\alpha \parallel \omega \left(\mathfrak{s}\right)\parallel +\beta \sum _{\mathfrak{i}=1}^n|{\omega }_{\mathfrak{i}}\left(\mathfrak{s}\right)|\right),\hspace{1em}\hfill \\ \hfill & \le (\alpha +\beta ){\displaystyle \frac{1}{\mathrm{\Gamma }\left(\delta \right(\mathfrak{r}\left)\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^{\mathfrak{r}}{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{\delta \left(\mathfrak{r}\right)-1}}\parallel \omega \left(\mathfrak{r}\right)\parallel ,\hspace{1em}\hfill \\ \hfill & =(\alpha +\beta ){}_{{\mathfrak{r}}_0}{\nabla }^{-\delta \left(\mathfrak{r}\right)}\parallel \omega \left(\mathfrak{r}\right)\parallel ,\hspace{1em}\hfill \end{array}$$

where $\alpha ={max}_{\mathfrak{i}=1,\hspace{1em}\dots ,\hspace{1em}n}\left\{d_{\mathfrak{i}}\right\}$ and $\beta ={max}_{\mathfrak{i}=1,\hspace{1em}\dots ,\hspace{1em}n}\{{\sum }_{\mathit{\ell }=1}^n|c_{\mathit{\ell }\mathfrak{i}}|l_{\mathfrak{i}}\}$.

Since $\alpha +\beta$ and $\parallel \omega \left(\mathfrak{r}\right)\parallel$ are positive, using the result of Theorem 1, we have:

$$\parallel \omega \left(\mathfrak{r}\right)\parallel \le 0\times F_{\overline{{\delta }_1}}(\alpha +\beta ,\hspace{1em}\mathfrak{r}-{\mathfrak{r}}_0).$$

(31)

It follows that, $\parallel \mathit{\ell }\left(\mathfrak{r}\right)-\mathfrak{y}\left(\mathfrak{r}\right)\parallel =0$, hence, $\mathit{\ell }\left(\mathfrak{r}\right)=\mathfrak{y}\left(\mathfrak{r}\right)$ for $\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}^T$. The proof is completed. □

Theorem 3.

Assuming $\left(H_1\right)$–$\left(H_3\right)$ are true, the unique fixed point of system (22) is finite time stable with regards to $\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}^T$.

Proof. 

Let be the unique fixed point of system (22) ${\mathit{\ell }}^{*}\in {\mathbb{R}}^n$, thus,

$$-d_{\mathfrak{i}}{\mathit{\ell }}_{\mathfrak{i}}^{*}+\sum _{\mathit{\ell }=1}^n{c}_{\mathfrak{i}\mathit{\ell }}{h}_{\mathit{\ell }}(\mathfrak{r},\hspace{1em}{\mathit{\ell }}_{\mathit{\ell }}^{*})+I_{\mathfrak{i}}=0,\hspace{1em}\mathfrak{i}=1,\hspace{1em}\dots ,\hspace{1em}n.$$

(32)

In what comes next, we will demonstrate that ${\mathit{\ell }}^{*}$ is finite time stable. Assuming $\mathit{\ell }\left(\mathfrak{r}\right))$ is any solution of system (22), then,

$$\begin{array}{cc}\hfill {}_{{\mathfrak{r}}_0}^C{\nabla }^{\delta \left(\mathfrak{r}\right)}& ({\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*})=-d_{\mathfrak{i}}({\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*})+\sum _{\mathit{\ell }=1}^n{c}_{\mathfrak{i}\mathit{\ell }}(h_{\mathit{\ell }}(\mathfrak{r},\hspace{1em}{\mathit{\ell }}_{\mathit{\ell }}\left(\mathfrak{r}\right))-h_{\mathit{\ell }}(\mathfrak{r},\hspace{1em}{\mathit{\ell }}_{\mathit{\ell }}^{*})).\hfill \end{array}$$

(33)

However, according to Definition 5, we have:

$$\begin{array}{cc}\hfill {}_{{\mathfrak{r}}_0}^C{\nabla }^{\delta \left(\mathfrak{r}\right)}|{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}|& ={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\delta \right(\mathfrak{r}\left)\right)}}\sum _{\mathfrak{s}={\mathfrak{r}}_0+1}^t{(\mathfrak{r}-\rho \left(\mathfrak{s}\right))}^{\overline{\delta \left(\mathfrak{r}\right)-1}}|{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{s}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*})|\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & =\left\{\begin{array}{c}{}_{{\mathfrak{r}}_0}^C{\nabla }^{\delta \left(\mathfrak{r}\right)}({\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}),\hspace{1em}\mathrm{if}{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}>0,\hspace{1em}\hfill \\ 0,\hspace{1em}\mathrm{if}{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}=0,\hspace{1em}\hfill \\ -{}_{{\mathfrak{r}}_0}^C{\nabla }^{\delta \left(\mathfrak{r}\right)}({\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}),\hspace{1em}\mathrm{if}{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}<0,\hspace{1em}\hfill \end{array}\right.\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & =sgn({\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}){}_{{\mathfrak{r}}_0}^C{\nabla }^{\delta \left(\mathfrak{r}\right)}({\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}).\hfill \end{array}$$

(36)

Therefore:

$$\begin{array}{cc}\hfill {}_{{\mathfrak{r}}_0}^C{\nabla }^{\delta \left(\mathfrak{r}\right)}|{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}|& =sgn({\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}){}_{{\mathfrak{r}}_0}^C{\nabla }^{\delta \left(\mathfrak{r}\right)}({\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}),\hspace{1em}\hfill \\ \hfill & =sgn({\mathit{\ell }}_{\mathfrak{i}}(\mathfrak{r})-{\mathit{\ell }}_{\mathfrak{i}}^{*})(-d_{\mathfrak{i}}({\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*})+\sum _{\mathit{\ell }=1}^n{c}_{\mathfrak{i}\mathit{\ell }}(h_{\mathit{\ell }}(\mathfrak{r},\hspace{1em}{\mathit{\ell }}_{\mathit{\ell }}\left(\mathfrak{r}\right))-h_{\mathit{\ell }}(\mathfrak{r},\hspace{1em}{\mathit{\ell }}_{\mathit{\ell }}^{*}))),\hspace{1em}\hfill \\ \hfill & =-d_{\mathfrak{i}}|{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}|+sgn({\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*})\sum _{\mathit{\ell }=1}^n{c}_{\mathfrak{i}\mathit{\ell }}(h_{\mathit{\ell }}(\mathfrak{r},\hspace{1em}{\mathit{\ell }}_{\mathit{\ell }}\left(\mathfrak{r}\right))-h_{\mathit{\ell }}(\mathfrak{r},\hspace{1em}{\mathit{\ell }}_{\mathit{\ell }}^{*})),\hspace{1em}\hfill \\ \hfill & \le -d_{\mathfrak{i}}|{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}|+\sum _{\mathit{\ell }=1}^n|c_{\mathfrak{i}\mathit{\ell }}|l_{\mathit{\ell }}|{\mathit{\ell }}_{\mathit{\ell }}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathit{\ell }}^{*}|.\hfill \end{array}$$

Using the fractional variable-order sum, We may deduce that:

$$\begin{array}{cc}\hfill |{\mathit{\ell }}_{\mathfrak{i}}& \left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}|\le -d_{\mathfrak{i}}{}_{{\mathfrak{r}}_0}{\nabla }^{-\delta \left(\mathfrak{r}\right)}|{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}|+\sum _{\mathit{\ell }=1}^n|c_{\mathfrak{i}\mathit{\ell }}|l_{\mathit{\ell }}{}_{{\mathfrak{r}}_0}{\nabla }^{-\delta \left(\mathfrak{r}\right)}|{\mathit{\ell }}_{\mathit{\ell }}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathit{\ell }}^{*}|+|{\mathit{\ell }}_{\mathfrak{i}}\left({\mathfrak{r}}_0\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}|.\hfill \end{array}$$

(37)

We may directly acquire:

$$\begin{array}{cc}\hfill \parallel \mathit{\ell }\left(\mathfrak{r}\right)-{\mathit{\ell }}^{*}\parallel & =\sum _{\mathfrak{i}=1}^n|{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}|,\hspace{1em}\hfill \\ \hfill & \le -d_{\mathfrak{i}}\sum _{\mathfrak{i}=1}^n{}_{{\mathfrak{r}}_0}{\nabla }^{-\delta \left(\mathfrak{r}\right)}|{\mathit{\ell }}_{\mathfrak{i}}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathfrak{i}}*|+\sum _{\mathfrak{i}=1}^n\sum _{\mathit{\ell }=1}^n|c_{\mathfrak{i}\mathit{\ell }}|l_{\mathit{\ell }}{}_{{\mathfrak{r}}_0}{\nabla }^{-\delta \left(\mathfrak{r}\right)}|{\mathit{\ell }}_{\mathit{\ell }}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathit{\ell }}^{*}|+\sum _{\mathfrak{i}=1}^n|{\mathit{\ell }}_{\mathfrak{i}}\left({\mathfrak{r}}_0\right)-{\mathit{\ell }}_{\mathfrak{i}}^{*}|,\hspace{1em}\hfill \\ \hfill & \le -\underset{\mathfrak{i}=1,\hspace{1em}\dots ,\hspace{1em}n}{min}{d}_{\mathfrak{i}}{}_{{\mathfrak{r}}_0}{\nabla }^{-\delta \left(\mathfrak{r}\right)}\parallel \mathit{\ell }\left(\mathfrak{r}\right)-{\mathit{\ell }}^{*}\parallel +\sum _{\mathfrak{i}=1}^n\underset{\mathit{\ell }=1,\hspace{1em}\dots ,\hspace{1em}n}{max}|c_{\mathfrak{i}\mathit{\ell }}|l_{\mathit{\ell }}{}_{{\mathfrak{r}}_0}{\nabla }^{-\delta \left(\mathfrak{r}\right)}\sum _{\mathit{\ell }=1}^n|{\mathit{\ell }}_{\mathit{\ell }}\left(\mathfrak{r}\right)-{\mathit{\ell }}_{\mathit{\ell }}^{*}|\hfill \\ \hfill & +\parallel \varphi -\mathit{\ell }*\parallel ,\hspace{1em}\hfill \\ \hfill & =\parallel \varphi -\mathit{\ell }*\parallel +\left(-\underset{\mathfrak{i}=1,\hspace{1em}\dots ,\hspace{1em}n}{min}{d}_{\mathfrak{i}}+\sum _{\mathfrak{i}=1}^n\underset{\mathit{\ell }=1,\hspace{1em}\dots ,\hspace{1em}n}{max}|c_{\mathfrak{i}\mathit{\ell }}|l_{\mathit{\ell }}\right){}_{{\mathfrak{r}}_0}{\nabla }^{-\delta \left(\mathfrak{r}\right)}\parallel \mathit{\ell }\left(\mathfrak{r}\right)-{\mathit{\ell }}^{*}\parallel .\hfill \end{array}$$

Given that $\parallel \varphi -{\mathit{\ell }}^{*}\parallel$, $-{min}_{\mathfrak{i}=1,\hspace{1em}\dots ,\hspace{1em}n}{d}_{\mathfrak{i}}+{\sum }_{\mathfrak{i}=1}^n{max}_{\mathit{\ell }=1,\hspace{1em}\dots ,\hspace{1em}n}|c_{\mathfrak{i}\mathit{\ell }}|l_{\mathit{\ell }}$, and $\parallel \mathit{\ell }\left(\mathfrak{r}\right)-{\mathit{\ell }}^{*}\parallel$ are all positive, we may derive from Theorem 1 and $\left(H_3\right)$ that (38) holds:

$$\begin{array}{cc}\hfill \parallel \mathit{\ell }\left(\mathfrak{r}\right)& -{\mathit{\ell }}^{*}\parallel \le \parallel \varphi -{\mathit{\ell }}^{*}\parallel F_{\overline{{\delta }_1}}\left(-\underset{\mathfrak{i}=1,\hspace{1em}\dots ,\hspace{1em}n}{min}{d}_{\mathfrak{i}}+\sum _{\mathfrak{i}=1}^n\underset{\mathit{\ell }=1,\hspace{1em}\dots ,\hspace{1em}n}{max}|c_{\mathfrak{i}\mathit{\ell }}|l_{\mathit{\ell }},\hspace{1em}\mathfrak{r}-{\mathfrak{r}}_0\right)<{\displaystyle \frac{ϵ}{\gamma }}.\hfill \end{array}$$

(38)

In line with Definition 6, this immediately shows that ${\mathit{\ell }}^{*}$ point of system (22) is finite time stable with regard to $\mathfrak{r}\in {\mathbb{N}}_{{\mathfrak{r}}_0+1}^T$. The proof is finished. □

Remark 1.

In [40], the author performed an asymptotic stability study of variable-order discrete neural networks. In [48,49], the authors examined the Mittag–Leffler stability of variable-order neural networks. Ref. [41] explored the uniform stability of discrete fractional variable-order neural networks. In contrast to prior studies, a new adequate condition has been constructed in this research by applying a generalized Gronwall-type inequality and the method of iteration, and the simulated examples in the next part will put the acquired findings to the test.

Remark 2.

In [30], the authors demonstrated that fractional discrete neural networks were finite-time stable utilizing the Mittag–Leffler matrix function technique. In certain practical applications, neural networks must be generated with only one stable equilibrium point. In the present research, we established an appropriate criterion for the stability of the targeted networks’ unique equilibrium point. Meanwhile, our approach varies from that of [20], where the author first showed the stability of the model that was suggested and then demonstrated the fact that this network has a unique equilibrium point based on additional criteria.

5. Numerical Simulations

Now, we shall apply theoretical stability conclusions to two numerical cases linked to variable-order discrete neural networks. Since most of the fractional variable-order difference equations do not exist analytic solutions, so approximation and numerical techniques must be used. A numerical sum for solving fractional variable-order difference equations was proposed. As shown below, we established explicit numerical formulations for the Nabla variable-order neural networks.

$$\left\{\begin{array}{c}{\mathit{\ell }}_1\left(\mathfrak{i}\right)={\mathit{\ell }}_1\left({\mathfrak{r}}_0\right)+{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\delta \left(\mathfrak{i}\right)\right)}}{\sum }_{\mathit{\ell }=1}^{\mathfrak{i}}{\displaystyle \frac{\mathrm{\Gamma }\left(\mathfrak{i}-\mathit{\ell }+\delta \left(\mathfrak{i}\right)\right)}{\mathrm{\Gamma }(\mathfrak{i}-\mathit{\ell }+1)}}\left(-d_1{\mathit{\ell }}_1\left(\mathfrak{i}\right)+{\sum }_{\mathit{\ell }=1}^n{c}_{1\mathit{\ell }}{h}_{\mathit{\ell }}(\mathfrak{i},\hspace{1em}{\mathit{\ell }}_{\mathit{\ell }}\left(j\right))+I_1\right),\hspace{1em}\hfill \\ \dots \hfill \\ {\mathit{\ell }}_n\left(\mathfrak{i}\right)={\mathit{\ell }}_n\left({\mathfrak{r}}_0\right)+{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\delta \left(\mathfrak{i}\right)\right)}}\sum _{\mathit{\ell }=1}^{\mathfrak{i}}{\displaystyle \frac{\mathrm{\Gamma }\left(\mathfrak{i}-\mathit{\ell }+\delta \left(\mathfrak{i}\right)\right)}{\mathrm{\Gamma }(\mathfrak{i}-\mathit{\ell }+1)}}\left(-d_n{\mathit{\ell }}_n\left(\mathfrak{i}\right)+\sum _{\mathit{\ell }=1}^n{c}_{n\mathit{\ell }}{h}_j(\mathfrak{i},\hspace{1em}{\mathit{\ell }}_{\mathit{\ell }}\left(\mathfrak{i}\right))+I_n\right).\hfill \end{array}\right.$$

(39)

Example 1.

We study the following discrete neural networks with variable order:

$$\left\{\begin{array}{c}{}_0^C{\nabla }^{\delta \left(\mathfrak{r}\right)}{\mathit{\ell }}_1\left(\mathfrak{r}\right)=-d_1{\mathit{\ell }}_1\left(\mathfrak{r}\right)+c_{11}sin\left({\mathit{\ell }}_1\left(\mathfrak{r}\right)\right)+c_{12}sin\left({\mathit{\ell }}_2\left(\mathfrak{r}\right)\right)+I_1,\hspace{1em}\hfill \\ {}_0^C{\nabla }^{\delta \left(\mathfrak{r}\right)}{\mathit{\ell }}_2\left(\mathfrak{r}\right)=-d_2{\mathit{\ell }}_2\left(\mathfrak{r}\right)+c_{21}sin\left({\mathit{\ell }}_1\left(\mathfrak{r}\right)\right)+c_{22}sin\left({\mathit{\ell }}_2\left(\mathfrak{r}\right)\right)+I_2.\hfill \end{array}\right.$$

(40)

Let be the following parameters

$$D=\left(\begin{array}{c}1.10\\ 00.9\end{array}\right),\hspace{1em}C=\left(\begin{array}{c}0.70.5\\ 0.5-0.6\end{array}\right),\hspace{1em}I=\left(\begin{array}{c}0\\ 0\end{array}\right),\hspace{1em}$$

(41)

as well as the variable-order function:

$$\delta \left(\mathfrak{r}\right)={\displaystyle \frac{|ln\left({\displaystyle \frac{1}{\mathfrak{r}+1}}\right)+1|}{10}},\hspace{1em}{\delta }_1=0.1,\hspace{1em}{\delta }_2=0.2433987.$$

(42)

We can see finite-time behavior within given parameters. Indeed, for

$$-\underset{\mathit{\ell }=1,\hspace{1em}\dots ,\hspace{1em}n}{min}{d}_{\mathit{\ell }}+\sum _{\mathfrak{i}=1}^n\underset{\mathit{\ell }=1,\hspace{1em}\dots ,\hspace{1em}n}{max}{l}_{\mathit{\ell }}|c_{\mathfrak{i}\mathit{\ell }}|=0.4,\hspace{1em}$$

(43)

$$F_{\overline{{\delta }_1}}\left(-\underset{\mathfrak{i}=1,\hspace{1em}\dots ,\hspace{1em}n}{min}{d}_{\mathfrak{i}}+\sum _{\mathfrak{i}=1}^n\underset{\mathit{\ell }=1,\hspace{1em}\dots ,\hspace{1em}n}{max}|c_{\mathfrak{i}\mathit{\ell }}|l_j,\hspace{1em}30\right)\le 1.172509622300451,\hspace{1em}$$

(44)

The activation functions satisfy assumption ($H_1$) with $l_i=1,\hspace{1em}$$i=1,\hspace{1em}2$. Take $\gamma =0.4$ and $ϵ=0.469003848920180.$ Then, it is easy to verify that $\left(H_2\right)$–$\left(H_3\right)$ hold, according to Theorem 2, system (40) has a unique equilibrium point which is finite time stable.

Example 2.

Let be the discrete neural networks

$$\left\{\begin{array}{c}{}_0^C{\nabla }^{\delta \left(\mathfrak{r}\right)}{\mathit{\ell }}_1\left(\mathfrak{r}\right)=-1.1{\mathit{\ell }}_1\left(\mathfrak{r}\right)+0.6tanh\left({\mathit{\ell }}_1\left(\mathfrak{r}\right)\right)+0.5tanh\left({\mathit{\ell }}_2\left(\mathfrak{r}\right)\right)-0.3tanh\left({\mathit{\ell }}_3\left(\mathfrak{r}\right)\right),\hspace{1em}\hfill \\ {}_0^C{\nabla }^{\delta \left(\mathfrak{r}\right)}{\mathit{\ell }}_2\left(\mathfrak{r}\right)=-1.2{\mathit{\ell }}_2\left(\mathfrak{r}\right)+0.2tanh\left({\mathit{\ell }}_1\left(\mathfrak{r}\right)\right)-0.6tanh\left({\mathit{\ell }}_2\left(\mathfrak{r}\right)\right)+0.5tanh\left({\mathit{\ell }}_3\left(\mathfrak{r}\right)\right),\hspace{1em}\hfill \\ {}_0^C{\nabla }^{\delta \left(\mathfrak{r}\right)}{\mathit{\ell }}_3\left(\mathfrak{r}\right)=-1.1{\mathit{\ell }}_3\left(\mathfrak{r}\right)+0.275tanh\left({\mathit{\ell }}_1\left(\mathfrak{r}\right)\right)+0.8tanh\left({\mathit{\ell }}_2\left(\mathfrak{r}\right)\right)-0.11tanh\left({\mathit{\ell }}_3\left(\mathfrak{r}\right)\right),\hspace{1em}\hfill \end{array}\right.$$

(45)

with the variable-order function as follows

$$\delta \left(\mathfrak{r}\right)=|{\displaystyle \frac{1}{6}}-e^{-{\displaystyle \frac{\mathfrak{r}}{4}}}|,\hspace{1em}{\delta }_1=0.05646\mathrm{and}{\delta }_2=0.83333.$$

(46)

Clearly, $l_j=1,\hspace{1em}j=1;2;3,\hspace{1em}$ the activation functions meets $\left(H_1\right)$. Also, $\left(H_2\right)$–$\left(H_3\right)$ hold for

$$-\underset{\mathit{\ell }=1,\hspace{1em}\dots ,\hspace{1em}n}{min}{d}_{\mathit{\ell }}+\sum _{\mathfrak{i}=1}^n\underset{\mathit{\ell }=1,\hspace{1em}\dots ,\hspace{1em}n}{max}{l}_{\mathit{\ell }}|c_{\mathfrak{i}\mathit{\ell }}|=0.9,\hspace{1em}$$

(47)

$$F_{\overline{{\delta }_1}}\left(-\underset{\mathfrak{i}=1,\hspace{1em}\dots ,\hspace{1em}n}{min}{d}_{\mathfrak{i}}+\sum _{\mathfrak{i}=1}^n\underset{\mathit{\ell }=1,\hspace{1em}\dots ,\hspace{1em}n}{max}|c_{\mathfrak{i}\mathit{\ell }}|l_{\mathit{\ell }},\hspace{1em}30\right)\le 1.142428052757200.$$

(48)

Hence, subject to Theorem 2, system (45) has an unique equilibrium point that is finite time stable when taking $\gamma =0.8$ and $ϵ=0.469003848920180$. We examine the next three numerical simulation scenarios: Case 1: Let $\mathit{\ell }\left(0\right)={(0.8,\hspace{1em}0.8,\hspace{1em}0.8)}^T$, Case 2: Let $\mathit{\ell }\left(0\right)={(0.1,\hspace{1em}0.5,\hspace{1em}0.2)}^T$ and Case 3 for the initial condition $\mathit{\ell }\left(0\right)={(1,\hspace{1em}-2,\hspace{1em}5)}^T$.

The following is the description of the results:

• Figure 1 shows the solutions of system (40), with the variable-order function $\delta \left(\mathfrak{r}\right)$ defined in (42) and the initial condition $\mathit{\ell }\left(0\right)={(0.4,\hspace{1em}-0.4)}^T$ and the set of parameters (41) and (42) and by Theorems 2 and 3, the unique equilibrium point ${\mathit{\ell }}^{*}={(0,\hspace{1em}0)}^T$ is finite time stable.
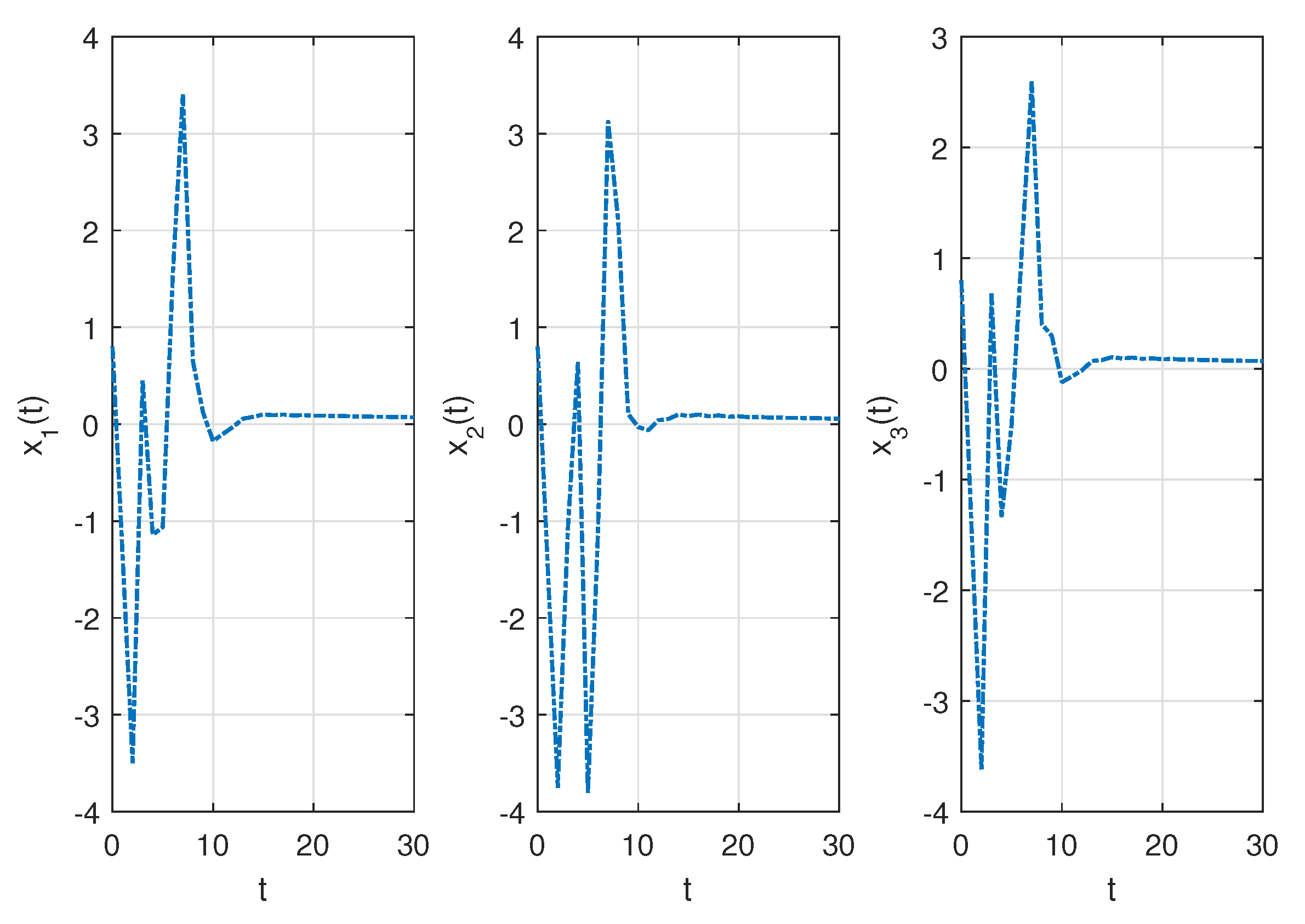
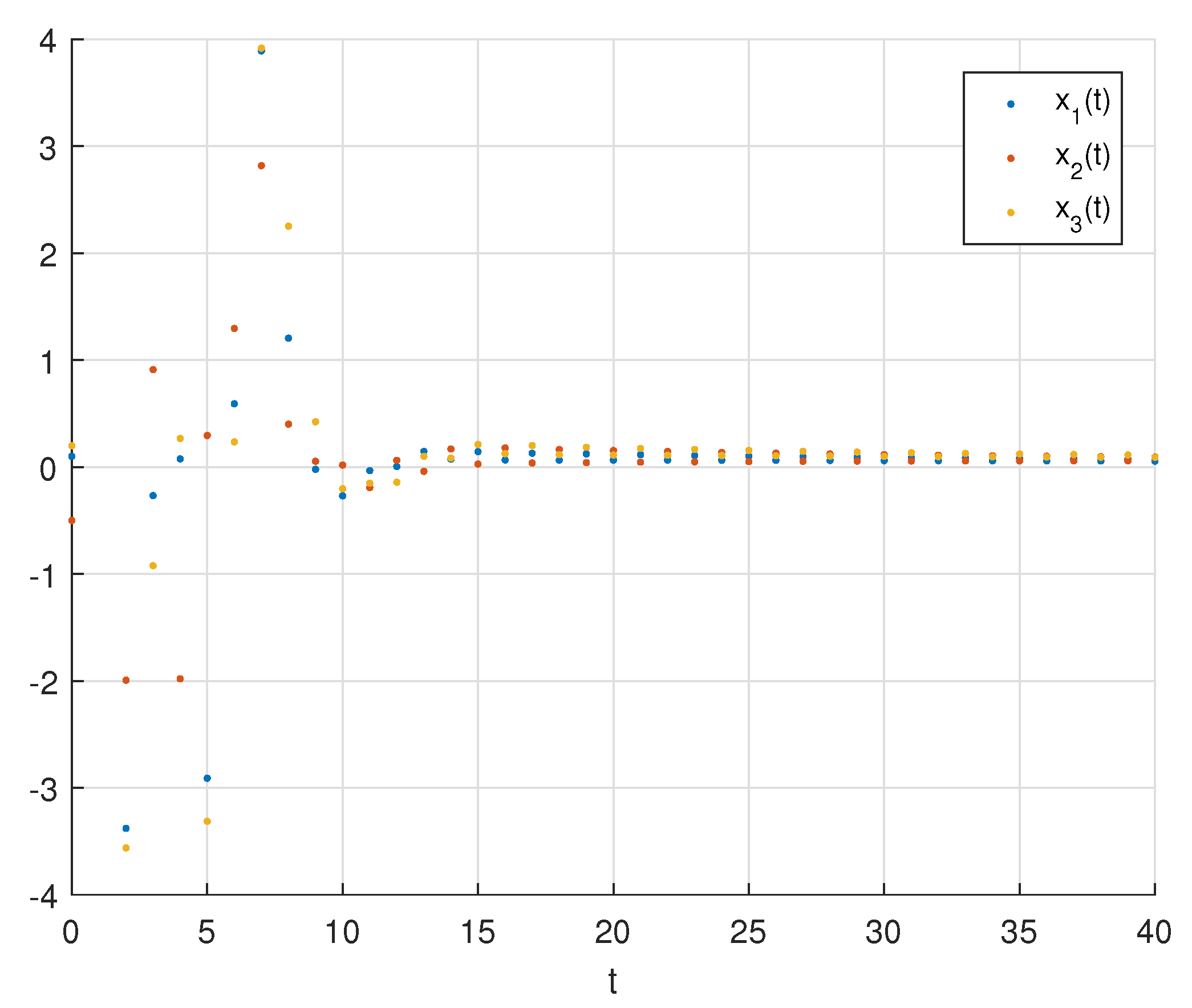
• Figure 2, Figure 3 and Figure 4 indicate that the unique equilibrium point ${\mathit{\ell }}^{*}={(0,\hspace{1em}0)}^T$ of the variable-order fractional neural networks (45), with the variable-order function $\delta \left(t\right)$ described in (2), and the chosen set of parameters, is stable in a finite time based on Theorems 2 and 3 for multiple initial conditions $\mathit{\ell }\left(0\right)={(0.8,\hspace{1em}0.8,\hspace{1em}0.8)}^T$, $\mathit{\ell }\left(0\right)={(0.1,\hspace{1em}0.5,\hspace{1em}0.2)}^T$ and $\mathit{\ell }\left(0\right)={(1,\hspace{1em}-2,\hspace{1em}5)}^T$, respectively.

6. Conclusions

The purpose of this study is to introduce the first generalized discrete variable-order Gronwall inequality in the sense of the Nabla fractional variable-order difference sum operator, in addition to discuss sufficient conditions that ensure the uniqueness and finite-time stability of non-linear nabla discrete variable-order neural networks based on the generalized discrete Gronwall inequality and the contracting mapping principle. We offer two numerical examples to demonstrate the suggested finite-time stability conclusions. We would like to emphasize that our approach can be extended to include more application, such as chaos and synchronization control in variable-order fractional discrete-time neural networks. It has been established that chaos exists in both the variable-order cases and the fractional logistic map. We may investigate the chaotic behavior of the new neural networks using a similar concept and analytical techniques involving the Jacobian matrix approach for calculating the Lyapunov exponent. Additionally, different chaotic synchronization and control rules can be developed in accordance with the stability criteria of this study.