Finite-Time Stabilization of Unstable Orbits in the Fractional Difference Logistic Map
Abstract
1. Introduction
2. Preliminaries
2.1. H-Ranks and Algebraic Complexity
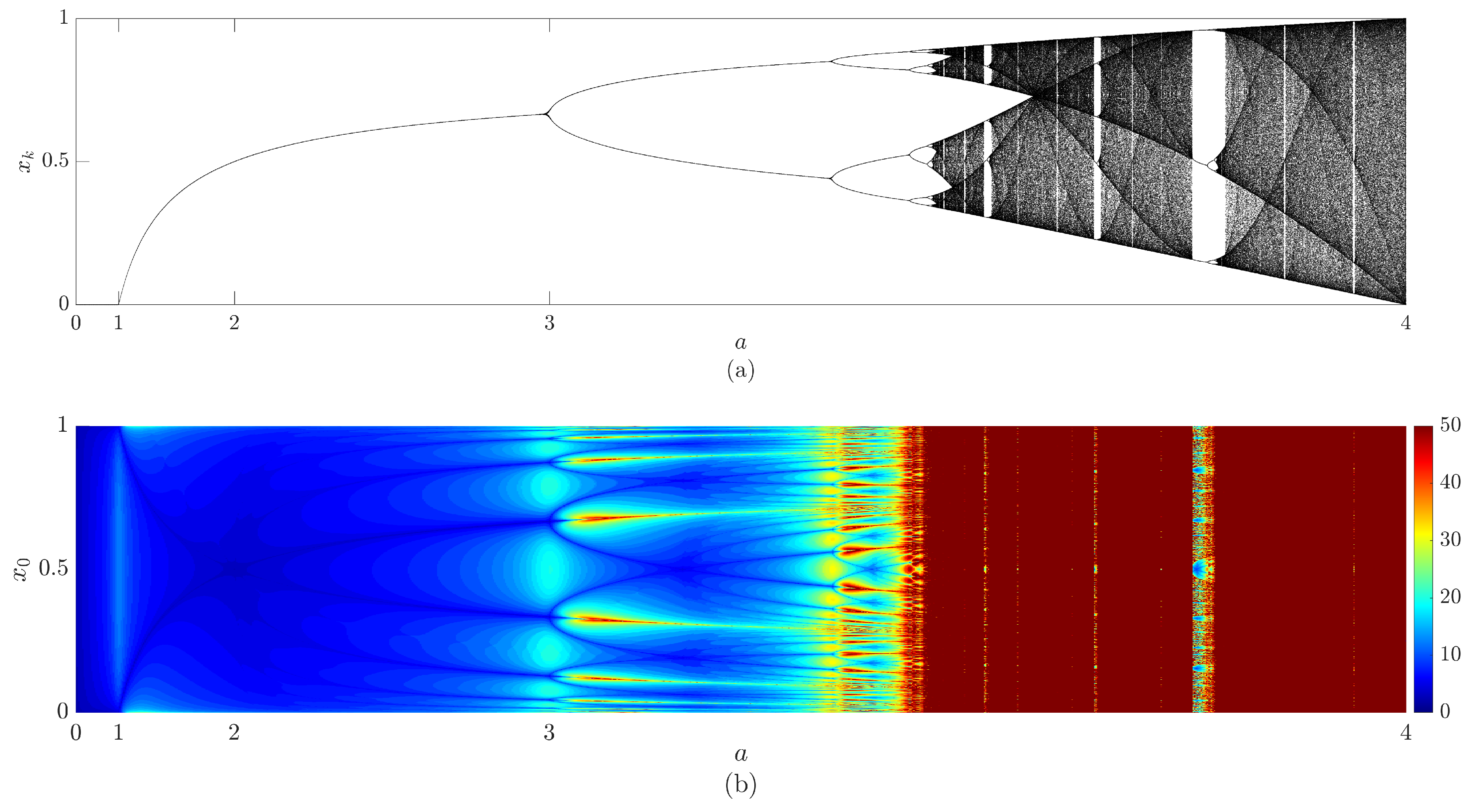
2.2. Classical Logistic Map and Types of Convergence
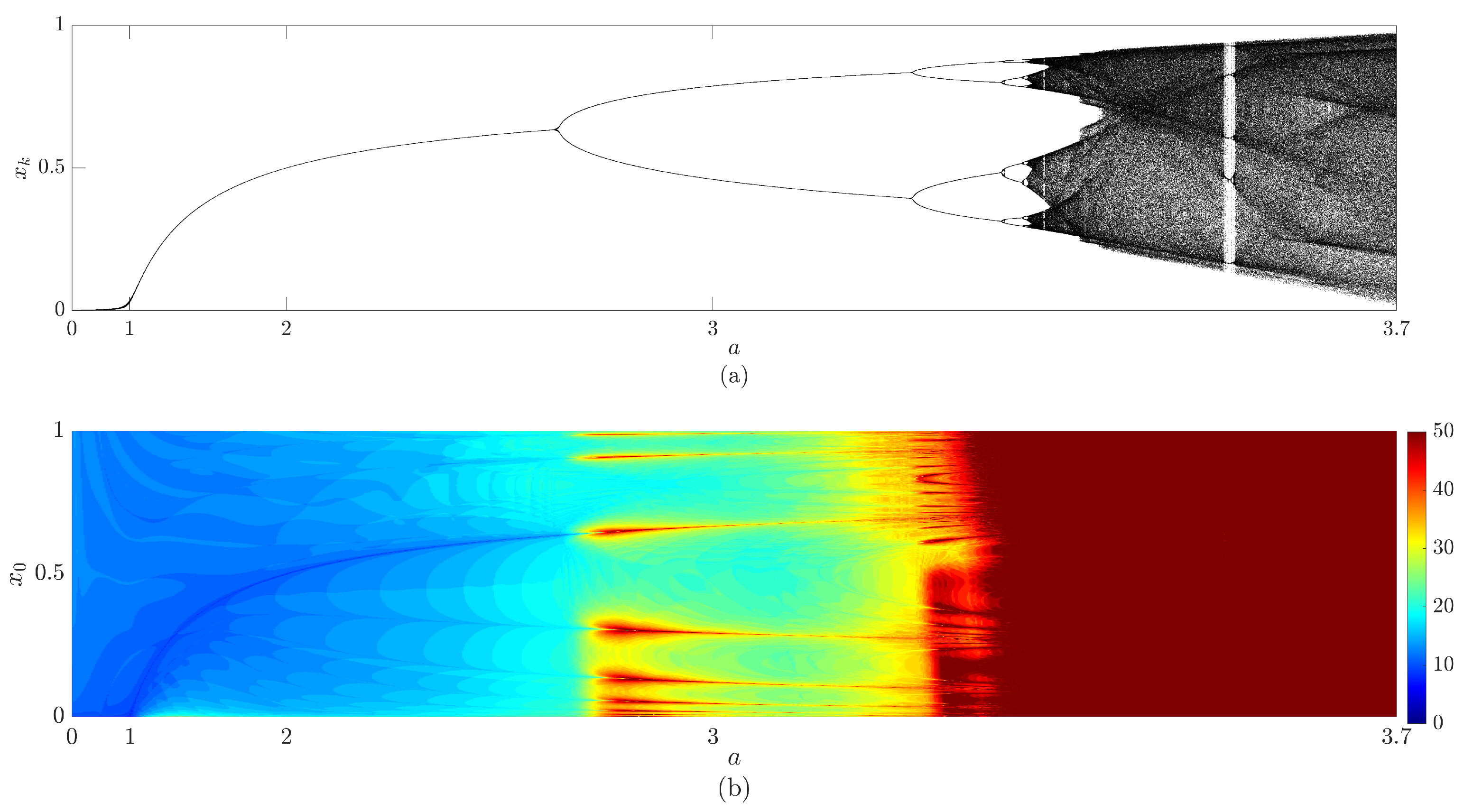
2.3. Fractional Logistic Map
3. The Unstable Orbits of the Fractional Difference Logistic Map
3.1. The Existence of the Unstable Period-1 Orbit at
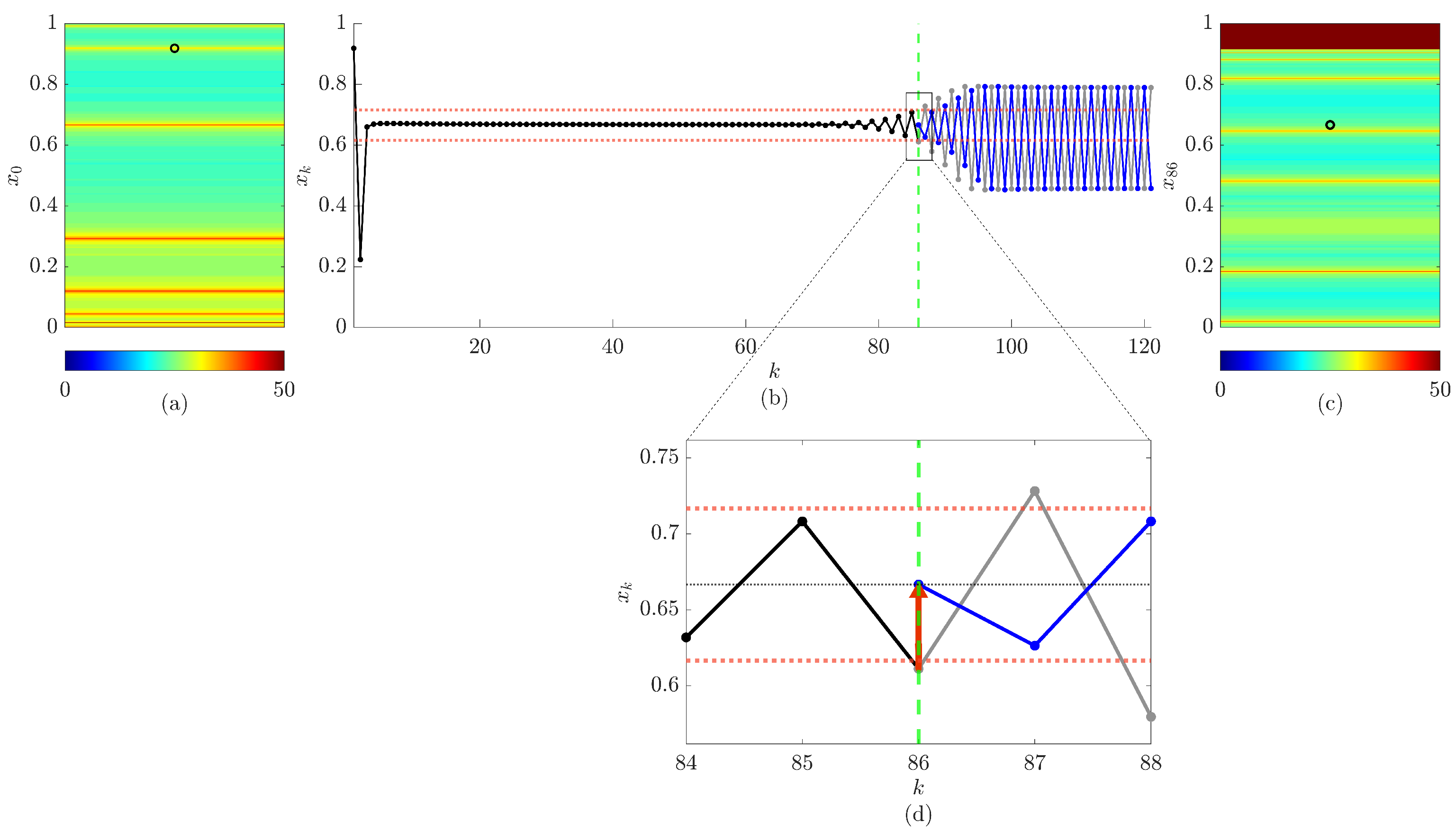
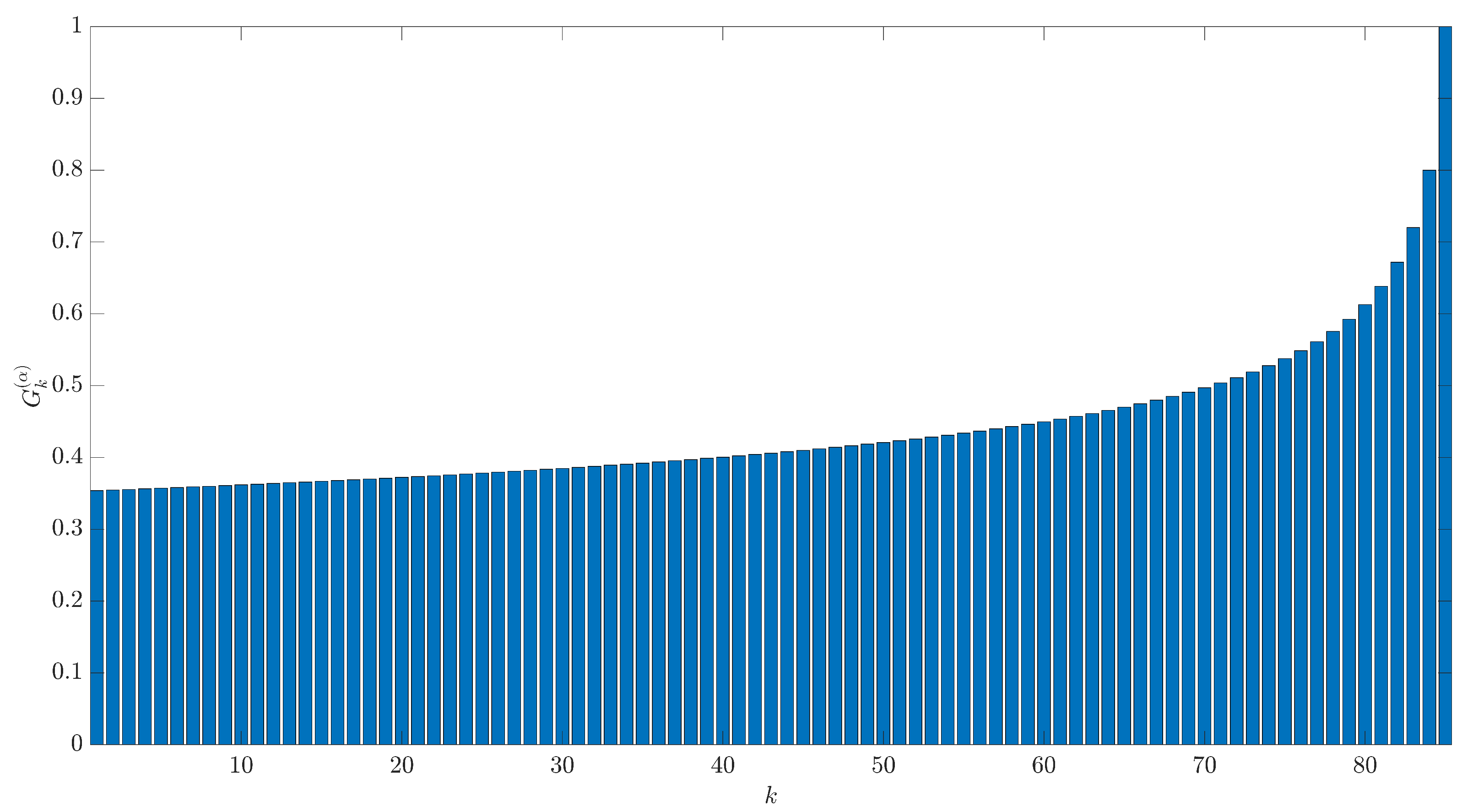
3.2. The Existence of the Non-Asymptotic Convergence to the Unstable Period-1 Orbit
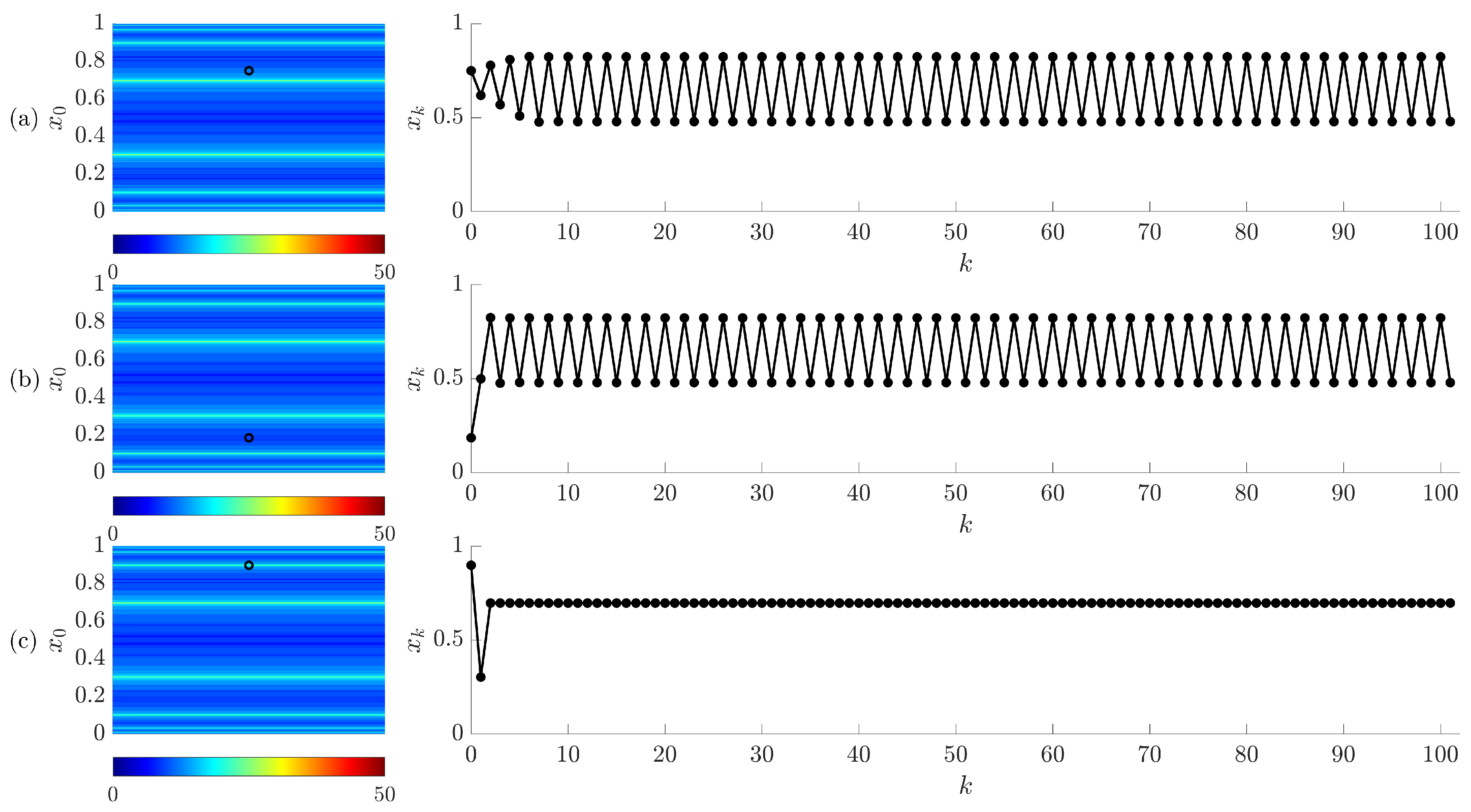
4. The Memory Effects and the Naive Control Scheme
4.1. The Naive Control Scheme for the Classical Logistic Map
4.2. The Naive Control Scheme for the Fractional Difference Logistic Map
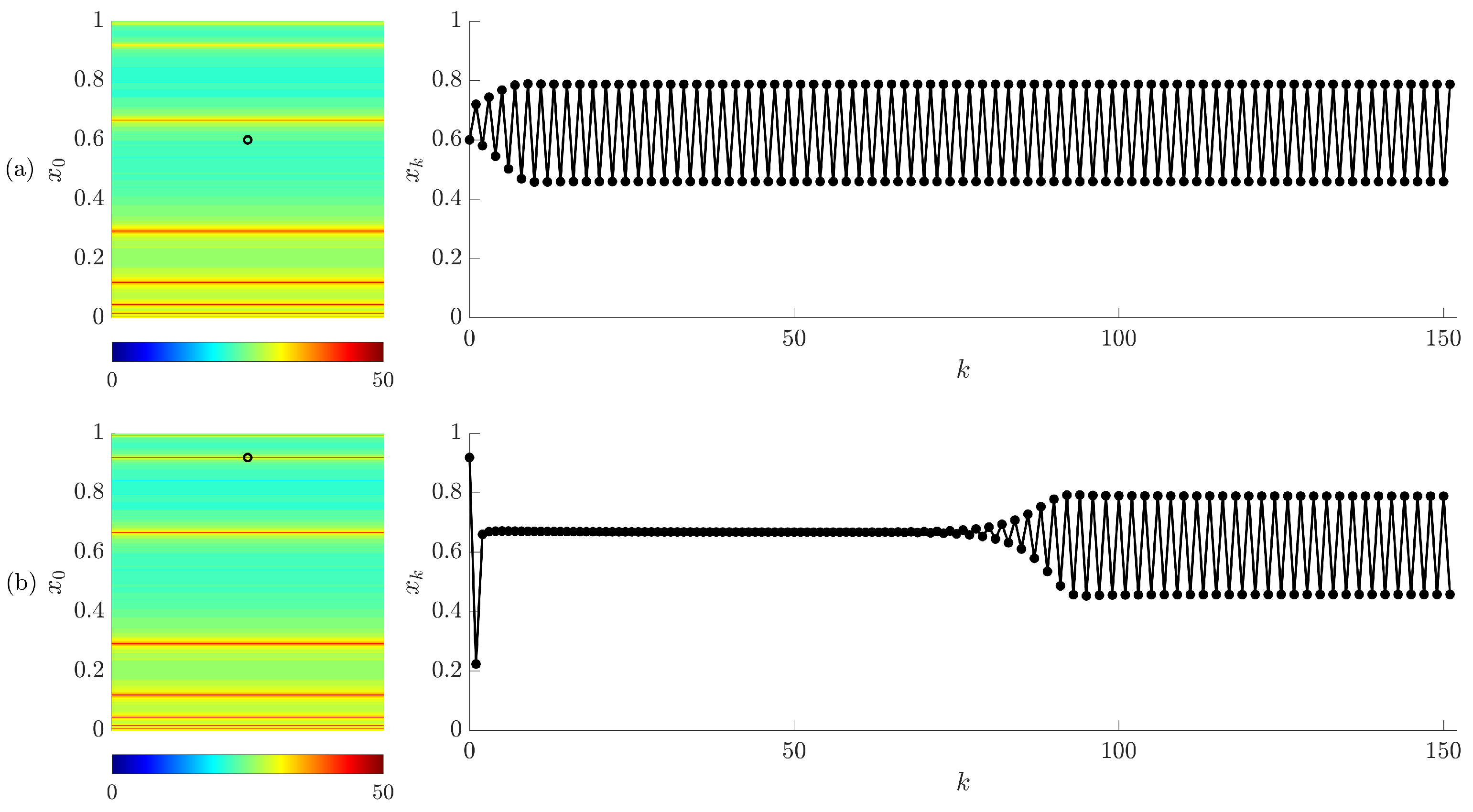
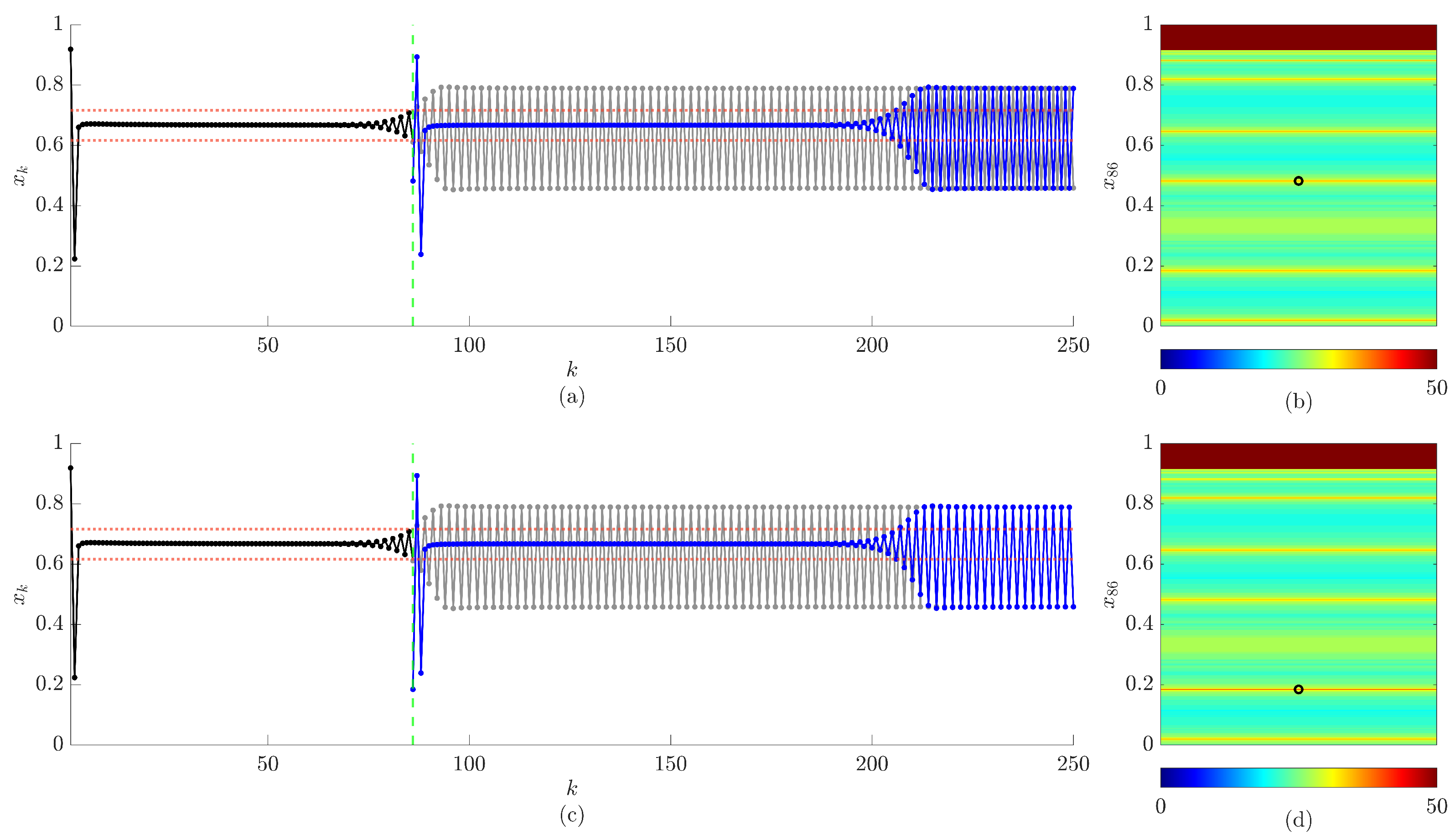
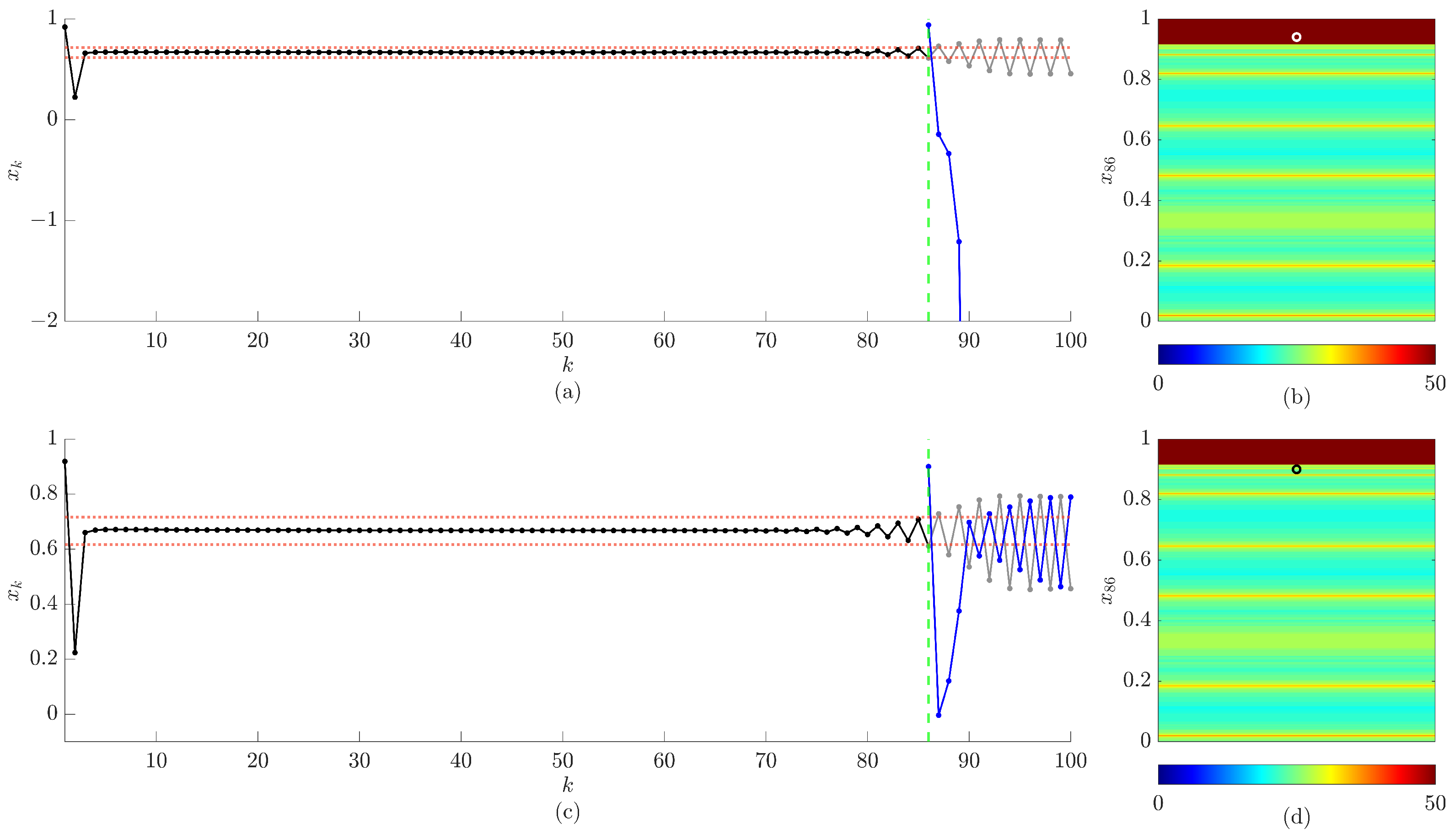
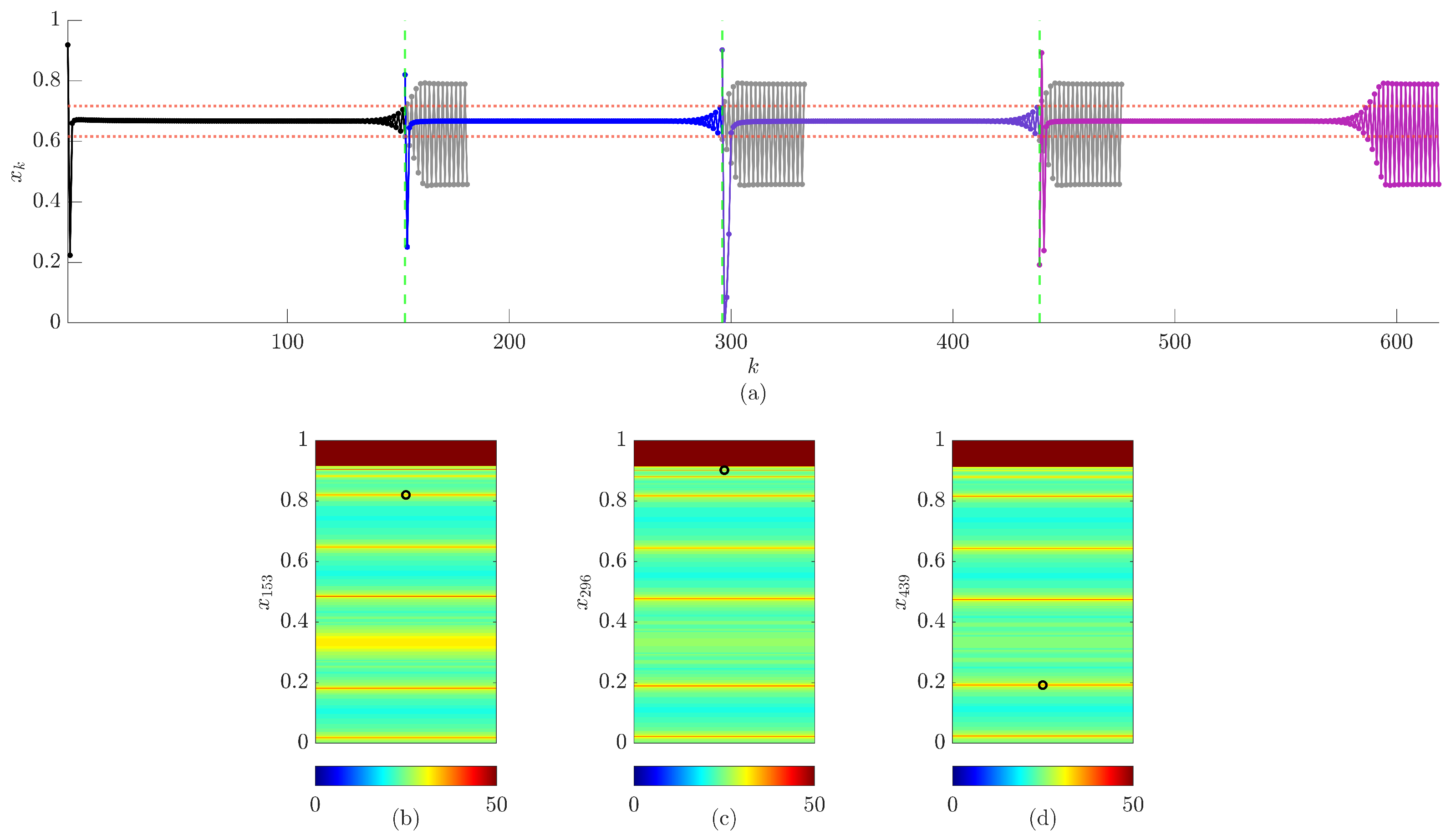
5. The Proposed Scheme Based on a Single Control Impulse
6. The Proposed Scheme Based on Multiple Control Impulses
7. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Galor, O. Discrete Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Smith, H.L.; Thieme, H.R. Dynamical Systems and Population Persistence; American Mathematical Soc.: Providence, RI, USA, 2011; Volume 118. [Google Scholar]
- Hasegawa, Y. Control Problems of Discrete-Time Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2013; Volume 447. [Google Scholar]
- Yang, X.; Deng, W.; Yao, J. Neural network based output feedback control for DC motors with asymptotic stability. Mech. Syst. Signal Process. 2022, 164, 108288. [Google Scholar] [CrossRef]
- Vinoth, S.; Sivasamy, R.; Sathiyanathan, K.; Unyong, B.; Vadivel, R.; Gunasekaran, N. A novel discrete-time Leslie–Gower model with the impact of Allee effect in predator population. Complexity 2022, 2022, 6931354. [Google Scholar] [CrossRef]
- Zheng, Y.; Yu, J. Stabilization of multi-rotation unstable periodic orbits through dynamic extended delayed feedback control. Chaos Solitons Fractals 2022, 161, 112362. [Google Scholar] [CrossRef]
- Rodríguez-Núñez, J.M.; de León, A.; Molinar-Tabares, M.E.; Flores-Acosta, M.; Castillo, S. Computational chaos control based on small perturbations for complex spectra simulation. Simulation 2022, 98, 835–846. [Google Scholar] [CrossRef]
- Hulka, T.; Matousek, R.; Lozi, R.P. Stabilization of Higher Periodic Orbits of Chaotic maps using Permutation-selective Objective Function. In Proceedings of the 2022 IEEE Workshop on Complexity in Engineering (COMPENG), IEEE, Florence, Italy, 18–20 July 2022; pp. 1–5. [Google Scholar]
- Bramburger, J.J.; Kutz, J.N.; Brunton, S.L. Data-driven stabilization of periodic orbits. IEEE Access 2021, 9, 43504–43521. [Google Scholar] [CrossRef]
- Weng, Y.; Zhang, Q.; Cao, J.; Yan, H.; Qi, W.; Cheng, J. Finite-time model-free adaptive control for discrete-time nonlinear systems. IEEE Trans. Circuits Syst. II Express Briefs 2023. [CrossRef]
- Edelman, M. Maps with power-law memory: Direct introduction and Eulerian numbers, fractional maps, and fractional difference maps. Handb. Fract. Calc. Appl. 2019, 2, 47–63. [Google Scholar]
- Chen, L.; Yin, H.; Yuan, L.; Machado, J.T.; Wu, R.; Alam, Z. Double color image encryption based on fractional order discrete improved Henon map and Rubik’s cube transform. Signal Process. Image Commun. 2021, 97, 116363. [Google Scholar] [CrossRef]
- Zhu, L.; Jiang, D.; Ni, J.; Wang, X.; Rong, X.; Ahmad, M.; Chen, Y. A stable meaningful image encryption scheme using the newly-designed 2D discrete fractional-order chaotic map and Bayesian compressive sensing. Signal Process. 2022, 195, 108489. [Google Scholar] [CrossRef]
- Liu, Z.; Xia, T.; Wang, T. Dynamic analysis of fractional-order six-order discrete chaotic mapping and its application in information security. Optik 2023, 272, 170356. [Google Scholar] [CrossRef]
- Coll, C.; Herrero, A.; Ginestar, D.; S’anchez, E. The discrete fractional order difference applied to an epidemic model with indirect transmission. Appl. Math. Model. 2022, 103, 636–648. [Google Scholar] [CrossRef]
- Abbes, A.; Ouannas, A.; Shawagfeh, N.; Grassi, G. The effect of the Caputo fractional difference operator on a new discrete COVID-19 model. Results Phys. 2022, 39, 105797. [Google Scholar] [CrossRef]
- Chu, Y.M.; Bekiros, S.; Zambrano-Serrano, E.; Orozco-L’opez, O.; Lahmiri, S.; Jahanshahi, H.; Aly, A.A. Artificial macro-economics: A chaotic discrete-time fractional-order laboratory model. Chaos Solitons Fractals 2021, 145, 110776. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, J.; He, S.; Sun, K. Discrete fracmemristor-based chaotic map by Grunwald–Letnikov difference and its circuit implementation. Chaos Solitons Fractals 2023, 171, 113429. [Google Scholar] [CrossRef]
- Edelman, M.; Jacobi, R. Power-Law Memory in Living Species and the Distribution of Lifespans. In Proceedings of the APS March Meeting Abstracts, Virtual, 15–19 March 2021; Volume 2021, p. L14-003. [Google Scholar]
- Zambrano-Serrano, E.; Bekiros, S.; Platas-Garza, M.A.; Posadas-Castillo, C.; Agarwal, P.; Jahanshahi, H.; Aly, A.A. On chaos and projective synchronization of a fractional difference map with no equilibria using a fuzzy-based state feedback control. Phys. Stat. Mech. Its Appl. 2021, 578, 126100. [Google Scholar] [CrossRef]
- Lu, Q.; Zhu, Y.; Li, B. Necessary optimality conditions of fractional-order discrete uncertain optimal control problems. Eur. J. Control. 2023, 69, 100723. [Google Scholar] [CrossRef]
- Yao, Y.; Wu, L.B. Backstepping control for fractional discrete-time systems. Appl. Math. Comput. 2022, 434, 127450. [Google Scholar] [CrossRef]
- Shahamatkhah, E.; Tabatabaei, M. Containment control of linear discrete-time fractional-order multi-agent systems with time-delays. Neurocomputing 2020, 385, 42–47. [Google Scholar] [CrossRef]
- Edelman, M. Universal fractional map and cascade of bifurcations type attractors. Chaos Interdiscip. J. Nonlinear Sci. 2013, 23, 033127. [Google Scholar] [CrossRef]
- Edelman, M. Fractional maps and fractional attractors. Part II: Fractional difference caputo α-families of maps. Discontinuity Nonlinearity Complex. 2015, 4, 391–402. [Google Scholar] [CrossRef]
- Kaslik, E.; Sivasundaram, S. Non-existence of periodic solutions in fractional-order dynamical systems and a remarkable difference between integer and fractional-order derivatives of periodic functions. Nonlinear Anal. Real World Appl. 2012, 13, 1489–1497. [Google Scholar] [CrossRef]
- Diblík, J.; Fečkan, M.; Pospíšil, M. Nonexistence of periodic solutions and S-asymptotically periodic solutions in fractional difference equations. Appl. Math. Comput. 2015, 257, 230–240. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A.; Powell, J.D. Feedback Control of Dynamic Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002; Volume 4. [Google Scholar]
- Piunovskiy, A.; Plakhov, A.; Torres, D.F.; Zhang, Y. Optimal impulse control of dynamical systems. Siam J. Control. Optim. 2019, 57, 2720–2752. [Google Scholar] [CrossRef]
- Lu, G.; Landauskas, M.; Ragulskis, M. Control of divergence in an extended invertible logistic map. Int. J. Bifurc. Chaos 2018, 28, 1850129. [Google Scholar] [CrossRef]
- Landauskas, M.; Ragulskis, M. A pseudo-stable structure in a completely invertible bouncer system. Nonlinear Dyn. 2014, 78, 1629–1643. [Google Scholar] [CrossRef]
- Navickas, Z.; Ragulskis, M.; Karaliene, D.; Telksnys, T. Weak and strong orders of linear recurring sequences. Comput. Appl. Math. 2018, 37, 3539–3561. [Google Scholar] [CrossRef]
- Petkevičiūtė-Gerlach, D.; Timofejeva, I.; Ragulskis, M. Clocking convergence of the fractional difference logistic map. Nonlinear Dyn. 2020, 100, 3925–3935. [Google Scholar] [CrossRef]
- Kurakin, V.; Kuzmin, A.; Mikhalev, A.; Nechaev, A. Linear recurring sequences over rings and modules. J. Math. Sci. 1995, 76, 2793–2915. [Google Scholar] [CrossRef]
- Bisgard, J. Analysis and Linear Algebra: The Singular Value Decomposition and Applications; American Mathematical Soc.: Providence, RI, USA, 2020; Volume 94. [Google Scholar]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef]
- Edelman, M. On stability of fixed points and chaos in fractional systems. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 023112. [Google Scholar] [CrossRef]
- Edelman, M. Evolution of systems with power-law memory: Do we have to die?(Dedicated to the Memory of Valentin Afraimovich). Demogr. Popul. Health Aging Health Expend. 2020, 50, 65–85. [Google Scholar]
- Edelman, M. Stability of fixed points in generalized fractional maps of the orders 0< α< 1. Nonlinear Dyn. 2023, 111, 10247–10254. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uzdila, E.; Telksniene, I.; Telksnys, T.; Ragulskis, M. Finite-Time Stabilization of Unstable Orbits in the Fractional Difference Logistic Map. Fractal Fract. 2023, 7, 570. https://doi.org/10.3390/fractalfract7080570
Uzdila E, Telksniene I, Telksnys T, Ragulskis M. Finite-Time Stabilization of Unstable Orbits in the Fractional Difference Logistic Map. Fractal and Fractional. 2023; 7(8):570. https://doi.org/10.3390/fractalfract7080570
Chicago/Turabian StyleUzdila, Ernestas, Inga Telksniene, Tadas Telksnys, and Minvydas Ragulskis. 2023. "Finite-Time Stabilization of Unstable Orbits in the Fractional Difference Logistic Map" Fractal and Fractional 7, no. 8: 570. https://doi.org/10.3390/fractalfract7080570
APA StyleUzdila, E., Telksniene, I., Telksnys, T., & Ragulskis, M. (2023). Finite-Time Stabilization of Unstable Orbits in the Fractional Difference Logistic Map. Fractal and Fractional, 7(8), 570. https://doi.org/10.3390/fractalfract7080570






