Solitary and Periodic Wave Solutions of the Space-Time Fractional Extended Kawahara Equation
Abstract
1. Introduction
2. Preliminaries
- Linearity: .
- .
- .
- If the function is -differentiable, then .
3. The Solution Method (JEF Expansion Method)
4. Demonstrations and Applications
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. Ser. 5 1895, 39, 422–443. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas, A.H.; Alharthi, M.R. Novel analytical cnoidal and solitary wave solutions of the extended Kawahara equation. Chaos Solit. Fractals 2021, 147, 110965. [Google Scholar] [CrossRef]
- Inc, M.; Parto-Haghighi, M.; Akinlar, M.A.; Chu, Y.M. New numerical solutions of fractional-order Korteweg-de Vries equation. Results Phys. 2020, 19, 103326. [Google Scholar] [CrossRef]
- Kumar, V.S.; Rezazadeh, H.; Eslami, M.; Izadi, F.; Osman, M.S. Jacobi elliptic function expansion method for solving KdV equation with conformable derivative and dual-power law nonlinearity. Int. J. Appl. Comput. Math. 2019, 5, 127. [Google Scholar] [CrossRef]
- Yaslan, H.C.; Girgin, A. New exact solutions for the conformable space-time fractional KdV, CDG, (2+ 1)-dimensional CBS and (2 + 1)-dimensional AKNS equations. J. Taibah Univ. Sci. 2019, 13, 1–8. [Google Scholar] [CrossRef]
- Korkmaz, A. On the wave solutions of conformable fractional evolution equations. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2018, 67, 68–79. [Google Scholar] [CrossRef]
- Zafar, A. The Expa function method and the conformable time-fractional KdV equations. Nonlinear Eng. 2019, 8, 728–732. [Google Scholar] [CrossRef]
- Kurt, A.; Tasbozan, O.; Durur, H. The exact solutions of conformable fractional partial differential equations using new sub equation method. Fundam. J. Math. Appl. 2019, 2, 173–179. [Google Scholar] [CrossRef]
- Hepson, O.E.; Korkmaz, A.; Hosseini, K.; Rezazadeh, H.; Eslami, M. An expansion based on Sine-Gordon equation to solve KdV and modified KdV equations in conformable fractional forms. Bol. Soc. Parana. Mat. 2022, 40, 1–10. [Google Scholar] [CrossRef]
- Yokuş, A. Comparison of Caputo and conformable derivatives for time-fractional Korteweg–de Vries equation via the finite difference method. Int. J. Mod. Phys. B 2018, 32, 1850365. [Google Scholar] [CrossRef]
- Karayer, H.H.; Demirhan, A.D.; Büyükkılıç, F. Analytical solutions of conformable time, space, and time-space fractional KdV equations. Turk. J. Phys. 2018, 42, 254–264. [Google Scholar] [CrossRef]
- Chung, W.S.; Hassanabadi, H.; Lütfüoğlu, B.C.; Kříž, J. Conformable fractional wave equation and conformable fractional KdV equation from the ordinary Newton equation with deformed translational symmetry. Waves Random Complex Media 2022, 1–12. [Google Scholar] [CrossRef]
- Dascioglu, A.; Culha, S.; Bayram, D.V. New analytical solutions of the space fractional KdV equation in terms of Jacobi elliptic functions. New Trends Math. Sci. 2017, 5, 232–241. [Google Scholar] [CrossRef]
- Ferdous, F.; Hafez, M.G. Nonlinear time fractional Korteweg-de Vries equations for the interaction of wave phenomena in fluid-filled elastic tubes. Eur. Phys. J. Plus 2018, 133, 384. [Google Scholar] [CrossRef]
- Yaslan, H.; Girgin, A. The extended tanh method for solving conformable space-time fractional KdV equations. Int. J. Nonlinear Anal. Appl. 2021, 12, 1181–1194. [Google Scholar]
- Thabet, H.; Kendre, S.; Peters, J. Travelling wave solutions for fractional Korteweg-de Vries equations via an approximate-analytical method. AIMS Math. 2019, 4, 1203–1222. [Google Scholar] [CrossRef]
- Nuruddeen, R.I. Multiple soliton solutions for the (3 + 1) conformable space–time fractional modified Korteweg–de-Vries equations. J. Ocean Eng. Sci. 2018, 3, 11–18. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S. Solitary wave solutions for time fractional third order modified KdV equation using two reliable techniques (G′/G)-expansion method and improved (G′/G)-expansion method. Phys. A Stat. Mech. Appl. 2016, 448, 265–282. [Google Scholar] [CrossRef]
- Abdulaziz, O.; Hashim, I.; Ismail, E.S. Approximate analytical solution to fractional modified KdV equations. Math. Comput. Model. 2009, 49, 136–145. [Google Scholar] [CrossRef]
- Akbulut, A.; Taşcan, F. Lie symmetries, symmetry reductions and conservation laws of time fractional modified Korteweg–de Vries (mKdV) equation. Chaos Solit. Fractals 2017, 100, 1–6. [Google Scholar] [CrossRef]
- Kurulay, M.; Bayram, M. Approximate analytical solution for the fractional modified KdV by differential transform method. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1777–1782. [Google Scholar] [CrossRef]
- Nazari-Golshan, A. Derivation and solution of space fractional modified Korteweg de Vries equation. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104904. [Google Scholar] [CrossRef]
- Zafar, A.; Seadawy, A.R. The conformable space-time fractional mKdV equations and their exact solutions. J. King Saud Univ. Sci. 2019, 31, 1478–1484. [Google Scholar] [CrossRef]
- Sabi’u, J.; Jibril, A.; Gadu, A.M. New exact solution for the (3 + 1) conformable space–time fractional modified Korteweg–de-Vries equations via Sine-Cosine method. J. Taibah Univ. Sci. 2019, 13, 91–95. [Google Scholar] [CrossRef]
- Uddin, M.H.; Akbar, M.A.; Khan, M.A.; Haque, M.A. Families of exact traveling wave solutions to the space time fractional modified KdV equation and the fractional Kolmogorov-Petrovskii-Piskunov equation. J. Mech. Contin. Math. Sci. 2018, 13, 17–33. [Google Scholar]
- Tasbozan, O.; Çenesiz, Y.; Kurt, A. New solutions for conformable fractional Boussinesq and combined KdV-mKdV equations using Jacobi elliptic function expansion method. Eur. Phys. J. Plus 2016, 131, 244. [Google Scholar] [CrossRef]
- Korkmaz, A. The Modified Kudryashov Method for the Conformable Time Fractional (3+ 1)-dimensional Kadomtsev-Petviashvili and the Modified Kawahara Equations. Preprints. Org 2016, 2016120004. [Google Scholar] [CrossRef]
- Çulha Ünal, S. Approximate Solutions of Time Fractional Kawahara Equation by Utilizing the Residual Power Series Method. Int. J. Appl. Comput. Math. 2022, 8, 78. [Google Scholar] [CrossRef]
- Yaslan, H.Ç. New analytic solutions of the conformable space–time fractional Kawahara equation. Optik 2017, 140, 123–126. [Google Scholar] [CrossRef]
- Shahen, N.H.M.; Bashar, M.H.; Tahseen, T.; Hossain, S. Solitary and rogue wave solutions to the conformable time fractional modified kawahara equation in mathematical physics. Adv. Math. Phys. 2021, 2021, 6668092. [Google Scholar] [CrossRef]
- Ünal, S.Ç.; Daşcıoğlu, A.; Bayram, D.V. New exact solutions of space and time fractional modified Kawahara equation. Phys. A Stat. Mech. Appl. 2020, 551, 124550. [Google Scholar] [CrossRef]
- Daşcıoğlu, A.; Çulha Ünal, S. New exact solutions for the space-time fractional Kawahara equation. Appl. Math. Model. 2021, 89, 952–965. [Google Scholar] [CrossRef]
- Safavi, M.; Khajehnasiri, A.A. Solutions of the modified Kawahara equation with time-and space-fractional derivatives. J. Mod. Methods Numer. Math. 2016, 7, 10–18. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas, A.H.; Alyousef, H.A.; Alharthi, M.R. Novel exact and approximate solutions to the family of the forced damped Kawahara equation and modeling strong nonlinear waves in a plasma. Chin. J. Phys. 2022, 77, 2454–2471. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas, A.H.; Alharthi, M.R. On the dissipative extended Kawahara solitons and cnoidal waves in a collisional plasma: Novel analytical and numerical solutions. Phys. Fluids 2021, 33, 106101. [Google Scholar] [CrossRef]
- Alyousef, H.A.; Salas, A.H.; Matoog, R.T.; El-Tantawy, S.A. On the analytical and numerical approximations to the forced damped Gardner Kawahara equation and modeling the nonlinear structures in a collisional plasma. Phys. Fluids 2022, 34, 103105. [Google Scholar] [CrossRef]
- Erdelyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1953; Volume 2. [Google Scholar]
- Hua-Mei, L. New exact solutions of nonlinear Gross–Pitaevskii equation with weak bias magnetic and time-dependent laser fields. Chin. Phys. 2005, 14, 251. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, T. A generalized F-expansion method and new exact solutions of Konopelchenko–Dubrovsky equations. Appl. Math. Comput. 2006, 183, 1190–1200. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, T. Variable-coefficient Jacobi elliptic function expansion method for (2+ 1)-dimensional Nizhnik–Novikov–Vesselov equations. Appl. Math. Comput. 2011, 218, 1308–1316. [Google Scholar] [CrossRef]
- Ünal, S.Ç.; Daşcioğlu, A.; BAYRAM, D.V. Jacobi elliptic function solutions of space-time fractional symmetric regularized long wave equation. Math. Sci. Appl. E-Notes 2021, 9, 53–63. [Google Scholar] [CrossRef]
- Daşcıoğlu, A.; Çulha Ünal, S.; Varol Bayram, D. New analytical solutions for space and time fractional Phi-4 equation. Naturengs 2020, 1, 30–46. [Google Scholar] [CrossRef]
- Ali, A.T. New generalized Jacobi elliptic function rational expansion method. J. Comput. Appl. Math. 2011, 235, 4117–4127. [Google Scholar] [CrossRef]

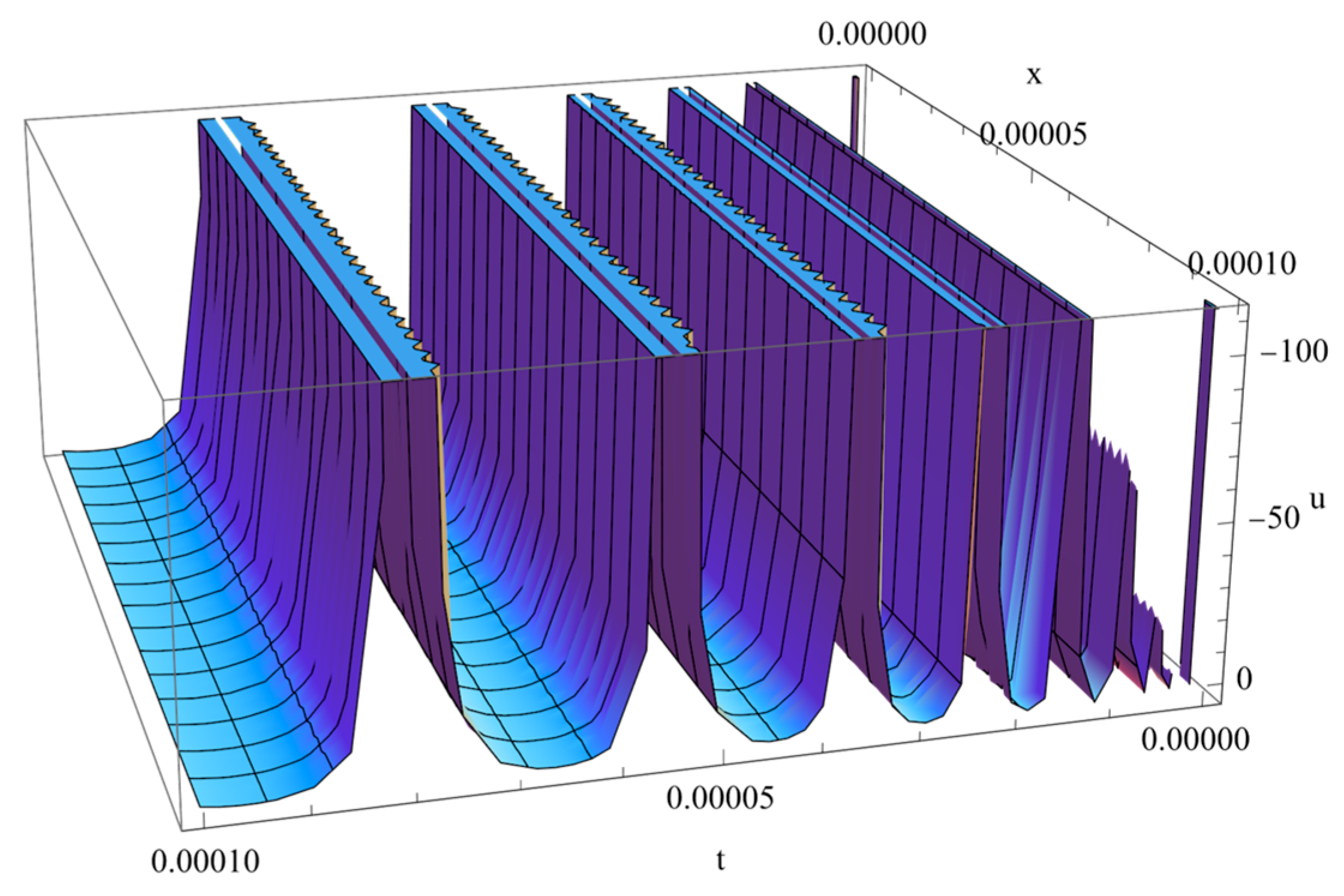
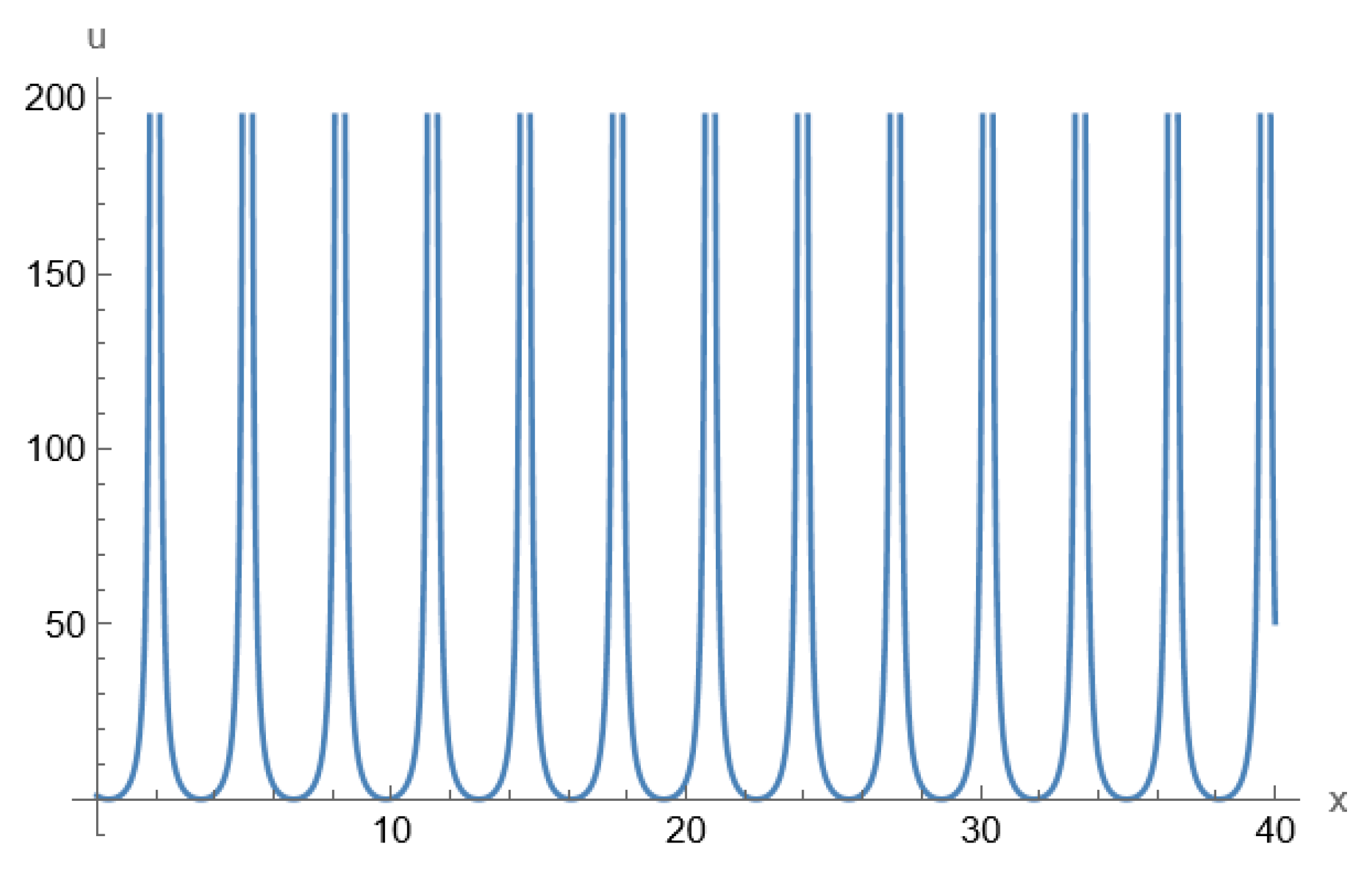
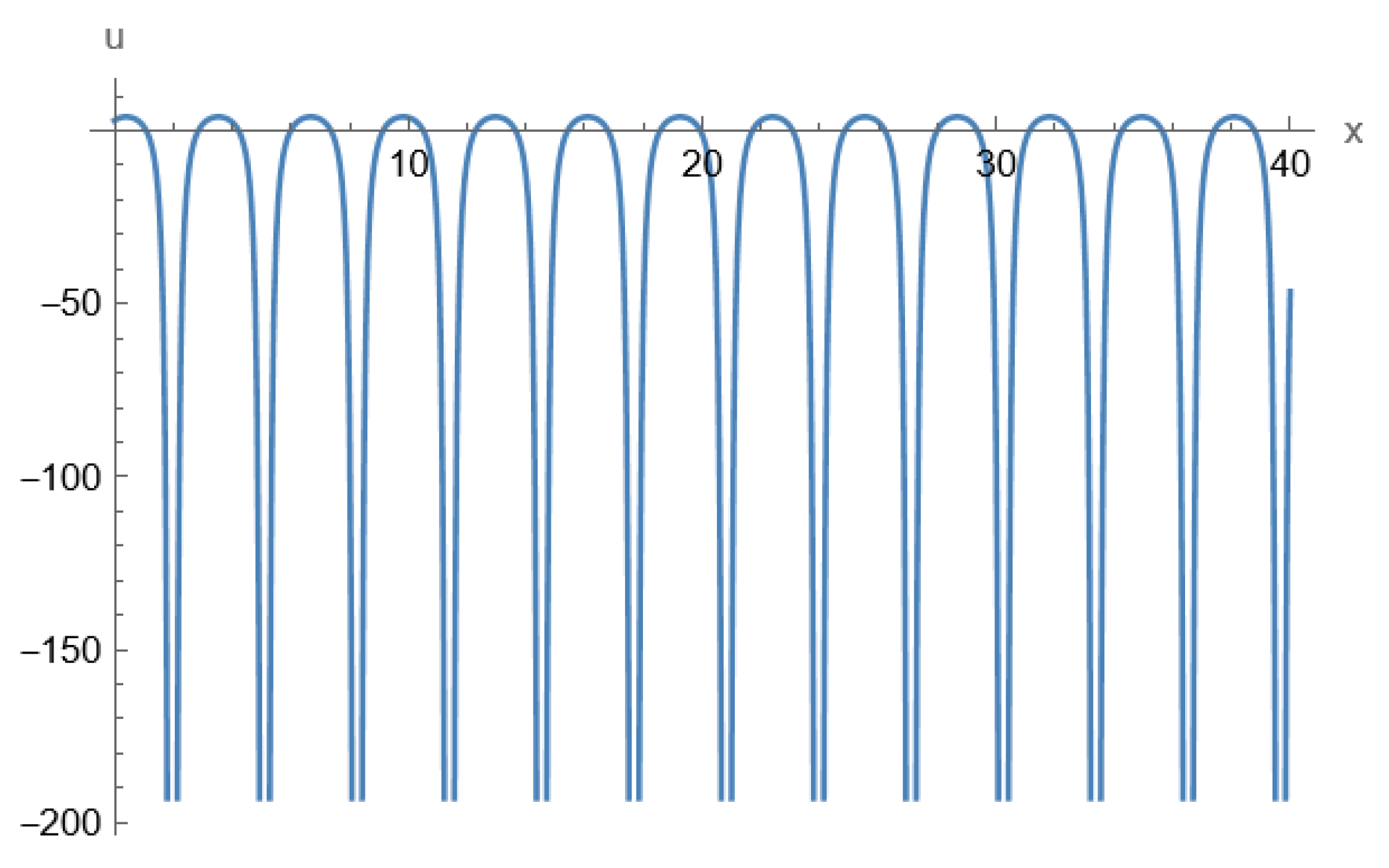
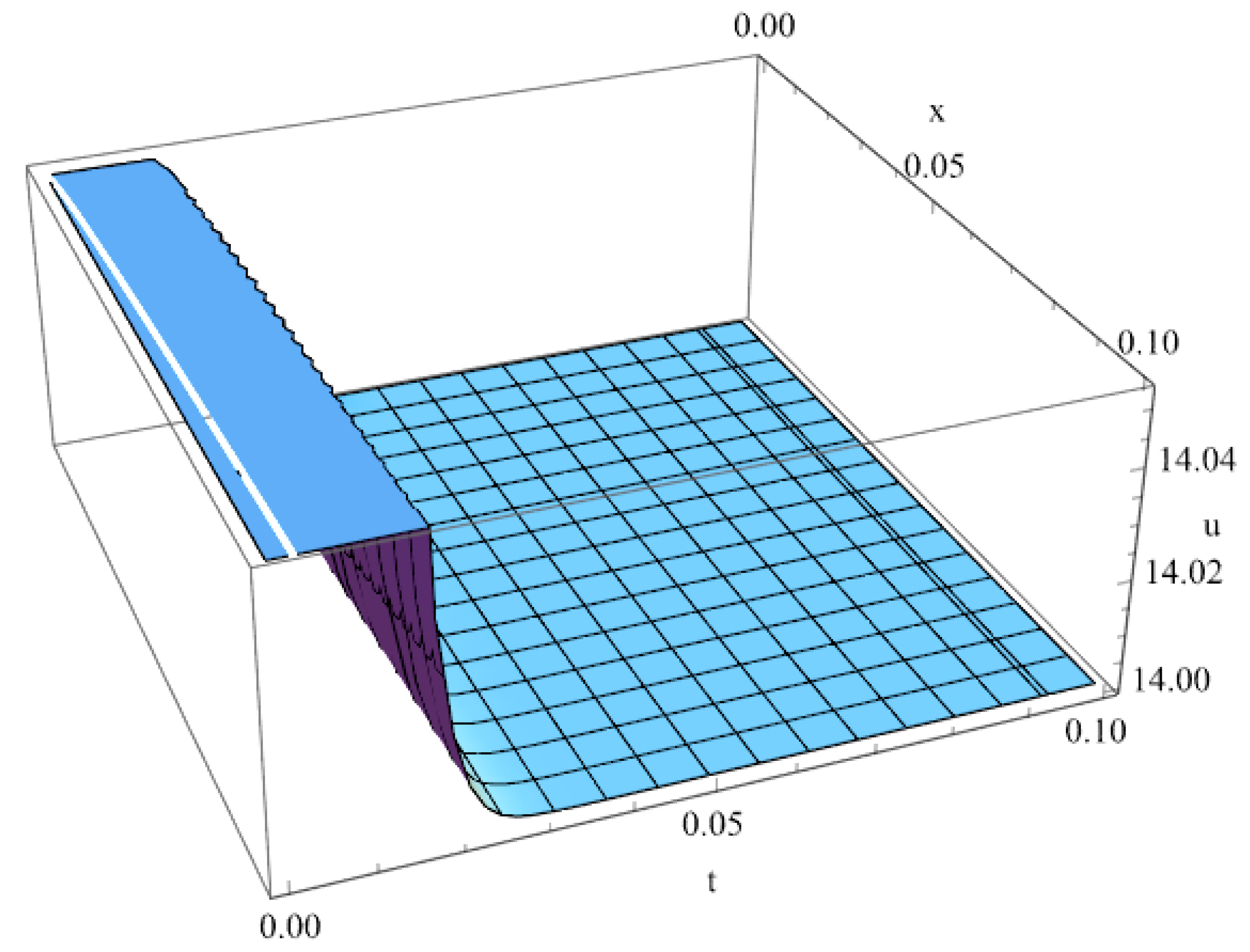
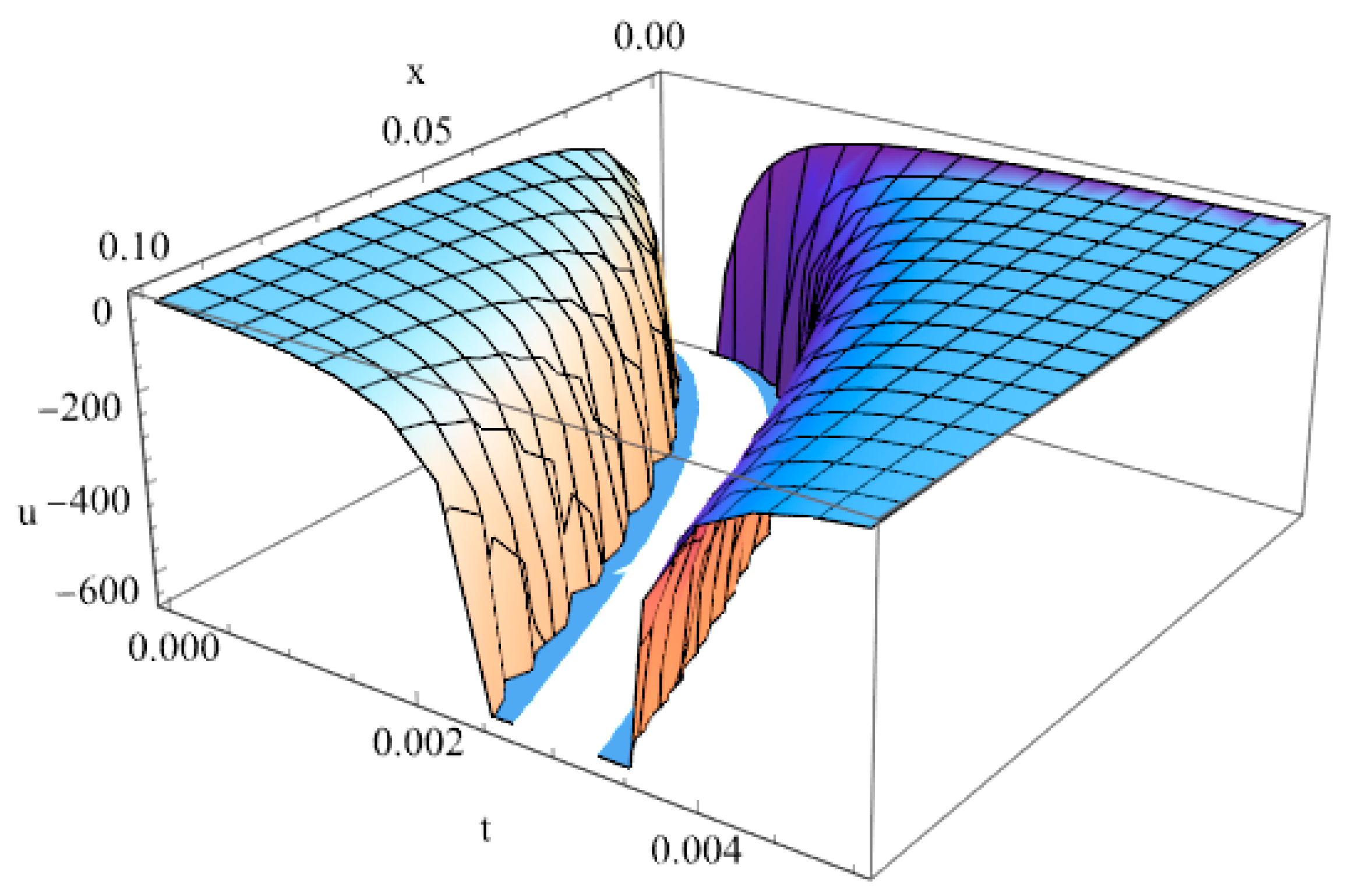
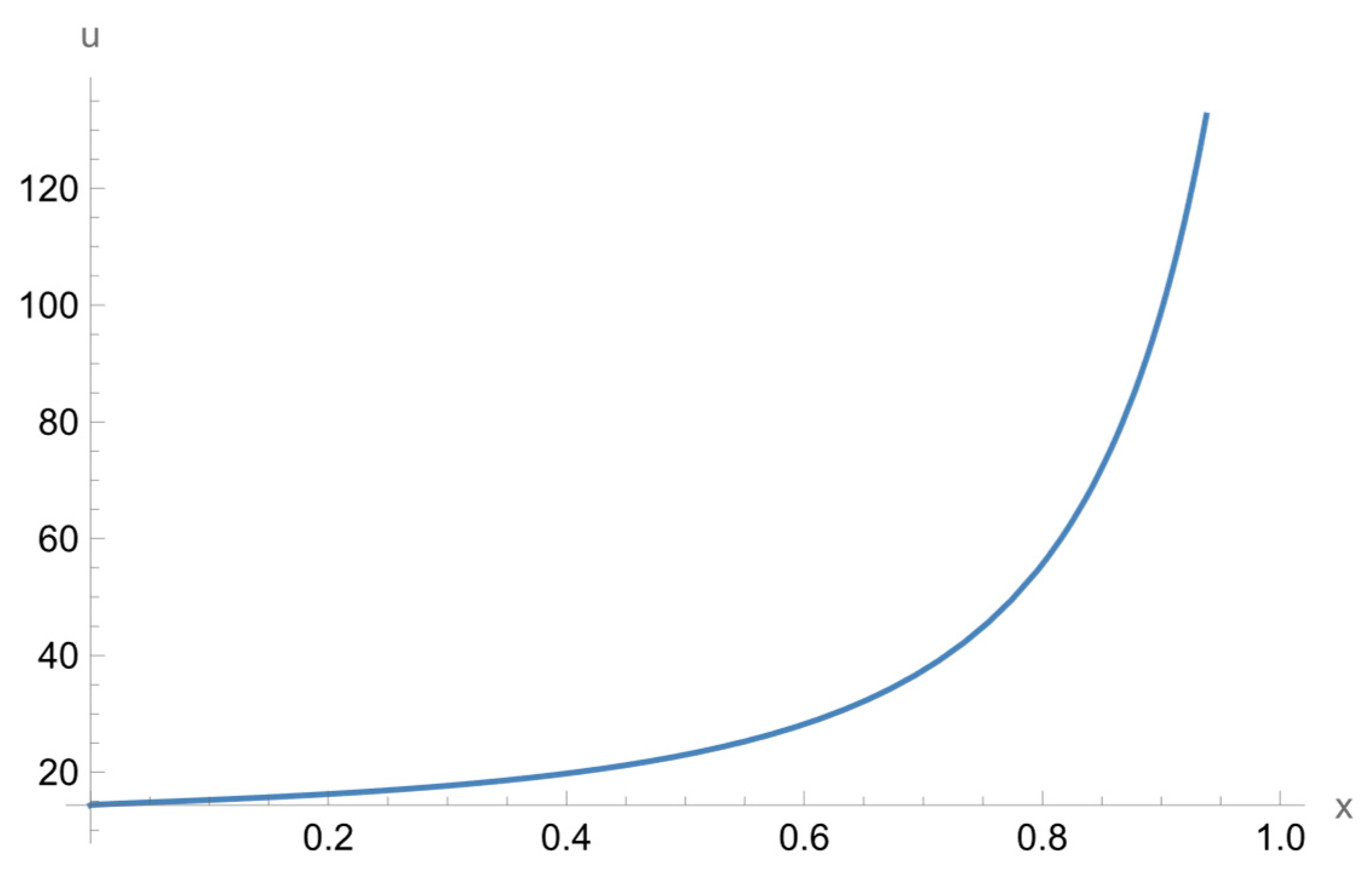
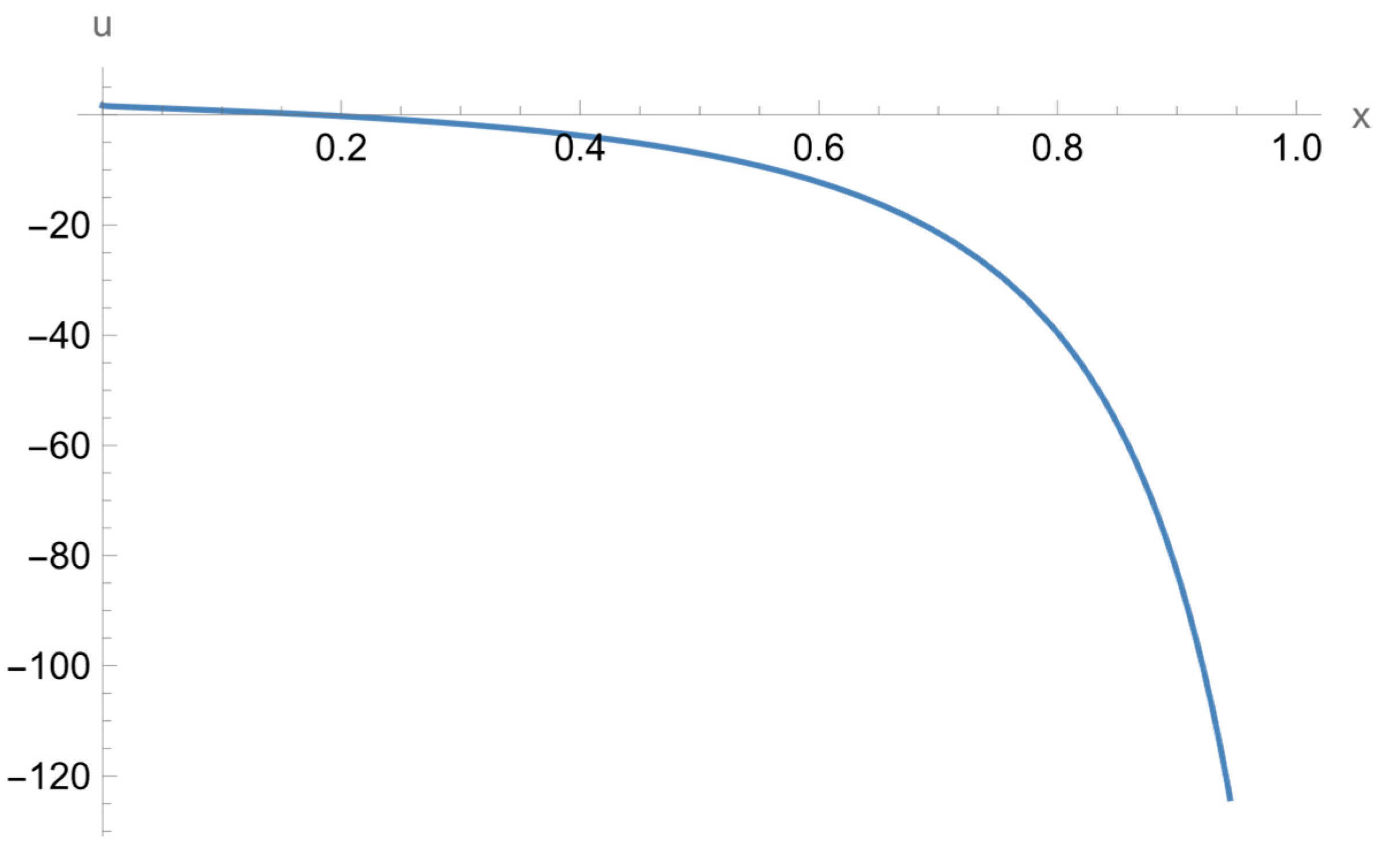
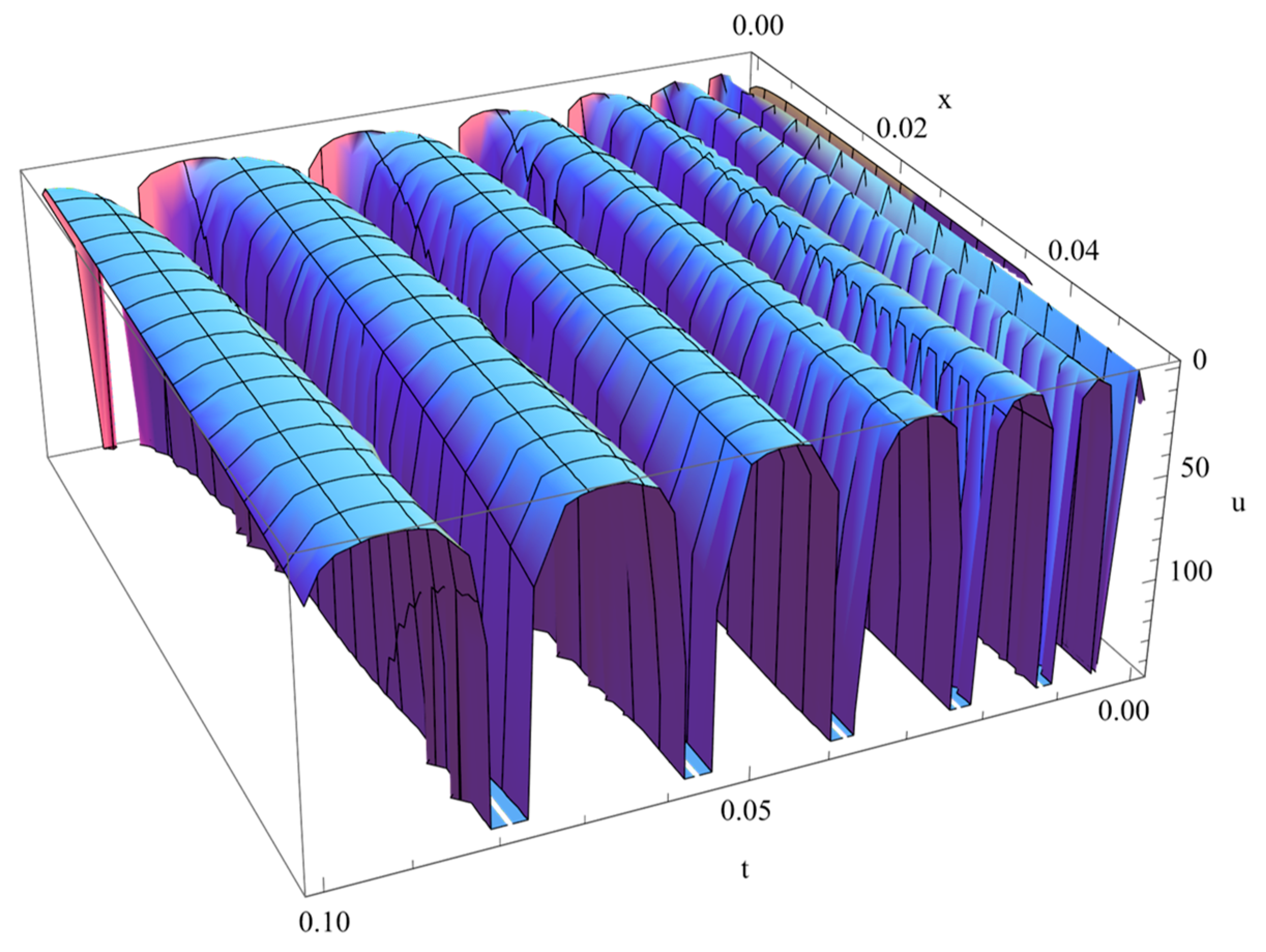
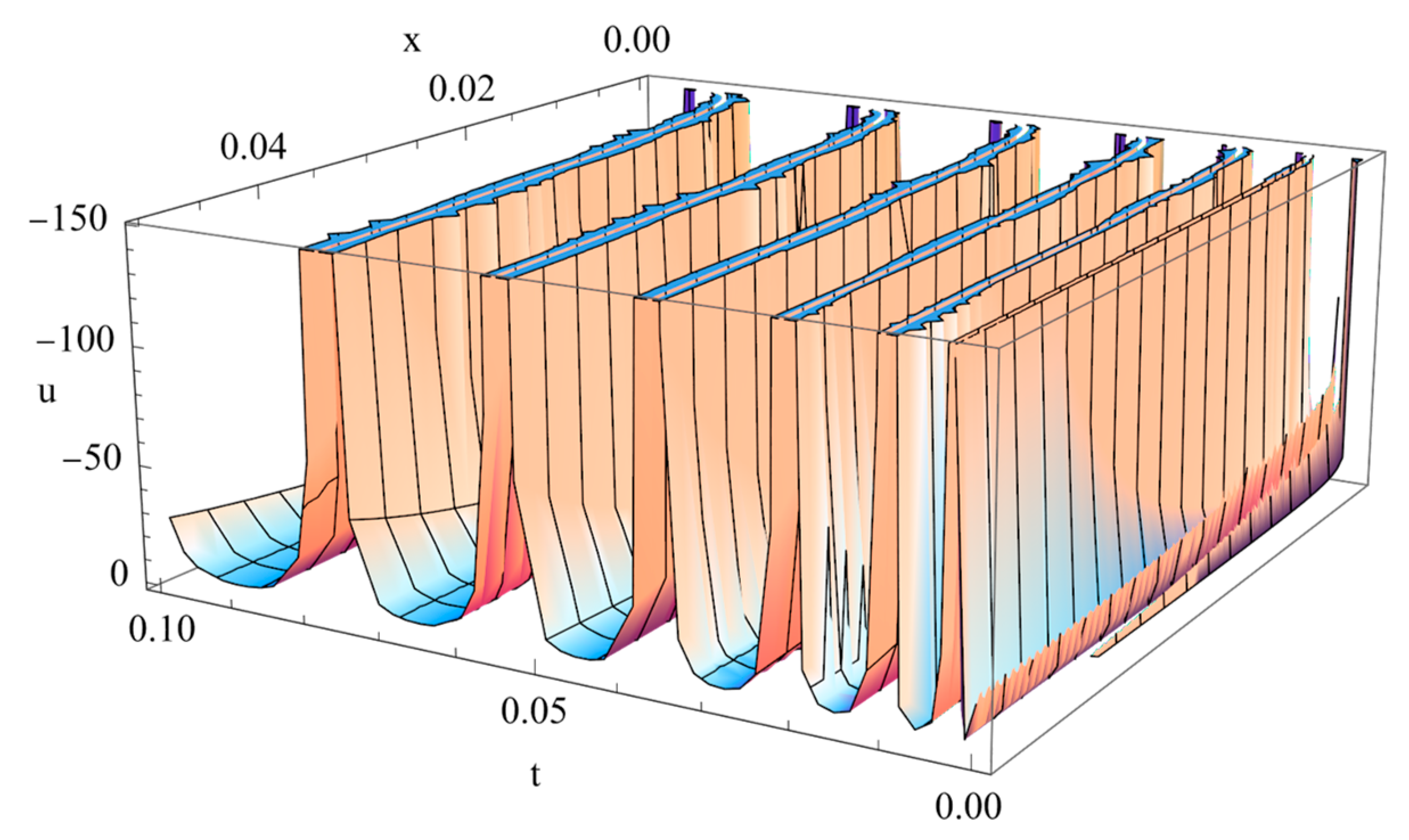
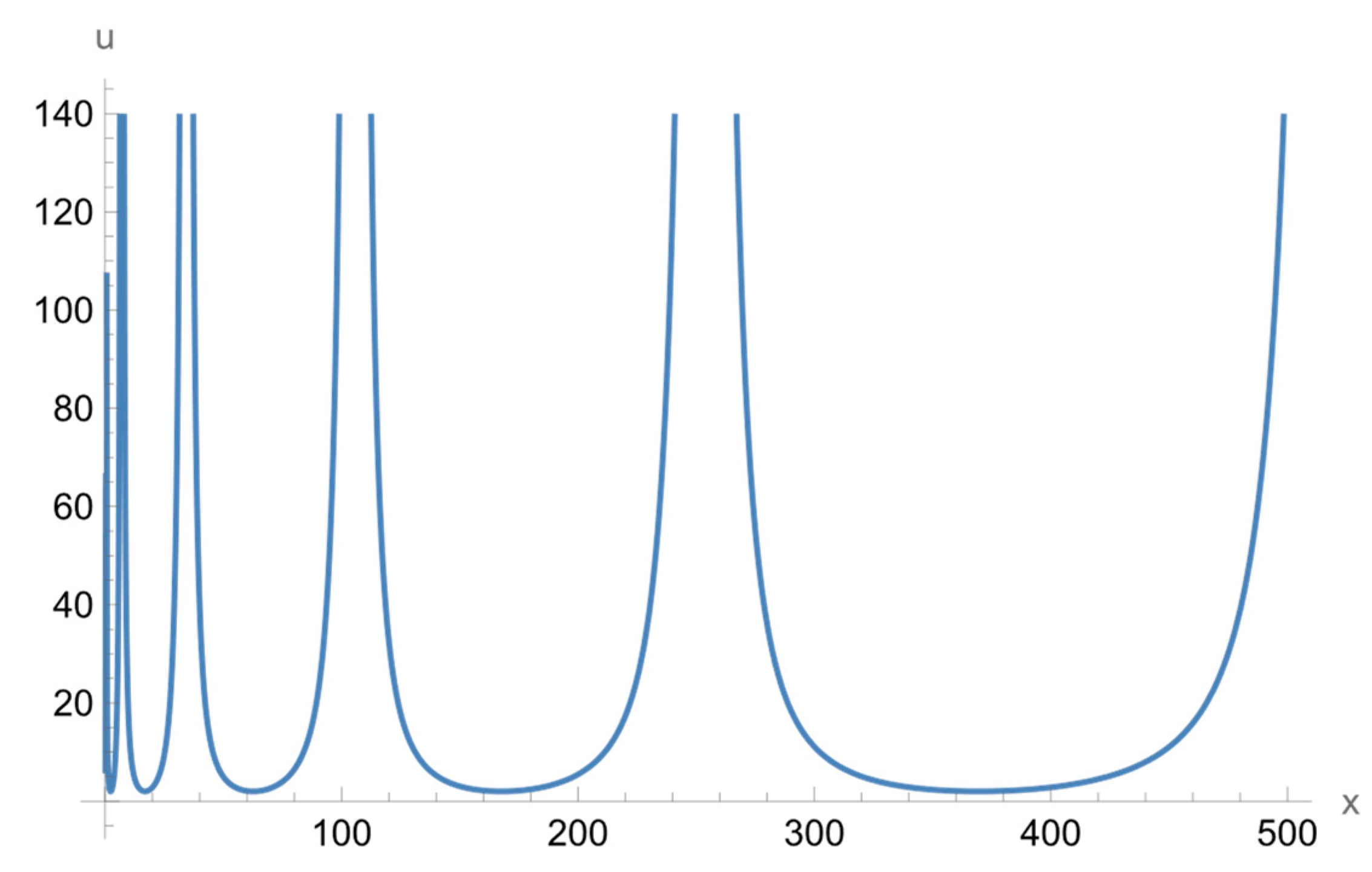
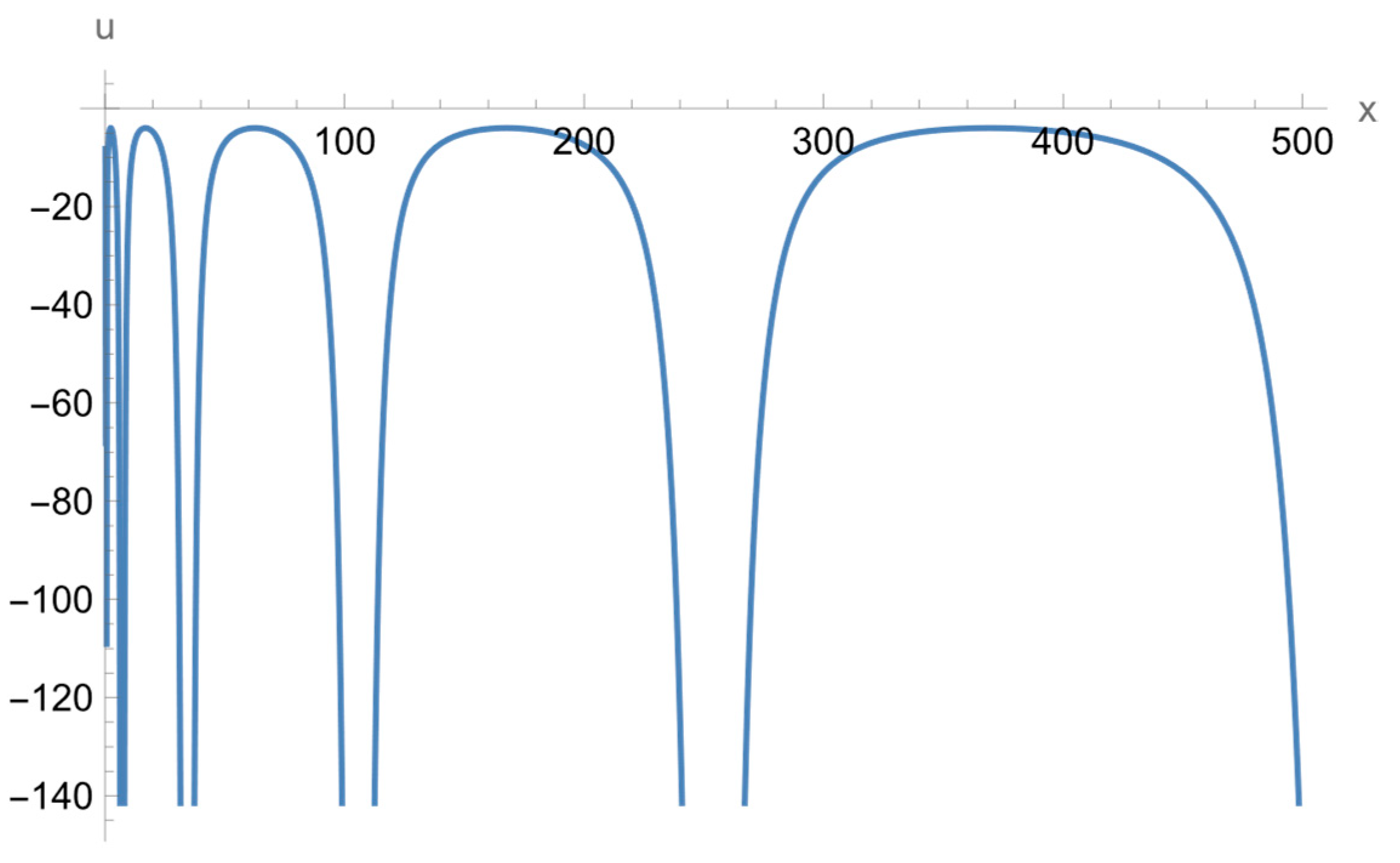
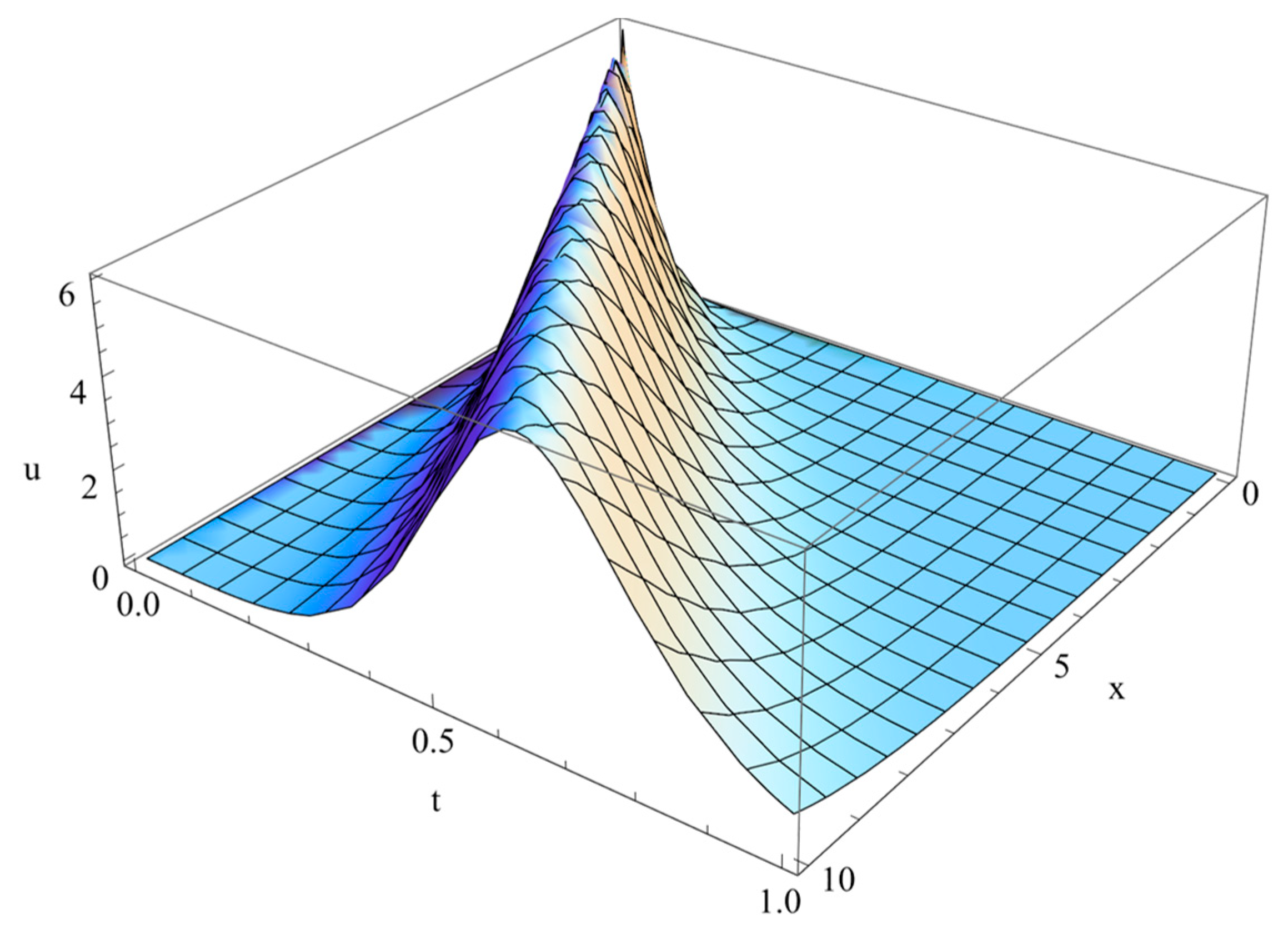
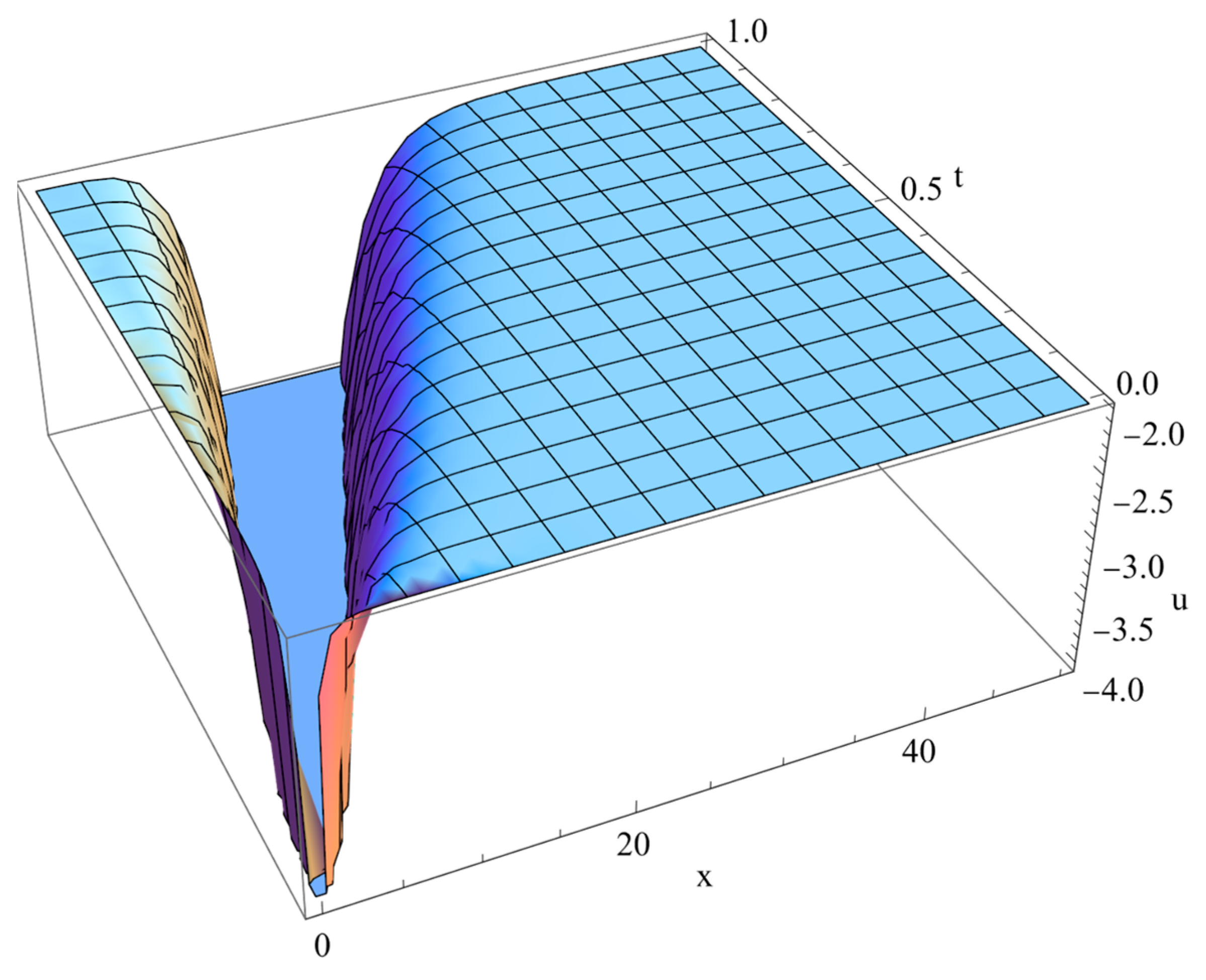
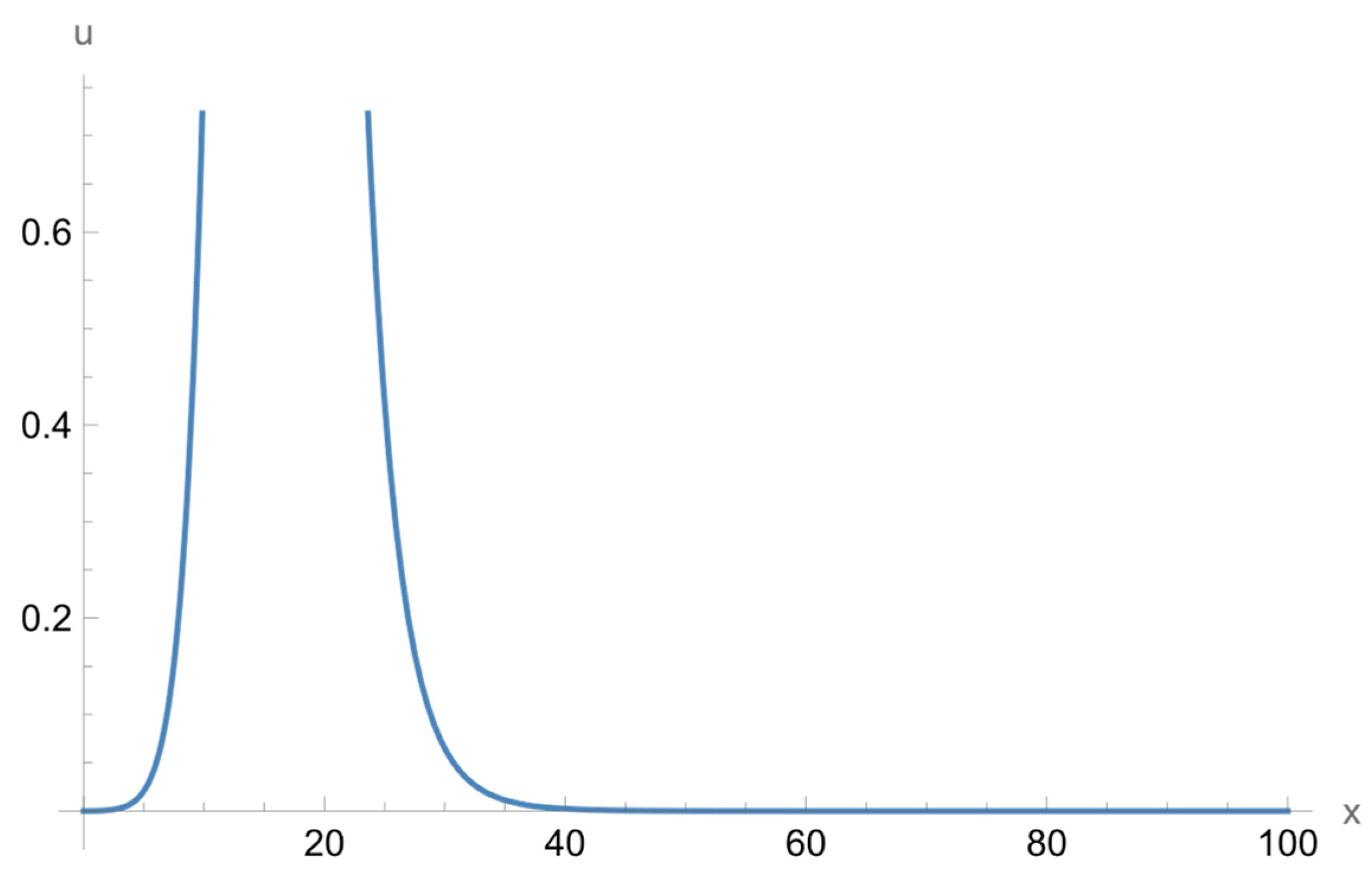

| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
| JEF | JEF | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 7 | 1 | |||||
| 2 | 8 | ||||||
| 3 | 1 | 9 | |||||
| 4 | 1 | 10 | |||||
| 5 | 11 | ||||||
| 6 | 1 | 12 |
| P | Q | R | Solutions | |
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | ||||
| 13 | ||||
| 14 | ||||
| 15 | ||||
| 16 | ||||
| 17 | ||||
| 18 | ||||
| 19 | ||||
| 20 | ||||
| 21 |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| 19 | ||
| 20 | ||
| 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varol, D. Solitary and Periodic Wave Solutions of the Space-Time Fractional Extended Kawahara Equation. Fractal Fract. 2023, 7, 539. https://doi.org/10.3390/fractalfract7070539
Varol D. Solitary and Periodic Wave Solutions of the Space-Time Fractional Extended Kawahara Equation. Fractal and Fractional. 2023; 7(7):539. https://doi.org/10.3390/fractalfract7070539
Chicago/Turabian StyleVarol, Dilek. 2023. "Solitary and Periodic Wave Solutions of the Space-Time Fractional Extended Kawahara Equation" Fractal and Fractional 7, no. 7: 539. https://doi.org/10.3390/fractalfract7070539
APA StyleVarol, D. (2023). Solitary and Periodic Wave Solutions of the Space-Time Fractional Extended Kawahara Equation. Fractal and Fractional, 7(7), 539. https://doi.org/10.3390/fractalfract7070539





