The Analytical Fractional Solutions for Coupled Fokas System in Fiber Optics Using Different Methods
Abstract
1. Introduction
2. M-Truncated Derivative
3. Traveling Wave Equation for FS-MTD
4. Exact Solutions of FS-MTD
4.1. EFE Method
4.2. JEF Method
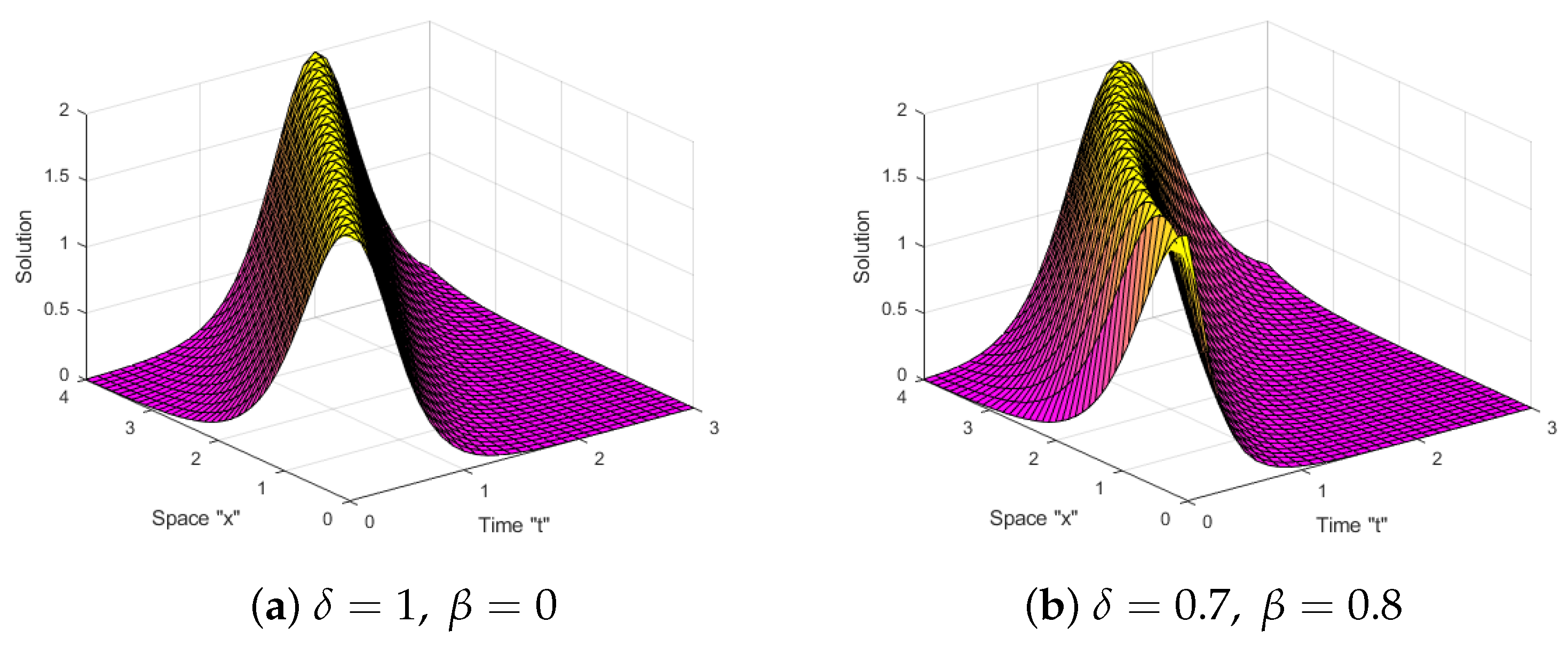
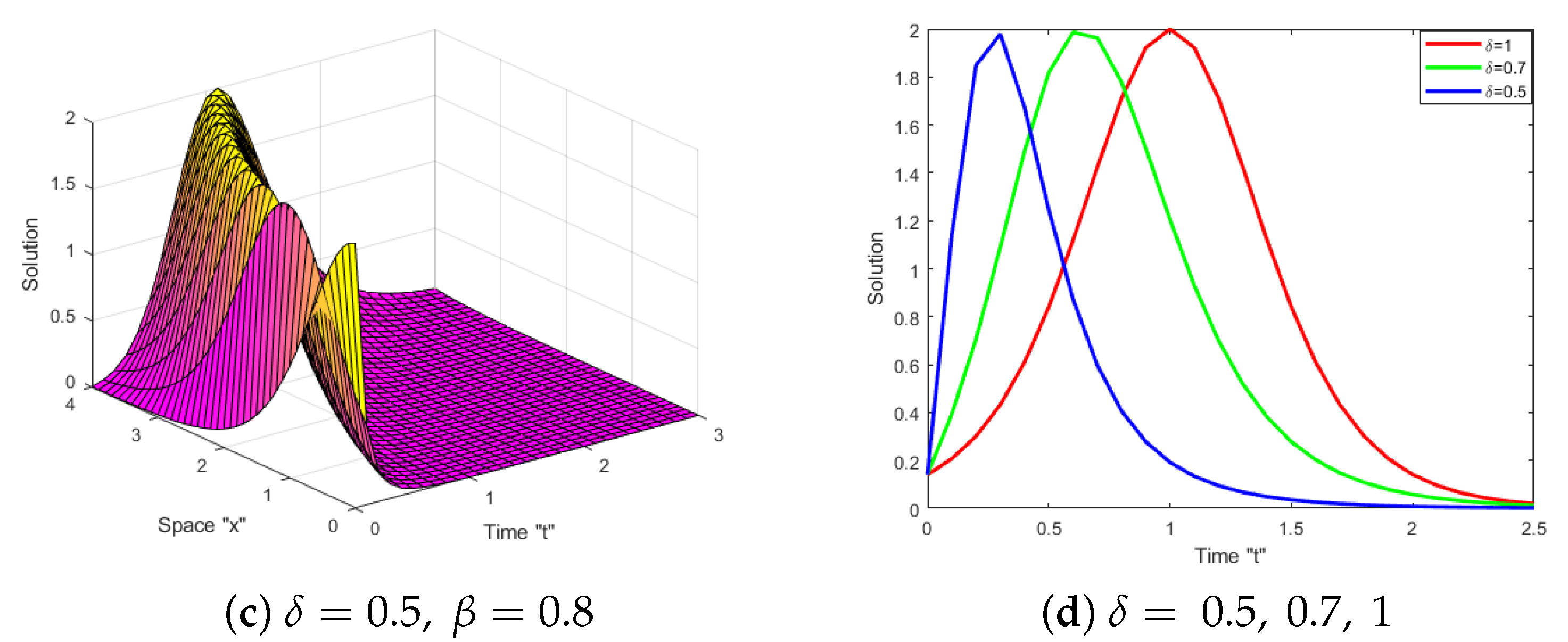
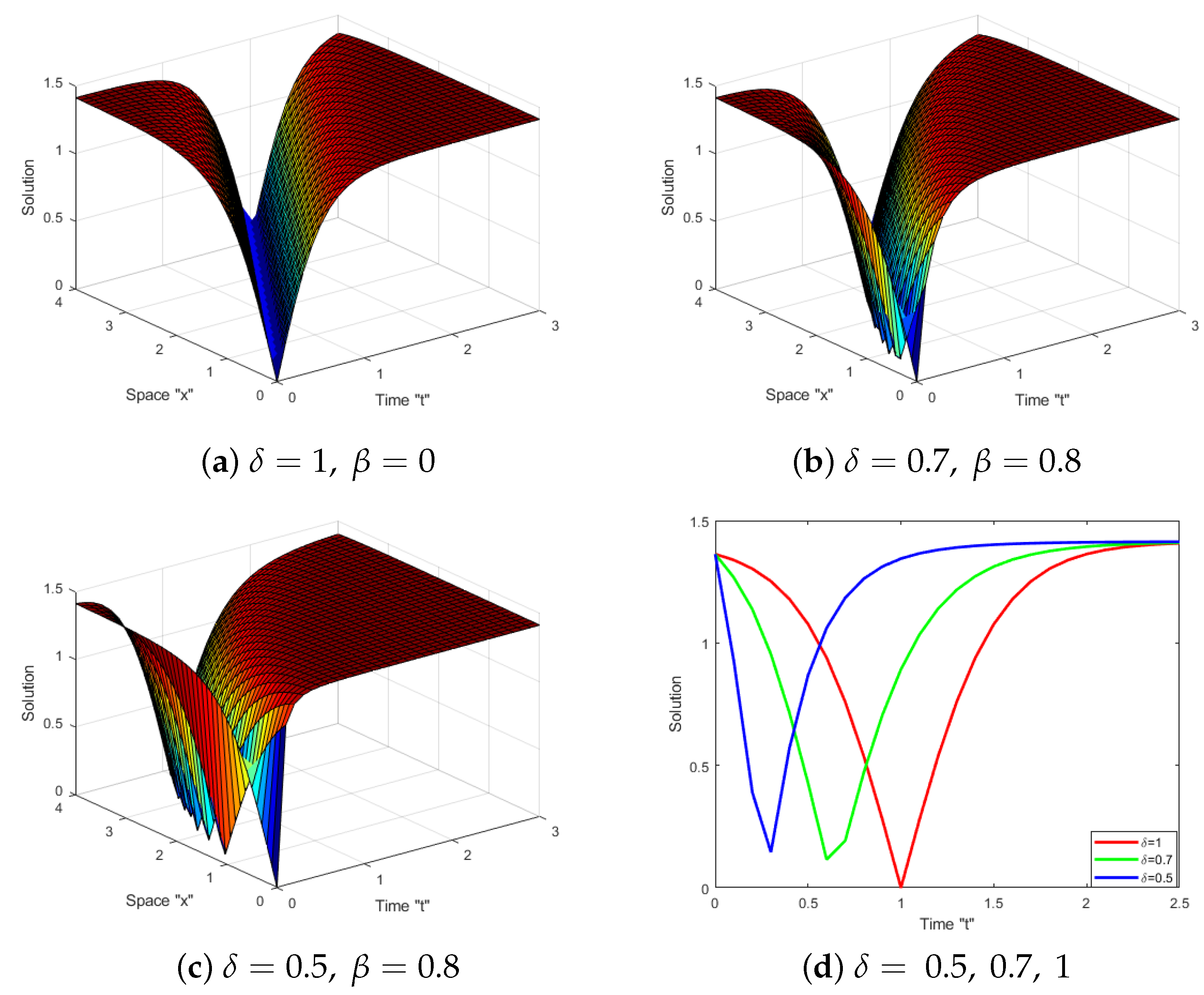
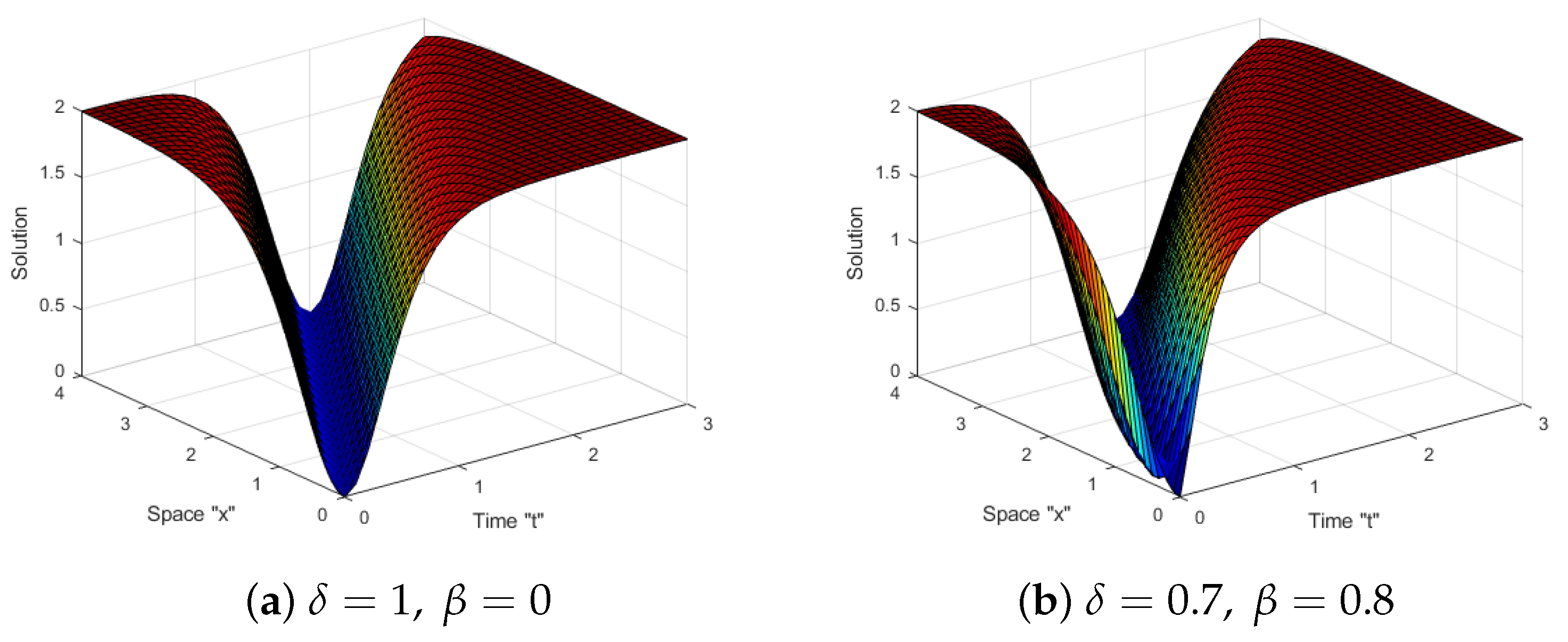
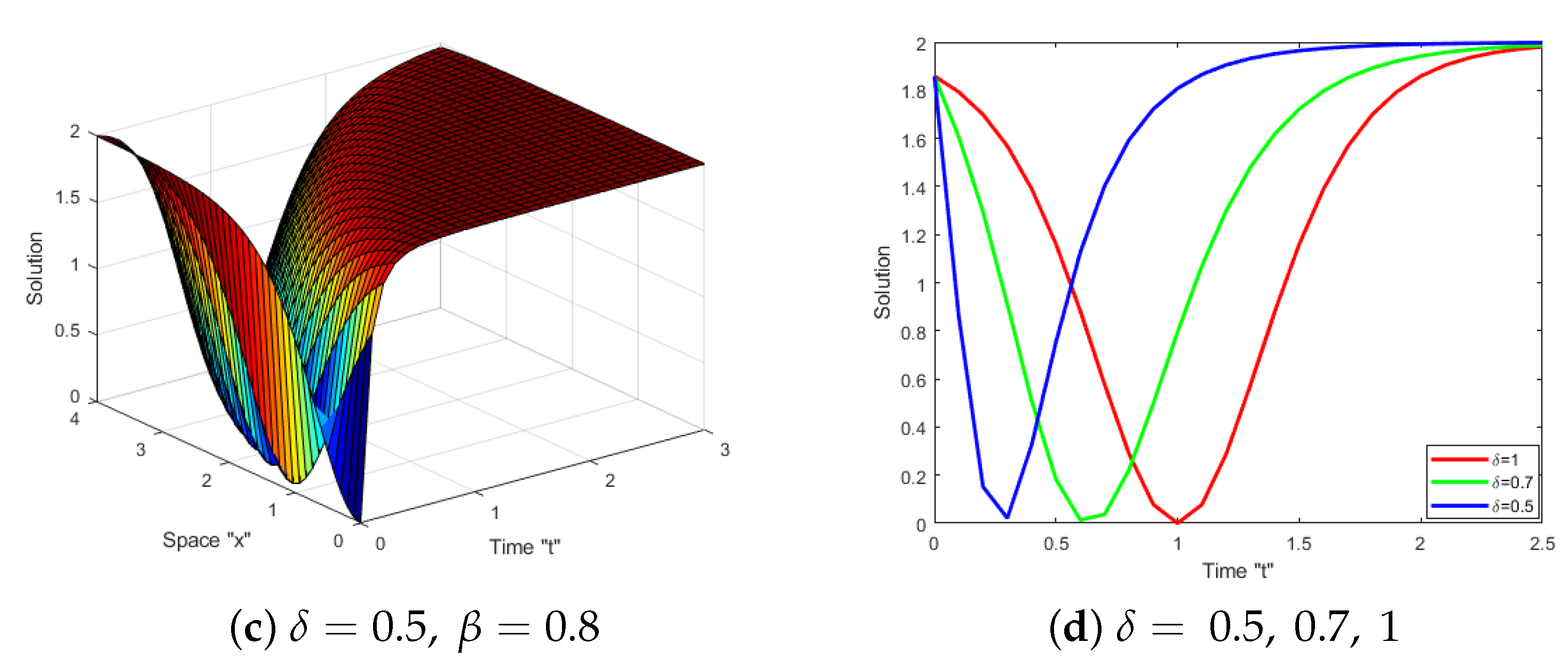
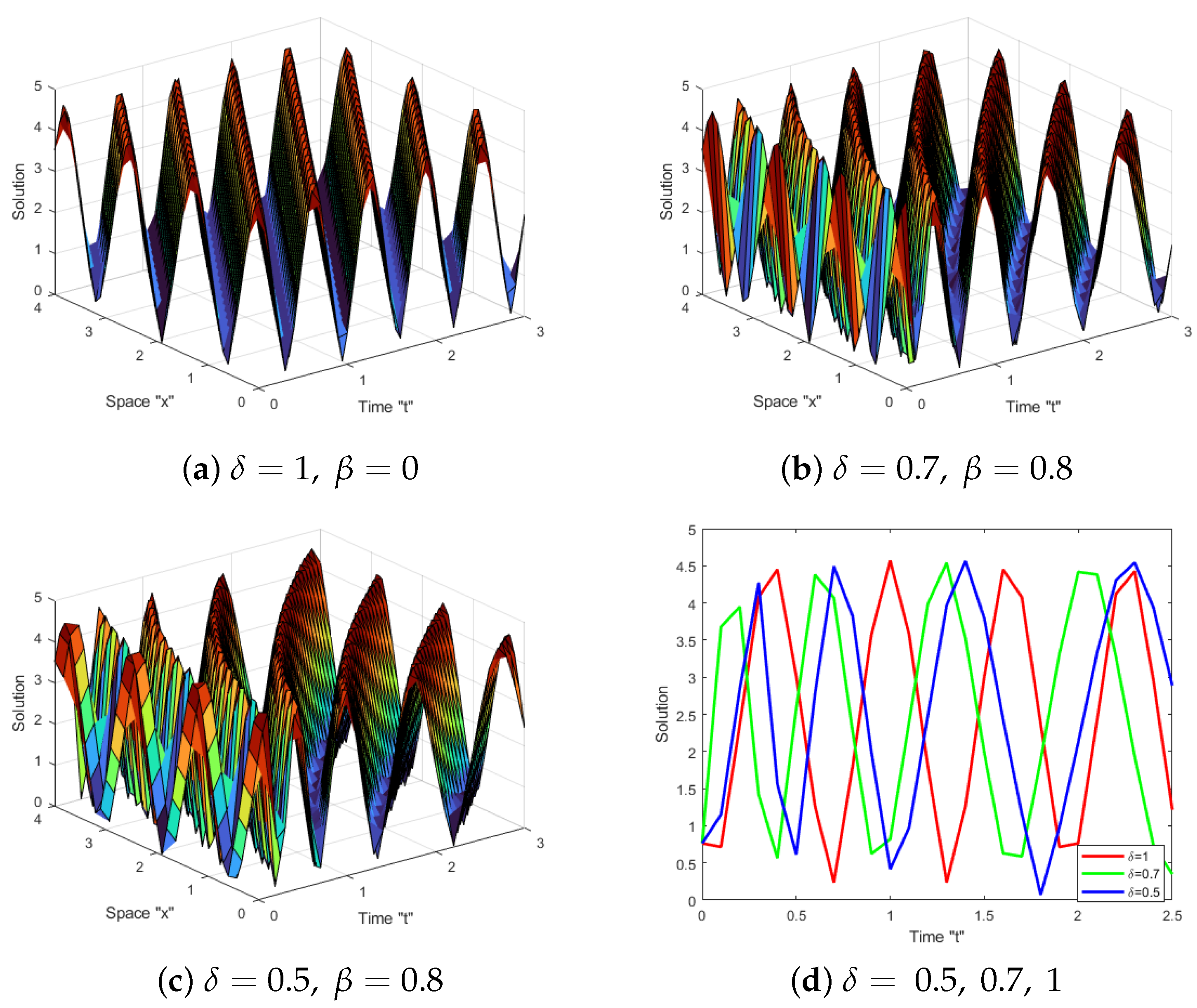
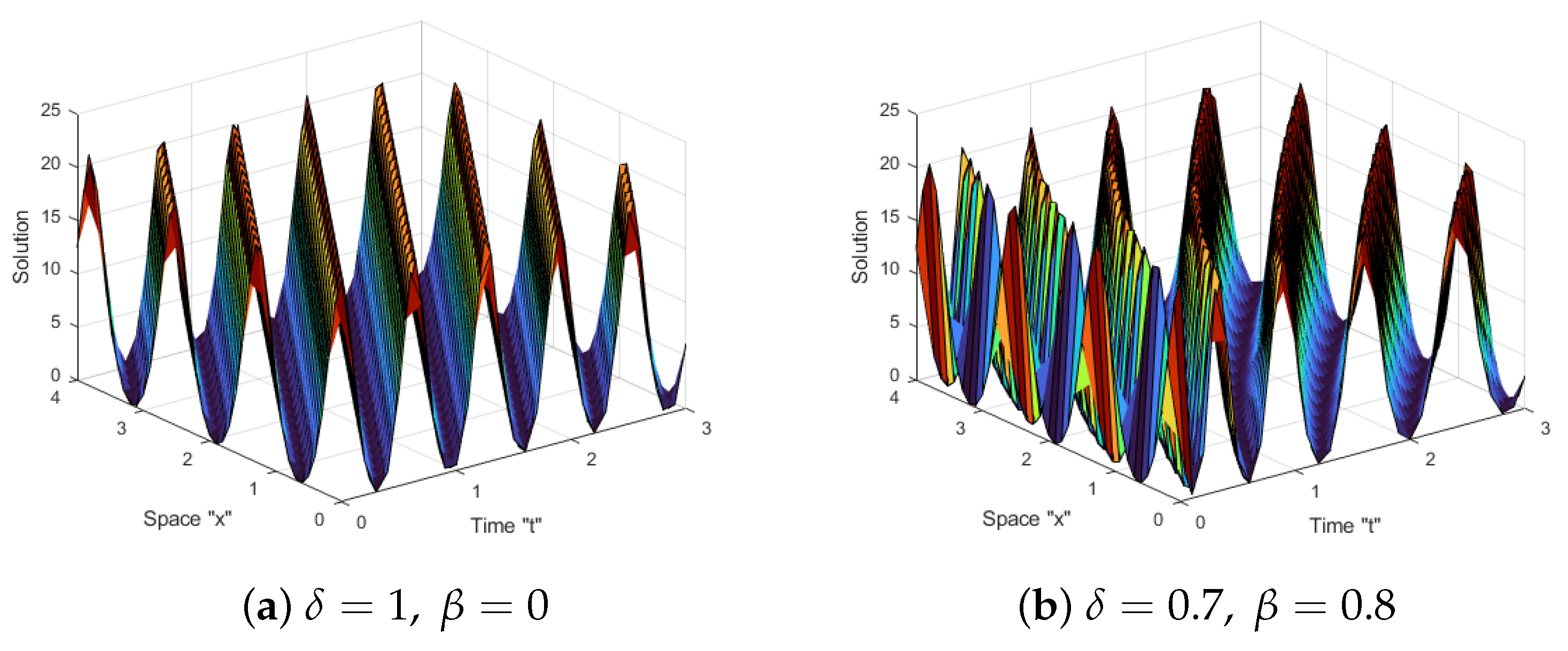
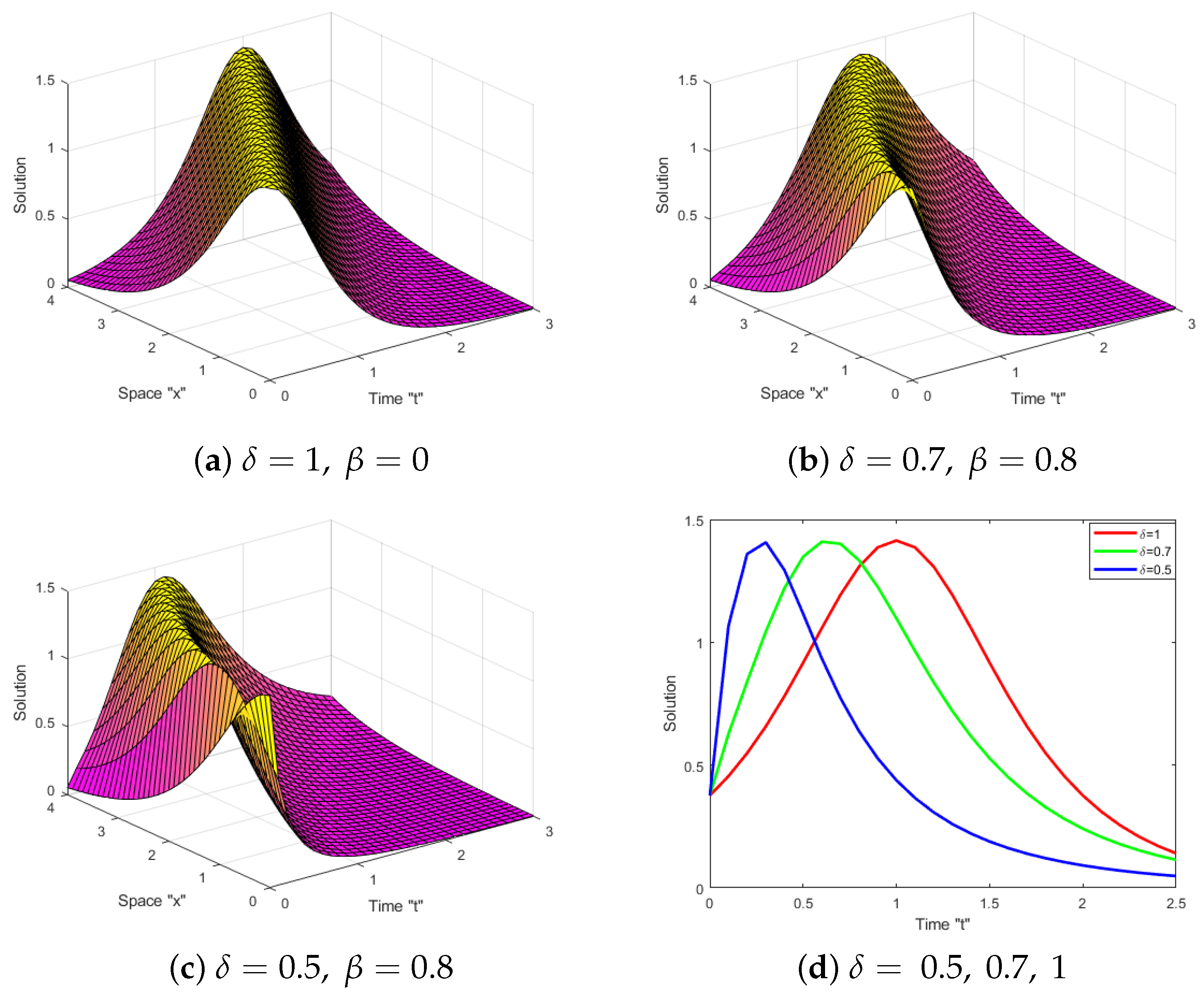
5. Effects of MTD on the Solutions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The (G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Zhang, H. New application of the (G′/G)-expansion method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3220–3225. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C. The Analytical Solutions of the Stochastic mKdV Equation via the Mapping Method. Mathematics 2022, 10, 4212. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. Multiplicative Brownian Motion Stabilizes the Exact Stochastic Solutions of the Davey-Stewartson Equations. Symmetry 2022, 14, 2176. [Google Scholar] [CrossRef]
- Yan, Z.L. Abunbant families of Jacobi elliptic function solutions of the dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18, 299–309. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The sine-cosine method for obtaining solutions with compact and noncompact structures. Appl. Math. A Comput. 2004, 159, 559–576. [Google Scholar] [CrossRef]
- Jiong, S. Auxiliary equation method for solving nonlinear partial differential equations. Phys. Lett. A 2003, 309, 387–396. [Google Scholar]
- Lu, B. The first integral method for some time fractional differential equations. J. Math. Anal. Appl. 2012, 395, 684–693. [Google Scholar] [CrossRef]
- Arnous, A.H.; Mirzazadeh, M. Application of the generalized Kudryashov method to Eckhaus equation. Nonlinear Anal. Model. Control 2016, 21, 577–586. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A. The exp(-ϕ(ς))-expansion method for finding travelling wave solutions of Vakhnenko-Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 2014, 5, 72–83. [Google Scholar]
- Fokas, A.S. On the simplest integrable equation in 2+ 1. Inverse Probl. 1994, 10, L19. [Google Scholar] [CrossRef]
- Shulman, E.I. On the integrability of equations of Davey Stewartson type. Teor. Mat. Fiz. 1983, 56, 131–136. [Google Scholar] [CrossRef]
- Rao, J.; Mihalache, D.; Cheng, Y.; He, J. Lump-soliton solutions to the Fokas system. Phys. Lett. A 2019, 383, 1138–1142. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.H.; Wu, J. Soliton solutions to the Fokas system arising in monomode optical fibers. Optik 2022, 251, 168319. [Google Scholar] [CrossRef]
- Tarla, S.; Ali, K.K.; Sun, T.C.; Yilmazer, R.; Osman, M.S. Nonlinear pulse propagation for novel optical solitons modeled by Fokas system in monomode optical fibers. Results Phys. 2022, 36, 1053. [Google Scholar] [CrossRef]
- Wang, K.J. Abundant exact soliton solutions to the Fokas system. Optik 2022, 249, 168265. [Google Scholar] [CrossRef]
- Zhang, P.L.; Wang, K.J. Abundant optical soliton structures to the Fokas system arising in monomode optical fibers. Open Phys. 2022, 20, 493–506. [Google Scholar] [CrossRef]
- Kaplan, M.; Akbulut, A.; Alqahtani, R.T. New Solitary Wave Patterns of the Fokas System in Fiber Optics. Mathematics 2023, 11, 1810. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. Abundant Solitary Wave Solutions for the Boiti–Leon–Manna–Pempinelli Equation with M-Truncated Derivative. Axioms 2023, 12, 466. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C. Solutions to the (4+1)-Dimensional Time-Fractional Fokas Equation with M-Truncated Derivative. Mathematics 2022, 11, 194. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Cesarano, C.; Al-Askar, F.M.; El-Morshedy, M. Solitary Wave Solutions for the Stochastic Fractional-Space KdV in the Sense of the M-Truncated Derivative. Mathematics 2022, 10, 4792. [Google Scholar] [CrossRef]
- Alshammari, M.; Hamza, A.E.; Cesarano, C.; Aly, E.S.; Mohammed, W.W. The Analytical Solutions to the Fractional Kraenkel–Manna–Merle System in Ferromagnetic Materials. Fractal Fract. 2023, 7, 523. [Google Scholar] [CrossRef]
- Yusuf, A.; Inc, M.; Baleanu, D. Optical Solitons with M-Truncated and Beta Derivatives in Nonlinear Optics. Front. Phys. 2019, 7, 126. [Google Scholar] [CrossRef]
- Akram, G.; Sadaf, M.; Zainab, I. Observations of fractional effects of β-derivative and M-truncated derivative for space time fractional Phi-4 equation via two analytical techniques. Chaos Solitons Fractals 2022, 154, 111645. [Google Scholar] [CrossRef]
- Katugampola, U.N. New approach to a generalized fractional integral. Appl. Math. Comput. 2011, 218, 860–865. [Google Scholar] [CrossRef]
- Katugampola, U.N. New approach to generalized fractional derivatives. Bull. Math. Anal. Appl. 2014, 6, 1–15. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Sousa, J.V.; de Oliveira, E.C. A new truncated Mfractional derivative type unifying some fractional derivative types with classical properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, W.W.; Cesarano, C.; Elsayed, E.M.; Al-Askar, F.M. The Analytical Fractional Solutions for Coupled Fokas System in Fiber Optics Using Different Methods. Fractal Fract. 2023, 7, 556. https://doi.org/10.3390/fractalfract7070556
Mohammed WW, Cesarano C, Elsayed EM, Al-Askar FM. The Analytical Fractional Solutions for Coupled Fokas System in Fiber Optics Using Different Methods. Fractal and Fractional. 2023; 7(7):556. https://doi.org/10.3390/fractalfract7070556
Chicago/Turabian StyleMohammed, Wael W., Clemente Cesarano, Elsayed M. Elsayed, and Farah M. Al-Askar. 2023. "The Analytical Fractional Solutions for Coupled Fokas System in Fiber Optics Using Different Methods" Fractal and Fractional 7, no. 7: 556. https://doi.org/10.3390/fractalfract7070556
APA StyleMohammed, W. W., Cesarano, C., Elsayed, E. M., & Al-Askar, F. M. (2023). The Analytical Fractional Solutions for Coupled Fokas System in Fiber Optics Using Different Methods. Fractal and Fractional, 7(7), 556. https://doi.org/10.3390/fractalfract7070556