On a System of Equations with General Fractional Derivatives Arising in Diffusion Theory
Abstract
1. Introduction
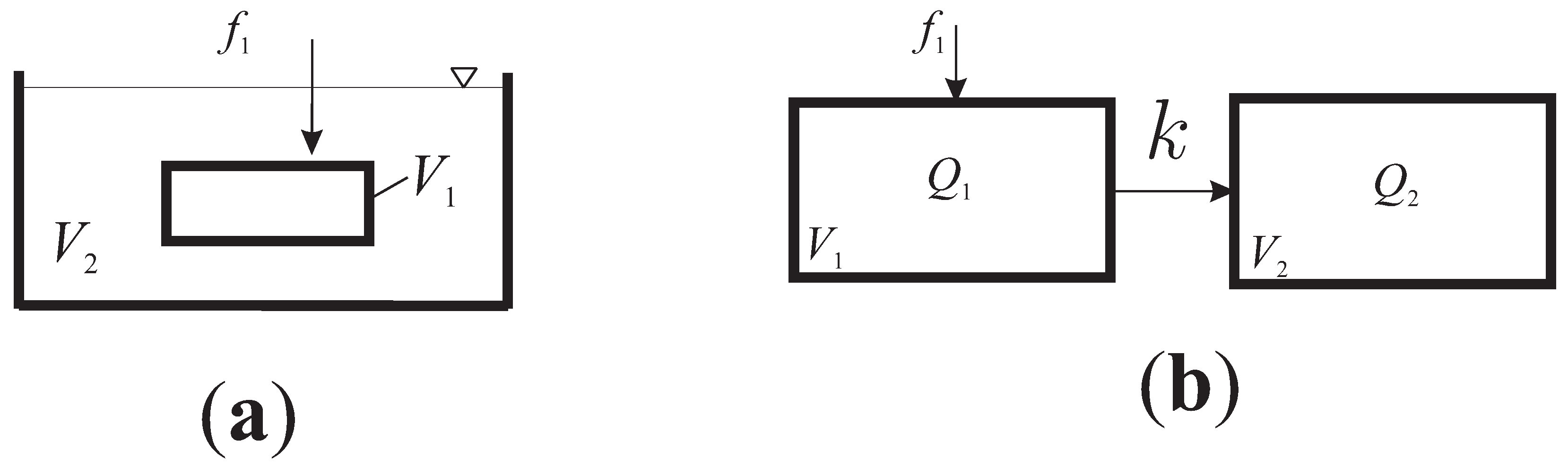
2. Two-Compartment System with General Fractional Derivatives
- Case I
- Case II
3. Solution of (10), (22) and (10), (23)
4. Numerical Results
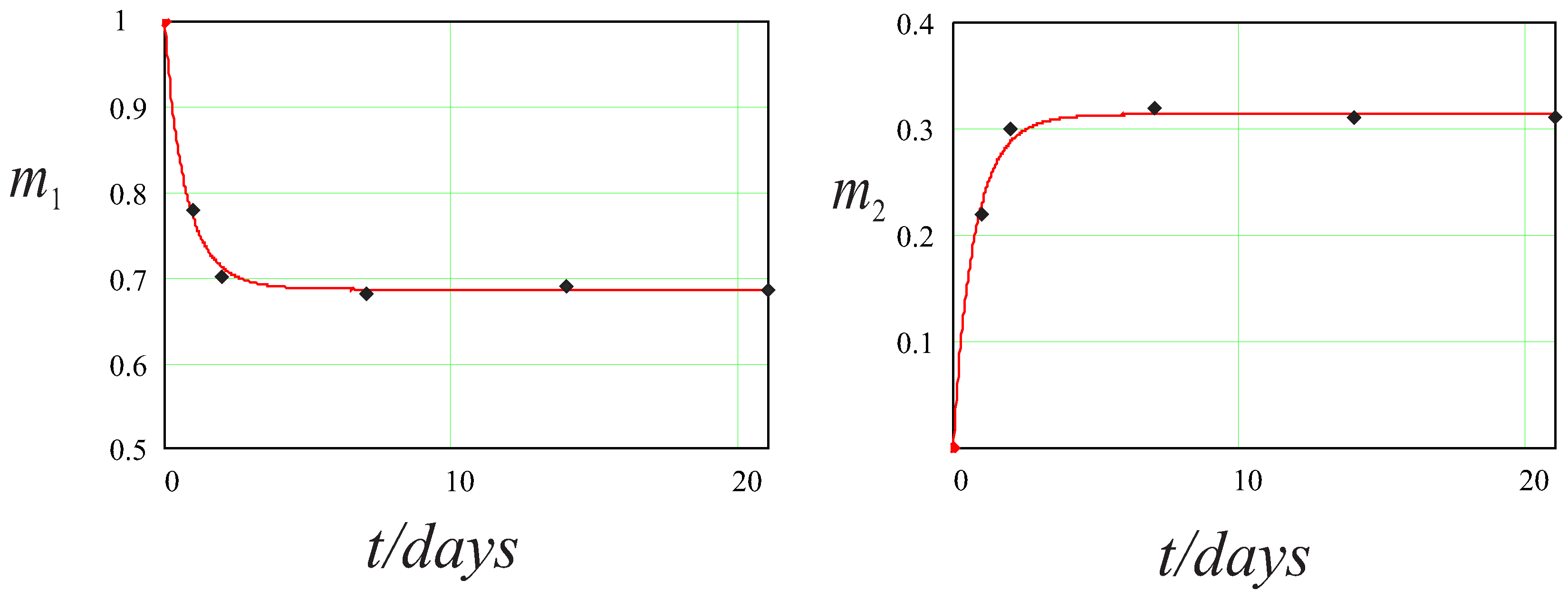
4.1. Gentamicin Release from Poly(vinyl Alcohol)/Chitosan/Gentamicin (PVA/CHI/Gent) Hydrogel
4.2. Gentamicin Release from Bioceramic Hydroxyapatite/Poly(vinyl Alcohol)/Chitosan/Gentamicin (HAP/PVA/CHI/Gent) Coating on Titanium
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rescigno, A. Foundations of Pharmacokinetics; Kluwer Academic Publishers: New York, NY, USA, 2003. [Google Scholar]
- Yadav, P.R.; Das, D.B.; Pattanayek, S.K. Coupled Diffusion-Binding-Deformation Modelling for Phase-Transition Microneedles-Based Drug Delivery. J. Pharm. Sci. 2023, 112, 1108–1118. [Google Scholar] [CrossRef] [PubMed]
- Kovacs, L.; Benyo, B.; Bokor, J.; Benyo, Z. Induced L2-norm minimization of glucose-insulin system for Type I diabetic patients. Comput. Methods Programs Biomed. 2011, 102, 105–118. [Google Scholar] [CrossRef] [PubMed]
- Drexler, D.; Kovacs, L.; Sapi, J.; Harmati, I.; Benyo, Z. Model-based analysis and synthesis of tumor growth under angiogenic inhibition: A case study. IFAC Proc. 2011, 44, 3753–3759. [Google Scholar] [CrossRef]
- Kiss, B.; Sapi, J.; Kovacs, L. Imaging method for model-based control of tumor diseases. In Proceedings of the IEEE 11th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 26–28 September 2013; pp. 271–275. [Google Scholar]
- Copot, D.; Ionescu, C. Drug delivery system for general anesthesia: Where are we? In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), San Diego, CA, USA, 5–8 October 2014; pp. 2452–2457. [Google Scholar]
- Ionescu, C.M.; Copot, D.; de Keyser, R. Anesthesiologist in the Loop and Predictive Algorithm to Maintain Hypnosis While Mimicking Surgical Disturbance. IFAC-Papers OnLine 2017, 50, 15080–15085. [Google Scholar] [CrossRef]
- Popovic, J.K.; Spasic, D.; Tosic, J.; Kolarovic, J.; Malti, R.; Mitic, I.M.; Pilipovic, S.; Atanackovic, T.M. Fractional model for pharmacokinetics of high dose methotrexate in children with acute lymphoblastic leukaemia. Commun. Nonlinear Sci. Numer. Simulat. 2015, 22, 451–471. [Google Scholar] [CrossRef]
- Dokoumetzidis, A.; Macheras, P. Fractional kinetics in drug absorption and disposition processes. J. Pharmacokinet. Pharmacodyn. 2009, 36, 165–178. [Google Scholar] [CrossRef]
- Dokoumetzidis, A.; Magin, R.; Macheras, P. A commentary on fractionalization of multi-compartmental models. J. Pharmacokinet. Pharmacodyn. 2010, 37, 203–207. [Google Scholar] [CrossRef]
- Verotta, D.J. Fractional compartmental models and multi-term Mittag-Leffler response functions. J. Pharmacokinet. Pharmacodyn. 2010, 37, 209–221. [Google Scholar] [CrossRef]
- Sopasakis, P.; Sarimveis, H.; Macheras, P.; Dokoumetzidis, A. Fractional calculus in pharmacokinetics. J. Pharmacokinet. Pharmacodyn. 2018, 45, 107–125. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.A.T.; Bates, J.H.T. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simulat. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Miskovic-Stankovic, V.; Janev, M.; Atanackovic, T.M. Two compartmental fractional derivative model with General fractional derivative. J. Pharmacokinet. Pharmacodyn. 2023, 50, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Popovic, J.K.; Atanackovic, M.T.; Pilipovic, A.S.; Rapaic, M.R.; Pilipovic, S.; Atanackovic, T.M. A new approach to the compartmental analysis in pharmacokinetics: Fractional time evolution of diclofenac. J. Pharmacokinet. Pharmacodyn. 2010, 37, 119–134. [Google Scholar] [CrossRef] [PubMed]
- Popovic, J.; Dolicanin, D.; Rapaic, M.; Popovic, S.L.; Pilipovic, S.; Atanackovic, T.M. A nonlinear two compartmental fractional derivative model. Eur. J. Drug Metab. Pharmacokinet. 2011, 36, 189–196. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.-J. General Fractional Derivatives, Theory, Methods and Applications; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- Yang, X.-J.; Gao, F.; Ju, Y. General Fractional Derivatives with Applications in Viscoelasticity; Elsevier: London, UK, 2020. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Atanackovic, T.M.; Pilipovic, S.; Stankovic, B.; Zorica, D. Fractional Calculus with Application in Mechanics: Vibrations and Diffusion Processes; ISTE: London, UK; John Wiley and Sons: New York, NY, USA, 2014. [Google Scholar]
- Atanackovic, T.M.; Pilipovic, S.; Stankovic, B.; Zorica, D. Fractional Calculus with Application in Mechanics: Wave Propagation, Impact and Variational Principles; ISTE: London, UK; John Wiley and Sons: New York, NY, USA, 2014. [Google Scholar]
- Tarasov, V.E. General Fractional Dynamics. Mathematics 2021, 9, 1464. [Google Scholar] [CrossRef]
- Kochubei, A.N. General fractional calculus, evolution equations, and renewal processes. Integral Equ. Oper. Theory 2011, 71, 583–600. [Google Scholar] [CrossRef]
- Luchko, Y. General Fractional Integrals and Derivatives of Arbitrary Order. Symmetry 2021, 13, 755. [Google Scholar] [CrossRef]
- Luchko, Y. Operational Calculus for the General Fractional derivative and its Applications. Fract. Calc. Appl. Anal. 2021, 24, 338–375. [Google Scholar] [CrossRef]
- Luchko, Y. On the 1st-Level General Fractional Derivatives of Arbitrary Order. Fractal Fract. 2023, 7, 183. [Google Scholar] [CrossRef]
- Luchko, Y. General fractional integrals and derivatives with the Sonine kernels. Mathematics 2021, 9, 594. [Google Scholar] [CrossRef]
- Samko, S.G.; Cardoso, R.P. Integral Equations of the First Kind of Sonine Type. Int. J. Math. Math. Sci. 2003, 57, 3609–3632. [Google Scholar] [CrossRef]
- Hanyga, A. A comment on a controversial issue: A generalized fractional derivative cannot have a regular kernel. Fract. Calc. Appl. Anal. 2020, 23, 211–223. [Google Scholar] [CrossRef]
- Zacher, R. Boundedness of weak solutions to evolutionary partial integro-differential equations with discontinuous coefficients. J. Math. Anal. Appl. 2008, 348, 137–149. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Atanackovic, T.M.; Pilipovic, S. Zener model with General fractional calculus: Thermodynamical Restrictions. Fractal. Fract. 2022, 6, 617. [Google Scholar] [CrossRef]
- Brezinski, C. Numerical Methods for Laplace Transform Inversion; Springer Science Business Media: New York, NY, USA, 2007. [Google Scholar]
- Djosic, M.; Jankovic, A.; Stevanovic, M.; Stojanovic, J.; Vukasinovic-Sekulic, M.; Kojic, V.; Miskovic-Stankovic, V. Hydroxyapatite/poly(vinyl alcohol)/chitosan coating with gentamicin for orthopedic implants. Mater. Chem. Phys. 2023, 303, 127766. [Google Scholar] [CrossRef]

| t (Days) | m calculated | m measured |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 0.72389 | 0.27611 |
| 2 | 0.33093 | 0.69067 |
| 4 | 0.2612 | 0.73880 |
| 7 | 0.2522 | 0.74771 |
| 14 | 0.25164 | 0.74836 |
| t (Days) | mcalculated | mmeasured |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 0.78 | 0.22 |
| 2 | 0.70 | 0.30 |
| 7 | 0.68 | 0.32 |
| 14 | 0.69 | 0.31 |
| 21 | 0.69 | 0.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miskovic-Stankovic, V.; Atanackovic, T.M. On a System of Equations with General Fractional Derivatives Arising in Diffusion Theory. Fractal Fract. 2023, 7, 518. https://doi.org/10.3390/fractalfract7070518
Miskovic-Stankovic V, Atanackovic TM. On a System of Equations with General Fractional Derivatives Arising in Diffusion Theory. Fractal and Fractional. 2023; 7(7):518. https://doi.org/10.3390/fractalfract7070518
Chicago/Turabian StyleMiskovic-Stankovic, Vesna, and Teodor M. Atanackovic. 2023. "On a System of Equations with General Fractional Derivatives Arising in Diffusion Theory" Fractal and Fractional 7, no. 7: 518. https://doi.org/10.3390/fractalfract7070518
APA StyleMiskovic-Stankovic, V., & Atanackovic, T. M. (2023). On a System of Equations with General Fractional Derivatives Arising in Diffusion Theory. Fractal and Fractional, 7(7), 518. https://doi.org/10.3390/fractalfract7070518







