A Light-Ray Approach to Fractional Fourier Optics

Abstract

A light ray in space is characterized by two vectors: (i) a transverse spatial vector associated with the point where the ray intersects a given spherical cap; (ii) an angular-frequency vector which defines the ray direction of propagation. Given a light ray propagating from a spherical emitter to a spherical receiver, a linear equation is established that links its representative vectors on the emitter and on the receiver. The link is expressed by means of a matrix which is not homogeneous, since it involves both spatial and angular variables (having distinct physical dimensions). Indeed, the matrix becomes a homogeneous rotation matrix after scaling the previous variables with appropriate dimensional coefficients. When applied to diffraction, in the framework of a scalar theory, the scaling operation results directly in introducing fractional-order Fourier transformations as mathematical expressions of Fresnel diffraction phenomena. Linking angular-frequency vectors and spatial frequencies results in an interpretation of the notion of a spherical angular spectrum. Accordance of both homogeneous and non-homogeneous ray matrices with the Huygens–Fresnel principle is examined. The proposed ray-matrix representation of diffraction is also applied to coherent imaging through a lens.

1. Introduction

The link between fractional-order Fourier transformations and Fresnel diffraction has been the subject of many articles since 1993 [1,2]. More generally, fractional-order Fourier transformations have been associated with various propagation issues in optics [3,4,5]. Those works fall into a subclass of Fourier optics, which we call fractional Fourier optics [2,4]. Among the various methods of fractional Fourier optics, some use matrix representations of light propagation (abcd matrices) for diffraction as well as for imaging through lenses [6]. They deal with ray vectors and square matrices, which are non-homogeneous matrices in the sense that they involve spatial variables as well as angular ones (matrix elements have distinct physical dimensions).

A way of introducing fractional-order Fourier transformations in optics is through Wigner distributions associated with optical fields, which are phase–space representations including both field amplitudes and their spectra (Fourier transforms) [7]. In such a case, the temptation is high to describe the effect of propagation or imaging as a geometrical isometry, e.g., a rotation. It should be clear that this may be done only on a homogeneous space, that is, after having defined an appropriate dimensional scaling of spatial and angular variables, so that reduced variables are dimensionless or have a common physical dimension.

In the present article we use ray vectors and matrices and look for conditions to transform them into homogeneous vectors and matrices. Since we are trying to represent diffraction phenomena, we shall consider coherent fields and, according to a scalar theory of diffraction, quadratic-phase factors have to be taken into account; the ray-matrix method we introduce is adapted to spherical emitters and receivers, a way of managing with those quadratic-phase factors [2].

We shall show that looking for transfer ray matrices being rotation matrices directly leads us to represent Fresnel diffraction phenomena by fractional-order Fourier transformations, in accordance with previous works [2]. We shall then interpret how the proposed ray-matrix method is in accordance with the Huygens–Fresnel principle.

The notion of a spherical angular spectrum [8] has been introduced as a generalization of the usual “planar” angular spectrum [9]. We shall show that a spherical angular spectrum can be simply interpreted in terms of the proposed ray-matrix theory. We shall eventually apply ray matrices to geometrical coherent imaging.

2. Space and Angular Variables and Their Transfers

According to a scalar theory of diffraction, the transfer of the optical-field amplitude from a usually plane emitter to a receiver at a given distance involves quadratic phase factors [2,9]. These factors can be handled by using spherical emitters or receivers, that is, spherical caps on which field amplitudes are considered [2,10,11]. We begin by adapting to spherical caps a light-ray representation that is currently used in paraxial geometrical optics, in which a light ray is represented by a transverse vector and by the angle made by the ray with the optical axis. Since emitters and receivers are spherical caps, calculi will be developed up to second order in the function of transverse and angular variables.

2.1. Angular Frequency and Light-Ray Representation

Let $\mathcal{A}$ be a spherical cap, whose vertex is Ω and center of curvature is C (Figure 1). The radius of curvature of $\mathcal{A}$ is $R_A=\overline{\Omega C}$ (an algebraic measure). Let P be a point on $\mathcal{A}$ and let p be the orthogonal projection of P on the plane $\mathcal{P}$ tangent to $\mathcal{A}$ at Ω. We choose Cartesian coordinates $x,y$ on $\mathcal{P}$, so that p is perfectly defined by the two-dimensional vector $\mathit{Sp}=\mathit{r}=(x_p,y_p)$.

Numbers $x_p$ and $y_p$ are the coordinates of p and we say that $\mathit{r}$ is the spatial variable associated with p. Given $\mathcal{A}$, coordinates $x_p$ and $y_p$ can also be used as coordinates of P on the sphere; in the following, indices will be dropped. (The former analysis holds true because the spherical cap $\mathcal{A}$ is less than half a sphere. In fact in the following, $\mathcal{A}$ will be close enough to $\mathcal{P}$ so that second-order approximations are legitimate.)

Let z be the axis along light propagation and let ${\mathit{e}}_x$, ${\mathit{e}}_y$ and ${\mathit{e}}_z$ be unit vectors along x, y and z, forming a direct basis (${\mathit{e}}_x\times {\mathit{e}}_y={\mathit{e}}_z$). Let ${\mathit{e}}_n$ be the unit vector, normal to $\mathcal{A}$ at P, so that the Euclidean scalar product ${\mathit{e}}_n·{\mathit{e}}_z$ is positive. We introduce the following unit vectors

$${\mathit{e}}_{\xi }=\frac{{\mathit{e}}_y\times {\mathit{e}}_n}{\left|\right|{\mathit{e}}_y\times {\mathit{e}}_n\left|\right|},{\mathit{e}}_{\eta }=\frac{{\mathit{e}}_n\times {\mathit{e}}_x}{\left|\right|{\mathit{e}}_n\times {\mathit{e}}_x\left|\right|},$$

(1)

such that ${\mathit{e}}_{\xi },{\mathit{e}}_{\eta },{\mathit{e}}_n$ form a direct basis (${\mathit{e}}_{\xi }\times {\mathit{e}}_{\eta }={\mathit{e}}_n$). We remark that ${\mathit{e}}_{\xi }$ and ${\mathit{e}}_{\eta }$ lie in the plane $\mathcal{T}$, tangent to $\mathcal{A}$ at P (Figure 2a).

Let us consider a light ray passing through P and let ${\mathit{e}}_u$ be the unit vector along the direction of propagation of the ray (Figure 2b). We define the direction cosines of ${\mathit{e}}_u$ with respect to ${\mathit{e}}_{\xi }$, ${\mathit{e}}_{\eta }$ and ${\mathit{e}}_n$ by

$$\xi =\cos {\theta }_{\xi },\eta =\cos {\theta }_{\eta },\zeta =\cos {\theta }_n,$$

(2)

where ${\theta }_{\xi }$ is the angle between ${\mathit{e}}_{\xi }$ and ${\mathit{e}}_u$, etc. (Figure 2b). Since ${\mathit{e}}_u$ is a unit vector, we have ${\xi }^2+{\eta }^2+{\zeta }^2=1$, so that ${\mathit{e}}_u$ is perfectly defined by $\xi$ and $\eta$ (because we impose $\zeta >0$, for waves propagating along positive z).

We call angular-frequency vector the two-dimensional vector Φ defined by

$$\mathit{\Phi }=(\xi ,\eta ).$$

(3)

The vector Φ is the projection of ${\mathit{e}}_u$ on the plane tangent to $\mathcal{A}$ at P (Figure 3). It is an element of ${\mathbb{R}}^2$ and has no physical dimension.

A light ray coming from $\mathcal{A}$ is perfectly defined by the ordered pair $(\mathit{r},\mathit{\Phi })$, so that we shall say “the ray $(\mathit{r},\mathit{\Phi })$”.

2.2. Ray Transfer

Let $\mathcal{B}$ be a spherical receiver at a distance D from $\mathcal{A}$ ($D=\overline{\Omega {\Omega }^{\prime }}$, where ${\Omega }^{\prime }$ is the vertex of $\mathcal{B}$). The radius of curvature of $\mathcal{B}$ is $R_B$. A ray $(\mathit{r},\mathit{\Phi })$ issued from P on $\mathcal{A}$ intersects $\mathcal{B}$ at $P^{\prime }$, where the ray is defined by $({\mathit{r}}^{\prime },{\mathit{\Phi }}^{\prime })$; our first task is to find the link between $(\mathit{r},\mathit{\Phi })$ and $({\mathit{r}}^{\prime },{\mathit{\Phi }}^{\prime })$, that is, between $(x,y,\xi ,\eta )$ and $(x^{\prime },y^{\prime },{\xi }^{\prime },{\eta }^{\prime })$.

We are looking for relations of the form $x^{\prime }=x^{\prime }(x,y,\xi ,\eta )$ ($x^{\prime }$ is a function of x, y, $\xi$ and $\eta$), ${\xi }^{\prime }={\xi }^{\prime }(x,y,\xi ,\eta )$, etc. and restrict ourselves to second-order approximations with respect to transverse variables, in accordance with the use of spherical caps, which are second approximations of emitters and receivers. We neglect terms whose order s are greater than or equal to 3. For example $x^{\prime }$ is written as

$$\begin{array}{ccc}\hfill x^{\prime }& =& a_0+a_{1}x+b_{1}y+c_1\xi +d_1\eta +a_2{x}^2+b_2{y}^2+e_{2}xy+c_2{\xi }^2+d_2{\eta }^2\hfill \\ & & +f_2\xi \eta +g_{2}x\xi +h_{2}x\eta +k_{2}y\xi +m_{2}y\eta .\hfill \end{array}$$

(4)

Now we remark that if we rotate $\mathcal{A}$ and $\mathcal{B}$ (Figure 4) by an angle $\pi$ around the z axis, we change $\mathit{r}$ into its opposite $-\mathit{r}$, and the same for Φ, ${\mathit{r}}^{\prime }$ and ${\mathit{\Phi }}^{\prime }$. Thus x, y, $\xi$ and $\eta$ are changed into their opposites, as well as $x^{\prime }$. Consequently $a_0$ and the second-order terms in Equation (4) must vanish so that, within a second-order approximation, $x^{\prime }$ is a linear function of x, y, $\xi$ and $\eta$, that is,

$$x^{\prime }=a_{1}x+b_{1}y+c_1\xi +d_1\eta .$$

(5)

The same can be done with $y^{\prime }$, ${\xi }^{\prime }$ and ${\eta }^{\prime }$, so that the relation between $(\mathit{r},\mathit{\Phi })$ and $({\mathit{r}}^{\prime },{\mathit{\Phi }}^{\prime })$ is linear. We adopt a matrix form and write

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ {\xi }^{\prime }\\ {\eta }^{\prime }\end{array}\right)=\left(\begin{array}{cccc}{a}_{11}& a_{12}& a_{13}& a_{14}\\ a_{21}& a_{22}& a_{23}& a_{24}\\ a_{31}& a_{32}& a_{33}& a_{34}\\ a_{41}& a_{42}& a_{43}& a_{44}\end{array}\right)\left(\begin{array}{c}x\\ y\\ \xi \\ \eta \end{array}\right).$$

(6)

The coefficients $a_{ij}$ can be determined by examining special cases, as follows.

i

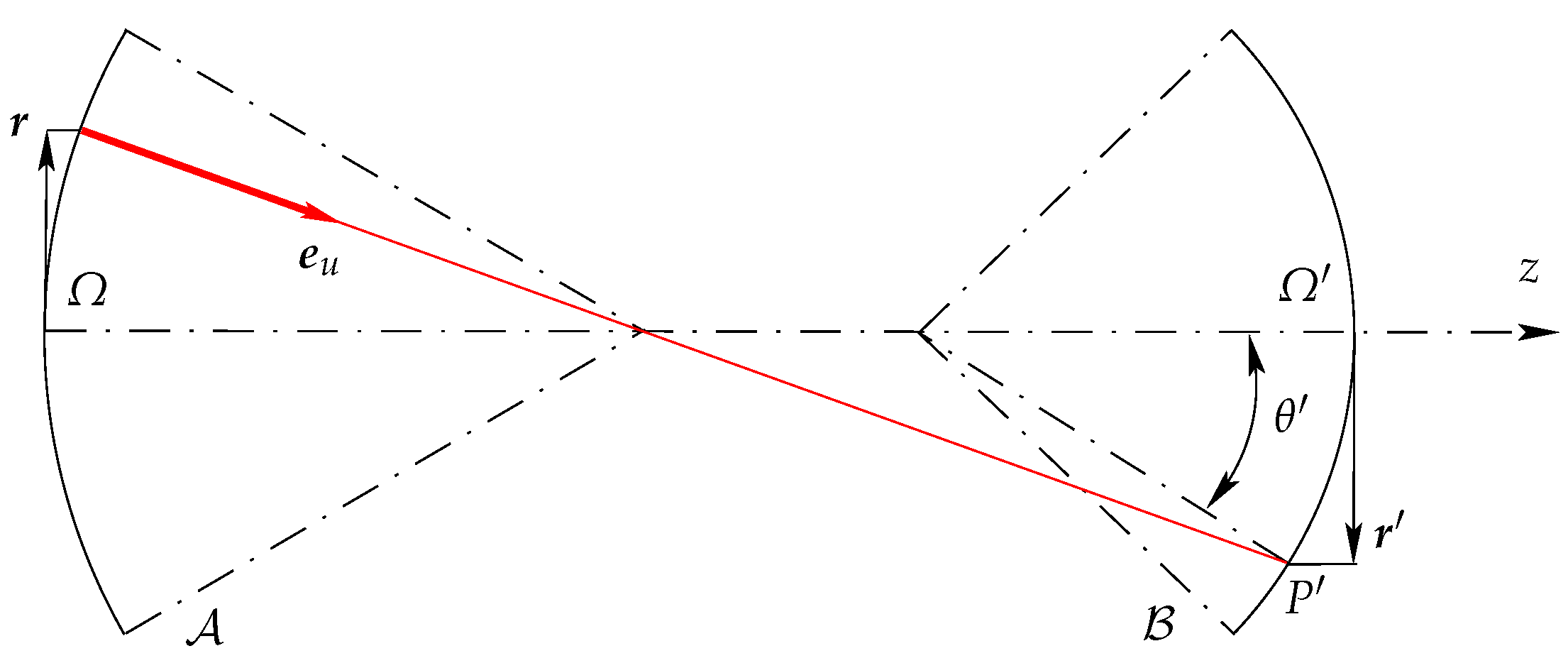
We first assume that $\mathit{r}=0$ (Figure 5). Then ${\mathit{r}}^{\prime }=D\mathit{\Phi }$ (second-order approximation in $\xi$ and $\eta$), that is $(x^{\prime },y^{\prime })=(D\xi ,D\eta )$, and we conclude by $a_{13}=a_{24}=D$, and $a_{14}=a_{23}=0$.

ii

We then assume that ${\mathit{e}}_u$ is in the x–z plane (Figure 5): ${\mathit{e}}_u=u_x{\mathit{e}}_x+u_z{\mathit{e}}_z$, with ${u_x}^2+{u_z}^2=1$. For $\mathit{r}=0$, we have $({\mathit{e}}_{\xi },{\mathit{e}}_{\eta },{\mathit{e}}_n)=({\mathit{e}}_x,{\mathit{e}}_y,{\mathit{e}}_z)$, so that

$$\mathit{\Phi }=(u_x,0).$$

(7)

We introduce the angle ${\theta }^{\prime }$ (Figure 5) and we obtain

$${\mathit{e}}_{{\xi }^{\prime }}={\mathit{e}}_x\cos {\theta }^{\prime }-{\mathit{e}}_z\sin {\theta }^{\prime },{\mathit{e}}_{{\eta }^{\prime }}={\mathit{e}}_y,{\mathit{e}}_n={\mathit{e}}_x\sin {\theta }^{\prime }+{\mathit{e}}_z\cos {\theta }^{\prime },$$

(8)

and

$${\mathit{\Phi }}^{\prime }=(u_x\cos {\theta }^{\prime }-u_z\sin {\theta }^{\prime },0).$$

(9)

In the limits of a second-order approximation, we have

$$\sin {\theta }^{\prime }=-\frac{D{u}_x}{R_B},\cos {\theta }^{\prime }=1-\frac{D^2{u_x}^2}{2{R_B}^2},$$

(10)

and then

$$u_x\cos {\theta }^{\prime }-u_z\sin {\theta }^{\prime }=\frac{D+R_B}{R_B}{u}_x,$$

(11)

so that

$$({\xi }^{\prime },0)={\mathit{\Phi }}^{\prime }=\frac{D+R_B}{R_B}\mathit{\Phi }=\frac{D+R_B}{R_B}(\xi ,0).$$

(12)

We conclude by $a_{34}=0$, and

$$a_{33}=\frac{D+R_B}{R_B}.$$

(13)

The same reasoning in the y–z plane leads to $a_{43}=0$ and

$$a_{44}=\frac{D+R_B}{R_B}.$$

(14)

iii

We now assume $\mathit{r}\ne 0$ and $\mathit{\Phi }=0$. Figure 6 shows that

$$(x^{\prime },y^{\prime })={\mathit{r}}^{\prime }=\frac{R_A-D}{R_A}\mathit{r}=\frac{R_A-D}{R_A}(x,y),$$

(15)

and we conclude by $a_{12}=a_{21}=0$ and

$$a_{11}=a_{22}=\frac{R_A-D}{R_A}.$$

(16)

iv

Finally, by choosing ${\mathit{e}}_u$ in the x–z plane, we have $\mathit{u}=u_x{\mathit{e}}_x+u_z{\mathit{e}}_z$ and we introduce ${\theta }^{\prime }$ (Figure 6) so that

$$\sin {\theta }^{\prime }=-\frac{r^{\prime }}{R_B},\cos {\theta }^{\prime }=1-\frac{r^{\prime 2}}{2{R_B}^2}.$$

(17)

We have

$${\mathit{\Phi }}^{\prime }=(u_x\cos {\theta }^{\prime }-u_z\sin {\theta }^{\prime },0).$$

(18)

We also have $u_x=r/R_A$, so that

$$u_x\cos {\theta }^{\prime }-u_z\sin {\theta }^{\prime }=\frac{r}{R_A}+\frac{R_A-D}{R_B}r=-\frac{D-R_A+R_B}{R_A{R}_B}r,$$

(19)

and

$$({\xi }^{\prime },0)={\mathit{\Phi }}^{\prime }=-\frac{D-R_A+R_B}{R_A{R}_B}\mathit{r}=\frac{R_A-R_B-D}{R_A{R}_B}(x,0).$$

(20)

We conclude by $a_{32}=0$ and

$$a_{31}=\frac{R_A-R_B-D}{R_A{R}_B}.$$

(21)

The same reasoning in the y–z leads to $a_{41}=0$ and

$$a_{42}=\frac{R_A-R_B-D}{R_A{R}_B}.$$

(22)

All the $a_{ij}$’s have been determined.

In conclusion, Equation (6) is explicitly written

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ {\xi }^{\prime }\\ {\eta }^{\prime }\end{array}\right)=\left(\begin{array}{cccc}{\displaystyle \frac{R_A-D}{R_A}}& 0& D& 0\\ \\ 0& {\displaystyle \frac{R_A-D}{R_A}}& 0& D\\ \\ {\displaystyle \frac{R_A-R_B-D}{R_A{R}_B}}& 0& {\displaystyle \frac{D+R_B}{R_B}}& 0\\ \\ 0& {\displaystyle \frac{R_A-R_B-D}{R_A{R}_B}}& 0& {\displaystyle \frac{D+R_B}{R_B}}\end{array}\right)\left(\begin{array}{c}x\\ y\\ \xi \\ \eta \end{array}\right).$$

(23)

With ${}^t(\mathit{r},\mathit{\Phi })={}^t(x,y,\xi ,\eta )$, a more concise form of Equation (23) is

$$\left(\begin{array}{c}{\mathit{r}}^{\prime }\\ {\mathit{\Phi }}^{\prime }\end{array}\right)=\left(\begin{array}{cc}{\displaystyle \frac{R_A-D}{R_A}}& D\\ \\ {\displaystyle \frac{R_A-R_B-D}{R_A{R}_B}}& {\displaystyle \frac{D+R_B}{R_B}}\end{array}\right)\left(\begin{array}{c}\mathit{r}\\ \mathit{\Phi }\end{array}\right),$$

(24)

Since the result is obtained for every point $(x,y)$ and every direction $(\xi ,\eta )$, we eventually point out that Equations (23) and (24) hold for skew rays as well as for meridional rays.

3. Rotations in a Reduced Phase Space

3.1. Defining Reduced Variables and an Angle of Rotation

The previous matrices—Equations (23) and (24)—are not homogeneous, because $\mathit{r}$ and ${\mathit{r}}^{\prime }$ are spatial vectors (their components are homogeneous to lengths) while Φ and ${\mathit{\Phi }}^{\prime }$ are physically dimensionless. We would like to express Equation (24) as

$$\left(\begin{array}{c}{\mathit{\rho }}^{\prime }\\ {\mathit{\varphi }}^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{array}\right)\left(\begin{array}{c}\mathit{\rho }\\ \mathit{\varphi }\end{array}\right),$$

(25)

where $\mathit{\rho }$, $\mathit{\varphi }$, ${\mathit{\rho }}^{\prime }$ and ${\mathit{\varphi }}^{\prime }$ are reduced variables that are dimensionless (from a physical point of view) and which replace $\mathit{r}$, Φ, $\mathit{r}$ and ${\mathit{\Phi }}^{\prime }$. (Mathematically, they are two-dimensional vectors, elements of ${\mathbb{R}}^2$.)

The square matrix in Equation (25) is a rotation matrix of angle $-\alpha$. We choose a rotation angle equal to $-\alpha$ to match $\alpha$ with the forthcoming fractional parameter $\alpha$ associated with a diffraction phenomenon. The value of the fractional parameter ($\alpha$ or $-\alpha$) is related to the definition of two-dimensional fractional-order Fourier transformations, according to Equation (48).

To express the matrix in Equation (24) as that in Equation (25), we set $\mathit{\rho }=A\mathit{r}$, ${\mathit{\rho }}^{\prime }=A^{\prime }{\mathit{r}}^{\prime }$, $\mathit{\varphi }=B\mathit{\Phi }$ and ${\mathit{\varphi }}^{\prime }=B^{\prime }\mathit{\Phi }$, where A, $A^{\prime }$, B and $B^{\prime }$ are positive real numbers. We should then have

$$\frac{A}{A^{\prime }}\cos \alpha =\frac{R_A-D}{R_A},$$

(26)

$$\frac{A}{B^{\prime }}\sin \alpha =-\frac{R_A-R_B-D}{R_A{R}_B},$$

(27)

$$\frac{B}{A^{\prime }}\sin \alpha =D,$$

(28)

$$\frac{B}{B^{\prime }}\cos \alpha =\frac{D+R_B}{R_B}.$$

(29)

Before calculating A, $A^{\prime }$, B and $B^{\prime }$, we define $\alpha$. Thus we introduce

$$J=\frac{(R_A-D)(D+R_B)}{D(D-R_A+R_B)},$$

(30)

and assume $J\ge 0$, so that we can choose $\alpha$, with $-\pi <\alpha <\pi$, such that

$${\cot }^2\alpha =\frac{(R_A-D)(D+R_B)}{D(D-R_A+R_B)}=J.$$

(31)

(If $J<0$, the parameter $\alpha$ becomes a complex number [2]).

To complete the definition of $\alpha$, we note that, according to Equation (28), the sign of $\alpha$ should be that of D and, according to Equations (26) and (28), the sign of $\cot \alpha$ should be the sign of $(R_A-D)D{R}_A$. Thus, in addition to Equation (31), we choose $\alpha$ such that $-\pi <\alpha <\pi$, and impose $\alpha D\ge 0$ and

$$\frac{R_{A}D}{R_A-D}\cot \alpha \ge 0.$$

(32)

On the other hand, we note that according to Equations (28) and (29) the sign of $\cot \alpha$ should also be the sign of $(R_B+D)D{R}_B$. To avoid inconsistency between Equations (26)–(29) and the previous definition of $\alpha$, we have to prove that $(R_A-D)D{R}_A$ and $(R_B+D)D{R}_B$ have the same sign. Actually, this is a consequence of the assumption $J\ge 0$. For a proof, we start with the identity $D(D-R_A-R_B)=R_A{R}_B-(R_A-D)(D+R_B)$ and deduce, for $J\ge 0$,

$$\frac{R_A{R}_B}{(R_A-D)(D+R_B)}=1+\frac{1}{J}\ge 1.$$

(33)

We then obtain

$$\frac{R_A{R}_B{D}^2}{(R_A-D)(D+R_B)}\ge 0,$$

(34)

and we conclude that $R_{A}D(R_A-D)$ and $R_{B}D(D+R_B)$ have the same sign. The definition of $\alpha$ is consistent with Equations (26)–(29).

So far A, $A^{\prime }$, B and $B^{\prime }$ are defined up to a multiplicative factor. We may choose additional conditions to define them more accurately: to make the link with diffraction, according to what has been done in a previous article [12], we shall impose

$$\mathit{\rho }·\mathit{\varphi }=\frac{1}{\lambda }\mathit{r}·\mathit{\Phi },$$

(35)

and

$${\mathit{\rho }}^{\prime }·{\mathit{\varphi }}^{\prime }=\frac{1}{\lambda }{\mathit{r}}^{\prime }·{\mathit{\Phi }}^{\prime }.$$

(36)

Under those conditions, we eventually deduce from Equations (26)–(29)

$$A^4=\frac{1}{{\lambda }^2{R_A}^2}\frac{(R_A-D)(D-R_A+R_B)}{D(D+R_B)},$$

(37)

$$B^4=\frac{{R_A}^2}{{\lambda }^2}\frac{D(D+R_B)}{(R_A-D)(D-R_A+R_B)},$$

(38)

$$A^{\prime 4}=\frac{1}{{\lambda }^2{R_B}^2}\frac{(D+R_B)(D-R_A+R_B)}{D(R_A-D)},$$

(39)

$$B^{\prime 4}=\frac{{R_B}^2}{{\lambda }^2}\frac{D(R_A-D)}{(D+R_B)(D-R_A+R_B)}.$$

(40)

(Proofs are given in Appendix A).

3.2. Interpreting Rotations in the Reduced Phase Space

We remark that Equation (23) can also be written

$$\left(\begin{array}{c}{x}^{\prime }\\ {\xi }^{\prime }\\ y^{\prime }\\ {\eta }^{\prime }\end{array}\right)=\left(\begin{array}{cccc}{\displaystyle \frac{R_A-D}{R_A}}& D& 0& 0\\ \\ {\displaystyle \frac{R_A-R_B-D}{R_A{R}_B}}& {\displaystyle \frac{D+R_B}{R_B}}& 0& 0\\ \\ 0& 0& {\displaystyle \frac{R_A-D}{R_A}}& D\\ \\ 0& 0& {\displaystyle \frac{R_A-R_B-D}{R_A{R}_B}}& {\displaystyle \frac{D+R_B}{R_B}}\end{array}\right)\left(\begin{array}{c}x\\ \xi \\ y\\ \eta \end{array}\right).$$

(41)

or equivalently, with reduced variables,

$$\left(\begin{array}{c}{\rho }_x^{\prime }\\ {\varphi }_x^{\prime }\\ {\rho }_y^{\prime }\\ {\varphi }_y^{\prime }\end{array}\right)=\left(\begin{array}{cccc}\cos \alpha & \sin \alpha & 0& 0\\ -\sin \alpha & \cos \alpha & 0& 0\\ 0& 0& \cos \alpha & \sin \alpha \\ 0& 0& -\sin \alpha & \cos \alpha \end{array}\right)\left(\begin{array}{c}{\rho }_x\\ {\varphi }_x\\ {\rho }_y\\ {\varphi }_y\end{array}\right),$$

(42)

where $\mathit{\rho }=({\rho }_x,{\rho }_y)$ and $\mathit{\varphi }=({\varphi }_x,{\varphi }_y)$.

Equation (42) shows that in the reduced phase-space the transfer from ray $(\mathit{r},\mathit{\Phi })$ to ray $({\mathit{r}}^{\prime },{\mathit{\Phi }}^{\prime })$ is represented by a four-dimensional rotation that splits into two rotations of angle $-\alpha$, each rotation operating in a two-dimensional subspace of the reduced phase space [12]. From a physical point of view, matrices in Equation (42) are dimensionless.

4. Link with Diffraction and Fractional Fourier Optics

4.1. General Transfer by Diffraction (Fresnel Phenomenon)

According to a scalar theory of diffraction, the field transfer from $\mathcal{A}$ to $\mathcal{B}$ is expressed as [2,10,11]

$$\begin{array}{ccc}\hfill U_B\left({\mathit{r}}^{\prime }\right)& =& \frac{\mathrm{i}}{\lambda D}\exp \left[-\frac{\mathrm{i}\pi }{\lambda }\left(\frac{1}{R_B}+\frac{1}{D}\right)r^{\prime 2}\right]\hfill \\ & & \times {\int }_{{\mathbb{R}}^2}\exp \left[-\frac{\mathrm{i}\pi }{\lambda }\left(\frac{1}{D}-\frac{1}{R_A}\right)r^2\right]\exp \left(\frac{2\mathrm{i}\pi }{\lambda D}{\mathit{r}}^{\prime }·\mathit{r}\right)U_A\left(\mathit{r}\right)\mathrm{d}\mathit{r},\hfill \end{array}$$

(43)

where $U_A$ is the field amplitude on $\mathcal{A}$, $U_B$ the field amplitude on $\mathcal{B}$ and $\mathrm{d}\mathit{r}=\mathrm{d}x\mathrm{d}y$. (A phase factor equal to $\exp (-2\mathrm{i}\pi D/\lambda )$ has been omitted).

We replace $\mathit{r}$ and ${\mathit{r}}^{\prime }$ by reduced variables $\mathit{\rho }$ and ${\mathit{\rho }}^{\prime }$, as defined in Section 3.1, and we use reduced field amplitudes defined by

$$V_A\left(\mathit{\rho }\right)=\sqrt{\left|\frac{R_{A}D}{R_A-D}\right|}{U}_A\left(\frac{\mathit{\rho }}{A}\right),$$

(44)

$$V_B\left({\mathit{\rho }}^{\prime }\right)=\sqrt{\left|\frac{R_{B}D}{R_B+D}\right|}{U}_B\left(\frac{{\mathit{\rho }}^{\prime }}{A^{\prime }}\right).$$

(45)

Then Equation (43) becomes (the proof is given in Appendix B):

$$V_B\left({\mathit{\rho }}^{\prime }\right)=\frac{\mathrm{i}}{\sin \alpha }\exp (-\mathrm{i}\pi {\rho }^{\prime 2}\cot \alpha ){\int }_{{\mathbb{R}}^2}\exp (-\mathrm{i}\pi {\rho }^2\cot \alpha )\exp \left(\frac{2\mathrm{i}\pi }{\sin \alpha }{\mathit{\rho }}^{\prime }·\mathit{\rho }\right)V_A\left(\mathit{\rho }\right)\mathrm{d}\mathit{\rho },$$

(46)

that is

$$V_B\left({\mathit{\rho }}^{\prime }\right)={\mathrm{e}}^{\mathrm{i}\alpha }{\mathcal{F}}_{\alpha }\left[V_A\right]\left({\mathit{\rho }}^{\prime }\right),$$

(47)

where ${\mathcal{F}}_{\alpha }$ denotes the fractional Fourier transformation of order $\alpha$, defined, for a two-dimensional function f, by [13,14]

$${\mathcal{F}}_{\alpha }\left[f\right]\left({\mathit{\rho }}^{\prime }\right)=\frac{\mathrm{i}{\mathrm{e}}^{-\mathrm{i}\alpha }}{\sin \alpha }\exp (-\mathrm{i}\pi {\rho }^{\prime 2}\cot \alpha ){\int }_{{\mathbb{R}}^2}\exp (-\mathrm{i}\pi {\rho }^2\cot \alpha )\exp \left(\frac{2\mathrm{i}\pi }{\sin \alpha }{\mathit{\rho }}^{\prime }·\mathit{\rho }\right)f\left(\mathit{\rho }\right)\mathrm{d}\mathit{\rho }.$$

(48)

Equation (47) is usually deduced in the framework of fractional Fourier optics [2], by choosing appropriate reduced variables and reduced field amplitudes. Reduced variables have been introduced here with the help of ray matrices by looking for homogeneous matrices. In other words, the basic equation that expresses diffraction in the framework of fractional Fourier optics has been established from the analysis of ray transfers from an emitter to a receiver and considering homogeneous ray matrices.

Equation (43) generally corresponds to a Fresnel-diffraction phenomenon [2]. Fraunhofer diffraction constitutes a special case and is the subject of the next section.

 Remark 1.

The integral in Equation (48) is a Lebesgue integral and the standard Fourier transformation $\mathcal{F}$ is obtained for $\alpha =\pi /2$. If $g\left(\mathit{\rho }\right)=\exp (-\mathrm{i}\pi {\rho }^2\cot \alpha )f\left(\mathit{\rho }\right)$, then $\left|g\right(\mathit{\rho }\left)\right|=\left|f\right(\mathit{\rho }\left)\right|$ and $|{\mathcal{F}}_{\alpha }\left[f\right]\left({\mathit{\rho }}^{\prime }\right)|$ is proportional to $|\mathcal{F}\left[g\right]({\mathit{\rho }}^{\prime }/\sin \alpha )|$, so that ${\mathcal{F}}_{\alpha }$ is defined in the same conditions as $\mathcal{F}$ and for the same classes of functions. In particular the fractional-order Fourier transformation can be extended to every tempered distribution T, according to $\langle {\mathcal{F}}_{\alpha }\left[T\right],\phi \rangle =\langle T,{\mathcal{F}}_{\alpha }\left[\phi \right]\rangle$, where φ is a rapidly decreasing test function. The space of tempered distributions is large enough to represent physical fields encountered in the electromagnetic theory of light, such as field amplitudes $U_A$, etc., of the present article.

4.2. Fraunhofer Diffraction

Fraunhofer diffraction [2] occurs when $R_A=D=-R_B$ (Figure 7). Then Equation (43) takes the form

$$U_B\left({\mathit{r}}^{\prime }\right)=\frac{\mathrm{i}}{\lambda D}{\int }_{{\mathbb{R}}^2}\exp \left(\frac{2\mathrm{i}\pi }{\lambda D}{\mathit{r}}^{\prime }·\mathit{r}\right)U_A\left(\mathit{r}\right)\mathrm{d}\mathit{r},$$

(49)

and involves a (standard) Fourier transform, that is

$$U_B\left({\mathit{r}}^{\prime }\right)=\frac{\mathrm{i}}{\lambda D}{\widehat{U}}_A\left(\frac{{\mathit{r}}^{\prime }}{\lambda D}\right).$$

(50)

The spherical cap $\mathcal{B}$ is called the Fourier sphere of $\mathcal{A}$ and will be denoted $\mathcal{F}$. Spherical caps $\mathcal{A}$ and $\mathcal{F}$ are (symmetrical) confocal spheres: the vertex of the one is the curvature center of the other ($R_F=-R_A$). We write

$$U_F\left({\mathit{r}}^{\prime }\right)=\frac{\mathrm{i}}{\lambda D}{\widehat{U}}_A\left(\frac{{\mathit{r}}^{\prime }}{\lambda D}\right)=\frac{\mathrm{i}}{\lambda R_A}{\widehat{U}}_A\left(\frac{{\mathit{r}}^{\prime }}{\lambda R_A}\right).$$

(51)

If $\tilde{f}$ denotes the function defined by $\tilde{f}\left(\mathit{r}\right)=f(-\mathit{r})$, from Equation (51) we deduce ($\mathit{F}$ is a spatial frequency):

$${\widehat{U}}_F\left(\mathit{F}\right)=\mathrm{i}\lambda R_A{\widehat{\widehat{U}}}_A\left(\lambda R_A\mathit{F}\right)=\mathrm{i}\lambda R_A{\tilde{U}}_A(-\lambda R_A\mathit{F}),$$

(52)

and then

$$U_A\left(\mathit{r}\right)=\frac{\mathrm{i}}{\lambda R_F}{\widehat{U}}_F\left(\frac{\mathit{r}}{\lambda R_F}\right),$$

(53)

which shows that $\mathcal{A}$ is the Fourier sphere of $\mathcal{F}$ (reciprocity property of Fourier spheres).

According to Equation (31) we have $\cot \alpha =0$ and for positive D we obtain $\alpha =\pi /2$: Equation (47) involves a (standard) Fourier transformation, as expected. To deal with reduced variables, we proceed as follows. We consider first that $R_A=-R_F\ne -D$ ($R_F=R_B$), so that according to Equations (37) and (39) we have

$$A^4=\frac{2R_A-D}{{\lambda }^2{R_A}^{2}D},A^{\prime 4}=\frac{2R_A-D}{{\lambda }^2{R_F}^{2}D}.$$

(54)

When D tends to $R_A$ we obtain then that $\mathit{\rho }$ tends to $\mathit{r}/\sqrt{\lambda R_A}$ and ${\mathit{\rho }}^{\prime }$ tends to ${\mathit{r}}^{\prime }/\sqrt{\lambda R_A}$. Hence, reduced variables are perfectly defined.

Thus, for $D>0$, Fraunhofer diffraction is decribed by a rotation of angle $-\alpha =-\pi /2$. If $D<0$, we obtain $\alpha =-\pi /2$; we have thus a virtual Fraunhofer diffraction, described by a rotation of angle $-\alpha =\pi /2$.

5. Link with the Spherical Angular Spectrum

5.1. The Notion of Spherical Angular Spectrum

The notion of a spherical angular spectrum is a generalization of the planar angular spectrum to spherical caps [8]. We shall provide an interpretation of the spherical angular spectrum by linking it with the previous analysis.

We begin by associating a light ray and a point on an emitter with a spatial frequency. Let $\mathcal{A}$ be a spherical emitter (or receiver) on which the field amplitude is

$$U_A\left(\mathit{r}\right)=U_0\exp (-2\mathrm{i}\pi {\mathit{F}}_0·\mathit{r}),$$

(55)

where $U_0$ is a dimensional constant. The vector ${\mathit{F}}_0$ is a spatial frequency.

According to Equation (51) the field amplitude on $\mathcal{F}$ (the Fourier sphere of $\mathcal{A}$) is

$$U_F\left({\mathit{r}}^{\prime }\right)=\frac{\mathrm{i}}{\lambda D}\delta \left(\frac{{\mathit{r}}^{\prime }}{\lambda D}-F_0\right)=\mathrm{i}\lambda D\delta ({\mathit{r}}^{\prime }-\lambda D{\mathit{F}}_0),$$

(56)

where $\delta$ denotes the (two-dimensional) Dirac distribution. We conclude that the wave emitted by $\mathcal{A}$ converges at the point $P^{\prime }$ of $\mathcal{F}$, such that ${\mathit{r}}^{\prime }=\lambda D{\mathit{F}}_0$ (Figure 8).

Let P be a point on $\mathcal{A}$. The ray $P{P}^{\prime }$ is defined by $(\mathit{r},{\mathit{\Phi }}_0)$. Since $D=R_A$ (Fourier sphere), Equation (24) gives $P^{\prime }$ as corresponding to ${\mathit{r}}^{\prime }=D{\mathit{\Phi }}_0$, so that

$${\mathit{\Phi }}_0=\lambda {\mathit{F}}_0.$$

(57)

Equation (57) leads us to introduce the notion of a spherical angular spectrum as follows. Let $U_A$ be the field amplitude on $\mathcal{A}$. The Fourier transform of $U_A$ (also called the spectrum of $U_A$) is ${\widehat{U}}_A\left(\mathit{F}\right)$. By changing $\mathit{F}$ into $\mathit{\Phi }=\lambda \mathit{F}$, we obtain the so-called spherical angular spectrum of $U_A$, denoted $S_A$ and such that

$$S_A\left(\mathit{\Phi }\right)=\frac{1}{{\lambda }^2}{\widehat{U}}_A\left(\frac{\mathit{\Phi }}{\lambda }\right)=\frac{1}{{\lambda }^2}{\int }_{{\mathbb{R}}^2}\exp \left(\frac{2\mathrm{i}\pi }{\lambda }\mathit{\Phi }·\mathit{r}\right)U_A\left(\mathit{r}\right)\mathrm{d}\mathit{r},$$

(58)

where the factor $1/{\lambda }^2$ has been introduced for the sake of homogeneity (that is, $S_A$ has the (physical) dimension of $U_A$).

If $\mathcal{A}$ becomes a plane, $S_A$ is the usual angular spectrum (up to a factor $1/{\lambda }^2$) [9]. According to classical Fourier optics, a plane wave is associated with each spatial frequency of the wave emitted by a planar object. The emitted wave is decomposed on a family of plane waves. Each plane wave propagates along a direction whose direction cosines are given by $(\cos {\theta }_x,\cos {\theta }_y)=\mathit{\Phi }=\lambda \mathit{F}$. The vector Φ is a constant.

The spherical angular spectrum is defined on a spherical emitter (or receiver). A spherical wave is associated with each spatial frequency on the spherical emitter, so that the emitted wave is decomposed on a family of spherical waves. Every spherical wave is weighted by an appropriate coefficient which is equal to the value of the angular spectrum for the associated spatial frequency. The law $\mathit{\Phi }=\lambda \mathit{F}$ still holds for spherical emitters (or receivers). However, on the basis of the analysis of Section 2, given a ray propagating along the unit vector ${\mathit{e}}_u$ and issued from a given point on an emitter, the angular frequency Φ should be interpreted as the projection of ${\mathit{e}}_u$ on the plane tangent to the emitter at the previous point.

5.2. Propagation of the Spherical Angular Spectrum

The transfer of the spherical angular spectrum from an emitter $\mathcal{A}$ (radius $R_A$) to a receiver $\mathcal{B}$ (radius $R_B$) at a distance D is given by [8]

$$\begin{array}{ccc}\hfill S_B\left({\mathit{\Phi }}^{\prime }\right)& =& \frac{\mathrm{i}{R}_A{R}_B}{\lambda (D-R_A+R_B)}\exp \left(\frac{-\mathrm{i}\pi R_B(R_A-D)}{\lambda (D-R_A+R_B)}{\mathit{\Phi }}^{\prime 2}\right)\hfill \\ & & \times {\int }_{{\mathbb{R}}^2}\exp \left(\frac{-\mathrm{i}\pi R_A(R_B+D)}{\lambda (D-R_A+R_B)}{\mathit{\Phi }}^2\right)\exp \left(\frac{2\mathrm{i}\pi R_A{R}_B}{\lambda (D-R_A+R_B)}{\mathit{\Phi }}^{\prime }·\mathit{\Phi }\right)S_A\left(\mathit{\Phi }\right)\mathrm{d}\mathit{\Phi }.\hfill \end{array}$$

(59)

If we make the following changes

$$D⟼\frac{D-R_A+R_B}{R_A{R}_B},$$

(60)

$$R_A⟼\frac{D-R_A+R_B}{R_{A}D},$$

(61)

$$R_B⟼\frac{D-R_A+R_B}{R_{B}D},$$

(62)

in Equation (43) and replace $\mathit{r}$ by Φ and ${\mathit{r}}^{\prime }$ by ${\mathit{\Phi }}^{\prime }$, we obtain Equation (59).

We use reduced (vectorial) variables $\mathit{\varphi }$ and ${\mathit{\varphi }}^{\prime }$, as defined in Section 3.1, and reduced spherical angular spectra $T_A$ and $T_B$ defined by

$$T_A\left(\mathit{\varphi }\right)=\sqrt{\left|\frac{R_A-D}{R_{A}D}\right|}{S}_A\left(\frac{\mathit{\varphi }}{B}\right),$$

(63)

$$T_B\left({\mathit{\varphi }}^{\prime }\right)=\sqrt{\left|\frac{R_B+D}{R_{B}D}\right|}{S}_B\left(\frac{{\mathit{\varphi }}^{\prime }}{B^{\prime }}\right),$$

(64)

so that the propagation of the spherical angular spectrum from $\mathcal{A}$ to $\mathcal{B}$ is expressed as

$$T_B\left({\mathit{\varphi }}^{\prime }\right)={\mathrm{e}}^{\mathrm{i}\alpha }{\mathcal{F}}_{\alpha }\left[T_A\right]\left({\mathit{\varphi }}^{\prime }\right).$$

(65)

The proof of Equation (65) is given in Appendix C.

Equation (65) can also be obtained in the framework of fractional Fourier optics [12]. It has been deduced here from the previous analysis, based on ray transfers and homogeneous matrices. Moreover, Equation (65) is similar to Equation (47), so that the spherical angular spectrum propagation is accomplished by a fractional Fourier transformation of order $\alpha$, as well as the field-amplitude propagation [8].

6. Accordance with the Huygens–Fresnel Principle

6.1. Expression with Non-Homogeneous Variables

In the framework of a scalar diffraction theory, the Huygens–Fresnel principle states that the (electric) field-amplitude transfer from an emitter $\mathcal{A}$ to a receiver $\mathcal{B}$ can be split into the transfer from $\mathcal{A}$ to $\mathcal{C}$, followed by the transfer from $\mathcal{C}$ to $\mathcal{B}$, where $\mathcal{C}$ is an arbitrary surface located between $\mathcal{A}$ and $\mathcal{B}$. We show in this section that the previous analysis, based on light rays and ray matrices, is in accordance with the principle.

We use the previous notations and variables: $\mathit{r}$ on $\mathcal{A}$ and ${\mathit{r}}^{\prime }$ on $\mathcal{B}$, and we introduce an intermediate spherical cap $\mathcal{C}$ whose radius is $R_C$ (Figure 9). A light ray on $\mathcal{C}$ is defined by $(\mathit{s},\mathit{\Psi })$. Let $D_1$ be the distance from $\mathcal{A}$ to $\mathcal{C}$ and $D_2$ the distance from $\mathcal{C}$ to $\mathcal{B}$, so that the distance from $\mathcal{A}$ to $\mathcal{B}$ is $D=D_1+D_2$. For the sake of convenience we assume $\mathcal{C}$ to be located between $\mathcal{A}$ and $\mathcal{B}$, but the analysis holds true for every $\mathcal{C}$; $\mathcal{C}$ might be a virtual emitter or receiver.

The spherical segment $\mathcal{C}$ is thought of as a receiver in the transfer from $\mathcal{A}$ to $\mathcal{C}$ and as an emitter in the transfer from $\mathcal{C}$ to $\mathcal{B}$. It should be clear that the same pair $(\mathit{s},\mathit{\Psi })$, taken on $\mathcal{C}$, can be used for describing both transfers.

The transfer from $\mathcal{A}$ to $\mathcal{C}$ is described by

$$\left(\begin{array}{c}\mathit{s}\\ \mathit{\Psi }\end{array}\right)=\left(\begin{array}{cc}{\displaystyle \frac{R_A-D_1}{R_A}}& D_1\\ \\ {\displaystyle \frac{D_1-R_A+R_C}{-R_A{R}_C}}& {\displaystyle \frac{D_1+R_C}{R_C}}\end{array}\right)\left(\begin{array}{c}\mathit{r}\\ \mathit{\Phi }\end{array}\right),$$

(66)

and the transfer from $\mathcal{C}$ to $\mathcal{B}$ by

$$\left(\begin{array}{c}{\mathit{r}}^{\prime }\\ {\mathit{\Phi }}^{\prime }\end{array}\right)=\left(\begin{array}{cc}{\displaystyle \frac{R_C-D_2}{R_C}}& D_2\\ \\ {\displaystyle \frac{D_2-R_C+R_B}{-R_B{R}_C}}& {\displaystyle \frac{D_2+R_B}{R_B}}\end{array}\right)\left(\begin{array}{c}\mathit{s}\\ \mathit{\Psi }\end{array}\right).$$

(67)

The combination of Equations (66) and (67) directly results in

$$\begin{array}{ccc}\hfill \left(\begin{array}{c}{\mathit{r}}^{\prime }\\ {\mathit{\Phi }}^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}{\displaystyle \frac{R_C-D_2}{R_C}}& D_2\\ \\ {\displaystyle \frac{D_2-R_C+R_B}{-R_B{R}_C}}& {\displaystyle \frac{D_2+R_B}{R_B}}\end{array}\right)\left(\begin{array}{cc}{\displaystyle \frac{R_A-D_1}{R_A}}& D_1\\ \\ {\displaystyle \frac{D_1-R_A+R_C}{-R_A{R}_C}}& {\displaystyle \frac{D_1+R_C}{R_C}}\end{array}\right)\left(\begin{array}{c}\mathit{r}\\ \mathit{\Phi }\end{array}\right)\hfill \\ & & \hfill \\ & =& \left(\begin{array}{cc}{\displaystyle \frac{R_A-D_1-D_2}{R_A}}& D_1+D_2\\ \\ {\displaystyle \frac{D_1+D_2-R_A+R_B}{-R_A{R}_B}}& {\displaystyle \frac{D_1+D_2+R_B}{R_B}}\end{array}\right)\left(\begin{array}{c}\mathit{r}\\ \mathit{\Phi }\end{array}\right),\hfill \end{array}$$

(68)

and, since $D=D_1+D_2$, Equation (68) is Equation (24) once more.

6.2. Expression with Homogeneous Variables

We examine now the accordance of the previous homogeneous ray-matrix representation with the Huygens–Fresnel principle. We have to compose two rotations whose angles are $-{\alpha }_1$ and $-{\alpha }_2$, and the result should be a rotation whose angle is $-\alpha =-{\alpha }_1-{\alpha }_2$. Nevertheless, the composition of the associated matrices physically makes sense only if reduced variables on $\mathcal{C}$ are the same for both transfers. The problem has already been analyzed [12] and the result is as follows: the composition makes sense if, and only if, the radius of $\mathcal{C}$ is $R_C$ such that

$$R_C=\frac{D_1(D_2+R_B)(R_A-D)+D_2(D+R_B)(R_A-D_1)}{D_1(R_A-D)+D_2(D+R_B)}.$$

(69)

Given an emitter $\mathcal{A}$ and a receiver $\mathcal{B}$, the result holds under rather strong conditions: (a) the field transfer from $\mathcal{A}$ to $\mathcal{B}$ is of real order; (b) intermediate caps (such as $\mathcal{C}$ above) belong to a family of spherical caps, whose curvature radii take only specific values, according to Equation (69). Such a result is actually close to the historical way in which Huygens conceived light propagation. Every point of an emitter emits ‘wavelets’ in the form of spherical lightwaves and the disturbance at a later instant is found on a wavefront, which is the envelope of the wavelets. Each point of the wavefront, in turn, re-emits wavelets whose envelope at a later instant provides the wavefront where the disturbance can be found. In this description of light propagation, an intermediate surface between an emitter and a receiver may not be an arbitrary cap, for the field on it has to correspond to an actual wavefront. Given a distance from the emitter, only one cap is then admissible and, in the metaxial theory, this cap is approximated as a sphere; its radius is given by Equation (69).

Such a situation corresponds to Gaussian beams [2]. A Gaussian beam can be seen as a sequence of spherical wavefronts ${\mathcal{W}}_{\alpha }$ on which the electric-field amplitude is represented by a Gaussian function (or more generally an Hermite–Gauss function). The field transfer from ${\mathcal{W}}_{{\alpha }_1}$ to ${\mathcal{W}}_{{\alpha }_2}$ (${\alpha }_1<{\alpha }_2$) can be seen as the composition of two field transfers from ${\mathcal{M}}_{{\alpha }_1}$ to ${\mathcal{M}}_{{\alpha }_3}$ and from ${\mathcal{M}}_{{\alpha }_3}$ to ${\mathcal{M}}_{{\alpha }_2}$, where ${\mathcal{M}}_{{\alpha }_3}$ is an intermediate wavefront, belonging to the previous family of wavefronts that constitute the Gaussian beam.

7. Coherent Imaging

Let $\mathcal{S}$ be a centered system that forms the image ${\mathcal{A}}^{\prime }$ of an arbitrary spherical cap $\mathcal{A}$. A ray issued from a point M on $\mathcal{A}$ is transformed into a ray on ${\mathcal{A}}^{\prime }$ and the issue is to establish the relationship between the two rays. We consider geometrical images in the meaning that we do not take into account diffraction by limited apertures of lenses (or refracting spherical caps, or mirrors).

We first examine image formation by a refracting sphere before we generalize to an arbitrary centered system.

7.1. Imaging by a Refracting Spherical Cap

We consider a refracting spherical cap $\mathcal{D}$ (radius $R_D$) separating two homogeneous and isotropic media with refractive indices n and $n^{\prime }$. We proceed in several steps that are as follows.

7.1.1. Matrix form of Snell’s Law (Refraction) [12]

A light ray $(\mathit{r},\mathit{\Phi }$) is incident on $\mathcal{D}$ at point M (coordinates $\mathit{r}$), see Figure 10. The refracted ray is written $({\mathit{r}}^{\prime },{\mathit{\Phi }}^{\prime })$ and, since it passes through M, we have ${\mathit{r}}^{\prime }=\mathit{r}$. If ${\mathit{e}}_n$ denotes the unit vector normal to $\mathcal{D}$ at M, the incident angle $\theta$ is the angle taken from ${\mathit{e}}_n$ to ${\mathit{e}}_u$, and the refracted angle ${\theta }^{\prime }$ is the angle from ${\mathit{e}}_n$ to ${\mathit{e}}_u^{\prime }$, where ${\mathit{e}}_u$ is along the incident ray and ${\mathit{e}}_u^{\prime }$ along the refracted ray (see Section 2). Since $\left|\right|\mathit{\Phi }\left|\right|=\left|\sin \theta \right|$, from the second part of Snell’s law ($n\sin \theta =n^{\prime }\sin {\theta }^{\prime }$), we obtain

$$n\left|\right|\mathit{\Phi }\left|\right|=n^{\prime }\left|\right|{\mathit{\Phi }}^{\prime }\left|\right|.$$

(70)

We assume $\mathit{\Phi }\ne 0$. According to the first part of Snell’s law, the incident and the refracted rays are in the plane of incidence, so that ${\mathit{e}}_u$, ${\mathit{e}}_u^{\prime }$ and ${\mathit{e}}_n$ are coplanar (Figure 10, right). Then Φ and ${\mathit{\Phi }}^{\prime }$, which are along the respective projections of ${\mathit{e}}_u$ and ${\mathit{e}}_u^{\prime }$ on the plane tangent to $\mathcal{D}$ at M, are colinear, and since $\theta$ and ${\theta }^{\prime }$ have the same sign, we obtain

$$n\mathit{\Phi }=n^{\prime }{\mathit{\Phi }}^{\prime },$$

(71)

which constitutes a vectorial form of Snell’s law and which holds also for $\mathit{\Phi }=0$.

Finally, the matrix form of Snell’s law is

$$\left(\begin{array}{c}{\mathit{r}}^{\prime }\\ {\mathit{\Phi }}^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& 0\\ \\ 0& {\displaystyle \frac{n}{n^{\prime }}}\end{array}\right)\left(\begin{array}{c}\mathit{r}\\ \mathit{\Phi },\end{array}\right)$$

(72)

and holds for meridional as well as for skew rays (as encountered when the refracting surface has a rotational symmetry).

7.1.2. Ray Transfer by a Refracting Spherical Cap

Let $\mathcal{A}$ be an emitter at a distance d from $\mathcal{D}$, in the object space; and let $\mathcal{B}$ be a receiver at a distance $d^{\prime }$ from $\mathcal{D}$, in the image space (we choose notations that are currently used in geometrical optics: $d=\overline{O{\Omega }_A}$ and $d^{\prime }=\overline{O{\Omega }_B}$, see Figure 11; the diffraction distance to be taken into account for the transfer from $\mathcal{A}$ to $\mathcal{D}$ is $D=-d$). A ray $(\mathit{r},\mathit{\Phi })$ on $\mathcal{A}$ becomes $(\mathit{s},\mathit{\Psi })$ on $\mathcal{D}$, then $({\mathit{s}}^{\prime },{\mathit{\Psi }}^{\prime })=(\mathit{s},{\mathit{\Psi }}^{\prime })$ after refraction and eventually $({\mathit{r}}^{\prime },{\mathit{\Phi }}^{\prime })$ on $\mathcal{B}$. We use Equations (24) and (72) to obtain

$$\left(\begin{array}{c}{\mathit{r}}^{\prime }\\ {\mathit{\Phi }}^{\prime }\end{array}\right)=\left(\begin{array}{cc}{\displaystyle \frac{R_D-d^{\prime }}{R_D}}& d^{\prime }\\ \\ {\displaystyle \frac{d^{\prime }-R_D+R_B}{-R_B{R}_D}}& {\displaystyle \frac{d^{\prime }+R_B}{R_B}}\end{array}\right)\left(\begin{array}{cc}1& 0\\ \\ 0& {\displaystyle \frac{n}{n^{\prime }}}\end{array}\right)\left(\begin{array}{cc}{\displaystyle \frac{R_A+d}{R_A}}& -d\\ \\ {\displaystyle \frac{d+R_A-R_D}{R_A{R}_D}}& {\displaystyle \frac{R_D-d}{R_D}}\end{array}\right)\left(\begin{array}{c}\mathit{r}\\ \mathit{\Phi }\end{array}\right),$$

(73)

from which we shall deduce the following results.

7.1.3. Conjugation Formula and Lateral Magnification

The receiver $\mathcal{B}$ becomes the image ${\mathcal{A}}^{\prime }$ of $\mathcal{A}$ if every ray passing through $\mathit{r}$ passes through ${\mathit{r}}^{\prime }$ after having crossed the refracting surface, that is, if ${\mathit{r}}^{\prime }$ does not depend on Φ. According to Equation (73), this happens if

$$-d\frac{R_D-d^{\prime }}{R_D}+\frac{n}{n^{\prime }}{d}^{\prime }\frac{R_D-d}{R_D}=0,$$

(74)

that is

$$\frac{n^{\prime }}{d^{\prime }}=\frac{n}{d}+\frac{n^{\prime }-n}{R_D}.$$

(75)

Equation (75) is a conjugation law of the refracting spherical cap.

From Equations (73) and (75) we deduce, in case of imaging,

$${\mathit{r}}^{\prime }=\left[1+\frac{d^{\prime }}{R_D}\left(\frac{n}{n^{\prime }}-1\right)+\frac{1}{R_A}\left(d-\frac{n}{n^{\prime }}{d}^{\prime }-\frac{d{d}^{\prime }}{R_D}+\frac{n}{n^{\prime }}\frac{d{d}^{\prime }}{R_D}\right)\right]\mathit{r}=\frac{n{d}^{\prime }}{n^{\prime }d}\mathit{r}.$$

(76)

The imaging lateral magnification is $m_{\mathrm{v}}=n{d}^{\prime }/n^{\prime }d$, a classical result of geometrical optics. (Subscript “v” indicates that $m_{\mathrm{v}}$ is the magnification between vertices of $\mathcal{A}$ and ${\mathcal{A}}^{\prime }$.)

We deduce that Equation (73) can be written as

$$\left(\begin{array}{c}{\mathit{r}}^{\prime }\\ {\mathit{\Phi }}^{\prime }\end{array}\right)=\left(\begin{array}{cc}{m}_{\mathrm{v}}& 0\\ a_{21}& a_{22}\end{array}\right)\left(\begin{array}{c}\mathit{r}\\ \mathit{\Phi }\end{array}\right),$$

(77)

where $a_{21}$ and $a_{22}$ remain to be determined.

7.1.4. Determination of $a_{22}$

From Equations (73) and (75) we deduce

$$\begin{array}{ccc}\hfill a_{22}& =& d\frac{d^{\prime }-R_D+R_B}{R_D{R}_B}+\frac{n}{n^{\prime }}\frac{(d^{\prime }+R_B)(R_D-d)}{R_D{R}_B}\hfill \\ & =& \frac{1}{R_D{R}_B}\left[d{d}^{\prime }-d{R}_D-\frac{n}{n^{\prime }}d{d}^{\prime }+\frac{n}{n^{\prime }}{d}^{\prime }{R}_D+R_B\left(d+\frac{n}{n^{\prime }}{R}_D-\frac{n}{n^{\prime }}d\right)\right]\hfill \\ & =& \frac{d}{d^{\prime }}=\frac{n}{n^{\prime }}\frac{1}{m_{\mathrm{v}}}.\hfill \end{array}$$

(78)

7.1.5. Conjugation of Curvature Centers (Double-Conjugation Law [2,10,11])

The spherical receiver ${\mathcal{A}}^{\prime }$ is the coherent geometrical image of the spherical emitter $\mathcal{A}$ if the field amplitude on ${\mathcal{A}}^{\prime }$ is equal to the field amplitude on $\mathcal{A}$ to within a scaling factor which is equal to the lateral magnification factor. As a consequence, the phase is preserved in the imaging process: if M and N are two points on the spherical cap $\mathcal{A}$, the images of which are $M^{\prime }$ and $N^{\prime }$ on ${\mathcal{A}}^{\prime }$, the phase difference between vibrations at $M^{\prime }$ and $N^{\prime }$ is equal to the phase difference between vibrations at M and N. The field amplitude on ${\mathcal{A}}^{\prime }$ is related to the field amplitude on $\mathcal{A}$ by

$$U_{A^{\prime }}\left({\mathit{r}}^{\prime }\right)=\frac{1}{m_{\mathrm{v}}}{U}_A\left(\frac{{\mathit{r}}^{\prime }}{m_{\mathrm{v}}}\right),$$

(79)

where $m_{\mathrm{v}}$ is the lateral magnification at vertices: if Ω is the vertex of $\mathcal{A}$ (with $d=\overline{O\Omega }$) and ${\Omega }^{\prime }$ the vertex of ${\mathcal{A}}^{\prime }$ (with $d^{\prime }=\overline{O{\Omega }^{\prime }}$), points Ω and ${\Omega }^{\prime }$ are conjugates, and d and $d^{\prime }$ are linked by Equation (75). The factor $1/m_{\mathrm{v}}$ before $U_A$ is necessary to express that the power of the whole object is also the power of the whole image: ${\int }_{{\mathbb{R}}^2}|U_{A^{\prime }}\left({\mathit{r}}^{\prime }\right){|}^2\mathrm{d}{\mathit{r}}^{\prime }={\int }_{{\mathbb{R}}^2}{\left|U_A\left(\mathit{r}\right)\right|}^2\mathrm{d}\mathit{r}$.

Let $\mathcal{F}$ be the Fourier sphere of $\mathcal{A}$, so that

$$U_F\left(\mathit{s}\right)=\frac{\mathrm{i}}{\lambda R_A}{\widehat{U}}_A\left(\frac{\mathit{s}}{\lambda R_A}\right).$$

(80)

From Equation (79) we deduce

$${\widehat{U}}_{A^{\prime }}\left(\mathit{F}\right)=m_{\mathrm{v}}{\widehat{U}}_A\left(m_{\mathrm{v}}\mathit{F}\right),$$

(81)

and if ${\mathcal{F}}^{\prime }$ denotes the Fourier sphere of ${\mathcal{A}}^{\prime }$ we have

$$U_{F^{\prime }}\left({\mathit{s}}^{\prime }\right)=\frac{\mathrm{i}}{{\lambda }^{\prime }{R}_{A^{\prime }}}{\widehat{U}}_{A^{\prime }}\left(\frac{{\mathit{s}}^{\prime }}{{\lambda }^{\prime }{R}_{A^{\prime }}}\right)=\frac{\mathrm{i}{m}_{\mathrm{v}}}{{\lambda }^{\prime }{R}_{A^{\prime }}}{\widehat{U}}_A\left(\frac{m_{\mathrm{v}}{\mathit{s}}^{\prime }}{{\lambda }^{\prime }{R}_{A^{\prime }}}\right)=m_{\mathrm{v}}\frac{\lambda R_A}{{\lambda }^{\prime }{R}_{A^{\prime }}}{U}_F\left(m_{\mathrm{v}}\frac{\lambda R_A{\mathit{s}}^{\prime }}{{\lambda }^{\prime }{R}_{A^{\prime }}}\right).$$

(82)

Equation (82) has the form $U_{F^{\prime }}\left({\mathit{s}}^{\prime }\right)=(1/m)U_F({\mathit{s}}^{\prime }/m)$, that is, the form of Equation (79): we conclude that the field amplitude on ${\mathcal{F}}^{\prime }$ is the coherent image of the field amplitude on $\mathcal{F}$, which means that the spherical cap ${\mathcal{F}}^{\prime }$ is the coherent image of $\mathcal{F}$. The vertices of $\mathcal{F}$ and ${\mathcal{F}}^{\prime }$, say C and $C^{\prime }$, are conjugates. Since C is also the curvature center of $\mathcal{A}$ and $C^{\prime }$ the curvature center of ${\mathcal{A}}^{\prime }$, we conclude that the spherical cap ${\mathcal{A}}^{\prime }$ is the coherent image of the spherical cap $\mathcal{A}$ if, and only if,

• The vertex of ${\mathcal{A}}^{\prime }$ is the paraxial image of the vertex of $\mathcal{A}$;
• The curvature center of ${\mathcal{A}}^{\prime }$ is the paraxial image of the curvature center of $\mathcal{A}$.

That constitutes the “double-conjugation law” of geometrical coherent imaging for a refracting spherical cap (a refracting plane constitutes a particular case: the curvature radius is infinite). The law also holds for mirrors and can be generalized to every centered system made up of refracting spheres and mirrors [2,10,11,15].

In Appendix B, we provide a pure geometrical proof of the conjugation of curvature centers for imaging by a refracting spherical cap (another geometrical proof has been given in a recent article [15]).

7.1.6. Determination of $a_{21}$

We consider a ray $(\mathit{r},\mathit{\Phi })$ on $\mathcal{A}$, such that $\mathit{\Phi }=0$. Then the ray passes through C (the curvature center of $\mathcal{A}$) and its image ray $({\mathit{r}}^{\prime },{\mathit{\Phi }}^{\prime })$ should pass through $C^{\prime }$, the center of ${\mathcal{A}}^{\prime }$, so that ${\mathit{\Phi }}^{\prime }=0$. Since the results holds true for every $\mathit{r}$, we must have $a_{21}=0$. (We provide an analytic checking of this result in Appendix E.)

Finally, we arrive at

$$\left(\begin{array}{c}{\mathit{r}}^{\prime }\\ {\mathit{\Phi }}^{\prime }\end{array}\right)=\left(\begin{array}{cc}{m}_{\mathrm{v}}& 0\\ \\ 0& {\displaystyle \frac{1}{m_{\mathrm{v}}}\frac{n}{n^{\prime }}}\end{array}\right)\left(\begin{array}{c}\mathit{r}\\ \mathit{\Phi }\end{array}\right).$$

(83)

We remark that

$$n\mathit{r}·\mathit{\Phi }=n^{\prime }{\mathit{r}}^{\prime }·{\mathit{\Phi }}^{\prime },$$

(84)

and, since $n\lambda =n^{\prime }{\lambda }^{\prime }$, from $\mathit{\Phi }=\lambda \mathit{F}$ we deduce

$$\mathit{r}·\mathit{F}={\mathit{r}}^{\prime }·{\mathit{F}}^{\prime }.$$

(85)

7.1.7. Radius Magnification

Let ${\mathcal{A}}^{\prime }$ (vertex ${\Omega }^{\prime }$, center $C^{\prime }$, radius $R_{A^{\prime }}=\overline{{\Omega }^{\prime }{C}^{\prime }}$) be the coherent image of $\mathcal{A}$ (vertex Ω, center C, radius $R_A=\overline{\Omega C}$) through a refracting spherical cap $\mathcal{D}$ (vertex O, radius $R_D$). Let us denote $q=\overline{OC}=d+R_A$ and $q=\overline{O{C}^{\prime }}=d^{\prime }+R_{A^{\prime }}$. Since C and $C^{\prime }$ are conjugates, we have

$$\frac{n^{\prime }}{q^{\prime }}=\frac{n}{q}+\frac{n^{\prime }-n}{R_D},$$

(86)

and the corresponding lateral magnification is

$$m_{\mathrm{c}}=\frac{n{q}^{\prime }}{n^{\prime }q}.$$

(87)

From Equation (82) we also deduce

$$m_{\mathrm{c}}=\frac{{\lambda }^{\prime }{R}_{A^{\prime }}}{m_{\mathrm{v}}\lambda R_A}=\frac{1}{m_{\mathrm{v}}}\frac{n}{n^{\prime }}\frac{R_{A^{\prime }}}{R_A},$$

(88)

and then

$$m_{\mathrm{r}}=\frac{R_{A^{\prime }}}{R_A}=\frac{n^{\prime }}{n}{m}_{\mathrm{v}}{m}_{\mathrm{c}},$$

(89)

where $m_{\mathrm{r}}$ is called the radius magnification [2,10,11].

The radius magnification law can also be deduced from vertex and center conjugation formulas, as shown in Appendix F.

7.2. Generalization to Centered Systems

A centered system $\mathcal{S}$ is the succession of refracting spherical caps ${\mathcal{D}}_i$, $i=1,...,I$, where ${\mathcal{D}}_i$ separates two media with respectives indices $n_{i-1}$ and $n_i$. We denote $n_0=n$ and $n_I=n^{\prime }$. Let ${\mathcal{A}}_0$ be an object (optically located in the medium of index n) and ${\mathcal{A}}_i$ (vertex ${\Omega }_i$, center $C_i$) be the intermediate image, that is, the image of ${\mathcal{A}}_{i-1}$ through ${\mathcal{D}}_i$. We denote ${\mathcal{A}}^{\prime }={\mathcal{A}}_I$, the final image (optically located in the medium of index $n^{\prime }$). We apply the double-conjugation law:

• Since ${\Omega }_i$ is the paraxial image of ${\Omega }_{i-1}$ through ${\mathcal{D}}_i$, we obtain that ${\Omega }^{\prime }={\Omega }_I$ is the paraxial image of ${\Omega }_0=\Omega$ through $\mathcal{S}$;
• Since $C_i$ is the paraxial image of $C_{i-1}$ through ${\mathcal{D}}_i$, we obtain that $C^{\prime }=C_I$ is the paraxial image of $C_0=C$ through $\mathcal{S}$.

We conclude that the double-conjugation law applies to $\mathcal{S}$.

A ray $(\mathit{r},\mathit{\Phi })=({\mathit{r}}_0,{\mathit{\Phi }}_0)$, issued from ${\mathcal{A}}_0$, becomes $({\mathit{r}}_i,{\mathit{\Phi }}_i)$ on ${\mathcal{A}}_i$, after refraction on ${\mathcal{D}}_i$. The final ray, on ${\mathcal{A}}^{\prime }$, is $({\mathit{r}}^{\prime },{\mathit{\Phi }}^{\prime })=({\mathit{r}}_I,{\mathit{\Phi }}_I)$.

For every i we have ${\mathit{r}}_i=m_i{\mathit{r}}_{i-1}$, so that

$${\mathit{r}}^{\prime }={\mathit{r}}_I=m_I{\mathit{r}}_{I-1}=m_I{m}_{I-1}{\mathit{r}}_{I-2}=\cdots =m_I{m}_{I-1}\cdots m_1{\mathit{r}}_0=m_{\mathrm{v}}\mathit{r},$$

(90)

where ${\displaystyle m_{\mathrm{v}}=\prod _{i=1}^{i=I}{m}_i}$ is the lateral magnification for the conjugation of Ω and ${\Omega }^{\prime }$. We also have

$$\frac{n}{n^{\prime }}=\frac{n}{n_1}\frac{n_1}{n_2}\cdots \frac{n_{I-2}}{n_{I-1}}\frac{n_{I-1}}{n^{\prime }}.$$

(91)

Equation (83) leads us to write

$$\left(\begin{array}{c}{\mathit{r}}^{\prime }\\ {\mathit{\Phi }}^{\prime }\end{array}\right)=\left(\begin{array}{c}{\mathit{r}}_I\\ {\mathit{\Phi }}_I\end{array}\right)=\prod _{i=1}^{i=I}\left(\begin{array}{cc}{m}_i& 0\\ \\ 0& {\displaystyle \frac{1}{m_i}\frac{n_{i-1}}{n_i}}\end{array}\right)\left(\begin{array}{c}{\mathit{r}}_0\\ {\mathit{\Phi }}_0\end{array}\right)=\left(\begin{array}{cc}{m}_{\mathrm{v}}& 0\\ \\ 0& {\displaystyle \frac{1}{m_{\mathrm{v}}}\frac{n}{n^{\prime }}}\end{array}\right)\left(\begin{array}{c}\mathit{r}\\ \mathit{\Phi }\end{array}\right),$$

(92)

because all previous square matrices are diagonal. Equation (92) is the generalization of Equation (83) to a centered system made up of refracting spherical caps. It can be proved to hold also for catadioptric systems.

The radius magnification law is

$$m_{\mathrm{r}}=\frac{R_{A^{\prime }}}{R_A}=\frac{R_I}{R_0}=\frac{R_I}{R_{I-1}}\frac{R_{I-1}}{R_{I-2}}\cdots \frac{R_2}{R_1}\frac{R_1}{R_0}=\prod _{i=1}^{i=I}\frac{n_i}{n_{i-1}}{m}_{\mathrm{v},i}{m}_{\mathrm{c},i}=\frac{n^{\prime }}{n}{m}_{\mathrm{v}}{m}_{\mathrm{c}},$$

(93)

and takes the same form as Equation (89).

7.3. Homogeneous Matrix Representation

Since ${\mathcal{F}}_0$ is the identity operator (${\mathcal{F}}_0\left[f\right]=f$, for every function f) and since ${\mathcal{F}}_{\pi }\left[f\right]\left({\mathit{\rho }}^{\prime }\right)=f(-{\mathit{\rho }}^{\prime })$, the imaging should be expressed by a fractional Fourier transform whose order is 0 or equal to $\pm \pi$. That holds true for both reduced spatial variable $\mathit{\rho }$ and angular frequency $\mathit{\varphi }$, because the field transfer and the angular-spectrum transfer are both expressed by fractional Fourier transforms of equal orders. The homogeneous ray matrix associated with imaging thus results to be such that

$$\left(\begin{array}{c}{\mathit{\rho }}^{\prime }\\ {\mathit{\varphi }}^{\prime }\end{array}\right)=\pm \left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}\mathit{\rho }\\ \mathit{\varphi }\end{array}\right).$$

(94)

In Appendix G, we prove that this is the case.

 Remark 2.

Square matrices in Equation (92) are homogenous since $m_{\mathrm{v}}$ and refractive indices n and $n^{\prime }$ are pure numbers. However, column vectors are not homogeneous. In Equation (94) all matrices are homogeneous.

 Remark 3

(Reduced form of Snell’s law). Snell’s law of refraction is expressed by Equation (72), which may be seen as an imaging between ray $(\mathit{r},\mathit{\Phi })$ and ray $({\mathit{r}}^{\prime },{\mathit{\Phi }}^{\prime })$, with ${\mathit{r}}^{\prime }=\mathit{r}$, so that the lateral magnification is $m_{\mathrm{v}}=1$. Then we have ${\mathit{\varphi }}^{\prime }=\mathit{\varphi }$, which constitutes the reduced form of Snell’s law.

8. Conclusions

Fractional Fourier optics is based on the representation of a Fresnel diffraction phenomenon by a fractional-order Fourier transformation. The transformation associated with a given diffraction phenomenon has been deduced here from a matrix representation of ray transfer from a spherical emitter to a spherical receiver by looking for homogeneous transfer matrices. When the field transfer is expressed by a real-order transformation, the ray matrix is a four-dimensional rotation matrix that splits into two rotations operating on two-dimensional subspaces of the reduced phase space. The analysis can be extended to complex orders; the previous rotation matrices become then two-dimensional hyperbolic-rotation matrices [12].