Thermal Conductivity of Fractal-Textured Foamed Concrete
Abstract
1. Introduction
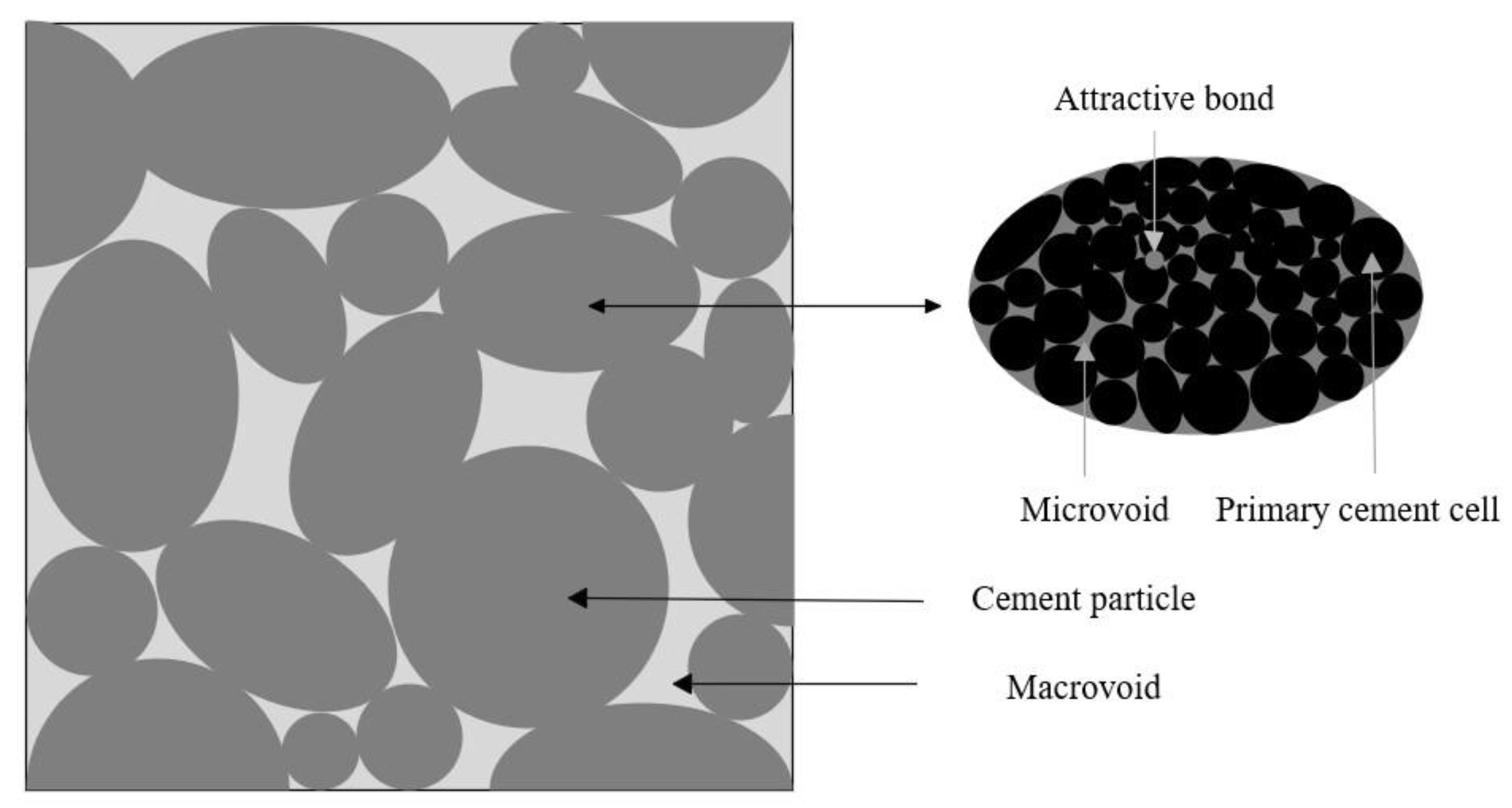
2. Theory
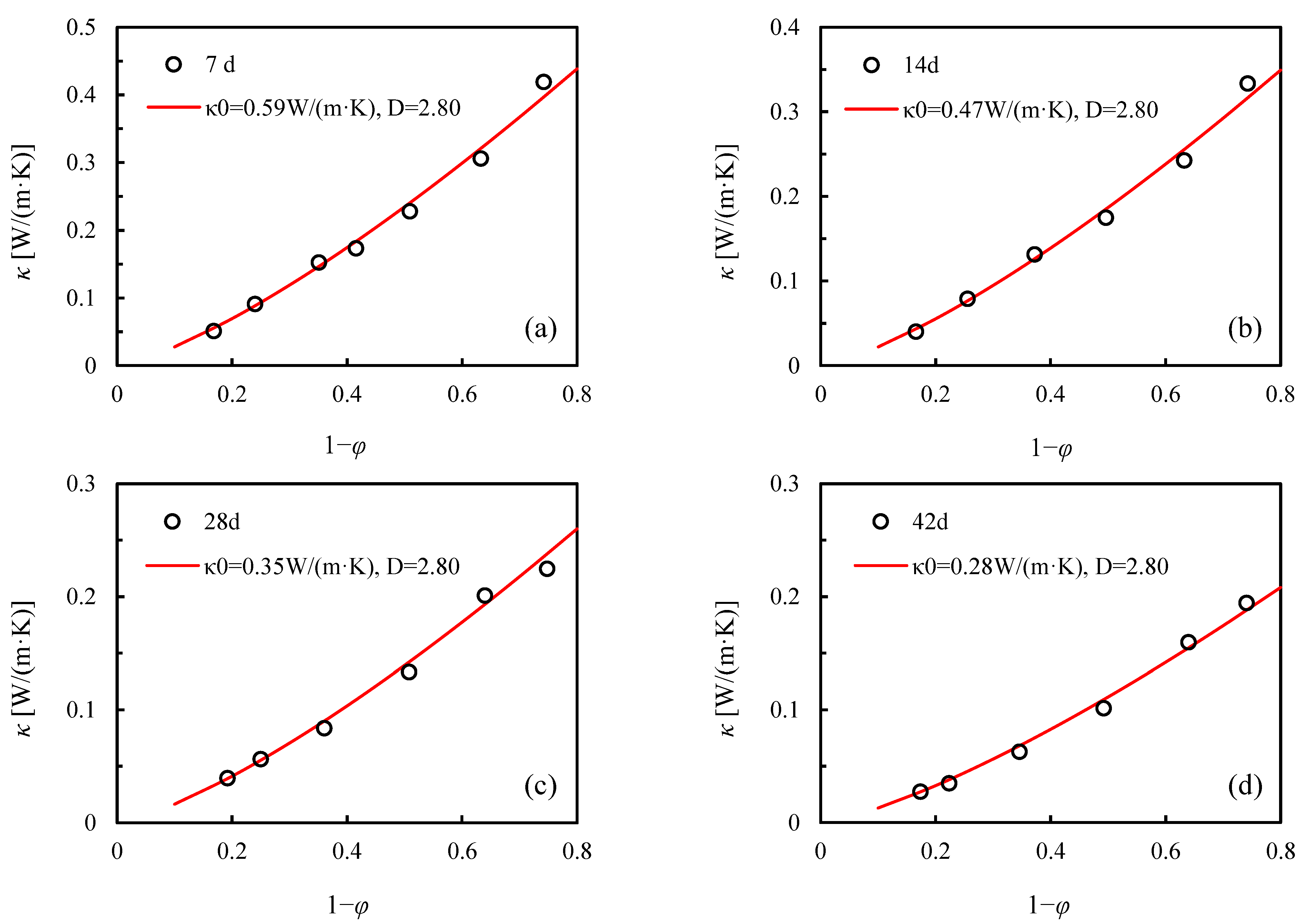
Relation of Thermal Conductivity to Porosity
3. Experiments
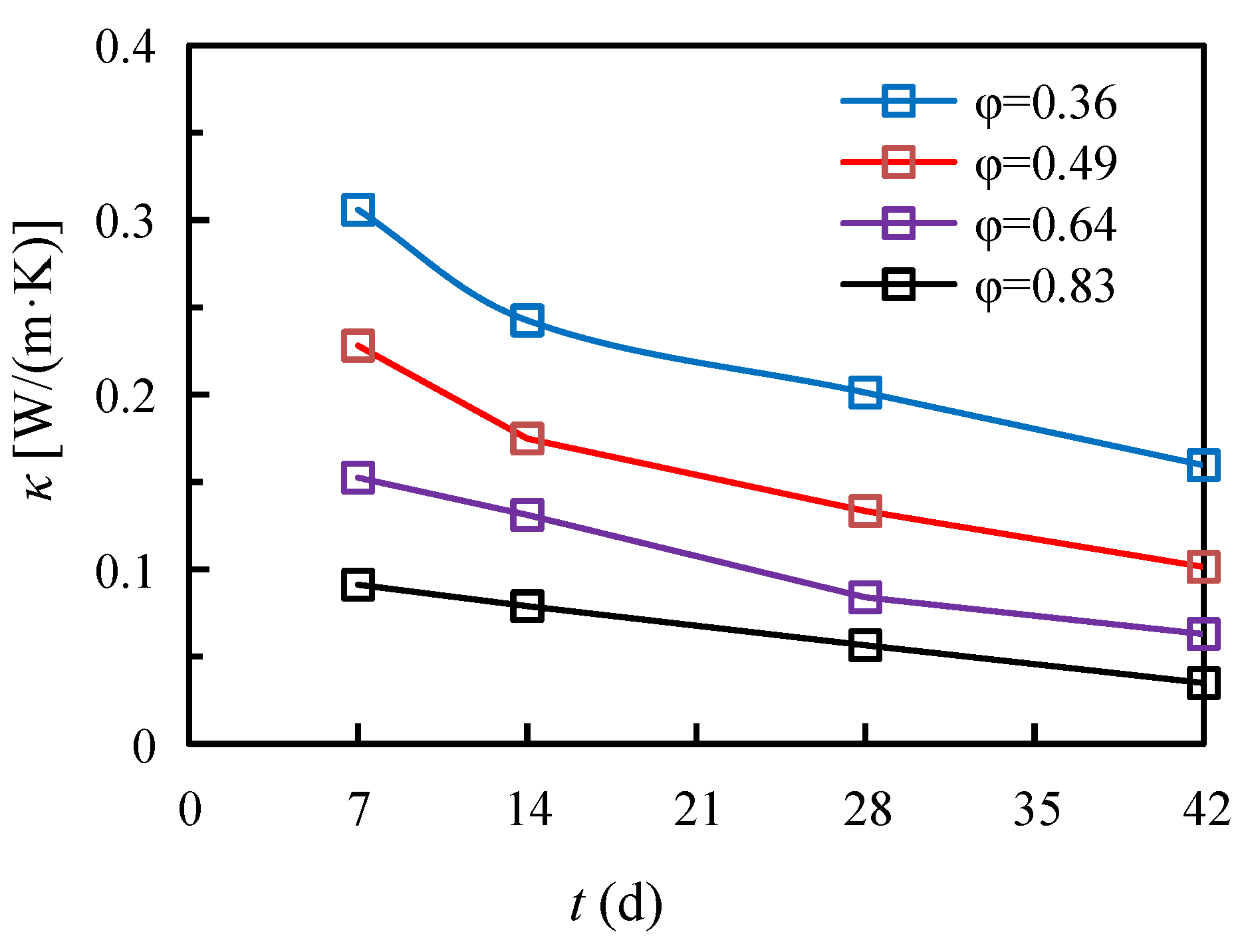
3.1. Thermal Conductivity Measurement
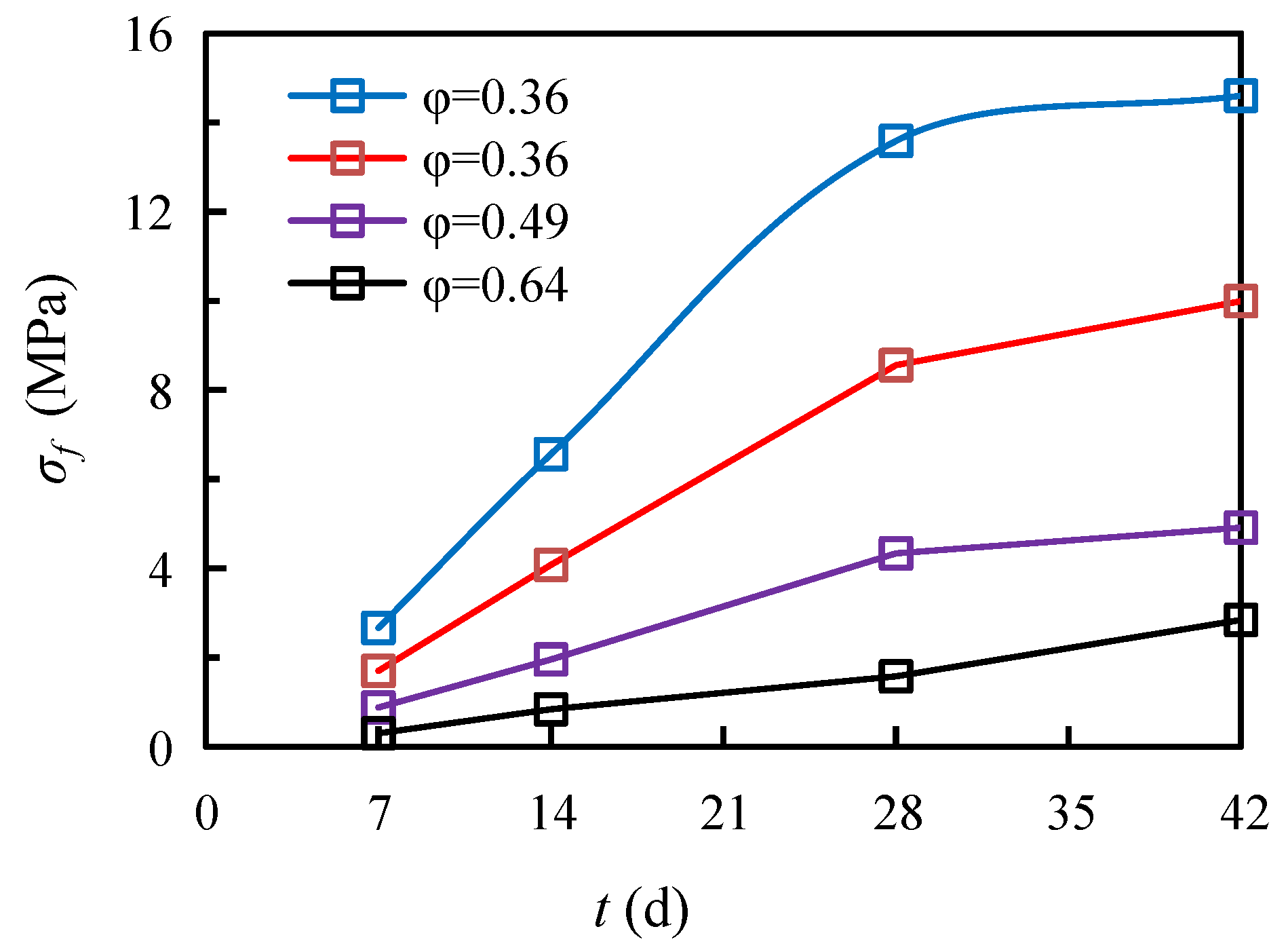
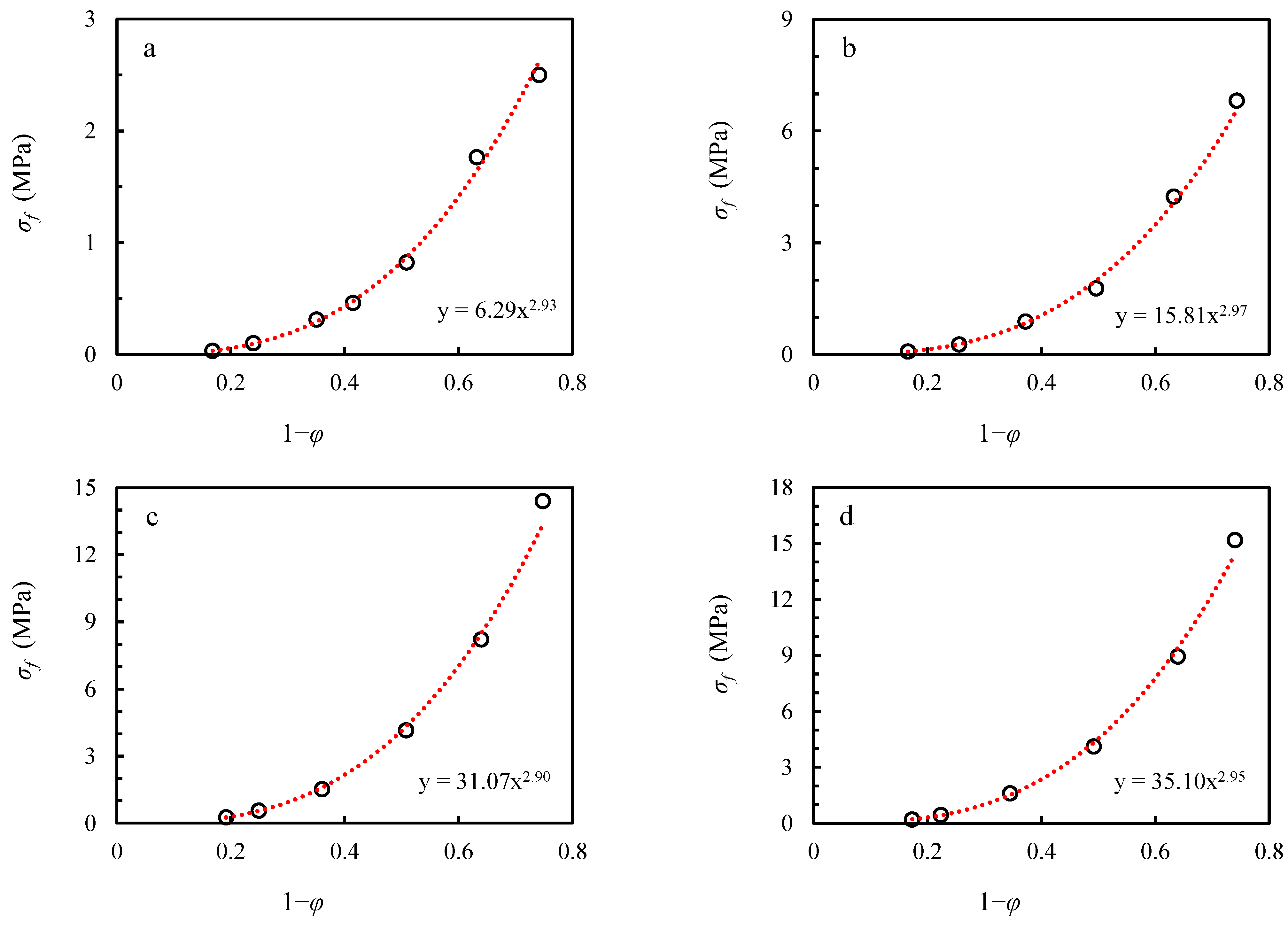
3.2. Compressive Strength Test
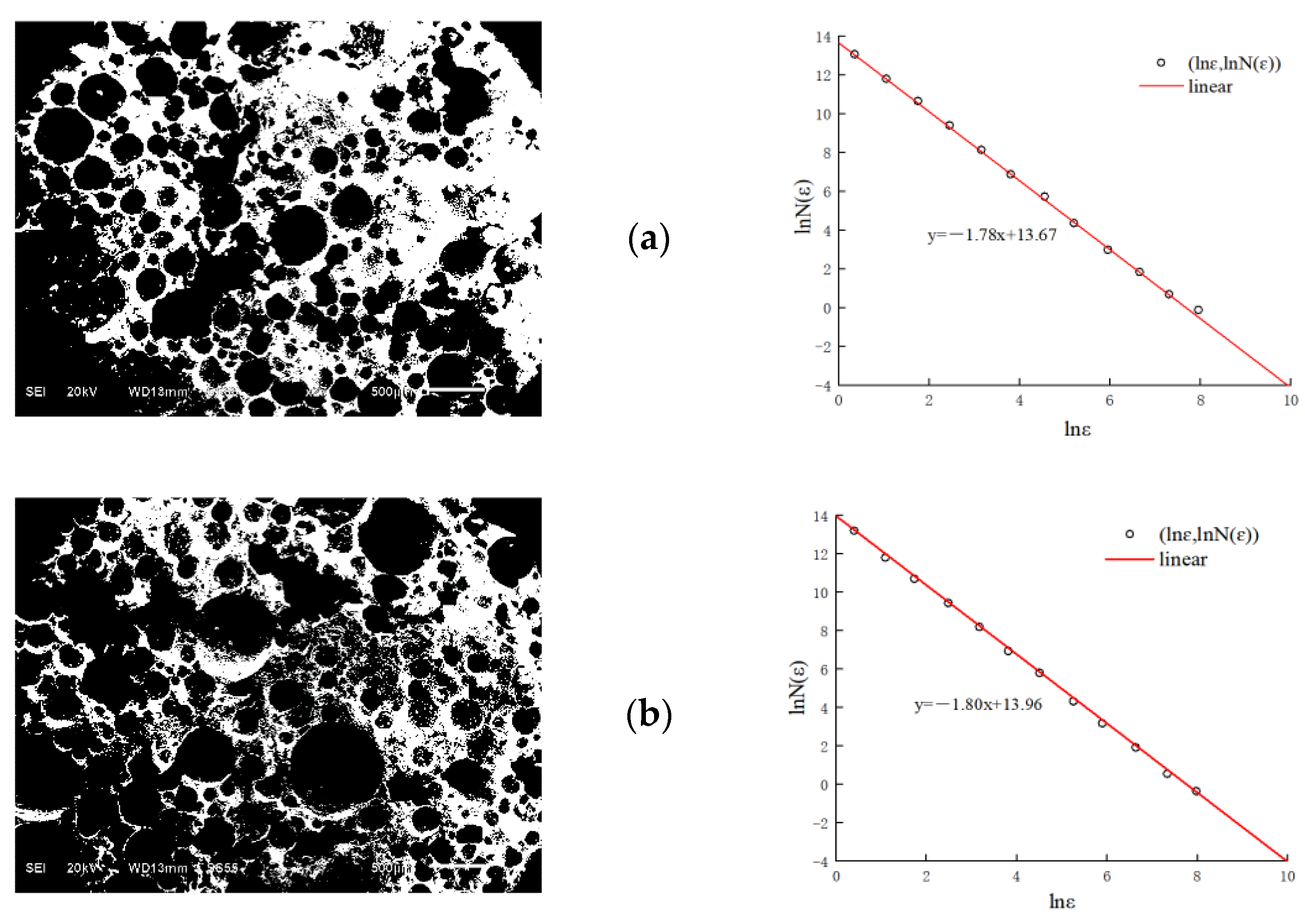
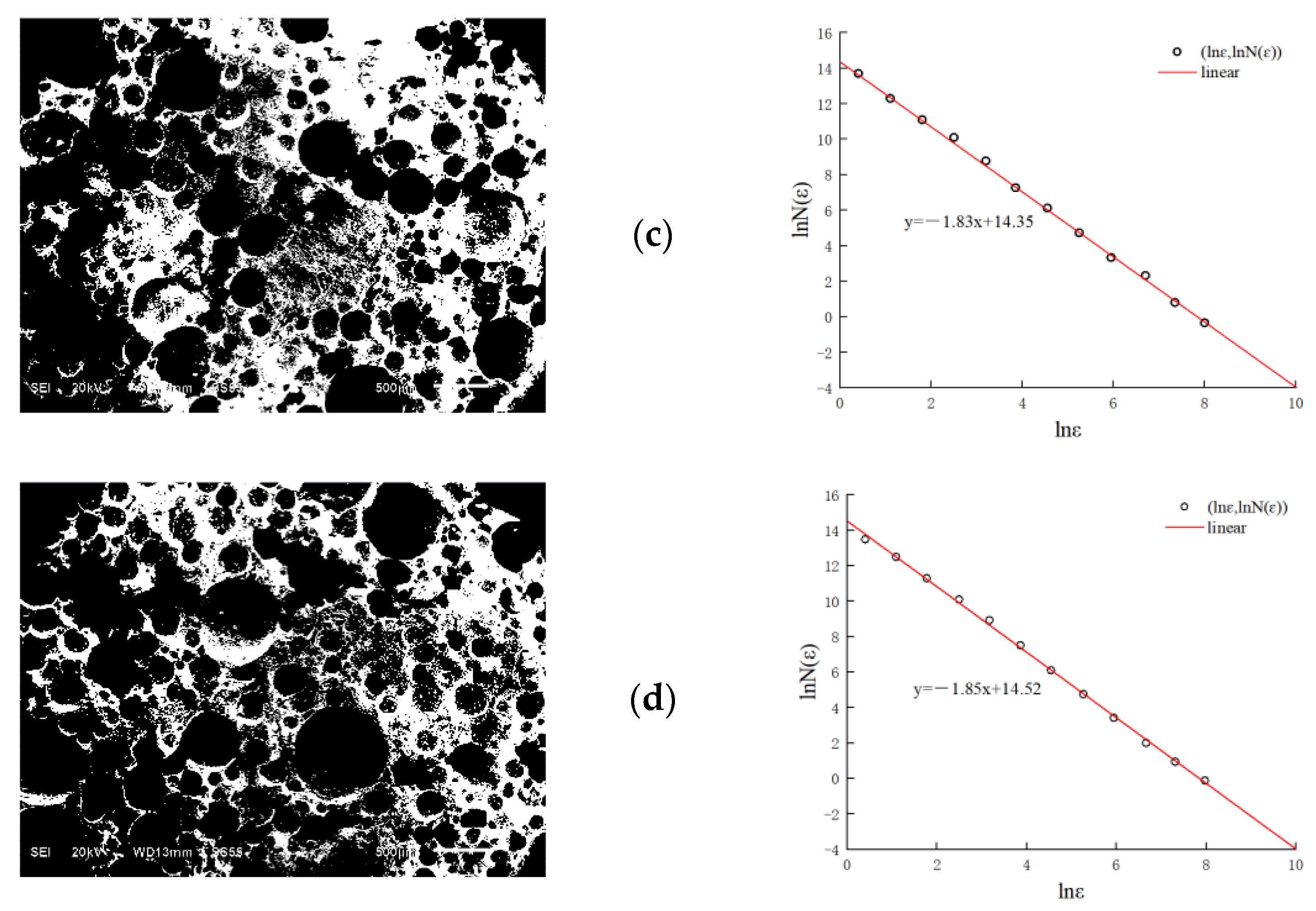
3.3. Scanning Electron Microscope Test
3.4. Calculation of Fractal Dimension of FC
3.5. Compressive Strength Method
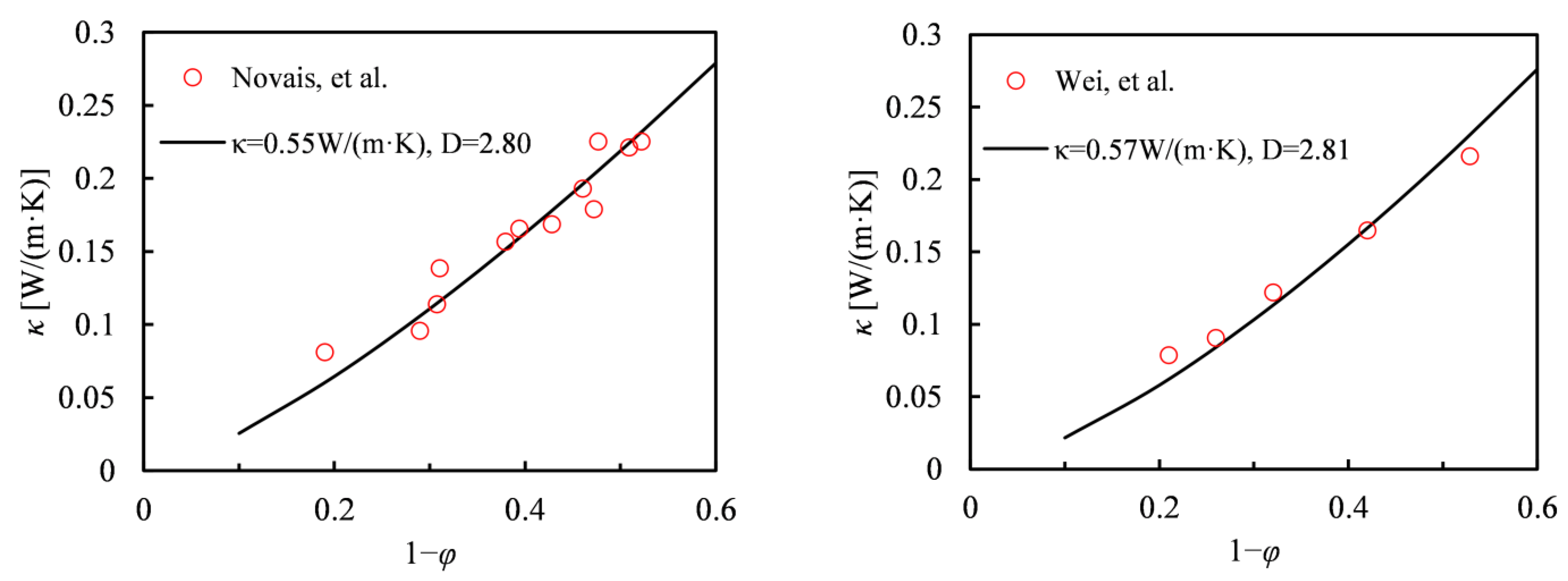
3.6. Validation of the Proposed Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raj, A.; Sathyan, D.; Mini, K.M. Physical and functional characteristics of foam concrete: A review. Constr. Build. Mater. 2019, 221, 787–799. [Google Scholar] [CrossRef]
- Shang, X.; Qu, N.; Li, J. Development and functional characteristics of novel foam concrete. Constr. Build. Mater. 2022, 324, 126666. [Google Scholar] [CrossRef]
- Nambiar, E.K.K.; Ramamurthy, K. Air-void characterisation of foam concrete. Cem. Concr. Res. 2007, 37, 221–230. [Google Scholar] [CrossRef]
- Ranjani, I.S.; Ramamurthy, K. Relative assessment of density and stability of foam produced with four synthetic surfactants. Mater. Struct. 2010, 43, 1317–1325. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, X.; Wang, L.; Li, Y. Foam concrete: A state-of-the-art and state-of-the-practice review. Adv. Mater. Sci. Eng. 2020, 2020, 6153602. [Google Scholar] [CrossRef]
- Raj, B.; Sathyan, S.; Madhavan, M.K.; Raj, A. Mechanical and durability properties of hybrid fiber reinforced foam concrete. Constr. Build. Mater. 2020, 245, 118373. [Google Scholar] [CrossRef]
- Babu, K.G.; Babu, D.S. Behaviour of lightweight expanded polystyrene concrete containing silica fume. Cem. Concr. Res. 2003, 33, 755–762. [Google Scholar] [CrossRef]
- Pei, W.; Zhang, M.; Lai, Y.; Yan, Z.; Li, S. Evaluation of the ground heat control capacity of a novel air-L-shaped TPCT-ground (ALTG) cooling system in cold regions. Energy 2019, 179, 655–668. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, X.; Li, S.; Wu, D.; Pei, W.; Lai, Y. Evaluating the cooling performance of crushed-rock interlayer embankments with unperforated and perforated ventilation ducts in permafrost regions. Energy 2015, 93, 874–881. [Google Scholar] [CrossRef]
- Li, S.; Wang, C.; Shi, L.; Yin, N. Statistical characteristics of the thermal conductivity of frozen clay at different water contents. Results Phys. 2019, 13, 102179. [Google Scholar] [CrossRef]
- Li, T.; Huang, F.; Zhu, J.; Tang, J.; Liu, J. Effect of foaming gas and cement type on the thermal conductivity of foamed concrete. Constr. Build. Mater. 2020, 231, 117197. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Q.; Shi, Y.; Zheng, G.; Li, Q.; Chen, H.; Cheng, X. Effects of different control methods on the mechanical and thermal properties of ultra-light foamed concrete. Constr. Build. Mater. 2020, 262, 120082. [Google Scholar] [CrossRef]
- Jhatial, A.A.; Goh, W.I.; Mohamad, N.; Rind, T.A.; Sandhu, A.R. Development of thermal insulating lightweight foamed concrete reinforced with polypropylene fibers. Arab. J. Sci. Eng. 2020, 45, 4067–4076. [Google Scholar] [CrossRef]
- Bi, J.; Chen, W.; Zhang, J.; Zhang, Y.; Fan, W.; Jia, B. A modified calculation model for the saturation-dependent thermal conductivity of fine-textured soils. Results Phys. 2019, 15, 102673. [Google Scholar] [CrossRef]
- Zhang, M.; Bi, J.; Chen, W.; Zhang, X.; Lu, J. Evaluation of calculation models for the thermal conductivity of soils. Int. Commun. Heat. Mass. 2018, 94, 14–23. [Google Scholar] [CrossRef]
- Miled, K.; Limam, O. Effective thermal conductivity of foam coconcreteHomogenization schemes vs experimental data and FEM simulations. Mech. Res. Commun. 2016, 76, 96–100. [Google Scholar] [CrossRef]
- Yuan, H.; Ge, Z.; Sun, R.; Xu, X.; Lu, Y.; Ling, Y.; Zhang, H. Drying shrinkage, durability, and microstructure of foamed concrete containing high-volume lime mud-fly ash. Constr. Build. Mater. 2022, 327, 126990. [Google Scholar] [CrossRef]
- Kim, J.S.; Chung, S.Y.; Han, T.S.; Stephan, D.; Elrahman, M.A. Mohamed, Correlation between microstructural characteristics from micro-CT of foamed concrete and mechanical behaviors evaluated by experiments and simulations. Cement Concr. Comp. 2020, 112, 103657. [Google Scholar] [CrossRef]
- Gancel, O.; Bilir, T.; Bademler, Z.; Ozbakkaloglu, T. A detailed review on foam concrete composites: Ingredients, properties, and microstructure. Appl. Sci. 2022, 12, 5752. [Google Scholar] [CrossRef]
- Demir, I.; Sevim, O.; Ozel, G.; Dogan, O. Microstructural, physical, and mechanical properties of aerated concrete containing fly ash under high temperature and pressure. Rev. Rom. Mater. 2020, 50, 240–249. [Google Scholar]
- Fu, J.; Yu, Y. Experimental study on pore characteristics and fractal dimension calculation of pore structure of aerated concrete block. Adv. Civil Eng. 2019, 2019, 8043248. [Google Scholar] [CrossRef]
- Lü, Q.; Qiu, Q.; Zheng, J.; Wang, J.; Zeng, Q. Fractal dimension of concrete incorporating silica fume and its correlations to pore structure, strength and permeability. Constr. Build. Mater. 2019, 228, 116986. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, Y. Compressive strength of fractal textured foamed concrete. Fractals 2019, 27, 1940003. [Google Scholar] [CrossRef]
- Yu, B. Analysis of Flow in Fractal Porous Media. Appl. Mech. Rev. 2008, 61, 050801. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, P.; Qiu, S.; Rao, B.; Yu, B. A generalized thermal conductivity model for unsaturated porous media with fractal geometry. Int. J. Heat. Mass. Transf. 2020, 152, 119540. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, B.; Zou, M.; Zhang, D. A Generalized Model for the Effective Thermal Conductivity of Unsaturated Porous Media Based on Self-Similarity. J. Porous. Media 2007, 10, 551–568. [Google Scholar] [CrossRef]
- Coórdoba, O.; Arias-Zugasti, M. Accurate and efficient calculation of multicomponent thermal diffusion coefficients and partial thermal conductivity based on kinetic theory. Combust. Flame 2022, 244, 112202. [Google Scholar] [CrossRef]
- Li, W.; Jiang, Y.; Liu, H.; Wang, C.; He, X.; He, F.; Li, M. Mullite fibers/whiskers hierarchical porous materials: Experimental characterization and fractal model to predict thermal conductivity. Ceram. Int. 2023, 49, 13657–13665. [Google Scholar] [CrossRef]
- Zhao, Z.; Feng, K.M.; Feng, Y.J. Theoretical calculation and analysis modeling for the effective thermal conductivity of Li4SiO4 pebble bed. Fusion Eng. Des. 2010, 85, 1975–1980. [Google Scholar] [CrossRef]
- Dubil, K.; Wolf, H.; Wetzel, T.; Dietrich, B. Development of a generalized thermal resistance model for the calculation of effective thermal conductivities in periodic open cellular structures (POCS). Int. J. Heat. Mass. Transf. 2022, 183, 122083. [Google Scholar] [CrossRef]
- Yuan, F.; He, Y.; Li, M.; Li, X. Study on the theoretical calculation method for the effective thermal conductivity of carbon nanotube composite molten salt for solar energy application. Sol. Energy Mat. Sol. C 2022, 238, 111631. [Google Scholar] [CrossRef]
- Krone, R.B. A Study of Rheologic Properties of Estuarial Sediments; Hydraulic Engineering Laboratory and Sanitary Engineering Research Laboratory, University of California: Berkeley, CA, USA, 1963. [Google Scholar]
- Xu, Y.; Jiang, H.; Chu, F.; Liu, C. Fractal model for surface erosion of cohesive sediments. Fractals 2014, 22, 1440006. [Google Scholar] [CrossRef]
- Son, M.; Hsu, T.J. The effect of variable yield strength and variable fractal dimension on flocculation of cohesive sediment. Water Res. 2009, 43, 3582–3592. [Google Scholar] [CrossRef]
- GB/T 32064-2015; Determination of Thermal Conductivity and Thermal Diffusivity of Building Matertials: Transient Plane Heat Sourse Method. State Administration for Market Regulation: Beijing, China, 2015.
- Novais, R.M.; Ascensão, G.; Buruberri, L.H.; Senff, L.; Labrincha, J.A. Influence of blowing agent on the fresh-and hardened-state properties of lightweight geopolymers. Mater. Des. 2016, 108, 551–559. [Google Scholar] [CrossRef]
- Wei, S.; Chen, Y.; Zhang, Y.; Jones, M.R. Characterization and simulation of microstructure and thermal properties of foamed concrete. Constr. Build. Mater. 2013, 47, 1278–1291. [Google Scholar] [CrossRef]
- Yang, K.H.; Lee, K.H.; Song, J.; Gong, M.H. Properties and sustainability of alkali-activated slag foamed concrete. J. Clean. Prod. 2014, 68, 226–233. [Google Scholar] [CrossRef]
- Hao, K.; Li, Y.; Zhang, N. Application of fractal dimension to activated sludge SEM images in MATLAB environment. Environ. Sci. Tec. 2020, 43, 22–27. (In Chinese) [Google Scholar]
- Buczkowski, S.; Kyriacos, S.; Nekka, F.; Cartilier, L. The modified box-counting method: Analysis of some characteristic parameters. Pattern Recogn. 1998, 31, 411–418. [Google Scholar] [CrossRef]
- Liebovitch, L.S.; Toth, T. A fast algorithm to determine fractal dimensions by box counting. Phys. Lett. A 1989, 141, 386–390. [Google Scholar] [CrossRef]
- Shibuichi, S.; Onda, T.; Satoh, N.; Tsujii, K. Super water-repellent surfaces resulting from fractal structure. J. Phys. Chem. 1996, 100, 19512–19517. [Google Scholar] [CrossRef]
- Balshin, M.Y. Relation of mechanical properties of powder metals and their porosity and ultimate properties of porous metal-ceramic materials. Dokl. Akad. Nauk. 1949, 6, 831–834. [Google Scholar]




| Cement | Fly Ash | Ore Powder | |
|---|---|---|---|
| SiO2 | 21.8 | 54.1 | 31.12 |
| Al2O3 | 4.15 | 25.3 | 13.87 |
| Fe2O3 | 4.52 | 6.96 | 15.38 |
| CaO | 65.5 | 8.73 | 26.61 |
| Na2O | 0.16 | 0.31 | 0.43 |
| K2O | 0.51 | 0.13 | 0.23 |
| SO3 | 1.73 | 0.61 | 0.33 |
| MgO | 1.09 | 2.07 | 8.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, G.; Li, H.; Zhou, Y.; Huang, Z. Thermal Conductivity of Fractal-Textured Foamed Concrete. Fractal Fract. 2023, 7, 475. https://doi.org/10.3390/fractalfract7060475
Xiang G, Li H, Zhou Y, Huang Z. Thermal Conductivity of Fractal-Textured Foamed Concrete. Fractal and Fractional. 2023; 7(6):475. https://doi.org/10.3390/fractalfract7060475
Chicago/Turabian StyleXiang, Guosheng, Huajian Li, Yinkang Zhou, and Zhe Huang. 2023. "Thermal Conductivity of Fractal-Textured Foamed Concrete" Fractal and Fractional 7, no. 6: 475. https://doi.org/10.3390/fractalfract7060475
APA StyleXiang, G., Li, H., Zhou, Y., & Huang, Z. (2023). Thermal Conductivity of Fractal-Textured Foamed Concrete. Fractal and Fractional, 7(6), 475. https://doi.org/10.3390/fractalfract7060475






