Generalized Thermoelastic Infinite Annular Cylinder under the Hyperbolic Two-Temperature Fractional-Order Strain Theory
Abstract
1. Introduction
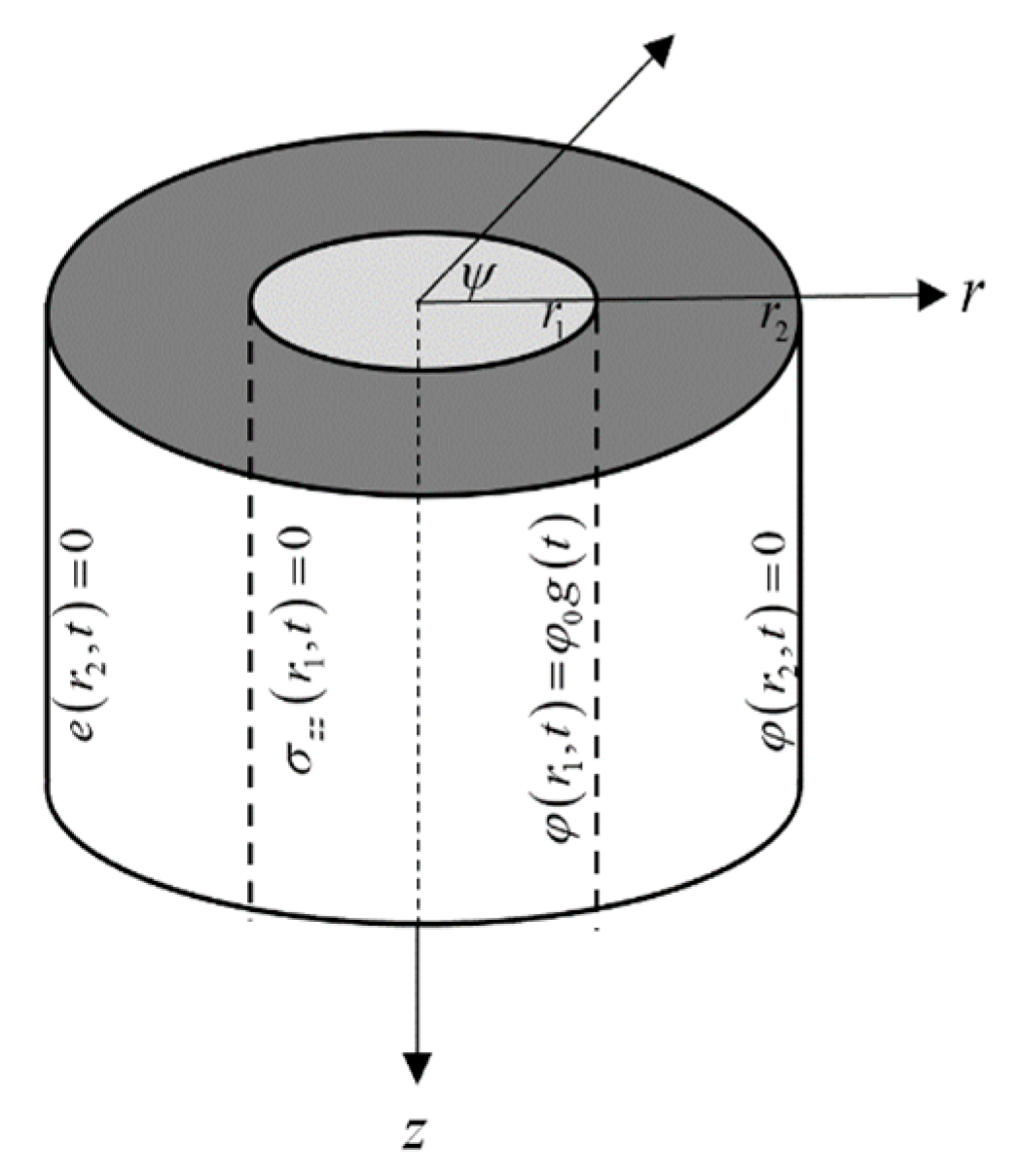
2. The Governing Equations
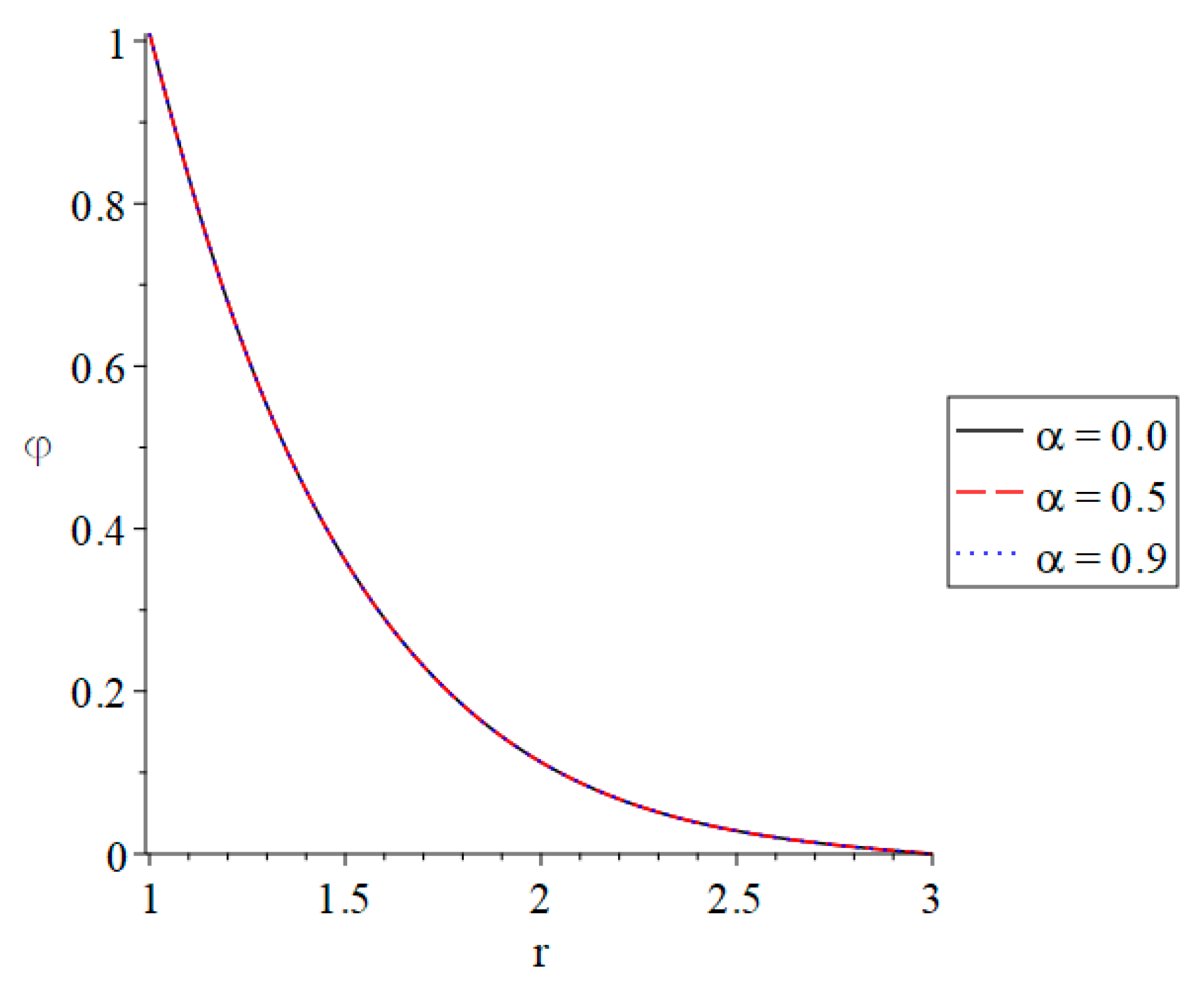
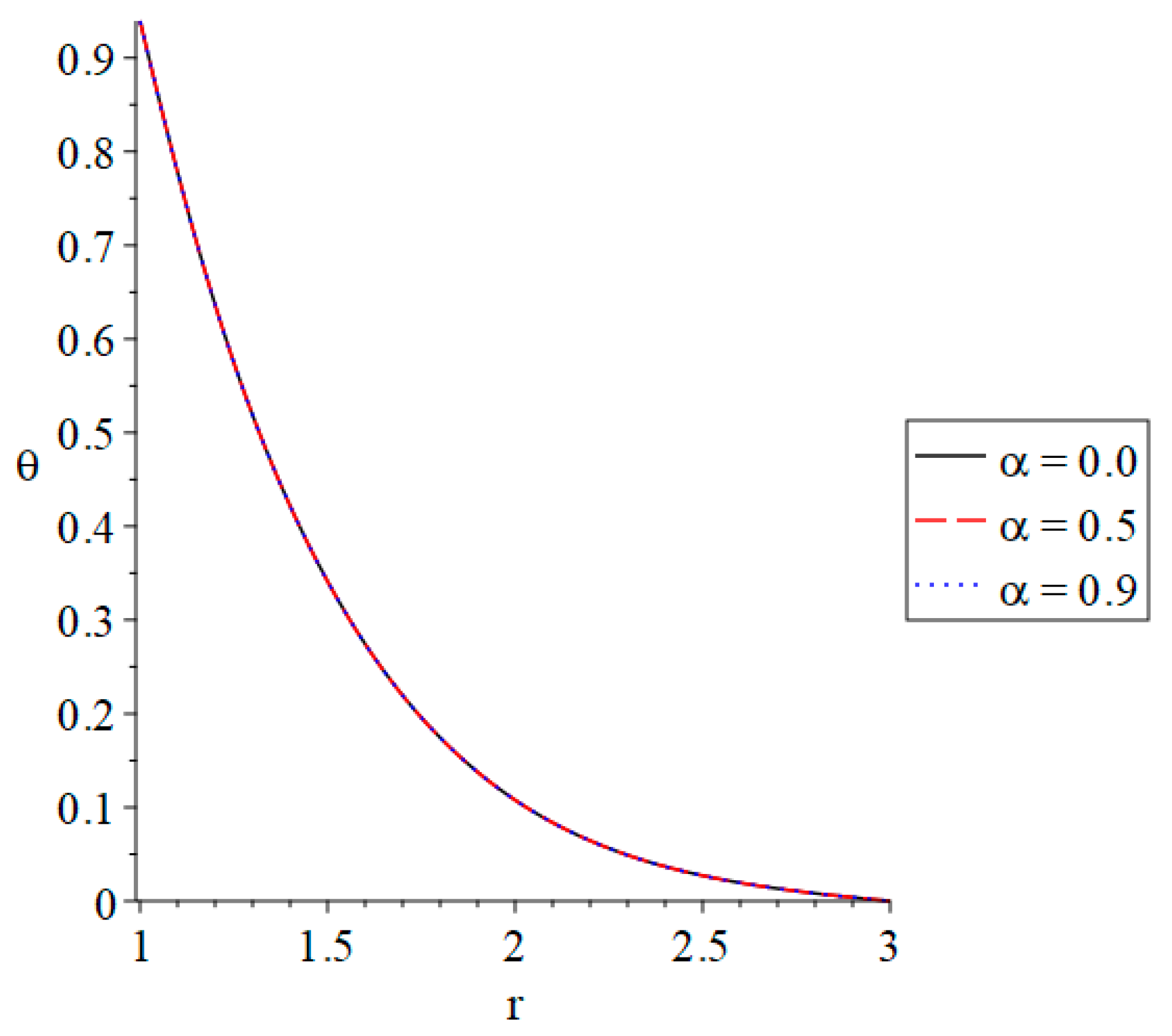
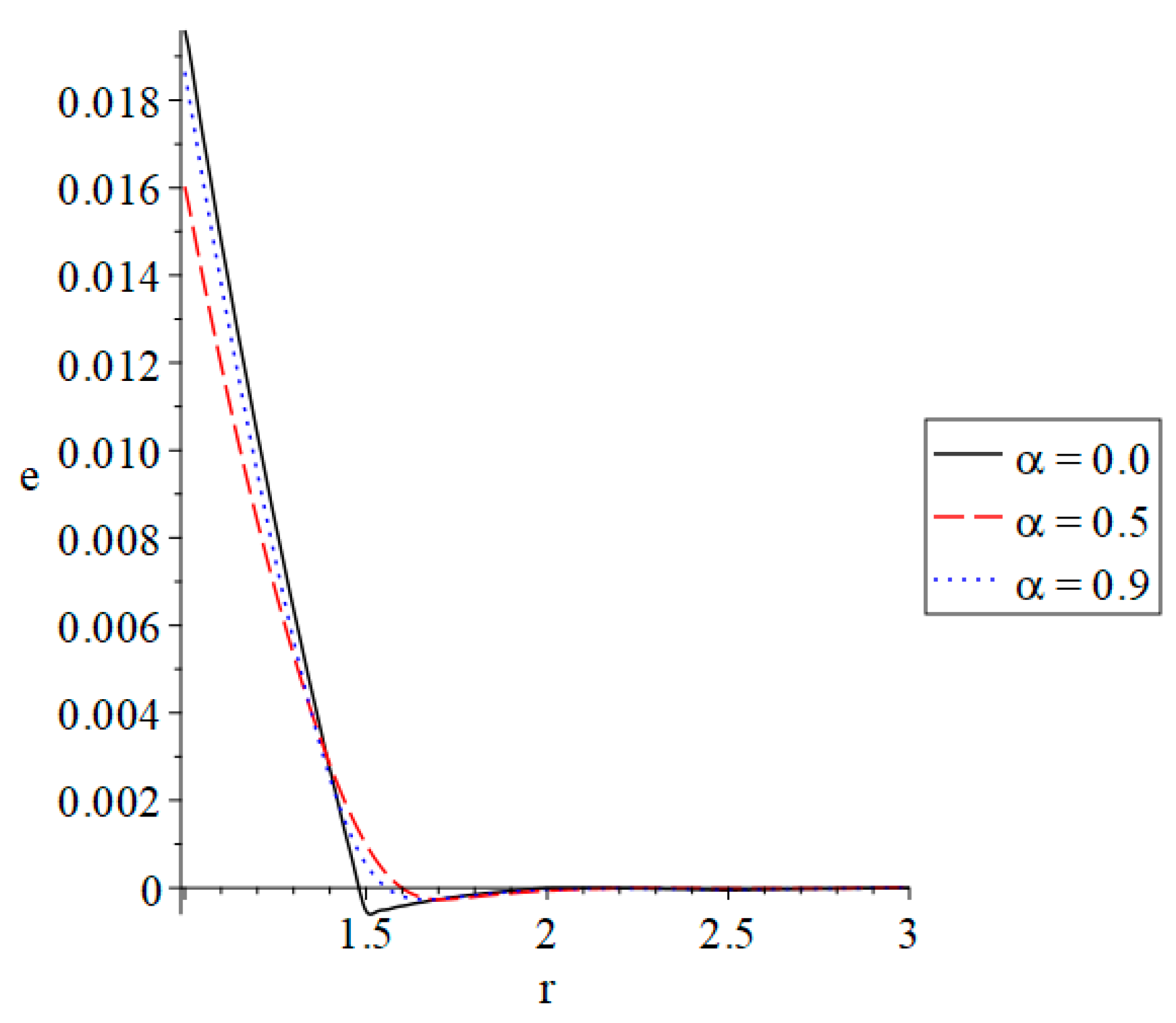
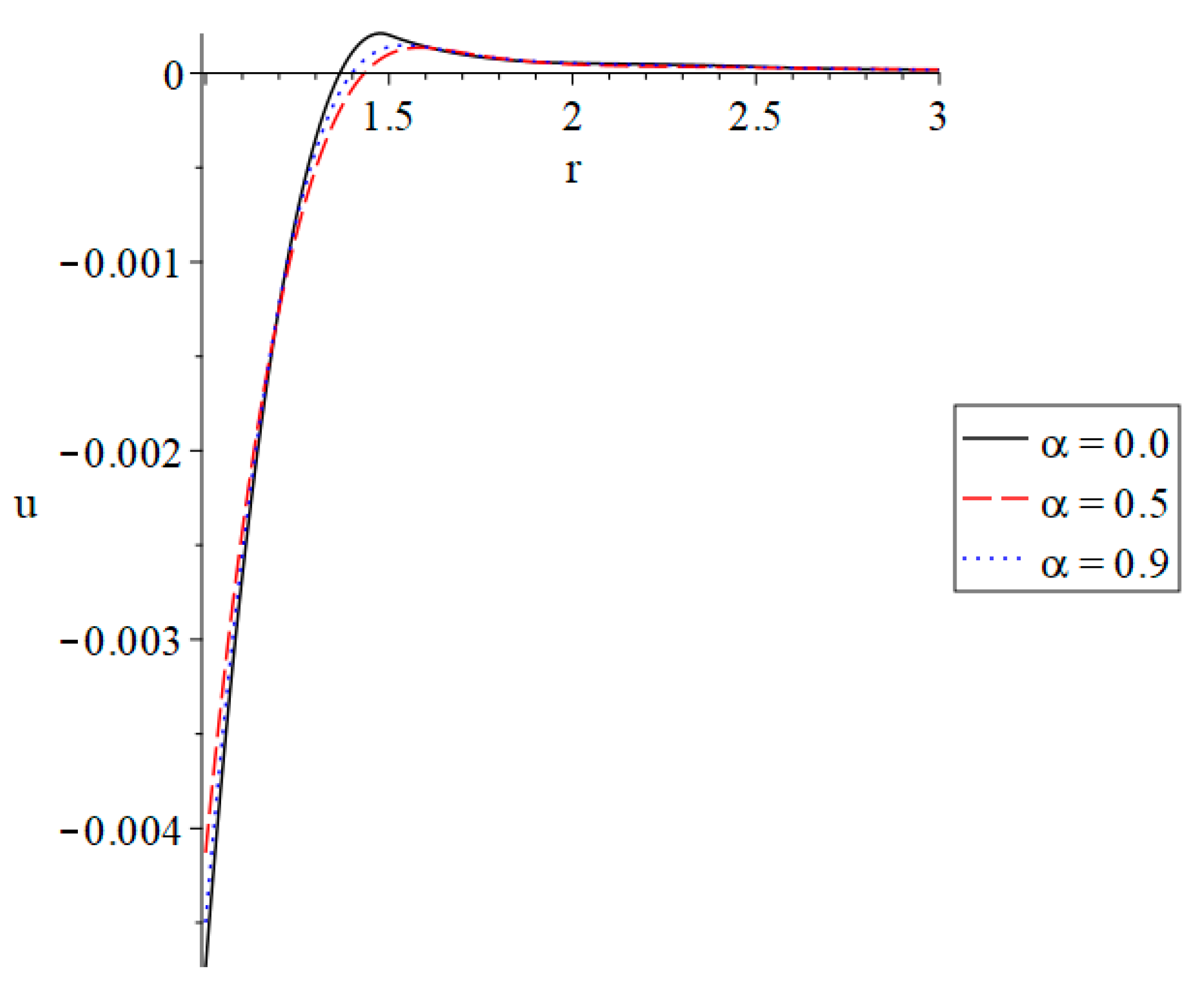
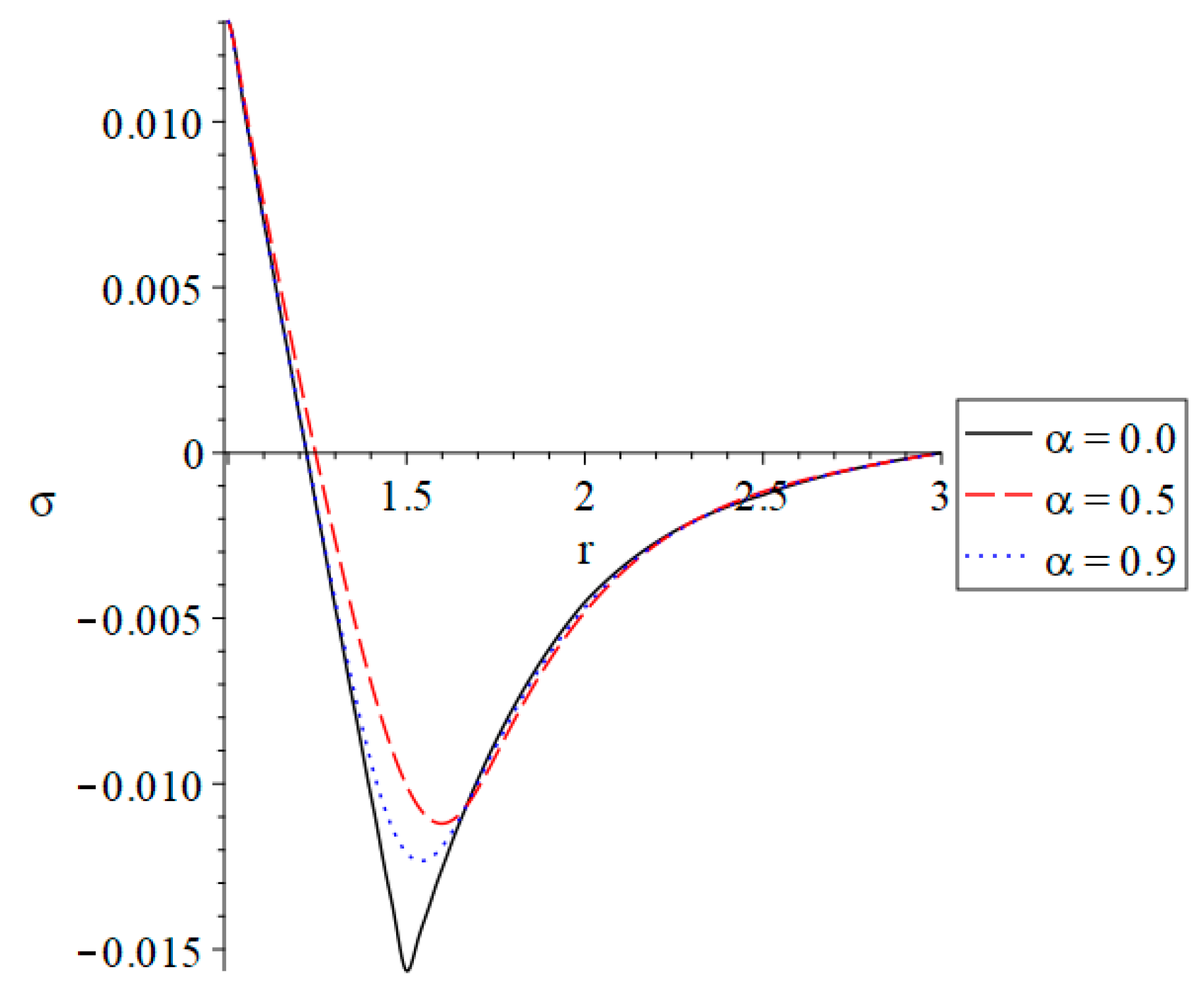
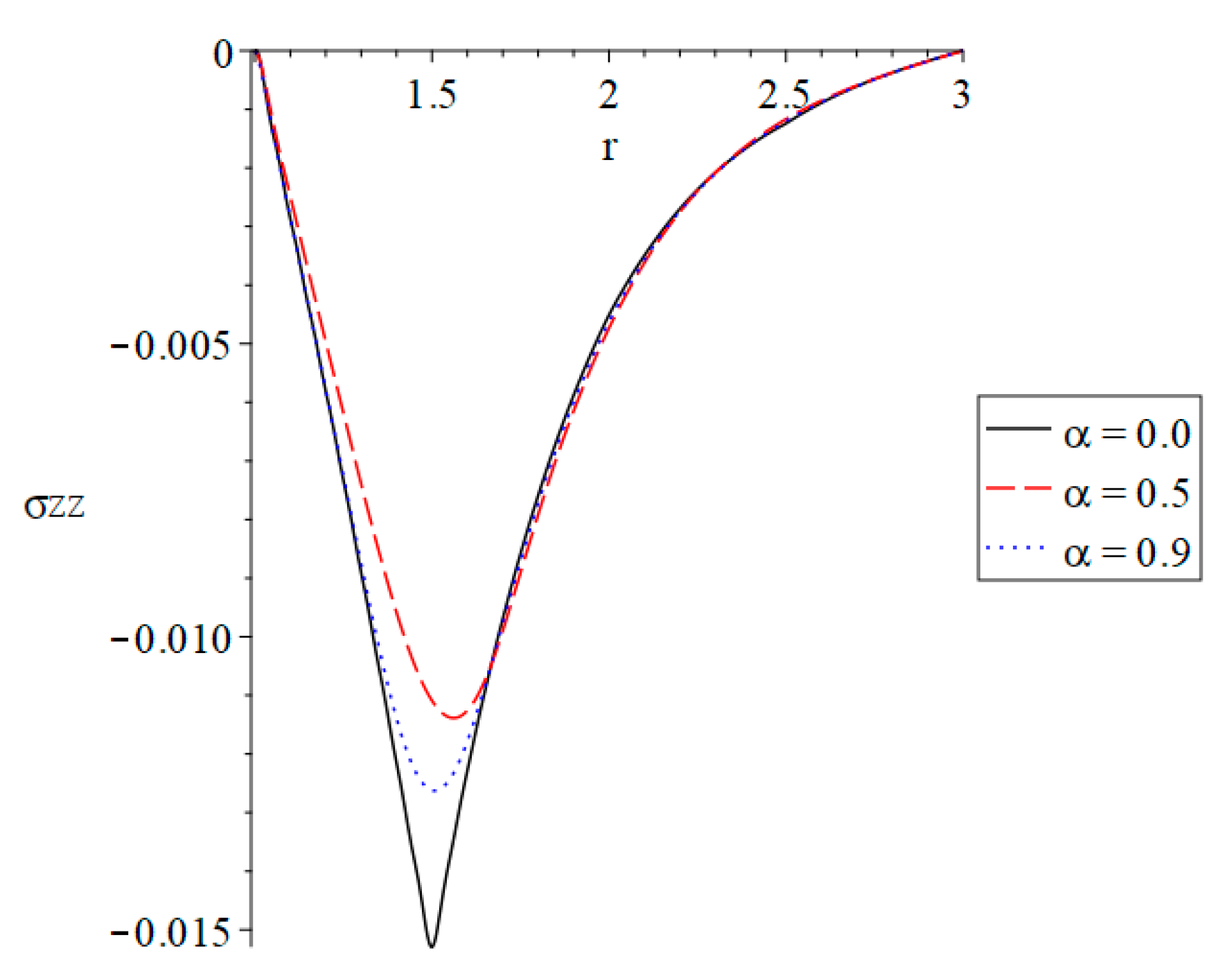
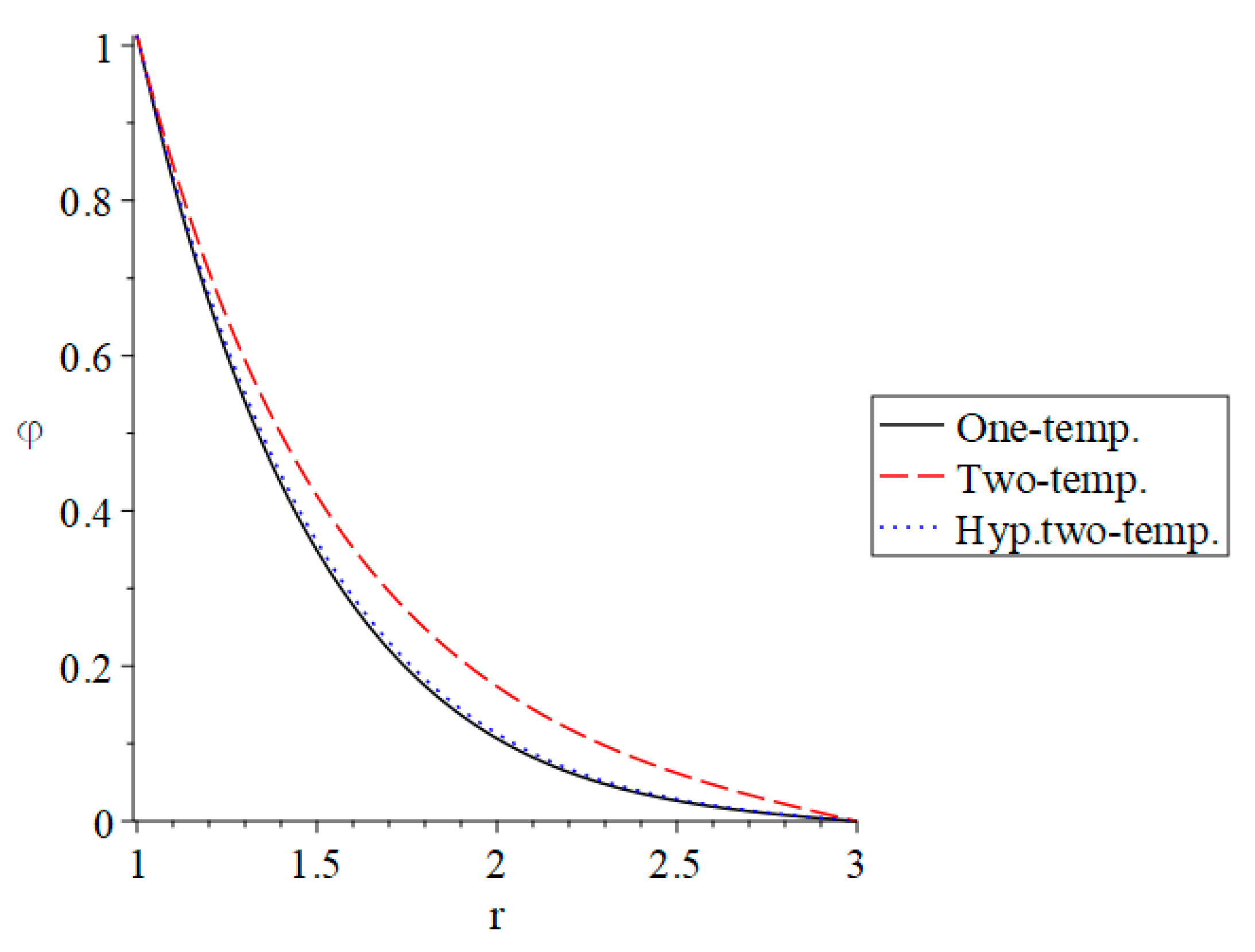
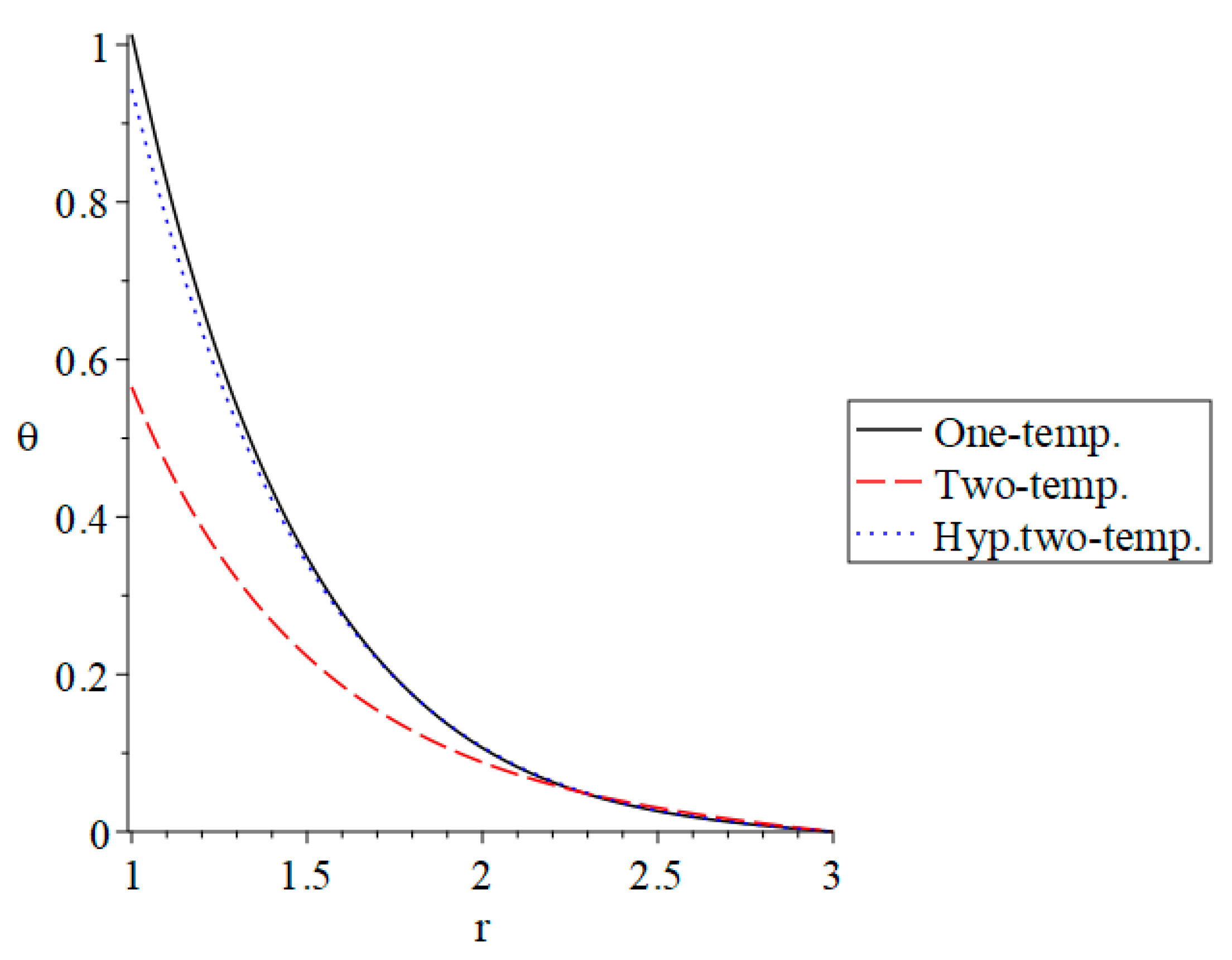
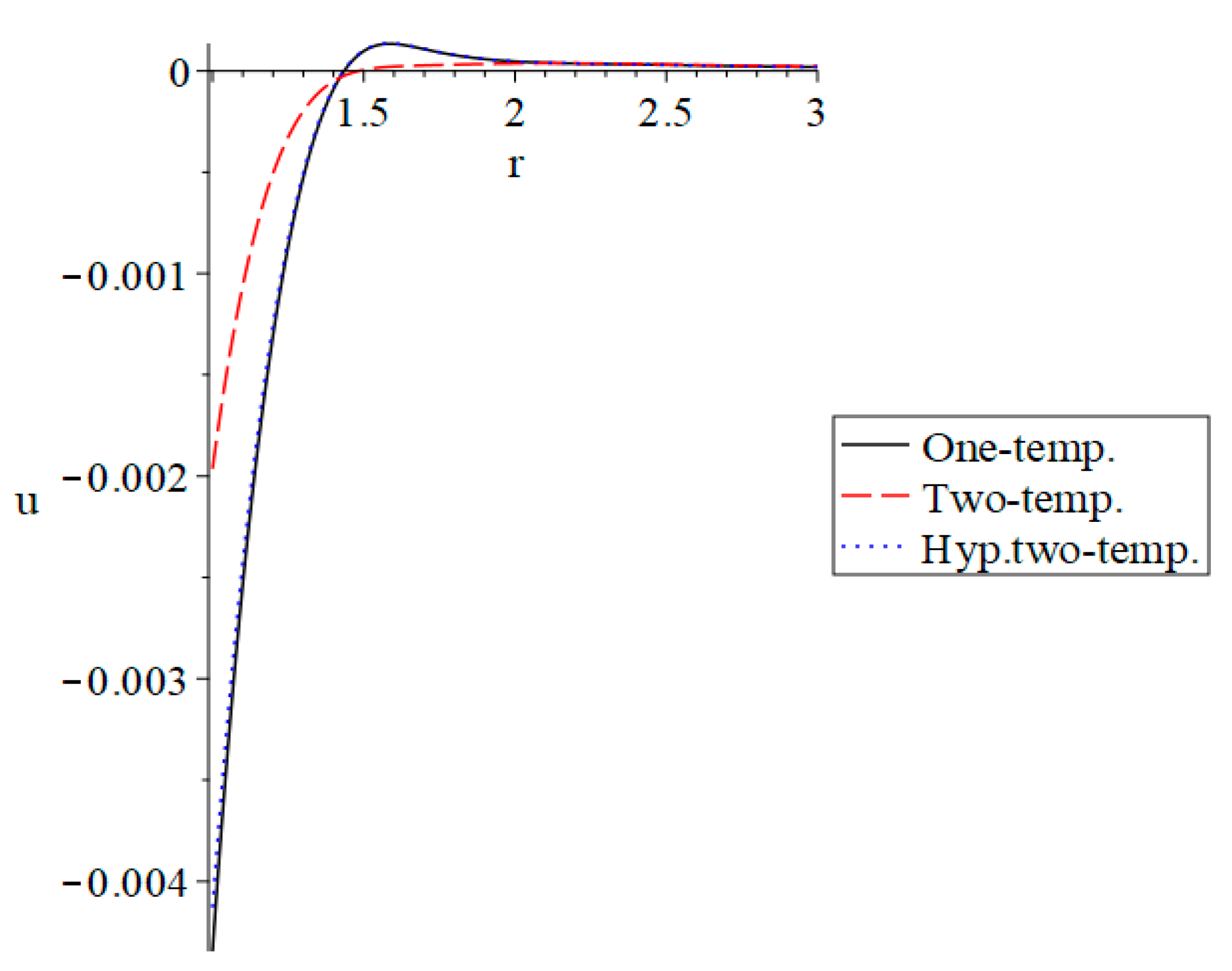
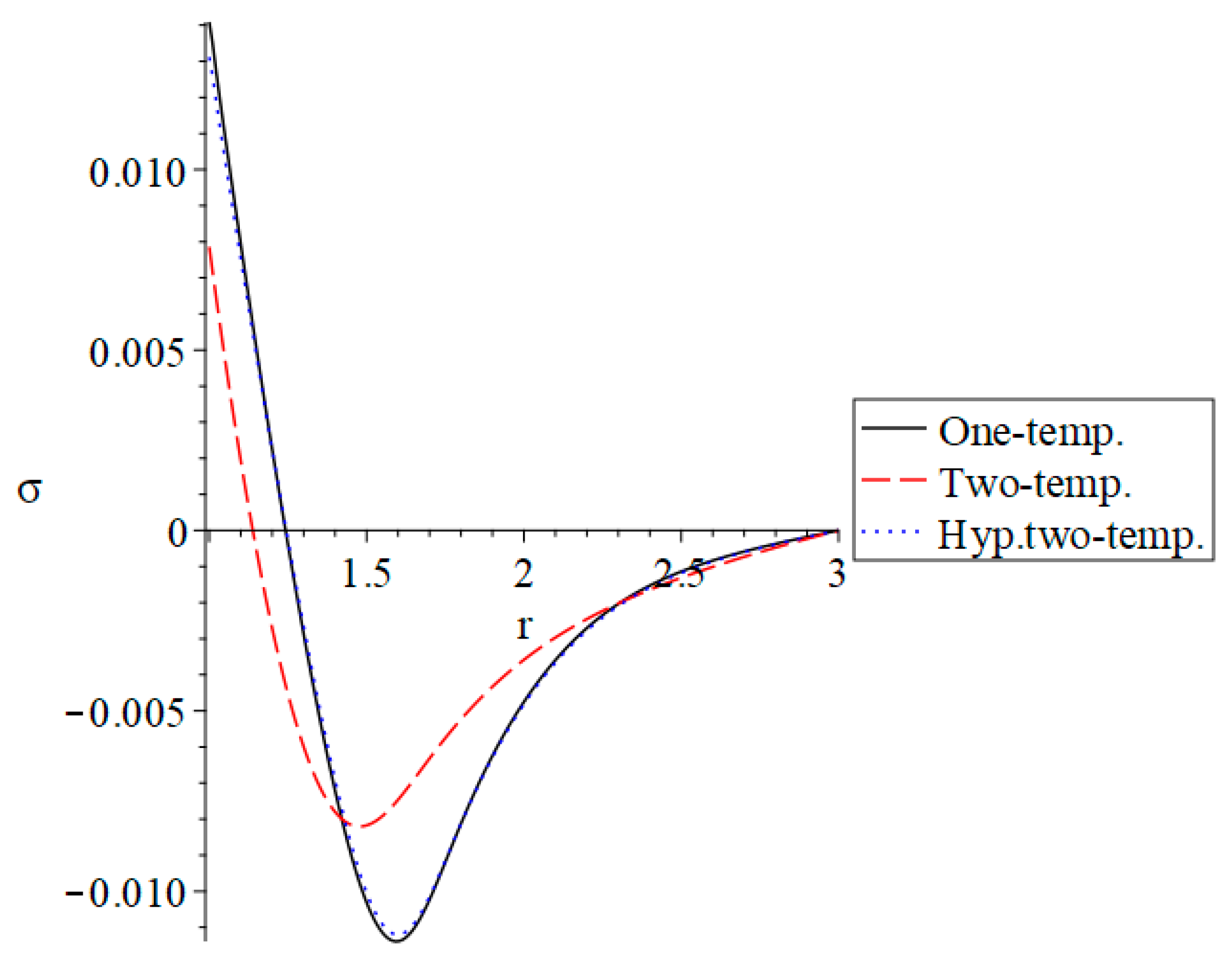
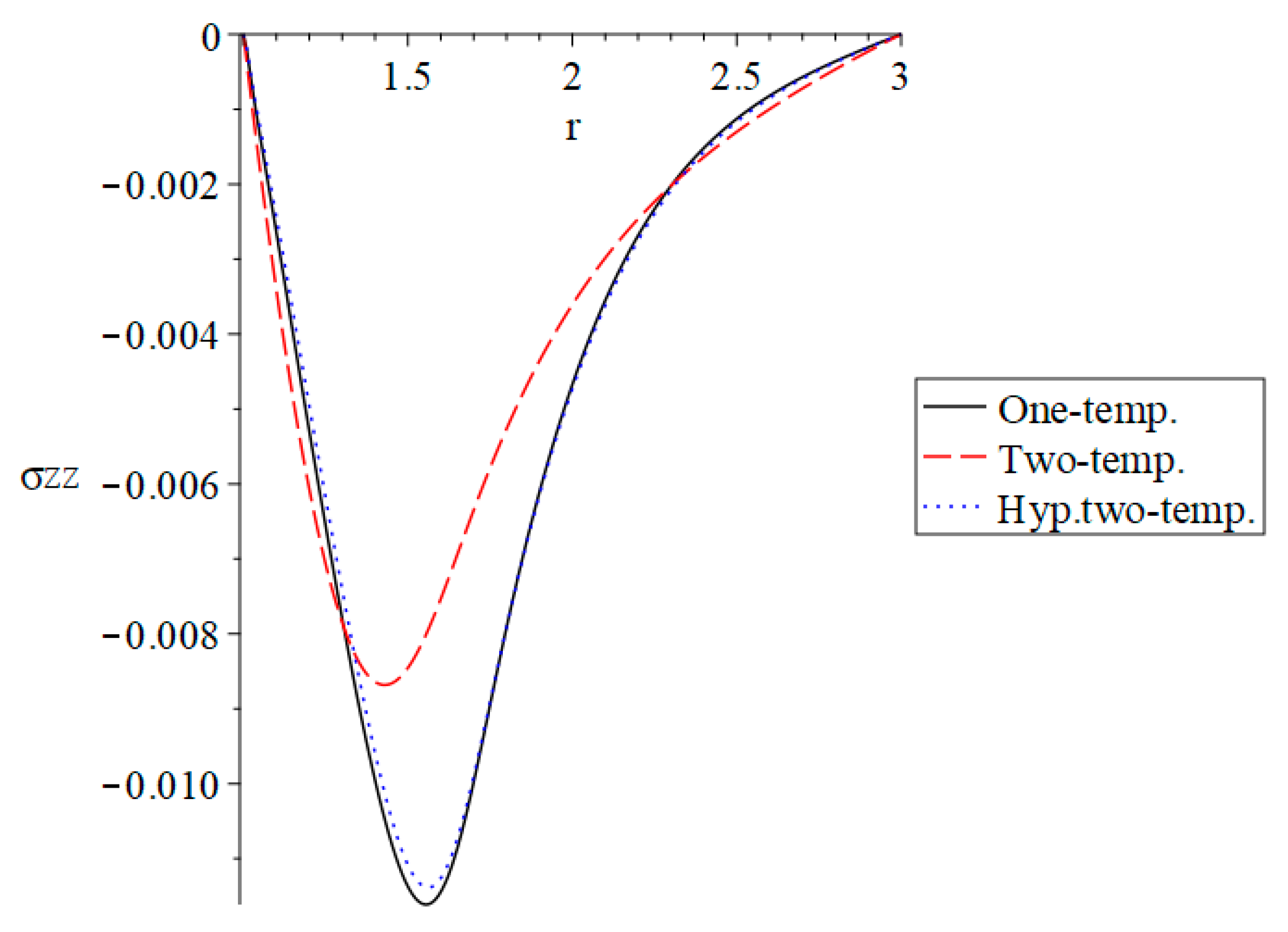
3. Numerical Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Specific heat at constant strain | |
| Longitudinal wave speed | |
| Hyperbolic two-temperature parameter | |
| Fractional derivative with respect to t with order | |
| Strain or volumetric deformation (dimensionless) | |
| Thermal conductivity | |
| Absolute temperature | |
| Absolute reference temperature | |
| Time | |
| Displacement functions | |
| The radius of the cylinder | |
| z-axis of the cylinder | |
| Coefficient of linear thermal expansion | |
| Fractional-order parameter (dimensionless) | |
| (dimensionless) | |
| = (dimensionless) | |
| The mechanical coupling constant (dimensionless) | |
| The thermoelastic coupling constant (dimensionless) | |
| Thermal viscosity | |
| Lamé’s constants | |
| Density | |
| Components of the stress tensor | |
| Thermal and mechanical relaxation times, respectively |
References
- Ray, S.S.; Atangana, A.; Noutchie, S.; Kurulay, M.; Bildik, N.; Kilicman, A. Fractional calculus and its applications in applied mathematics and other sciences. Math. Probl. Eng. 2014, 2014, 849395. [Google Scholar] [CrossRef]
- Sene, N. Fractional SIRI model with delay in context of the generalized Liouville–Caputo fractional derivative. Math. Model. Soft Comput. Epidemiol. 2020, 107, 107–125. [Google Scholar]
- Imran, M.; Shah, N.A.; Khan, I.; Aleem, M. Applications of non-integer Caputo time fractional derivatives to natural convection flow subject to arbitrary velocity and Newtonian heating. Neural Comput. Appl. 2018, 30, 1589–1599. [Google Scholar] [CrossRef]
- Khan, I.; Ali Shah, N.; Vieru, D. Unsteady flow of generalized Casson fluid with fractional derivative due to an infinite plate. Eur. Phys. J. Plus 2016, 131, 181. [Google Scholar] [CrossRef]
- Khan, I.; Ali Shah, N.; Mahsud, Y.; Vieru, D. Heat transfer analysis in a Maxwell fluid over an oscillating vertical plate using fractional Caputo-Fabrizio derivatives. Eur. Phys. J. Plus 2017, 132, 194. [Google Scholar] [CrossRef]
- Ali, F.; Saqib, M.; Khan, I.; Ahmad Sheikh, N. Application of Caputo-Fabrizio derivatives to MHD free convection flow of generalized Walters’-B fluid model. Eur. Phys. J. Plus 2016, 131, 377. [Google Scholar] [CrossRef]
- Shen, F.; Tan, W.; Zhao, Y.; Masuoka, T. The Rayleigh–Stokes problem for a heated generalized second grade fluid with fractional derivative model. Nonlinear Anal. Real World Appl. 2006, 7, 1072–1080. [Google Scholar] [CrossRef]
- Ganie, A.H.; Saeed, A.M.; Saeed, S.; Ali, U. The Rayleigh–Stokes Problem for a Heated Generalized Second-Grade Fluid with Fractional Derivative: An Implicit Scheme via Riemann–Liouville Integral. Math. Probl. Eng. 2022, 2022, 6948461. [Google Scholar] [CrossRef]
- Riaz, M.B.; Imran, M.; Shabbir, K. Analytic solutions of Oldroyd-B fluid with fractional derivatives in a circular duct that applies a constant couple. Alex. Eng. J. 2016, 55, 3267–3275. [Google Scholar] [CrossRef]
- Saad, K.M.; Baleanu, D.; Atangana, A. New fractional derivatives applied to the Korteweg–de Vries and Korteweg–de Vries–Burger’s equations. Comput. Appl. Math. 2018, 37, 5203–5216. [Google Scholar] [CrossRef]
- Xue, Z.-N.; Yu, Y.-J.; Li, X.-Y.; Tian, X.-G. Nonlocal thermoelastic analysis with fractional order strain in multilayered structures. J. Therm. Stress. 2018, 41, 80–97. [Google Scholar] [CrossRef]
- Sur, A.; Kanoria, M. Fractional order generalized thermoelastic functionally graded solid with variable material properties. J. Solid Mech. 2014, 6, 54–69. [Google Scholar]
- Sidhardh, S.; Patnaik, S.; Semperlotti, F. Thermodynamics of fractional-order nonlocal continua and its application to the thermoelastic response of beams. Eur. J. Mech.-A/Solids 2021, 88, 104238. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Tzou, D.; Guo, Z.-Y. Nonlocal behavior in thermal lagging. Int. J. Therm. Sci. 2010, 49, 1133–1137. [Google Scholar] [CrossRef]
- Zhou, H.; Li, P.; Fang, Y. Single-phase-lag thermoelastic damping models for rectangular cross-sectional micro-and nano-ring resonators. Int. J. Mech. Sci. 2019, 163, 105132. [Google Scholar] [CrossRef]
- Chen, P.J.; Gurtin, M.E. On a theory of heat conduction involving two temperatures. Z. Für Angew. Math. Und Phys. ZAMP 1968, 19, 614–627. [Google Scholar] [CrossRef]
- Warren, W.; Chen, P. Wave propagation in the two temperature theory of thermoelasticity. Acta Mech. 1973, 16, 21–33. [Google Scholar] [CrossRef]
- Youssef, H.M. Theory of two-temperature-generalized thermoelasticity. IMA J. Appl. Math. 2006, 71, 383–390. [Google Scholar] [CrossRef]
- Youssef, H.M.; Elsibai, K.A. On the theory of two-temperature thermoelasticity without energy dissipation of Green–Naghdi model. Appl. Anal. 2015, 94, 1997–2010. [Google Scholar] [CrossRef]
- Alzahrani, F.S.; Abbas, I.A. Fractional order GL model on thermoelastic interaction in porous media due to pulse heat flux. Geomech. Eng. 2020, 23, 217–225. [Google Scholar]
- Abbas, I.A. Fractional order GN model on thermoelastic interaction in an infinite fibre-reinforced anisotropic plate containing a circular hole. J. Comput. Theor. Nanosci. 2014, 11, 380–384. [Google Scholar] [CrossRef]
- Abbas, I.A.; Youssef, H.M. Two-temperature generalized thermoelasticity under ramp-type heating by finite element method. Meccanica 2013, 48, 331–339. [Google Scholar] [CrossRef]
- Youssef, H.M. A two-temperature generalized thermoelastic medium subjected to a moving heat source and ramp-type heating: A state-space approach. J. Mech. Mater. Struct. 2010, 4, 1637–1649. [Google Scholar] [CrossRef]
- El-Bary, A.A.; Youssef, H.M.; Nasr MA, E. Hyperbolic Two-Temperature Generalized Thermoelastic Infinite Medium with Cylindrical Cavity Subjected to Non-Gaussian Laser Beam. J. Umm Al-Qura Univ. Eng. Archit. 2022, 13, 62–69. [Google Scholar] [CrossRef]
- Youssef, H.M. Two-dimensional problem of a two-temperature generalized thermoelastic half-space subjected to ramp-type heating. Comput. Math. Model. 2008, 19, 201–216. [Google Scholar] [CrossRef]
- Youssef, H.M. Two-temperature generalized thermoelastic infinite medium with cylindrical cavity subjected to moving heat source. Arch. Appl. Mech. 2010, 80, 1213–1224. [Google Scholar] [CrossRef]
- Youssef, H.M.; El-Bary, A.A. Theory of Hyperbolic Two-Temperature Generalized Thermoelasticity. Mater. Phys. Mech. 2018, 40, 158–171. [Google Scholar]
- Magin, R.L.; Royston, T.J. Fractional-order elastic models of cartilage: A multi-scale approach. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 657–664. [Google Scholar] [CrossRef]
- Youssef, H.M. Theory of generalized thermoelasticity with fractional order strain. J. Vib. Control 2016, 22, 3840–3857. [Google Scholar] [CrossRef]
- Ezzat, M.A.; El-Karamany, A.S.; El-Bary, A.A. Two-temperature theory in Green–Naghdi thermoelasticity with fractional phase-lag heat transfer. Microsyst. Technol. 2018, 24, 951–961. [Google Scholar] [CrossRef]
- Youssef, H.M. Generalized thermoelasticity of an infinite body with a cylindrical cavity and variable material properties. J. Therm. Stress. 2005, 28, 521–532. [Google Scholar] [CrossRef]
- Youssef, H.M. Problem of generalized thermoelastic infinite medium with cylindrical cavity subjected to a ramp-type heating and loading. Arch. Appl. Mech. 2006, 75, 553–565. [Google Scholar] [CrossRef]
- Ezzat, M.; El-Bary, A. Effects of variable thermal conductivity and fractional order of heat transfer on a perfect conducting infinitely long hollow cylinder. Int. J. Therm. Sci. 2016, 108, 62–69. [Google Scholar] [CrossRef]
- Youssef, H.M. Two-Temperature Generalized Thermoelastic Infinite Medium with Cylindrical Cavity Subjected to Different Types of Thermal Loading. WSEAS Trans. Heat Mass Transf. 2006, 1, 769. [Google Scholar]
- Ezzat, M.A.; Youssef, H.M. Generalized Magneto-Thermoelasticity for an Infinite Perfect Conducting Body with A Cylindrical Cavity. Mater. Phys. Mech. 2013, 18, 156–170. [Google Scholar]
- Povstenko, Y. Fractional Thermoelasticity; Springer: Berlin/Heidelberg, Germany, 2015; Volume 219. [Google Scholar]
- Tzou, D.Y. A unified field approach for heat conduction from macro-to micro-scales. J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Youssef, H.M. Thermal shock problem of a generalized thermoelastic solid sphere affected by mechanical damage and thermal diffusion. J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Youssef, H.M. State-space approach on generalized thermoelasticity for an infinite material with a spherical cavity and variable thermal conductivity subjected to ramp-type heating. Can. Appl. Math. Quaterly 2005, 13, 4. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Lehaibi, E.A.N. Generalized Thermoelastic Infinite Annular Cylinder under the Hyperbolic Two-Temperature Fractional-Order Strain Theory. Fractal Fract. 2023, 7, 476. https://doi.org/10.3390/fractalfract7060476
Al-Lehaibi EAN. Generalized Thermoelastic Infinite Annular Cylinder under the Hyperbolic Two-Temperature Fractional-Order Strain Theory. Fractal and Fractional. 2023; 7(6):476. https://doi.org/10.3390/fractalfract7060476
Chicago/Turabian StyleAl-Lehaibi, Eman A. N. 2023. "Generalized Thermoelastic Infinite Annular Cylinder under the Hyperbolic Two-Temperature Fractional-Order Strain Theory" Fractal and Fractional 7, no. 6: 476. https://doi.org/10.3390/fractalfract7060476
APA StyleAl-Lehaibi, E. A. N. (2023). Generalized Thermoelastic Infinite Annular Cylinder under the Hyperbolic Two-Temperature Fractional-Order Strain Theory. Fractal and Fractional, 7(6), 476. https://doi.org/10.3390/fractalfract7060476





