Abstract
The Wiener process was used to explore the (2 + 1)-dimensional chiral nonlinear Schrödinger equation (CNLSE). This model outlines the energy characteristics of quantum physics’ fractional Hall effect edge states. The sine-Gordon expansion technique (SGET) was implemented to extract stochastic solutions for the CNLSE through multiplicative noise effects. This method accurately described a variety of solitary behaviors, including bright solitons, dark periodic envelopes, solitonic forms, and dissipative and dissipative–soliton-like waves, showing how the solutions changed as the values of the studied system’s physical parameters were changed. The stochastic parameter was shown to affect the damping, growth, and conversion effects on the bright (dark) envelope and shock-forced oscillatory wave energy, amplitudes, and frequencies. In addition, the intensity of noise resulted in enormous periodic envelope stochastic structures and shock-forced oscillatory behaviors. The proposed technique is applicable to various energy equations in the nonlinear applied sciences.
1. Introduction
The important features of new solitonic envelopes form a foundation for the novel scientific energy universe, which is of great importance for a number of disciplines, including plasma physics, solid-state physics, telecommunications, superfluidity, quantum mechanics, and astrophysical dynamics [1,2,3,4,5,6]. These types of solution have attracted particular attention from physicists, mathematicians, and engineers [7,8,9,10,11,12]. Several new analytical methods, such as the —expansion approach, sub-equation approach, enhanced modified extended tanh-expansion approach have been used to obtain several nonlinear energy structures, which have been used to investigate the influence of physical parameters on energy and wave properties [13,14,15]. However, in recent decades there has been significant interest in understanding energy equations via the study of nonlinear Schrödinger equation dynamics in nature [16,17].
The investigation of chiral wave structures has a significant role in the developments of quantum mechanisms, specially in Hall-effect applications. Biswas obtained topological and nontopological solitons for a chiral NLSE model with time-dependent and constant coefficients [18]. Alharbi et al. investigated the dynamical Brownian stochastic CNLSE in two dimensions [19]. It was noted that the random noise parameter modulated the solitonic structures. Moreover, the Brownian noise affected the solitary features and produced distorted beak oscillatory shocks. Javid and Raza [20], explained the dark and singular solitons obtained from the (1 + 2) CNLSE using an M-simple-equation and the exp-expansion methods. It was reported that the solution movements and phase shift mainly depended on the signs of the equation constants. Eslami [21] studied the (1 + 2) CNLSE solutions using a trial solution technique. It was noted that, in this model, the stationary and singular soliton were retrieved. In addition, the structures were produced via constraint conditions for the equation coefficients.Recently, due to its increasingly widespread application, numerous analytical and numerical techniques have been developed for deterministic and stochastic NPDEs, such as the unified solver approach [22], Crank–Nicolson method [23], improved modified extended tanh-function method [24], implicit meshless method [25], finite difference method [26], adaptive moving mesh method [27], and operational matrix method [28].
The dominant model considered in this work is the (2 + 1)-dimensional CNLSE using a noise term. In this investigation, the nonlinear Schrödinger equations (NLSEs) were restricted using random noise effects, which have important nonlinear energy applications in superfluidity, quantum mechanics, plasma space, optical fibers, and other fields of science. The NLSE is described as wave propagations affected by the Kerr effect, dispersion, and group velocity. The solitonic solutions for NLSEs become important in nonlinearity energy studies. Recently, the NLSEs forced or damped with random noises using stochastic soliton solutions have become an important representative tool for explaining the propagations of a wave in solid state physics, chemical engineering, fiber communications, nuclear physics, and solid-state and energy physics [29,30,31].
We consider the -dimensional CNLSE [20,21]:
denotes a complex function in time t and the directions x, y, and are the coefficient of dispersion; & denote the coefficients of the nonlinear coupling terms; and denotes the noise strength. represents the time derivative of the Wiener process [32]. Equation (1) cannot be integrated using the inverse scattering transform approach because it fails the Painleve integrability condition. It is also worth noting that Equation (1) is not invariant under Galilean transformation. There have been several studies carried out for Equation (1) when there is no stochastic influence [21,33,34,35,36].
In the present research, by using the sine-Gordon expansion approach, we provide some important stochastic solutions to the 2D CNLSE induced by multiplicative noise in the Itô sense. The suggested technique offers a number of benefits, including the ability to use freely physical parameters to deliver accurate solutions in an explicit form. Clarifying the impact of the noise on the obtained solutions is one of the most intriguing points. We also show how certain chosen stochastic solutions affected the nonlinear dynamics of the model. To the best of our knowledge, no one has ever utilized the proposed technique to solve the (2 + 1)-dimensional CNLSE in the Itô sense.
This paper is structured as follows: Section 2 introduces a description of the proposed method and the Wiener process. Section 3 provides the stochastic solutions to the 2D stochastic CNLSE. Section 4 presents an explanation of the gained stochastic solution. The conclusions are summarized in Section 5.
2. Preliminaries
In this section we introduce the abbreviation of the sine-Gordon expansion approach [37] and the Wiener process.
2.1. Description of the Method
Consider the sine-Gordon equation [37]
where and is a non-zero real number. Utilizing the wave transform
Equation (2) is reduced to
Multiplying on both sides of Equation (4) and integrating it one time yields
K is the constant of integration. Setting , and into Equation (5) yields
Choosing , Equation (6) becomes
The solution of Equation (7) is given as follows:
Now, consider the following NPDEs:
Using the wave transformation:
w is the wave speed, Equation (10) is reduced to the following ODE:
It is assumed that the solution of Equation (11) can be written as
Considering Equations (8) and (9), Equation (12) can be written as follows:
The value of N is determined by utilizing the homogeneous balance principle. Superseding Equation (13) into Equation (11), and comparing the terms, yields a system of algebraic equations. Solving these equations, gives the traveling wave solutions of Equation (10).
2.2. Wiener Process
A stochastic process is a mathematical model of the possible future manifestations of a random phenomena when it first occurs [38]. The Wiener process is an example of a continuous-time stochastic process. This process meets the following requirements:
- (i)
- is a continuous functions of ,
- (ii)
- For is independent of increments,
- (iii)
- has a normal distribution through mean 0 and variance .
The distributional derivative of the Wiener process is the white noise in time. It is delta correlated in the sense that
is the Dirac mass. As the Dirac mass has a constant Fourier transform, the term “white noise” was coined. White noise is frequently thought of as a mathematical idealization of occurrences such as sudden, large fluctuations. It should be underlined that the Itô lemma is used to calculate the time derivative of stochastic processes as follows:
where represents the time derivative of stochastic processes, while denotes a differentiable function. Thus, this illustrates how has changed in a short amount of time . The Itô lemma for the Wiener process is represented as
One can construct the stochastic integral in a variety of ways. The most familiar types of a stochastic integral are those by Itô and Stratonovich. When the integral is calculated at the left-end point, it is said to have an Itô stochastic integral. When the stochastic integral is calculated at the midpoint, it is referred to as a Stratonovich stochastic integral [39].
3. The Stochastic Solutions for Equation (1)
Utilizing wave transformation [20]:
, denote the frequencies in x and y directions, and symbolize the soliton frequency and phase constant. In addition, and are wave numbers in x and y directions and is a traveling velocity.
Setting Equation (14) into Equation (1) produces
for the imaginary part and
for the real part, , and . Equation (16) provides the soliton solutions under the condition
Balancing the highest order derivative term and highest nonlinear term in Equation (16) yields N = 1. Thus, the solution of Equation (16) takes the form:
Substituting , , and into Equation (16) and setting the coefficients of the hyperbolic functions to zero produces a system of algebraic equations, which yields
Family I:
The stochastic solutions of Equation (16) are
Thus, the stochastic dark solutions for Equation (1) are
, .
Family II:
The stochastic solutions of Equation (16) are
Hence, the stochastic bright solutions for Equation (1) are
, .
Family III:
4. Results and Discussion
An effective and particular -dimension CNLSE stochastic solution has been achieved using SGET. Since CNLSE denotes the quantum fractional Hall-effect edge states [40,41,42]. Thus, new solitary forms have been studied in view of the constants and coefficients , , and the strength of noise . The perfect constitutional behaviors of solutions obtained for Equation (1) are a dark envelope, periodic envelopes, solitons, localized super soliton, dissipative shock-like, symmetric solitons, oscillatory shocks, etc. In neglecting noise effects, Equation (1) produces the following forms:
Here, the 3D solution profiles CNLSE have been informed by the physical values of , and for the absence on . In view of Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, a 3D plot of the obtained solitary forms with and t is given. Equation (25) describes the dark periodic envelopes, and super and solitonic profiles, as in Figure 1, Figure 2, Figure 3 and Figure 4. The dynamical behavior of Figure 1 shows that a dark envelope is produced for the x axis and a pure periodic wave for the t axis. In addition, a bright soliton wave is directed at the positive x axis generated in Figure 2. In Figure 3 and Figure 4 a plot of Equation (25) with the x and y axis is shown, and a narrow dissipative wave with symmetric periodic waves in the x, y axis and a bright soliton which is directed toward the negative x axis are given. For solution (26), some new physical description solutions are introduced in Figure 5, Figure 6, Figure 7 and Figure 8. A bright periodic envelope and a positive solitonic structure directed toward the negative x axis are illustrated in Figure 5 and Figure 6. Some important symmetric compressive-rarefactive solitons are produced for the x and y axis, as shown in Figure 7. In Figure 8, a positive soliton directed at the positive x axis is obtained. For solution (27), a combination of dissipative–soliton waves is created, as seen in Figure 9 and Figure 10. These dissipative behaviors are displayed in a symmetric manner with a solitonic shape, as shown in Figure 9, and in the center of the periodic solitary waves, as seen in Figure 10. The presented simulation diagrams for certain model solutions (1) were produced using Matlab Release 18.
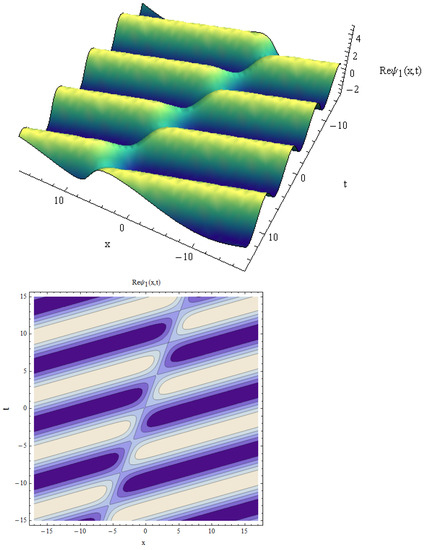
Figure 1.
Real part of vs. for , .
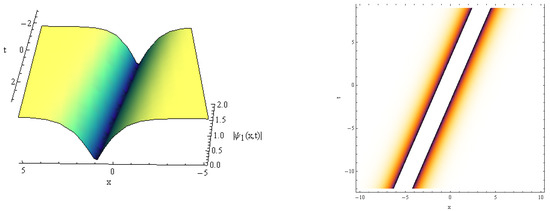
Figure 2.
vs. for , , .
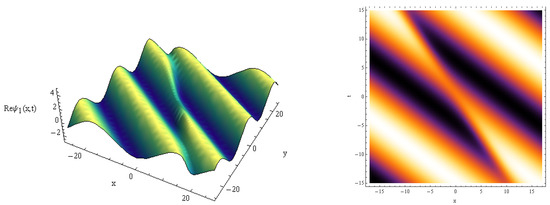
Figure 3.
Real part of vs. for , , .
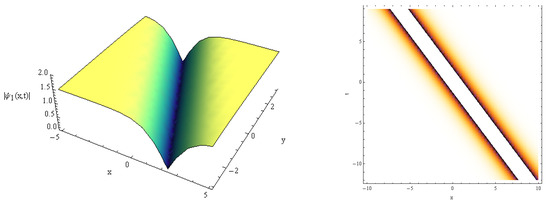
Figure 4.
vs. for , , .
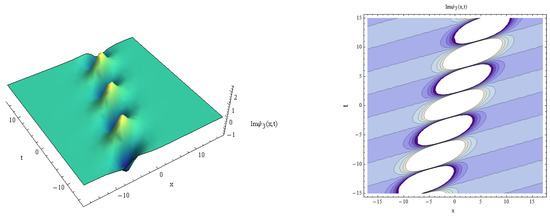
Figure 5.
Imaginary part of vs. for , .
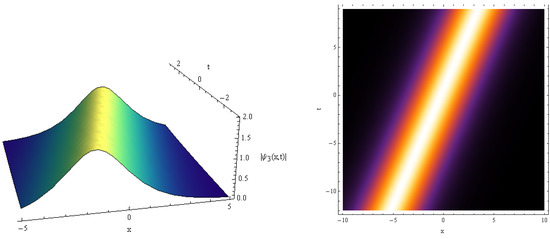
Figure 6.
vs. for , .
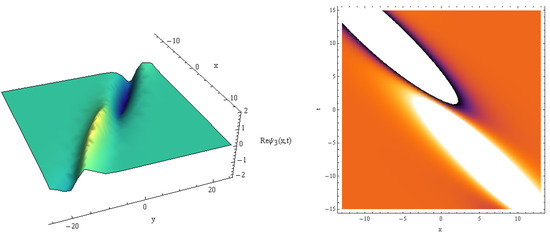
Figure 7.
Real part of vs. for , , .
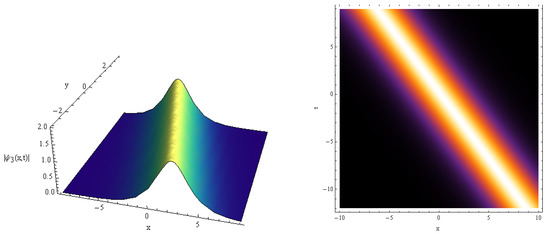
Figure 8.
vs. for , .
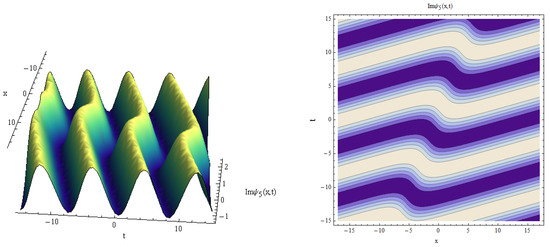
Figure 9.
Imaginary part of vs. for , .
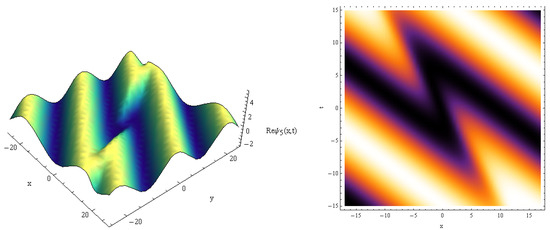
Figure 10.
Real part of vs. for , , , .
The effects of noise on the features of the solitary type solutions were investigated, which may be damped or grow with t. Equation (20) changes with t and the noise amplitude for a positive value, as shown in Figure 11. It was shown that, by increasing , the dark envelope amplitudes decrease for the positive t axis and increase for the negative t axis, without changes of frequency, as seen in Figure 11.
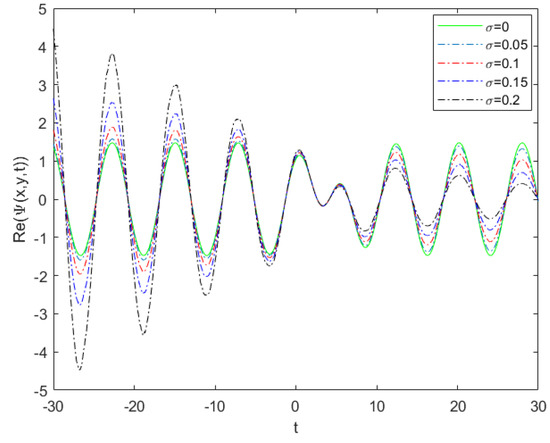
Figure 11.
Real stochstic solution (20) vs. for , , , .
For a negative value, the same effect is produced with changes of the wave frequency, as in Figure 12. Moreover, solution (22) is plotted with time t and for a positive value, as shown in Figure 13. By increasing , the envelope solitary form was converted to a shock-forced oscillatory wave. For a negative value, the amplitudes increased and the wave was converted to a huge bright periodic envelope wave, as in Figure 14.
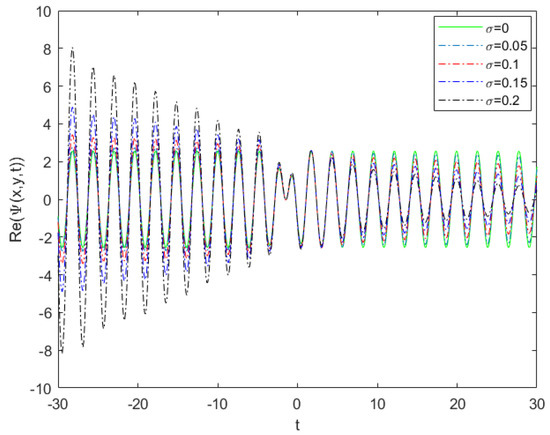
Figure 12.
Real stochstic solution (20) vs. for , , .
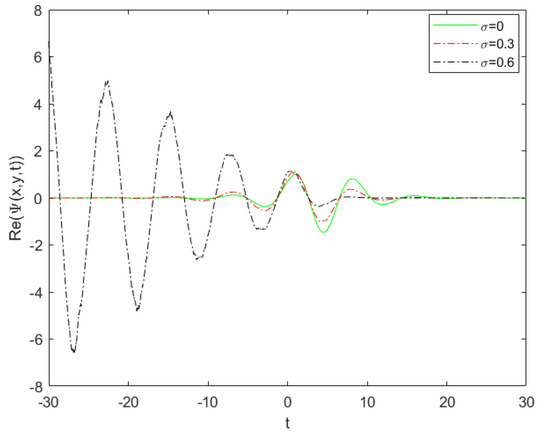
Figure 13.
Real stochstic solution (22) vs. for , .
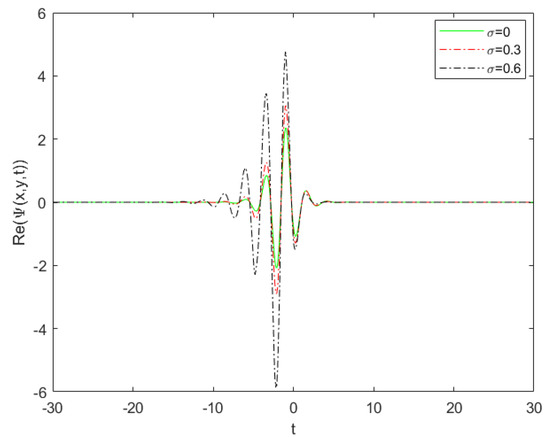
Figure 14.
Real stochstic solution (22) vs. for , .
In view of the importance of the solutions found in this work, which give an accurate description of many types of solitary behavior, such as dark periodic envelopes, solitonic forms, bright solitons, and dissipative and dissipative–soliton-like waves, they demonstrate the accuracy of the solutions with a change of the values of the physical parameters of the studied system. This facilitates the process of comparison with previous studies. Our results are consistent with the dark and bright solutions in [18] in the case of an equation with constant coefficients, as well as the dark solutions and the dissipative solutions of [21]. In addition, our results are in agreement with [20], but the conception of the results in this work gives a distinctive description of the change of wave behaviors between the solitons, shocks, and the periodic forms for a change of system parameters, while neglecting noise strength. On the other hand, the noise strength produces shock-forced oscillatory behaviors and huge bright periodic envelope stochastic structures.
Remark 1.
- The solver proposed in this study can be applied to large classes of nonlinear stochastic partial differential equations (NSPDEs).
- The suggested solver is simple to implement for solving stochastic fractional NPDEs.
Remark 2.
Despite the fact that the suggested technique was implemented for all classes of NSPDEs that were transformed to Equation (16), it failed to solve other classes of NSPDEs, which is regarded as a drawback of the proposed approach.
5. Conclusions
A 2D stochastic CNLSE has been delivered using SGET. The CNLSE denoting the quantum fractional Hall effect edge states was solved utilizing SGET to describe solitary wave structures. New solutions for the absence of the noise term describe behaviors in the form of bright and dark periodic envelopes, and dissipative and dissipative–soliton-like waves, depending on the studied system’s physical parameters. These solutions could be useful for quantum fractional Hall effect edge states. The effects of noise on the structural behavior of energy waves were investigated.The noise parameter modulated the wave attitude as amplitude variations, frequency fluctuations, and energy wave conversions. The present results may be important for Hall effect studies in quantum physics.
Author Contributions
H.G.A.: Conceptualization, Software, Formal analysis, Writing—original draft. A.F.A.: Conceptualization, Data curation, Writing—original draft. E.K.E.-S.: Conceptualization, Software, Formal analysis, Writing—review editing. M.A.E.A.: Conceptualization, Software, Formal analysis, Writing—review editing. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through project number (IF2/PSAU/2022/01/22803).
Data Availability Statement
Data sharing not applicable to this article, as no datasets were generated or analyzed during the current study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Younis, M.; Ali, S.; Mahmood, S.A. Solitons for compound KdV Burgers equation with variable coefficients and power law nonlinearity. Nonlinear Dyn. 2015, 81, 1191–1196. [Google Scholar] [CrossRef]
- Alharbi, A.; Almatrafi, M.B. Exact solitary wave and numerical solutions for geophysical KdV equation. J. King Saud Univ.-Sci. 2022, 34, 102087. [Google Scholar] [CrossRef]
- Alharbi, A.R.; Abdelrahman, M.A.E.; Almatrafi, M.B. Analytical and numerical investigation for the DMBBM equation. CMES-Comput. Model. Eng. Sci. 2020, 122, 743–756. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Almatrafi, M.B.; Alharbi, A.R. Fundamental solutions for the coupled KdV system and its stability. Symmetry 2020, 12, 429. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Abdo, N.F. On the nonlinear new wave solutions in unstable dispersive environments. Phys. Scr. 2020, 95, 045220. [Google Scholar] [CrossRef]
- Ullah, N.; Asjad, M.I.; Hussanan, A.; Akgül, A.; Alharbi, W.R.; Algarni, H.; Yahia, I.S. Novel waves structures for two nonlinear partial differential equations arising in the nonlinear optics via Sardar-subequation method. Alex. Eng. J. 2023, 71, 105–113. [Google Scholar] [CrossRef]
- Biswas, A.; Konar, S. Introduction to Non-Kerr Law Optical Solitons; Chapman and Hall, CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Mirzazadeh, Q.Z.Q.M.; Ekici, M.; Sonmezoglu, A. Analytical study of solitons in non-Kerr nonlinear negative-index materials. Nonlinear Dyn. 2016, 86, 623–638. [Google Scholar]
- Inc, M.; Aliyu, A.I.; Yusuf, A.; Bayram, M.; Baleanu, D. Optical solitons to the (n+1)-dimensional nonlinear Schrödinger’s equation with Kerr law and power law nonlinearities using two integration schemes. Mod. Lett. B 2019, 33, 1950223. [Google Scholar] [CrossRef]
- Kuo, C.K.; Ghanbari, B. Resonant multi-soliton solutions to new (3+1)-dimensional Jimbo-Miwa equations by applying the linear superposition principle. Nonlinear Dyn. 2019, 96, 459–464. [Google Scholar] [CrossRef]
- Almatrafi, M.B.; Alharbi, A.; Tunç, C. Constructions of the soliton solutions to the good Boussinesq equation. Adv. Differ. Equ. 2020, 2020, 629. [Google Scholar] [CrossRef]
- Shaikh, T.S.; Baber, M.Z.; Ahmed, N.; Shahid, N.; Akgül, A.; la Sen, M.D. On the soliton solutions for the stochastic Konno–Oono system in magnetic field with the presence of noise. Mathematics 2023, 11, 1472. [Google Scholar] [CrossRef]
- Younis, M.; Rizvi, S.T.R. Dispersive dark optical soliton in (2+1)-dimensions by -expansion with dual-power law nonlinearity. Optik 2015, 126, 5812–5814. [Google Scholar] [CrossRef]
- Khodadad, F.S.; Nazari, F.; Eslami, M.; Rezazadeh, H. Soliton solutions of the conformable fractional Zakharov-Kuznetsov equation with dual-power law nonlinearity. Opt. Quantum Electron. 2017, 49, 384. [Google Scholar] [CrossRef]
- Ashraf, R.; Ashraf, F.; Akgül, A.; Ashraf, S.; Alshahrani, B.; Mahmoud, M.; Weera, W. Some new soliton solutions to the (3+1)-dimensional generalized KdV-ZK equation via enhanced modified extended tanh-expansion approach. Alex. Eng. J. 2023, 69, 303–309. [Google Scholar] [CrossRef]
- Li, B.Q. Phase transitions of breather of a nonlinear Schrödinger equation in inhomogeneous optical fiber system. Optik 2020, 217, 164670. [Google Scholar] [CrossRef]
- Li, B.Q.; Ma, Y.L. Extended generalized Darboux transformation to hybrid rogue wave and breather solutions for a nonlinear Schrödinger equation. Appl. Math. Comput. 2020, 386, 125469. [Google Scholar] [CrossRef]
- Biswas, A. chiral solitons in 1+2 dimensions. Int. J. Theor. Phys 2009, 48, 3403–3409. [Google Scholar] [CrossRef]
- Alharbi, Y.F.; El-Shewy, E.K.; Abdelrahman, M.A.E. Effects of Brownian noise strength on new chiral solitary structures. J. Low Freq. Noise Vib. Act. Control. 2022, 42. [Google Scholar] [CrossRef]
- Javid, A.; Raza, N. Chiral solitons of the (1 + 2)-dimensional nonlinear Schrödinger’s equation. Mod. Phys. Lett. B 2019, 33, 1950401. [Google Scholar] [CrossRef]
- Eslami, M. Trial solution technique to chiral nonlinear Schrödinger’s equation in(1+2)-dimensions. Nonlinear Dyn. 2016, 85, 813–816. [Google Scholar] [CrossRef]
- Alomair, R.A.; Hassan, S.Z.; Abdelrahman, M.A.E. A new structure of solutions to the coupled nonlinear Maccari’s systems in plasma physics. AIMS Math. 2022, 7, 8588–8606. [Google Scholar] [CrossRef]
- Samadyar, N.; Ordokhani, Y.; Mirzaee, F. The couple of Hermite-based approach and Crank-Nicolson scheme to approximate the solution of two dimensional stochastic diffusion-wave equation of fractional order. Eng. Anal. Bound. Elem. 2020, 118, 285–294. [Google Scholar] [CrossRef]
- Almatrafi, M.B. Solitary wave solutions to a fractional model using the improved modified extended tanh-function method. Fractal Fract. 2023, 7, 252. [Google Scholar] [CrossRef]
- Mirzaee, F.; Samadyar, N. Numerical solution of time fractional stochastic Korteweg-de Vries equation via implicit meshless approach. Iran. J. Sci. Technol. Trans. A Sci. 2019, 43, 2905–2912. [Google Scholar] [CrossRef]
- Mirzaee, F.; Rezaei, S.; Samadyar, N. Numerical solution of two-dimensional stochastic time-fractional sine-Gordon equation on non-rectangular domains using finite difference and meshfree methods. Eng. Anal. Bound. Elem. 2021, 127, 53–63. [Google Scholar] [CrossRef]
- Almatrafi, M.B.; Alharbi, A. New soliton wave solutions to a nonlinear equation arising in plasma physics. Comput. Model. Eng. Sci. 2023, 137, 827–841. [Google Scholar] [CrossRef]
- Samadyar, N.; Ordokhani, Y.; Mirzaee, F. Hybrid Taylor and block-pulse functions operational matrix algorithm and its application to obtain the approximate solution of stochastic evolution equation driven by fractional Brownian motion. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105346. [Google Scholar] [CrossRef]
- Dalfovo, F.; Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of Bose-Einstein condensation in trapped gases. Rev. Mod. Phys. 1999, 71, 463. [Google Scholar] [CrossRef]
- Nakkeeran, K. Bright and dark optical solitons in fiber media with higher-order effects. Chaos Solitons Fractals 2002, 13, 673–679. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Sohaly, M.A.; Alharbi, Y.F. Fundamental stochastic solutions for the conformable fractional NLSE with spatiotemporal dispersion via exponential distribution. Phys. Scr. 2021, 96, 125223. [Google Scholar] [CrossRef]
- Mirzaee, F.; Sayevand, K.; Rezaei, S.; Samadyar, N. Finite difference and spline approximation for solving fractional stochastic advection-diffusion equation. Iran. J. Sci. Technol. A Sci. 2021, 45, 607–617. [Google Scholar] [CrossRef]
- Nishino, A.; Umeno, Y.; Wadati, M. Chiral nonlinear Schrödinger equation. Chaos Solitons Fractals 1998, 9, 1063–1069. [Google Scholar] [CrossRef]
- Tsitsas, N.L.; Lakhtakia, A.; Frantzeskakis, D.J. Vector solitons in nonlinear isotropic chiral metamaterials. J. Phys. A Math. Theor. 2011, 44, 435203. [Google Scholar] [CrossRef]
- Ismail, M.S.; Al-Basyouni, K.S.; Aydin, A. Conservative finite difference schemes for the chiral nonlinear Schrödinger equation. Bound. Value Probl. 2015, 89, 2015. [Google Scholar] [CrossRef]
- Younis, M.; Cheemaa, N.; Mahmood, S.A.; Rizvi, S.T.R. On optical solitons: The chiral nonlinear Schrödinger equation with perturbation and Bohm potential. Opt. Quant. Electron. 2016, 48, 542. [Google Scholar] [CrossRef]
- Yan, C. A simple transformation for nonlinear waves. Phys. Lett. A 1996, 224, 77–84. [Google Scholar] [CrossRef]
- Karatzas, I.; Shreve, S.E. Brownian Motion and Stochastic Calculus, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- ∅ksendal, B. Stochastic Differential Equations: An Introduction with Applications, 6th ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Griguolo, L.; Seminara, D. Chiral solitons from dimensional reduction of Chern-Simons gauged nonlinear Schrödinger equation: Classical and quantum aspects. Nucl. Phys. B 1998, 516, 467–498. [Google Scholar] [CrossRef]
- Lee, J.H.; Lin, C.K.; Pashev, O.K. Shock waves, chiral solitons and semi-classical limit of one-dimensional anyons. Chaos Solitons Fractals 2004, 19, 109–128. [Google Scholar] [CrossRef]
- Aglietti, U.; Griguolo, L.; Jackiw, R.; Pi, S.Y.; Semirara, D. Anyons and Chiral Solitons on a Line. Phys. Rev. Lett. 1996, 77, 44064409. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).