New Versions of Midpoint Inequalities Based on Extended Riemann–Liouville Fractional Integrals
Abstract
1. Introduction
2. Preliminaries
3. Main Outcomes
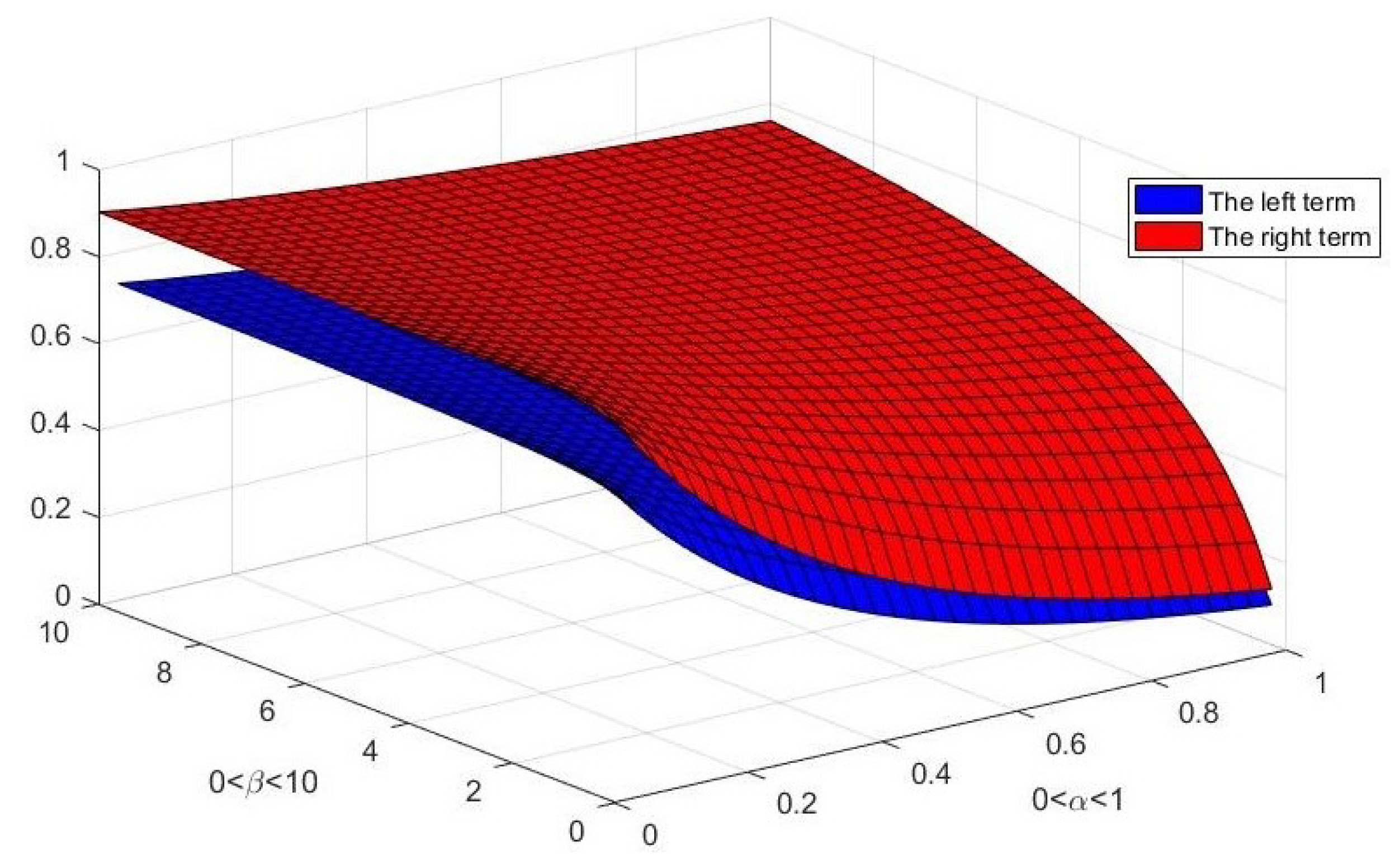
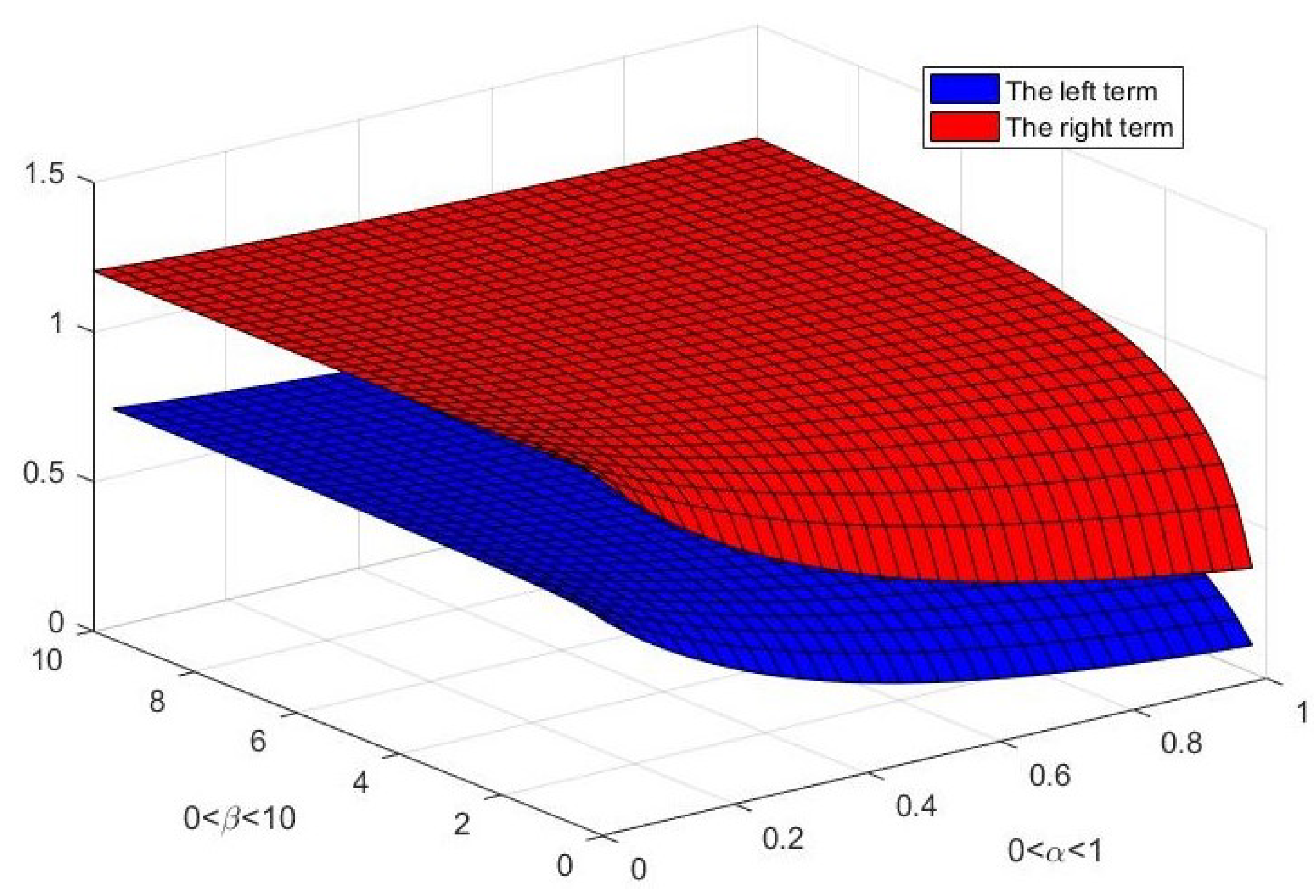
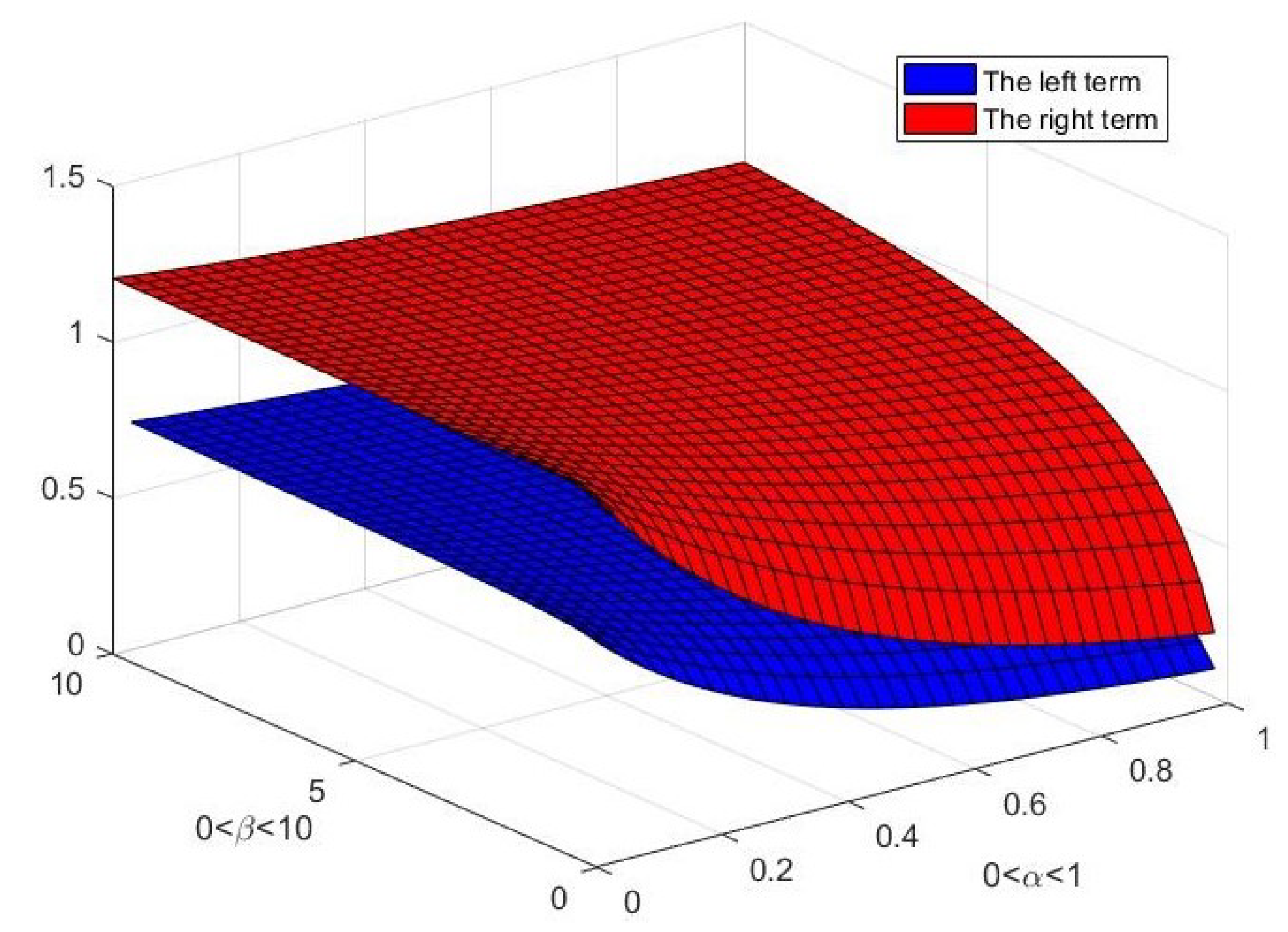
4. Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2016. [Google Scholar]
- Anastassiou, G.A. Generalized Fractional Calculus: New Advancements and Applications; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers: Redding, CA, USA, 2006. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivative with non-local and non-singular kernel. Therm. Sci. 2016, 20, 757–763. [Google Scholar] [CrossRef]
- Sezer, S. The Hermite-Hadamard inequality for s-Convex functions in the third sense. AIMS Math. 2021, 6, 7719–7732. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Baleanu, D. Integration by parts and its applications of a new nonlocal fractional derivative with Mittag-Leffler nonsingular kernel. J. Nonlinear Sci. Appl. 2017, 10, 1098–1107. [Google Scholar] [CrossRef]
- Krishna, V.; Maenner, E. Convex Potentials with an Application to Mechanism Design. Econometrica 2001, 69, 1113–1119. [Google Scholar] [CrossRef]
- Okubo, S.; Isihara, A. Inequality for convex functions in quantum-statistical mechanics. Physica 1972, 59, 228–240. [Google Scholar] [CrossRef]
- Peajcariaac, J.; Tong, Y. Convex Functions, Partial Orderings, and Statistical Applications; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Murota, K.; Tamura, A. New characterizations of M-convex functions and their applications to economic equilibrium models with indivisibilities. Discret. Appl. Math. 2003, 131, 495–512. [Google Scholar] [CrossRef]
- Tariq, M.; Ahmad, H.; Sahoo, S.K.; Aljoufi, L.S.; Awan, S.K. A novel comprehensive analysis of the refinements of Hermite-Hadamard type integral inequalities involving special functions. J. Math. Comput. Sci. 2022, 26, 330–348. [Google Scholar] [CrossRef]
- Raees, M.; Anwar, M.; Farid, G. Error bounds associated with different versions of Hadamard inequalities of mid-point type. J. Math. Comput. Sci. 2021, 23, 213–229. [Google Scholar] [CrossRef]
- Hyder, A.; Barakat, M.A.; Fathallah, A.; Cesarano, C. Further Integral Inequalities through Some Generalized Fractional Integral Operators. Fractal Fract. 2021, 5, 282. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Set, E.; Yaldiz, H.; Basak, N. Hermite—Hadamard’s inequalities for fractional integrals and related fractional inequalities. Math. Comput. Model. 2013, 57, 2403–2407. [Google Scholar] [CrossRef]
- Set, E. New inequalities of Ostrowski type for mappings whose derivatives are s-convex in the second sense via fractional integrals. Comput. Math. Appl. 2012, 63, 1147–1154. [Google Scholar] [CrossRef]
- Budak, H.; Hezenci, F.; Kara, H. On parameterized inequalities of Ostrowski and Simpson type for convex functions via generalized fractional integrals. Math. Methods Appl. Sci. 2021, 44, 12522–12536. [Google Scholar] [CrossRef]
- Hyder, A.; Budak, H.; Almoneef, A.A. Further midpoint inequalities via generalized fractional operators in Riemann-Liouville sense. Fractal Fract. 2022, 6, 496. [Google Scholar] [CrossRef]
- Hadamard, J. Etude sur les propriétés des fonctions entières et en particulier d’une fonction considérée par Riemann. J. Math. Pures Appl. 1893, 58, 171–215. [Google Scholar]
- Jarad, F.; Uğurlu, E.; Abdeljawad, T.; Baleanu, D. On a new class of fractional operators. Adv. Differ. Equ. 2017, 2017, 247. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Yildirim, H. On Hermite-Hadamard type inequalities for Riemann-Liouville fractional integrals. Miskolc Math. Notes 2016, 7, 1049–1059. [Google Scholar] [CrossRef]
- Set, E.; Choi, J.; Gözpinar, A. Hermite–Hadamard Type Inequalities for New Conformable Fractional Integral Operator, Research- Gate Preprint. 2018. Available online: https://www.researchgate.net/publication/322936389 (accessed on 8 May 2012).
- Gözpınar, A. Some Hermite-Hadamard type inequalities for convex functions via new fractional conformable integrals and related inequalities. AIP Conf. Proc. 2018, 1991, 020006. [Google Scholar]
- Budak, H.; Kapucu, R. New generalization of midpoint type inequalities for fractional integral. An. Stiint¸. Univ. Al. I. Cuza Ia¸si. Mat. (N.S.) 2021. [Google Scholar] [CrossRef]
- Qaisar, S.; Hussain, S. On Hermite-Hadamard type inequalities for functions whose first derivative absolute values are convex and concave. Fasc. Math. 2017, 58, 155–166. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hyder, A.-A.; Budak, H.; Barakat, M.A. New Versions of Midpoint Inequalities Based on Extended Riemann–Liouville Fractional Integrals. Fractal Fract. 2023, 7, 442. https://doi.org/10.3390/fractalfract7060442
Hyder A-A, Budak H, Barakat MA. New Versions of Midpoint Inequalities Based on Extended Riemann–Liouville Fractional Integrals. Fractal and Fractional. 2023; 7(6):442. https://doi.org/10.3390/fractalfract7060442
Chicago/Turabian StyleHyder, Abd-Allah, Hüseyin Budak, and Mohamed A. Barakat. 2023. "New Versions of Midpoint Inequalities Based on Extended Riemann–Liouville Fractional Integrals" Fractal and Fractional 7, no. 6: 442. https://doi.org/10.3390/fractalfract7060442
APA StyleHyder, A.-A., Budak, H., & Barakat, M. A. (2023). New Versions of Midpoint Inequalities Based on Extended Riemann–Liouville Fractional Integrals. Fractal and Fractional, 7(6), 442. https://doi.org/10.3390/fractalfract7060442







