FPGA Implementation of Parameter-Switching Scheme to Stabilize Chaos in Fractional Spherical Systems and Usage in Secure Image Transmission
Abstract
1. Introduction
- (i)
- A digital realization of a parameter-switching scheme to stabilize chaos in fractional-order and spherical chaotic nonlinear systems using Grünwald–Letnikov for the numerical approximation and VHDL as the hardware description language.
- (ii)
- A master–slave-based synchronization of fractional-order and spherical nonlinear systems using the Hamiltonian system with an observer-based approach for the purpose of communication.
- (iii)
- A methodology developed to implement a secure image transmission system on Xilinx and Intel FPGA cards using the parameter-switching technique as a decryption mechanism. The implementation was achieved on two FPGA cards, namely Xilinx’s Artix-7 AC701 and Intel’s Cyclone V.
2. Theoretical Framework
2.1. Grünwald–Letnikov Numerical Method
2.2. Fractional-Order Chaotic Spherical System
2.3. Parameter-Switching Technique
2.4. Hamiltonian System
3. Numerical Implementations
3.1. Chaos Control in FOCSS
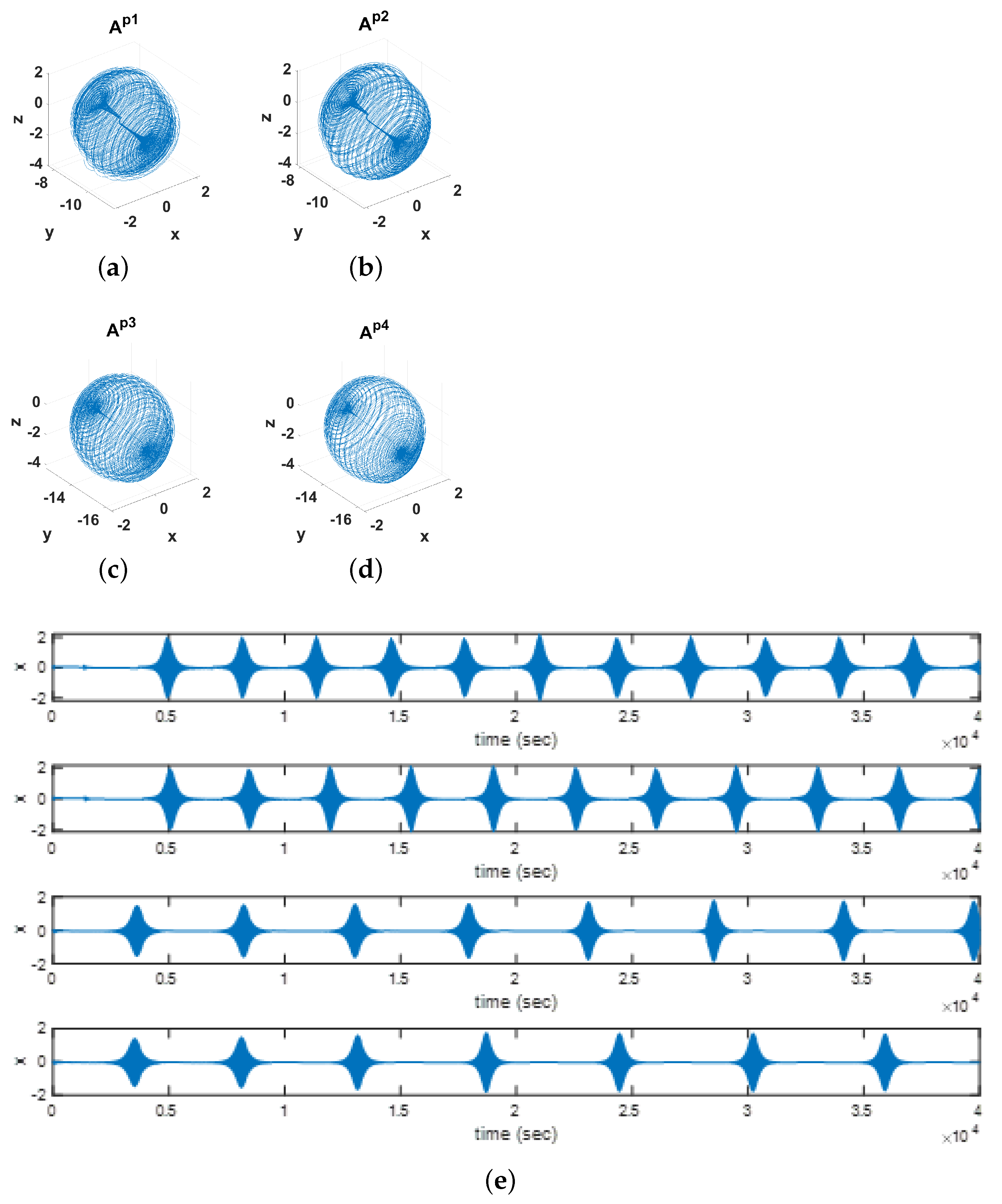
3.1.1. Case 1: Four Control Parameters
- , which are the corresponding weights of ; and
- , which are the chaotic attractors corresponding to .
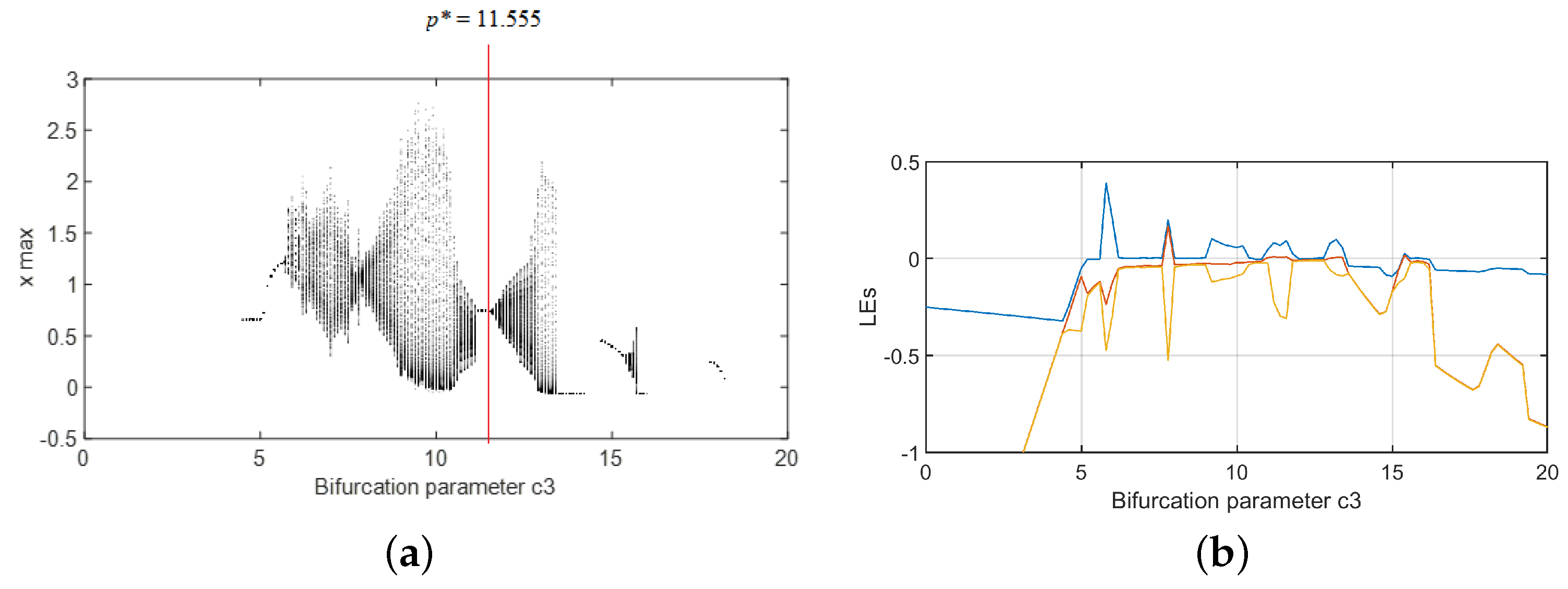
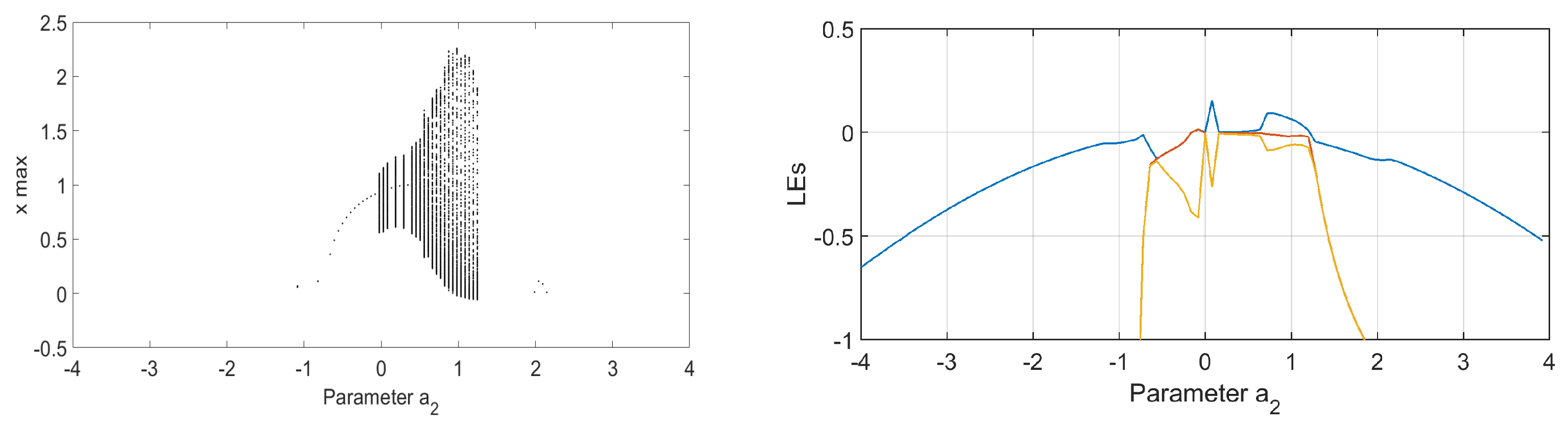
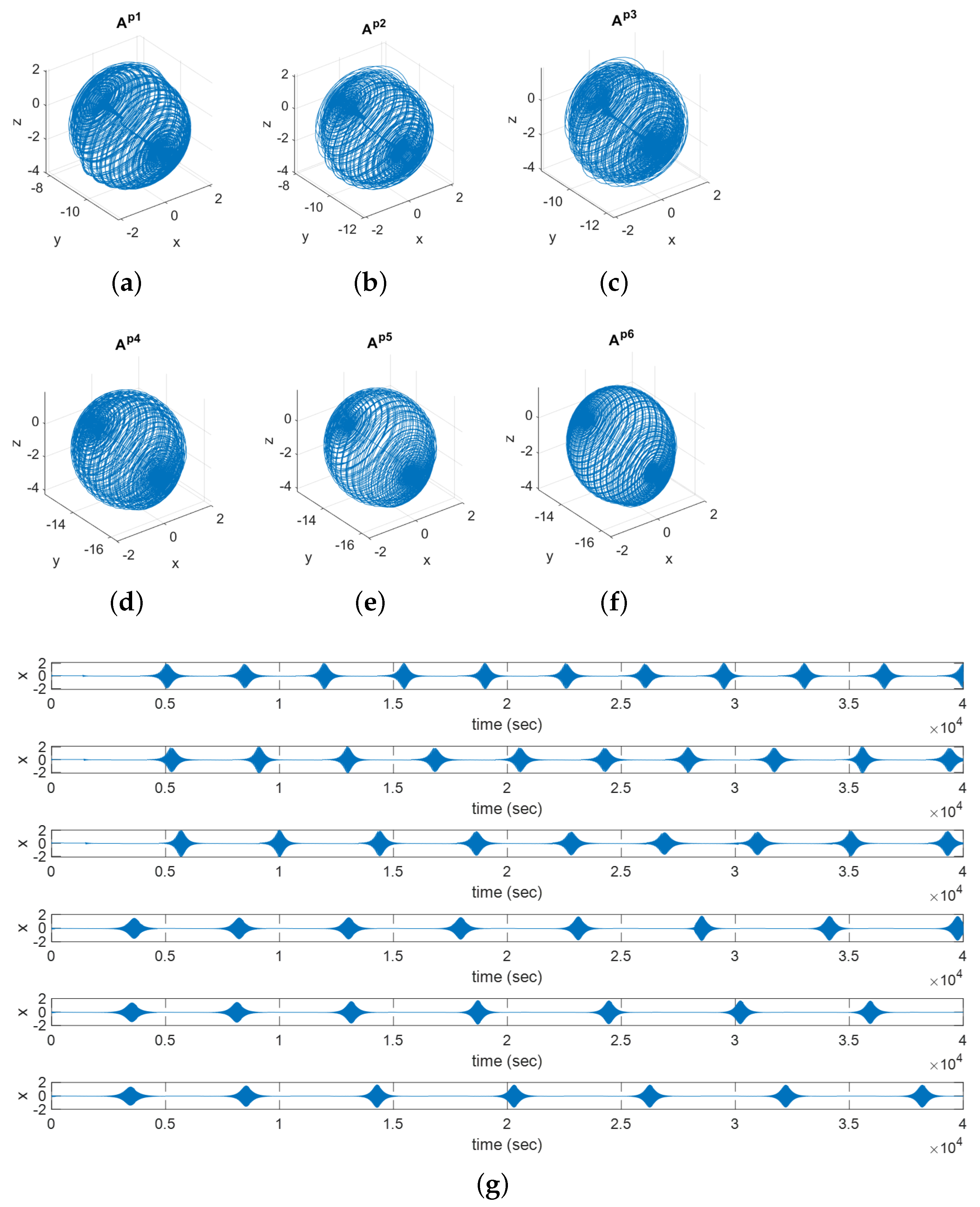
3.1.2. Case 2: Six Control Parameters
- , which are selected from the chaotic regions of the FOCSS (14);
- , which are the corresponding weights of ; and
- , which are the chaotic attractors corresponding to .
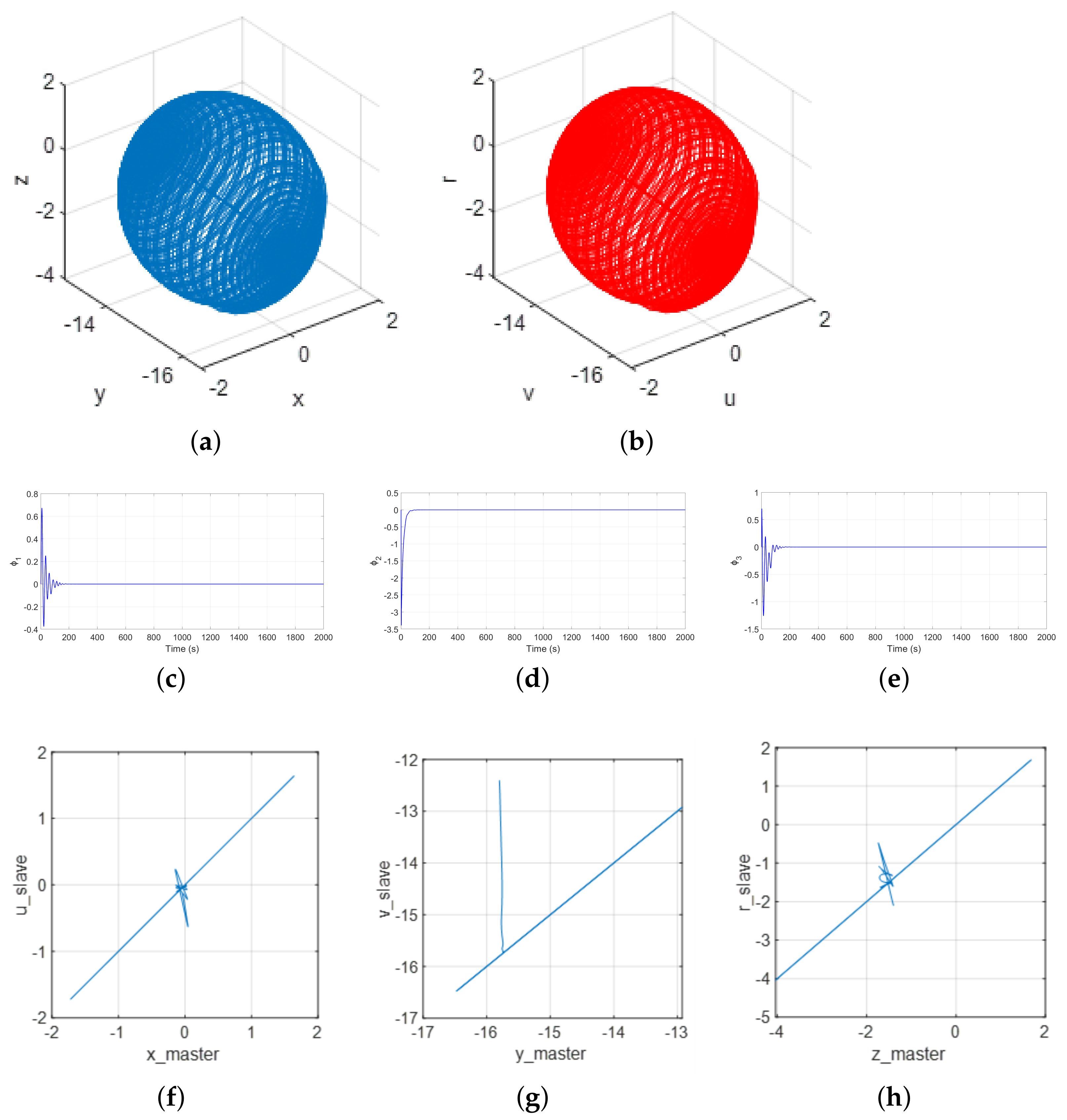
3.2. Synchronization of FOCSSs
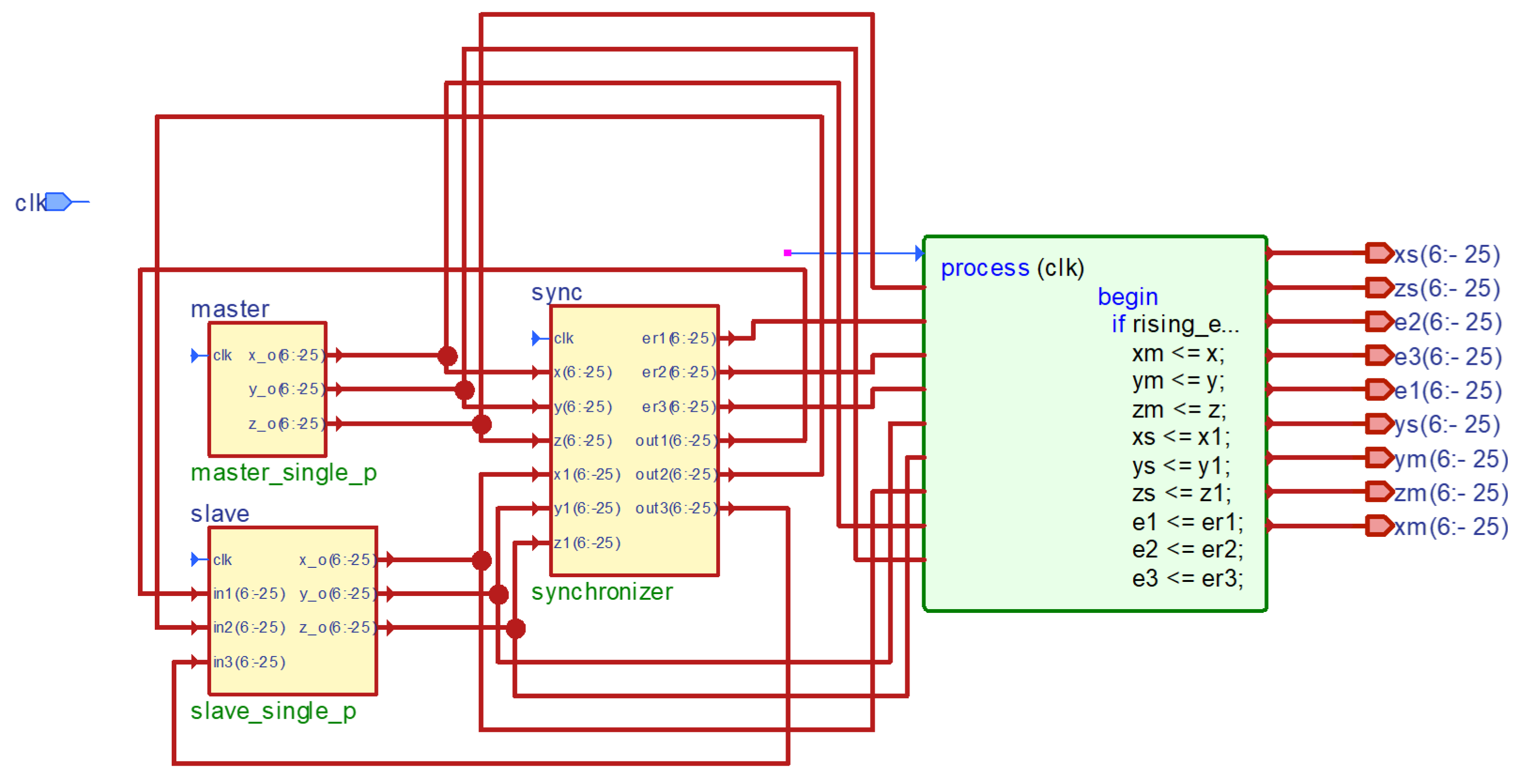
4. VHDL Implementations
4.1. Chaos Control in FOCSS
4.2. Synchronization of FOCSSs
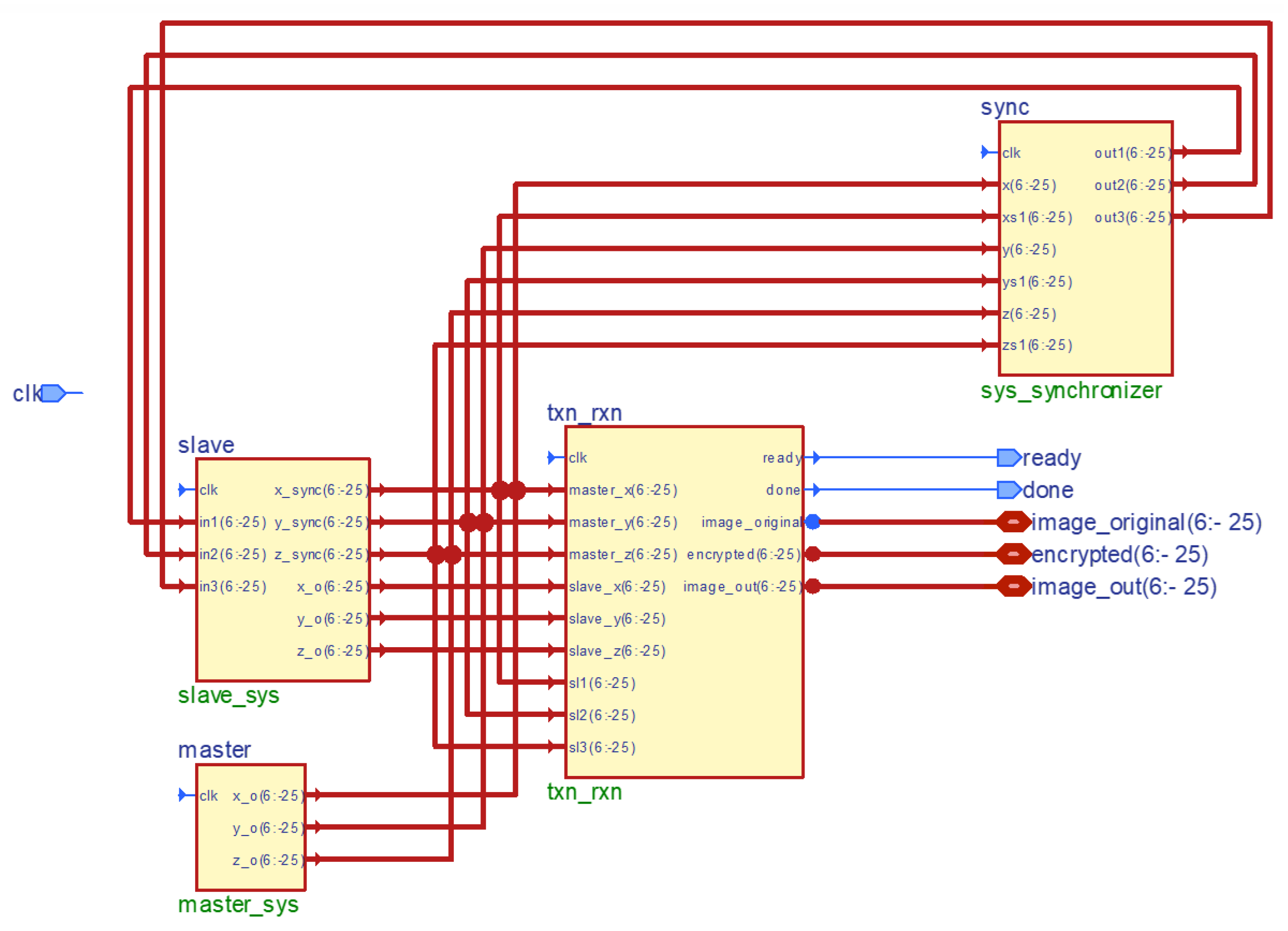
5. Secure Image Transmission System
6. Discussion
6.1. Consumption of Logical Resources
6.2. Performance Analysis
6.3. Comparison with Other Works
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ALM | Adaptive Logic Module |
| CLB | Configurable Logic Block |
| DSP | Digital Signal Processor |
| FDE | Fractional Differential Equation |
| FMCS | Fractional Memristive Chaotic System |
| FOCSS | Fractional-Order Chaotic Spherical System |
| FONLS | Fractional-Order Nonlinear System |
| FOS | Fractional-Order System |
| FPGA | Field Programmable Gate Array |
| I/O | Input/Output |
| IVP | Initial Value Problem |
| LE | Lyapunov Exponent |
| LUT | Look-up Table |
| MLE | Maximum Lyapunov Exponent |
| N/A | Not Available |
| NECS | No-equilibrium Chaotic System |
| NMCS | New Multi-scroll Chua’s System |
| RGB | Red, Green, Blue |
| UPO | Unstable Periodic Orbit |
| VHDL | VHSIC Hardware Description Language |
References
- Machado, J.A.T. The Evolution of Fractional Calculus. Chaos Theory Appl. 2022, 4, 59–63. [Google Scholar]
- Stanisławski, R. Fractional Systems: State-of-the-Art. In Fractional Dynamical Systems: Methods, Algorithms and Applications; Studies in Systems, Decision and Control; Kulczycki, P., Korbicz, J., Kacprzyk, J., Eds.; Springer: Cham, Switzerland, 2022; Volume 402. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Ghasemi-Nasrabady, A.; Eftekhari, A. Numerical Study of Singular Fractional Lane–Emden Type Equations Arising in Astrophysics. J. Astrophys. Astron. 2019, 40, 1–12. [Google Scholar]
- Cruz-Duarte, J.M.; Guia-Calderon, M.; Rosales-Garcia, J.J.; Correa, R. Determination of a Physically Correct Fractional-order Model for Electrolytic Computer-grade Capacitors. Math. Method Appl. Sci. 2020, 44, 4366–4380. [Google Scholar]
- Nigmatullin, R.R.; Lino, P.; Maione, G. “Fuzzy” Calculus: The Link Between Quantum Mechanics and Discrete Fractional Operators. Fract. Calc. Appl. Anal. 2020, 23, 764–786. [Google Scholar]
- Fadaei, Y.; Ahmadi, A.; Fekri, K.; Masoumi, R.; Radunskaya, A. A Fractional-order Model for Chronic Lymphocytic Leukemia and Immune System Interactions. Math. Method Appl. Sci. 2020, 44, 391–406. [Google Scholar]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Assiri, T.; Atangana, A. Optimal control for cancer treatment mathematical model using Atangana–Baleanu–Caputo Fractional Derivative. Adv. Differ. Equ. 2020, 2020, 1–21. [Google Scholar]
- Frunzo, L.; Garra, R.; Giusti, A.; Luongo, V. Modeling Biological Systems with an Improved Fractional Gompertz Law. Commun. Nonlinear Sciience Numer. Simul. 2019, 74, 260–267. [Google Scholar]
- Tarasova, V.V.; Tarasov, V.E. Productivity with Fatigue and Long Memory: Fractional Calculus Approach. Int. J. Appl. Comput. Math. 2019, 5, 16. [Google Scholar]
- Chen, S.Y.; Yang, M.C. Nonlinear Contour Tracking of a Voice Coil Motors-Driven Dual-Axis Positioning Stage Using Fuzzy Fractional PID Control with Variable Orders. Math. Probl. Eng. 2021, 2021, 6697942. [Google Scholar]
- Sibtain, D.; Murtaza, A.F.; Ahmed, N.; Sher, H.A.; Gulzar, M.M. Multi Control Adaptive Fractional Order PID Control Approach for PV/Wind Connected Grid System. Int. Trans. Electr. Energy Syst. 2021, 31, e12809. [Google Scholar]
- Wang, G.; Liu, Y.; Wu, Y.; Su, X. Symmetry Analysis for a Seventh-order Generalized Kdv Equation and its Fractional Version in Fluid Mechanics. Fractals 2020, 28, 2050044. [Google Scholar]
- Javadi, M.; Noorian, M.A.; Irani, S. Stability Analysis of Pipes Conveying Fluid with Fractional Viscoelastic Model. Meccanica 2019, 54, 399–410. [Google Scholar]
- Gulgowski, J.; Kwiatkowski, D.; Stefanski, T.P. Signal Propagation in Electromagnetic Media Modelled by the Two-Sided Fractional Derivative. Fractal Fract. 2021, 5, 10. [Google Scholar]
- Shi, L.; Qiu, L.; Huang, X.; Zhang, F.; Wang, D.; Zhou, L.; Gao, J. Characterization of Si-BCB Transmission Line at Millimeter-Wave Frequency by Compact Fractional-order Equivalent Circuit Model. Int. J. Microw. Comput.-Aided Eng. 2019, 29, e21685. [Google Scholar]
- Poincaré, H. Méthode Nouvelles de la Mécanique Céleste. In New Methods of Celestial Mechanics in History of Modem Physics; Goroff, D.L., Translator; Springer: New York, NY, USA, 1992. [Google Scholar]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar]
- Khalil, N.; Sarhan, A.; Alshewimy, M.A.M. An efficient color/grayscale image encryption scheme based on hybrid chaotic maps. Opt. Laser Technol. 2021, 143, 107326. [Google Scholar]
- Mukherjee, S. New Insights Into Chaos Based Image Encryption & Its Application. J. Math. Sci. Comput. Math. 2023, 4, 241–264. [Google Scholar]
- Montero-Canela, R.; Zambrano-Serrano, E.; Tamariz-Flores, E.I.; Muñoz-Pacheco, J.M.; Torrealba-Meléndez, R. Fractional Chaos-Based Cryptosystem for Generating Encryption Keys in Ad Hoc Networks. Ad Hoc Netw. 2020, 97, 102005. [Google Scholar]
- Mozaffari, A.; Emami, M.; Fathi, A. Comprehensive Investigation into the Performance, Robustness, Scalability and Convergence of Chaos-Enhanced Evolutionary Algorithms with Boundary Constraint. Artif. Intell. Rev. 2019, 52, 2319–2380. [Google Scholar]
- Saifullah, S.; Ali, A.; Goufo, E.F.D. Investigation of complex behaviour of fractal fractional chaotic attractor with mittag-leffler Kernel. Chaos Solitons Fractals 2021, 152, 111332. [Google Scholar]
- Lin, H.; Wang, C.; Sun, Y.; Wang, T. Generating n-Scroll Chaotic Attractors From a Memristor-Based Magnetized Hopfield Neural Network. IEEE Trans. Circuits Syst. Ii: Express Briefs 2023, 70, 311–315. [Google Scholar] [CrossRef]
- Amster, P.; Alliera, C. Control of Pyragas Applied to a Coupled System with Unstable Periodic Orbits. Bull. Math. Biol. 2018, 80, 2897–2916. [Google Scholar]
- Din, Q.; Elsadany, A.A.; Ibrahim, S. Bifurcation Analysis and Chaos Control in a Second Order Rational Difference Equation. Int. J. Nonlinear Sci. Numer. Simul. 2018, 19, 53–68. [Google Scholar]
- Anikushin, M.; Romanov, A. Hidden and unstable periodic orbits as a result of homoclinic bifurcations in the Suarez–Schopf delayed oscillator and the irregularity of ENSO. Phys. Nonlinear Phenom. 2023, 445, 133653. [Google Scholar]
- Wu, Y.; Qiao, S.; Yao, D. A hybrid chaotic controller integrating hip stiffness modulation and reinforcement learning-based torque control to stabilize passive dynamic walking. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2023, 237, 673–691. [Google Scholar]
- Gholami, M.; Ghaziani, R.K.; Eskandari, Z. Three-dimensional fractional system with the stability condition and chaos control. Math. Model. Numer. Simul. Appl. 2022, 2, 41–47. [Google Scholar] [CrossRef]
- Cetinkaya, A.; Hayakawa, T.; bin Mohd Taib, M.A.F. Stabilizing unstable periodic orbits with delayed feedback control in act-and-wait fashion. Syst. Control. Lett. 2018, 113, 71–77. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Yu, J.L. Stabilization of multi-rotation unstable periodic orbits through dynamic extended delayed feedback control. Chaos Solitons Fractals 2022, 161, 112362. [Google Scholar] [CrossRef]
- Adeyemi, V.A.; Núñez-Pérez, J.C.; Sandoval-Ibarra, Y.; Pérez-Pinal, F.J.; Tlelo-Cuautle, E. FPGA Realization of the Parameter-Switching Method in the Chen Oscillator and Application in Image Transmission. Symmetry 2021, 13, 923. [Google Scholar]
- Nuñez-Perez, J.C.; Adeyemi, V.A.; Sandoval-Ibarra, Y.; Pérez-Pinal, F.J.; Tlelo-Cuautle, E. FPGA Realization of Spherical Chaotic System with Application in Image Transmission. Math. Probl. Eng. 2021, 2021, 5532106. [Google Scholar]
- Dridi, F.; Assad, S.E.; Youssef, W.E.H.; Machhout, M.; Lozi, R. The Design and FPGA-Based Implementation of a Stream Cipher Based on a Secure Chaotic Generator. Appl. Sci. 2021, 11, 625. [Google Scholar]
- Hagras, E.A.A.; Saber, M. Low power and high-speed FPGA Implementation for 4D Memristor Chaotic System for Image Encryption. Multimed. Tools Appl. 2020, 79, 23203–23222. [Google Scholar]
- Guillén-Fernández, O.; Meléndez-Cano, A.; Tlelo-Cuautle, E.; Núñez-Pérez, J.C.; Rangel-Magdaleno, J.J. On the Synchronization Techniques of Chaotic Oscillators and Their FPGA-Based Implementation for Secure Image Transmission. PLoS ONE 2019, 14, e0209618. [Google Scholar]
- Dridi, F.; Assad, S.E.; Hadj, Y.W.E.; Machhout, M. Design, Hardware Implementation on FPGA and Performance Analysis of Three Chaos-Based Stream Ciphers. Fractal Fract. 2023, 7, 197. [Google Scholar]
- Lahcene, M.; Noureddine, C.; Lorenz, P.; Ali-Pacha, A. Securing information using a proposed reliable chaos-based stream cipher: With real-time FPGA-based wireless connection implementation. Nonlinear Dyn. 2023, 111, 801–830. [Google Scholar]
- Al-Musawi, W.A.; Al-Ibadi, M.A.A.; Wali, W.A. Artificial intelligence techniques for encrypt images based onthe chaotic system implemented on field-programmable gate. Iaes Int. J. Artif. Intell. 2023, 12, 347–356. [Google Scholar]
- Lin, H.; Wang, C.; Yu, F.; Xu, C.; Hong, Q.; Yao, W.; Sun, Y. An Extremely Simple Multiwing Chaotic System: Dynamics Analysis, Encryption Application, and Hardware Implementation. IEEE Trans. Ind. Electron. 2021, 68, 12708–12719. [Google Scholar] [CrossRef]
- Wu, G.C.; Deng, Z.G.; Baleanu, D.; Zeng, D.Q. New variable-order fractional chaotic systems for fast image encryption. Chaos 2019, 29, 083103. [Google Scholar]
- Chen, L.; Yin, H.; Huang, T.; Yuan, L.; Zheng, S.; Yin, L. Chaos in fractional-order discrete neural networks with application to image encryption. Neural Netw. 2020, 125, 174–184. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, C.; Sun, J.; Yu, F. A Chaotic Image Encryption Method Based on the Artificial Fish Swarms Algorithm and the DNA Coding. Mathematics 2020, 11, 767. [Google Scholar] [CrossRef]
- Gokyildirim, A.; Kocamaz, U.E.; Uyaroglu, Y.; Calgan, H. A novel five-term 3D chaotic system with cubic nonlinearity and its microcontroller-based secure communication implementation. Aeu-Int. J. Electron. Commun. 2023, 160, 154497. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, Z. Grid-scroll memristive chaotic system with application to image encryption. Chaos, Solitons Fractals 2023, 170, 113341. [Google Scholar] [CrossRef]
- Platas-Garza, M.A.; Zambrano-Serrano, E.; Rodríguez-Cruz, J.R.; Posadas-Castillo, C. Implementation of an encrypted-compressed image wireless transmission scheme based on chaotic fractional-order systems. Chin. J. Phys. 2021, 71, 22–37. [Google Scholar] [CrossRef]
- Hu, C.; Tian, Z.; Wang, Q.; Zhang, X.; Liang, B.; Jian, C.; Wu, X. A memristor-based VB2 chaotic system: Dynamical analysis, circuit implementation, and image encryption. Optik 2022, 269, 169878. [Google Scholar] [CrossRef]
- Guillén-Fernández, O.; Tlelo-Cuautle, E.; Fraga, L.G.d.; Sandoval-Ibarra, Y.; Nuñez-Perez, J.C. An Image Encryption Scheme Synchronizing Optimized Chaotic Systems Implemented on Raspberry Pis. Mathematics 2022, 10, 1907. [Google Scholar] [CrossRef]
- MacDonald, C.L.; Bhattacharya, N.; Sprouse, B.P.; Silva, G.A. Efficient Computation of the Grünwald–Letnikov Fractional Diffusion Derivative Using Adaptive Time Step Memory. J. Of. Comput. Phys. 2015, 297, 221–236. [Google Scholar]
- Zhou, Y.; Wang, J.N. The Nonlinear Rayleigh-Stokes Problem with Riemann-Liouville Fractional Derivative. Math. Methods Appl. Sci. 2021, 44, 2431–2438. [Google Scholar]
- Almeida, R. A Caputo Fractional Derivative of a Function with Respect to Another Function. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 460–481. [Google Scholar]
- Petráš, I. Modeling and Numerical Analysis of Fractional-Order Bloch Equations. Comput. Math. Appl. 2011, 61, 341–356. [Google Scholar]
- Wang, Z.; Sun, Y.; Cang, S. A 3-D Spherical Chaotic Attractor. Acta Phys. Pol. Ser. B 2011, 42, 235–247. [Google Scholar]
- Danca, M.-F.; Chattopadhyay, J. Chaos Control of Hastings-Powell Model by Combining Chaotic Motions. Chaos 2016, 26, 043106. [Google Scholar]
- Lai, J.W.; Cheong, K.H. Parrondo’s Paradox from Classical to Quantum: A Review. Nonlinear Dyn. 2020, 100, 849–861. [Google Scholar]
- Li, Y.; Li, Z.; Ma, M.; Wang, M. Generation of Grid Multi-Wing Chaotic Attractors and its Application in Video Secure Communication System. Multimed. Tools Appl. 2020, 79, 29161–29177. [Google Scholar]
- Askar, S.; Karawia, A.; Al-Khedhairi, A.; Alammar, F. An Algorithm of Image Encryption Using Logistic and Two-Dimensional Chaotic Economic Maps. Entropy 2019, 21, 44. [Google Scholar]
- Shakiba, A. A Novel Randomized Bit-Level Two-Dimensional Hyperchaotic Image Encryption Algorithm. Multimed. Tools Appl. 2020, 79, 32575–32605. [Google Scholar]
- Cao, C.; Sun, K.; Liu, W. A Novel Bit-Level Image Encryption Algorithm Based on 2d-LICM Hyperchaotic Map. Signal Process. 2018, 143, 122–133. [Google Scholar]
- Zhang, G.; Liu, Q. A novel image encryption method based on total shuffling scheme. Opt. Commun. 2015, 284, 2775–2780. [Google Scholar]
- Gong, L.; Qiu, K.; Deng, C.; Zhou, N. An Image compression and encryption algorithm based on chaotic system and compressive sensing. Opt. Laser Technol. 2019, 115, 257–267. [Google Scholar]
- Kulsoon, A.; Xiao, D.; Abbas, S.A. An efficient and noise resistive selective image encryption scheme for gray images based on chaotic maps and DNA complementary rules. Multimed. Tools Appl. 2016, 75, 1–23. [Google Scholar]
- Yu, F.; Shen, H.; Zhang, Z.; Huang, Y.; Cai, S.; Du, S. A new multi-scroll Chua’s circuit with composite hyperbolic tangent-cubic nonlinearity: Complex dynamics, Hardware implementation and Image encryption application. Integration 2021, 81, 71–83. [Google Scholar]
- Mohamed, S.M.; Sayed, W.S.; Madian, A.H.; Radwan, A.G.; Said, L.A. An Encryption Application and FPGA Realization of a Fractional Memristive Chaotic System. Electronics 1219, 12, 1219. [Google Scholar] [CrossRef]
- Lai, Q.; Zhang, H.; Kuate, P.D.K.; Xu, G.; Zhao, X.W. Analysis and implementation of no-equilibrium chaotic system with application in image encryption. Appl. Intell. 2022, 52, 11448–11471. [Google Scholar]










| FPGA | Resources | Available | RGB Image | Grayscale Image | ||
|---|---|---|---|---|---|---|
| Used | Consumed (%) | Used | Consumed (%) | |||
| Artix-7 AC701 | LUTs (CLB) | 133,800 | 86,230 | 64 | 92,627 | 69 |
| Memory LUTs (Kb) | 2888 | 0 | 0 | 0 | 0 | |
| Registers | 267,600 | 2127 | 0.79 | 2127 | 0.79 | |
| I/O Pins | 500 | 195 | 39 | 195 | 39 | |
| Block RAMs (Kb) | 13,140 | 0 | 0 | 0 | 0 | |
| DSPs | 740 | 120 | 16 | 120 | 16 | |
| Cyclone V | LUTs (ALM) | 113,560 | 94,019 | 83 | 101,416 | 89 |
| Memory LUTs (Kb) | 1,717 | 0 | 0 | 0 | 0 | |
| Registers | 454,240 | 420 | 0.09 | 422 | 0.09 | |
| I/O Pins | 616 | 195 | 32 | 195 | 32 | |
| Block RAMs (Kb) | 12,200 | 0 | 0 | 0 | 0 | |
| DSPs | 342 | 96 | 28 | 96 | 28 | |
| This Work | Ref. [56] | Ref. [57] | Ref. [58] |
|---|---|---|---|
| Chaotic State | Images | Correlation | Jaccard Similarity | Jaccard Distance | |||
|---|---|---|---|---|---|---|---|
| RGB | Grayscale | RGB | Grayscale | RGB | Grayscale | ||
| x | Original and encrypted | 0.0511 | 0.0392 | 0.0062 | 0.0059 | 0.9938 | 0.9941 |
| Original and recovered | 1 | 1 | 1 | 1 | 0 | 0 | |
| y | Original and encrypted | 0.2178 | 0.0694 | 0.0069 | 0.0060 | 0.9931 | 0.9940 |
| Original and recovered | 1 | 1 | 1 | 1 | 0 | 0 | |
| z | Original and encrypted | 0.0762 | 0.0422 | 0.0063 | 0.0059 | 0.9937 | 0.9941 |
| Original and recovered | 1 | 1 | 1 | 1 | 0 | 0 | |
| Chaotic State | RGB | Grayscale |
|---|---|---|
| x | 7.9981 | 7.9965 |
| y | 7.9908 | 7.9961 |
| z | 7.9918 | 7.9916 |
| Metric | Variance of 0.01 | Variance of 0.001 | Variance of 0.0001 | |||
|---|---|---|---|---|---|---|
| RGB | Grayscale | RGB | Grayscale | RGB | Grayscale | |
| Correlation coefficient | 0.7451 | 0.6961 | 0.9071 | 0.8743 | 0.9682 | 0.9556 |
| SNR | 15 dB | 15 dB | 25 dB | 25 dB | 35 dB | 35 dB |
| Percentage recovery | 75% | 70% | 90% | 87% | 96% | 95% |
| Parameters | This Work | Ref. [62] | Ref. [63] | Ref. [64] | |
|---|---|---|---|---|---|
| Chaotic system | FOCSS | FOCSS | NMCS | FMCS | NECS |
| FPGA | Artix-7 | Artix-7 | Virtex-6 | Artix-7 | Cyclone IV |
| Image | RGB | Grayscale | RGB | RGB | RGB/Grayscale |
| Image size | 320 × 240 | 640 × 480 | 256 × 256 | 256 × 256 | 256 × 256 |
| LUTs | 86,230 | 92,627 | 15,978 | 23,929 | 32,983 |
| Registers | 2127 | 2127 | 21,057 | 4599 | 450 |
| I/O pins | 195 | 195 | 16 | N/A | 66 |
| DSPs | 120 | 120 | 20 | 144 | 84 |
| Language | VHDL | VHDL | VHDL | Verilog | VHDL |
| Numerical approximation | Grünwald– Letnikov | Grünwald– Letnikov | RK4 | Grünwald– Letnikov | RK4 |
| Order | Fractional | Fractional | Integer | Fractional | Integer |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adeyemi, V.-A.; Tlelo-Cuautle, E.; Sandoval-Ibarra, Y.; Nuñez-Perez, J.-C. FPGA Implementation of Parameter-Switching Scheme to Stabilize Chaos in Fractional Spherical Systems and Usage in Secure Image Transmission. Fractal Fract. 2023, 7, 440. https://doi.org/10.3390/fractalfract7060440
Adeyemi V-A, Tlelo-Cuautle E, Sandoval-Ibarra Y, Nuñez-Perez J-C. FPGA Implementation of Parameter-Switching Scheme to Stabilize Chaos in Fractional Spherical Systems and Usage in Secure Image Transmission. Fractal and Fractional. 2023; 7(6):440. https://doi.org/10.3390/fractalfract7060440
Chicago/Turabian StyleAdeyemi, Vincent-Ademola, Esteban Tlelo-Cuautle, Yuma Sandoval-Ibarra, and Jose-Cruz Nuñez-Perez. 2023. "FPGA Implementation of Parameter-Switching Scheme to Stabilize Chaos in Fractional Spherical Systems and Usage in Secure Image Transmission" Fractal and Fractional 7, no. 6: 440. https://doi.org/10.3390/fractalfract7060440
APA StyleAdeyemi, V.-A., Tlelo-Cuautle, E., Sandoval-Ibarra, Y., & Nuñez-Perez, J.-C. (2023). FPGA Implementation of Parameter-Switching Scheme to Stabilize Chaos in Fractional Spherical Systems and Usage in Secure Image Transmission. Fractal and Fractional, 7(6), 440. https://doi.org/10.3390/fractalfract7060440









