Coupled System of Fractional Impulsive Problem Involving Power-Law Kernel with Piecewise Order

Abstract

In this research paper, we study a coupled system of piecewise-order differential equations (DEs) with variable kernel and impulsive conditions. DEs with variable kernel have high flexibility due to the freedom of changing the kernel. We study existence and stability theory and derive sufficient conditions for main results of the proposed problem. We apply Scheafer’s fixed point theorem and Banach fixed point theorem for the result of at least one and unique solution, respectively. In addition, stability results based on the Ulam–Hyers concept are derived. Being a coupled system of piecewise fractional-order DEs with variable kernel and impulsive effects, the obtained results have multi-dimension applications. To demonstrate the applications, we apply the derived results to a numerical problem.

1. Introduction

Fractional calculus has become an active area of research. In the last two to three decades, fractional calculus has given much importance by researchers due to the non-local and global nature of the differential operators it involves. These operators have the ability to describe the dynamical behavior of a natural phenomena with a high degree of accuracy which have successfully been applied in numerous directions as in [1,2,3,4,5]. For its basic history and some applications, we recommend the books [6,7]. In view of the aforementioned importance fractional differential equations (FDEs) and, more specifically, the coupled systems of FDEs, these are considered as key tools of applied mathematics which are used to develop differential models for high complex systems. For instance, we refer to quantum evolution of complex systems [8], Duffing system [9], anomalous diffusion [10], fractional Lorenz system [11], secure communication and control processing [12]. Similarly, their applications can be observed in applied electrical engineering, mathematical biology, chemical theory, static dynamics, etc.

Here, it should be kept in mind that many real-world phenomena do not have a unique behavior and, rather, exhibit a variety of behaviors, including economic fluctuations, comparable molecular dynamics behaviors, earthquakes, etc. To achieve better results in the aforementioned process, researchers have increasingly used various operators for the mathematical modeling of such processes. In this regard, researchers have introduced various fractional differential operators to describe the crossover behaviours of different phenomenons more comprehensively. For example, author [13] has investigated some classes of impulsive fractional-order problems and discussed the exact solutions, and short-memory cases. In the same way, short memory fractional-order DEs were introduced for the first time [14]: variable-order DEs are the natural extension of classical DEs and were also given much attention in subsequent years (see [15,16]). Here, one thing should kept in mind that fractional derivatives include memory and genetic effects, which play a crucial part in investigations of many real world dynamical problems (see [17]). Almost all the definitions of fractional derivative have different kernels which are either singular or non-singular. For instance, the Caputo derivative and Riemann–Liouville derivative have a singular kernel, the Caputo–Fabrizio derivative has a non-singular exponential decay kernel [18], and the Atangana–Baleanu–Caputo derivative has a non-singular Mittag–Leffler kernel [19]. In all these definitions, the kernels are constant. On the other hand, the usual fractional calculus has long memory effects which result in difficulties with long-term calculation. In addition, the long memory with power law is described using the mathematical tools of usual fractional calculus which contains the fractional-order derivatives and integrals.

Motivated from the above discussion, researchers have introduced the concept of piecewise fractional-order derivatives to address the problem with short memory. Therefore, researchers are using two stages to deal the memory process. One stage is devoted to permanent retention of short memory. The second stage is related to a simple model of fractional derivative. Here, it is interesting that short memory can be applied to improve performance and efficiency to explain physical phenomena more brilliantly (see [20]). Therefore, the concept of piecewise derivative with fractional-order has been used recently in many papers; we refer to [21,22,23]. Recently, a new concept of fractional derivative with piecewise-order and variable kernel has been introduced. This concept has high flexibility due to the freedom of changing the kernel [24]. These definitions are suitable in physical systems whose properties are based on the dynamics with memory effects which show change in their behavior across the time interval. The mentioned concept has been extended to boundary value problems in [25].

On other hand, differential equations with impulsive behavior have acquired applications in many applied fields of sciences; for example, physical problems that keep instantaneous changes and discontinuous jumps are modeled via impulsive DEs. The existence theory of DEs with impulsive effects has been enticing to many researchers. For instance, authors [26] investigated the three-point boundary value problem (BVP) with impulsive conditions using a fixed-point approach. In addition, a coupled system of BVPs with impulsive conditions has been studied via fixed theory in [27]. The impulsive problem of fractional-order evolution equations has been investigated using the tools of nonlinear functional analysis (see [28]). In the same way, multi-point BVP of FDEs with impulsive conditions has been studied for the existence theory in [29]. All the mentioned studies indicate that researchers have studied various impulsive problems by using fixed-point theory and tools of functional analysis under the fixed fractional-order derivative.

We first convert the considered system to an equivalent variable-order integral system. We use fixed-point theorems due to Banach and Scheafer’s to develop sufficient conditions for the existence and uniqueness of solution to the considered problem. Also, stability is an important consequence of optimization theory and numerical functional analysis, therefore we also establish some results by using Ulam-Hyers (UH) concept. The mentioned stability was introduced by Ulam in 1940, and explained further by Hyers in 1941 (see [30]). Later on the aforesaid stability was increasingly studied by other researchers for different problems (see [31,32,33,34]).

2. Presentation of our Problem

Here, we remark that coupled systems have been considered in many investigations of real world problems. For instance, authors [35] studied network-based leader-following consensus of nonlinear multi-agent coupled systems by using distributed impulsive control. In the same way, researchers [36] used coupled systems under impulsive conditions to investigate a process of saturated control problems. Moreover, a coupled system with impulsive conditions addressing networks problems has been studied for stability theory in [37]. Therefore, motivated from the aforementioned discussion, in this paper, we investigate a coupled system of Caputo fractional piecewise-order impulsive problem with a variable kernel, as given in (1). Here, the order is piecewise and the kernel has an variable power. The considered problem is described as the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {}^c{D}_{\left[x\right]}^{\varrho \left(x\right)}w\left(x\right)=f(x,u\left(x\right),w\left(x\right)),x\in \mathbb{S}=[0,T],x\ne x_i,\hfill \\ & w\left(0\right)=w_0+\rho \left(w\right),\hfill \\ & \Delta w\left(x\right){\mid }_{x=x_i}=w\left(x_i^{+}\right)-w\left(x_i^{-}\right)=w\left(x_i^{+}\right)-w\left(x_i\right)\hfill \\ & ={\mathcal{I}}_{i}w\left(x_i^{-}\right),i=1,...m,\hfill \\ & {}^c{D}_{\left[x\right]}^{\varrho \left(x\right)}u\left(x\right)=\mathcal{F}(x,w\left(x\right),u\left(x\right)),x\in \mathbb{S}=[0,T],x\ne x_i,\hfill \\ & i=1,\dots ,\aleph ,0<\varrho \left(x\right)\le 1,\hfill \\ & u\left(0\right)=u_0+\varphi \left(u\right),\hfill \\ & \Delta u\left(x\right){\mid }_{x=x_i}=u\left(x_i^{+}\right)-u\left(x_i^{-}\right)=u\left(x_i^{+}\right)-u\left(x_i\right)\hfill \\ & ={\overline{\mathcal{I}}}_{i}u\left(x_i^{-}\right),i=1,...m.\hfill \end{array}\right.\end{array}$$

(1)

The variable-order $\varrho \left(x\right)$ is defined as a finite sequence of real numbers in the interval $(0,1]$ as

$$\varrho \left(x\right)=\left\{\begin{array}{c}{\varrho }_0,0<x\le x_1\\ {\varrho }_1,x_1<x\le x_2\\ ⋮\\ {\varrho }_m,x_m<x\le T\end{array}\right.$$

(2)

The Caputo derivative, ${}^c{D}_{\left[x\right]}^{{\varrho }_i,g_i}u\left(x\right)$ of order ${\varrho }_i$ of function $u\left(x\right)$ with respect to a finite sequence of nonnegative increasing functions $g_i$; $(i=0,1,\dots ,m)$, is defined by

$${}^c{D}_{\left[x\right]}^{\varrho \left(x\right)}u\left(x\right)=\left\{\begin{array}{c}{}^c{D}_{\left[x\right]}^{{\varrho }_0,g_0}u\left(x\right),0<x\le x_1\\ {}^c{D}_{\left[x\right]}^{{\varrho }_1,g_1}u\left(x\right),x_1<x\le x_2\\ ⋮\\ {}^c{D}_{\left[x\right]}^{{\varrho }_m,g_m}u\left(x\right),x_m<x\le T\end{array}\right.$$

(3)

$f,\mathcal{F}:\mathbb{S}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ are given piecewise continuous functions, ${\mathcal{I}}_{\ell },{\overline{\mathcal{I}}}_{\ell }:\mathbb{R}\to \mathbb{R},$ are impulsive continuous functions, $u_0\in \mathbb{R},$$x_{\ell }$ satisfy $0=x_0<x_1<...<x_m<x_{m+1}=T,$$\Delta w{\mid }_{x=x_{\ell }}=w\left(x_{\ell }^{+}\right)-w\left(x_{\ell }^{-}\right)=w\left(x_{\ell }^{+}\right)-w\left(x_{\ell }\right)$, $w\left(x_{\ell }^{+}\right)={lim}_{\nu \to 0^{+}}w(x_{\ell }+\nu ),w\left(x^{-}\right)={lim}_{\nu \to 0^{-}}w(x_{\ell }+\nu )$ and $\Delta u{\mid }_{x=x_{\ell }}=u\left(x_{\ell }^{+}\right)-u\left(x_{\ell }^{-}\right)=u\left(x_{\ell }^{+}\right)-u\left(x_{\ell }\right)$, $u\left(x_{\ell }^{+}\right)={lim}_{\nu \to 0^{+}}u(x_{\ell }+\nu ),u\left(x^{-}\right)={lim}_{\nu \to 0^{-}}u(x_{\ell }+\nu ).$ Also, $\left[x\right]=x_{\ell }$ if $x\in (x_{\ell },x_{\ell +1}],$ $\ell =0,1,...$ and $x_0=0.$

The rest of the paper is organized as follows: A detailed introduction is given in Section 1. The presentation of the problem is given in Section 2. Section 3 is devoted to the existence theory. Section 4 is related to stability results. Section 5 is devoted to application and its discussion. Section 6 consists of the conclusion. Preliminaries results are given in Appendix A. Appendix B is devoted to the proof of Lemma 1.

3. Existence Theory

This part is devoted to derive sufficient results for the existence theory.

We define the Banach spaces by

$$\begin{array}{c}\hfill {\mathcal{E}}_1=\{w:\mathbb{S}\to \mathbb{R}:w\in C({\mathbb{S}}_{\mathbb{k}},\mathbb{R})\mathrm{and}w\left(x_{\mathbb{k}}^{+}\right),w\left(x_{\mathbb{k}}^{-}\right),\\ \hfill \mathrm{there}\mathrm{exists}\Delta w\left(x_{\mathbb{k}}\right)=w\left(x_{\mathbb{k}}^{+}\right)-w\left(x_{\mathbb{k}}^{-}\right)\mathrm{for}\mathbb{k}=1,2,\dots ,\aleph \},\end{array}$$

and

$$\begin{array}{c}\hfill {\mathcal{E}}_2=\{u:\mathbb{S}\to \mathbb{R}:u\in C({\mathbb{S}}_{\mathbb{k}},\mathbb{R}),\mathrm{and}u\left(x_{\mathbb{k}}^{+}\right),u\left(x_{\mathbb{k}}^{-}\right),\\ \hfill \mathrm{there}\mathrm{exists}\Delta u\left(x_{\mathbb{k}}\right)=u\left(x_{\mathbb{k}}^{+}\right)-u\left(x_{\mathbb{k}}^{-}\right)\mathrm{for}\mathbb{k}=1,2,\dots ,\aleph \}\end{array}$$

with respect to the norms $∥w∥={max}_{x\in \mathbb{S}}\left|w\left(x\right)\right|$ and $∥u∥={max}_{x\in \mathbb{S}}\left|u\left(x\right)\right|.$ Then, the product space, denoted by $\mathcal{E}$, i.e, ${\mathcal{E}}_1\times {\mathcal{E}}_2=\mathcal{E}$, is also a Banach space with the norm given by $\parallel (w,u)\parallel =\parallel w\parallel +\parallel u\parallel .$ We set ${\mathbb{S}}^{\prime }:=\mathbb{S}\backslash \{x_1,...,x_{\aleph }\}.$

Lemma 1. 

Let $\varrho \in (0,1]$ and let $\phi :\mathbb{S}\to \mathbb{R}$ be continuous. A function $w\in \mathcal{E}$ is solution of the fractional integral equation

$$w\left(x\right)=\left\{\begin{array}{cc}& w_0+\rho \left(w\right)+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}\phi \left(z\right)dz,ifx\in [0,x_1],\hfill \\ & w_0+\rho \left(w\right)+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^{x_1}{h}_0^{\prime }\left(z\right){(h_0\left(x_1\right)-h_0\left(z\right))}^{{\varrho }_0-1}\phi \left(z\right)dz\hfill \\ & +\frac{1}{\Gamma \left({\varrho }_1\right)}{\int }_{x_1}^x{h}_1^{\prime }\left(z\right){(h_1\left(x\right)-h_1\left(z\right))}^{{\varrho }_1-1}\phi \left(z\right)dz+{\mathcal{I}}_{1}w\left(x_1^{-}\right),ifx\in (x_1,x_2],\hfill \\ & ⋮\hfill \\ & w_0+\rho \left(w\right)+\sum _{i=1}^{\mathbb{k}}{\mathcal{I}}_{i}w\left(x_i^{-}\right)+\sum _{i=1}^{\mathbb{k}}\frac{1}{\Gamma \left({\varrho }_{i-1}\right)}{\int }_{x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}\phi \left(z\right)dz\hfill \\ & +\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}\phi \left(z\right)dz,ifx\in (x_{\mathbb{k}},x_{\mathbb{k}+1}],\mathbb{k}=1,\dots ,\aleph .\hfill \end{array}\right.$$

(4)

if and only if it is a solution of the impulsive problem:

$$\begin{array}{ccc}\hfill {}^c{D}_{\left[x\right]}^{\varrho \left(x\right)}w\left(x\right)& =& \phi \left(x\right),x\in \mathbb{S},\hfill \\ \hfill t& \ne & x_{\mathbb{k}},\mathbb{k}=1,\dots ,\aleph ,\hfill \end{array}$$

(5)

$$\begin{array}{c}\hfill \Delta w\left(x_{\mathbb{k}}\right)=w\left(x_{\mathbb{k}}^{+}\right)-w\left(x_{\mathbb{k}}^{-}\right)=w\left(x_{\mathbb{k}}^{+}\right)-w\left(x_{\mathbb{k}}\right)={\mathcal{I}}_{\mathbb{k}}w\left(x_{\mathbb{k}}^{-}\right),\mathbb{k}=1,\dots ,\aleph ,\end{array}$$

(6)

$$w\left(0\right)=w_0+\rho \left(w\right),$$

(7)

where $\left[x\right]=x_{\mathbb{k}}$ if $x\in (x_{\mathbb{k}},x_{\mathbb{k}+1}],$$\mathbb{k}=0,1,...$ and $x_0=0.$

Proof. 

The proof is given in Appendix B. □

Corollary 1. 

As a consequence of Lemma 1, the solution of the coupled system (1) is given by

$$\left\{\begin{array}{cc}& w\left(x\right)=\left\{\begin{array}{cc}& w_0+\rho \left(w\right)+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}f(z,u\left(z\right),w\left(z\right))dz,ifx\in [0,x_1],\hfill \\ & w_0+\rho \left(w\right)+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^{x_1}{h}_0^{\prime }\left(z\right){(h_0\left(x_1\right)-h_0\left(z\right))}^{{\varrho }_0-1}f(z,u\left(z\right),w\left(z\right))dz\hfill \\ & +\frac{1}{\Gamma \left({\varrho }_1\right)}{\int }_{x_1}^x{h}_1^{\prime }\left(z\right){(h_1\left(x\right)-h_1\left(z\right))}^{{\varrho }_1-1}f(z,u\left(z\right),w\left(z\right))dz+{\mathcal{I}}_{1}w\left(x_1^{-}\right)ifx\in (x_1,x_2],\hfill \\ & ⋮\hfill \\ & w_0+\rho \left(w\right)+\sum _{i=1}^{\mathbb{k}}{\mathcal{I}}_{i}w\left(x_i^{-}\right)+\sum _{i=1}^{\mathbb{k}}\frac{1}{\Gamma \left({\varrho }_{i-1}\right)}{\int }_{x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}\hfill \\ & \times f(z,u\left(z\right),w\left(z\right))dz+\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}f(z,u\left(z\right),w\left(z\right))dz,\hfill \\ & ifx\in (x_{\mathbb{k}},x_{\mathbb{k}+1}],\mathbb{k}=1,\dots ,\aleph .\hfill \end{array}\right.\hfill \\ & u\left(x\right)=\left\{\begin{array}{cc}& u_0+\varphi \left(u\right)+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}\mathcal{F}(z,u\left(z\right),w\left(z\right))dz,ifx\in [0,x_1],\hfill \\ & u_0+\varphi \left(u\right)+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^{x_1}{h}_0^{\prime }\left(z\right){(h_0\left(x_1\right)-h_0\left(z\right))}^{{\varrho }_0-1}\mathcal{F}(z,u\left(z\right),w\left(z\right))dz\hfill \\ & +\frac{1}{\Gamma \left({\varrho }_1\right)}{\int }_{x_1}^x{h}_1^{\prime }\left(z\right){(h_1\left(x\right)-h_1\left(z\right))}^{{\varrho }_1-1}\mathcal{F}(z,u\left(z\right),w\left(z\right))dz+{\mathcal{I}}_{1}u\left(x_1^{-}\right)ifx\in (x_1,x_2],\hfill \\ & ⋮\hfill \\ & u_0+\varphi \left(u\right)+\sum _{i=1}^{\mathbb{k}}{\mathcal{I}}_{i}u\left(x_i^{-}\right)+\sum _{i=1}^{\mathbb{k}}\frac{1}{\Gamma \left({\varrho }_{i-1}\right)}{\int }_{x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}\hfill \\ & \times \mathcal{F}(z,u\left(z\right),w\left(z\right))dz+\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}\mathcal{F}(z,u\left(z\right),w\left(z\right))dz,\hfill \\ & ifx\in (x_{\mathbb{k}},x_{\mathbb{k}+1}],\mathbb{k}=1,\dots ,\aleph .\hfill \end{array}\right.\hfill \end{array}\right.$$

(8)

Now to go ahead for the main results, we define the following operators

$$\mathcal{N}=\left({\mathcal{N}}_1,{\mathcal{N}}_2\right):{\mathcal{E}}_1\times {\mathcal{E}}_2\to {\mathcal{E}}_1\times {\mathcal{E}}_2$$

by

$$\mathcal{N}(w,u)=\left({\mathcal{N}}_{1}w,{\mathcal{N}}_{2}u\right).$$

Which may be expressed as

$$\left({\mathcal{N}}_{1}w\right)\left(x\right)=\left\{\begin{array}{cc}& w_0+\rho \left(w\right)+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}f(z,u\left(z\right),w\left(z\right))dz,ifx\in [0,x_1],\hfill \\ & w_0+\rho \left(w\right)+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^{x_1}{h}_0^{\prime }\left(z\right){(h_0\left(x_1\right)-h_0\left(z\right))}^{{\varrho }_0-1}f(z,u\left(z\right),w\left(z\right))dz\hfill \\ & +\frac{1}{\Gamma \left({\varrho }_1\right)}{\int }_{x_1}^x{h}_1^{\prime }\left(z\right){(h_1\left(x\right)-h_1\left(z\right))}^{{\varrho }_1-1}f(z,u\left(z\right),w\left(z\right))dz+{\mathcal{I}}_{1}w\left(x_1^{-}\right)ifx\in (x_1,x_2],\hfill \\ & ⋮\hfill \\ & w_0+\rho \left(w\right)+\sum _{i=1}^{\mathbb{k}}{\mathcal{I}}_{i}w\left(x_i^{-}\right)+\sum _{i=1}^{\mathbb{k}}\frac{1}{\Gamma \left({\varrho }_{i-1}\right)}{\int }_{x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}\hfill \\ & \times f(z,u\left(z\right),w\left(z\right))dz+\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}f(z,u\left(z\right),w\left(z\right))dz,\hfill \\ & ifx\in (x_{\mathbb{k}},x_{\mathbb{k}+1}],\mathbb{k}=1,\dots ,\aleph ,\hfill \end{array}\right.$$

(9)

and

$$\left({\mathcal{N}}_{2}u\right)\left(x\right)=\left\{\begin{array}{cc}& u_0+\varphi \left(u\right)+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}\mathcal{F}(z,u\left(z\right),w\left(z\right))dz,ifx\in [0,x_1],\hfill \\ & u_0+\varphi \left(u\right)+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^{x_1}{h}_0^{\prime }\left(z\right){(h_0\left(x_1\right)-h_0\left(z\right))}^{{\varrho }_0-1}\mathcal{F}(z,u\left(z\right),w\left(z\right))dz\hfill \\ & +\frac{1}{\Gamma \left({\varrho }_1\right)}{\int }_{x_1}^x{h}_1^{\prime }\left(z\right){(h_1\left(x\right)-h_1\left(z\right))}^{{\varrho }_1-1}\mathcal{F}(z,u\left(z\right),w\left(z\right))dz+{\mathcal{I}}_{1}u\left(x_1^{-}\right)ifx\in (x_1,x_2],\hfill \\ & ⋮\hfill \\ & u_0+\varphi \left(u\right)+\sum _{i=1}^{\mathbb{k}}{\mathcal{I}}_{i}u\left(x_i^{-}\right)+\sum _{i=1}^{\mathbb{k}}\frac{1}{\Gamma \left({\varrho }_{i-1}\right)}{\int }_{x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}\hfill \\ & \times \mathcal{F}(z,u\left(z\right),w\left(z\right))dz+\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}\mathcal{F}(z,u\left(z\right),w\left(z\right))dz,\hfill \\ & ifx\in (x_{\mathbb{k}},x_{\mathbb{k}+1}],\mathbb{k}=1,\dots ,\aleph .\hfill \end{array}\right.$$

(10)

Prior to proving the main results, we give the following accompanying hypotheses:

Hypothesis 1. 

For $f,\mathcal{F}:\mathbb{S}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$, let there exist constants $k_f,k_{\mathcal{F}}>0,$ so that for any $x\in \mathbb{S}$ and $(u,w),(u^{*},w^{*})\in {\mathcal{E}}_1\times {\mathcal{E}}_2,$ we have

$$\left|f(x,u,w)-f(x,u^{*},w^{*})\right|\le k_f(\left|u-u^{*}\right|+\left|w-w^{*}\right|),$$

and

$$\left|\mathcal{F}(x,u,w)-\mathcal{F}(x,u^{*},w^{*})\right|\le k_{\mathcal{F}}(\left|u-u^{*}\right|+\left|w-w^{*}\right|).$$

Hypothesis 2. 

For ${\mathcal{I}}_{\mathbb{k}},{\overline{\mathcal{I}}}_{\mathbb{k}}:\mathbb{R}\to \mathbb{R},$ and any $(w,u),(w^{*},u^{*})\in {\mathcal{E}}_1\times {\mathcal{E}}_2,$, let there exist constants $k_{\mathcal{I}},k_{\overline{\mathcal{I}}}>0,$ so that

$$\left|{\mathcal{I}}_{\mathbb{k}}\left(w\right)-{\mathcal{I}}_{\mathbb{k}}\left(w^{*}\right)\right|\le k_{\mathcal{I}}\left|w-w^{*}\right|$$

and

$$\left|{\overline{\mathcal{I}}}_{\mathbb{k}}\left(u\right)-{\overline{\mathcal{I}}}_{\mathbb{k}}\left(u^{*}\right)\right|\le k_{\overline{\mathcal{I}}}\left|u-u^{*}\right|,\mathbb{k}=1,...,\aleph .$$

Hypothesis 3. 

There exist bounded functions ${\mathbb{B}}_w,{\mathbb{C}}_w,{\mathbb{D}}_w,{\mathbb{B}}_u,{\mathbb{C}}_u,{\mathbb{D}}_u\in C(\mathbb{S},\mathbb{R}),$ so that

$$\left|f(x,u,w)\right|\le {\mathbb{B}}_w\left(x\right)+{\mathbb{C}}_w\left(x\right)\left|u\right|+{\mathbb{D}}_w\left(x\right)\left|w\right|, \mathit{for}\mathit{each}(x,u,w)\in \mathbb{S}\times \mathbb{R}\times \mathbb{R}$$

and

$$\left|\mathcal{F}(x,u,w)\right|\le {\mathbb{B}}_u\left(x\right)+{\mathbb{C}}_u\left(x\right)\left|u\right|+{\mathbb{D}}_u\left(x\right)\left|w\right|, \mathit{for}\mathit{each}(x,u,w)\in \mathbb{S}\times \mathbb{R}\times \mathbb{R}.$$

Hypothesis 4. 

There exist ${\eta }_1,{\eta }_2$ and ${\eta }_3,{\eta }_4>0,$ so that

$$\left|{\mathcal{I}}_{\mathbb{k}}\left(w\right)\right|\le {\eta }_1+{\eta }_2\left|w\right|,$$

$$\left|{\overline{\mathcal{I}}}_{\mathbb{k}}\left(u\right)\right|\le {\eta }_3+{\eta }_4\left|u\right|;\mathbb{k}=1,...,\aleph ,u\in \mathbb{R}.$$

Hypothesis 5. 

There exist constants $k_{\rho },k_{\varphi }>0,$ so that

$$\left|\rho \left(w\left(x\right)\right)\right|\le k_{\rho }$$

and

$$\left|\varphi \left(u\left(x\right)\right)\right|\le k_{\varphi }.$$

Hypothesis 6. 

There exist constants $k_{\rho }^{*},k_{\varphi }^{*}>0,$ so that

$$|\rho \left(w\left(x\right)\right)-\rho \left(w^{*}\left(x\right)\right)|\le k_{\rho }^{*}\left|w-w^{*}\right|$$

and

$$|\varphi \left(u\left(x\right)\right)-\varphi \left(u^{*}\left(x\right)\right)|\le k_{\varphi }^{*}\left|u-u^{*}\right|.$$

Theorem 1. 

Let $f:\mathbb{S}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ be continuous and $\left(H_3\right)-\left(H_4\right)$ hold. If

$$\zeta \ge max\left(\frac{{\Delta }_0+k+\mathbb{B}\mathbb{P}}{1-\xi \mathbb{P}},\frac{{\Delta }_0+k+\aleph \eta +\mathbb{Q}\mathbb{B}}{1-\left(\aleph {\eta }^{*}+\xi \mathbb{Q}\right)}\right),$$

(11)

then the impulsive problem (1) has a solution in $\mathcal{E}.$

Proof. 

We apply Theorem A1 to show that $\mathcal{N}$ as defined in 9 has a fixed point. We set $\mathcal{B}=\{(w,u)\in {\mathcal{E}}_1\times {\mathcal{E}}_2:∥(w,u)∥\le \zeta \}.$ This operator, $\mathcal{N}$, is a closed, bounded and convex subset of $\mathcal{B}$, and it is verified in the following steps.

Step1: In every step, we discuss two cases.

$\mathbf{Case}\mathbf{I}$

According to (9), for $(w,u)\in {\mathcal{B}}_{\zeta }$ and $x\in [0,x_1]$, we have

$$\begin{array}{ccc}\hfill \left|{\mathcal{N}}_{1}w\left(x\right)\right|& \le & \left|w_0\right|+\left|\rho \left(w\right(x\left)\right)\right|+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}\left|f(z,u(z),w(z\left)\right)\right|dz\hfill \\ & \le & \left|w_0\right|+k_{\rho }+\frac{\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}dz\hfill \\ & \le & \left|w_0\right|+k_{\rho }+\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)\frac{{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\hfill \\ & \le & \left|w_0\right|+k_{\rho }+\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)\frac{{(h_0\left(T\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\hfill \end{array}$$

(12)

Similarly, using (10), for $(w,u)\in {\mathcal{B}}_{\zeta }$ and $x\in [0,x_1]$, we have

$$\begin{array}{ccc}\hfill \left|{\mathcal{N}}_{2}u\left(x\right)\right|& \le & \left|u_0\right|+k_{\varphi }+\left({\mathbb{B}}_u+{\mathbb{C}}_u∥u∥+{\mathbb{D}}_u∥w∥\right)\frac{{(h_0\left(T\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\hfill \end{array}$$

(13)

From (12) and (13), we have

$$\begin{array}{ccc}\hfill ∥{\mathcal{N}}_1(w,u)∥+∥{\mathcal{N}}_2(w,u)∥& \le & \left|w_0\right|+\left|u_0\right|+k_{\rho }+k_{\varphi }+({\mathbb{B}}_u+{\mathbb{B}}_w+({\mathbb{C}}_u+{\mathbb{C}}_w)∥u∥\hfill \\ & +& ({\mathbb{D}}_u+{\mathbb{D}}_w)∥w∥)\frac{{(h_0\left(T\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}.\hfill \end{array}$$

(14)

Or

$$\begin{array}{ccc}\hfill {∥\mathcal{N}(w,u)∥}_{\mathcal{E}}& \le & {\Delta }_0+k+\mathbb{B}\frac{{(h_0\left(T\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}+\xi ∥(w,u)∥\frac{{(h_0\left(T\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\hfill \\ & \le & \zeta ,\hfill \end{array}$$

(15)

where

$$\begin{array}{c}\hfill \zeta \ge \frac{{\Delta }_0+k+\mathbb{B}\mathbb{P}}{1-\xi \mathbb{P}}.\end{array}$$

Thus, $\mathcal{N}(w,u)$ is bounded, and hence, $\mathcal{N}(w,u)\in \mathcal{B}$, which implies that $\mathcal{N}\left(\mathcal{B}\right)\subseteq \mathcal{B}.$

$\mathbf{Case}\mathbf{II}$

In addition, for interval $(x_{\mathbb{k}},x_{\mathbb{k}+1}],$$\mathbb{k}=1,\dots ,\aleph ,$ we have

$$\begin{array}{cc}\hfill & \left|\mathcal{N}w\left(x\right)\right|\le \left|w_0\right|+\left|\rho \left(w\right(x\left)\right)\right|+\sum _{0<x_{\mathbb{k}}<x}\left|{\mathcal{I}}_{\mathbb{k}}w\left(x_{\mathbb{k}}^{-}\right)\right|\hfill \\ & +\sum _{i=1}^{\mathbb{k}}\frac{1}{\Gamma \left({\varrho }_{i-1}\right)}{\int }_{x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}\left|f(z,u(z),w(z\left)\right)\right|dz\hfill \\ & +\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}\left|f(z,u(z),w(z\left)\right)\right|dz\hfill \end{array}$$

(16)

Using assumption (H${}_3$), (H${}_5$) and result (16), we have

$$\begin{array}{cc}\hfill & \left|{\mathcal{N}}_{1}w\left(x\right)\right|\le \left|w_0\right|+k_{\rho }+\sum _{0<x_{\mathbb{k}}<x}\left({\eta }_1+{\eta }_2\left|w\left(x_{\mathbb{k}}^{-}\right)\right|\right)\hfill \\ & +\sum _{i=1}^{\mathbb{k}}\frac{\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)}{\Gamma \left({\varrho }_{i-1}\right)}{\int }_{x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}dz\hfill \\ & +\frac{\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}dz\hfill \\ & \le \left|w_0\right|+k_{\rho }+\aleph \left({\eta }_1+{\eta }_2∥w∥\right)+\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)\hfill \\ & \times \left(\sum _{i=1}^{\mathbb{k}}\frac{{(h_{i-1}\left(x_i\right)-h_{i-1}\left(x_{i-1}\right))}^{{\varrho }_{i-1}}}{\Gamma ({\varrho }_{i-1}+1)}+\frac{{(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(x_{\mathbb{k}}\right))}^{{\varrho }_{\mathbb{k}}}}{\Gamma ({\varrho }_{\mathbb{k}}+1)}\right).\hfill \end{array}$$

(17)

Similarly, we obtain the following result for the second operator

$$\begin{array}{cc}\hfill & \left|{\mathcal{N}}_{2}u\left(x\right)\right|\le \left|u_0\right|+k_{\varphi }+\aleph \left({\eta }_1+{\eta }_2∥w∥\right)+\aleph \left({\eta }_3+{\eta }_4∥u∥\right)+\left({\mathbb{B}}_u+{\mathbb{C}}_u∥u∥+{\mathbb{D}}_u∥w∥\right)\hfill \\ & \times \left(\sum _{i=1}^{\mathbb{k}}\frac{{(h_{i-1}\left(x_i\right)-h_{i-1}\left(x_{i-1}\right))}^{{\varrho }_{i-1}}}{\Gamma ({\varrho }_{i-1}+1)}+\frac{{(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(x_{\mathbb{k}}\right))}^{{\varrho }_{\mathbb{k}}}}{\Gamma ({\varrho }_{\mathbb{k}}+1)}\right).\hfill \end{array}$$

(18)

Using the notations as used in Case I, we have, from (17) and (18),

$$\begin{array}{cc}\hfill & ∥{\mathcal{N}}_1(w,u)∥+∥{\mathcal{N}}_2(w,u)∥\le {\Delta }_0+k+\aleph \eta \hfill \\ & +\mathbb{B}\left(\sum _{i=1}^{\mathbb{k}}\frac{{(h_{i-1}\left(x_i\right)-h_{i-1}\left(x_{i-1}\right))}^{{\varrho }_{i-1}}}{\Gamma ({\varrho }_{i-1}+1)}+\frac{{(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(x_{\mathbb{k}}\right))}^{{\varrho }_{\mathbb{k}}}}{\Gamma ({\varrho }_{\mathbb{k}}+1)}\right)\hfill \\ & +\aleph {\eta }^{*}{∥(w,u)∥}_{\mathcal{E}}+\left(\sum _{i=1}^{\mathbb{k}}\frac{{(h_{i-1}\left(x_i\right)-h_{i-1}\left(x_{i-1}\right))}^{{\varrho }_{i-1}}}{\Gamma ({\varrho }_{i-1}+1)}+\frac{{(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(x_{\mathbb{k}}\right))}^{{\varrho }_{\mathbb{k}}}}{\Gamma ({\varrho }_{\mathbb{k}}+1)}\right)\xi ∥(w,u)∥\hfill \\ & \le {\Delta }_0+k+\aleph \eta +\mathbb{B}\left(\sum _{i=1}^{\mathbb{k}}\frac{{(h_{i-1}\left(x_i\right)-h_{i-1}\left(x_{i-1}\right))}^{{\varrho }_{i-1}}}{\Gamma ({\varrho }_{i-1}+1)}+\frac{{(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(x_{\mathbb{k}}\right))}^{{\varrho }_{\mathbb{k}}}}{\Gamma ({\varrho }_{\mathbb{k}}+1)}\right)\hfill \\ & +\left(\aleph {\eta }^{*}+\xi \left(\sum _{i=1}^{\mathbb{k}}\frac{{(h_{i-1}\left(x_i\right)-h_{i-1}\left(x_{i-1}\right))}^{{\varrho }_{i-1}}}{\Gamma ({\varrho }_{i-1}+1)}+\frac{{(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(x_{\mathbb{k}}\right))}^{{\varrho }_{\mathbb{k}}}}{\Gamma ({\varrho }_{\mathbb{k}}+1)}\right)\right)\zeta \hfill \\ & \le \zeta ,\hfill \end{array}$$

(19)

where $\eta ={\eta }_1+{\eta }_3$ and ${\eta }^{*}=max({\eta }_2,{\eta }_4).$

Now for sake of simplicity, let us denote ${\sum }_{i=1}^{\mathbb{k}}\frac{{(h_{i-1}\left(x_i\right)-h_{i-1}\left(x_{i-1}\right))}^{{\varrho }_{i-1}}}{\Gamma ({\varrho }_{i-1}+1)}+\frac{{(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(x_{\mathbb{k}}\right))}^{{\varrho }_{\mathbb{k}}}}{\Gamma ({\varrho }_{\mathbb{k}}+1)}$ by $\mathbb{Q}$. Then, we have

$$\begin{array}{cc}\hfill & {∥\mathcal{N}(w,u)∥}_{\mathcal{E}}\le \frac{{\Delta }_0+k+\aleph \eta +\mathbb{Q}\mathbb{B}}{1-\left(\aleph {\eta }^{*}+\xi \mathbb{Q}\right)}\le \zeta ,\hfill \end{array}$$

(20)

Now if

$$\begin{array}{c}\hfill \zeta \ge max\left(\frac{{\Delta }_0+k+\mathbb{B}\mathbb{P}}{1-\xi \mathbb{P}},\frac{{\Delta }_0+k+\aleph \eta +\mathbb{Q}\mathbb{B}}{1-\left(\aleph {\eta }^{*}+\xi \mathbb{Q}\right)}\right),\end{array}$$

then, ${∥\mathcal{N}(w,u)∥}_{\mathcal{E}}\le \zeta .$ This means that $\mathcal{N}$ maps ${\mathcal{B}}_{\zeta }$ onto itself.

Step 2: $\mathcal{N}$ is continuous.

Let ${\left\{w_s\right\}}_{s\in \mathbb{N}}$ be a sequence, so that $w_s\to w$ on ${\mathcal{B}}_{\zeta }.$ The continuity of $f(·,u,w),$$\mathcal{F}(·,u,w),$${\mathcal{I}}_{\mathbb{k}}\left(w\right)$, ${\overline{\mathcal{I}}}_{\mathbb{k}}\left(w\right)$, $\rho \left(w\right)$ and $\varphi \left(u\right)$ imply that $f(·,u_s,w_s)\to f(·,u,w),$$\mathcal{F}(·,u_s,w_s)\to \mathcal{F}(·,u,w),$${\mathcal{I}}_{\mathbb{k}}\left(w_s\right)\to {\mathcal{I}}_{\mathbb{k}}\left(w\right),$${\overline{\mathcal{I}}}_{\mathbb{k}}\left(w_s\right)\to {\overline{\mathcal{I}}}_{\mathbb{k}}\left(w\right),$$\rho \left(w_s\right)\to \rho \left(w\right)$ and $\varphi \left(u_s\right)\to \varphi \left(u\right)$ as $s\to \infty .$ Moreover, for each $x\in [0,x_1]$,

$$\begin{array}{ccc}& & \left|{\mathcal{N}}_1(w_s\left(x\right),u_s\left(x\right))-{\mathcal{N}}_1(w\left(x\right),u\left(x\right))\right|\le \left|\rho \left(w_s\left(x\right)\right)-\rho \left(w\left(x\right)\right)\right|\hfill \\ & +& \frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}\left|f(z,u_s\left(z\right),w_s\left(z\right))-f(z,u\left(z\right),w\left(z\right))\right|dz.\hfill \end{array}$$

Using the assumptions and simplifying, we have

$$\begin{array}{ccc}\hfill & & ∥{\mathcal{N}}_1(w_s,u_s)-{\mathcal{N}}_1(w,u)∥\hfill \\ & \le & k_{\rho }^{*}∥w_s-w∥+\frac{k_f}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}\left(∥u_s-u∥+∥w_s-w∥\right)dz\hfill \\ & \le & k_{\rho }^{*}∥w_s-w∥+\frac{k_f{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\left(∥u_s-u∥+∥w_s-w∥\right).\hfill \end{array}$$

(21)

Similarly, we obtain

$$\begin{array}{ccc}\hfill & & ∥{\mathcal{N}}_2(w_s,u_s)-{\mathcal{N}}_2(w,u)∥\hfill \\ & \le & k_{\varphi }^{*}∥u_s-u∥+\frac{k_f{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\left(∥u_s-u∥+∥w_s-w∥\right).\hfill \end{array}$$

(22)

Looking at the inequalities (21) and (22), we see that as $s\to \infty ,$$w_s$ and $u_s$ converge to w and u, respectively. This implies that ${\mathcal{N}}_1(w_s,u_s)\to {\mathcal{N}}_1(w,u)$ and ${\mathcal{N}}_2(w_s,u_s)\to {\mathcal{N}}_2(w,u).$ This means that ${\mathcal{N}}_1$ and ${\mathcal{N}}_2$ are continuous. Consequently, the operator $\mathcal{N}$ is continuous at $x\in [0,x_1]$. In the same way, we may show that $\mathcal{N}$ is continuous at $x\in (x_{\mathbb{k}},x_{\mathbb{k}+1}],$$\mathbb{k}=1,\dots ,\aleph .$

Step 3: $\mathcal{N}$ maps bounded sets onto equi-continuous sets of $\mathcal{E}$.

$\mathbf{Case}\mathbf{I}$

Assume that ${\mathcal{B}}_{\zeta }$ is a bounded set as in Steps 1 and 2, and $w\in {\mathcal{B}}_{\zeta }.$ For arbitrary ${\tau }_1,{\tau }_2\in [0,x_1],$${\tau }_1<{\tau }_2$, we obtain

$$\begin{array}{ccc}\hfill & & \left|{\mathcal{N}}_1(w,u)\left({\tau }_2\right)-{\mathcal{N}}_1(w,u)\left({\tau }_1\right)\right|\le \left|\rho \left(w\left({\tau }_2\right)\right)-\rho \left(w\left({\tau }_1\right)\right)\right|\hfill \\ & +& \frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^{{\tau }_1}{h}_0^{\prime }\left(z\right)\left({(h_0\left({\tau }_2\right)-h_0\left(z\right))}^{{\varrho }_0-1}-{(h_0\left({\tau }_1\right)-h_0\left(z\right))}^{{\varrho }_0-1}\right)\left|f(z,u(z),w(z\left)\right)\right|dz\hfill \\ & & +\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_{{\tau }_1}^{{\tau }_2}{h}_0^{\prime }\left(z\right){(h_0\left({\tau }_2\right)-h_0\left(z\right))}^{{\varrho }_0-1}\left|f(z,u(z),w(z\left)\right)\right|dz\hfill \\ & \le & ∥\rho \left(w\left({\tau }_2\right)\right)-\rho \left(w\left({\tau }_1\right)\right)∥+\frac{\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)}{(\Gamma \left({\varrho }_0\right)}\hfill \\ & \times & {\int }_0^{{\tau }_1}{h}_0^{\prime }\left(z\right)\left({(h_0\left({\tau }_1\right)-h_0\left(z\right))}^{{\varrho }_0-1}-{(h_0\left({\tau }_2\right)-h_0\left(z\right))}^{{\varrho }_0-1}\right)dz\hfill \\ & & +\frac{\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)}{\Gamma \left({\varrho }_0\right)}{\int }_{{\tau }_1}^{{\tau }_2}{h}_0^{\prime }\left(z\right){(h_0\left({\tau }_2\right)-h_0\left(z\right))}^{{\varrho }_0-1}dz\hfill \\ & \le & ∥\rho \left(w\left({\tau }_2\right)\right)-\rho \left(w\left({\tau }_1\right)\right)∥+\frac{\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)}{\Gamma ({\varrho }_0+1)}\hfill \\ & & \times \left({(h_0\left({\tau }_2\right)-h_0\left({\tau }_1\right))}^{{\varrho }_0}+{(h_0\left({\tau }_1\right)-h_0\left(0\right))}^{{\varrho }_0}-{(h_0\left({\tau }_2\right)-h_0\left(0\right))}^{{\varrho }_0}\right)\hfill \\ \hfill & +& \frac{\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)}{\Gamma ({\varrho }_0+1)}{(h_0\left({\tau }_2\right)-h_0\left({\tau }_1\right))}^{{\varrho }_0}\hfill \\ & \le & ∥\rho \left(w\left({\tau }_2\right)\right)-\rho \left(w\left({\tau }_1\right)\right)∥+\frac{2\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)}{\Gamma ({\varrho }_0+1)}{(h_0\left({\tau }_2\right)-h_0\left({\tau }_1\right))}^{{\varrho }_0}.\hfill \end{array}$$

(23)

Similarly, we obtain

$$\begin{array}{ccc}\hfill & & \left|{\mathcal{N}}_2(w,u)\left({\tau }_2\right)-{\mathcal{N}}_2(w,u)\left({\tau }_1\right)\right|\hfill \\ & \le & ∥\varphi \left(u\left({\tau }_2\right)\right)-\varphi \left(u\left({\tau }_1\right)\right)∥+\frac{2\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)}{\Gamma ({\varrho }_0+1)}{(h_0\left({\tau }_2\right)-h_0\left({\tau }_1\right))}^{{\varrho }_0}.\hfill \end{array}$$

(24)

Since $h_0$ is continuous, $\left|{\mathcal{N}}_{1}w\left({\tau }_2\right)-{\mathcal{N}}_{1}w\left({\tau }_1\right)\right|\to 0$ and $\left|{\mathcal{N}}_{2}w\left({\tau }_2\right)-{\mathcal{N}}_{2}w\left({\tau }_1\right)\right|\to 0$ as ${\tau }_2\to {\tau }_1$.

$\mathbf{Case}\mathbf{II}$

By and large, for $x\in (x_{\mathbb{k}},x_{\mathbb{k}+1}],$ $\mathbb{k}=1,\dots ,\aleph$, we get the accompanying inequality

$$\begin{array}{ccc}\hfill & & \left|{\mathcal{N}}_1(w,u)\left({\tau }_2\right)-{\mathcal{N}}_1(w,u)\left({\tau }_1\right)\right|\le \left|\rho \left(w\left({\tau }_2\right)\right)-\rho \left(w\left({\tau }_1\right)\right)\right|+\sum _{0<x_{\mathbb{k}}<{\tau }_2-{\tau }_1}\left|{\mathcal{I}}_{\mathbb{k}}w\left(x_{\mathbb{k}}^{-}\right)\right|\hfill \\ & & +\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^{{\tau }_1}{h}_{\mathbb{k}}^{\prime }\left(z\right)\left({(h_{\mathbb{k}}\left({\tau }_1\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}-{(h_{\mathbb{k}}\left({\tau }_2\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}\right)\hfill \\ & & \times \left|f(z,u(z),w(z\left)\right)\right|dz+\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{{\tau }_1}^{{\tau }_2}{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left({\tau }_2\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}\left|f(z,u(z),w(z\left)\right)\right|dz\hfill \\ & \le & ∥\rho \left(w\left({\tau }_2\right)\right)-\rho \left(w\left({\tau }_1\right)\right)∥+\aleph \left({\tau }_2-{\tau }_1\right)\left({\eta }_1+{\eta }_2\zeta \right)+\frac{\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)}{\Gamma ({\varrho }_{\mathbb{k}}+1)}\hfill \\ & \times & \left({(h_{\mathbb{k}}\left({\tau }_2\right)-h_{\mathbb{k}}\left({\tau }_1\right))}^{{\varrho }_{\mathbb{k}}}+{(h_{\mathbb{k}}\left({\tau }_1\right)-h_{\mathbb{k}}\left(x_{\mathbb{k}}\right))}^{{\varrho }_{\mathbb{k}}}-{(h_{\mathbb{k}}\left({\tau }_2\right)-h_{\mathbb{k}}\left(x_{\mathbb{k}}\right))}^{{\varrho }_{\mathbb{k}}}\right)\hfill \\ & +& \frac{\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)}{\Gamma ({\varrho }_{\mathbb{k}}+1)}\left[{(h_{\mathbb{k}}\left({\tau }_2\right)-h_{\mathbb{k}}\left({\tau }_1\right))}^{{\varrho }_{\mathbb{k}}}\right]\hfill \\ & \le & ∥\rho \left(w\left({\tau }_2\right)\right)-\rho \left(w\left({\tau }_1\right)\right)∥+\aleph \left({\tau }_2-{\tau }_1\right)\left({\eta }_1+{\eta }_2\zeta \right)+\frac{2\left({\mathbb{B}}_w+{\mathbb{C}}_w∥u∥+{\mathbb{D}}_w∥w∥\right)}{\Gamma ({\varrho }_{\mathbb{k}}+1)}\hfill \\ & \times & {(h_{\mathbb{k}}\left({\tau }_2\right)-h_{\mathbb{k}}\left({\tau }_1\right))}^{{\varrho }_{\mathbb{k}}}.\hfill \end{array}$$

(25)

Similarly, we obtain

$$\begin{array}{ccc}\hfill & & \left|{\mathcal{N}}_2(w,u)\left({\tau }_2\right)-{\mathcal{N}}_2(w,u)\left({\tau }_1\right)\right|\le ∥\varphi \left(u\left({\tau }_2\right)\right)-\varphi \left(u\left({\tau }_1\right)\right)∥+\aleph \left({\tau }_2-{\tau }_1\right)\left({\eta }_3+{\eta }_4\zeta \right)\hfill \\ & +& \frac{2\left({\mathbb{B}}_u+{\mathbb{C}}_u∥u∥+{\mathbb{D}}_u∥w∥\right)}{\Gamma ({\varrho }_{\mathbb{k}}+1)}{(h_{\mathbb{k}}\left({\tau }_2\right)-h_{\mathbb{k}}\left({\tau }_1\right))}^{{\varrho }_{\mathbb{k}}}.\hfill \end{array}$$

(26)

Since $h_{\mathbb{k}}$ ($\mathbb{k}=1,2,...,\aleph$) is continuous, that is

$$\left|{\mathcal{N}}_1(w,u)\left({\tau }_2\right)-{\mathcal{N}}_1(w,u)\left({\tau }_1\right)\right|\to 0$$

and

$$\left|{\mathcal{N}}_2(w,u)\left({\tau }_2\right)-{\mathcal{N}}_2(w,u)\left({\tau }_1\right)\right|\to 0\mathrm{as}{\tau }_2\to {\tau }_1.$$

Hence, ${\mathcal{N}}_1(w,u)$, ${\mathcal{N}}_2(w,u)$ are equi-continuous. Consequently $\mathcal{N}(w,u)$ is equi-continuous on $\mathbb{S}$.

On the other hand, according to Step 1, $\mathcal{N}{\mathcal{B}}_{\zeta }\subset {\mathcal{B}}_{\zeta }$ is uniformly bounded. Hence, applying the Ascoli–Arzela theorem, the family $\left\{\mathcal{N}(w,u):(w,u)\in {\mathcal{B}}_{\zeta }\right\}$ is a relatively compact subset of $\mathcal{E}$. Thus, $\mathcal{N}:\mathcal{P}\mathcal{C}\to \mathcal{P}\mathcal{C}$ is completely continuous. As a consequence of Steps 1–3 together with the Ascoli–Arzela theorem, we conclude that $\mathcal{N}$ has a fixed point in ${\mathcal{B}}_{\zeta }$ which indicates that the impulsive problem (1) has a solution in $\mathcal{E}$. □

Theorem 2. 

If $\left(H_1\right),$$\left(H_2\right)$ and $\left(H_6\right)$ hold with the following condition

$$max({\chi }_1,{\chi }_2)<1,$$

(27)

where

$${\chi }_1=k_{\rho }^{*}+k_{\varphi }^{*}+2(k_f+k_{\mathcal{F}})\frac{{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)},$$

and

$${\chi }_2=k_{\rho }^{*}+k_{\varphi }^{*}+\aleph (k_{\mathcal{I}}+k_{\overline{\mathcal{I}}})+2(k_f+k_{\mathcal{F}})\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)},$$

then, the impulsive problem (1) has a unique solution in $\mathcal{E}.$

Proof. 

Let $\mathcal{N}$ be the operator defined by (9). Then, $\mathcal{N}:\mathcal{P}\mathcal{C}\to \mathcal{P}\mathcal{C}$ is well defined by Theorem 1. Next, we will utilize Banach’s contraction theorem to demonstrate that $\mathcal{N}$ has a fixed point.

$\mathbf{Case}\mathbf{I}$

For arbitrary $(w,u),(w^{*},u^{*})\in \mathcal{E}$ and $x\in [0,x_1],$ we obtain

$$\begin{array}{cc}& \left|{\mathcal{N}}_1(w,u)\left(x\right)-{\mathcal{N}}_1(w^{*},u^{*})\left(x\right)\right|\le \left|\rho \left(w\left(x\right)\right)-\rho \left(w^{*}\left(x\right)\right)\right|+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}\hfill \\ & \times \left|f(z,u\left(z\right),w\left(z\right))-f(z,u^{*}\left(z\right),w^{*}\left(z\right))\right|dz\hfill \\ & \le k_{\rho }^{*}\left|w\left(x\right)-w^{*}\left(x\right)\right|+\frac{k_f}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}\hfill \\ & \times \left(\left|u-u^{*}\right|+\left|w-w^{*}\right|\right)dz\hfill \\ & \le \left(k_{\rho }^{*}+\frac{k_f{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\right)∥w-w^{*}∥+\frac{k_f{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}∥u-u^{*}∥.\hfill \end{array}$$

(28)

Thus, we have

$$\begin{array}{cc}& \left|{\mathcal{N}}_1(w,u)\left(x\right)-{\mathcal{N}}_1(w^{*},u^{*})\left(x\right)\right|\hfill \\ & \le \left(k_{\rho }^{*}+\frac{k_f{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\right)∥w-w^{*}∥+\frac{k_f{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}∥u-u^{*}∥.\hfill \end{array}$$

(29)

Similarly

$$\begin{array}{cc}& \left|{\mathcal{N}}_2(w,u)\left(x\right)-{\mathcal{N}}_2(w^{*},u^{*})\left(x\right)\right|\hfill \\ & \le \left(k_{\varphi }^{*}+\frac{k_{\mathcal{F}}{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\right)∥u-u^{*}∥+\frac{k_{\mathcal{F}}{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}∥w-w^{*}∥.\hfill \end{array}$$

(30)

From (29) and (30), we have

$$\begin{array}{cc}& ∥\mathcal{N}(w,u)-\mathcal{N}(w^{*},u^{*})∥\hfill \\ & \le \left(k_{\rho }^{*}+k_{\varphi }^{*}+2(k_f+k_{\mathcal{F}})\frac{{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\right)\left(∥w-w^{*}∥+∥u-u^{*}∥\right).\hfill \end{array}$$

(31)

$\mathbf{Case}\mathbf{II}$

For $x\in (x_{\mathbb{k}},x_{\mathbb{k}+1}],$$\mathbb{k}=1,\dots ,\aleph ,$ we have

$$\begin{array}{cc}& \left|{\mathcal{N}}_{1}w\left(x\right)-{\mathcal{N}}_1{w}^{*}\left(x\right)\right|\hfill \\ & \le \left|\rho \left(w\left(x\right)\right)-\rho \left(w^{*}\left(x\right)\right)\right|+\sum _{0<x_{\mathbb{k}}<x}\left|{\mathcal{I}}_{\mathbb{k}}w\left(x_{\mathbb{k}}^{-}\right)-{\mathcal{I}}_{\mathbb{k}}{w}^{*}\left(x_{\mathbb{k}}^{-}\right)\right|\hfill \\ & +\sum _{i=1}^{\mathbb{k}}\frac{1}{\Gamma \left({\varrho }_{i-1}\right)}\int {x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}\left|f(z,u\left(z\right),w\left(z\right))-f(z,u^{*}\left(z\right),w^{*}\left(z\right))\right|dz\hfill \\ & +\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}\left|f(z,u\left(z\right),w\left(z\right))-f(z,u^{*}\left(z\right),w^{*}\left(z\right))\right|dz\hfill \\ & \le k_{\rho }^{*}\left|w\left(x\right)-w^{*}\left(x\right)\right|+\sum _{0<x_{\mathbb{k}}<x}{k}_{\mathcal{I}}\left|w\left(x_{\mathbb{k}}^{-}\right)-w^{*}\left(x_{\mathbb{k}}^{-}\right)\right|\hfill \\ & +\sum _{i=1}^{\mathbb{k}}\frac{k_f}{\Gamma \left({\varrho }_{i-1}\right)}{\int }_{x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}\left(\left|u-u^{*}\right|+\left|w-w^{*}\right|\right)|dz\hfill \\ & +\frac{k_f}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}\left(\left|u-u^{*}\right|+\left|w-w^{*}\right|\right)dz\hfill \\ & \le k_{\rho }^{*}∥w-w^{*}∥+\aleph k_{\mathcal{I}}∥w-w^{*}∥+k_f\left(∥u-u^{*}∥+∥w-w^{*}∥\right)\hfill \\ & \times \left(\sum _{i=1}^{\mathbb{k}}\frac{{(h_{i-1}\left(x_i\right)-h_{i-1}\left(x_{i-1}\right))}^{{\varrho }_{i-1}}}{\Gamma ({\varrho }_{i-1}+1)}+\frac{{(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(x_{\mathbb{k}}\right))}^{{\varrho }_{\mathbb{k}}}}{\Gamma ({\varrho }_{\mathbb{k}}+1)}\right)\hfill \\ & \le k_{\rho }^{*}∥w-w^{*}∥+\aleph k_{\mathcal{I}}∥w-w^{*}∥+k_f\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\left(∥u-u^{*}∥+∥w-w^{*}∥\right).\hfill \end{array}$$

(32)

Thus

$$\begin{array}{c}\hfill ∥{\mathcal{N}}_1(w,u)-{\mathcal{N}}_1(w^{*},u^{*})∥\le k_f\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}∥u-u^{*}∥\\ \hfill +\left(k_{\rho }^{*}+\aleph k_{\mathcal{I}}+k_f\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)∥w-w^{*}∥.\end{array}$$

(33)

Similarly

$$\begin{array}{c}\hfill ∥{\mathcal{N}}_2(w,u)-{\mathcal{N}}_2(w^{*},u^{*})∥\le k_{\mathcal{F}}\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}∥w-w^{*}∥\\ \hfill +\left(k_{\varphi }^{*}+\aleph k_{\overline{\mathcal{I}}}+k_{\mathcal{F}}\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)∥u-u^{*}∥.\end{array}$$

(34)

From (33) and (34), we have

$$\begin{array}{c}\hfill ∥\mathcal{N}(w,u)-\mathcal{N}(w^{*},u^{*})∥\le (k_{\rho }^{*}+k_{\varphi }^{*}+\aleph (k_{\mathcal{I}}+k_{\overline{\mathcal{I}}})\\ \hfill +2(k_f+k_{\mathcal{F}})\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)})\left(∥w-w^{*}∥+∥u-u^{*}∥\right).\end{array}$$

(35)

Now if

$$max({\chi }_1,{\chi }_2)<1,$$

where

$${\chi }_1=k_{\rho }^{*}+k_{\varphi }^{*}+2(k_f+k_{\mathcal{F}})\frac{{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)},$$

and

$${\chi }_2=k_{\rho }^{*}+k_{\varphi }^{*}+\aleph (k_{\mathcal{I}}+k_{\overline{\mathcal{I}}})+2(k_f+k_{\mathcal{F}})\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)},$$

then, $\mathcal{N}$ is strict contraction on $\mathcal{E}$. It follows from Banach’s contraction theorem that the impulsive FDE (1) has a unique solution on $\mathbb{S}.$  □

4. Stability Analysis of Problem (1)

In this main section, we derive some results about stability analysis for the proposed problem (1). Prior to the proof of main results, we give definitions of Hyers–Ulam (H–U) stability and some remarks.

Consider an operator $\mathcal{N}:\mathcal{E}\to \mathcal{E},$ defined by

$$\mathcal{N}\left(w\right)=w;w\in \mathcal{E}.$$

(36)

Definition 1. 

The solution w of problem (36) is H–U stable. If we find a constant $\mathbf{C}>0$, so that for any $ϵ>0$ and any solution $w\in \mathcal{E}$ of the inequality

$$\left\{\begin{array}{c}|w-\mathcal{N}(w\left)\right|\le ϵ,\hfill \end{array}\right.$$

(37)

there exists unique solution $\overline{w}$ of Equation (36) in $\mathcal{E}$, so that the following relation satisfies

$$\parallel \overline{w}-w\parallel \le \mathbf{C}ϵ.$$

Definition 2. 

The solution of problem (36) is G–H–U stable if we find

$$\theta :(0,\infty )\to (0,\infty ),\theta \left(0\right)=0$$

so that for any solution of the inequality (37), the following relation satisfies

$$\parallel \overline{w}-w\parallel \le \mathbf{C}\theta \left(ϵ\right).$$

Remark 1. 

w is the solution in $\mathcal{E}$ for the inequality (37), iff there exists a function $\varkappa \in \mathcal{E}$ which is independent of solution $(w,u)$, so that for any t

 $\left(i\right)$

 $\left|\varkappa \right(x\left)\right|\le ϵ,$  $|{\varkappa }_n|\le ϵ,$

 $\left(ii\right)$

${}^c{D}_{\left[x\right]}^{\varrho \left(x\right)}w\left(x\right)=f(x,u\left(x\right),w\left(x\right))+\varkappa \left(x\right),$

 $\left(iii\right)$

${}^c{D}_{\left[x\right]}^{\varrho \left(x\right)}u\left(x\right)=\mathcal{F}(x,u\left(x\right),w\left(x\right))+\varkappa \left(x\right),$

 $\left(iv\right)$

 $\Delta w\left(x_i\right)={\mathcal{I}}_i\left(w\left(x_i^{-}\right)\right)+{\varkappa }_n,$  $n=1,\dots ,k.$

 $\left(v\right)$

 $\Delta u\left(x_i\right)=\overline{{\mathcal{I}}_i}\left(u\left(x_i^{-}\right)\right)+{\varkappa }_n,$  $n=1,\dots ,k.$

By Remark 1, we have the following perturbed problem

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {}^c{D}_{\left[x\right]}^{\varrho \left(x\right)}w\left(x\right)=f(x,u\left(x\right),w\left(x\right))+\varkappa \left(x\right),x\in \mathbb{S}=[0,T],x\ne x_i,\hfill \\ & w\left(0\right)=w_0+\rho \left(w\right),\hfill \\ & \Delta w\left(x_i\right)={\mathcal{I}}_i\left(w\left(x_i^{-}\right)\right)+{\varkappa }_n,i=1,...m,\hfill \\ & {}^c{D}_{\left[x\right]}^{\varrho \left(x\right)}u\left(x\right)=\mathcal{F}(x,w\left(x\right),u\left(x\right))+\varkappa \left(x\right),x\in \mathbb{S}=[0,T],x\ne x_i,\hfill \\ & i=1,\dots ,\aleph ,0<\varrho \left(x\right)\le 1,\hfill \\ & u\left(0\right)=u_0+\varphi \left(u\right),\hfill \\ & \Delta u\left(x_i\right)={\overline{\mathcal{I}}}_i\left(u\left(x_i^{-}\right)\right)+{\varkappa }_n,i=1,...m.\hfill \end{array}\right.\end{array}$$

(38)

Lemma 2. 

The solution of the perturbed problem (38) satisfies the following relations

$$\left\{\begin{array}{cc}& w\left(x\right)-\left(w_0+\rho \left(w\right)+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}f(z,u\left(z\right),w\left(z\right))dz\right)\hfill \\ & \le \frac{ϵ{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)},ifx\in [0,x_1],\hfill \\ & ⋮\hfill \\ & w\left(x\right)-(w_0+\rho \left(w\right)+\sum _{i=1}^{\mathbb{k}}{\mathcal{I}}_{i}w\left(x_i^{-}\right)+\sum _{i=1}^{\mathbb{k}}\frac{1}{\Gamma \left({\varrho }_{i-1}\right)}{\int }_{x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}\hfill \\ & \times f(z,u\left(z\right),w\left(z\right))dz+\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}f(z,u\left(z\right),w\left(z\right))dz)\hfill \\ & \le \left(\mathbb{k}+\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)ϵ,\hfill \\ & ifx\in (x_{\mathbb{k}},x_{\mathbb{k}+1}],\mathbb{k}=1,\dots ,\aleph ,\hfill \end{array}\right.$$

(39)

and

$$\left\{\begin{array}{cc}& u\left(x\right)-\left(u_0+\varphi \left(u\right)+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}\mathcal{F}(z,u\left(z\right),w\left(z\right))dz\right)\hfill \\ & \le \frac{ϵ{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)},ifx\in [0,x_1],\hfill \\ & ⋮\hfill \\ & u\left(x\right)-(u_0+\varphi \left(u\right)+\sum _{i=1}^{\mathbb{k}}{\mathcal{I}}_{i}u\left(x_i^{-}\right)+\sum _{i=1}^{\mathbb{k}}\frac{1}{\Gamma \left({\varrho }_{i-1}\right)}{\int }_{x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}\hfill \\ & \times \mathcal{F}(z,u\left(z\right),w\left(z\right))dz+\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}\mathcal{F}(z,u\left(z\right),w\left(z\right))dz)\hfill \\ & \le \left(\mathbb{k}+\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)ϵ,\hfill \\ & ifx\in (x_{\mathbb{k}},x_{\mathbb{k}+1}],\mathbb{k}=1,\dots ,\aleph .\hfill \end{array}\right.$$

(40)

Proof. 

The proof can be obtained by applying Lemma A2 repeatedly as in the proof of Lemma 1. □

Theorem 3. 

If $\left(H_1\right),$$\left(H_2\right)$ and $\left(H_6\right)$ hold with the following condition

$$max({\chi }_1,{\chi }_2)<1,$$

where

$${\chi }_1=k_{\rho }^{*}+k_{\varphi }^{*}+2(k_f+k_{\mathcal{F}})\frac{{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)},$$

and

$${\chi }_2=k_{\rho }^{*}+k_{\varphi }^{*}+\aleph (k_{\mathcal{I}}+k_{\overline{\mathcal{I}}})+2(k_f+k_{\mathcal{F}})\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)},$$

then, problem (1) is H–U stable.

Proof. 

Let $w^{*}$ be any solution of set of inequalities (37) and w be the unique solution of problem (1). Then, from integral Equations (8) and (39), we have

$$\begin{array}{cc}& \left|w\left(x\right)-w^{*}\left(x\right)\right|\le \left|\rho \left(w\left(x\right)\right)-\rho \left(w^{*}\left(x\right)\right)\right|+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}\hfill \\ & \times \left|f(z,u\left(z\right),w\left(z\right))-f(z,u^{*}\left(z\right),w^{*}\left(z\right))\right|dz+\frac{1}{\Gamma \left({\varrho }_0\right)}{\int }_0^x{h}_0^{\prime }\left(z\right){(h_0\left(x\right)-h_0\left(z\right))}^{{\varrho }_0-1}\left|\varkappa \left(z\right)\right|dz\hfill \\ & \le \left(k_{\rho }^{*}+\frac{k_f{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\right)∥w-w^{*}∥+\frac{k_f{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}∥u-u^{*}∥\hfill \\ & +\frac{ϵ{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}.\hfill \end{array}$$

(41)

Thus, for $x\in [0,x_1],$ we have

$$\begin{array}{cc}& ∥w-w^{*}∥\le \left(k_{\rho }^{*}+\frac{k_f{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\right)∥w-w^{*}∥+\frac{k_f{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}∥u-u^{*}∥\hfill \\ & +\frac{ϵ{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}.\hfill \end{array}$$

(42)

Similarly, for $x\in [0,x_1],$ we have

$$\begin{array}{cc}& ∥u-u^{*}∥\le \left(k_{\varphi }^{*}+\frac{k_{\mathcal{F}}{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\right)∥w-w^{*}∥+\frac{k_{\mathcal{F}}{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}∥u-u^{*}∥\hfill \\ & +\frac{ϵ{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}.\hfill \end{array}$$

(43)

Adding (42) and (43), we have

$$\begin{array}{cc}& ∥w-w^{*}∥+∥u-u^{*}∥\le \left(k_{\rho }^{*}+\frac{k_f{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\right)∥w-w^{*}∥+\frac{k_f{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}∥u-u^{*}∥\hfill \\ & +\frac{ϵ{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\hfill \\ & \le (k_{\rho }^{*}+k_{\varphi }^{*}+2(k_f\hfill \\ & +k_{\mathcal{F}})\frac{{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)})\left(∥w-u∥+∥w^{*}-u^{*}∥\right)+\frac{ϵ{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}.\hfill \end{array}$$

(44)

That implies

$$\begin{array}{cc}& ∥w-w^{*}∥+∥u-u^{*}∥\le \left(k_{\rho }^{*}+k_{\varphi }^{*}+2(k_f+k_{\mathcal{F}})\frac{{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\right)\left(∥w-u∥+∥w^{*}-u^{*}∥\right)\hfill \\ & +\frac{ϵ{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}.\hfill \end{array}$$

(45)

From which we obtain

$$\begin{array}{cc}& ∥(w,u)-(w^{*},u^{*})∥\le \frac{\frac{ϵ{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}}{1-{\chi }_1},\hfill \end{array}$$

(46)

where ${\chi }_1=\left(k_{\rho }^{*}+k_{\varphi }^{*}+2(k_f+k_{\mathcal{F}})\frac{{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)}\right)$ is assumed to be less than one.

By and large, for $x\in (x_{\mathbb{k}},x_{\mathbb{k}+1}],$$\mathbb{k}=1,\dots ,\aleph ,$ we have

$$\begin{array}{cc}& \left|w\left(x\right)-w^{*}\left(x\right)\right|\hfill \\ & \le \left|\rho \left(w\left(x\right)\right)-\rho \left(w^{*}\left(x\right)\right)\right|+\sum _{0<x_{\mathbb{k}}<x}\left|{\mathcal{I}}_{\mathbb{k}}w\left(x_{\mathbb{k}}^{-}\right)-{\mathcal{I}}_{\mathbb{k}}{w}^{*}\left(x_{\mathbb{k}}^{-}\right)\right|\hfill \\ & +\sum _{i=1}^{\mathbb{k}}\frac{1}{\Gamma \left({\varrho }_{i-1}\right)}{\int }_{x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}\left|f(z,u\left(z\right),w\left(z\right))-f(z,u^{*}\left(z\right),w^{*}\left(z\right))\right|dz\hfill \\ & +\sum _{i=1}^{\mathbb{k}}\frac{1}{\Gamma \left({\varrho }_{i-1}\right)}{\int }_{x_{i-1}}^{x_i}{h}_{i-1}^{\prime }\left(z\right){(h_{i-1}\left(x_i\right)-h_{i-1}\left(z\right))}^{{\varrho }_{i-1}-1}\left|\varkappa \left(z\right)\right|dz\hfill \\ & +\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}\left|f(z,u\left(z\right),w\left(z\right))-f(z,u^{*}\left(z\right),w^{*}\left(z\right))\right|dz\hfill \\ & +\frac{1}{\Gamma \left({\varrho }_{\mathbb{k}}\right)}{\int }_{x_{\mathbb{k}}}^x{h}_{\mathbb{k}}^{\prime }\left(z\right){(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(z\right))}^{{\varrho }_{\mathbb{k}}-1}\left|\varkappa \left(z\right)\right|dz\hfill \\ & \le k_{\rho }^{*}∥w-w^{*}∥+\aleph k_{\mathcal{I}}∥w-w^{*}∥+k_f\left(∥u-u^{*}∥+∥w-w^{*}∥\right)\hfill \\ & \times \left(\sum _{i=1}^{\mathbb{k}}\frac{{(h_{i-1}\left(x_i\right)-h_{i-1}\left(x_{i-1}\right))}^{{\varrho }_{i-1}}}{\Gamma ({\varrho }_{i-1}+1)}+\frac{{(h_{\mathbb{k}}\left(x\right)-h_{\mathbb{k}}\left(x_{\mathbb{k}}\right))}^{{\varrho }_{\mathbb{k}}}}{\Gamma ({\varrho }_{\mathbb{k}}+1)}\right)+\left(\mathbb{k}+\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)ϵ\hfill \\ & \le k_{\rho }^{*}∥w-w^{*}∥+\aleph k_{\mathcal{I}}∥w-w^{*}∥+k_f\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\left(∥u-u^{*}∥+∥w-w^{*}∥\right)\hfill \\ & +\left(\mathbb{k}+\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)ϵ.\hfill \end{array}$$

(47)

Thus, we have

$$\begin{array}{cc}& ∥w-w^{*}∥\hfill \\ & \le k_f\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}∥u-u^{*}∥+\left(k_{\rho }^{*}+\aleph k_{\mathcal{I}}+k_f\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)∥w-w^{*}∥\hfill \\ & +\left(\mathbb{k}+\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)ϵ.\hfill \end{array}$$

(48)

Similarly, we have

$$\begin{array}{cc}& ∥u-u^{*}∥\hfill \\ & \le k_{\mathcal{F}}\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}∥w-w^{*}∥+\left(k_{\varphi }^{*}+\aleph k_{\overline{\mathcal{I}}}+k_{\mathcal{F}}\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)∥u-u^{*}∥\hfill \\ & +\left(\mathbb{k}+\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)ϵ.\hfill \end{array}$$

(49)

From (48) and (49), we have

$$\begin{array}{cc}& ∥w-w^{*}∥+∥u-u^{*}∥\le \left(k_{\rho }^{*}+k_{\varphi }^{*}+\aleph (k_{\mathcal{I}}+k_{\overline{\mathcal{I}}})+2(k_f+k_{\mathcal{F}})\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)\hfill \\ & \times \left(∥w-w^{*}∥+∥u-u^{*}∥\right)+\left(\mathbb{k}+\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)ϵ.\hfill \end{array}$$

(50)

Which implies that

$$\begin{array}{cc}& ∥(w,u)-(w^{*},u^{*})∥\le \frac{\left(\mathbb{k}+{\sum }_{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)ϵ}{1-{\chi }_2}.\hfill \end{array}$$

(51)

where ${\chi }_2=\left(k_{\rho }^{*}+k_{\varphi }^{*}+\aleph (k_{\mathcal{I}}+k_{\overline{\mathcal{I}}})+2(k_f+k_{\mathcal{F}}){\sum }_{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)$ is assumed to be less than one. Equivalently, (51) can be written as

$$\begin{array}{cc}& ∥(w,u)-(w^{*},u^{*})∥\le \mathbf{C}ϵ,\hfill \end{array}$$

where

$$\begin{array}{cc}& \mathbf{C}=\frac{\left(\mathbb{k}+{\sum }_{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)}{1-\left(k_{\rho }^{*}+k_{\varphi }^{*}+\aleph (k_{\mathcal{I}}+k_{\overline{\mathcal{I}}})+2(k_f+k_{\mathcal{F}}){\sum }_{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}\right)}.\hfill \end{array}$$

This shows that problem (1) is H–U stable. □

Lemma 3. 

By setting $\theta \left(ϵ\right)=\mathbf{C}\left(ϵ\right);$$\theta \left(0\right)=0,$ problem (1) becomes G–H–U stable.

5. Application and Discussion

In this section, we apply our main results to the following numerical problem to verify the applications of the main results. We also plot graphs for its solution and functions $\varrho$ and h for illustration purposes.

Example 1. 

$$\left\{\begin{array}{cc}\hfill & {}^c{D}_{\left[x\right]}^{\varrho \left(x\right)}w\left(x\right)=\frac{e^{-\pi x}}{20}+\frac{(x-\frac{1}{5})}{28}\left(\left|u\right(x\left)\right|+sin\left(\right|w\left(x\right)\left|\right)\right),\hfill \\ & x\in [0,1],x\ne x_k,k=1,2,\dots ,9.\hfill \\ & {}^c{D}_{\left[x\right]}^{\varrho \left(x\right)}u\left(x\right)=\frac{e^{-\pi x}}{25}+\frac{(x-\frac{1}{5})}{20}\left(\left|w\right(x\left)\right|+cos\left(\right|u\left(x\right)\left|\right)\right),\hfill \\ & x\in [0,1],x\ne x_k,k=1,2,\dots ,9.\hfill \\ & \Delta w\left(x_k\right)=\frac{1}{25}w\left(x_k^{-}\right),\Delta u\left(x_k\right)=\frac{1}{40}u\left(x_k^{-}\right),\hfill \\ & w\left(0\right)=\frac{w}{22+\left|w\right|}+0.025,u\left(0\right)=\frac{u}{30+\left|u\right|}+1,\hfill \end{array}\right.$$

(52)

where $\varrho =\frac{1}{2},$${\mathbb{S}}_0=[0,\frac{1}{5}]$, ${\mathbb{S}}_1=(\frac{1}{5},1]$.

Set

$$f(x,u\left(x\right),w\left(x\right))=\frac{e^{-\pi x}}{20}+\frac{(x-\frac{1}{3})}{30}\left(\left|u\right(x\left)\right|+sin\left(\right|w\left(x\right)\left|\right)\right);u,w\in {\mathrm{R}}^{+},$$

and

$$\mathcal{F}(x,u\left(x\right),w\left(x\right))=\frac{e^{-\pi x}}{25}+\frac{(x-\frac{1}{5})}{20}\left(\left|w\right(x\left)\right|+cos\left(\right|u\left(x\right)\left|\right)\right),$$

$${\mathcal{I}}_i\left(w\right)=\frac{1}{50}w;w\in {\mathrm{R}}^{+},i=1,2,$$

and

$$\rho \left(w\right)=\frac{w}{22+\left|w\right|},\varphi \left(u\right)=\frac{u}{30+\left|u\right|}.$$

Assuming $\aleph =2$ ($\mathbb{k}=1,2$), we have

$$\begin{array}{c}\hfill {}^c{D}_{\left[x\right]}^{\varrho \left(x\right)}w\left(x\right)=\left\{\begin{array}{cc}& {}^c{D}_{\left[x\right]}^{{\varrho }_0,h_0}w\left(x\right),0<x\le x_1,\hfill \\ & {}^c{D}_{\left[x\right]}^{{\varrho }_1,h_1}w\left(x\right),x_1<x\le x_2\hfill \\ & {}^c{D}_{\left[x\right]}^{{\varrho }_2,h_2}w\left(x\right),x_2<x\le 1,\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill {}^c{D}_{\left[x\right]}^{\varrho \left(x\right)}u\left(x\right)=\left\{\begin{array}{cc}& {}^c{D}_{\left[x\right]}^{{\varrho }_0,h_0}u\left(x\right),0<x\le x_1,\hfill \\ & {}^c{D}_{\left[x\right]}^{{\varrho }_1,h_1}u\left(x\right),x_1<x\le x_2\hfill \\ & {}^c{D}_{\left[x\right]}^{{\varrho }_2,h_2}u\left(x\right),x_2<x\le 1;\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \varrho \left(x\right)=\left\{\begin{array}{cc}& {\varrho }_0=\frac{1}{4},0<x\le \frac{1}{3},\hfill \\ & {\varrho }_1=\frac{1}{3},\frac{1}{3}<x\le \frac{1}{2},\hfill \\ & {\varrho }_2=\frac{1}{2},\frac{1}{2}<x\le 1.\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill h\left(x\right)=\left\{\begin{array}{cc}& h_0\left(x\right)=\frac{x}{3},0<x\le \frac{1}{3},\hfill \\ & h_1\left(x\right)=2^x,\frac{1}{3}<x\le \frac{1}{2},\hfill \\ & h_2\left(x\right)=e^x,\frac{1}{2}<x\le 1.\hfill \end{array}\right.\end{array}$$

Let $w,\overline{w}\in {\mathrm{R}}^{+}$ and $x\in [0,1].$ Then,

$$\begin{array}{cc}\hfill & \left|f(x,u\left(x\right),w\left(x\right))-f(x,\overline{u}\left(x\right),\overline{w}\left(x\right))\right|\hfill \\ & \le \frac{(x-\frac{1}{5})}{28}\left(\left|\right|u\left(x\right)-\overline{u}\left(x\right)\left|\right|+|sin(\left|w\left(x\right)\right|)-sin\left(\overline{w}\left(x\right)\right)|\right)\hfill \\ & \le \frac{1}{35}\left(\left|\right|u\left(x\right)-\overline{u}\left(x\right)\left|\right|+|sin(\left|w\left(x\right)\right|)-sin\left(\overline{w}\left(x\right)\right)|\right).\hfill \end{array}$$

(53)

Similarly, we have

$$\begin{array}{cc}\hfill & \left|\mathcal{F}(x,u\left(x\right),w\left(x\right))-\mathcal{F}(x,\overline{u}\left(x\right),\overline{w}\left(x\right))\right|\hfill \\ & \le \frac{(x-\frac{1}{5})}{20}\left(\left|\right|w\left(x\right)-\overline{w}\left(x\right)\left|\right|+|cos(\left|u\left(x\right)\right|)-cos\left(\overline{u}\left(x\right)\right)|\right)\hfill \\ & \le \frac{1}{25}\left(\left|\right|w\left(x\right)-\overline{w}\left(x\right)\left|\right|+|cos(\left|u\left(x\right)\right|)-cos\left(\overline{u}\left(x\right)\right)|\right).\hfill \end{array}$$

(54)

Using $\left(H_1\right)$, from (53) and (54), we obtain $k_f=\frac{1}{35}$ and $k_{\mathcal{F}}=\frac{1}{25}.$ By $\left(H_2\right)$,

$$\begin{array}{ccc}\hfill \left|{\mathcal{I}}_i\left(w\right)-{\mathcal{I}}_i\left(\overline{w}\right)\right|& \le & \frac{1}{25}\left|w-\overline{w}\right|,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \left|{\overline{\mathcal{I}}}_i\left(u\right)-{\overline{\mathcal{I}}}_i\left(\overline{u}\right)\right|& \le & \frac{1}{40}\left|u-\overline{u}\right|.\hfill \end{array}$$

Using $\left(H_2\right),$ we get $k_{\mathcal{I}}=\frac{1}{25},$$k_{\overline{\mathcal{I}}}=\frac{1}{40},$

By $\left(H_6\right),$ we have

$$\begin{array}{ccc}\hfill \left|\rho \left(w\right)-\rho \left(\overline{w}\right)\right|& =& \left|\frac{w}{22+\left|w\right|}-\frac{\overline{w}}{22+|\overline{w}|}\right|\hfill \\ & \le & \frac{22\left|w-\overline{w}\right|}{(22+|w\left|\right)(22+|\overline{w}\left|\right)}\le \frac{1}{22}\left|w-\overline{w}\right|,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \left|\varphi \left(u\right)-\varphi \left(\overline{u}\right)\right|& =& \left|\frac{u}{30+\left|u\right|}-\frac{\overline{u}}{30+|\overline{u}|}\right|\hfill \\ & \le & \frac{30\left|u-\overline{u}\right|}{(30+|u\left|\right)(30+|\overline{u}\left|\right)}\le \frac{1}{30}\left|u-\overline{u}\right|.\hfill \end{array}$$

Which implies $k_{\varphi }^{*}=\frac{1}{30}.$ Using the derived values, one may show that

$$max({\chi }_1,{\chi }_2)<1,$$

where

$${\chi }_1=k_{\rho }^{*}+k_{\varphi }^{*}+2(k_f+k_{\mathcal{F}})\frac{{(h_0\left(x_1\right)-h_0\left(0\right))}^{{\varrho }_0}}{\Gamma ({\varrho }_0+1)},$$

and

$${\chi }_2=k_{\rho }^{*}+k_{\varphi }^{*}+\aleph (k_{\mathcal{I}}+k_{\overline{\mathcal{I}}})+2(k_f+k_{\mathcal{F}})\sum _{i=0}^{\mathbb{k}}\frac{{(h_i\left(T\right)-h_i\left(x_i\right))}^{{\varrho }_i}}{\Gamma ({\varrho }_i+1)}.$$

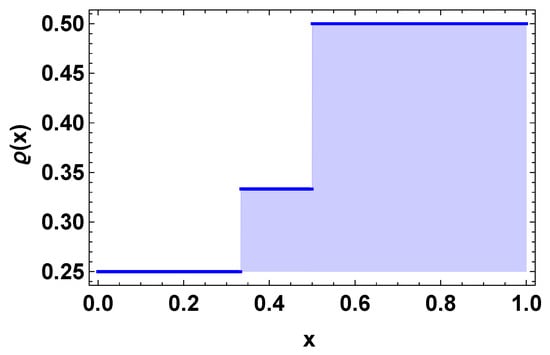
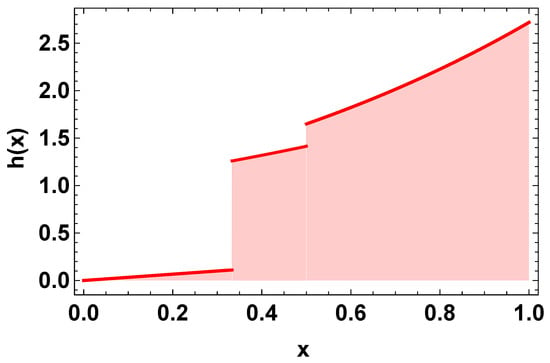
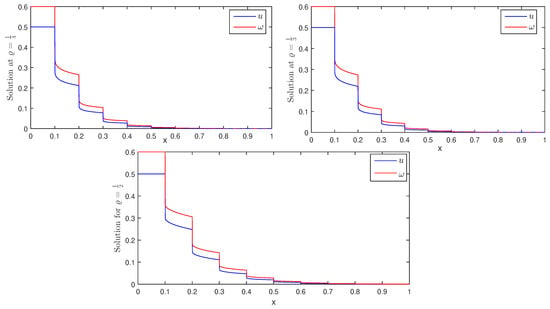
Hence, by Theorem 2, the numerical problem (52) has a unique solution, and by Theorem 3, it is H–U stable. We have presented the piecewise graphs of function ϱ in Figure 1. The graph looks like a stair function. Moreover, the piecewise variable-order graphs for different pieces have been presented in Figure 2. The solution under the impulsive conditions and having piecewise variable-order has been plotted in Figure 3. The impulsive points are given as $0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9.$ From the graph of solution, the crossover behaviors in the dynamics of the considered problem can be observed clearly at the given impulsive points. Hence, DEs with variable kernel have high flexibility due to the freedom of changing the kernel. This manuscript has a multiple stage structure. The problem investigated here has Caputo-type piecewise fractional-order derivative and a variable kernel. It can prove interesting for to readers and researchers working in this area.

Figure 1. Plot for function $\varrho$ in Example 1.

Figure 2. Plot for function h in Example 1.

Figure 3. Solution representation of problem (52) in Example 1.

6. Conclusions

In this work, we have studied a coupled system of piecewise-order differential equations (DEs) with a variable kernel and impulsive conditions. The theoretical analysis is based on Scheafer’s and Banach fixed-point theorems. For stability results, H–U’s concept has been applied. The derived results have been applied to a numerical problem which illustrates the applicability of the main results. The contents of the paper generalize many results already studied in the literature. For the future, the reader should easily extend the results studied in [38,39] under the variable-order with a kernel of variable exponents. In addition, this concept can be extended to various problems of FDEs involving Caputo–Fabrizio or Atangana–Baleanu fractional differential operator with impulsive conditions and variable exponents.