Abstract
This paper proposes an efficient load frequency control (LFC) technique based on a fractional-order proportional–integral–derivative–accelerator with a low-pass filter compensator (FOPIDA-LPF) controller, which can also be accurately referred to as the PIλDND2N2 controller. A trustworthy metaheuristic optimization algorithm, known as the gray wolf optimizer (GWO), is used to fine-tune the suggested PIλDND2N2 controller parameters. Moreover, the proposed PIλDND2N2 controller is designed for the LFC of a self-contained hybrid maritime microgrid system (HMμGS) containing solid oxide fuel cell energy units, a marine biodiesel generator, renewable energy sources (RESs), non-sensitive loads, and sensitive loads. The proposed controller enables the power system to deal with random variations in load and intermittent renewable energy sources. Comparisons with various controllers used in the literature demonstrate the excellence of the proposed PIλDND2N2 controller. Additionally, the proficiency of GWO optimization is checked against other powerful optimization techniques that have been extensively researched: particle swarm optimization and ant lion optimization. Finally, the simulation results performed by the MATLAB software prove the effectiveness and reliability of the suggested PIλDND2N2 controller built on the GWO under several contingencies of different load perturbations and random generation of RESs. The proposed controller can maintain stability within the system, while also greatly decreasing overshooting and minimizing the system’s settling time and rise time.
1. Introduction
The world strives to transition to a low-carbon life where electricity is produced from clean, renewable energy sources (RESs) at reasonable prices to meet daily demands. An increasing number of countries are dedicated to attaining net-zero emissions by the mid-century or shortly after that [1]. Marine energy is the most abundant untapped renewable energy source; the energy of the waves and winds in the oceans and seas meet the world’s needs several times over [2]. Recently, shipboard power systems (SPSs), such as those installed in ships, ferries, warships, vessels, and other marine gear, have considerably grown in size along with their power demands. Lately, due to the rising costs of fossil fuels and progressively tighter emission regulations, modern shipbuilding industries are currently considering how to power all-electric ships (AES). As a result, they should focus on using integrated electric propulsion systems such as steam turbine propulsion, wind propulsion, and solar propulsion, which would allow the ships’ load needs to be met from the same power source. Such systems are also expected to eliminate the need for a separate generation system for these loads and establish a unified electrical platform. The notion of AESs using electric propulsion and integrated power systems (IPSs) has piqued interest in the global shipbuilding industry [3,4].
Recently, there has been growing interest in integrating energy storage systems (ESSs) and RESs into SPSs to reduce sailing costs, thus making such a system increasingly composed of a hybrid marine microgrid system (HMGS). In contrast, the frequency instability issue arises due to the intermittent nature of renewable energy sources (RESs) [5]. To solve this issue, numerous researchers have been working on using energy storage systems such as batteries, superconducting magnetic energy storage systems (SMES), and ultracapacitors as backup resources within hybrid power systems. Nevertheless, cost, conservation, and dumping concerns prevent battery energy storage from being widely used. On the contrary, the flow of costly helium liquid is a significant obstacle for SMES. For such cases, the dynamic tuning of controllable loads such as freezers (FRZ) and heat pumps (HP) may be necessary to reduce the volatility produced by RESs’ deployments. Therefore, the marine bio-diesel generator (MBG) and the non-toxic and eco-friendly solid oxide fuel cell (SOFC) can be considered as supplementary sets in these HMGSs in the standalone operation mode. Furthermore, to counteract the sporadic and erratic nature of RESs, much emphasis is placed in the literature on the appropriate size of various RESs/ESSs within HMGS [6,7]. However, less emphasis has been placed on developing control techniques for frequency regulation and power management in these HMGS [5,6,7,8].
On the other hand, after the tremendous development witnessed by DC microgrids, the attention of those in charge of the marine ship industry turned to work on the shift in ship power systems from AC systems to DC microgrids. However, moving completely from the AC networks to the DC microgrids is difficult, so this process needs time. During this time, hybrid systems that depend on AC and DC systems can be implemented [9,10,11].
In electrical grids, frequency is mainly governed by active power, whereas voltage is primarily regulated by reactive power. As a result, the control standpoint of power systems may be split into two main categories. The first focuses on active power control along with frequency, while the second concerns reactive power control along with voltage [12]. Due to its relevance, frequency control in electrical grids has recently received much attention. Frequency control is included in the primary, secondary, and tertiary stages. The main mission of primary frequency control is intercepting the decline of the frequency to avoid the tripping operation of the under/over frequency protection relays [13]. The responsibility of taking the action of the primary controller is assigned directly to the governor. While the main task of secondary frequency control, which is usually named automatic generation control (AGC) or load frequency control (LFC), is frequency regulation, according to an acceptable range. The main job of tertiary frequency control is to dispatch generating units and auxiliary reserves after a severe disturbance. While RESs are becoming more common in electrical power networks, one of the main challenges that this type of resource faces is the uncertainty of the generated active power, resulting in frequency fluctuations. In addition to demand stochasticity, which is already a permanent source of frequency fluctuations, such fluctuations urgently require more resilient and optimal LFC methods to deal with such problems [14].
Numerous control approaches were proposed to address the LFC issue of power systems with RESs’ penetration by applying distinctive controllers such as proportional–integral (PI) [15], proportional–integral–derivative (PID) [16], proportional–integral–derivative–acceleration (PIDA) [17], fractional-order PID (FOPID) [18], intelligent fractional-order integral [19], ultralocal model control incorporated with LFC [20], non-integer order PID (NOPID) [21], model predictive control [22], non-integer order model predictive control [23], etc. Recently, various innovative control techniques were published in the literature, such as a modified PID controller structure based on the grasshopper optimization algorithm [24], adaptive sliding mode control [25], a fuzzy logic controller [26], and sampled-data control [27]. Although the aforementioned control techniques gave a good response in the frequency regulation of power systems, their designs did not consider the low-inertia issue of modern power systems resulting from the high penetration of RESs. Moreover, most of these studies did not consider the intermittent nature of RESs for short-term frequency stability. The marine microgrid can be categorized as a low-inertia microgrid containing intermittent RESs [5]. Recently, the authors of [28] proposed a linear matrix inequality (LMI) controller approach to handle the LFC issue in maritime microgrids. Likewise, the authors of [29] suggested a fractional-order fuzzy proportional–derivative-one plus integral controller to handle the LFC issues in marine microgrids. Moreover, the HMµG studied in [29] does not consider RESs and non-critical loads. The above-mentioned LMI controller and fractional-order controller have a highly complex structure that results in a long-elapsed time, which would not be practical for actual implementation. Likewise, the authors of [30] investigated a sine–cosine wavelet technique for the frequency regulation of a mobile MµG. Moreover, the above-mentioned control strategy is intricately designed. Additionally, these studies do not consider the power-sharing among RESs and non-critical loads such as heaters and FRZ. Recently, the authors of [5] proposed a two-stage controller, PI-one plus proportional–derivative PI − (1 + PD) controller, to enhance the frequency stability of the MµG. The proposed two-stage controller was designed using the grasshopper optimization algorithm (GOA), which outperformed the genetic algorithm (GA), particle swarm optimization (PSO), firefly algorithm (FA), and cultural algorithm (CA). Motivated by all of the above, this work presents a new, less complicated multi-stage PDND2N2 controller for the LFC of the MµGs, which performs better at transient error reduction in system disturbances.
Aside from controller design, optimal controller parameter modification is a crucial stage for improving system dynamics. As a result, various heuristic algorithmic techniques, such as the genetic algorithm (GA) [15], particle swarm optimization (PSO) [16], the butterfly algorithmic technique (BOA) [18], the mine blast technique (MBA) [31], the cuckoo search technique (CS), the firefly technique (FA) [32], and the flower pollination technique (FPA) [33], are employed to adjust the controllers’ parameters [8,34]. This work uses a reliable metaheuristic optimization algorithm, called the gray wolf optimizer (GWO) [35], to optimize the proposed PIλDND2N2 controller.
The following points serve to highlight the main contribution of this work.
- This study proposes a new PIλDND2N2 controller for the LFC of a self-contained HMμGS, where the proposed controller structure is based on the combination of a PIDND2N2 controller and fractional-order integration.
- The proposed PIλDND2N2 controller is optimally designed using a reliable metaheuristic optimization algorithm, the GWO.
- The proficiency of the GWO algorithm is checked against other powerful optimization techniques that were extensively researched: ant lion optimization (ALO) and PSO.
- For assessing the performance of the suggested controller, the utilized PIλDND2N2 controller’s performance is compared to the performances of other controllers used in the literature under load/RESs fluctuations.
- Finally, the proposed controller allows the power system to mitigate the random load variations and intermittent fluctuations that occur in renewable energy power. As a result, the system stability increases, which significantly reduces overshooting and minimizes the settling time and rise time of the system.
The remaining sections of the article are listed as follows: In Section 2, the considered system, including all its components, is described and modeled. The suggested controller structure and the objective function used for the optimization problem are detailed in Section 3. Section 4 provides an overview of the optimization algorithm used to fine-tune the gains of the proposed controllers. Section 5 provides the simulation results performed by the MATLAB program and their comments. Finally, in Section 6, the paper’s findings are summarized.
2. System Modeling
The suggested HMGS, shown in Figure 1, is schematically described in this section. Furthermore, the studied hybrid system model includes AWPG, WDG, MBG, SOFC, and thermostatically controlled HP and FRZ components. The following subsection discusses the modeling of the intended HMGS. Table 1 presents the values of the studied HMGS parameters.
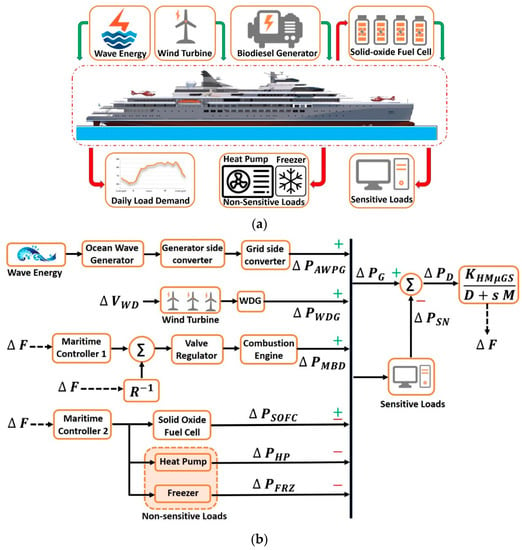
Figure 1.
The studied HMµGS: (a) simplified model of the HMµGS and (b) dynamic model of the HMGS.

Table 1.
The studied HMG parameters.
2.1. Archimedes Wave Power Generation (AWPG)
For the proposed HMGS, AWPG is based on using a permanent magnet synchronous generator (PMSG). As such, the active speed and force of the studied AWPG can be expressed as [36]
The sinusoidal wave strength can be expressed as [5]
The AWPG linearized transfer function can be written as
2.2. Wind-Driven Generation (WDG)
Wind power output depends on the wind velocity and the wind turbine (WT)’s inherent identification due to the unpredictable nature of variable speed induction generators. As a result, the producible mechanical power of WDG [37] could be represented as
For the considered wind station, the rate of change in WDG can be expressed as [38]
The WDG transfer function can be written as
2.3. Marine Bio-Diesel Generator (MBG)
The power generation from a modern MBG set is equivalent to that of a regular diesel generator. Furthermore, the inherently non-toxic, environmentally benign, and good air quality properties of the proposed materials are motivating the considerations for their usage as proposed in this study. MBG’s linearized model is defined as follows (see Figure 2) [39]:
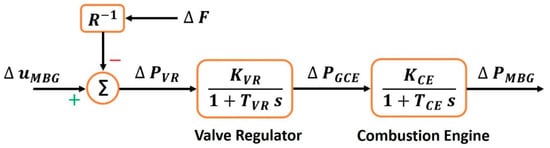
Figure 2.
MBG’s response model of the studied HMGS.
2.4. Solid Oxide Electrolyte Fuel Cell (SOFC)
Generally, a SOFC is an energy storage device that produces electricity by converting oxygen (O2) and concentrated organic hydrogen (H2) energy using a porcelain-based electrolyte and two electrodes. Due to its higher efficiency (i.e., 80%), temperature, and reduced polluting gas emissions, it is gaining popularity among other fuel cell units. The linearized SOFC model is expressed as [5]
2.5. Non-Sensitive Loads (Heat Pump (HP) and Freezer (FRZ))
Due to their better-regulating capability, HP and FRZ are controllable loads that could be used for load frequency regulation and, thus, enhance the HMGS stability. The HP and FRZ transfer functions can be expressed as [5]
2.6. Dynamic Model of the Proposed HMGS
According to the suggested HMGS, as described in Figure 1b, the change in power difference (ΔPD) between the net generated power (ΔPG) and the sensitive load power demand (ΔPSN) could be expressed as
As a result, the model of HMGS frequency response can be stated as
3. Proposed Control Methodology and Objective Function
Over the past few decades, research in control engineering has increasingly been conducted since the introduction of fractional-order (FO) control by I. Podlubny [40]. Using the fractional operators in the controller allows for the general differential and integral notation of any real number. There are two definitions to describe the FO concept. The first is Riemann–Liouville to define the order derivative of a function f(t), as demonstrated in (19) [41].
where is the Gamma function, the parameter q is bounded as n − 1 < q < n, q is the order of the FO calculus, and lb and ub are the lower and upper bands, respectively.
Then, taking the Laplace transformation for the fractional Riemann–Liouville derivative yields the following [19]:
The second definition associated with the basic FO concept is Caputo’s definition, by which the time-domain representation for q order of a function f(t) can be expressed as
Again, taking the Laplace transformation for Equation (21) yields Equation (22), which indicates the integral order has an initial condition and denotes the physical meaning.
where s is the Laplace operator.
The recursive approximation is usually applied to implement the fractional-order definition [42]. The Laplace transformation of the qth derivative is
where
and N is the approximation order of an effective frequency range [].
3.1. Controller Structure
The conventional PID controller has only three parameters to be tuned. The fractional-order PID controller has five parameters, meaning two extra parameters of the integral and fractional orders, λ and µ. Compared to a conventional PID [43], these parameters can enhance the controller’s transient time, stability, and steady-state errors. In addition, they increase the degree of freedom of the controller. The complete transfer function of the fractional-order PID controller (FOPID) is given as
Here, the complete transfer function of the PIλDND2N2 controller is given in (25). Its structure is depicted in Figure 3. It merges two controller forms as PIDND2N2, which allows system stability and amplification to reduce overshoots, minimizing system settling time and rise time [44]. The second controller is the fractional integrator to reduce the rise time and steady-state error in the system, where λ has a range of [0, 2].
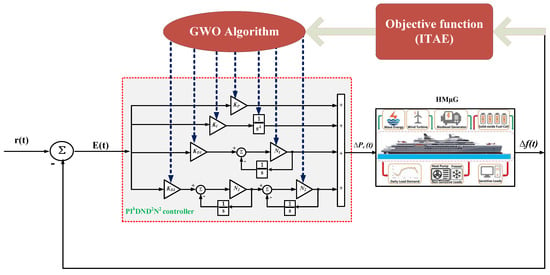
Figure 3.
Structure of the proposed optimal PIλDND2N2 controller-based GWO for the studied HMGS.
3.2. Formulation of the Objective Function (J)
In this study, the proposed control system of the investigated HMGS aims to achieve three main tasks:
- Enabling the RESs to produce the maximum possible power by utilizing their converters/interfacing devices;
- Controlling the extracted power from dispatchable units (SOFC and MBG);
- Controlling the input power of thermostatic non-sensitive loads (HP and FRZ).
As such, the provided control system is equipped with modern optimization approaches to instantaneously tune its parameters, ensuring active power balancing for keeping the reliability and stability of the HMGS. The formulation of the objective function (J) is critical to achieving the optimal dynamics of the system. This research selects the objective function of the integral time absolute error (ITAE), as shown in (26).
Subject to
where i = 1, 2. The proportion (), integral (), and differential () gains were tuned in the range of [0, 10]. While the fractional-order operator of the integral controller (λ) and the coefficient of the derivative filter (N) were tuned in the range of [0, 2] and [50, 1000], respectively.
4. Overview of the Gray Wolf Optimization (GWO) Algorithm
Realistically, computational difficulties may arise in discovering globally optimum solutions from an enormous solution space. Consequently, heuristic optimization algorithms were developed to discover feasible solutions within a vast solution space efficiently. Moreover, recent research in meta-heuristic optimization methods, such as that discussed in Section 1, introduced effective techniques for handling complex, real-time, and nonlinear problems.
The valuable feature of the GWO method over other well-known meta-heuristic algorithms is that its function does not require specific input parameters. Furthermore, it is simple and devoid of computational complexity. Its advantages also include the ease with which the GWO algorithm can be translated into programming languages and the ease with which the GWO algorithm can be understood. The authors attempted to develop and fine-tune the suggested load frequency controllers on the proposed HMGS based on GWO optimization.
GWO emulates the natural hunting mechanism and leadership hierarchy of gray wolves (GWs). GWs adapt to living in sets (5–12 on average). As described in [33], four types of GWs, α (alpha), β (beta), δ (delta), and Ω (omega), are used to simulate the hierarchy of leadership. Furthermore, the prey-hunting process in the GWO algorithm consists of three primary strategies: seeking, encircling, and attacking. For modeling the GWs behavioral patterns, α was deemed the fittest solution, followed by β and δ, and the other remaining solutions are categorized as Ω. In GWO, hunting (optimization) operations are driven by α, β, and δ wolves, with Ω always following these three wolves. Both Equations (28) and (29) are used to model the behavior of GW encircling prey.
where
t: current iteration; and
: victim’s current position,
while and are the coefficient vectors, which are determined by Equations (30) and (31), respectively.
where and are two random vectors between [0, 1], while, over each course of the iteration, the component linearly decreases from 2 to 0.
During the hunting process, which is primarily directed by alphas, the GWs’ positions are updated. Even though alphas are the principal actors in the hunting process, betas and deltas do occasionally participate. To determine the GWs’ optimum positions, the three best solutions (for α, β, and δ) are stored, while the rest of the solutions, including Ω, are competing. Equations (32)–(34) are used to update the positions of the GWs.
It can be seen that the final position varies within the circle that is entirely identified by the α, β, and δ in the search area. In contrast, other GWs update their position by forecasting the prey position. Two parameters are considered to mathematically express the modeling of the approaching methodology to the prey: that decreases linearly from 2 to 0 and that would be in the range of [−, ]. When is between [−1, 1], the search agent’s next position could be any position between the prey and the current position.
So, in GWO, the optimum search depends on the positions of α, β, and δ. They diverge while searching for prey and converge while attacking it. Mathematically, when 1 or −1, the search agent diverges to prey. Another variable in GWO that aids the exploration mechanism is named ; according to Equation (31), the value of varies between [0, 2], which affects defining the distance of the prey, as in Equation (29). As a result, GWO exhibits more random behavior, enhancing exploration and avoiding local optima. The overall flowchart of the GWO algorithm is presented in Figure 4; more details on GWO are given in [35].
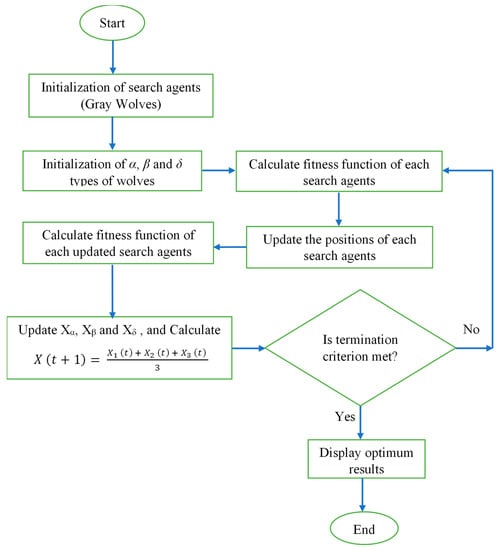
Figure 4.
Overall flowchart of GWO algorithm.
5. Results of the Simulation and Discussion
The performance of the proposed PIλDND2N2 controller based on the GWO algorithm is verified in that it enhances the frequency stability of the considered HMGS. The numerical results of the studied system are executed using MATLAB/Simulink® software to assess the robustness and efficacy of the proposed PIλDND2N2 controller. To carry out the optimization (i.e., the GWO algorithm) process, its code is executed in an m-file and interfaced with the HMGS model built by the Simulink model. The simulation program runs on a laptop with an Intel® Core i5-2.6 GHz processor and 8.0 GB RAM. Moreover, the proficiency of the GWO algorithm used to obtain the optimal parameters of the proposed LFC-based PIλDND2N2 controller is verified by comparing its performance with that of the other optimization algorithms used in the literature (e.g., ALO and PSO algorithms). Moreover, the outperformance of the proposed PIλDND2N2 controller is validated over that of the conventional PID controller, which was designed using different optimization algorithms. Under numerous different operating circumstances, the frequency regulation of the considered HMGS is validated using the following scenarios.
Scenario 1: Investigation of the proposed PIλDND2N2 controller using various optimization algorithms.
The effectiveness of the GWO algorithm used to fine-tune the suggested PIλDND2N2 controllers’ parameters in the considered HMGS is confirmed by evaluating its effectiveness against the other optimization algorithms used in the literature (e.g., ALO and PSO algorithms). This scenario is addressed in the following three different operation cases:
Case A: Assessment of system performance in the event of a sudden load change.
In this case, the proposed PIλDND2N2 controllers in the considered HMGS are fine-tuned using the proposed GWO algorithm, in addition to the other two optimization algorithms (i.e., ALO and PSO algorithms), considering a 20% sudden load change in the sensitive load demand at t = 5 s. Additionally, this case considers the studied system without RESs (i.e., AWPG and WDG). The optimization algorithms used are set with 100 iterations and 30 search agents. The optimal parameters of the proposed PIλDND2N2 controllers, which are designed using various optimization algorithms (i.e., GWO, ALO, and PSO), are given in Table 2. Figure 5 shows the convergence curve of the optimization algorithms that are used. The proposed GWO algorithm outperforms the other algorithms in terms of convergence characteristics and objective function. Figure 6 shows the frequency deviation of the considered HMGS with the proposed PIλDND2N2 controllers, which were designed using various optimization algorithms under the operating conditions of this case. The results show that the suggested controller based on the GWO algorithm gives superior performance, with less overshoot, less undershoot, and a faster settling time than other optimization algorithms (i.e., ALO and PSO).

Table 2.
The optimal parameters of the proposed PIλDND2N2 controllers using various optimization algorithms.
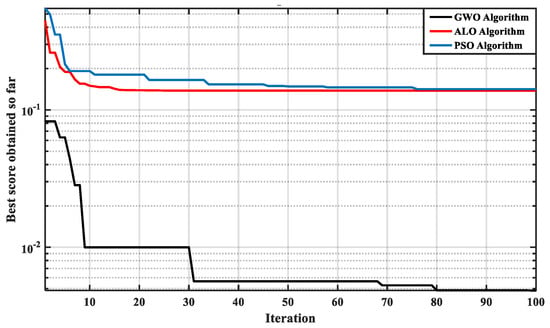
Figure 5.
The convergence curve of the optimization algorithms used.
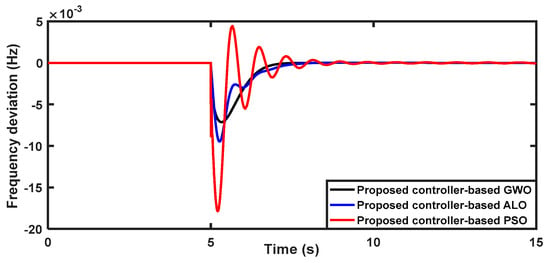
Figure 6.
System frequency deviation for Scenario 1, Case A.
Case B: Assessment of system performance in the event of a sudden load change and the fixed generation of RESs.
In this case, the performance of the considered HMGS with the proposed PIλDND2N2 controllers, which are designed using various optimization algorithms, is examined under a 0.2 pu sudden load change in the sensitive load demand at t = 0 s onwards, a 0.1 pu of WDG during (0 ˂ t ˂ 100 s) and 0.15 pu at t = 100 s onwards, and a 0.1 pu of AWPG at t = 0 s onwards. Table 2 indicates the optimal parameters of the proposed controllers designed using the various optimization algorithms used in this case. Figure 7 displays the frequency deviation of the investigated grid with the proposed PIλDND2N2 controllers based on various optimization algorithms. Figure 7 makes it clear that the investigated HMGS with the suggested PIλDND2N2 controllers based on the GWO algorithm is more efficient and reliable than using other optimization algorithms across all the difficulties encountered by the system.
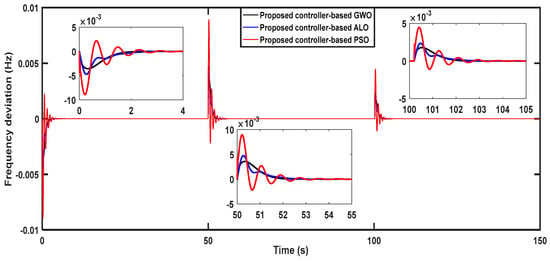
Figure 7.
System frequency deviation for Scenario 1, Case B.
Case C: Assessment of system performance in the event of a random load change as well as random RESs generation.
Under this case study, a random generation of WDG and AWPG, as shown in Figure 8, and a random load change in the sensitive load demand, as shown in Figure 9, are considered to examine the studied HMGS with the proposed PIλDND2N2 controllers, which are designed using various optimization algorithms. The profile of the load change in the sensitive load demand shown in Figure 9 was obtained using the random load model shown in Figure 10, which was extracted from [45]. The optimal gains of the suggested controllers designed using the various optimization algorithms used in this case are given in Table 2. Figure 11 shows the frequency deviation of the analyzed system with the suggested PIλDND2N2 controllers based on various optimization algorithms. The simulation results show that the suggested PIλDND2N2 controllers based on the GWO algorithm could dampen the high-frequency deviations resulting from high load/RESs fluctuations compared to other optimization algorithms. Therefore, the proposed PIλDND2N2 controllers based on the GWO algorithm give superior performance in improving the frequency stability of the considered HMGS than using the other optimization algorithms used in the literature. The system performance specifications in terms of maximum undershoot (MUS), maximum overshoot (MOS), and maximum settling time (Ts) for the investigated system are given in Table 3. From these numerical results, it is evident that the suggested PIλDND2N2 controllers based on the GWO algorithm surpass the other employed algorithms, leading to superior results. Therefore, it is most suitable for the frequency regulation of the considered HMGS.
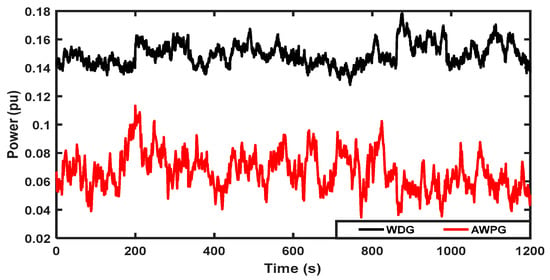
Figure 8.
Power profile of WDG and AWPG.
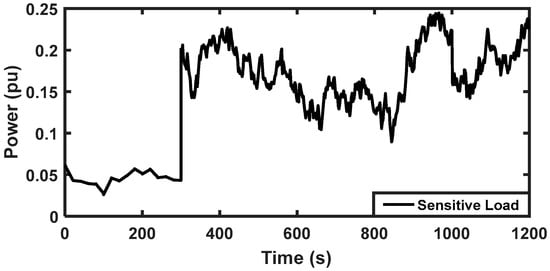
Figure 9.
Random load change in sensitive load demand.
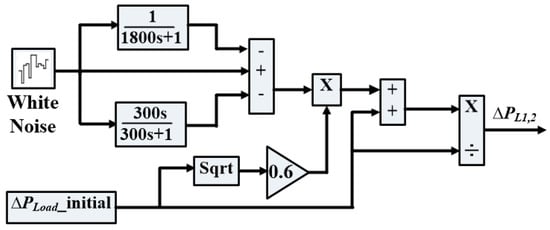
Figure 10.
The random load model using MATLAB/Simulink [45].
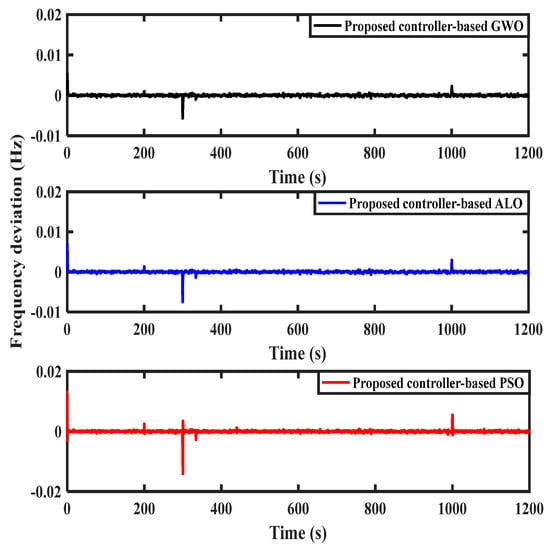
Figure 11.
System frequency deviation for Scenario 1, Case C.

Table 3.
System performance specification for Scenario 1, under various optimization algorithms.
Scenario 2: Comparison of the suggested PIλDND2N2 controller’s performance and the PID controller designed using various optimization algorithms.
To validate the superiority of the suggested PIλDND2N2 controller based on the GWO algorithm, its performance is compared with both the PID controller based on the GWO algorithm and the PID controller based on the GOA [5]. The optimal parameters of the suggested PIλDND2N2 controllers based on the GWO and other compared PID controllers are given in Table 4. This scenario is addressed in the following three different operation cases:

Table 4.
The optimal parameters of the suggested PIλDND2N2 controllers and the compared PID controllers.
Case A: Assessment of system performance inthe event of a sudden load change.
The performance of the considered HMGS with the suggested PIλDND2N2 controllers based on the GWO algorithm is compared with the PID controller based on the GWO algorithm and the PID controller based on the GOA [5] under a 20% sudden load change in the sensitive load demand at t = 5 s. Additionally, this case considers the studied system without RESs (i.e., AWPG and WDG). Figure 12 shows the system frequency deviation using each of the suggested PIλDND2N2 controllers based on the GWO algorithm, the PID controller based on the GWO algorithm, and the PID controller based on the GOA [5]. The results demonstrate that the suggested PIλDND2N2 controller performs better than the other PID controllers. Moreover, the proposed controller exhibits optimal performance by achieving reduced overshoot, reduced undershoot, and a faster settling time than the other used controllers.
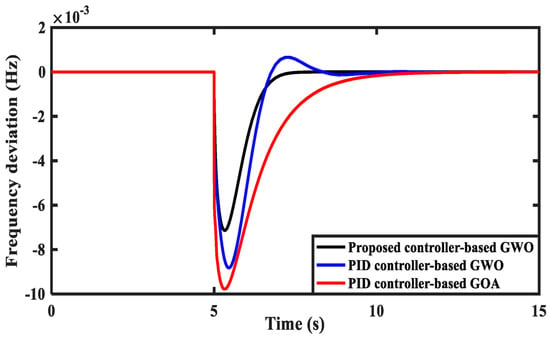
Figure 12.
System frequency deviation for Scenario 2, Case A [5].
Case B: System performance evaluation in the event of a random load change as well as random RESs generation.
To evaluate the effectiveness and robustness of the suggested PIλDND2N2 controllers based on the GWO algorithm, the random generation of WDG and AWPG shown in Figure 8 and the random load change in the sensitive load demand shown in Figure 9 are considered in the studied HMGS. Moreover, the optimal parameters of the suggested PIλDND2N2 controllers based on the GWO and the other compared PID controllers used in this case are given in Table 4. Figure 13 displays the frequency deviation of the system studied with the suggested PIλDND2N2 controllers based on the GWO algorithm. As shown in Figure 13, the proposed PIλDND2N2 controller shows a reliable behavior compared to the PID controller based on the GWO algorithm and the PID controller based on the GOA [5], despite the high load/RESs fluctuations. The system performance specifications in terms of the MOS, MUS, and Ts for the investigated system under Scenario 2 are given in Table 5. This analysis shows that the suggested PIλDND2N2 controllers based on the GWO algorithm give better results than the PID controller based on the GWO algorithm and the PID controller based on the GOA [5]. Therefore, it is most suitable for the frequency regulation of the considered HMGS when considering high load/RESs fluctuations.
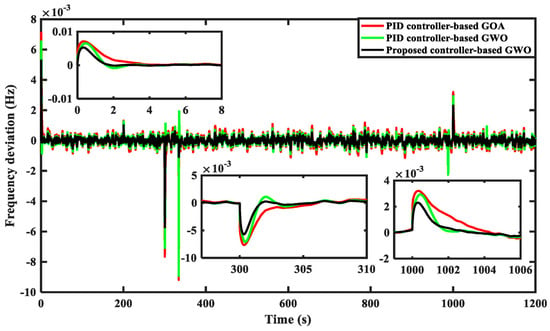
Figure 13.
System frequency deviation for Scenario 2, Case B [5].

Table 5.
System performance specification for Scenario 2.
6. Conclusions
This paper discussed supporting the frequency response of the low-inertia self-contained hybrid maritime microgrid system containing a marine biodiesel generator and renewable energy sources by proposing a combination of a PIDND2N2 controller and a fractional-order integration, referred to as a PIλDND2N2 controller. The associated gains of the suggested PIDND2N2 controller were optimally computed using the gray wolf optimization approach. The simulation results validated that the proposed controller provides optimal dynamic stability metrics compared to the conventional controllers based on PID controllers. In addition, the proposed controller allowed the power system to mitigate the random load variations and intermittent fluctuations that occur in renewable energy power. By employing the proposed controller, the system could maintain stability and avoid fluctuations, resulting in a reduction in overshooting by over 19%. Additionally, the settling time and rise time of the system were shortened by more than 71%, leading to more efficient and effective performance. Future work will focus on distributing the inertia property required for the maritime microgrid to compensate for the high penetration of RESs among the distributed energy resources in the power system. Moreover, the robust integral scheme for the nonlinear system can be applied to handle the mismatch uncertainties in the system.
Author Contributions
Conceptualization, methodology, writing—original draft: F.M.A., G.M., A.B., K.S.S.A. and M.R. Investigation, validation, software: G.M. and A.B. Visualization: G.M., A.B. and M.R. Writing—review and editing: F.M.A., A.B., G.M., K.S.S.A. and M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the University of Tabuk, grant number S-1443-0207 (https://www.ut.edu.sa/en/Deanship/scientific-research/Pages/default.aspx (accessed on 1 April 2023)).
Data Availability Statement
Data are available from the authors upon reasonable request.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at the University of Tabuk for funding this work through grant no. S-1443-0207.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| AESs | All-Electric Ships |
| AGC | Automatic Generation Control |
| ALO | Ant Lion Optimization |
| AWPG | Archimedes Wave Power Generation |
| BOA | Butterfly Optimization Algorithmic |
| CS | Cuckoo Search |
| ESSs | Energy Storage Systems |
| FA | Firefly Algorithm |
| FO | Fractional Order |
| FOPID | Fractional Order Proportional–Integral–Derivative |
| FPA | Flower Pollination Algorithm |
| FRZ | Freezers |
| GA | Genetic Algorithm |
| GOA | Grasshopper Optimization Algorithmic |
| GWs | Gray Wolves |
| GWO | Gray Wolf Optimizer |
| HMμGS | Hybrid Maritime Microgrid System |
| HP | Heat Pump |
| IPS | Integrated Power System |
| ITAE | Integral Time Absolute Error |
| LFC | Load Frequency Control |
| LMI | Linear Matrix Inequality |
| MBA | Mine Blast Algorithm |
| MBG | Marine Bio-diesel Generator |
| MµG | Maritime Microgrid |
| MOS | Maximum Overshoot |
| MUS | Maximum Under Shoot |
| NOPID | Non-integer Order Proportional–Integral–Derivative |
| PI | Proportional–Integral |
| PID | Proportional–Integral–Derivative |
| PI-(1 + PD) | PI-one plus Proportional–Derivative |
| PIDND2N2 | Proportional–Integral–Derivative with low-pass filter-derivative with two low-pass filter controllers |
| PIλDND2N2 | PIDND2N2 controller with fractional order integration |
| PMSG | Permanent Magnet Synchronous Generator |
| PSO | Particle Swarm Optimization |
| RESs | Renewable Energy Sources |
| SOFC | Solid Oxide Fuel Cell |
| SPS | Shipboard Power Systems |
| SMES | Superconducting Magnetic Energy Storage systems |
| WDG | Wind-Driven Generation |
| WTs | Wind Turbines |
| Valve Regulator Gain | |
| Combustion Engine Gain | |
| Time delay of Valve Regulator (s) | |
| constant Time of Combustion Engine (s) | |
| WDG gain | |
| WDG Time constant (s) | |
| AWPG gain | |
| AWPG Time constant(s) | |
| SOFC gain | |
| SOFC Time constant (s) | |
| HP gain | |
| HP Time constant (s) | |
| FRZ gain | |
| FRZ Time constant (s) | |
| M | Moment of inertia of HMG (s) |
| D | Damping co-factor of HMGS (p.u./Hz) |
| Velocity of floater-generator set (m/s) | |
| Floater-translator set movement (m) | |
| Wave strengths (N) | |
| Overall mass (kg) | |
| Damping factor of synchronous generator (N s/m) | |
| Damping factor of AWPG (N s/m) | |
| Spring coefficient (N/m) | |
| Magnitude of wave strength | |
| Radial frequency of wave strength | |
| Air density (Kg/m3) | |
| Radius of turbine (m) | |
| Wind speed (m/s) | |
| Extractable power coefficient of WT | |
| Tip speed ratio | |
| Pitch angle | |
| Change in input error of MBG | |
| Output control signal of the controller |
References
- Net Zero by 2050 A Roadmap for the Global Energy Sector; International Energy Agency: Paris, France, 2021.
- Marine Power Systems. Available online: https://www.marinepowersystems.co.uk/marine-energy/ (accessed on 17 March 2022).
- Guerrero, J.M.; Jin, Z.; Liu, W.; Othman, M. Shipboard Microgrids: Maritime Islanded Power Systems Technologies. In Proceedings of the International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Aalborg, Denmark, 28–30 June 2016. [Google Scholar]
- Thongam, J.s.; Tarbouchi, M.; Okou, A.F.; Bouchard, D.; Beguenane, R. All-Electric Ships-A Review of the Present State of the Art. In Proceedings of the IEE, Eighth International Conference and Exhibition on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 27–30 March 2013. [Google Scholar]
- Latif, A.; Hussain, S.M.S.; Das, D.C.; Ustun, T.S. Double stage controller optimization for load frequency stabilization in hybrid wind-ocean wave energy based maritime microgrid system. Appl. Energy 2020, 282, 116171. [Google Scholar] [CrossRef]
- Maleki, A.; Askarzadeh, A. Optimal sizing of a PV/wind/diesel system with battery storage for electrification to an off-grid remote region: A case study of Rafsanjan, Iran. Sustain. Energy Technol. Assess. 2014, 7, 147–153. [Google Scholar] [CrossRef]
- Lan, H.; Wen, S.; Hong, Y.-Y.; Yu, D.C.; Zhang, L. Optimal sizing of hybrid PV/diesel/battery in ship power system. Appl. Energy 2015, 158, 26–34. [Google Scholar] [CrossRef]
- Maleki, A.; Askarzadeh, A. Artificial bee swarm optimization for optimum sizing of a stand-alone PV/WT/FC hybrid system considering LPSP concept. Sol. Energy 2014, 107, 227–235. [Google Scholar] [CrossRef]
- Haseltalab, A.; Wani, F.; Negenborn, R.R. Multi-level model predictive control for all-electric ships with hybrid power generation. Int. J. Electr. Power Energy Syst. 2022, 135, 107484. [Google Scholar] [CrossRef]
- Caravella, T.; Austell, C.; Brady-Alvarez, C.; Elsaiah, S. Hybrid Maritime Microgrids: A Quest for Future Onboard Integrated Marine Power Systems. In Innovation in Energy Systems—New Technologies for Changing Paradigms; IntechOpen: Rijeka, Croatia, 2019. [Google Scholar] [CrossRef]
- Othman, M.; Anvari-Moghaddam, A.; Guerrero, J.M. Hybrid shipboard microgrids: System architectures and energy management aspects. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 6801–6806. [Google Scholar] [CrossRef]
- Magdy, G.; Shabib, G.; Elbaset, A.A.; Mitani, Y. Renewable Power Systems Dynamic Security. Power Syst. 2020, 44, 1–13. [Google Scholar] [CrossRef]
- Magdy, G.; Shabib, G.; Elbaset, A.A.; Mitani, Y. A Novel Coordination Scheme of Virtual Inertia Control and Digital Protection for Microgrid Dynamic Security Considering High Renewable Energy Penetration. In IET Renewable Power Generation; Institution of Engineering and Technology (IET): London, UK, 2019; Volume 54513, pp. 462–474. [Google Scholar] [CrossRef]
- Alhelou, H.H.; Hamedani-Golshan, M.-E.; Zamani, R.; Heydarian-Forushani, E.; Siano, P. Challenges and Opportunities of Load Frequency Control in Conventional, Modern and Future Smart Power Systems: A Comprehensive Review. Energies 2018, 11, en11102497. [Google Scholar] [CrossRef]
- Das, D.C.; Roy, A.K.; Sinha, N. GA based frequency controller for solar thermal–diesel–wind hybrid energy generation/energy storage system. Int. J. Electr. Power Energy Syst. 2012, 43, 262–279. [Google Scholar] [CrossRef]
- Das, D.C.; Sinha, N.; Roy, A.K. Automatic Generation Control of an Organic Rankine Cycle Solar-Thermal/Wind-Diesel Hybrid Energy System. Energy Technol. 2014, 2, 721–731. [Google Scholar] [CrossRef]
- Kumar, M.; Hote, Y.V. Robust IMC-PIDA Controller Design for Load Frequency Control of a Time delayed Power System. In Proceedings of the IEEE 58th Conference on Decision and Control (CDC), Nice, France, 1 December 2019; pp. 8380–8385. [Google Scholar] [CrossRef]
- Nour, M.; Magdy, G.; Chaves-Ávila, J.P.; Sánchez-Miralles, Á.; Jurado, F. A new two-stage controller design for frequency regulation of low-inertia power system with virtual synchronous generator. J. Energy Storage 2023, 62, 106952. [Google Scholar] [CrossRef]
- Zaid, S.A.; Bakeer, A.; Magdy, G.; Albalawi, H.; Kassem, A.M.; El-Shimy, M.E.; AbdelMeguid, H.; Manqarah, B. A New Intelligent Fractional-Order Load Frequency Control for Interconnected Modern Power Systems with Virtual Inertia Control. Fractal Fract. 2023, 7, 62. [Google Scholar] [CrossRef]
- Bakeer, A.; Magdy, G.; Chub, A.; Jurado, F.; Rihan, M. Optimal Ultra-Local Model Control Integrated with Load Frequency Control of Renewable Energy Sources Based Microgrids. Energies 2022, 15, 9177. [Google Scholar] [CrossRef]
- Latif, A.; Das, D.C.; Barik, A.K.; Ranjan, S. Maiden co-ordinated load frequency control strategy for ST-AWEC-GEC-BDDG based independent three-area interconnected microgrid system with the combined effect of diverse energy storage and DC link using BOA optimized PFOID controller. IET Renew. Power Gener. 2019, 13, 2634–2646. [Google Scholar] [CrossRef]
- Magdy, G.; Bakeer, A.; Alhasheem, M. Robust decentralized model predictive load-frequency control design for time-delay renewable power systems. Int. J. Emerg. Electr. Power Syst. 2021, 22, 617–628. [Google Scholar] [CrossRef]
- Chen, M.-R.; Zeng, G.-Q.; Dai, Y.-X.; Lu, K.-D.; Bi, D.-Q. Fractional-Order Model Predictive Frequency Control of an Islanded Microgrid. Energies 2019, 12, 84. [Google Scholar] [CrossRef]
- Nosratabadi, S.M.; Bornapour, M.; Gharaei, M.A. Grasshopper optimization algorithm for optimal load frequency control considering predictive Functional Modified PID controller in restructured multi-resource multi-area power system with Redox Flow Battery units. Control Eng. Pract. 2019, 89, 204–227. [Google Scholar] [CrossRef]
- Guo, J. Application of a novel adaptive sliding mode control method to the load frequency control. Eur. J. Control 2020, 2020, 172–178. [Google Scholar] [CrossRef]
- Jalali, N.; Razmi, H.; Doagou-Mojarrad, H. Optimized fuzzy self-tuning PID controller design based on Tribe-DE optimization algorithm and rule weight adjustment method for load frequency control of interconnected multi-area power systems. Appl. Soft Comput. 2020, 93, 106424. [Google Scholar] [CrossRef]
- Shang-Guan, X.; He, Y.; Zhang, C.; Jiang, L.; Spencer, J.W.; Wu, M. Sampled-data based discrete and fast load frequency control for power systems with wind power. Appl. Energy 2020, 259, 114202. [Google Scholar] [CrossRef]
- Vafamand, N.; Khooban, M.H.; Dragicevic, T.; Boudjadar, J.; Asemani, M.H. Time-delayed stabilizing secondary load frequency control of shipboard microgrids. IEEE Syst. J. 2019, 13, 3233–3241. [Google Scholar] [CrossRef]
- Khooban, M.-H.; Dragicevic, T.; Blaabjerg, F.; Delimar, M. Shipboard Microgrids: A Novel Approach to Load Frequency Control. IEEE Trans. Sustain. Energy 2018, 9, 843–852. [Google Scholar] [CrossRef]
- Khooban, M.-H.; Gheisarnejad, M.; Vafamand, N.; Jafari, M.; Mobayen, S.; Dragicevic, T.; Boudjadar, J. Robust Frequency Regulation in Mobile Microgrids: HIL Implementation. IEEE Syst. J. 2019, 13, 4281–4291. [Google Scholar] [CrossRef]
- Ranjan, S.; Das, D.C.; Latif, A.; Sinha, N. LFC for autonomous hybrid microgrid system of 3 unequal renewable areas using mine blast algorithm. Int. J. Renew. Energy Res. 2018, 8, 1297–1308. [Google Scholar]
- Latif, A.; Pramanik, A.; Das, D.C.; Hussain, I.; Ranjan, S. Plug in hybrid vehicle-wind-diesel autonomous hybrid power system: Frequency control using FA and CSA optimized controller. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 1147–1158. [Google Scholar] [CrossRef]
- Hussain, I.; Ranjan, S.; Das, D.C.; Sinha, N. Performance Analysis of Flower Pollination Algorithm Optimized PID Controller for Wind-PV-SMES-BESS-Diesel Autonomous Hybrid Power System. Int. J. Renew. Energy Res. 2017, 7, 643–651. [Google Scholar]
- Latif, A.; Suhail Hussain, S.M.; Das, D.C.; Ustun, T.S. State-of-the-art of controllers and soft computing techniques for regulated load frequency management of single/multi-area traditional and renewable energy based power systems. Appl. Energy 2020, 266, 114858. [Google Scholar] [CrossRef]
- Mirjalili, S.S.; Mirjalili, M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Hasanien, M.H. Whale optimisation algorithm for automatic generation control of interconnected modern power systems including renewable energy sources. IET Gener. Transm. Distrib. 2018, 12, 607–614. [Google Scholar] [CrossRef]
- Rihan, M.; Nasrallah, M.; Hasanin, B. Performance analysis of grid-integrated brushless doubly fed reluctance generator-based wind turbine: Modelling, control and simulation. SN Appl. Sci. 2020, 2, 114. [Google Scholar] [CrossRef]
- Lee, D.-J.; Wang, L. Small-Signal Stability Analysis of an Autonomous Hybrid Renewable Energy Power Generation/Energy Storage System Part I: Time-Domain Simulations. IEEE Trans. Energy Convers. 2008, 23, 311–320. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; El-Hameed, M.A. Efficient frequency controllers for autonomous two-area hybrid microgrid system using social-spider optimizer. IET Gener. Transm. Distrib. 2017, 11, 637–648. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and fractional-order controllers. In Proceedings of the International Conference of Francophone d’Automatique, Grenoble, France, 19–23 September 1994. [Google Scholar]
- Morsali, J.; Zare, K.; Tarafdar Hagh, M. Applying fractional order PID to design TCSC-based damping controller in coordination with automatic generation control of interconnected multi-source power system. Eng. Sci. Technol. Int. J. 2017, 20, 1–17. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. In IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications; IEEE: New York, NY, USA, 2000; Volume 47, pp. 25–39. [Google Scholar] [CrossRef]
- Moschos, I.; Parisses, C. A novel optimal PIλDND2N2 controller using coyote optimization algorithm for an AVR system. Eng. Sci. Technol. Int. J. 2022, 26, 100991. [Google Scholar] [CrossRef]
- Agrawal, K.; Negi, R.; Singh, N. Dynamically tuned PIDD2 controller for single-link flexible manipulator. In Lecture Notes in Electrical Engineering; Springer: Singapore, 2019; pp. 907–924. [Google Scholar]
- Magdy, G.; Shabib, G.; Elbaset, A.A.; Mitani, Y. Renewable power systems dynamic security using a new coordination of frequency control strategy based on virtual synchronous generator and digital frequency protection. Int. J. Electr. Power Energy Syst. 2019, 109, 351–368. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).