Analysis of a Fractional-Order Model for African Swine Fever with Effect of Limited Medical Resources
Abstract
1. Introduction
2. Qualitative Analysis of System (1)
2.1. The Existence and Uniqueness of a Positive Solution
2.2. The Basic Reproduction Number and the Existence of Equilibriums
2.3. The Stability of the Disease-Free Equilibrium
2.4. The Stability of Endemic Equilibrium
3. Numerical Simulations
4. Discussion
- ◊
- If , then the disease-free equilibrium is the unique equilibrium of system (1) and it is asymptotically stable within .
- ◊
- If , then may be stable for a relatively small value of , or it may be unstable for a relatively large value of ; and the endemic equilibrium appears.
- ◊
- If , then the endemic equilibrium exists and it may be stable for some values of or unstable for other values of .
- ◊
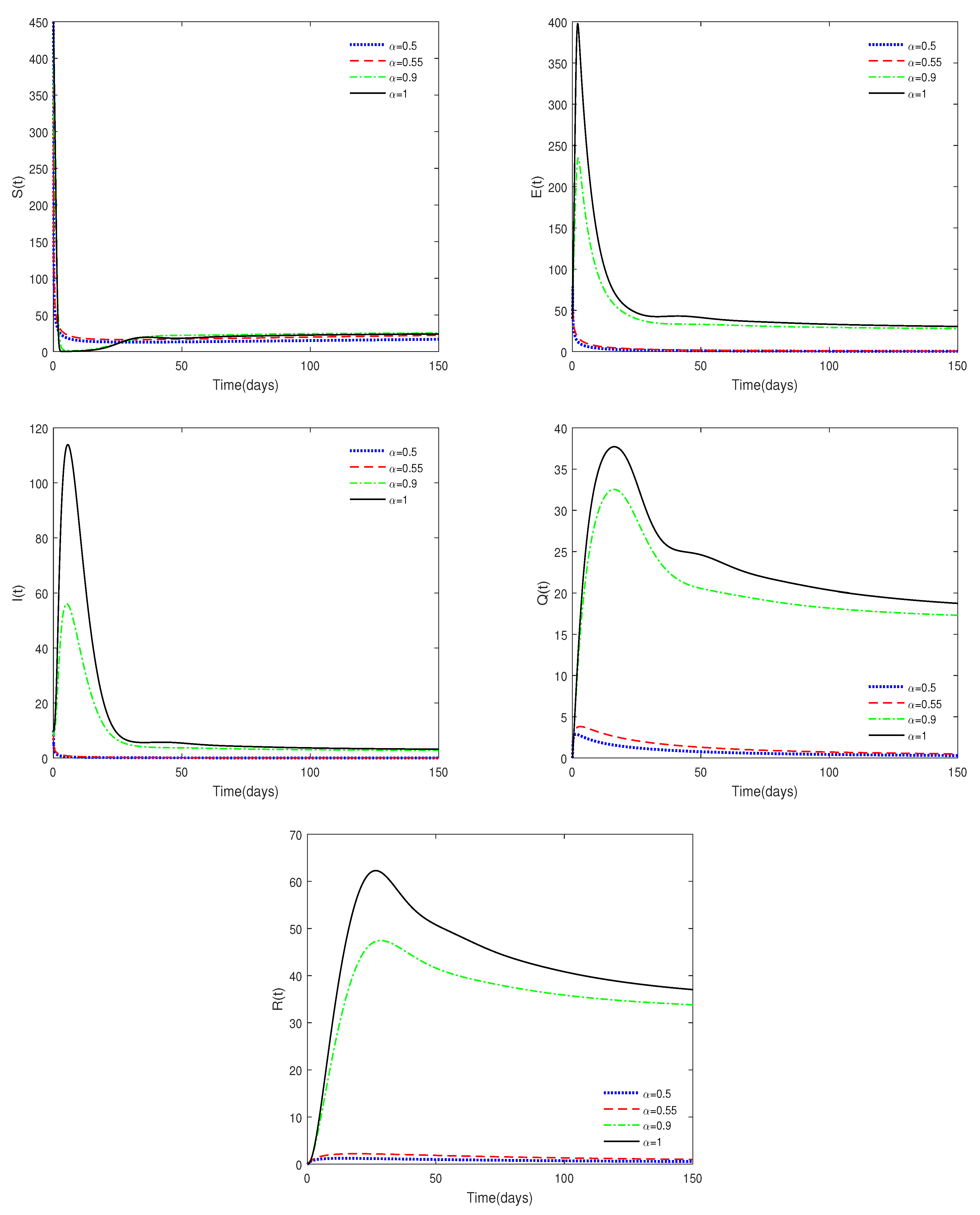
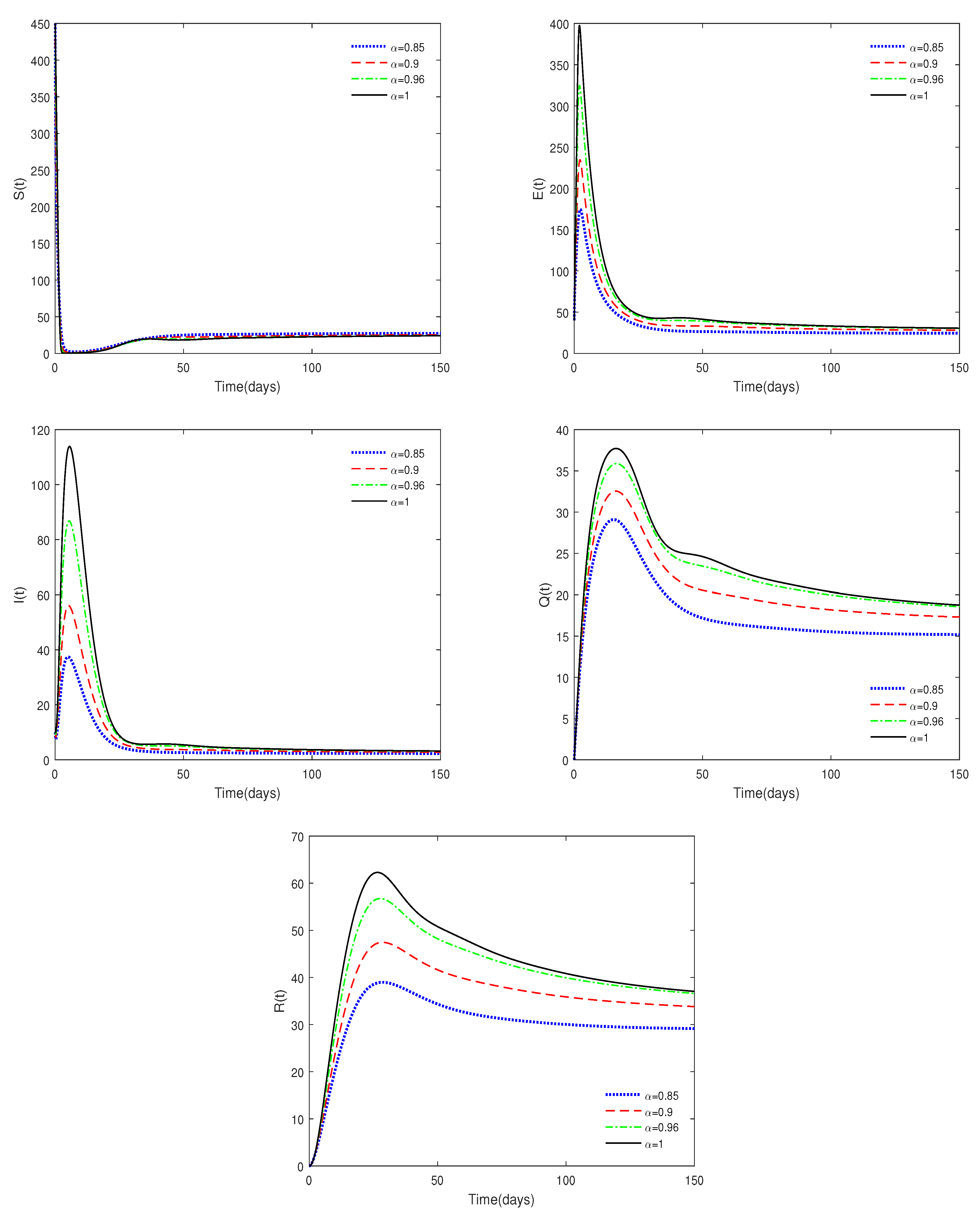
- Figure 1 and Figure 2 show that the values of and are crucial to the dynamics of the system. If , then the disease-free equilibrium is always stable for different values of . If , then the disease-free equilibrium may be stable for a relatively small value of ; while it is unstable with a relatively large value of . This result shows the difference between fractional-order systems and integer-order systems.
- ◊
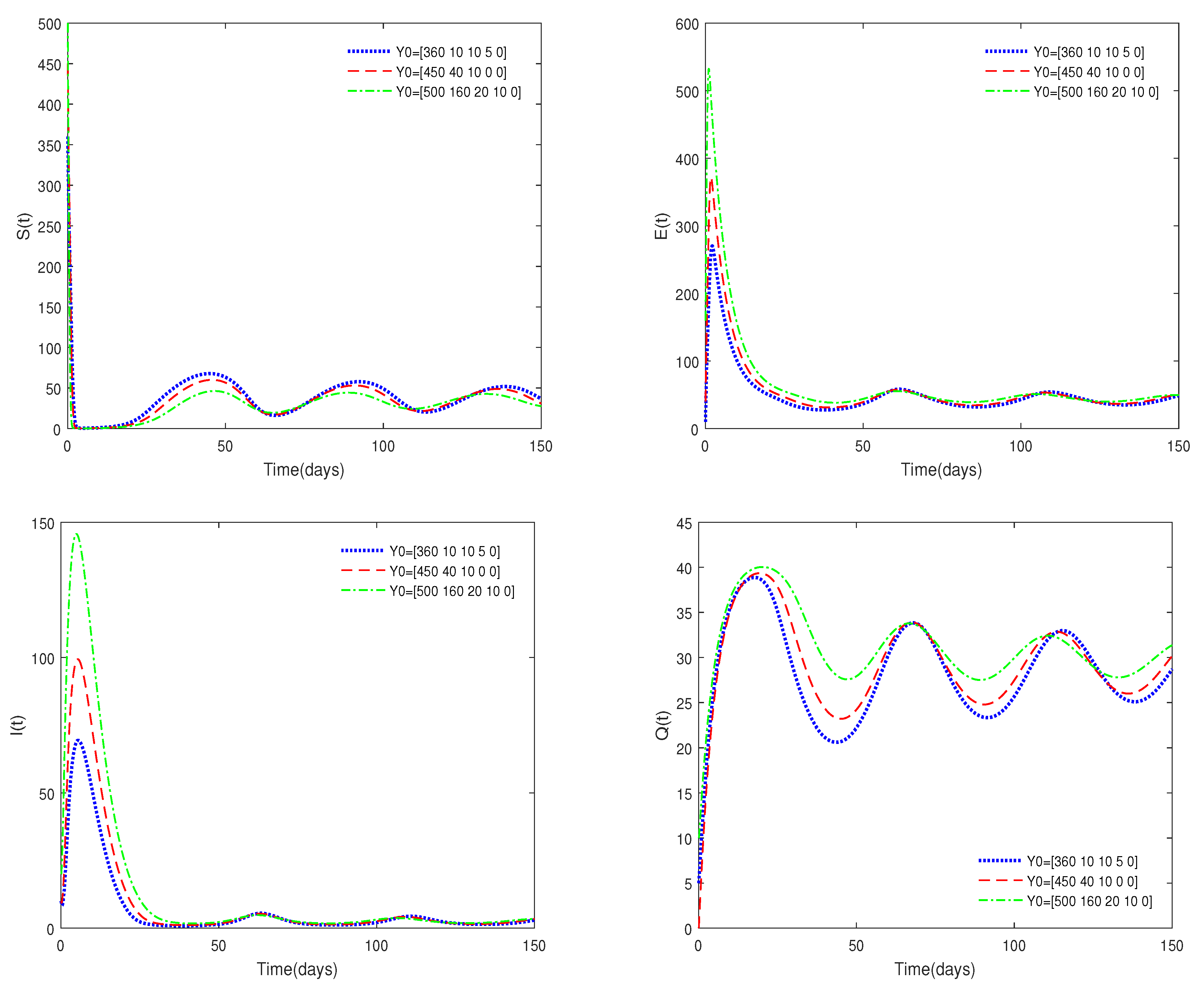
- Figure 3 shows that if the Routh–Hurwitz conditions are satisfied, then the endemic equilibrium is stable for different values of . Figure 4 shows that the endemic equilibrium may be unstable if the Routh–Hurwitz conditions are not satisfied. Figure 5 shows that the initial values are not important to the stability of the endemic equilibrium .
- ◊
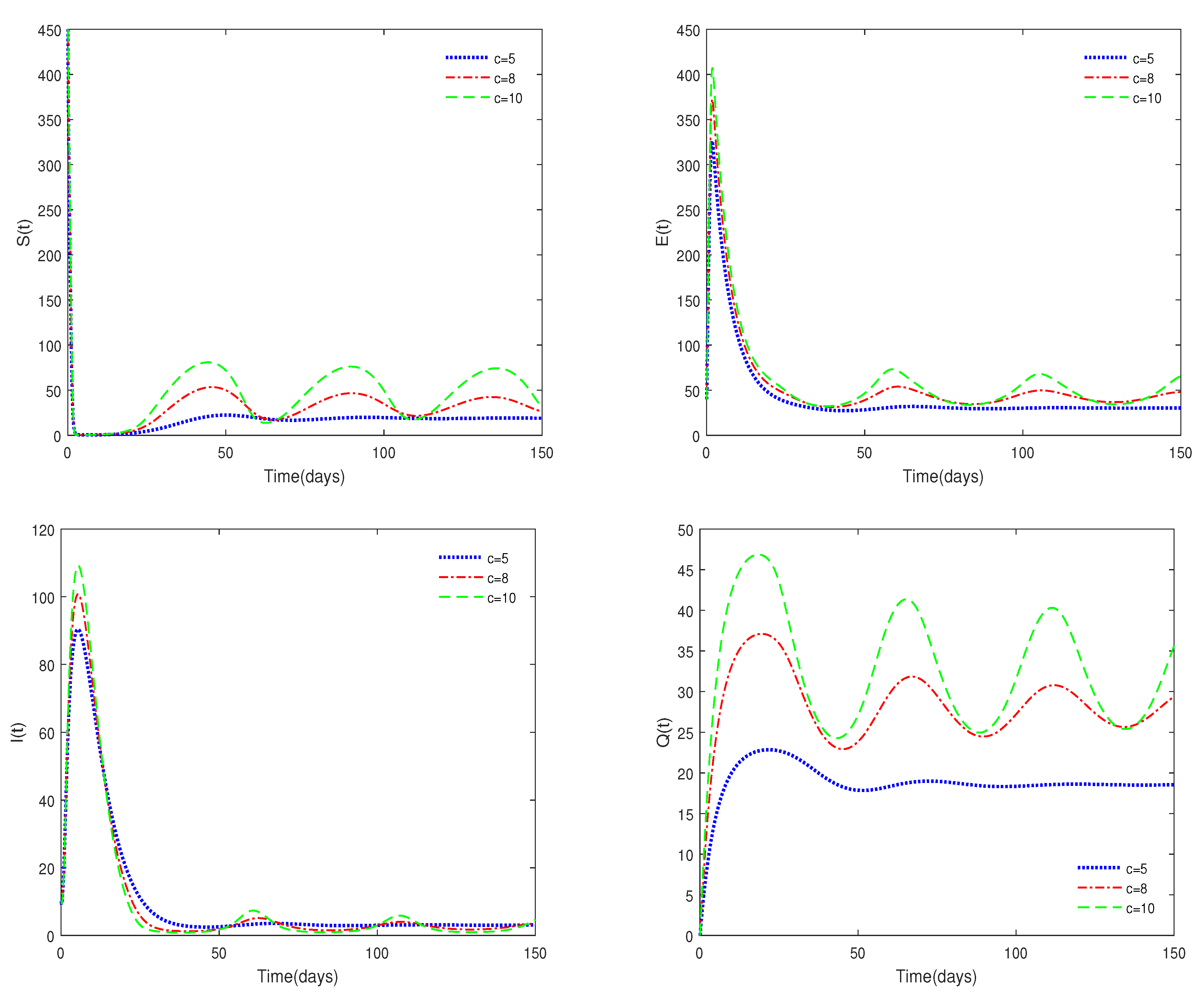
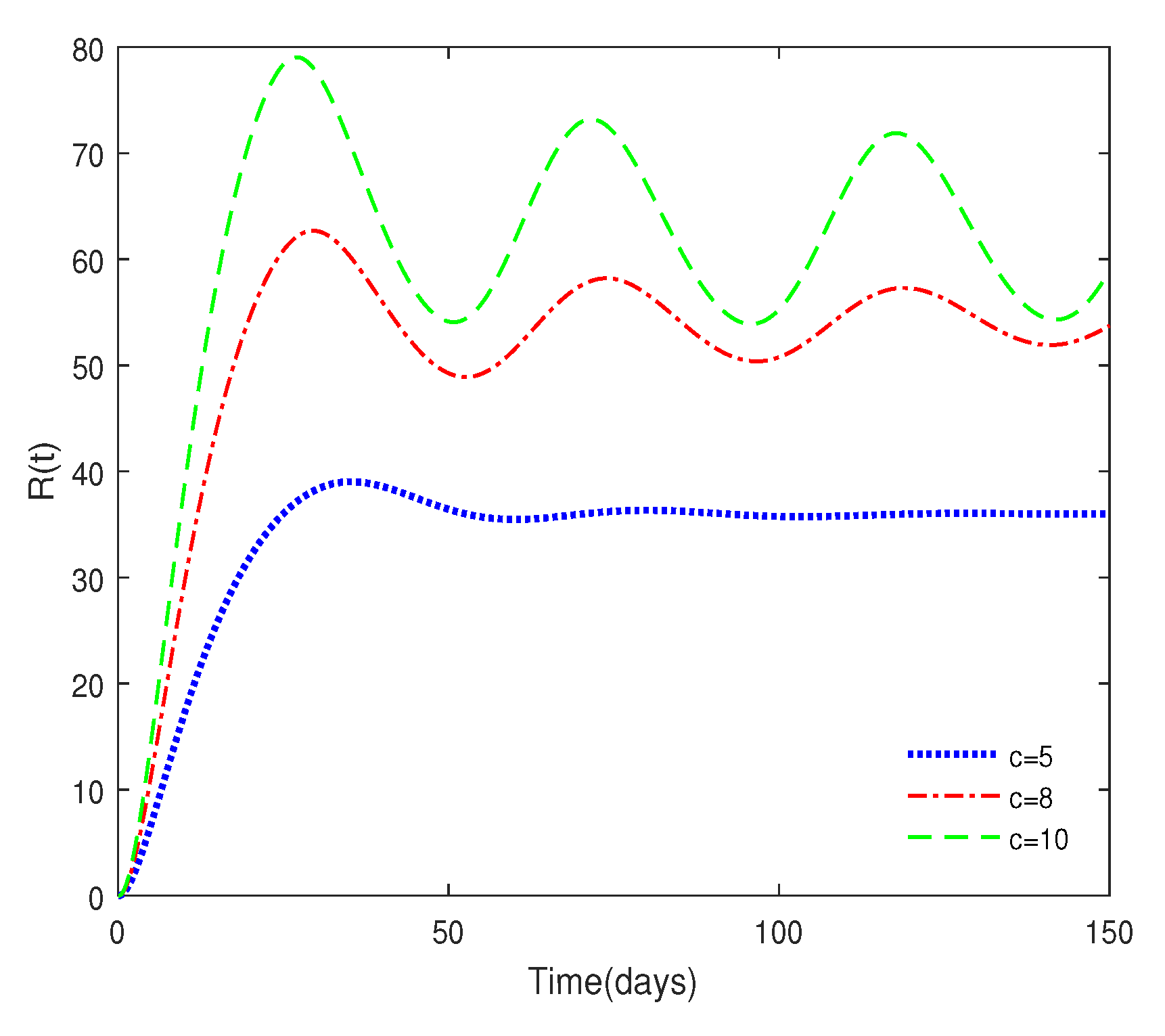
- Figure 6 shows that medical resources are important for controlling the transmission of the disease.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, C.; Zhang, B. Diagnosis of African swine fever and its prevention and control measures. Swine Ind. Sci. 2020, 37, 96–98. (In Chinese) [Google Scholar]
- Li, T.; Yu, X.; Li, F. The prevalent, diagnosis, prevention and control of African swine fever. Mod. Agric. Ind. Technol. Syst. 2019, 5, 23–25. [Google Scholar]
- Lu, Y.; Pawelek, K.; Liu, S. A stage-structured predator-prey model with predation over juvenile prey. Appl. Math. Comput. 2016, 297, 115–130. [Google Scholar] [CrossRef]
- Zhang, W.; Meng, X. Stochastic analysis of a novel nonautonomous periodic SIRI epidemic system with random disturbances. Physica A 2018, 492, 1290–1301. [Google Scholar] [CrossRef]
- Zhou, W.; Xiao, Y.; Heffernan, J. A two-thresholds policy to interrupt transmission of West Nile Virus to birds. J. Theor. Biol. 2019, 463, 22–46. [Google Scholar] [CrossRef] [PubMed]
- Lv, Y.; Pei, Y.; Yuan, R. Complete global analysis of a diffusive NPZ model with age structure in zooplankton. Nonlinear Anal. Real World Appl. 2019, 46, 274–297. [Google Scholar] [CrossRef]
- Pietschmann, J.; Guinat, C.; Beer, M.; Pronin, V.; Tauscher, K.; Petrov, A.; Keil, G.; Blome, S. Course and transmission characteristics of oral low-dose infection of domestic pigs and European wild boar with a caucasian African swine fever virus isolate. Arch. Virol. 2015, 160, 1657–1667. [Google Scholar] [CrossRef]
- Guinat, C.; Gubbins, S.; Vergne, T.; Gonzales, J.L.; Dixon, L.; Pfeiffer, D.U. Experimental pig-to-pig transmission dynamics for African swine fever virus, Georgia 2007/1 strain. Epidemiol. Infect. 2016, 144, 25–34. [Google Scholar] [CrossRef]
- Mur, L.; Sánchez-Vizcaíno, J.M.; Fernández-Carrión, E.; Jurado, C.; Rolesu, S.; Feliziani, F.; Laddomada, A.; Martínez-López, B. Understanding African swine fever infection dynamics in Sardinia using a spatially explicit transmission model in domestic pig farms. Transbound. Emerg. Dis. 2017, 65, 123–134. [Google Scholar] [CrossRef]
- Barongo, M.B.; Bishop, R.P.; Fèvre, E.M.; Knobel, D.L.; Ssematimba, A. A mathematical model that simulates control options for African swine fever virus (ASFV). PLoS ONE 2016, 11, e0158658. [Google Scholar] [CrossRef]
- Zhang, X.; Rong, X.; Li, J.; Fan, M.; Wang, Y.; Sun, X.; Huang, B.; Zhu, H. Modeling the outbreak and control of African swine fever virus in large-scale pig farms. J. Theor. Biol. 2021, 526, 110798. [Google Scholar] [CrossRef]
- Song, H.; Li, J.; Jin, Z. Nonlinear dynamic modelling and analysis of African swine fever with culling in China. Commun. Nonlinear Sci. Numer. Simul. 2023, 117, 106915. [Google Scholar] [CrossRef]
- Magin, R.; Abdullah, O.; Baleanu, D.; Zhou, X. Anomalous diffusion expressed through fractional order differential operators in the Bloch-Torrey equation. J. Magn. Reson. 2008, 190, 255–270. [Google Scholar] [CrossRef] [PubMed]
- Hilfer, R. Application of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Laskin, N.; Zaslavsky, G. Nonlinear fractional dynamics on a lattice with long range interactions. Phys. A Stat. Mech. Its Appl. 2006, 368, 38–54. [Google Scholar] [CrossRef]
- Copot, D.; De Keyser, R.; Derom, E.; Ortigueira, M.; Ionescu, C.M. Reducing bias in fractional order impedance estimation for lung function evaluation. Biomed. Signal Process. Control 2018, 39, 74–80. [Google Scholar] [CrossRef]
- Alidousti, J.; Ghaziani, R. Spiking and bursting of a fractional order of the modified FitzHugh-Nagumo neuron model. Math. Model. Comput. Simulations 2017, 9, 390–403. [Google Scholar] [CrossRef]
- Rihan, F.; Rahman, D. Delay differential model for tumour-immune dynamics with HIV infection of CD4+ T-cells. Int. J. Comput. Math. 2013, 90, 594–614. [Google Scholar] [CrossRef]
- Shi, R.; Lu, T.; Wang, C. Dynamic analysis of a fractional-order model for HIV with drug-resistance and CTL immune response. Math. Comput. Simul. 2021, 188, 509–536. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Mohammed, Z.N.; Baleanu, D. Optimal control for variable order fractional HIV/AIDS and malaria mathematical models with multi-time delay. Alex. Eng. J. 2020, 59, 3149–3162. [Google Scholar] [CrossRef]
- Ortigueira, M. Fractional calculus for scientists and engineers. Lect. Notes Electr. Eng. 2011, 84, 101–121. [Google Scholar]
- Doha, E.H.; Bhrawy, A.H.; Ezz-Eldien, S.S. A new Jacobi operational matrix: An application for solving fractional differential equations. Appl. Math. Model. 2012, 36, 4931–4943. [Google Scholar] [CrossRef]
- Muresan, C.; Ionescu, C.; Folea, S.; Keyser, R.D. Fractional order control of unstable processes: The magnetic levitation study case. Nonlinear Dyn. 2015, 80, 1761–1772. [Google Scholar] [CrossRef]
- Cao, Y.; Nikan, O.; Avazzadeh, Z. A localized meshless technique for solving 2D nonlinear integro-differential equation with multi-term kernels. Appl. Numer. Math. 2023, 183, 140–156. [Google Scholar] [CrossRef]
- Salama, F.M.; Ali, N.H.M.; Hamid, N.N.A. Fast O(N) hybrid Laplace transform-finite difference method in solving 2D time fractional diffusion equation. J. Math. Comput. Sci. 2021, 23, 110–123. [Google Scholar] [CrossRef]
- Jassim, H.K.; Hussain, M.A.S. On approximate solutions for fractional system of differential equations with Caputo-Fabrizio fractional op-erator. J. Math. Comput. Sci. 2021, 23, 58–66. [Google Scholar] [CrossRef]
- Akrama, T.; Abbasb, M.; Alia, A. A numerical study on time fractional Fisher equation using an extended cubic B-spline approximation. J. Math. Comput. Sci. 2021, 22, 85–96. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Cui, J.; Mu, X.; Wan, H. Saturation recovery leads to multiple endemic equilibria and backward bifurcation. J. Theor. Biol. 2008, 254, 275–283. [Google Scholar] [CrossRef]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: London, UK, 1993. [Google Scholar]
- Odibat, Z.; Shawagfeh, N. Generalized Taylors formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar]
- Mao, S.; Xu, R.; Li, Y. A fractional order SIRS model with standard incidence rate. J. Beihua Univ. Nat. Sci. 2012, 12, 379–382. [Google Scholar]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef]
- van Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental systems of disease transmis-sion. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Kou, C.; Yan, Y.; Liu, J. Stability analysis for fractional differential equations and their applications in the models of HIV-1 infection. Comput. Model. Eng. Sci. 2009, 39, 301–317. [Google Scholar]



| Variables | Descriptions | |
|---|---|---|
| Density of the susceptible population | ||
| Density of the exposed population | ||
| Density of the infection population | ||
| Density of the quarantined population | ||
| Density of the recovered population | ||
| Parameters | Descriptions | Values |
| The constant recruitment rates of population | [1, 1.75] | |
| Effective contact rate between the susceptible and the infection population | [0.001, 0.3] | |
| The average rate at which an individual passes through the incubation period | [0.12, 0.35] | |
| Recovery rate of the quarantined | [0.01, 0.8] | |
| The constant rate at which the recovered population become susceptible | [0.01, 0.3] | |
| d | Death rate due to the disease | [0.002, 0.0035] |
| Natural death rate | [0.08, 0.25] | |
| c | The maximum isolation rate per unit of time | [1, 10] |
| b | The infection scale | [1, 5] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, R.; Li, Y.; Wang, C. Analysis of a Fractional-Order Model for African Swine Fever with Effect of Limited Medical Resources. Fractal Fract. 2023, 7, 430. https://doi.org/10.3390/fractalfract7060430
Shi R, Li Y, Wang C. Analysis of a Fractional-Order Model for African Swine Fever with Effect of Limited Medical Resources. Fractal and Fractional. 2023; 7(6):430. https://doi.org/10.3390/fractalfract7060430
Chicago/Turabian StyleShi, Ruiqing, Yang Li, and Cuihong Wang. 2023. "Analysis of a Fractional-Order Model for African Swine Fever with Effect of Limited Medical Resources" Fractal and Fractional 7, no. 6: 430. https://doi.org/10.3390/fractalfract7060430
APA StyleShi, R., Li, Y., & Wang, C. (2023). Analysis of a Fractional-Order Model for African Swine Fever with Effect of Limited Medical Resources. Fractal and Fractional, 7(6), 430. https://doi.org/10.3390/fractalfract7060430








