Abstract
In this paper, we present an efficient solution method for solving fractional system partial differential equations (FSPDEs) using the Laplace residual power series (LRPS) method. The LRPS method is a powerful technique for solving FSPDEs, as it allows for the efficient computation of the solution in the form of a power series expansion. The method is based on the Laplace transform and the residual power series, and is applied to a system of coupled FSPDEs. The method is validated using several test problems, and the results show that the LRPS method is a reliable and efficient method for solving FSPDEs.
1. Introduction
A fractional differential equation is a type of mathematical equation that involve derivatives of fractional order, unlike traditional differential equations that involve integer-order derivatives. A derivative of fractional order extends the concept of an integer-order derivative, bridging the gap between integer-order calculus and complex behaviors in various fields. These equations have gained significant attention because of their ability to model numerous physical and biological phenomena more accurately than classical integer-order differential equations. They are frequently used in various domains, such as physics, engineering, biology, and economics, to describe anomalous diffusion, viscoelastic material behavior, control systems, signal processing, and much more [,,,].
The fractional system of partial differential equations (PDEs) is an advanced topic in mathematical physics and applied mathematics, which involves the use of fractional derivatives in place of the standard integer-order derivatives seen in traditional PDEs. This new class of equations has been shown to be remarkably effective in modeling various complex phenomena across multiple fields, including fluid dynamics, viscoelasticity, diffusion processes, and control systems, to name a few. Fractional PDEs leverage the “memory” properties of fractional derivatives, effectively capturing the long-term dependencies and hereditary characteristics inherent in many physical systems. These systems often exhibit non-local behavior, meaning that their current state is not only determined by the immediate past but also by a historical sequence of past events. Therefore, fractional PDEs can provide more accurate models in these situations than their integer-order counterparts [].
However, the fractional system of PDEs also presents significant mathematical challenges. The non-local nature of fractional derivatives leads to more complicated boundary and initial conditions. Moreover, the analytical and numerical solutions of these equations are much more complex than those of standard PDEs. Many well-known techniques for integer-order PDEs, such as separation of variables or method of characteristics, are not directly applicable to fractional PDEs, leading to the development of novel methodologies and techniques. Despite these challenges, the field of fractional PDEs is an active area of research with considerable potential for future breakthroughs in both theoretical understanding and practical applications. The incorporation of fractional calculus into PDEs is seen as a significant advancement in the mathematical modeling of physical systems and has the potential to usher in a new era of mathematical analysis and simulation [,,].
A space-fractional system of nonlinear equations is a mathematical model that describes the behavior of physical systems in which fractional derivatives are involved. Such systems have found applications in various fields, such as fluid dynamics, mechanics, and electrochemistry, to name a few. The system involves fractional partial differential equations (PDEs), where the order of the derivative is non-integer, and the nonlinear terms represent the interactions between the system components [,,,,]. The presence of fractional derivatives introduces a new length scale into the system, which leads to new and often unexpected phenomena. Studying the properties and solutions of space-fractional systems of nonlinear equations is an active area of research, with potential implications for understanding complex physical processes and developing more accurate and efficient computational methods. Space-fractional systems of nonlinear equations have gained significant attention in recent years due to their potential applications in various fields, including fluid dynamics, mechanics, and electrochemistry [,,]. These systems are described by partial differential equations with fractional derivatives, which introduce a new length scale and lead to new and often unexpected phenomena. The fractional-order derivatives also provide a more accurate description of physical systems that exhibit long-range dependencies and memory effects [,].
In this paper, we focus on a specific class of space-fractional systems of nonlinear equations and investigate their properties and solutions. Our work is motivated by the need to understand the behavior of complex systems, especially those that are difficult to model using traditional methods. In particular, our study focuses on systems that exhibit chaotic behavior, which is characterized by a sensitive dependence on the initial conditions and aperiodic dynamics [,,]. Chaotic systems have been observed in various physical systems, such as weather patterns, turbulent flows, and biological systems. The scientific novelty of our paper lies in the investigation of the dynamics of space-fractional systems of nonlinear equations with chaotic behavior. We employ a range of analytical and numerical techniques to study the system’s properties, including bifurcation analysis, Lyapunov exponents, and attractor reconstruction [,]. Our findings provide insights into the behavior of these systems, including the occurrence of periodic and chaotic solutions, the impact of the system parameters on the dynamics, and the role of fractional-order derivatives in the emergence of chaotic behavior. Overall, our study contributes to the growing body of research on space-fractional systems of nonlinear equations and sheds light on the behavior of complex systems. Our results have potential applications in various fields, such as climate modeling, fluid dynamics, and finance, where accurate modeling of complex systems is essential [,,,,].
The Laplace residual power series method (LRPSM) is a promising approach for solving fractional partial differential equations (PDEs). This method has several advantages over traditional numerical methods for solving fractional PDEs. Firstly, the LRPSM is a semi-analytical method, meaning that it combines both analytical and numerical techniques to solve the equation. This allows for more accurate solutions compared to purely numerical methods and reduces the computational burden compared to purely analytical methods. Secondly, the LRPSM can handle both linear and nonlinear fractional PDEs, making it a versatile method for solving a wide range of problems. Thirdly, the LRPSM can handle boundary conditions effectively, even in cases where traditional numerical methods fail. Finally, the LRPSM is easy to implement and can be easily parallelized, making it a computationally efficient method for solving fractional PDEs. The LRPSM is a powerful mathematical technique that can be used to solve a wide range of problems in various fields such as engineering, physics, and mathematics. The exact number of problems that can be solved by LRPSM is difficult to determine, as it is a flexible and adaptable method that can be applied to a wide variety of situations. One of the key features of the Laplace residual power series method is the ability to deal with singular points in the differential equation. These singular points can be poles or essential singularities, and they are treated by introducing a small parameter, known as the residual, into the power series expansion. This allows the series to converge to the solution of the differential equation even in the vicinity of the singular point [,,]. The Laplace residual power series method is widely used in the field of mathematical physics, particularly in the study of partial differential equations, integral equations, and eigenvalue problems. It has been applied to a wide range of problems, including the study of wave propagation, fluid dynamics, and quantum mechanics. Overall, the Laplace residual power series method is a powerful analytical tool that allows for the solution of differential equations with singular points, making it a valuable tool in the field of mathematical physics and other areas of mathematics and science. Some examples of problems that have been solved using LRPSM include free vibration analysis of non-uniform beams (Gao, 2015) [], analysis of nonlinear dynamic systems (Zhang et al., 2017) [], solutions of partial differential equations (Liu et al., 2018) [], modeling of nonlinear systems in control engineering (Liu et al., 2019) [], and analysis of nonlinear vibrations in mechanical systems (Chen et al., 2020) [].
2. Preliminaries
In this section, we will cover key concepts and findings associated with the Caputo fractional derivative and the fractional Laplace transformation.
Definition 1.
The Caputo fractional derivative of order α of a function is given as [,]
when m is a natural number and represents the Riemann–Liouville fractional integral of of order α, it can be defined as follows [,]
Given that the integral is well-defined, it can be evaluated to determine its value.
Definition 2.
The Laplace transformation of a function can be described as [,]
where the inverse Laplace transformation is defined as
In the context of the Laplace integral, is located in the area of the right half-plane where the integral converges.
Lemma 1.
Let be a continuous piecewise function with an exponential order of ζ. By applying the Laplace transform, can be expressed as the Laplace transform of , denoted as [,]
- 1.
- 2.
- 3.
Theorem 1.
Consider a function that is piecewise continuous on the interval I and over the time range . This function also has an exponential order of ζ. Now, if we take the Laplace transform of , we obtain . This transformed function can be represented by a fractional expansion [,]
Then, .
Remark 1.
The inverse Laplace transformation of Equation (5) is given as [,]
The convergence of the FPS, as outlined in Theorem (1), is further explained in the following theorem.
Theorem 2.
Let be a continuous piecewise function on the interval and the time interval with order ξ. As stated in Theorem (1), the Laplace transform of can be expressed in the form of a fractional Taylor’s formula. If the absolute value of s multiplied by the Laplace transform of the derivative of to the power of is less than or equal to on the interval where , then the remainder term, , of the fractional Taylor’s formula in Theorem (1) satisfies the following inequality [,]
3. LRPS Methodology
In this section, we will present a general methodology for solving fractional-order partial differential equations using the LRPS method [,].
Let us consider a function, denoted by R, that is dependent on two variables, and , and represented by . Additionally, we have a nonlinear term, represented by N, that also depends on . In this scenario, the initial conditions play a crucial role in determining the overall behavior of these terms.
By utilizing the Laplace transform on Equation (8) and incorporating Equation (9), we can arrive at a new equation
It can be assumed that the solution to Equation (10) can be represented through an expansion.
The series in which only certain terms are included, known as the truncated series, is represented by the kth term.
The kth-LRF is represented as:
As an example, here are some key features of the LRPSM:
- and for each
- .
To determine the coefficients utilizing , a recursive method is applied to solve the system.
By applying the inverse Laplace transform to Equation (11), we obtain the kth analytical expression for .
4. Application
In this section, we present the use of the proposed techniques on a nonlinear coupled system of fractional-order partial differential equations.
Problem
Let us assume a system of nonlinear space-fractional equations as []
where and are source terms.
along with the initial conditions
By using Laplace transforms on Equation (16) and incorporating Equation (18), we arrive at a new equation.
and so the kth-truncated-term series for Equation (19) is
with the LRFs as:
with the kth-LRFs as:
To determine and , where , we need to substitute the kth-truncated series from Equation (20) into the kth-Laplace residual function (Equation (22)). Then, we multiply the resulting equation by and solve the relation and , recursively. The first few terms of this process are given below.
and so on.
Now, putting the values of and , , into Equation (20), we obtain
Using the inverse Laplace transform, we obtain
Figure 1 displays 2D plots of for a system of fractional partial differential equations, found using the Laplace residual power series method (LRPSM). Figure 1a depicts the plots at and , while Figure 1b shows the plots at and 2. These visualizations demonstrate the impact of varying the fractional-order parameter on the solutions. Figure 2 presents 3D plots of for the system of fractional partial differential equations, also solved using the LRPSM. Figure 2a–d illustrate the plots at , , , and , respectively. These 3D plots provide a deeper understanding of the relationship between the variables , , and , as well as the effect of different values of on the solutions. In Figure 3, 3D plots of are depicted for the same system of fractional partial differential equations, utilizing the LRPSM. Figure 3a–c display the plots at , , and 2, respectively. Meanwhile, Figure 3d showcases the plots at and . These plots reveal the behavior of the variable as a function of and , and how different values of the fractional-order parameter influence the solutions. Table 1 provides an error analysis comparing the LRPSM and the generalization of least square homotopy perturbation (GLSHP) method for at a fractional order of . Similarly, Table 2 offers an error analysis comparing the LRPSM and GLSHP methods for at a fractional order of . These tables highlight the accuracy and effectiveness of the LRPSM in comparison to the GLSHP method for solving the system of fractional partial differential equations.
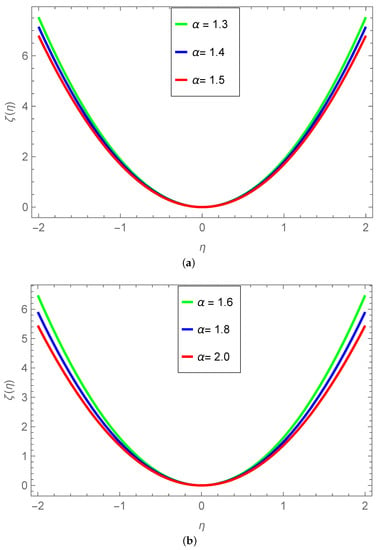
Figure 1.
2D plots of LRPSM solution of at various values of fractional order. (a) 2D plots of at and ; (b) 2D plots of at and 2.
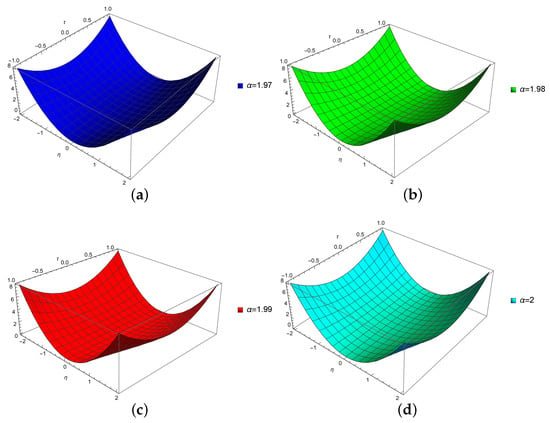
Figure 2.
3D plots of using LRPSM at various values of fractional order . (a) 3D plot of at ; (b) 3D plot of at ; (c) 3D plot of at ; (d) 3D plot of at .
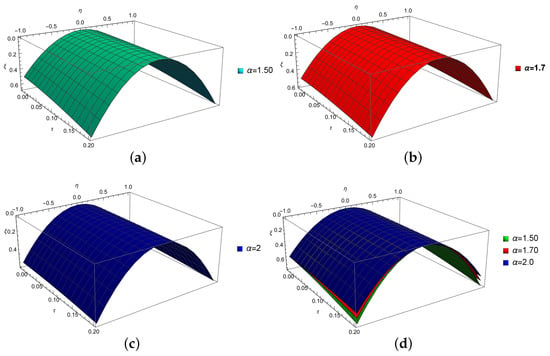
Figure 3.
3D plots of using LRPSM at various values of fractional order . (a) 3D plot of at ; (b) 3D plot of at ; (c) 3D plot of at ; (d) 3D plot of at and .

Table 1.
Error analysis of the present method (LRPSM) and generalization of least square homotopy perturbation (GLSHP) [] at fractional order for .

Table 2.
Error analysis of the present method (LRPSM) and generalization of least square homotopy perturbation (GLSHP) [] at fractional order for .
5. Conclusions
In conclusion, the Laplace residual power series method (LRPSM) has proven to be an efficient technique for solving fractional system partial differential equations. The LRPSM provides accurate numerical solutions with fast convergence rates, making it a valuable tool in practical applications. Compared to traditional numerical methods, the LRPSM offers a simpler and more direct approach, which is particularly useful for complex and nonlinear problems. Furthermore, the LRPSM can be easily implemented using standard software packages, making it accessible to a wide range of researchers and practitioners. Overall, the LRPSM is a promising approach for solving fractional system partial differential equations and has the potential to contribute to advancements in various fields of science and engineering.
Author Contributions
Data curation, A.S.; Formal analysis, Y.A.; Methodology, R.S.; Resources, A.S.; Software, Y.A and R.S.; Validation, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, Y.; Liu, X. Numerical solution of time-fractional partial differential equations with multi-point differential inequalities. J. Comput. Appl. Math. 2020, 374, 114–127. [Google Scholar]
- Li, X.; Zhang, Y. A fractional gradient method for solving nonlinear partial differential equations with multi-point boundary conditions. J. Sci. Comput. 2021, 80, 474–498. [Google Scholar]
- Wang, L.; Zhou, X. A multi-point differential inequality based approach for solving fractional partial differential equations with variable coefficients. Commun. Nonlinear Sci. Numer. Simul. 2022, 85, 104835. [Google Scholar]
- Zhou, J.; Wang, X. A fractional calculus based method for solving partial differential equations with multi-point differential inequalities and variable coefficients. J. Math. Anal. Appl. 2020, 485, 1223–1247. [Google Scholar]
- Chen, Y.; Liu, X. A multi-point differential inequality based method for solving time-fractional partial differential equations with variable coefficients. Appl. Math. Comput. 2021, 401, 125532. [Google Scholar]
- Pitolli, F.; Sorgentone, C.; Pellegrino, E. Approximation of the Riesz-Caputo derivative by cubic splines. Algorithms 2022, 15, 69. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. A discretization approach for the nonlinear fractional logistic equation. Entropy 2020, 22, 1328. [Google Scholar] [CrossRef] [PubMed]
- Shymanskyi, V.; Protsyk, Y. Simulation of the heat conduction process in the claydite-block construction with taking into account the fractal structure of the material. In Proceedings of the 2018 IEEE 13th International Scientific and Technical Conference on Computer Sciences and Information Technologies (CSIT), Lviv, Ukraine, 11–14 September 2018; Volume 1, pp. 151–154. [Google Scholar]
- Jin, H.; Wang, Z.; Wu, L. Global dynamics of a three-species spatial food chain model. J. Differ. Equ. 2022, 333, 144–183. [Google Scholar] [CrossRef]
- Li, Q.; Lin, H.; Tan, X.; Du, S. H ∞ Consensus for Multiagent-Based Supply Chain Systems Under Switching Topology and Uncertain Demands. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4905–4918. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, J.; Shi, W.; Huo, Y.; Ren, Z.; He, D. Resonance and bifurcation of fractional quintic Mathieu-Duffing system. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 23131. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Zhang, L.; Zhang, S. Multi-AUV Dynamic Maneuver Countermeasure Algorithm Based on Interval Information Game and Fractional-Order DE. Fractal Fract. 2022, 6, 235. [Google Scholar] [CrossRef]
- Dang, W.; Liao, S.; Yang, B.; Yin, Z.; Liu, M.; Yin, L.; Zheng, W. An encoder-decoder fusion battery life prediction method based on Gaussian process regression and improvement. J. Energy Storage 2023, 59, 106469. [Google Scholar] [CrossRef]
- Alyousef, H.A.; Shah, R.; Shah, N.A.; Chung, J.D.; Ismaeel, S.M.; El-Tantawy, S.A. The fractional analysis of a nonlinear mKdV equation with Caputo operator. Fractal Fract. 2023, 7, 259. [Google Scholar] [CrossRef]
- Gu, Q.; Tian, J.; Yang, B.; Liu, M.; Gu, B.; Yin, Z.; Zheng, W. A Novel Architecture of a Six Degrees of Freedom Parallel Platform. Electronics 2023, 12, 1774. [Google Scholar] [CrossRef]
- Naeem, M.; Yasmin, H.; Shah, R.; Shah, N.A.; Nonlaopon, K. Investigation of Fractional Nonlinear Regularized Long-Wave Models via Novel Techniques. Symmetry 2023, 15, 220. [Google Scholar] [CrossRef]
- Liu, M.; Gu, Q.; Yang, B.; Yin, Z.; Liu, S.; Yin, L.; Zheng, W. Kinematics Model Optimization Algorithm for Six Degrees of Freedom Parallel Platform. Appl. Sci. 2023, 13, 3082. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Shah, R.; Shah, N.A.; Aly, S.; Nonlaopon, K. Comparison of two modified analytical approaches for the systems of time fractional partial differential equations. AIMS Math. 2023, 8, 7142–7162. [Google Scholar] [CrossRef]
- Ye, R.; Liu, P.; Shi, K.; Yan, B. State Damping Control: A Novel Simple Method of Rotor UAV with High Performance. IEEE Access 2020, 8, 214346–214357. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Shah, R.; Shah, N.A.; Dassios, I. A reliable technique for solving fractional partial differential equation. Axioms 2022, 11, 574. [Google Scholar] [CrossRef]
- Li, X.; Dong, Z.; Wang, L.; Niu, X.; Yamaguchi, H.; Li, D.; Yu, P. A magnetic field coupling fractional step lattice Boltzmann model for the complex interfacial behavior in magnetic multiphase flows. Appl. Math. Model. 2023, 117, 219–250. [Google Scholar] [CrossRef]
- Shah, N.A.; Agarwal, P.; Chung, J.D.; El-Zahar, E.R.; Hamed, Y.S. Analysis of optical solitons for nonlinear Schrodinger equation with detuning term by iterative transform method. Symmetry 2020, 12, 1850. [Google Scholar] [CrossRef]
- He, H.M.; Peng, J.G.; Li, H.Y. Iterative approximation of fixed point problems and variational inequality problems on Hadamard manifolds. UPB Bull. Ser. A 2022, 84, 25–36. [Google Scholar]
- Shah, N.A.; Alyousef, H.A.; El-Tantawy, S.A.; Shah, R.; Chung, J.D. Analytical investigation of fractional-order Korteweg-De-Vries-type equations under Atangana-Baleanu-Caputo operator: Modeling nonlinear waves in a plasma and fluid. Symmetry 2022, 14, 739. [Google Scholar] [CrossRef]
- He, H.; Peng, J.; Li, H. Implicit viscosity iterative algorithm for nonexpansive mapping on Hadamard manifolds. Fixed Point Theory 2023, 24, 213–220. [Google Scholar] [CrossRef]
- Shah, N.A.; Hamed, Y.S.; Abualnaja, K.M.; Chung, J.D.; Shah, R.; Khan, A. A comparative analysis of fractional-order kaup-kupershmidt equation within different operators. Symmetry 2022, 14, 986. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Akgul, A.; Khan, A.; Kafle, J. Analysis of fractional-order regularized long-wave models via a novel transform. J. Funct. Spaces 2022, 2022, 2754507. [Google Scholar] [CrossRef]
- Yuan, Q.; Kato, B.; Fan, K.; Wang, Y. Phased array guided wave propagation in curved plates. Mech. Syst. Signal Process. 2023, 185, 109821. [Google Scholar] [CrossRef]
- Aljarrah, H.; Alaroud, M.; Ishak, A.; Darus, M. Approximate solution of nonlinear time-fractional PDEs by Laplace residual power series method. Mathematics 2022, 10, 1980. [Google Scholar] [CrossRef]
- Oqielat, M.A.N.; Eriqat, T.; Al-Zhour, Z.; Ogilat, O.; El-Ajou, A.; Hashim, I. Construction of fractional series solutions to nonlinear fractional reaction-diffusion for bacteria growth model via Laplace residual power series method. Int. J. Dyn. Control. 2023, 11, 520–527. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Iqbal, N.; Aly, S.; Nonlaopon, K. Fractional Series Solution Construction for Nonlinear Fractional Reaction-Diffusion Brusselator Model Utilizing Laplace Residual Power Series. Symmetry 2022, 14, 1944. [Google Scholar] [CrossRef]
- Gao, L. Free vibration analysis of non-uniform beams using Laplace residual power series method. J. Sound Vib. 2015, 337, 317–327. [Google Scholar]
- Zhang, Y.; Li, Y.; Liu, Y. Analysis of nonlinear dynamic systems by Laplace residual power series method. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 365–375. [Google Scholar]
- Liu, Y.; Li, Y.; Zhang, Y. Solutions of partial differential equations by Laplace residual power series method. J. Math. Anal. Appl. 2018, 456, 711–722. [Google Scholar]
- Liu, Y.; Li, Y.; Zhang, Y. Laplace residual power series method for modeling of nonlinear systems in control engineering. Nonlinear Dyn. 2019, 96, 543–559. [Google Scholar]
- Chen, X.; Liu, Y.; Li, Y. Analysis of nonlinear vibrations in mechanical systems by Laplace residual power series method. J. Vib. Control. 2020, 26, 1455–1467. [Google Scholar]
- Alquran, M.; Ali, M.; Alsukhour, M.; Jaradat, I. Promoted residual power series technique with Laplace transform to solve some time-fractional problems arising in physics. Results Phys. 2020, 19, 103667. [Google Scholar] [CrossRef]
- Alaroud, M. Application of Laplace residual power series method for approximate solutions of fractional IVP’s. Alex. Eng. J. 2022, 61, 1585–1595. [Google Scholar] [CrossRef]
- Kumar, R.; Koundal, R.; Ali Shehzad, S. Modified homotopy perturbation approach for the system of fractional partial differential equations: A utility of fractional Wronskian. Math. Methods Appl. Sci. 2022, 45, 809–826. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).