High-Dimensional Chaotic Lorenz System: Numerical Treatment Using Changhee Polynomials of the Appell Type
Abstract
1. Introduction
- We describe the proposed 9Dim chaotic Lorenz system using a theoretical and numerical simulation.
- Particular attention is given to using ACPs to provide a suitable formula for the Caputo fractional (CF) derivative.
- The recommended method and this approximation are used to convert the model into a set of algebraic equations. Through the use of the Newton iteration method, this system is numerically solved.
- With alternative values for the parameter r and varied values for the fractional order , we provide a numerical simulation of the model under consideration using the suggested methodology.
- The REF is then introduced to calculate the solution’s error. Additionally, we compared the solution produced by the suggested method with that produced by (RK4) and other previously published research.
2. Preliminaries
2.1. Definitions in Fractional Calculus
2.2. Some Concepts of Changhee Polynomials
3. Approximation of the Derivative Dν via ACPs
4. Numerical Implementation
5. Numerical Simulation and Discussion
5.1. Graphical and Tabular Findings
5.2. Discussion and Recommendations
- The proposed method is demonstrated in Figure 1 to be an effective way to solve the proposed model in its fractional version in the Caputo sense.
- In Figure 3, we can note that there is excellent agreement between our technique and the RK4 method in this special case with the integer derivative , and this indicates that the proposed method is suitable.
- Through the results in Figure 4, we can increase the speed of the numerical computation by controlling the order of approximation m to improve the results as well as the efficiency of the given scheme.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lorenz, E. Deterministic nonperiodic flow. J. Atmospheric Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Rossler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Ispolatov, I.; Madhok, V.; Allende, S.; Doebeli, M. Chaos in high-dimensional dissipative dynamical systems. Sci. Rep. 2015, 5, 12506. [Google Scholar] [CrossRef] [PubMed]
- Odibat, Z.M.; Bertelle, C.; Aziz-Alaoui, M.A.; Duchamp, G.H.E. A multi-step differential transform method and application to non-chaotic or chaotic systems. Comput. Math. Appl. 2010, 59, 1462–1472. [Google Scholar] [CrossRef]
- Lozi, R.; Pogonin, V.A.; Pchelintsev, A.N. A new accurate numerical method of approximation of chaotic solutions of dynamical model equations with quadratic nonlinearities. Chaos Solitons Fractals 2016, 91, 108–114. [Google Scholar] [CrossRef]
- Zhou, X.; Li, J.; Wang, Y.; Zhang, W. Numerical simulation of a class of hyperchaotic system using Barycentric Lagrange interpolation collocation method. Complexity 2019, 2019, 1739785. [Google Scholar] [CrossRef]
- Eftekhari, S.A.; Jafari, A.A. Numerical simulation of chaotic dynamical systems by the method of differential quadrature. Sci. Iran. 2012, 19, 1299–1315. [Google Scholar] [CrossRef]
- Khader, M.M.; Mustafa, I.; Adel, M.; Ali, M. Numerical solutions to the fractional-order wave equation. Int. J. Mod. Phys. C 2023, 34, 2350067. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Youssri, Y.H. Sixth-Kind Chebyshev Spectral Approach for Solving Fractional Differential Equations. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 191–203. [Google Scholar] [CrossRef]
- Adel, M.; Srivastava, H.M.; Khader, M.M. Implementation of an accurate method for the analysis and simulation of electrical R-L circuits. Math. Meth. Appl. Sci. 2023, 46, 8362–8371. [Google Scholar] [CrossRef]
- Adel, M.; Khader, M.M.; Assiri, T.A.; Kaleel, W. Numerical simulation for COVID-19 model using a multidomain spectral relaxation technique. Symmetry 2023, 15, 931. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Khader, M.M.; Adel, M. On the fundamental equations for modeling neuronal dynamics. J. Adv. Res. 2014, 5, 253–259. [Google Scholar] [CrossRef] [PubMed]
- Abd-Elhameed, W.M.; Youssri, Y.H. Spectral Tau algorithm for certain coupled system of fractional differential equations via generalized Fibonacci polynomial sequence. Iran. J. Sci. Technol. Trans. A Sci. 2019, 43, 543–554. [Google Scholar] [CrossRef]
- Anjam, Y.N.; Shafqat, R.; Sarris, I.E.; Rahma, M.; Touseef, S.; Arshad, M. A fractional order investigation of smoking model using CF-differential operator. Fractal Fract. 2022, 6, 623. [Google Scholar] [CrossRef]
- Ibrahim, Y.F.; El-Bar, S.E.A.; Khader, M.M.; Adel, M. Studying and simulating the fractional COVID-19 model using an efficient spectral collocation approach. Fractal Fract. 2023, 7, 307. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Saadatmandi, A.; Dehghan, M. A new operational matrix for solving fractional-order differential equations. Comput. Math. Appl. 2010, 59, 1326–1336. [Google Scholar] [CrossRef]
- Kim, D.S.; Kim, T.; Seo, J.J. A note on Changhee polynomials and numbers. Adv. Stud. Theor. Phys. 2013, 7, 993–1003. [Google Scholar] [CrossRef]
- Lee, J.G.; Jang, L.C.; Seo, J.J.; Choi, S.K.; Kwon, H.I. On Appell-type Changhee polynomials and numbers. Adv. Differ. Equ. 2016, 1, 1–10. [Google Scholar] [CrossRef]
- Kreyszig, E. Introductory Functional Analysis with Applications; Wiley: New York, NY, USA, 1978; Volume 1. [Google Scholar]
- Reiterer, P.; Lainscsek, C.; Sch, F.; Maquet, J. A nine-dimensional Lorenz system to study high-dimensional chaos. J. Phys. A Math. Gen. 1998, 31, 7121–7139. [Google Scholar] [CrossRef]
- El-Hawary, H.M.; Salim, M.S.; Hussien, H.S. Ultraspherical integral method for optimal control problems governed by ordinary differential equations. J. Glob. Optim. 2003, 25, 283–303. [Google Scholar] [CrossRef]
- Alqhtani, M.; Khader, M.M.; Saad, K.M. Numerical simulation for a high-dimensional chaotic Lorenz system based on Gegenbauer wavelet polynomials. Mathematics 2023, 2, 472. [Google Scholar] [CrossRef]
- Kouagou, J.N.; Dlamini, P.G.; Simelane, S.M. On the multi-domain compact finite difference relaxation method for high dimensional chaos: The nine-dimensional Lorenz system. Alex. Eng. J. 2020, 59, 2617–2625. [Google Scholar] [CrossRef]

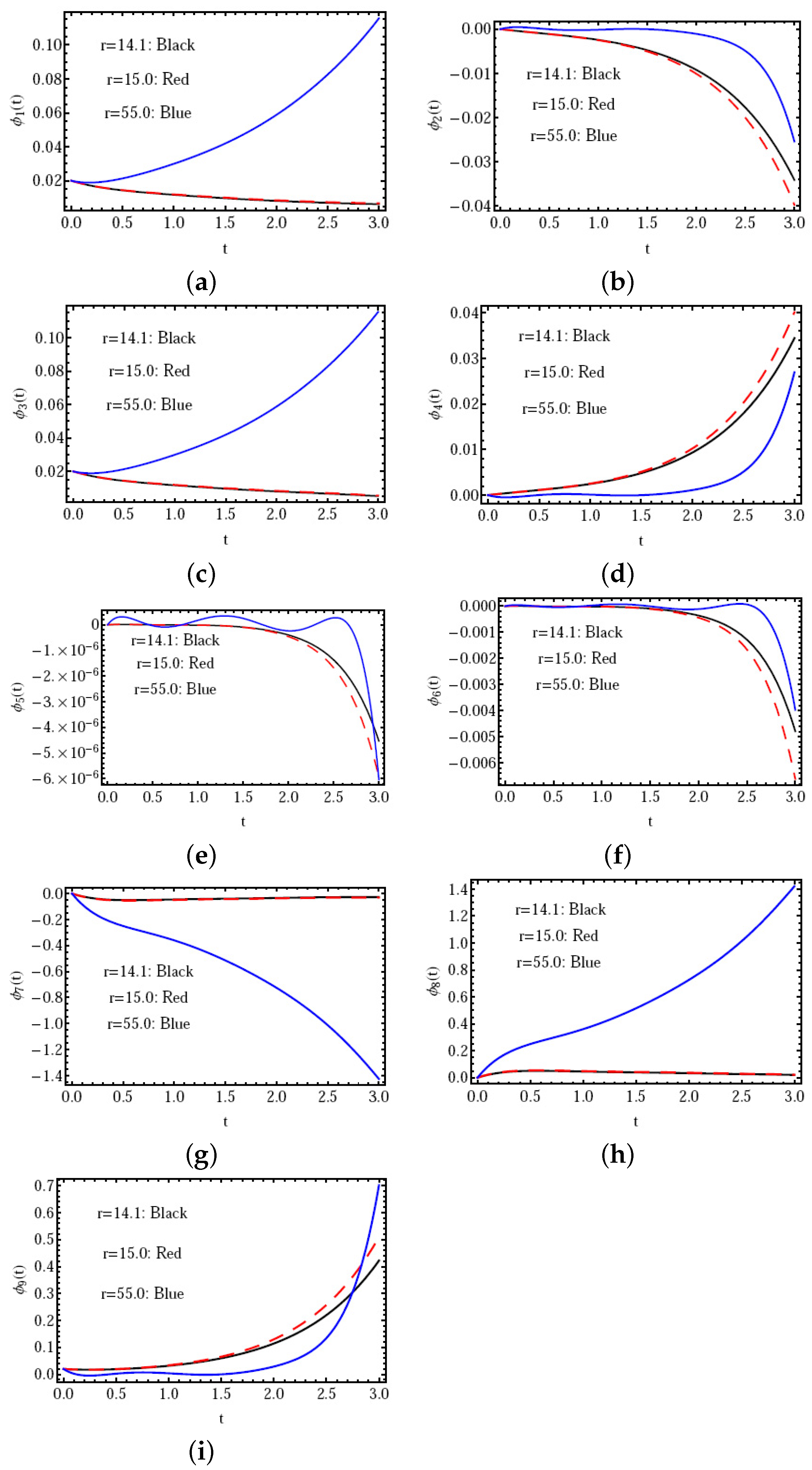
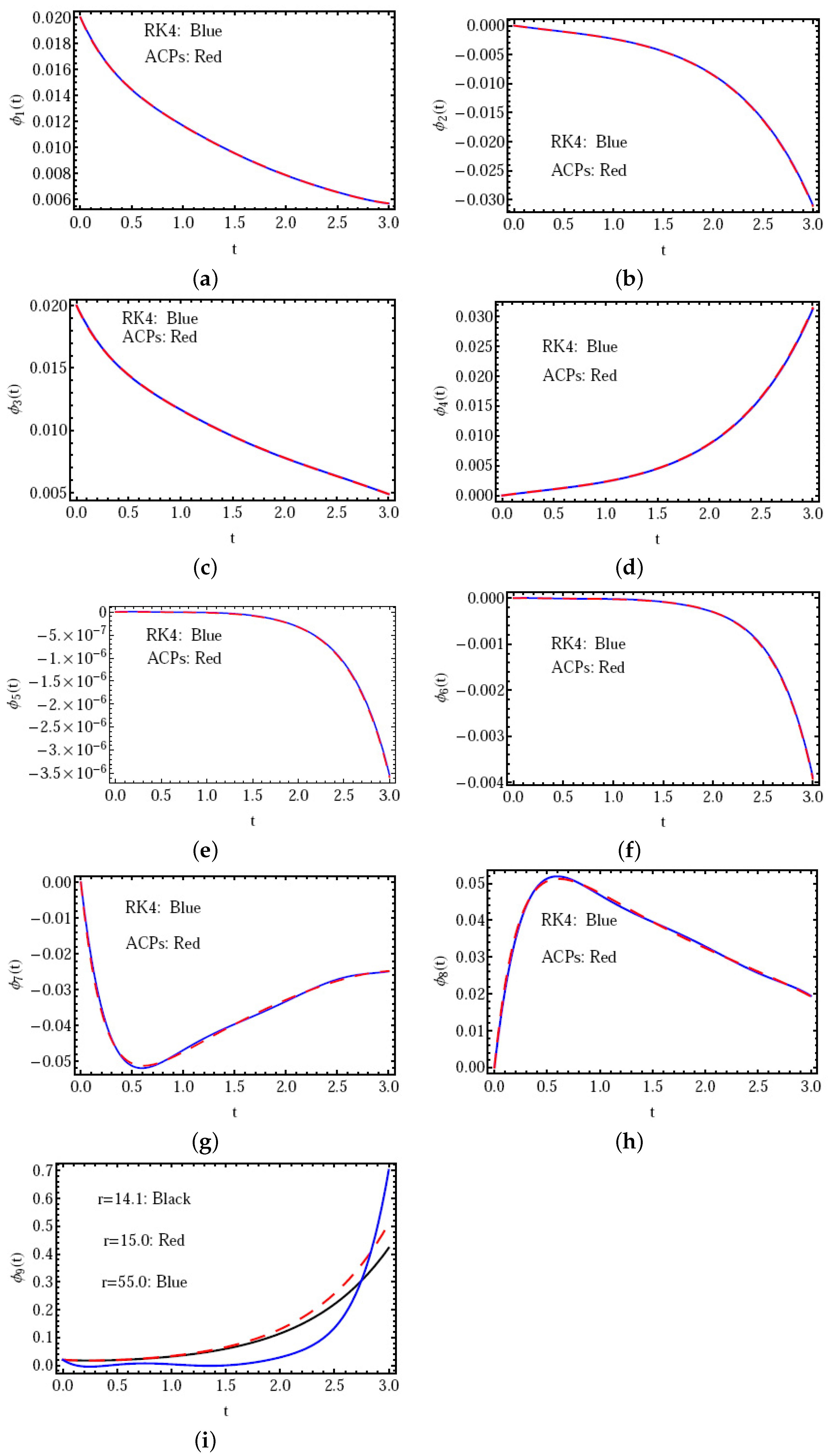
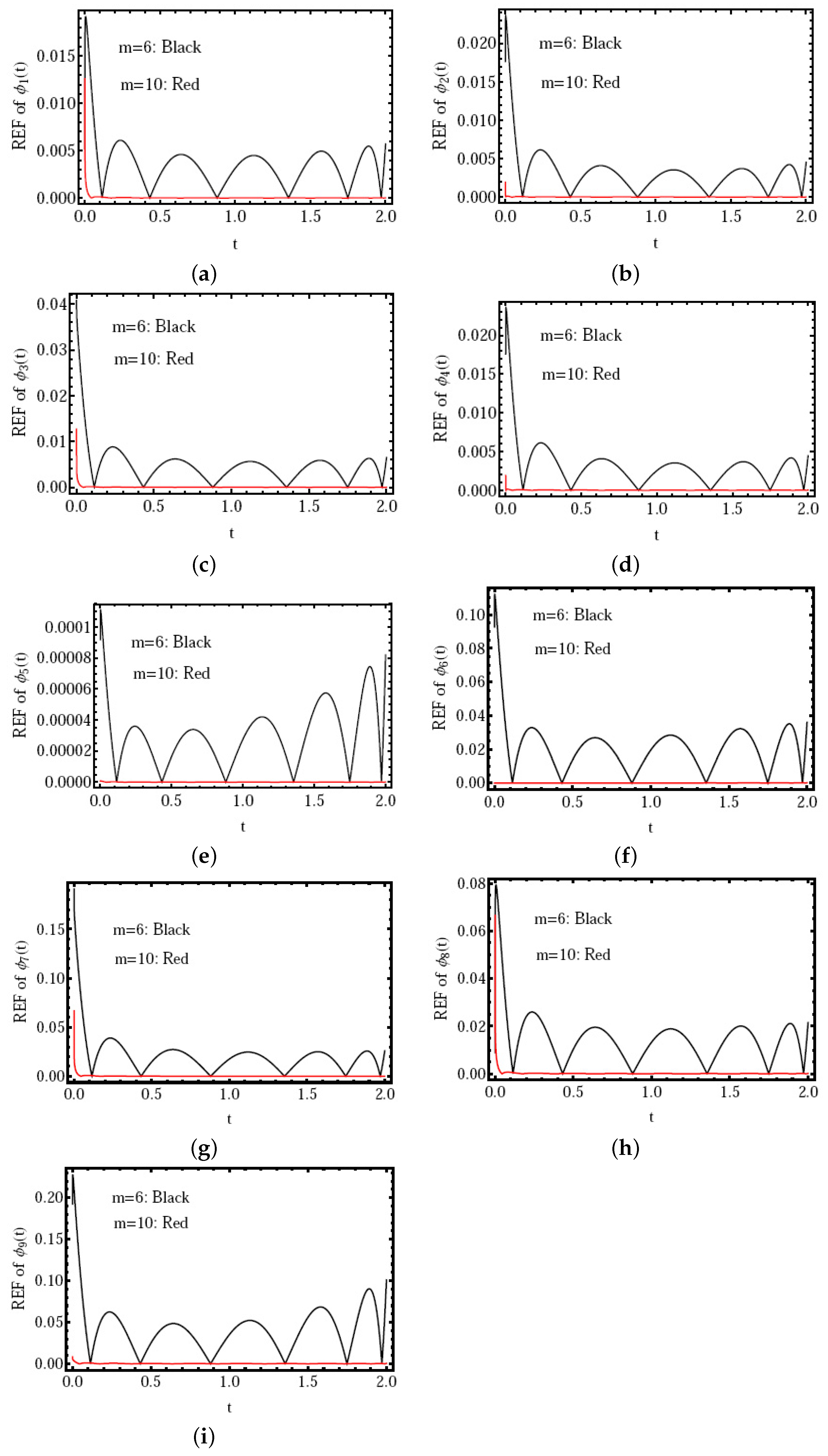

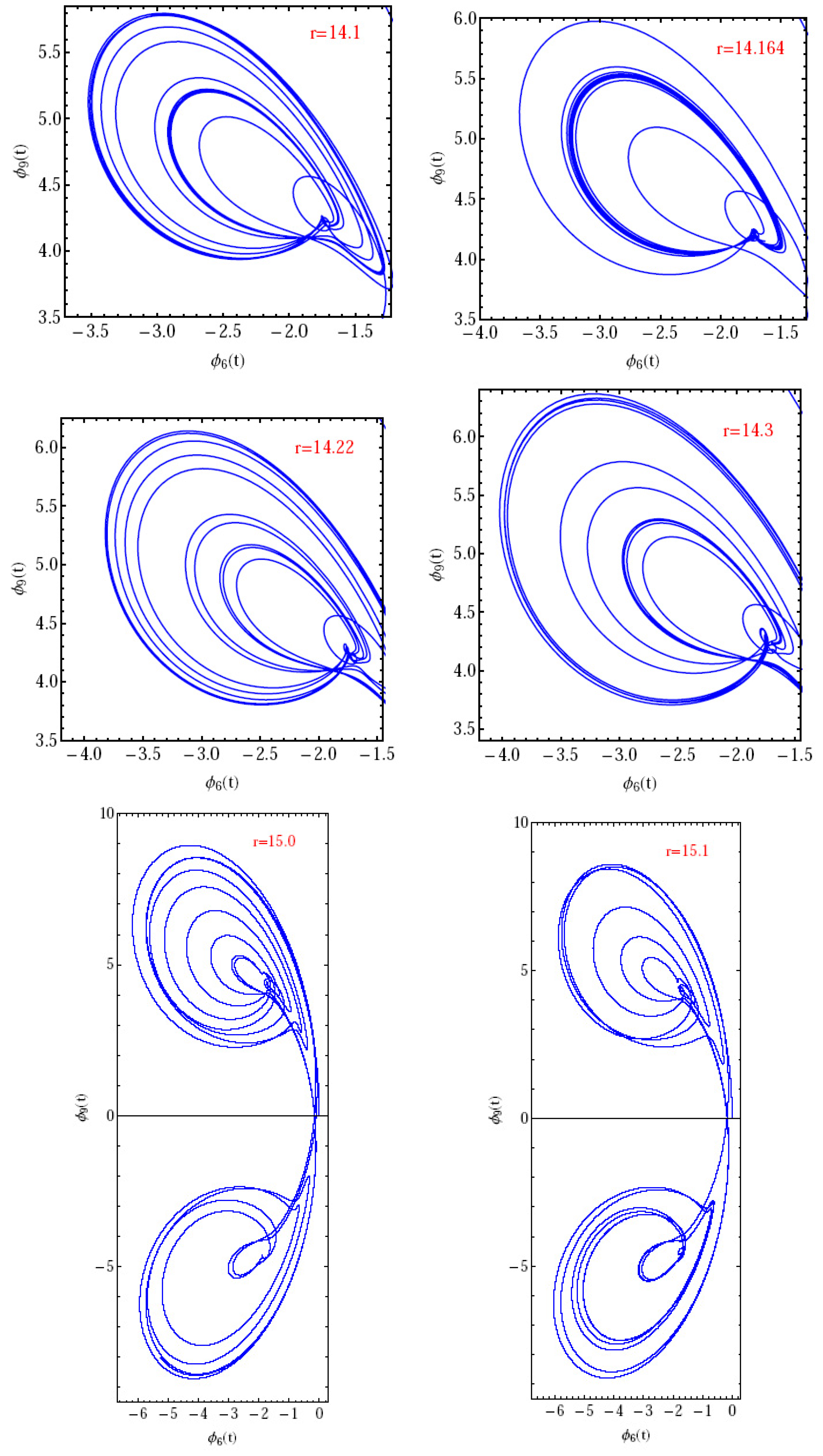
| t | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 2.52 | 4.02 | 6.85 | 2.29 | 3.90 | 0.82 | 0.73 | 5.68 | 4.85 |
| 0.0 | 3.65 | 5.96 | 4.65 | 0.85 | 5.97 | 9.65 | 4.05 | 6.90 | 5.02 |
| 0.2 | 4.55 | 3.62 | 3.95 | 3.35 | 1.25 | 7.50 | 1.90 | 7.30 | 0.60 |
| 0.2 | 5.01 | 1.50 | 2.38 | 1.95 | 7.65 | 6.05 | 5.62 | 6.95 | 6.02 |
| 0.4 | 6.26 | 0.05 | 1.05 | 4.50 | 8.98 | 5.66 | 7.58 | 4.28 | 3.95 |
| 0.4 | 7.95 | 7.99 | 3.95 | 6.65 | 0.05 | 3.80 | 6.95 | 3.98 | 7.65 |
| 0.6 | 7.28 | 7.98 | 5.26 | 7.28 | 8.96 | 2.58 | 5.29 | 2.24 | 4.96 |
| 0.6 | 6.65 | 6.29 | 7.95 | 8.32 | 8.85 | 0.29 | 8.95 | 2.24 | 8.53 |
| 0.8 | 4.95 | 6.68 | 5.02 | 7.95 | 9.95 | 8.02 | 4.05 | 3.03 | 1.95 |
| 0.8 | 3.75 | 5.50 | 4.32 | 5.26 | 0.25 | 7.95 | 6.50 | 4.74 | 3.62 |
| 1.0 | 1.65 | 2.32 | 0.29 | 3.26 | 1.65 | 4.00 | 4.00 | 5.65 | 6.85 |
| 1.0 | 2.01 | 3.85 | 3.96 | 2.95 | 2.75 | 3.90 | 2.80 | 4.85 | 3.96 |
| t | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 3.95 | 4.02 | 0.85 | 1.78 | 5.42 | 9.01 | 4.32 | 2.85 | 3.85 |
| 0.0 | 6.65 | 6.82 | 7.33 | 0.75 | 2.65 | 4.50 | 3.65 | 1.85 | 2.99 |
| 0.2 | 5.85 | 5.85 | 1.65 | 0.26 | 8.96 | 4.85 | 3.65 | 6.95 | 1.68 |
| 0.2 | 4.65 | 1.95 | 2.95 | 5.65 | 9.00 | 7.65 | 0.75 | 4.32 | 2.09 |
| 0.4 | 5.11 | 3.95 | 3.65 | 9.95 | 0.85 | 1.01 | 4.32 | 0.75 | 1.00 |
| 0.4 | 0.02 | 9.26 | 6.96 | 2.85 | 1.95 | 0.85 | 7.98 | 6.98 | 4.35 |
| 0.6 | 2.02 | 3.98 | 4.25 | 5.85 | 6.65 | 1.50 | 0.95 | 2.28 | 3.66 |
| 0.6 | 1.12 | 2.54 | 0.29 | 5.58 | 1.74 | 7.00 | 6.62 | 5.85 | 4.97 |
| 0.8 | 3.32 | 3.75 | 4.85 | 5.78 | 0.12 | 1.85 | 6.50 | 6.52 | 4.29 |
| 0.8 | 4.85 | 4.95 | 3.95 | 7.96 | 3.96 | 5.22 | 1.52 | 4.85 | 0.85 |
| 1.0 | 3.85 | 4.68 | 1.24 | 8.98 | 5.85 | 2.05 | 3.65 | 8.98 | 6.65 |
| 1.0 | 5.01 | 2.96 | 3.95 | 4.36 | 3.29 | 0.55 | 0.01 | 8.85 | 2.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adel, M.; Khader, M.M.; Algelany, S. High-Dimensional Chaotic Lorenz System: Numerical Treatment Using Changhee Polynomials of the Appell Type. Fractal Fract. 2023, 7, 398. https://doi.org/10.3390/fractalfract7050398
Adel M, Khader MM, Algelany S. High-Dimensional Chaotic Lorenz System: Numerical Treatment Using Changhee Polynomials of the Appell Type. Fractal and Fractional. 2023; 7(5):398. https://doi.org/10.3390/fractalfract7050398
Chicago/Turabian StyleAdel, Mohamed, Mohamed M. Khader, and Salman Algelany. 2023. "High-Dimensional Chaotic Lorenz System: Numerical Treatment Using Changhee Polynomials of the Appell Type" Fractal and Fractional 7, no. 5: 398. https://doi.org/10.3390/fractalfract7050398
APA StyleAdel, M., Khader, M. M., & Algelany, S. (2023). High-Dimensional Chaotic Lorenz System: Numerical Treatment Using Changhee Polynomials of the Appell Type. Fractal and Fractional, 7(5), 398. https://doi.org/10.3390/fractalfract7050398







