Dynamic Properties for a Second-Order Stochastic SEIR Model with Infectivity in Incubation Period and Homestead-Isolation of the Susceptible Population
Abstract
1. Introduction
2. Existence of Ergodic Stationary Distribution
3. Extinction
4. Density Function Analysis of Model (3)
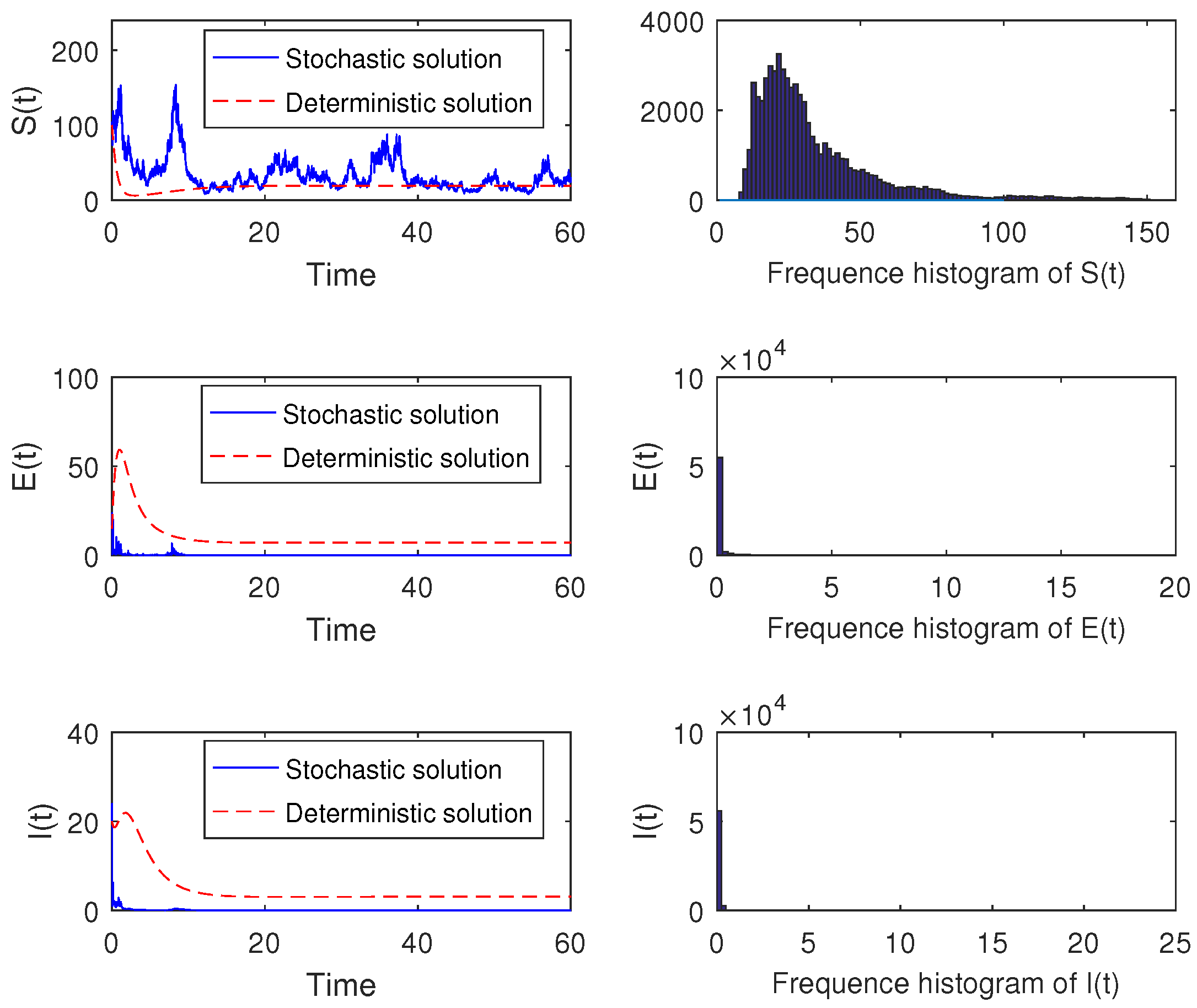
5. Numerical Tests
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- WHO. Weekly Epidemiological and Operational Updates January 2022. Available online: https://www.who.int/publications/m/item/weekly-epidemiological-update-on-covid-19 (accessed on 20 November 2022).
- Zhou, B.; Jiang, D.; Dai, Y.; Hayat, T. Stationary distribution and density function expression for a stochastic SIQRS epidemic model with temporary immunity. Nonlinear Dyn. 2021, 105, 931–955. [Google Scholar] [CrossRef]
- Ida, A.; Oharu, S.; Oharu, Y. A mathematical approach to HIV infection dynamics. J. Comput. Appl. Math. 2007, 204, 172–186. [Google Scholar] [CrossRef]
- Jiao, J.; Liu, Z.; Cai, S. Dynamics of an SEIR model with infectivity in incubation period and homestead-isolation on the susceptible. Appl. Math. Lett. 2020, 107, 106442. [Google Scholar] [CrossRef]
- Mao, X.; Marion, G.; Renshaw, E. Environmental Brownian noise suppresses explosions in population dynamics. Stoch. Proc. Appl. 2002, 97, 95–110. [Google Scholar] [CrossRef]
- Zhou, B.; Han, B.; Jiang, D. Ergodic property, extinction and density function of a stochastic SIR epidemic model with nonlinear incidence and general stochastic perturbations. Chaos Solitons Fractals 2021, 152, 111338. [Google Scholar] [CrossRef]
- Lowen, A.C.; Steel, J. Roles of humidity and temperature in shaping influenza seasonality. J. Virol. 2014, 88, 7692–7695. [Google Scholar] [CrossRef]
- Beddington, J.R.; May, R.M. Harvesting natural populations in a randomly fluctuating environment. Science 1977, 197, 463–465. [Google Scholar] [CrossRef]
- Li, X.; Song, G.; Xia, Y.; Yuan, C. Dynamical behaviors of the tumor-immune system in a stochastic environment. SIAM J. Appl. Math. 2019, 79, 2193–2217. [Google Scholar] [CrossRef]
- Cai, Y.; Kang, Y.; Banerjee, M.; Wang, W. A stochastic epidemic model incorporating media coverage. Commun. Math. Sci. 2016, 14, 893–910. [Google Scholar] [CrossRef]
- Mu, X.; Jiang, D.; Alsaedi, A. Dynamical behavior of a stochastic microorganism flocculation model with nonlinear perturbation. Qual. Theor. Dyn. Syst. 2022, 21, 42. [Google Scholar] [CrossRef]
- Han, B.; Jiang, D.; Hayat, T.; Alsaedi, A.; Ahmad, B. Stationary distribution and extinction of a stochastic staged progression AIDS model with staged treatment and second-order perturbation. Chaos Solitons Fractals 2020, 140, 110238. [Google Scholar] [CrossRef]
- Zhou, B.; Han, B.; Jiang, D.; Hayat, T.; Alsaedi, A. Ergodic stationary distribution and extinction of a staged progression HIV/AIDS infection model with nonlinear stochastic perturbations. Nonlinear Dyn. 2022, 107, 3863–3886. [Google Scholar] [CrossRef]
- Zhou, B.; Zhang, X.; Jiang, D. Dynamics and density function analysis of a stochastic SVI epidemic model with half saturated incidence rate. Chaos Solitons Fractals 2020, 137, 109865. [Google Scholar] [CrossRef]
- Han, B.; Jiang, D.; Zhou, B.; Hayat, T.; Alsaedi, A. Stationary distribution and probability density function of a stochastic SIRSI epidemic model with saturation incidence rate and logistic growth. Chaos Solitons Fractals 2021, 142, 110519. [Google Scholar] [CrossRef]
- Zhou, B.; Jiang, D.; Dai, Y.; Hayat, T.; Alsaedi, A. Stationary distribution and probability density function of a stochastic SVIS epidemic model with standard incidence and vaccination strategies. Chaos Solitons Fractals 2021, 143, 110601. [Google Scholar] [CrossRef]
- Ge, J.; Zuo, W.; Jiang, D. Stationary distribution and density function analysis of a stochastic epidemic HBV model. Math. Comput. Simul. 2022, 191, 232–255. [Google Scholar] [CrossRef]
- Han, B.; Zhou, B.; Jiang, D.; Hayat, T.; Alsaedi, A. Stationary solution, extinction and density function for a high-dimensional stochastic SEI epidemic model with general distributed delay. Appl. Math. Comput. 2021, 405, 126236. [Google Scholar] [CrossRef]
- Lu, M.; Wang, Y.; Jiang, D. Stationary distribution and probability density function analysis of a stochastic HIV model with cell-to-cell infection. Appl. Math. Comput. 2021, 410, 126483. [Google Scholar] [CrossRef]
- Lv, X.; Meng, X.; Wang, X. Extinction and stationary distribution of an impulsive stochastic chemostat model with nonlinear perturbation. Chaos Solitons Fractals 2018, 110, 273–279. [Google Scholar] [CrossRef]
- Ji, C.; Jiang, D. Dynamics of a stochastic density dependent predator-prey system with Beddington-DeAngelis functional response. J. Math. Anal. Appl. 2011, 381, 441–453. [Google Scholar] [CrossRef]
- Khasminskii, R. Stochastic Stability of Differential Equations; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Liu, Q.; Jiang, D. Stationary distribution and extinction of a stochastic SIR model with nonlinear perturbation. Appl. Math. Lett. 2017, 73, 8–15. [Google Scholar] [CrossRef]
- Qi, H.; Meng, X. Mathematical modeling, analysis and numerical simulation of HIV: The influence of stochastic environmental fluctuations on dynamics. Math. Comput. Simul. 2021, 187, 700–719. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, M. Optimal impulsive harvesting strategy of a stochastic Gompertz model in periodic environments. Appl. Math. Lett. 2022, 125, 107733. [Google Scholar] [CrossRef]
- Liu, M.; Bai, C. Optimal harvesting of a stochastic mutualism model with regime-switching. Appl. Math. Comput. 2020, 373, 125040. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, S.; Zhang, T. A predator-prey model with different response functions to juvenile and adult prey in deterministic and stochastic environments. Appl. Math. Comput. 2022, 413, 126598. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Q. Threshold behavior in a stochastic SVIR model with general incidence rates. Appl. Math. Lett. 2021, 121, 107403. [Google Scholar] [CrossRef]
- Lu, C.; Liu, H.; Zhang, D. Dynamics and simulations of a second order stochastically perturbed SEIQV epidemic model with saturated incidence rate. Chaos Solitons Fractals 2021, 152, 111312. [Google Scholar] [CrossRef]
- Lu, C. Dynamical analysis and numerical simulations on a crowley-Martin predator-prey model in stochastic environment. Appl. Math. Comput. 2022, 413, 126641. [Google Scholar] [CrossRef]
- Liu, M. Optimal harvesting of Stochastic Population Models with Periodic Coefficients. J. Nonlinear Sci. 2022, 32, 23. [Google Scholar] [CrossRef]
- Song, M.; Zuo, W.; Jiang, D.; Hayat, T. Stationary distribution and ergodicity of a stochastic cholera model with multiple pathways of transmission. J. Frankl. Inst. 2020, 357, 10773–10798. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and Applications; Horwood Publishing: Chichester, UK, 1997. [Google Scholar]
- Roozen, H. An asymptotic solution to a two-dimensional exit problem arising in population dynamics. SIAM J. Appl. Math. 1989, 49, 1793. [Google Scholar] [CrossRef]
- Tian, X.; Ren, C. Linear equations, superposition principle and complex exponential notation. Coll. Phys. 2004, 23, 23–25. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Liu, H.; Zhou, J. Dynamic Properties for a Second-Order Stochastic SEIR Model with Infectivity in Incubation Period and Homestead-Isolation of the Susceptible Population. Fractal Fract. 2023, 7, 365. https://doi.org/10.3390/fractalfract7050365
Lu C, Liu H, Zhou J. Dynamic Properties for a Second-Order Stochastic SEIR Model with Infectivity in Incubation Period and Homestead-Isolation of the Susceptible Population. Fractal and Fractional. 2023; 7(5):365. https://doi.org/10.3390/fractalfract7050365
Chicago/Turabian StyleLu, Chun, Honghui Liu, and Junhua Zhou. 2023. "Dynamic Properties for a Second-Order Stochastic SEIR Model with Infectivity in Incubation Period and Homestead-Isolation of the Susceptible Population" Fractal and Fractional 7, no. 5: 365. https://doi.org/10.3390/fractalfract7050365
APA StyleLu, C., Liu, H., & Zhou, J. (2023). Dynamic Properties for a Second-Order Stochastic SEIR Model with Infectivity in Incubation Period and Homestead-Isolation of the Susceptible Population. Fractal and Fractional, 7(5), 365. https://doi.org/10.3390/fractalfract7050365