Analysis of Damage Characteristics for Skarn Subjected to Freeze-Thaw Cycles Based on Fractal Theory
Abstract
1. Introduction
- Xu et al. [3] conducted freeze-thaw cycling tests on red sandstone and shale and obtained the variation patterns between the number of cycles and the strength and deformation parameters of the rock masses.
- Inigo A.C. et al. [4] investigated the mechanical properties of Spanish granite under different numbers of freeze-thaw cycles by means of indoor tests using chromatic coordinates and acoustic tests.
- Long et al. [5] prepared interrupted joint specimens with different joint dips and rock bridge lengths using similar materials, and obtained the deterioration damage characteristics of the various types of specimens and their influence laws on the compressive strength and damage modes.
- Yamabe et al. [6] conducted a thermal expansion strain test and corresponding rock mechanics experiments within one freeze-thaw cycle on the Sirahama sandstone in Japan and obtained the relationship between the number of cycles and strength and deformation.
- Kodama J. et al. [7] studied the effect of rock moisture content and temperature on the mechanical properties of frozen rocks and specifically analyzed the extent of the effect.
- Gao et al. [8] proposed a new segmental intrinsic structure model by examining the stress–strain relationship of sandstone under different numbers of freeze-thaw weathering cycles.
- Huang et al. [9] studied the pore structure changes and physical and mechanical property deterioration of red sandstone under freeze-thaw cycles and concluded that the growth of large pores may play a dominant role in freeze-thaw damage and strength deterioration.
- Seyed Zanyar et al. [10] established an empirical equation between the triaxial compressive strength and the number of freeze-thaw cycles for calcareous schist samples from an Angouran open pit by analyzing the test results of triaxial compressive strength under freeze-thaw cycles.
- On the other hand, Zhang Huimei et al. [11] carried out freeze-thaw cycling tests and CT (computed tomography) scanning tests on red sandstone as the research object. Based on three-dimensional reconstruction, the damage pattern of the red sandstone specimens during freezing and thawing, and the development characteristics of the internal pores, were analyzed.
- Park et al. [12] used X-ray and CT scan images and electron microscopy to study the changes in the internal fine structure of rocks under the action of freeze-thaw cycles.
- Feng et al. [13] extracted the microscopic pore structure parameters of sandstone under the freeze-thaw effect based on CT scan tests; the functional relationship between the number of freeze-thaw cycles and the coefficient of freezing and thawing of the pore particles was established.
- Zhou et al. [14], based on NMR (nuclear magnetic resonance) and impact loading tests of freeze-thaw sandstones, analyzed the microstructural damage and the characteristics of the dynamic mechanical parameters’ evolution of the rocks under freeze-thaw action.
- Zhang et al. [17] studied the damage deterioration of rock’s mechanical properties and fine structure caused by freeze-thaw cycling action on saturated red sandstone.
- Javad et al. [18] investigated the damage behavior of Tasmanian sandstone under different numbers of freeze-thaw cycles and explored the damage mechanism of Tasmanian sandstone subjected to various freeze-thaw cycles in UCS (uniaxial compressive strength) and BTS (Brazilian tensile strength) tests.
- Zhu et al. [23] conducted a fractal study of rock damage under blasting loads and defined the degree of damage in terms of the fractal dimension to provide a new way to study the damage evolution of rocks under blasting action.
- Based on fractal theory, Luo et al. [24] studied the distribution characteristics of blasting blockiness in medium-deep holes and obtained a prediction model of blasting blockiness distribution.
- Liu et al. [25] applied the fractal theory to the various stages of mineral processing and introduced a variety of fractal laws for each process step.
- Shan et al. [26] investigated the fractality characteristics of oil-rich kerogen destruction under microwave–water interaction and quantitatively described the fracture expansion pattern of the specimen with the help of the fractal dimension.
- Yu et al. [27] used fractal theory combined with medical images to provide a practical method for describing complex structures and behaviors in living organisms.
- Li et al. [28] quantified the brain development images of infants and children based on fractal theory. All these fields have achieved more fruitful results due to the intervention of fractal methods. In addition, for rocks, as a natural, porous material, fractal theory provides a new method for the quantitative analysis of their internal pore structure and crack nodularity.
- M.N. Bagde et al. [29] proposed a better method of rock classification based on the fractal approach.
- The fractal characterization of the evolution of microstructural features of sandstones under dry and wet cycles was carried out by Zhou et al. [30].
- Ren et al. [31] explored the fractal characteristics of perforated rock masses based on acoustic emission tests and the fractal dimension.
2. Methodology
2.1. Experiments
2.1.1. Specimen Preparation
2.1.2. Specimen Grouping
2.1.3. Experimental Program
- (1)
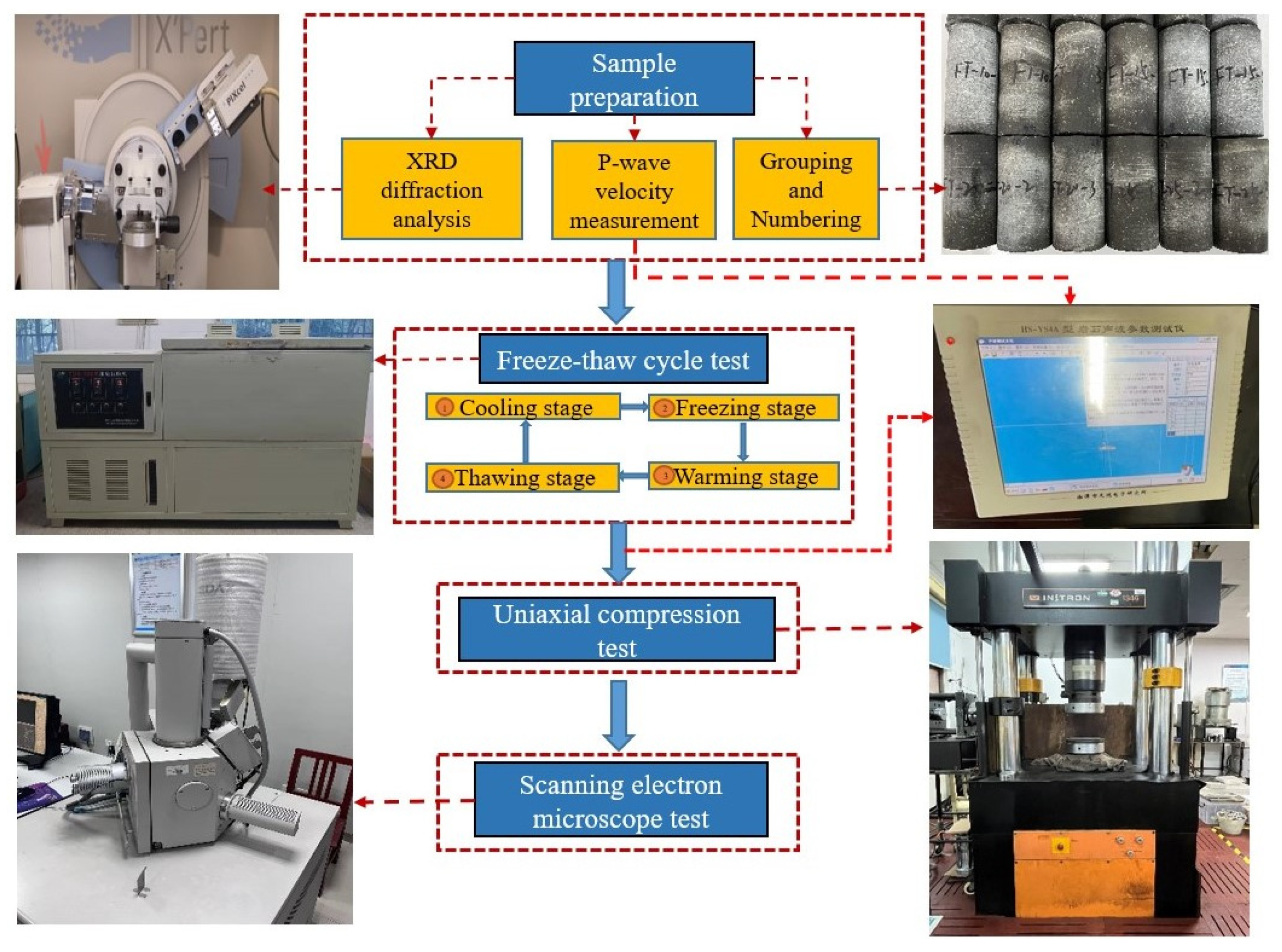
- After the sampling was completed, the quality and diameter of the rock samples were tested first, and the rock samples with obvious defects such as fractures on the surface were rejected. Then, based on the XRD component analysis test, the specimens with large differences and that did not meet the test requirements were rejected. The 18 rock samples that met the test requirements were grouped and numbered in the format of FT-X-Y (X is the number of corresponding cycles, Y is the serial number).
- (2)
- Except for the rock sample with freeze-thaw cycle number 0, all other rock samples were put into the TDS-300 freeze-thaw cycle tester (Donghua Test Equipment Co., Suzhou, China), the corresponding freezing and thawing temperatures were set, and then the samples were removed after completing the corresponding freeze-thaw cycle number.
- (3)
- (The P-wave velocity test was carried out again on the specimens after the freeze-thaw treatment using the HS-YS4A Rock Acoustic Wave Parameter Tester (Tianhong Electronics Research Institute, Xiangtan, China) to obtain the P-wave velocity values of the specimens after the freeze-thaw.
- (4)
- Uniaxial compression testing of rock samples was conducted using the Instron 1346 Electro-Hydraulic Servo Universal Testing Machine (INSTRON Corporation, Norwood, MA, USA). The test machine was loaded using displacement control loading and a loading rate of 0.1 mm/min to obtain the stress–strain curve during the uniaxial compression of the specimen.
- (5)
- The SEM test was carried out with an FEG-Quanta 200 environmental scanning electron microscope (FEI Corporation, Hillsboro, OR, USA) on the fine structure of the crushed rock samples after the uniaxial compression test under different cycle times, and the SEM images of the rock samples under different freeze-thaw cycle times were obtained.
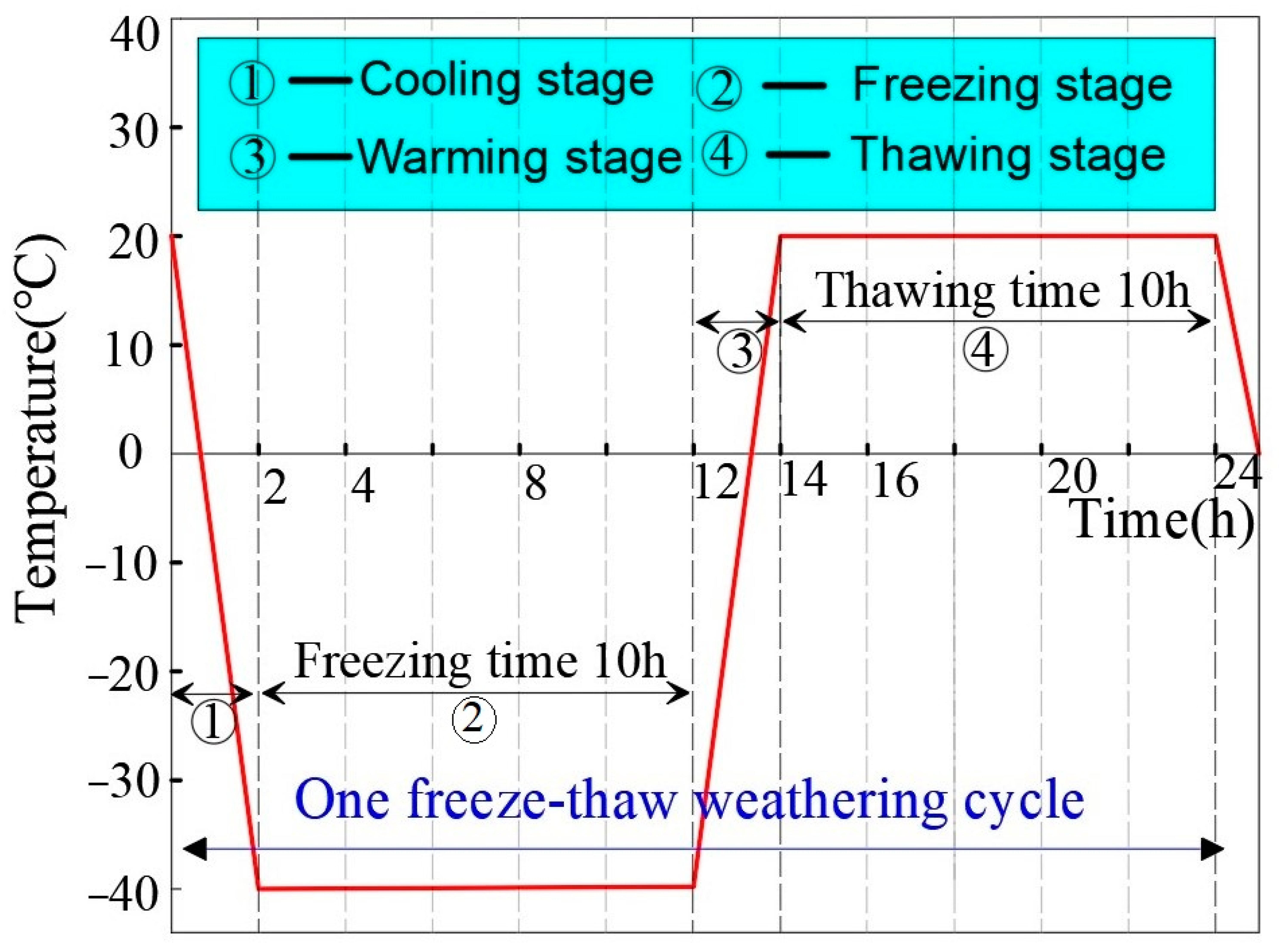
2.2. Fractal
- (1)
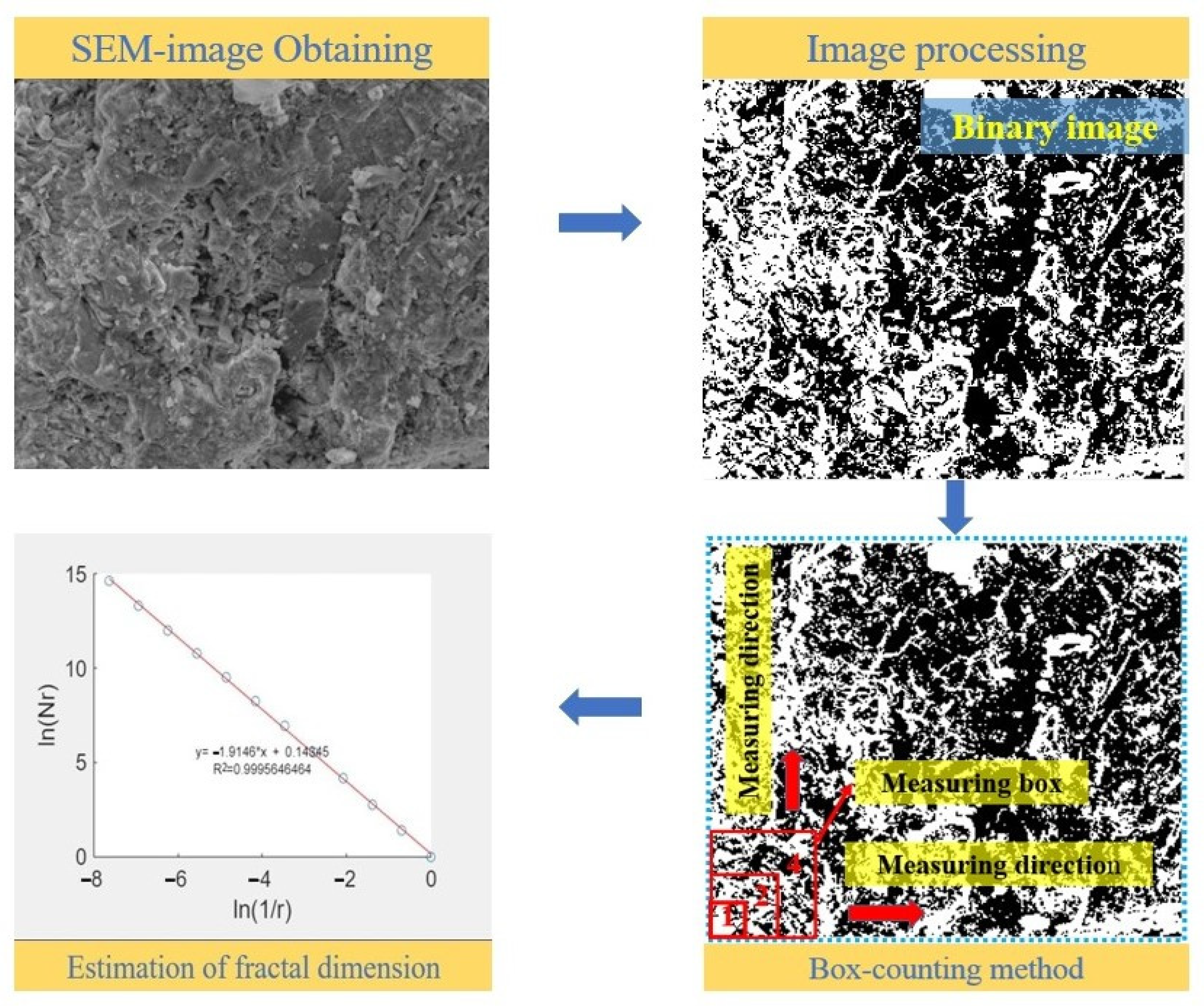
- Image processing: The “gradient” function in the Matlab software environment is used to convert the SEM image into a grayscale image, and then the grayscale image is binarized, with the white area representing the particulate matter and the black area representing the crack network in the black-and-white image.
- (2)
- Box dimension method calculation: The fractal dimension of the crack network in the SEM image is calculated using the box-dimension counting method, and each region in the binary image is covered by a sequence of square grids of scale r. The number of regions containing black or white parts is recorded as N(r), which is usually taken as r = 1, 2, 4, …, 2i (i = 0, 1, 2, 3, …); from the image perspective, the dimensions of 1, 2, 4, …, 2i pixels are taken as the edge length to divide the image; and finally, the number of boxes N(1), N(2), N(4), …, N(2i) is obtained.
- (3)
- When r tends to 0, the fractal dimension of the box dimension method is obtained as:where f is the value of the fractal dimension measured by the box dimension.Because only a finite number of side lengths r can be taken for practical applications, the double logarithmic coordinates have a good linear relationship:where f is the slope of the line (i.e., the fractal dimension of the image) and h is the intercept.
3. Experimental Results
3.1. Physical Parameter Degradation Characteristics
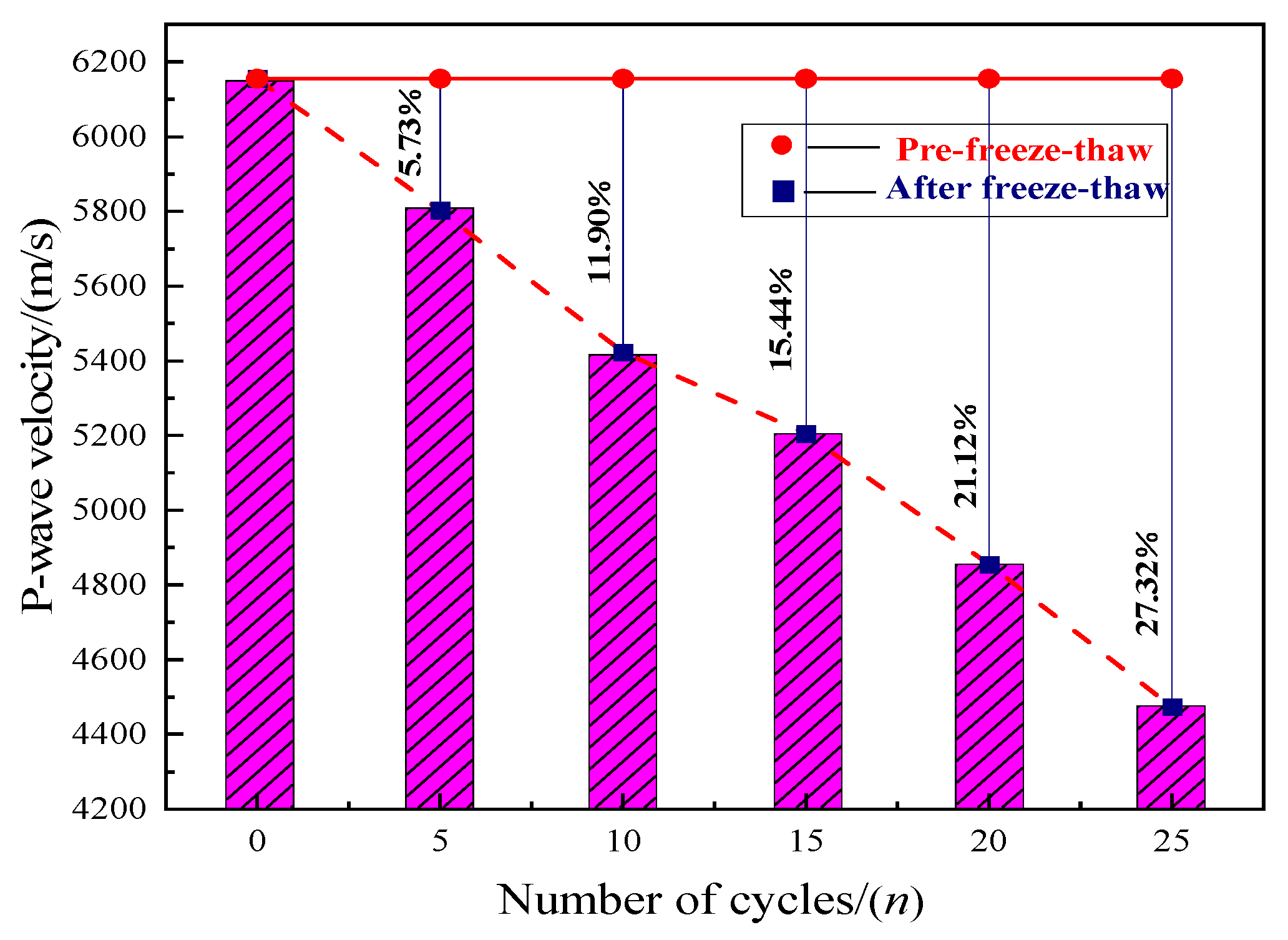
3.1.1. P-Wave Velocity
3.1.2. Quality Change
3.2. Mechanical Parameter Degradation Characteristics
3.2.1. Stress–Strain Curve
3.2.2. Uniaxial Compressive Strength
3.2.3. Modulus of Elasticity and Poisson’s Ratio

3.3. Freeze-Thaw Damage Analysis of Rocks Based on Scanning Electron Microscopy
3.4. Calculation of the Fractal Dimension Based on SEM Images
4. Discussion
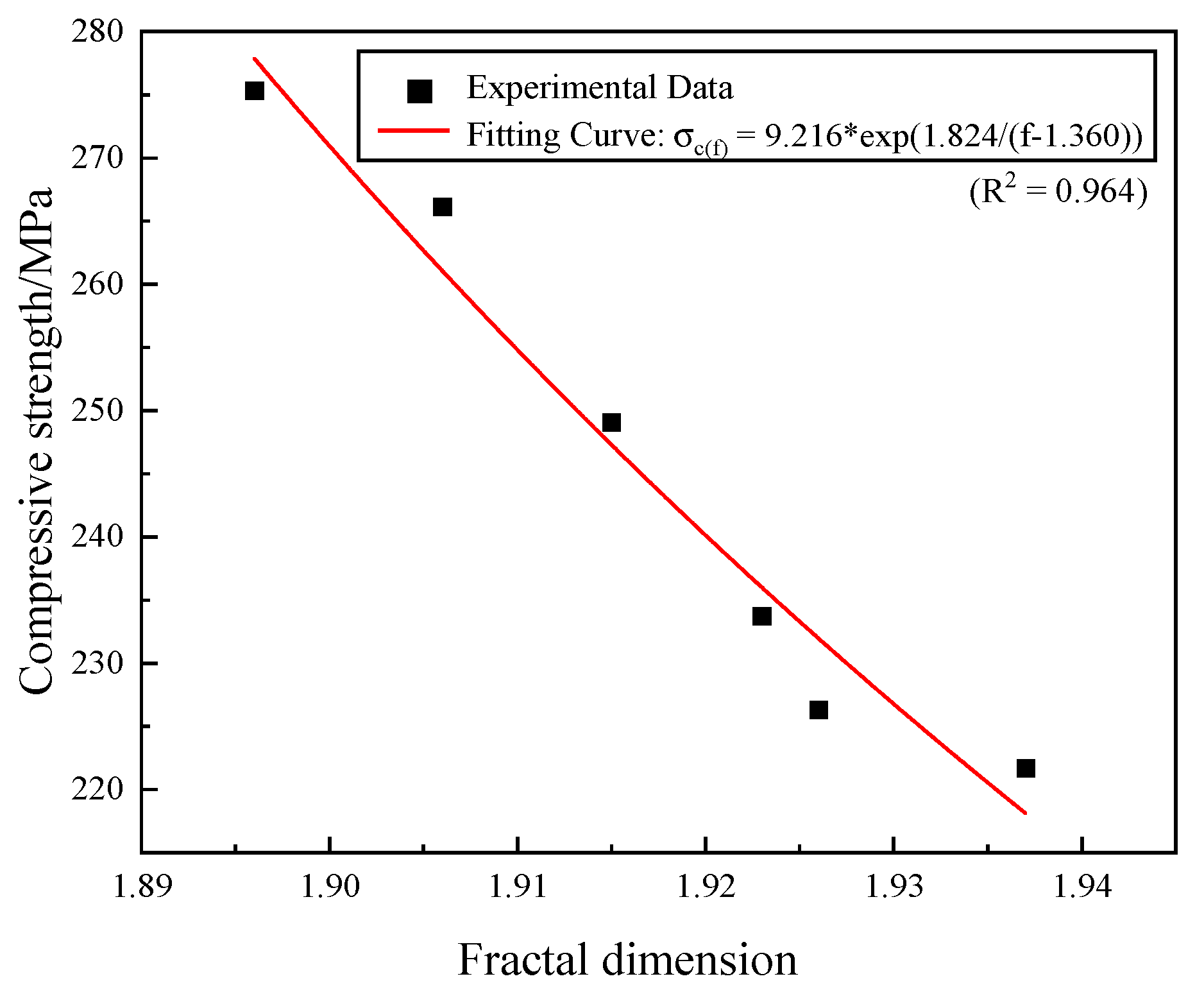
4.1. Correlation Analysis of Fractal Dimension and Rock Physical Property Parameters
4.2. Analysis of Freeze-Thaw Damage Mechanism
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shen, Y.J.; Yang, G.S.; Rong, T.L.; Jia, H.L.; Wang, M.; Liu, H. Analysis of localized damage effect and end fracture characteristics of single fracture type sandstone under the action of freeze-thaw cycles. J. Rock Mech. Eng. 2017, 36, 562–570. [Google Scholar]
- Yang, G.S.; Pu, Y.B.; Ma, W. Study on the extension of rock damage under freeze-thaw environment conditions in cold regions. Exp. Mech. 2002, 17, 220–226. [Google Scholar]
- Xu, G.M.; Liu, Q.S.; Peng, W.W.; Chang, X.X. Experimental study of basic mechanical properties of rocks under low temperature action. J. Rock Mech. Eng. 2006, 25, 2502–2508. [Google Scholar]
- Iñigo, A.C.; García-Talegón, J.; Vicente-Tavera, S.; Martín-González, S.; Casado-Marín, S.; Vargas-Muñoz, M.; Pérez-Rodríguez, J.L. Colour and ultrasound propagation speed changes by different ageing of freezing/thawing and cooling/heating in granitic materials. Cold Reg. Sci. Technol. 2013, 85, 71–78. [Google Scholar] [CrossRef]
- Long, S.G.; Xu, J.T.; Li, R.J.; Liu, X.; Chen, J. Damage and mechanical properties of intermittent jointed rock masses under freeze-thaw action. J. Disaster Prev. Mitig. Eng. 2023, 3, 1–7. [Google Scholar]
- Yamabe, T.; Neaupane, K.M. Determination of some thermo-mechanical properties of Sirahama sandstone under subzero temperature condition. Int. J. Rock Mech. Min. Sci. 2001, 38, 1029–1034. [Google Scholar] [CrossRef]
- Kodama, J.; Goto, T.; Fujii, Y.; Hagan, O. The effects of water content, temperature and loading rate on strength and failure process of frozen rocks. Int. J. Rock Mech. Min. Sci. 2013, 62, 1–13. [Google Scholar] [CrossRef]
- Gao, F.; Xiong, X.; Xu, C.; Zhou, K.P. Mechanical property deterioration characteristics and a new constitutive model for rocks subjected to freeze-thaw weathering process. Int. J. Rock Mech. Min. Sci. 2021, 140, 104642. [Google Scholar] [CrossRef]
- Huang, S.; Yu, S.; Ye, Y.; Ye, Z.; Cheng, A. Pore structure change and physico-mechanical properties deterioration of sandstone suffering freeze-thaw actions. Constr. Build. Mater. 2022, 330, 127200. [Google Scholar] [CrossRef]
- Mousavi SZ, S.; Tavakoli, H.; Moarefvand, P.; Rezaei, M. Assessing the effect of freezing-thawing cycles on the results of the triaxial compressive strength test for calc-schist rock. Int. J. Rock Mech. Min. Sci. 2019, 123, 104090. [Google Scholar] [CrossRef]
- Zhang, H.M.; Wang, H.; Zhang, J.F.; Cheng, S.F.; Zhou, H.W. Characterization of fine-scale damage in freeze-thaw rocks at CT scale. J. Liaoning Univ. Eng. Technol. Nat. Sci. Ed. 2020, 39, 51–56. [Google Scholar]
- Park, J.; Hyun, C.U.; Park, H.D. Changes in microstructure and physical properties of rocks caused by artificial freeze–thaw action. Bull. Eng. Geol. Environ. 2015, 74, 555–565. [Google Scholar] [CrossRef]
- Feng, Q.; Hou, S.; Liu, W.; Zhang, S.; Li, W.; Tian, M. Study on the simulation method and mesoscopic characteristics of rock freeze-thaw damage. Comput. Geotech. 2023, 153, 105038. [Google Scholar] [CrossRef]
- Zhou, K.; Bin, L.; Li, J.L.; Deng, H.; Bin, F. Microscopic damage and dynamic mechanical properties of rock under freeze–thaw environment. Trans. Nonferr. Met. Soc. China 2015, 25, 1254–1261. [Google Scholar] [CrossRef]
- Li, J.L.; Zhu, L.Y.; Zhou, K.P.; Liu, H.W.; Cao, S.P. Characterization of pore structure damage in sandstone under freeze-thaw action. Geotech. Mech. 2019, 40, 3524–3532. [Google Scholar]
- Li, J.L.; Zhou, K.P.; Zhang, Y.M.; Xu, Y. Experimental study on freeze-thaw damage of rock pore structure based on nuclear magnetic resonance technique. J. Rock Mech. Eng. 2012, 31, 1208–1214. [Google Scholar]
- Zhang, N.; Zhao, W.Z.; Luo, S.L.; Wang, S.D.; Wang, R.C.; Li, X.L. Mineral analysis of freeze-thaw red sandstone damage characteristics based on uniaxial compression and scanning electron microscopy experiments. J. Build. Sci. Eng. 2022, 3, 1–9. [Google Scholar]
- Perfect, E. Fractal models for the fragmentation of rocks and soils: A review. Eng. Geol. 1997, 48, 185–198. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Passoja, D.E.; Paullay, A.J. Fractal character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Chen, P.P.; Qi, L.H.; Zhang, X.B.; Ma, L.; Yang, G.; Qi, J. Analysis of heat–moisture coupling transfer for unsaturated soil under freezing and thawing based on fractal theory. Cold Reg. Sci. Technol. 2023, 206, 103744. [Google Scholar] [CrossRef]
- Ma, B.Y.; Hu, Q.H.; Yang, S.Y.; Zhang, T.; Qiao, H.; Meng, M.; Zhu, X.; Sun, X. Pore structure typing and fractal characteristics of lacustrine shale from Kongdian Formation in East China. J. Nat. Gas Sci. Eng. 2021, 85, 103709. [Google Scholar] [CrossRef]
- Jiang, S.F.; Su, Y. Application of fractal theory in the field of civil engineering. Eng. Mech. 2009, 26, 148–152. [Google Scholar]
- Zhu, W.H.; Ming, F.; Song, C.Z. Fractal Study of Rock Damage Destruction under Blasting Load. Geotech 2011, 32, 3131–3135. [Google Scholar]
- Luo, H.H.; Yang, R.S.; Ma, X.M. Study on the distribution characteristics of blockiness in fan-shaped deep hole blasting in Shilu iron ore mine. J. Min. Saf. Eng. 2023, 40, 371–377. [Google Scholar]
- Liu, X.R.; Zhou, W.G.; Xie, G.Y.; Peng, Y.L.; Liang, L.; Li, Y.J. The basis of application of fractal theory in mineral processing and research progress. J. China Coal Soc. 2023. [Google Scholar] [CrossRef]
- Shan Peng, F.; Yang, P.; Lai, X.P.; Sun, H.Q.; Guo, Z.A.; Gu, H.L.; Li, W.; Zhang, S. Experiment on the progressive damage law of oil-rich coal rocks under microwave-water interaction. J. Rock Mech. Eng. 2023. [Google Scholar] [CrossRef]
- Yu, K.J.; Li, C. A Study on The Application of Matlab-Based Fractal Theory in Medicine. Software 2019, 40, 111–116. [Google Scholar] [CrossRef]
- Li, H.H.; Luo, L.P.; Huang, L. Quantitative analysis of medical images of normal brain development in infants and children based on fractal theory. J. Biomed. Eng. 2011, 28, 18–21. [Google Scholar]
- Bagde, M.N.; Raina, A.K.; Chakraborty, A.K.; Jethwa, J.L. Rock mass characterization by fractal dimension. Eng. Geol. 2002, 63, 141–155. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Cai, X.; Ma, D.; Chen, L.; Wang, S.; Tan, L. Dynamic tensile properties of sandstone subjected to wetting and drying cycles. Constr. Build. Mater. 2018, 182, 215–232. [Google Scholar] [CrossRef]
- Ren, J.J.; Zhang, W.L.; Ma, J. Experimental study on butterfly shape of failure zone and fractal characteristics of rock burst. Eng. Fail. Anal. 2022, 140, 106636. [Google Scholar] [CrossRef]
- GBT 50266-2013; Standard for Test Methods of Engineering Rock Mass. Standardization Administration of China: Beijing, China, 2013.
- Kulatilake, P.H.S.W.; Fiedler, R.; Panda, B.B. Box fractal dimension as a measure of statistical homogeneity of jointed rock masses. Eng. Geol. 1997, 48, 217–229. [Google Scholar] [CrossRef]
- Aia, T.; Zhang, R.; Zhou, H.W. Box-counting methods to directly estimate the fractal dimension of a rock surface. Appl. Surf. Sci. 2014, 314, 610–621. [Google Scholar] [CrossRef]
- Wu, M.; Wang, W.; Shi, D.; Song, Z.; Li, M.; Luo, Y. Improved box-counting methods to directly estimate the fractal dimension of a rough surface. Measurement 2021, 177, 109303. [Google Scholar] [CrossRef]
- Yahaghi, J.; Liu, H.; Chan, A.; Fukuda, D. Experimental and numerical studies on failure behaviours of sandstones subject to freeze-thaw cycles. Transp. Geotech. 2021, 31, 100655. [Google Scholar] [CrossRef]
- Bour, O.; Davy, P.; Darcel, C.; Odling, O. A statistical scaling model for fracture network geometry, with validation on a multiscale mapping of a joint network (Hornelen Basin, Norway). J. Geophys. Res. Solid Earth 2002, 107, ETG 4-1–ETG 4-12. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, S.; Weng, L.; Wang, L.; Li, Z.; Xu, L. Fractal analysis of cracking in a clayey soil under freeze–thaw cycles. Eng. Geol. 2016, 208, 93–99. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Yao, J.; Gong, F.; Li, X.; Du, K.; Tao, M.; Huang, L.; Du, S. Experimental investigation of rock breakage by a conical pick and its application to non-explosive mechanized mining in deep hard rock. Int. J. Rock Mech. Min. Sci. 2019, 122, 104063. [Google Scholar] [CrossRef]
- Lin, Z.J.; Niu, F.J.; Liu, H.; Lu, J.H. Influence of cyclic freezing and thawing on the physical and mechanical properties of permafrost road base boulders. Rock Soil Mech. 2011, 32, 1369–1375. [Google Scholar]
- Li, J.-L.; Zhou, K.-P.; Liu, W.-J.; Deng, H.-W. NMR research on deterioration characteristics of microscopic structure of sandstones in freeze−thaw cycles. Trans. Nonferr. Met. Soc. China 2016, 26, 2997–3003. [Google Scholar] [CrossRef]
- Tan, H.; Song, Y.J.; Guo, X.X.; Meng, F.D.; Han, D.Y.; Sun, Y.W. Study on fine view damage and strain localization in freeze-thaw fractured sandstone. Chin. J. Rock Mech. Eng. 2022, 41, 2485–2495. [Google Scholar]
- Yang, G.S.; Shen, Y.J.; Jia, H.L.; Wei, Y.; Zhang, H.M.; Liu, H. Multiscale study and progress of mechanical properties of rock damage in freeze-thaw environment. Chin. J. Rock Mech. Eng. 2018, 37, 545–558. [Google Scholar]
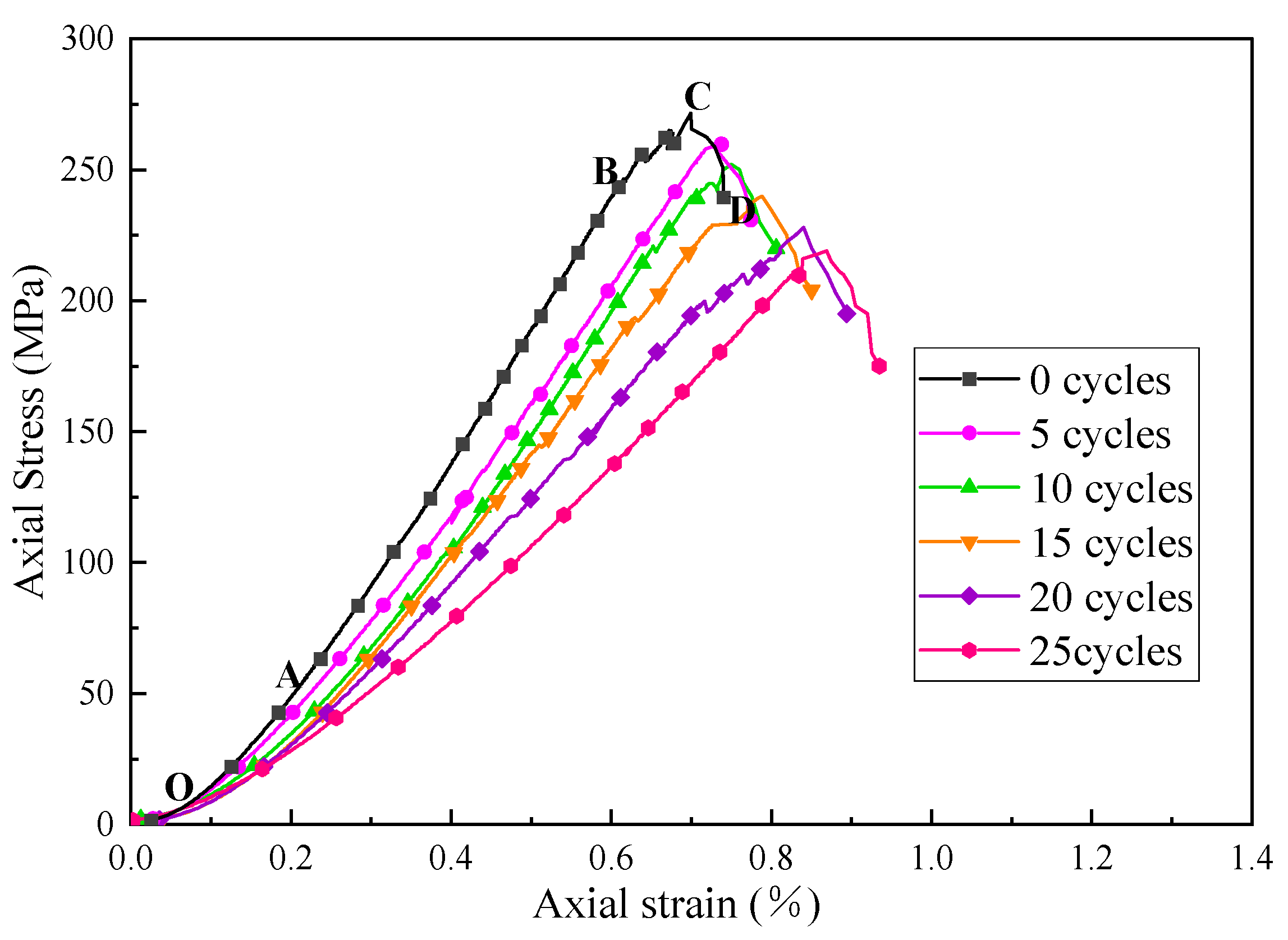
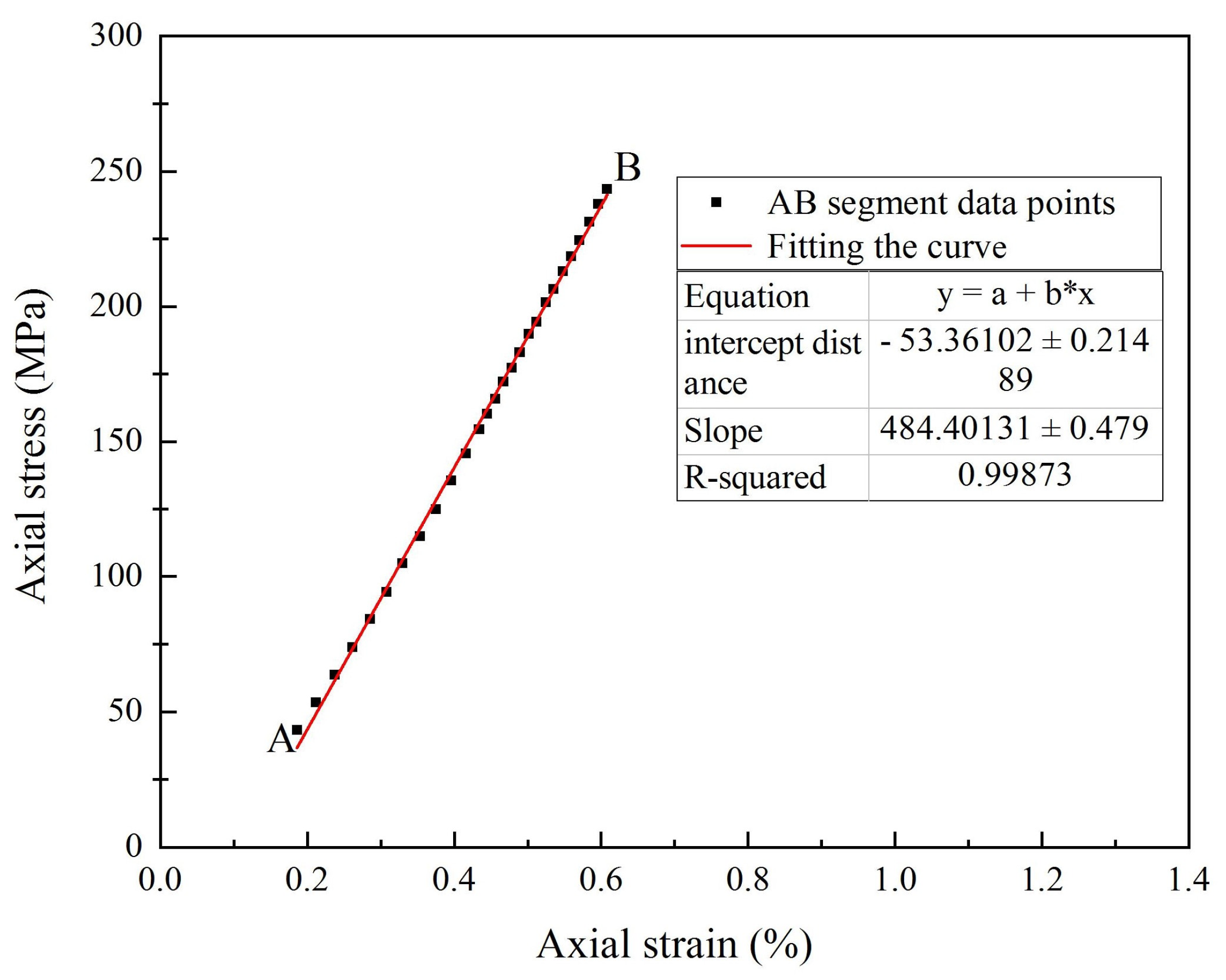


| Mineral/% | Pyroxene | Feldspar | Chlorite | Mica | Quartz | |
|---|---|---|---|---|---|---|
| Number | ||||||
| No.1 | 51.6 | 20.8 | 15.3 | 8.5 | 3.8 | |
| No.2 | 53.4 | 19.5 | 14.5 | 9.1 | 3.5 | |
| No.3 | 48.9 | 18.3 | 16.7 | 12.8 | 3.9 | |
| Number of Cycles/n | Specimen Number | Before Freezing and Thawing/g | After Freezing and Thawing/g | Poor Quality/g | Mass Change Rate/% | Average Mass Change Rate/% |
|---|---|---|---|---|---|---|
| 0 | FT-0-1 | 569.51 | 569.51 | 0 | 0 | 0 |
| FT-0-2 | 583.5 | 583.5 | 0 | 0 | ||
| FT-0-3 | 585.38 | 585.38 | 0 | 0 | ||
| 5 | FT-5-1 | 581.49 | 585.69 | 4.2 | 0.72 | 0.85 |
| FT-5-2 | 556.17 | 562.26 | 6.09 | 1.09 | ||
| FT-5-3 | 579.18 | 583.36 | 4.18 | 0.72 | ||
| 10 | FT-10-1 | 557.64 | 565.83 | 8.19 | 1.47 | 1.27 |
| FT-10-2 | 578.71 | 583.86 | 5.15 | 0.89 | ||
| FT-10-3 | 582.15 | 590.68 | 8.53 | 1.47 | ||
| 15 | FT-15-1 | 578.17 | 587.86 | 9.69 | 1.68 | 1.75 |
| FT-15-2 | 553.91 | 562.98 | 9.07 | 1.64 | ||
| FT-15-3 | 557.15 | 567.96 | 10.81 | 1.94 | ||
| 20 | FT-20-1 | 582.35 | 586.89 | 4.54 | 0.78 | 0.96 |
| FT-20-2 | 582.81 | 587.54 | 4.73 | 0.81 | ||
| FT-20-3 | 582.14 | 589.64 | 7.5 | 1.29 | ||
| 25 | FT-25-1 | 580.53 | 584.65 | 4.12 | 0.71 | 0.57 |
| FT-25-2 | 578.04 | 581.34 | 3.3 | 0.57 | ||
| FT-25-3 | 584.8 | 587.38 | 2.58 | 0.44 |
| Number of Cycles/n | Specimen Number | Peak Compressive Strength/MPa | Average Peak Compressive Strength/MPa | Loss Rate/% |
|---|---|---|---|---|
| 0 | FT-0-1 | 279.18 | 275.35 | 0 |
| FT-0-2 | 270.63 | |||
| FT-0-3 | 276.25 | |||
| 5 | FT-5-1 | 269.48 | 266.15 | 3.35 |
| FT-5-2 | 265.02 | |||
| FT-5-3 | 263.97 | |||
| 10 | FT-10-1 | 244.83 | 249.05 | 9.56 |
| FT-10-2 | 250.95 | |||
| FT-10-3 | 251.37 | |||
| 15 | FT-15-1 | 228.49 | 233.75 | 15.12 |
| FT-15-2 | 237.55 | |||
| FT-15-3 | 235.21 | |||
| 20 | FT-20-1 | 222.46 | 226.35 | 17.81 |
| FT-20-2 | 225.21 | |||
| FT-20-3 | 231.38 | |||
| 25 | FT-25-1 | 217.03 | 221.69 | 19.50 |
| FT-25-2 | 221.89 | |||
| FT-25-3 | 226.16 |
| Number of Cycles/n | Specimen Number | Modulus of Elasticity/GPa | Average Modulus of Elasticity/GPa | Loss Rate/% | Poisson’s Ratio |
|---|---|---|---|---|---|
| 0 | 0-1 | 42.71 | 42.78 | 0 | 0.22 |
| 0-2 | 43.95 | ||||
| 0-3 | 41.68 | ||||
| 5 | 5-1 | 37.49 | 41.06 | 4.02 | 0.20 |
| 5-2 | 42.95 | ||||
| 5-3 | 42.74 | ||||
| 10 | 10-1 | 42.74 | 40.09 | 6.28 | 0.18 |
| 10-2 | 38.38 | ||||
| 10-3 | 40.67 | ||||
| 15 | 15-1 | 42.14 | 39.52 | 7.62 | 0.17 |
| 15-2 | 36.02 | ||||
| 15-3 | 40.41 | ||||
| 20 | 20-1 | 39.74 | 38.88 | 9.11 | 0.17 |
| 20-2 | 37.23 | ||||
| 20-3 | 39.67 | ||||
| 25 | 25-1 | 38.41 | 38.56 | 9.86 | 0.16 |
| 25-2 | 39.04 | ||||
| 25-3 | 38.23 |
| Number of Cycles | Fitting Formula | Goodness of Fit | Fractal Dimension |
|---|---|---|---|
| 0 | y = −1.8964x + 0.1714 | R2 = 0.999 | 1.896 |
| 5 | y = −1.906x + 0.1570 | R2 = 0.999 | 1.906 |
| 10 | y = −1.9146x + 0.1434 | R2 = 0.999 | 1.915 |
| 15 | y = −1.923x + 0.1394 | R2 = 0.999 | 1.923 |
| 20 | y = −1.9257x + 0.1303 | R2 = 0.999 | 1.926 |
| 25 | y = −1.9371x + 0.1121 | R2 = 0.999 | 1.937 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Tan, S.; Yang, C.; Chen, H.; Lin, Y. Analysis of Damage Characteristics for Skarn Subjected to Freeze-Thaw Cycles Based on Fractal Theory. Fractal Fract. 2023, 7, 354. https://doi.org/10.3390/fractalfract7050354
Li J, Tan S, Yang C, Chen H, Lin Y. Analysis of Damage Characteristics for Skarn Subjected to Freeze-Thaw Cycles Based on Fractal Theory. Fractal and Fractional. 2023; 7(5):354. https://doi.org/10.3390/fractalfract7050354
Chicago/Turabian StyleLi, Jielin, Shuaijie Tan, Chun Yang, Hui Chen, and Yun Lin. 2023. "Analysis of Damage Characteristics for Skarn Subjected to Freeze-Thaw Cycles Based on Fractal Theory" Fractal and Fractional 7, no. 5: 354. https://doi.org/10.3390/fractalfract7050354
APA StyleLi, J., Tan, S., Yang, C., Chen, H., & Lin, Y. (2023). Analysis of Damage Characteristics for Skarn Subjected to Freeze-Thaw Cycles Based on Fractal Theory. Fractal and Fractional, 7(5), 354. https://doi.org/10.3390/fractalfract7050354










