A New Perspective on Predicting Roughness of Discontinuity from Fractal Dimension D of Outcrops
Abstract
1. Introduction
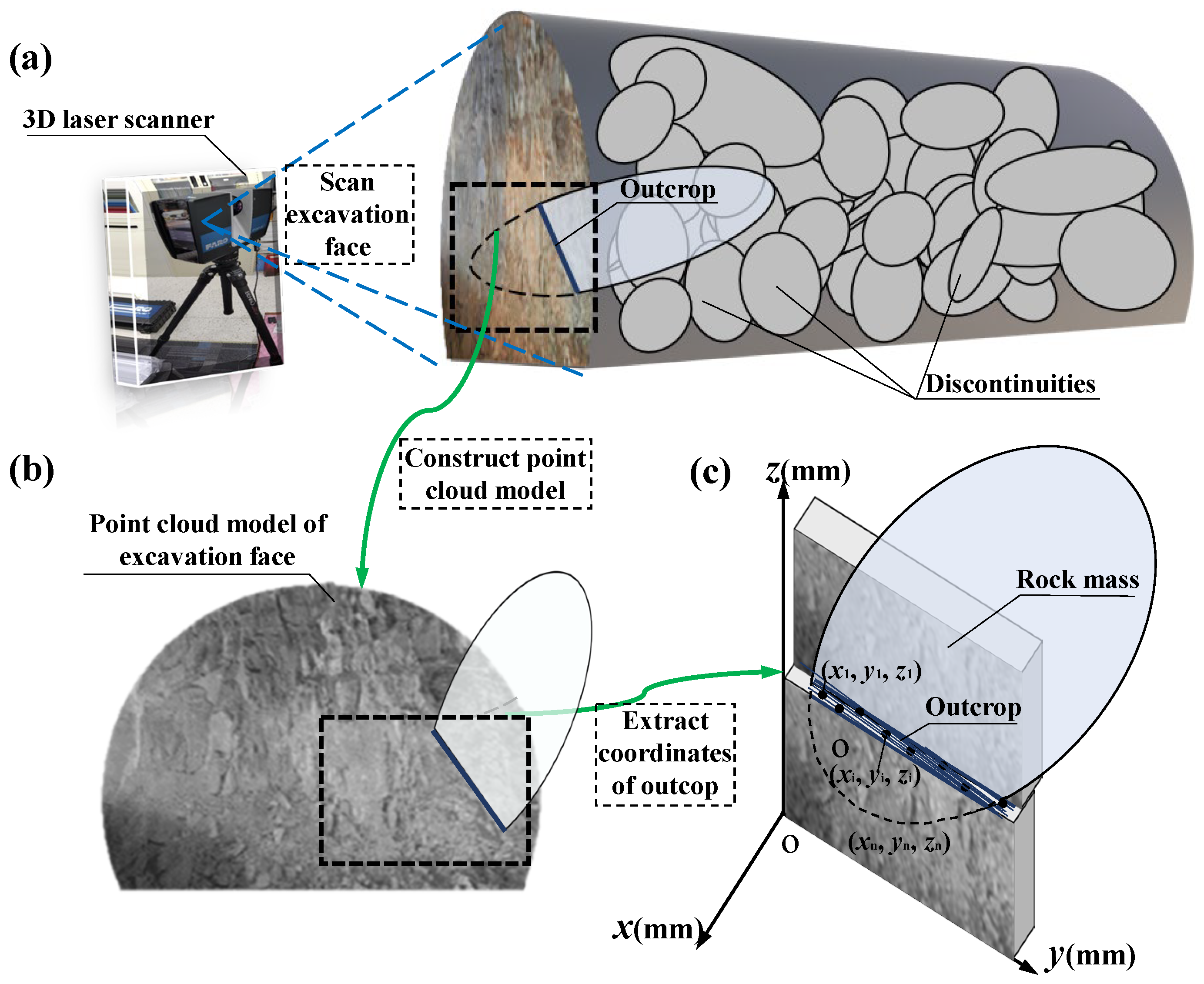
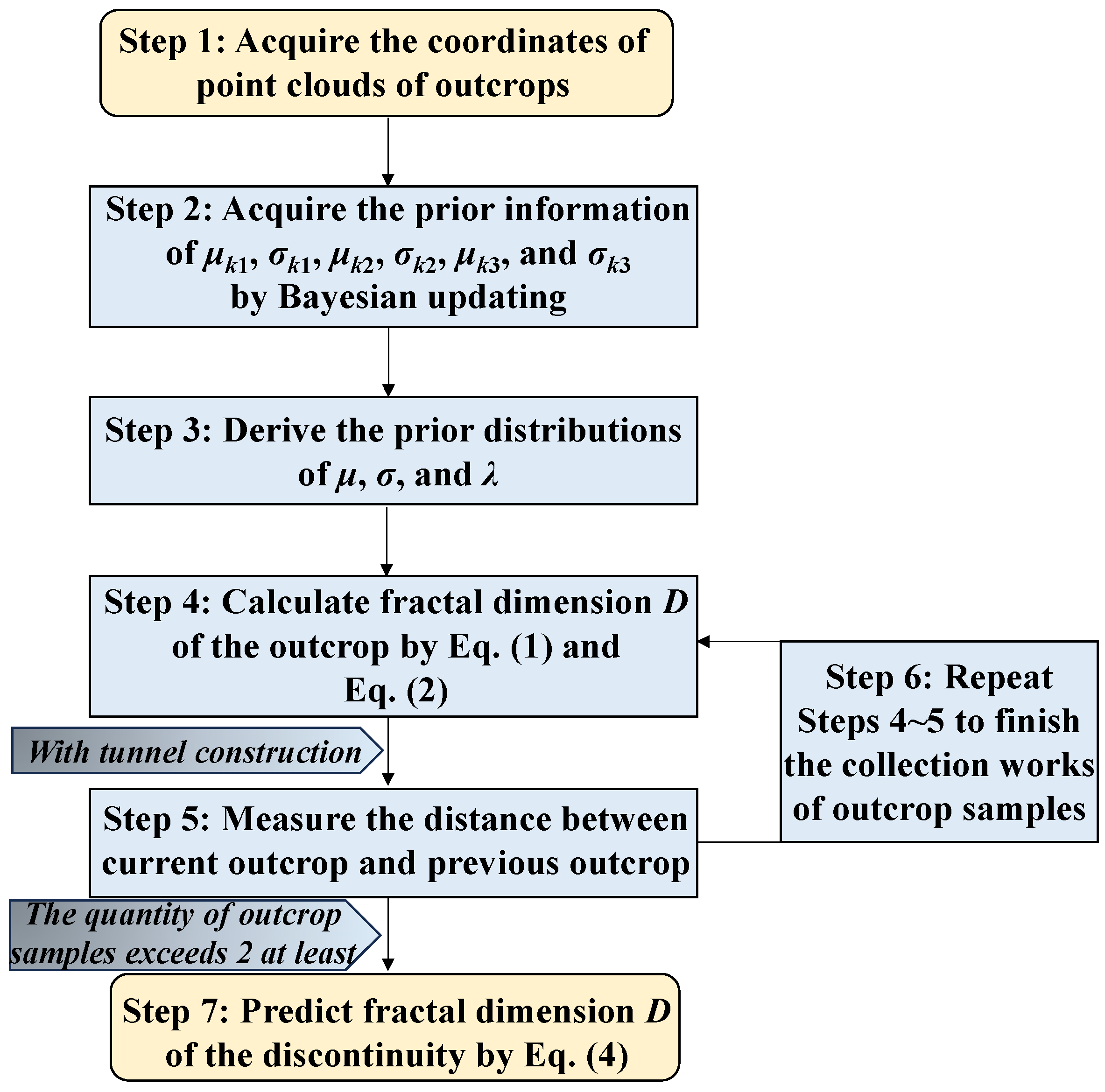
2. Measurement of Fractal Dimension D of Outcrops
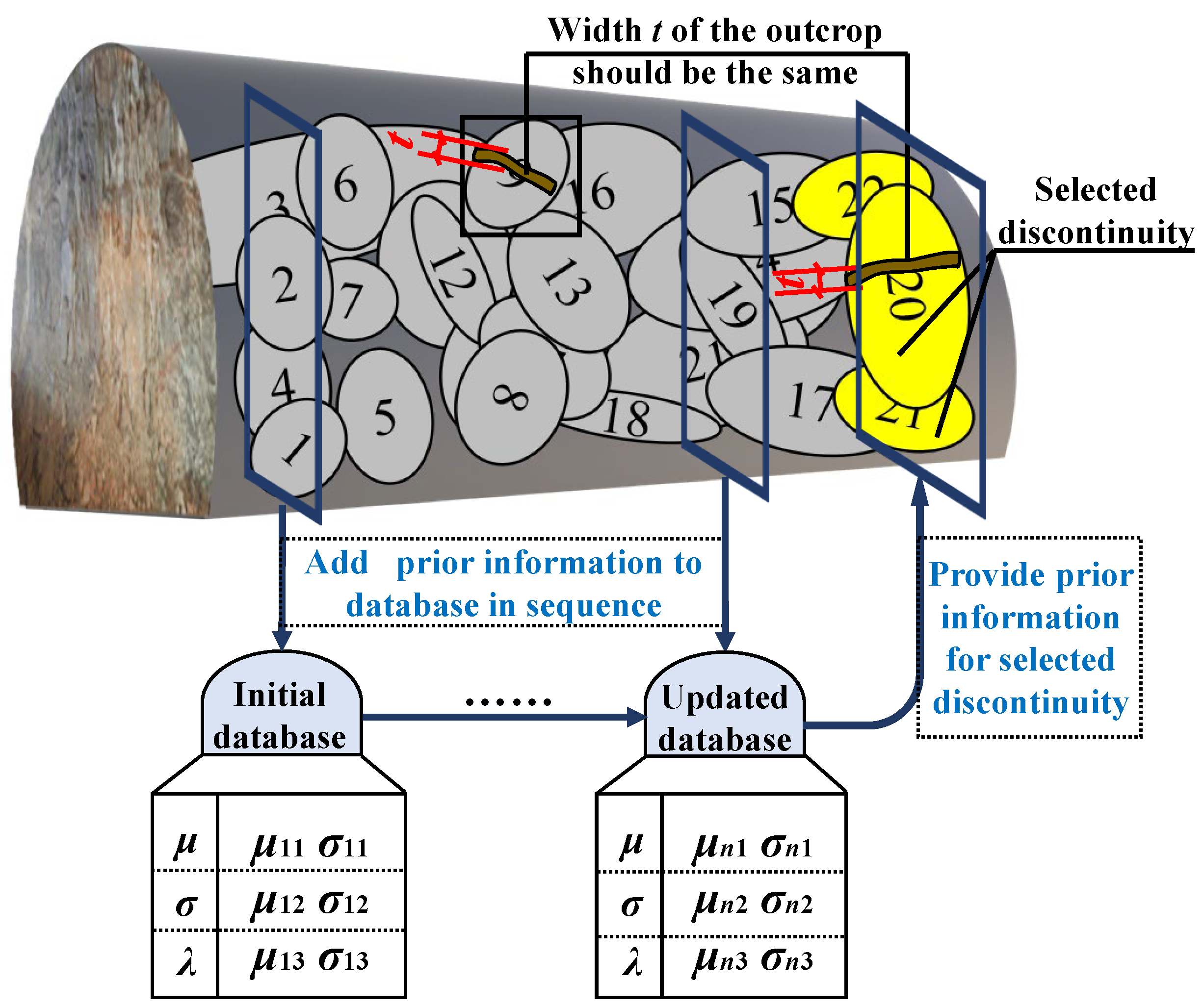
2.1. Measurement of Coordinates of Outcrops
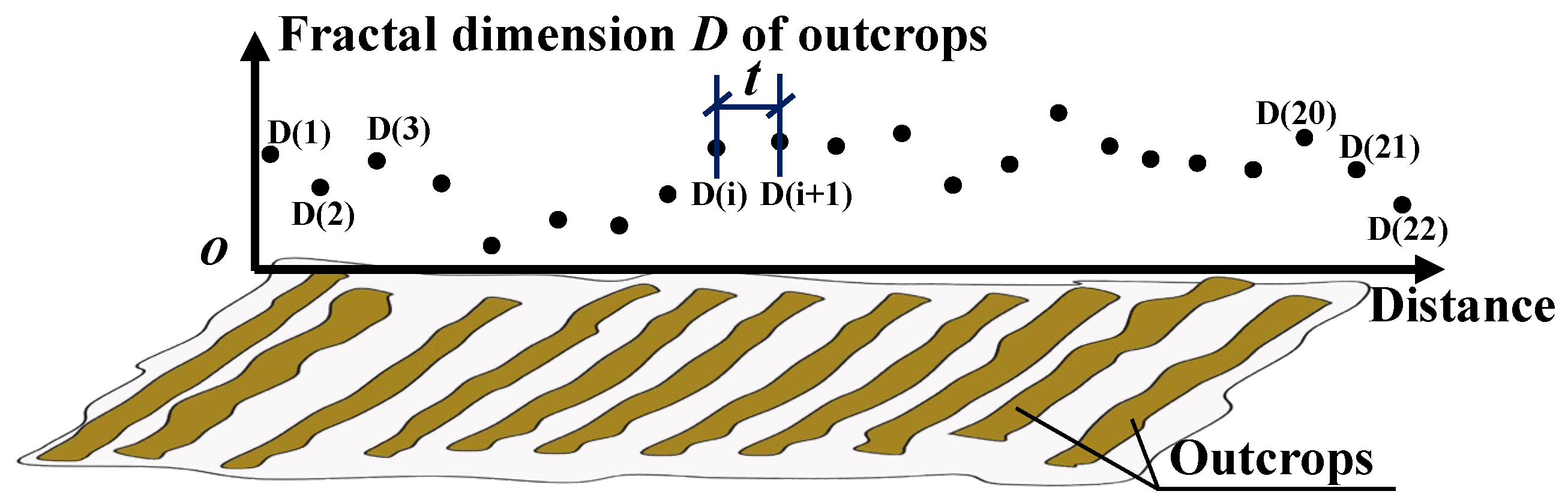
2.2. Calculation Method of Fractal Dimension D
3. Prediction of Fractal Dimension D of Discontinuity
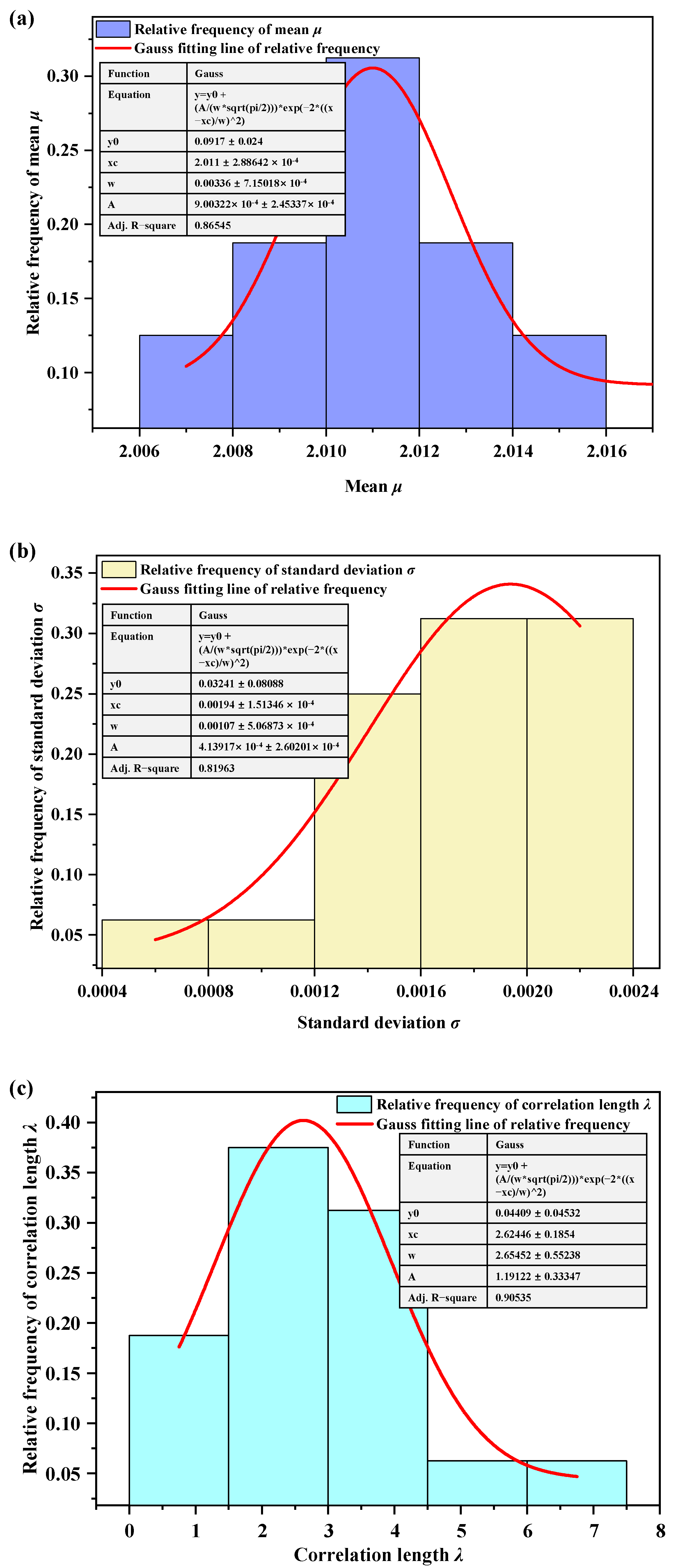
3.1. Discretization of Random Field of Fractal Dimension D
3.2. Establishment of Prediction Model of Fractal Dimension D
4. Verification of Proposed Method and Sensitivity Analysis of Correlation Function and Discontinuity Size in Predicting Results
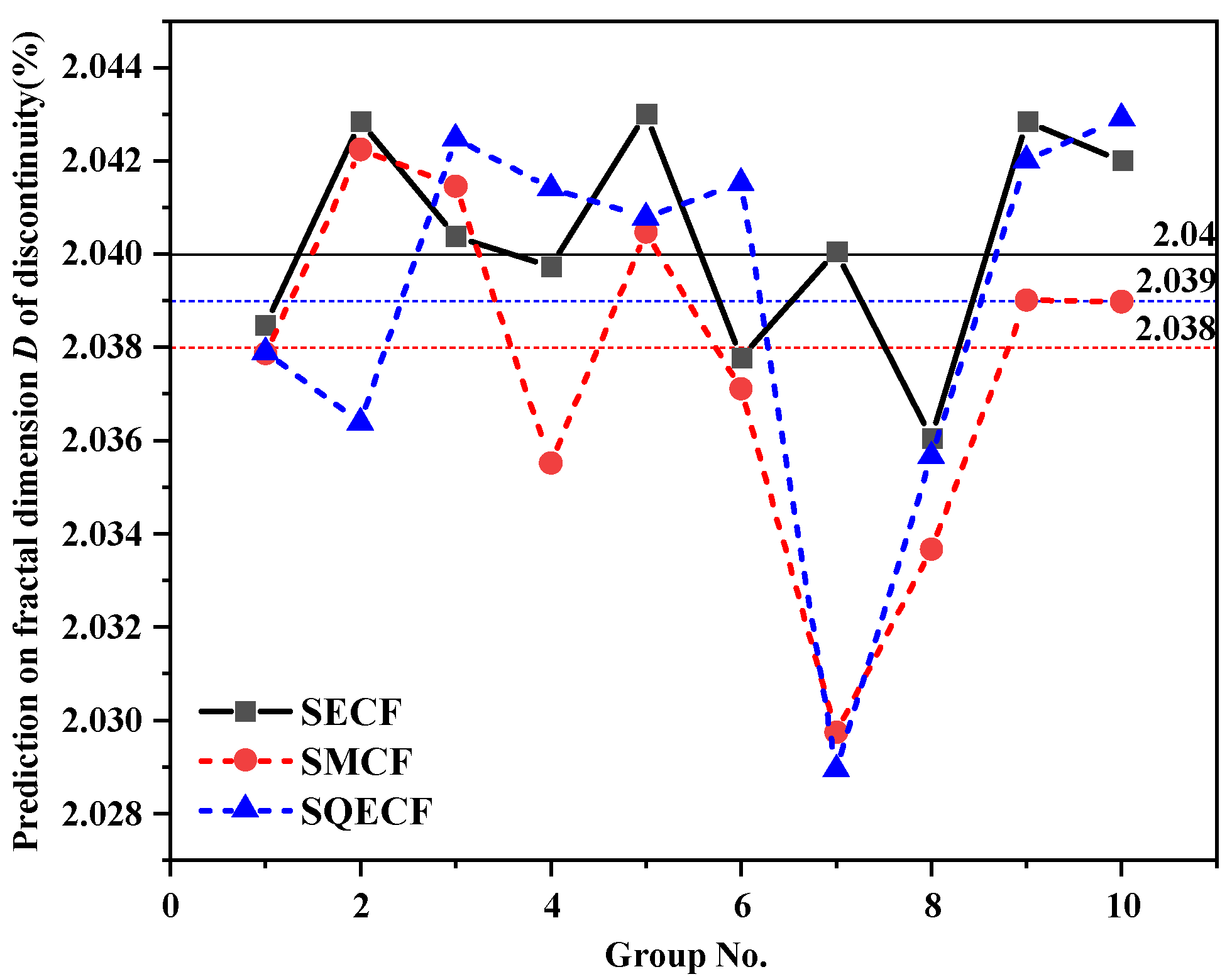
4.1. Verification of Proposed Method for Discontinuity Sample
4.2. Study on Sensitivity of Correlation Function in Prediction Results
4.3. Study on Sensitivity of Discontinuity Size in Predicting Fractal Dimension D
5. Conclusions
- (1)
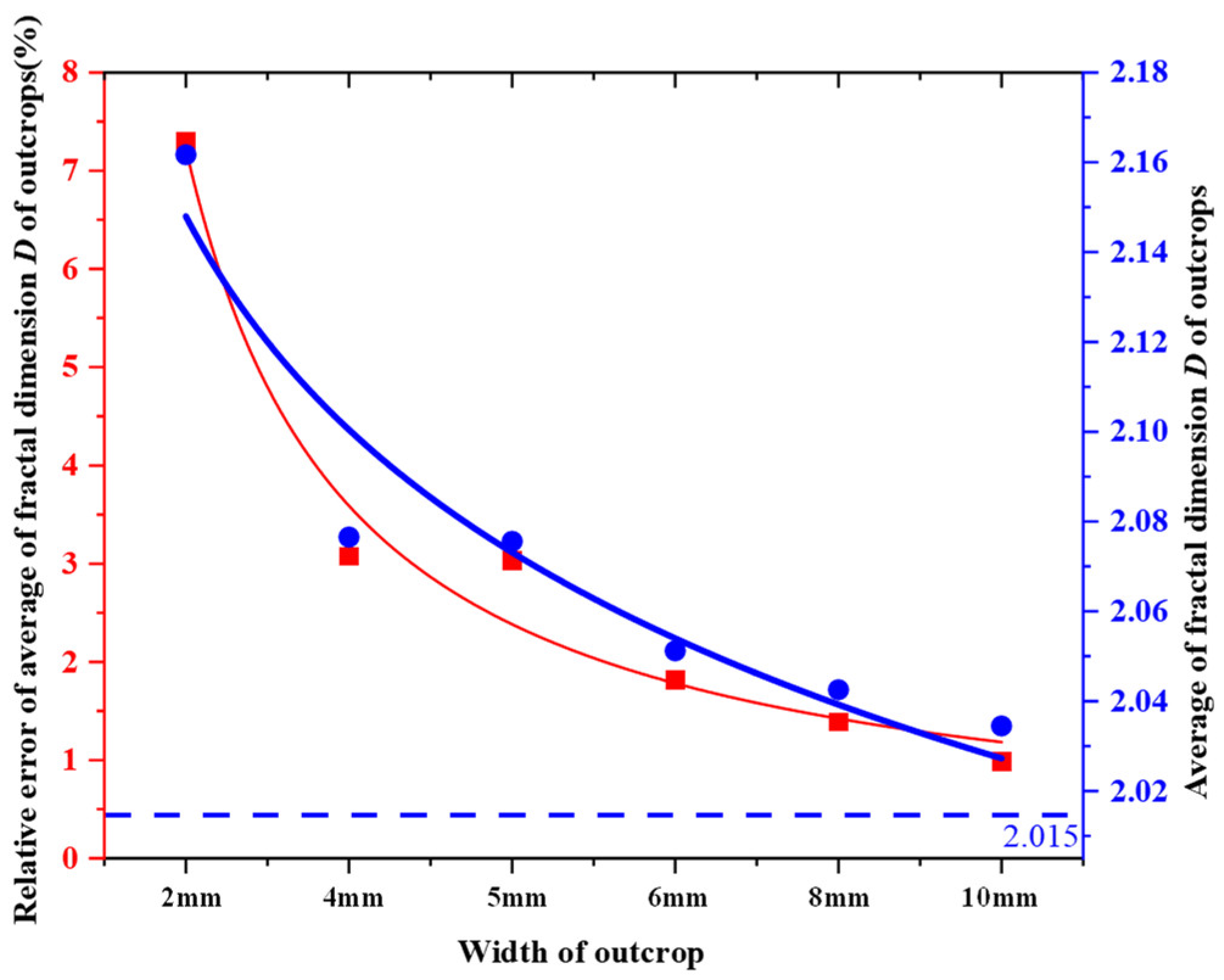
- For determining the optimal width of the outcrop, the widths of 2 mm, 4 mm, 5 mm, 6 mm, 8 mm, and 10 mm are used for analysis. Considering the trade-off of the between the width of outcrop and the error, the width of 4 mm is selected to conduct follow-up analysis in our case.
- (2)
- The prediction model of the fractal dimension D is established based on Bayesian theory, according to [9]. For deriving the prior distribution in the model, Bayesian updating is adopted for dynamically determining the prior information of μ, σ, and λ.
- (3)
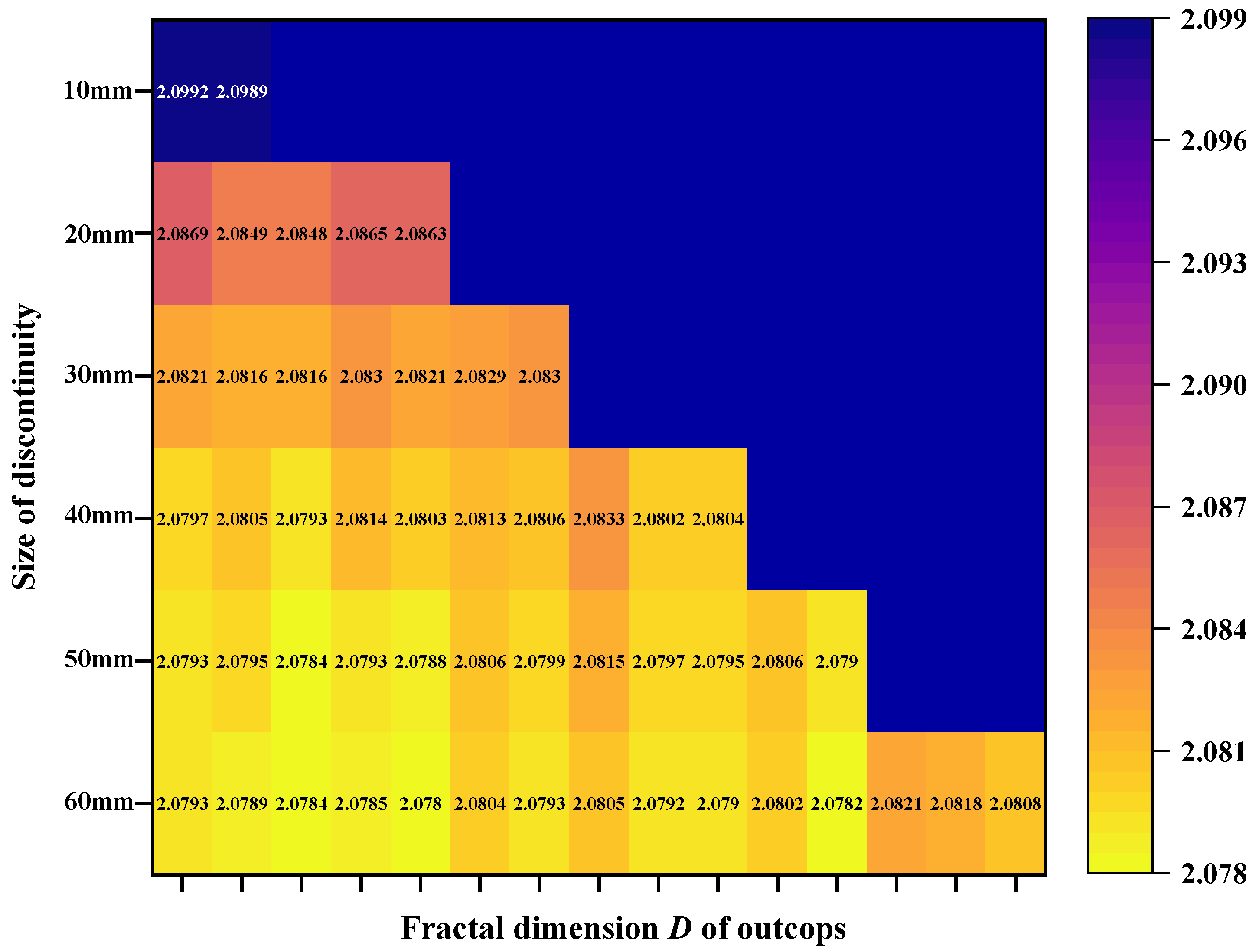
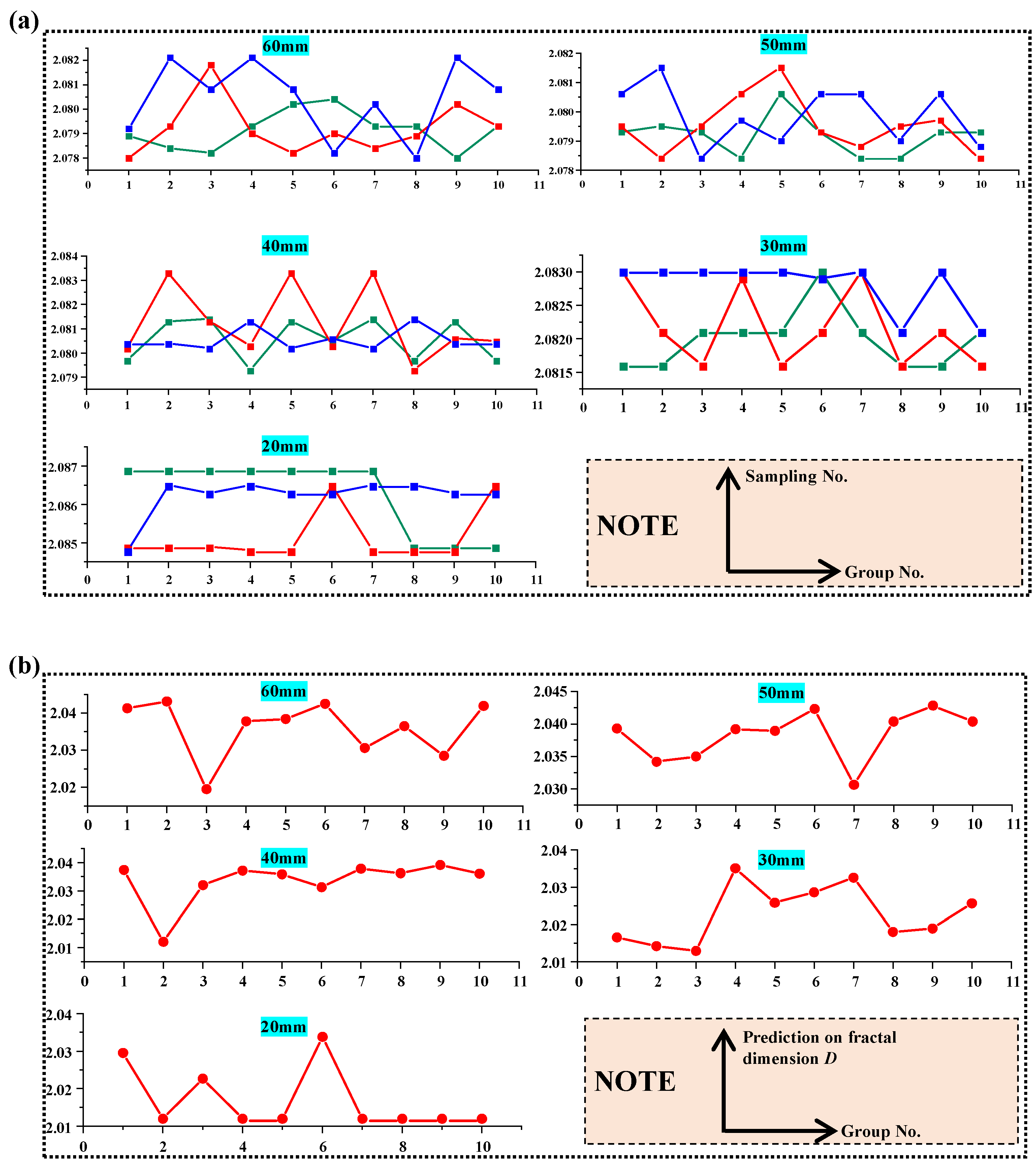
- The proposed method is verified by the discontinuity sample, which can be applied to the engineering for predicting the fractal dimension D of the discontinuity. For the GSI standard, the level of the roughness of the discontinuity (Rr) can be evaluated as 1. For choosing the appropriate sampling size in the study, the sampling sizes of 2, 3, 4, and 5 are studied. It is found that when the sampling size is relatively large, the prediction value of fractal dimension D of the discontinuity may be approximately coincident with the prior information. In addition, when the sampling size is relatively small, the prediction results are not necessarily less accurate than those obtained using a large sampling size.
- (4)
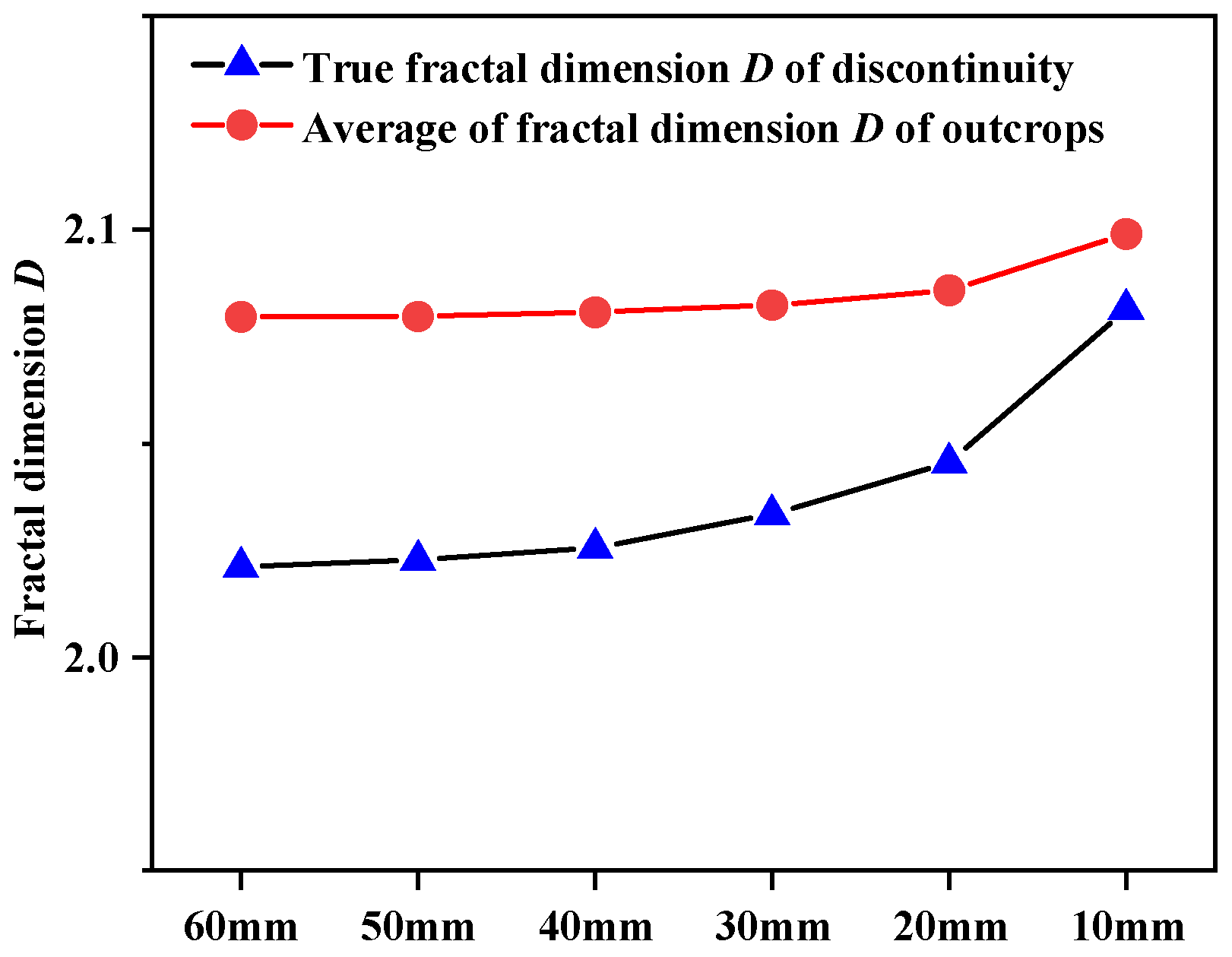
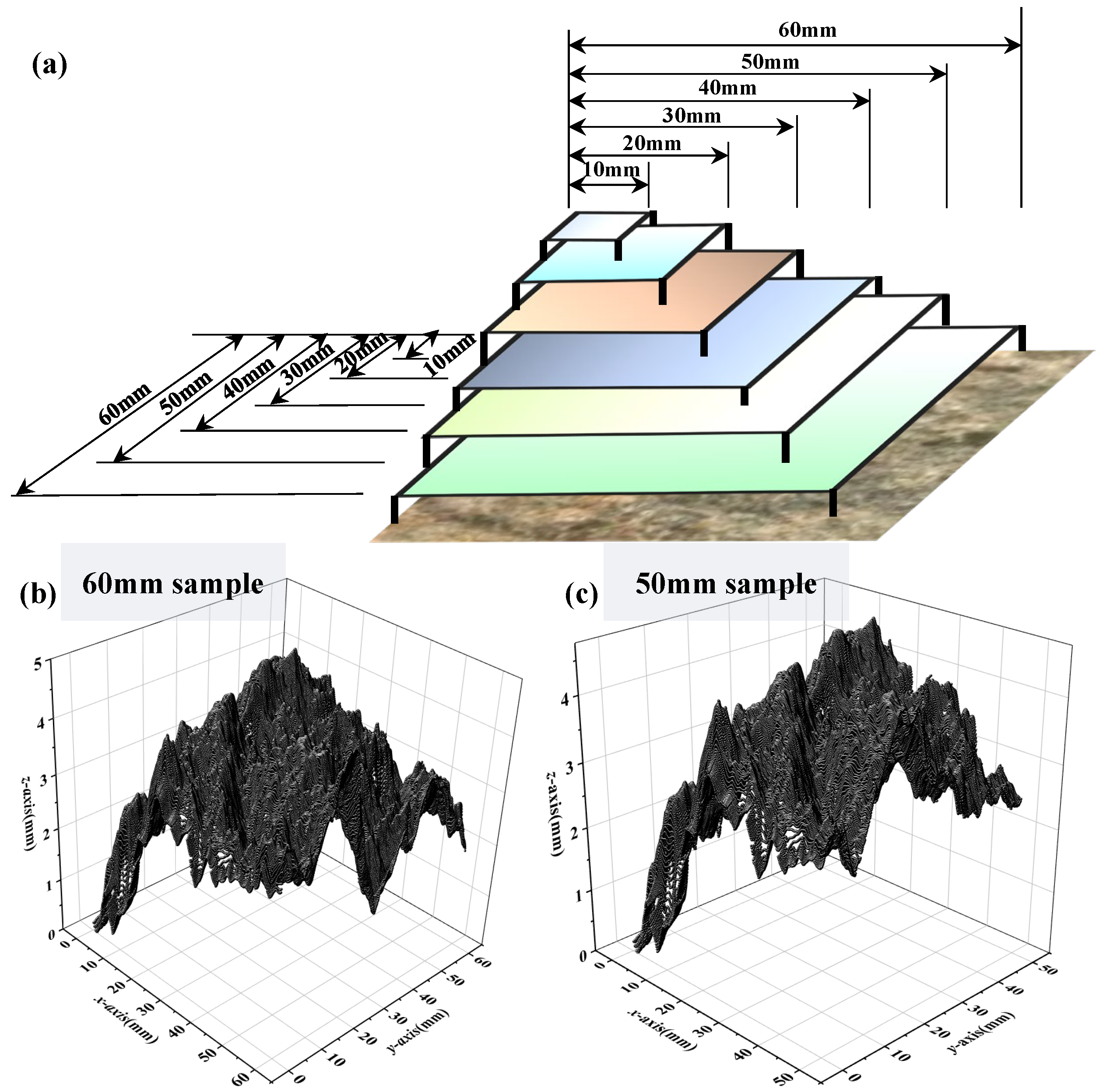
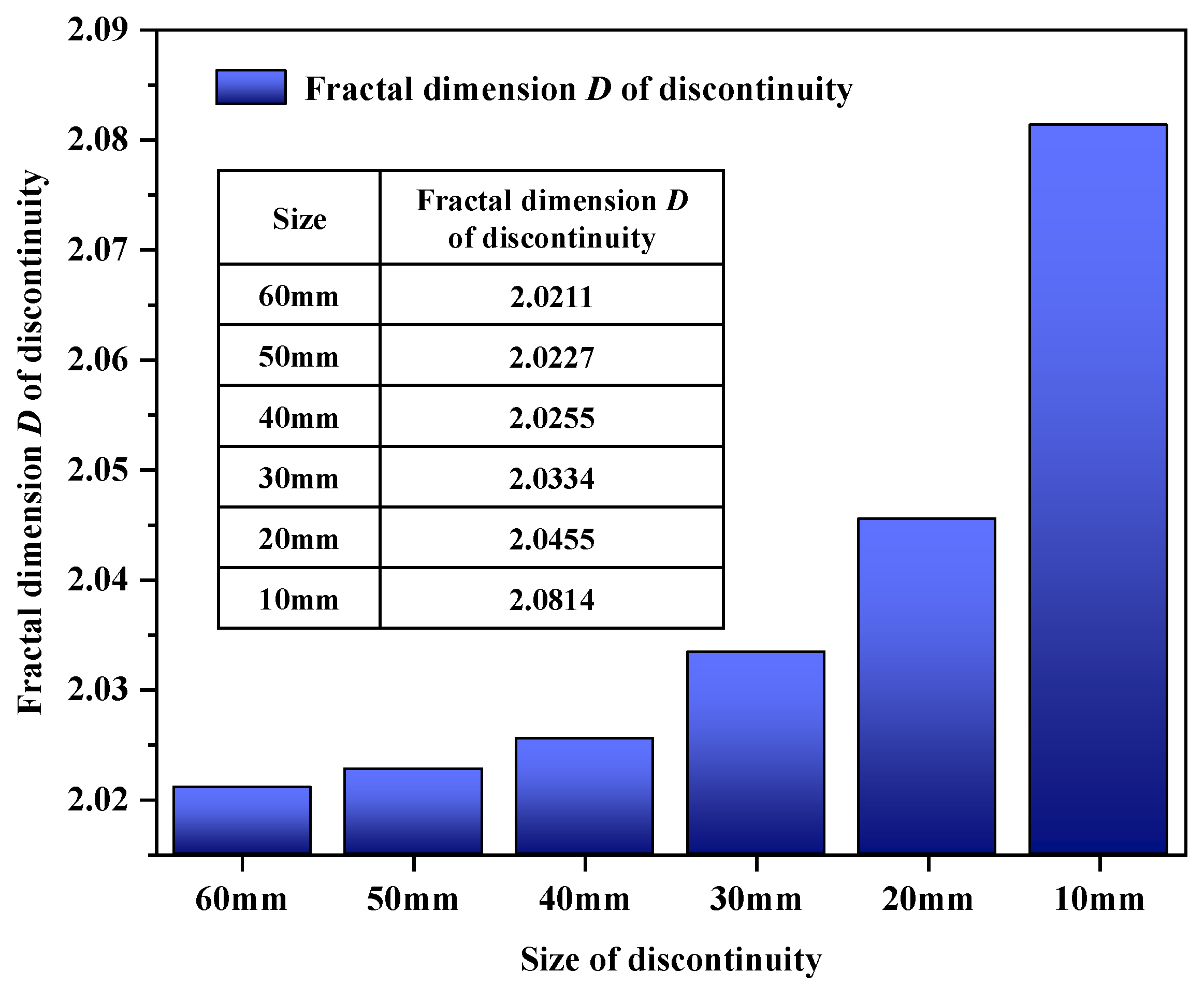
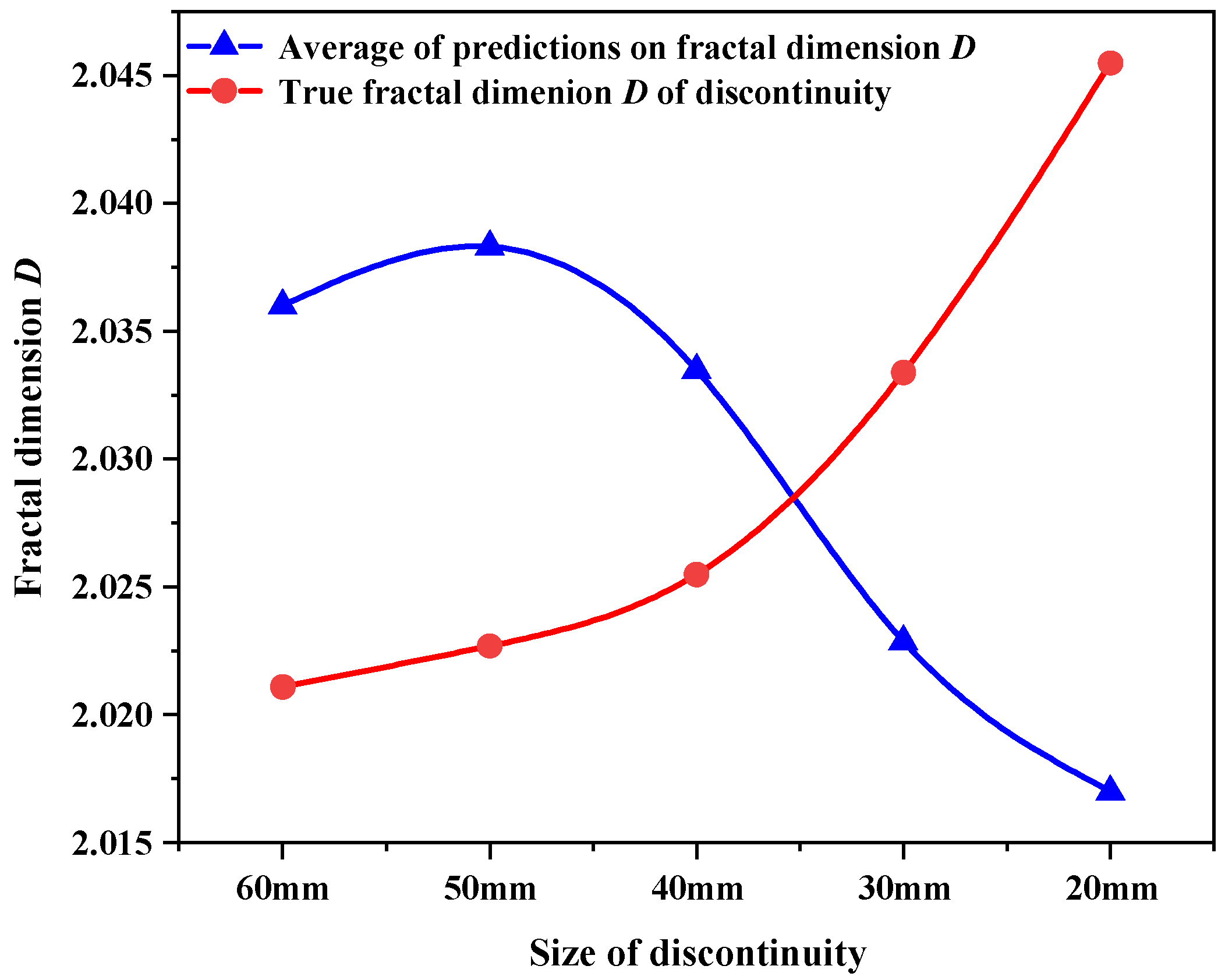
- The sensitivities of the correlation function on the prediction results are analyzed, and the result proves that the correlation function does not affect the prediction results of the fractal dimension D of the discontinuity. The size effect of the discontinuity on the fractal dimension D is analyzed by using discontinuity samples of 10 mm, 20 mm, 30 mm, 40 mm, 50 mm, and 60 mm. The research results indicate that the distances between the samples should also be considered with the application of the method, which means that the proposed method may be well applied to a relatively large size of the discontinuity, but not applied to a small size of the discontinuity.
- (5)
- There exists an intersection point between two lines represented by the prediction results and the true fractal dimension D, which may be affected simultaneously by the size of the discontinuity, the derivation of the prior information, and the extraction of the random samples. It may be necessary to further study the intersection point for better predicting the fractal dimension D of the discontinuity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bieniawski, Z.T. Engineering classification of jointed rock masses. Trans. S. Afr. Inst. Civ. Eng. 1973, 15, 335–344. [Google Scholar]
- Hoek, E.; Brown, E.T. The Hoek-Brown failure criterion and GSI—2018 edition. J. Rock Mech. Geotech. Eng. 2019, 11, 445–463. [Google Scholar] [CrossRef]
- Liu, X.G.; Zhu, W.C.; Yu, Q.L.; Chen, S.J.; Li, R.F. Estimation of the joint roughness coefficient of rock joints by consideration of two-order asperity and its application in double-joint shear tests. Eng. Geol. 2017, 220, 243–255. [Google Scholar] [CrossRef]
- Diaz, M.; Kim, K.Y.; Yeom, S.; Zhuang, L.; Park, S.; Min, K.B. Surface roughness characterization of open and closed rock joints in deep cores using X-ray computed tomography. Int. J. Rock Mech. Min. Sci. 2017, 98, 10–19. [Google Scholar] [CrossRef]
- Cai, Y.; Tang, H.M.; Wang, D.J.; Wen, T. A method for estimating the surface roughness of rock discontinuities. Math. Probl. Eng. 2018, 2018, 9835341. [Google Scholar] [CrossRef]
- Magsipoc, E.; Zhao, Q.; Grasselli, G. 2D and 3D roughness characterization. Rock Mech. Rock Eng. 2020, 53, 1495–1519. [Google Scholar] [CrossRef]
- Zhang, G.C.; Karakus, M.; Tang, H.M.; Ge, Y.F.; Jiang, Q.Q. Estimation of joint roughness coefficient from three-dimensional discontinuity surface. Rock Mech. Rock Eng. 2017, 50, 2535–2546. [Google Scholar] [CrossRef]
- Ban, L.R.; Zhu, C.; Qi, C.Z.; Tao, Z.G. New roughness parameters for 3D roughness of rock joints. Bull. Eng. Geol. Environ. 2019, 78, 4505–4517. [Google Scholar] [CrossRef]
- Zhang, Q.; Pei, Y.C.; Wang, X.J.; Li, X.J.; Shen, Y.X. Probabilistic prediction on three-dimensional roughness of discontinuity based on two-dimensional traces under rock tunnel excavation based on Bayesian theory. Undergr. Space, 2023; under review. [Google Scholar]
- Cao, T.; Xiao, A.C.; Wu, L.; Mao, L.G. Automatic fracture detection based on terrestrial laser scanning data: A new method and case study. Comput. Geosci. 2017, 106, 209–216. [Google Scholar] [CrossRef]
- Pan, D.D.; Li, S.C.; Xu, Z.H.; Zhang, Y.C.; Lin, P.; Li, H.Y. A deterministic-stochastic identification and modelling method of discrete fracture networks using laser scanning: Development and case study. Eng. Geol. 2019, 262, 105310. [Google Scholar] [CrossRef]
- Wang, C.; Yong, R.; Luo, Z.; Du, S.; Karakus, M.; Huang, C. A novel method for determining the three-dimensional roughness of rock joints based on profile slices. Rock Mech. Rock Eng. 2023, 56, 4303–4327. [Google Scholar] [CrossRef]
- Ge, Y.F.; Kulatilake, P.; Tang, H.M.; Xiong, C.R. Investigation of natural rock joint roughness. Comput. Geotech. 2014, 55, 290–305. [Google Scholar] [CrossRef]
- Li, X.J.; Chen, Z.Y.; Chen, J.Q.; Zhu, H.H. Automatic characterization of rock mass discontinuities using 3D point clouds. Eng. Geol. 2019, 259, 105131. [Google Scholar] [CrossRef]
- Guo, J.T.; Liu, S.J.; Zhang, P.N.; Wu, L.X.; Zhou, W.H.; Yu, Y.N. Towards semi-automatic rock mass discontinuity orientation and set analysis from 3D point clouds. Comput. Geosci. 2017, 103, 164–172. [Google Scholar] [CrossRef]
- Gefen, Y.; Aharony, A.; Mandelbrot, B.B. Phase-transitions on fractals.1. quasilinear lattices. J. Phys. A Math. Gen. 1983, 16, 1267–1278. [Google Scholar] [CrossRef]
- Gefen, Y.; Meir, Y.; Mandelbrot, B.B.; Aharony, A. Geometric implementation of hypercubic lattices with noninteger dimensionality by use of low lacunarity fractal lattices. Phys. Rev. Lett. 1983, 50, 145–148. [Google Scholar] [CrossRef]
- Clarke, K.C. Computation of the fractal dimension of topographic surfaces using the triangular prism surface-area method. Comput. Geosci. 1986, 12, 713–722. [Google Scholar] [CrossRef]
- Xie, H.P.; Wang, J.A.; Stein, E. Direct fractal measurement and multifractal properties of fracture surfaces. Phys. Lett. A 1998, 242, 41–50. [Google Scholar] [CrossRef]
- Xie, H.P.; Wang, J.A. Direct fractal measurement of fracture surfaces. Int. J. Solids Struct. 1999, 36, 3073–3084. [Google Scholar] [CrossRef]
- Zhou, H.W.; Xie, H. Direct estimation of the fractal dimensions of a fracture surface of rock. Surf. Rev. Lett. 2003, 10, 751–762. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, H.; Xie, H. Improved cubic covering method for fractal dimensions of a fracture surface of rock. Chin. J. Rock Mech. Eng. 2005, 24, 3192–3196. [Google Scholar]
- Ai, T.; Zhang, R.; Zhou, H.W.; Pei, J.L. Box-counting methods to directly estimate the fractal dimension of a rock surface. Appl. Surf. Sci. 2014, 314, 610–621. [Google Scholar] [CrossRef]
- Wu, M.Y.; Wang, W.S.; Shi, D.; Song, Z.L.; Li, M.H.; Luo, Y.F. Improved box-counting methods to directly estimate the fractal dimension of a rough surface. Measurement 2021, 177, 109303. [Google Scholar] [CrossRef]
- Kwaśny, W. A modification of the method for determination of surface fractal dimension and multifractal analysis. J. Achiev. Mater. Manuf. Eng. 2009, 33, 115–125. [Google Scholar]
- Zhu, H.; Zhang, L.M.; Xiao, T.; Li, X.Y. Generation of multivariate cross-correlated geotechnical random fields. Comput. Geotech. 2017, 86, 95–107. [Google Scholar] [CrossRef]
- Wang, Q.; Ren, X.D.; Li, J. Modeling of unstable creep failure of spatial variable rocks subjected to sustained loading. Comput. Geotech. 2022, 148, 104847. [Google Scholar] [CrossRef]
- Vanmarcke, E.H. Probabilistic modeling of soil profiles. J. Geotech. Eng. Div. 1977, 103, 1227–1246. [Google Scholar] [CrossRef]
- Chen, D.F.; Xu, D.P.; Ren, G.F.; Jiang, Q.; Liu, G.F.; Wan, L.P.; Li, N. Simulation of cross-correlated non-Gaussian random fields for layered rock mass mechanical parameters. Comput. Geotech. 2019, 112, 104–119. [Google Scholar] [CrossRef]
- Yuan, J.; Papaioannou, I.; Straub, D. Probabilistic failure analysis of infinite slopes under random rainfall processes and spatially variable soil. Georisk 2019, 13, 20–339. [Google Scholar] [CrossRef]
- Wang, Y.; Au, S.-K.; Cao, Z. Bayesian approach for probabilistic characterization of sand friction angles. Eng. Geol. 2010, 114, 354–363. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Z. Probabilistic characterization of young’s modulus of soil using equivalent samples. Eng. Geol. 2013, 159, 106–118. [Google Scholar] [CrossRef]
- Papaioannou, I.; Straub, D. Reliability updating in geotechnical engineering including spatial variability of soil. Comput. Geotech. 2012, 42, 44–51. [Google Scholar] [CrossRef]
- Targoutzidis, A. A Monte Carlo simulation for the assessment of Bayesian updating in dynamic systems. Reliab. Eng. Syst. Saf. 2012, 100, 125–132. [Google Scholar] [CrossRef]
- Straub, D.; Papaioannou, I. Bayesian updating with structural reliability methods. J. Eng. Mech. 2015, 141, 04014134. [Google Scholar] [CrossRef]
- Huang, J.S.; Zeng, C.; Kelly, R. Back analysis of settlement of teven road trial embankment using Bayesian updating. Georisk 2019, 13, 320–325. [Google Scholar] [CrossRef]
- Rahimi, M.; Shafieezadeh, A.; Wood, D.; Kubatko, E.J.; Dormady, N.C. Bayesian calibration of multi-response systems via multivariate Kriging: Methodology and geological and geotechnical case studies. Eng. Geol. 2019, 260, 105248. [Google Scholar] [CrossRef]
- Hu, B.A.; Gong, Q.M.; Zhang, Y.Q.; Yin, Y.H.; Chen, W.J. Characterizing uncertainty in geotechnical design of energy piles based on Bayesian theorem. Acta Geotech. 2022, 17, 4191–4206. [Google Scholar] [CrossRef]
- Tian, H.M.; Cao, Z.J.; Li, D.Q.; Du, W.Q.; Zhang, F.P. Efficient and flexible Bayesian updating of embankment settlement on soft soils based on different monitoring datasets. Acta Geotech. 2022, 17, 1273–1294. [Google Scholar] [CrossRef]
- Sönmez, H.; Ulusay, R. A discussion on the Hoek-Brown failure criterion and suggested modifications to the criterion verified by slope stability case studies. Yerbilimleri 2002, 26, 77–99. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Pei, Y.; Shen, Y.; Wang, X.; Lai, J.; Wang, M. A New Perspective on Predicting Roughness of Discontinuity from Fractal Dimension D of Outcrops. Fractal Fract. 2023, 7, 496. https://doi.org/10.3390/fractalfract7070496
Zhang Q, Pei Y, Shen Y, Wang X, Lai J, Wang M. A New Perspective on Predicting Roughness of Discontinuity from Fractal Dimension D of Outcrops. Fractal and Fractional. 2023; 7(7):496. https://doi.org/10.3390/fractalfract7070496
Chicago/Turabian StyleZhang, Qi, Yuechao Pei, Yixin Shen, Xiaojun Wang, Jingqi Lai, and Maohui Wang. 2023. "A New Perspective on Predicting Roughness of Discontinuity from Fractal Dimension D of Outcrops" Fractal and Fractional 7, no. 7: 496. https://doi.org/10.3390/fractalfract7070496
APA StyleZhang, Q., Pei, Y., Shen, Y., Wang, X., Lai, J., & Wang, M. (2023). A New Perspective on Predicting Roughness of Discontinuity from Fractal Dimension D of Outcrops. Fractal and Fractional, 7(7), 496. https://doi.org/10.3390/fractalfract7070496





