Hermite Wavelet Method for Nonlinear Fractional Differential Equations
Abstract
1. Introduction
2. Foundations
3. Hermite Wavelets (HWs)
4. Function Approximation of HWs
5. Convergence Analysis
6. Operational Matrices of HWs
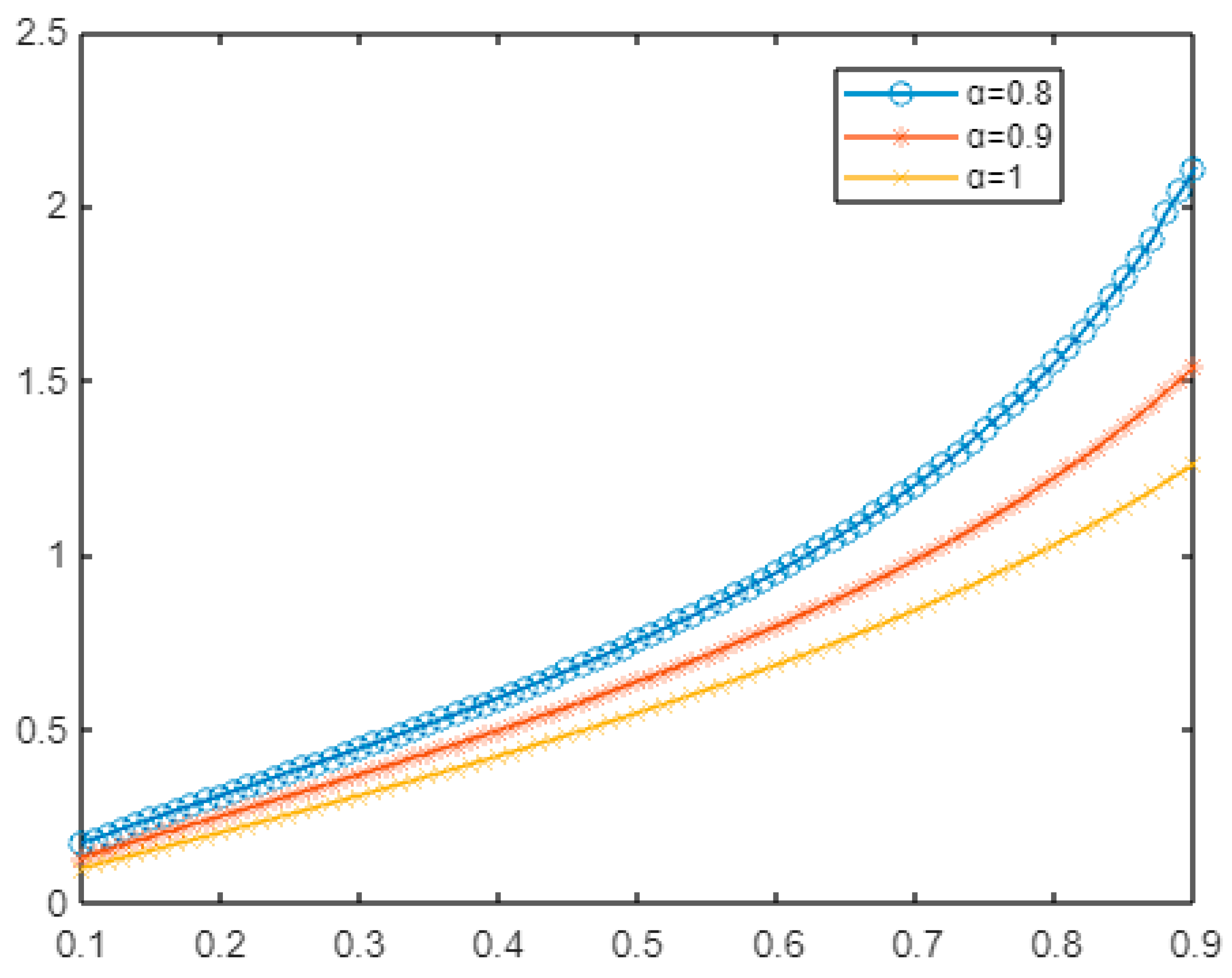
7. Numeric Solution Examples
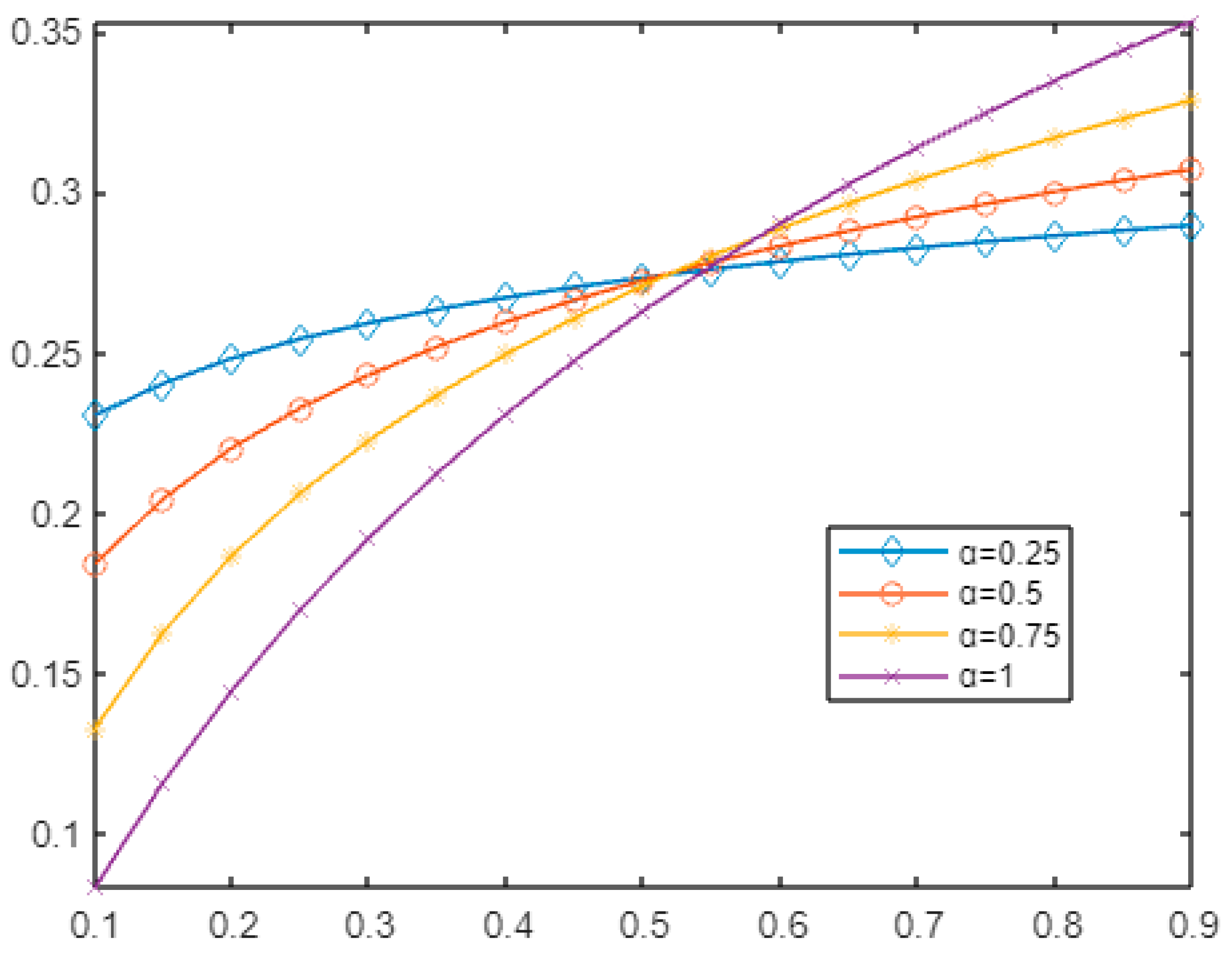
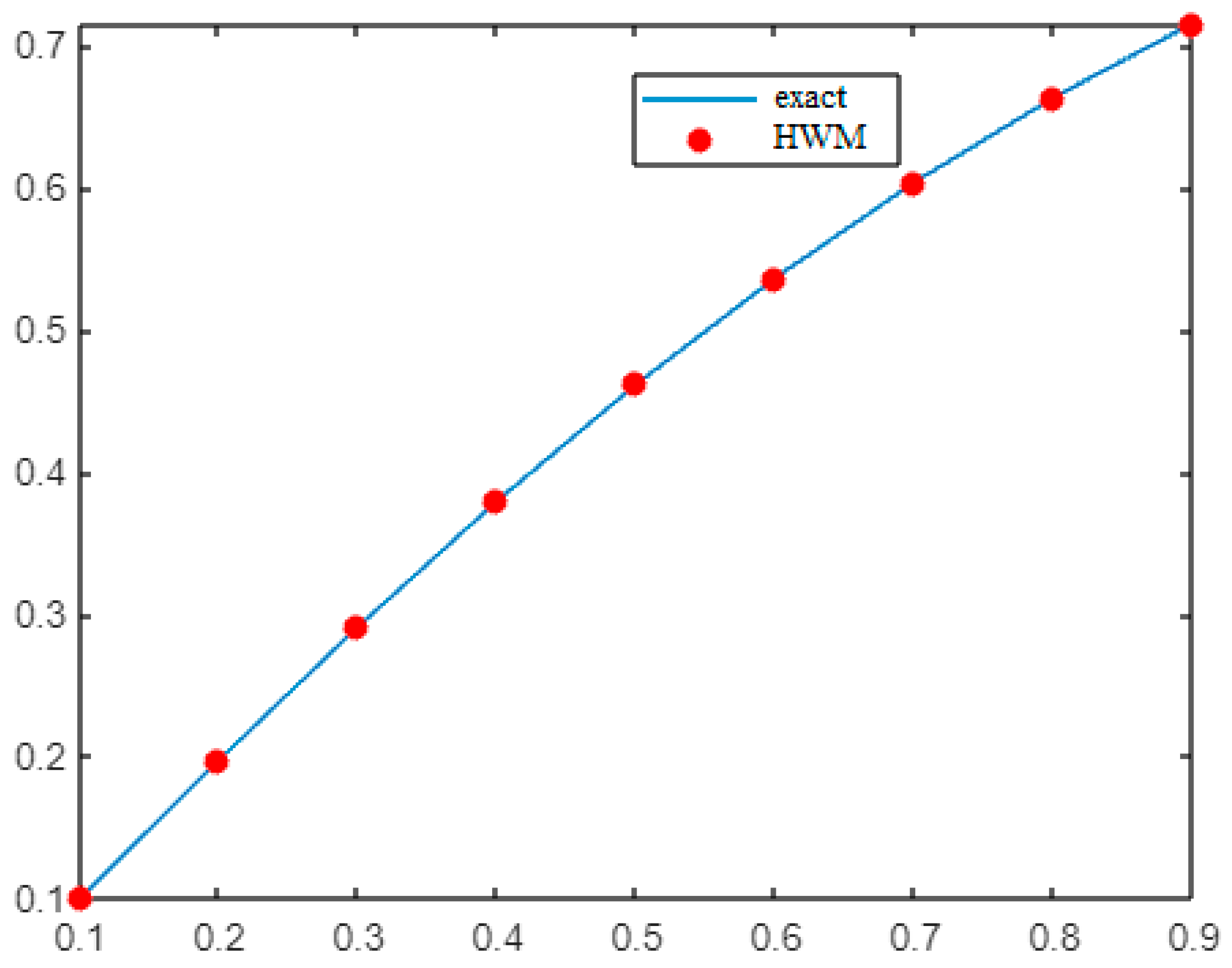
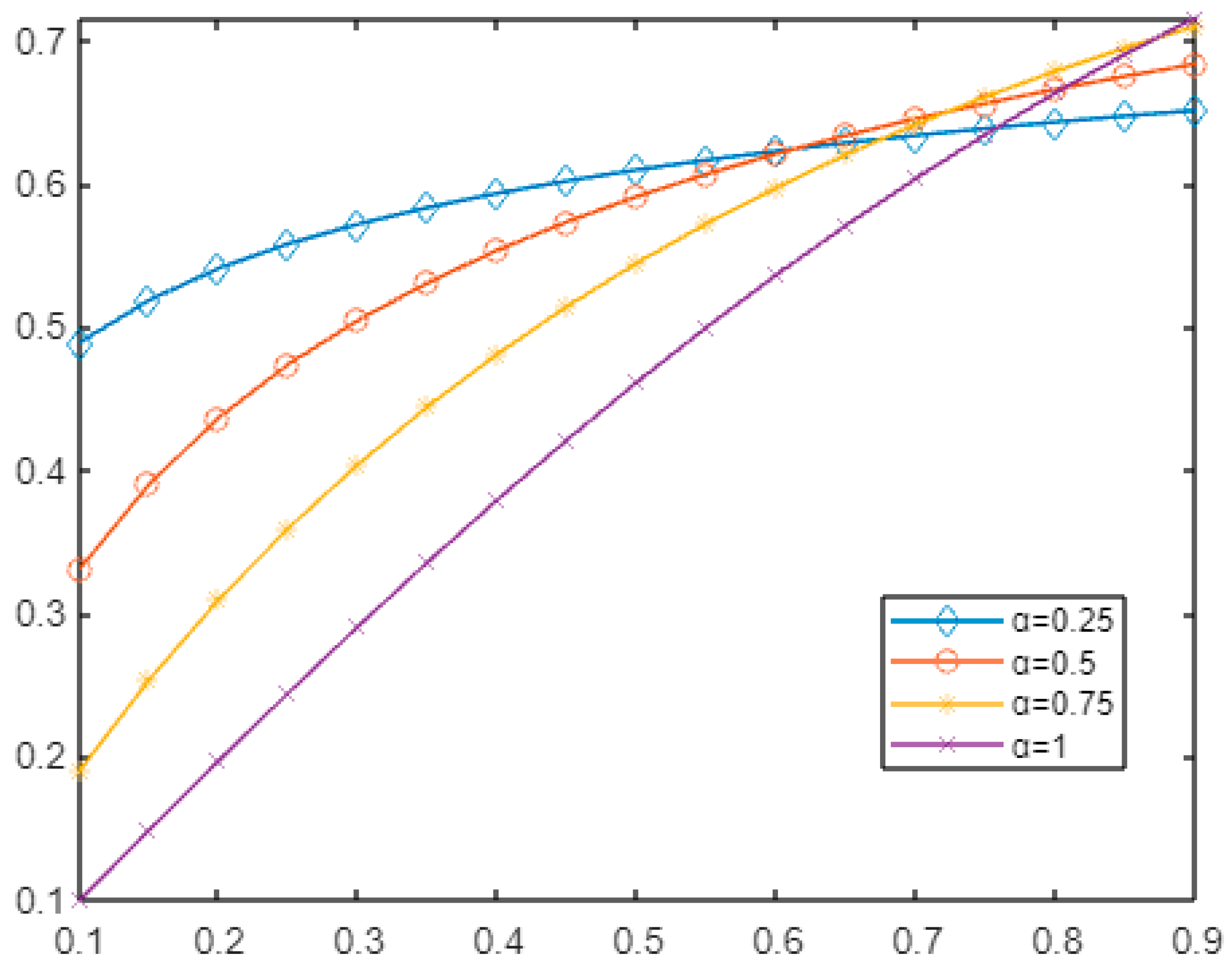
- Example 1:
- Example 2:
- Example 3:
- Example 4:
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arikoğlu, A.; Özkol, İ. Solution of fractional differential equations by using differential transform method. Chaos Solitons Fractals 2007, 34, 1473–1481. [Google Scholar] [CrossRef]
- Li, X. Numerical solution of fractional differential equations using cubic B-spline wavelet collocation method. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3934–3946. [Google Scholar] [CrossRef]
- Erturk, V.S.; Momani, S. Solving systems of fractional differential equations using differential transform method. J. Comput. Appl. Math. 2008, 215, 142–151. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Numerical comparison of methods for solving linear differential equations of fractional order. Chaos Solitons Fractals 2007, 31, 1248–1255. [Google Scholar] [CrossRef]
- Babolian, E.; Vahidi, A.R.; Shoja, A. An efficient method for nonlinear fractional differential equations: Combination of the Adomian decomposition method and Spectral method. Indian J. Pure Appl. Math. 2014, 45, 1017–1028. [Google Scholar] [CrossRef]
- Yang, S.; Xiao, A.; Su, H. Convergence of the variational iteration method for solving multi-order fractional differential equations. Comput. Math. Appl. 2010, 60, 2871–2879. [Google Scholar] [CrossRef]
- Kumar, S.; Gupta, V. An application of variational iteration method for solving fuzzy time-fractional diffusion equations. Neural. Comput. Appl. 2021, 33, 17659–17668. [Google Scholar] [CrossRef]
- Huang, J.; Tang, Y.; Vazquez, L. Convergence analysis of a block-by-block method for fractional differential equations. Numer. Math. Theory Methods Appl. 2012, 5, 229–241. [Google Scholar] [CrossRef]
- Mokhtary, P.; Ghoreishi, F.; Srivastava, H.M. The Müntz-Legendre Tau method for fractional differential equations. Appl. Math. Model. 2016, 40, 671–684. [Google Scholar] [CrossRef]
- Tural-Polat, S.N.; Dincel, A.T. Numerical solution method for multi-term variable order fractional differential equations by shifted chebyshev polynomials of the third kind. Alex. Eng. J. 2022, 61, 5145–5153. [Google Scholar] [CrossRef]
- Azarnavid, B.; Emamjomeh, M.; Nabati, M. A shooting like method based on the shifted Chebyshev polynomials for solving nonlinear fractional multi-point boundary value problem. Chaos Solitons Fractals 2022, 159. in press. [Google Scholar] [CrossRef]
- Fambri, F.; Dumbser, M. Spectral semi-implicit and space-time discontinuous Galerkin methods for the incompressible Navier-Stokes equations on staggered Cartesian grids. Appl. Numer. Math. 2016, 110, 41–74. [Google Scholar] [CrossRef]
- Yüzbaşi, S. Numerical solution of the Bagley-Torvik equation by the Bessel collocation method. Math. Method Appl. Sci. 2013, 36, 300–312. [Google Scholar] [CrossRef]
- Pindza, E.; Owolabi, K.M. Fourier spectral method for higher order space fractional reaction-diffusion equations. Commun. Nonlinear Sci. 2016, 40, 112–128. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Abu Arqub, O. Computational algorithm for solving fredholm time-fractional partial integro differential equations of dirichlet functions type with error estimates. Appl. Math. Comput. 2019, 342, 280–294. [Google Scholar]
- Al-Smadi, M.; Abu Arqub, O.; Gaith, M. Numerical simulation of telegraph and Cattaneo fractional-type models using adaptive reproducing kernel framework. Math. Methods Appl. Sci. 2021, 44, 8472–8489. [Google Scholar] [CrossRef]
- Bengochea, G. Operational solution of fractional differential equations. Appl. Math. Lett. 2014, 32, 48–52. [Google Scholar] [CrossRef]
- Luchko, Y.; Gorenflo, R. An operational method for solving fractional differential equations with the Caputo derivatives. Acta Math. Vietnam. 1999, 24, 207–233. [Google Scholar]
- Li, M.; Zhao, W. Solving Abel’s type integral equation with Mikusinski’s operator of fractional order. Adv. Math. Phys. 2013, 2013, 806984. [Google Scholar]
- Xu, X.Y.; Xu, D. Legendre wavelets method for approximate solution of fractional-order differential equations under multi-point boundary conditions. Int. J. Comput. Math. 2018, 95, 998–1014. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. An efficient approximate method for solving delay fractional optimal control problems. Nonlinear Dynam. 2016, 86, 1649–1661. [Google Scholar] [CrossRef]
- Rehman, M.U.; Khan, R.A. A numerical method for solving boundary value problems for fractional differential equations. Appl. Math. Model. 2012, 36, 894–907. [Google Scholar] [CrossRef]
- Shiralashetti, S.C.; Hanaji, S.I. Taylor wavelet collocation method for Benjamin–Bona–Mahony partial differential equations. Results Appl. Math. 2021, 9, 100139. [Google Scholar] [CrossRef]
- Shiralashetti, S.C.; Kumbinarasaiah, S. CAS wavelets analytic solution and Genocchi polynomials numerical solutions for the integral and integro-differential equations. J. Interdiscip. Math. 2019, 22, 201–218. [Google Scholar] [CrossRef]
- Kumbinarasaiah, S.; Mundewadi, R.A. Numerical solution of fractional-order integro-differential equations using Laguerre wavelet method. J. Optim. Theory Appl. 2022, in press. [Google Scholar] [CrossRef]
- Behera, S.; Saha Ray, S. Euler wavelets method for solving fractional-order linear Volterra–Fredholm integro-differential equations with weakly singular kernels. Comp. Appl. Math. 2021, 40, 1–30. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, Y. Second Chebyshev wavelet operational matrix of integration and its application in the calculus of variations. Int. J. Comput. Math. 2013, 90, 2338–2352. [Google Scholar] [CrossRef]
- Lal, S.; Sharma, R.P. Approximation of function belonging to generalized Hölder’s class by first and second kind Chebyshev wavelets and their applications in the solutions of Abel’s integral equations. Arab. J. Math. 2021, 10, 157–174. [Google Scholar] [CrossRef]
- Shiralashetti, S.C.; Kumbinarasaiah, S. Hermite wavelets operational matrix of integration for the numerical solution of nonlinear singular initial value problems. Alex. Eng. J. 2018, 57, 2591–2600. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Kilicman, A.; Al Zhour, Z.A.A. Kronecker operational matrices for fractional calculus and some applications. Appl. Math. Comput. 2007, 187, 250–265. [Google Scholar] [CrossRef]
- Li, Y.; Sun, N. Numerical solution of fractional differential equations using the generalized block pulse operational matrix. Comput. Math. Appl. 2011, 62, 1046–1054. [Google Scholar] [CrossRef]
- Saad, K.M.; Al-Shomrani, A.A. An application of homotopy analysis transform method for Riccati differential equation of fractional order. J. Fract. Calc. Appl. 2016, 7, 61–72. [Google Scholar]
- Odibat, Z.; Momani, S. Modifed homotopy perturbation method: Application to quadratic Riccati diferential equation of fractional order. Chaos Solitons Fractals 2008, 36, 167–174. [Google Scholar] [CrossRef]
- Sakar, M. Iterative reproducing kernel Hilbert spaces method for Riccati differential equations. J. Comput. Appl. Math. 2017, 309, 163–174. [Google Scholar] [CrossRef]
- Li, X.Y.; Wu, B.Y.; Wang, R.T. Reproducing kernel method for fractional Riccati differential equations. Abstr. Appl. 2014, 2014, 970967. [Google Scholar] [CrossRef]
- Yüzbaşı, S. Numerical solutions of fractional Riccati type differential equations by means of the Bernstein polynomials. Appl. Math. Comput. 2013, 219, 6328–6343. [Google Scholar] [CrossRef]
- Sakar, M.G.; Akgül, A.; Baleanu, D. On solutions of fractional Riccati differential equations. Adv. Differ. Equ. 2017, 39, 1–10. [Google Scholar] [CrossRef]
- Li, Y.; Sun, N.; Zheng, B.; Wang, Q.; Zhang, Y. Wavelet operational matrix method for solving the Riccati differential equation. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 483–493. [Google Scholar] [CrossRef]
| t | ||||
|---|---|---|---|---|
| 0 | 5.27 × 10−4 | 1.40 × 10−4 | 3.58 × 10−5 | 9.01 × 10−6 |
| 0.1 | 5.23 × 10−4 | 1.31 × 10−4 | 3.32 × 10−5 | 8.32 × 10−6 |
| 0.2 | 4.15 × 10−4 | 1.09 × 10−4 | 2.71 × 10−5 | 6.56 × 10−6 |
| 0.3 | 3.29 × 10−4 | 7.49 × 10−5 | 1.88 × 10−5 | 4.80 × 10−6 |
| 0.4 | 1.77 × 10−4 | 4.36 × 10−5 | 9.96 × 10−6 | 2.62 × 10−6 |
| 0.5 | 1.94 × 10−4 | 2.37 × 10−5 | 3.11 × 10−6 | 6.66 × 10−7 |
| 0.6 | 1.74 × 10−4 | 4.29 × 10−5 | 9.86 × 10−6 | 2.81 × 10−6 |
| 0.7 | 3.41 × 10−4 | 7.54 × 10−5 | 1.90 × 10−5 | 4.93 × 10−6 |
| 0.8 | 4.26 × 10−4 | 1.17 × 10−4 | 2.91 × 10−5 | 7.17 × 10−6 |
| 0.9 | 5.68 × 10−4 | 1.43 × 10−4 | 3.70 × 10−5 | 9.22 × 10−6 |
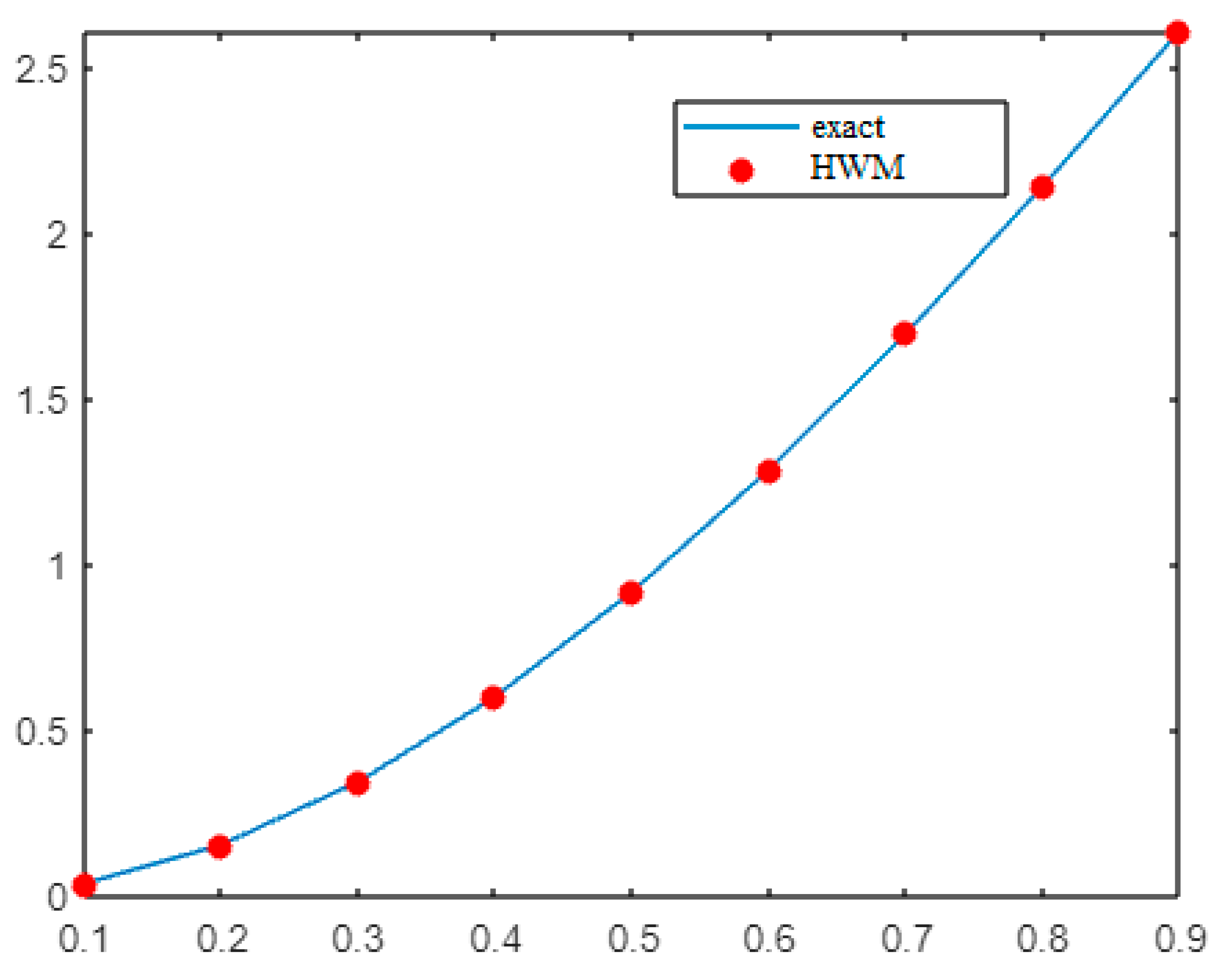
| t | [32] | [4] | [4] | [1] | ||
|---|---|---|---|---|---|---|
| 0.1 | 0.039750 | 0.039752 | 0.039754 | 0.039874 | 0.039874 | 0.039473 |
| 0.2 | 0.157036 | 0.157038 | 0.157043 | 0.158512 | 0.158512 | 0.157703 |
| 0.3 | 0.347370 | 0.347371 | 0.347373 | 0.353625 | 0.353625 | 0.352402 |
| 0.4 | 0.604695 | 0.604696 | 0.604699 | 0.622083 | 0.622083 | 0.620435 |
| 0.5 | 0.921768 | 0.921768 | 0.921768 | 0.960047 | 0.960047 | 0.957963 |
| 0.6 | 1.290457 | 1.290456 | 1.290458 | 1.363093 | 1.363093 | 1.360551 |
| 0.7 | 1.702008 | 1.702007 | 1.702007 | 1.826257 | 1.826257 | 1.823267 |
| 0.8 | 2.147287 | 2.147285 | 2.147286 | 2.344224 | 2.344224 | 2.340749 |
| 0.9 | 2.617001 | 2.616999 | 2.616998 | 2.911278 | 2.911278 | 2.907324 |
| t | |||||
|---|---|---|---|---|---|
| 0 | 3.79 × 10−4 | 4.57 × 10−5 | 5.67 × 10−6 | 7.07 × 10−7 | 8.83 × 10−8 |
| 0.1 | 6.20 × 10−5 | 3.38 × 10−5 | 8.23 × 10−6 | 1.78 × 10−6 | 4.48 × 10−7 |
| 0.2 | 2.87 × 10−4 | 7.03 × 10−5 | 1.51 × 10−5 | 3.80 × 10−6 | 9.89 × 10−7 |
| 0.3 | 3.63 × 10−4 | 9.45 × 10−5 | 2.67 × 10−5 | 6.64 × 10−6 | 1.61 × 10−6 |
| 0.4 | 7.33 × 10−4 | 1.52 × 10−4 | 3.84 × 10−5 | 1.01 × 10−5 | 2.52 × 10−6 |
| 0.5 | 2.26 × 10−3 | 3.72 × 10−4 | 7.51 × 10−5 | 1.68 × 10−5 | 3.97 × 10−6 |
| 0.6 | 1.25 × 10−3 | 3.76 × 10−4 | 9.34 × 10−5 | 2.24 × 10−5 | 5.61 × 10−6 |
| 0.7 | 2.39 × 10−3 | 5.92 × 10−4 | 1.36 × 10−4 | 3.43 × 10−5 | 8.75 × 10−6 |
| 0.8 | 3.17 × 10−3 | 8.29 × 10−4 | 2.26 × 10−4 | 5.64 × 10−5 | 1.38 × 10−5 |
| 0.9 | 6.76 × 10−3 | 1.41 × 10−3 | 3.58 × 10−4 | 9.36 × 10−5 | 2.34 × 10−5 |
| t | |||||
|---|---|---|---|---|---|
| 0 | 1.00 × 10−3 | 4.47 × 10−4 | 1.54 × 10−4 | 4.54 × 10−5 | 1.24 × 10−5 |
| 0.1 | 1.90 × 10−3 | 3.63 × 10−4 | 9.31 × 10−5 | 2.49 × 10−5 | 6.20 × 10−6 |
| 0.2 | 6.26 × 10−4 | 1.73 × 10−4 | 4.97 × 10−5 | 1.24 × 10−5 | 3.00 × 10−6 |
| 0.3 | 4.34 × 10−4 | 1.08 × 10−4 | 2.34 × 10−5 | 5.90 × 10−6 | 1.53 × 10−6 |
| 0.4 | 1.24 × 10−4 | 4.97 × 10−5 | 1.23 × 10−5 | 2.81 × 10−6 | 7.05 × 10−7 |
| 0.5 | 1.04 × 10−4 | 7.99 × 10−6 | 8.56 × 10−7 | 6.21 × 10−7 | 2.10 × 10−7 |
| 0.6 | 2.26 × 10−5 | 2.09 × 10−6 | 3.80 × 10−7 | 2.84 × 10−8 | 5.79 × 10−9 |
| 0.7 | 5.47 × 10−5 | 1.25 × 10−5 | 2.42 × 10−6 | 6.12 × 10−7 | 1.64 × 10−7 |
| 0.8 | 6.02 × 10−5 | 1.51 × 10−5 | 4.29 × 10−6 | 1.06 × 10−6 | 2.58 × 10−7 |
| 0.9 | 9.23 × 10−5 | 1.98 × 10−5 | 4.98 × 10−6 | 1.29 × 10−6 | 3.23 × 10−7 |
| t | MHPM [34] | IRKHSM [35] | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 6.40 × 10−5 | 3.24 × 10−5 | 7.88 × 10−6 | 1.71 × 10−6 | 4.31 × 10−7 | 1.10 × 10−8 | 0 | 9.05 × 10−6 |
| 0.2 | 2.44 × 10−4 | 5.91 × 10−5 | 1.29 × 10−5 | 3.25 × 10−6 | 8.42 × 10−7 | 1.12 × 10−7 | 0 | 1.72 × 10−5 |
| 0.3 | 2.71 × 10−4 | 6.82 × 10−5 | 1.85 × 10−5 | 4.60 × 10−6 | 1.13 × 10−6 | 2.10 × 10−7 | 1.00 × 10−6 | 2.38 × 10−5 |
| 0.4 | 3.64 × 10−4 | 8.24 × 10−5 | 2.06 × 10−5 | 5.29 × 10−6 | 1.32 × 10−6 | 2.82 × 10−7 | 5.00 × 10−6 | 2.85 × 10−5 |
| 0.5 | 3.92 × 10−4 | 9.67 × 10−5 | 2.33 × 10−5 | 5.68 × 10−6 | 1.40 × 10−6 | 3.28 × 10−7 | 3.90 × 10−5 | 3.11 × 10−5 |
| 0.6 | 3.35 × 10−4 | 8.53 × 10−5 | 2.13 × 10−5 | 5.29 × 10−6 | 1.32 × 10−6 | 3.46 × 10−7 | 1.93 × 10−4 | 3.17 × 10−5 |
| 0.7 | 3.05 × 10−4 | 7.56 × 10−5 | 1.90 × 10−5 | 4.75 × 10−6 | 1.19 × 10−6 | 3.31 × 10−7 | 7.37 × 10−4 | 3.07 × 10−5 |
| 0.8 | 2.62 × 10−4 | 6.47 × 10−5 | 1.58 × 10−5 | 3.95 × 10−6 | 9.93 × 10−7 | 2.96 × 10−7 | 2.33 × 10−3 | 2.81 × 10−5 |
| 0.9 | 1.84 × 10−4 | 5.03 × 10−5 | 1.25 × 10−5 | 3.06 × 10−6 | 7.65 × 10−7 | 2.48 × 10−7 | 6.37 × 10−3 | 2.32 × 10−5 |
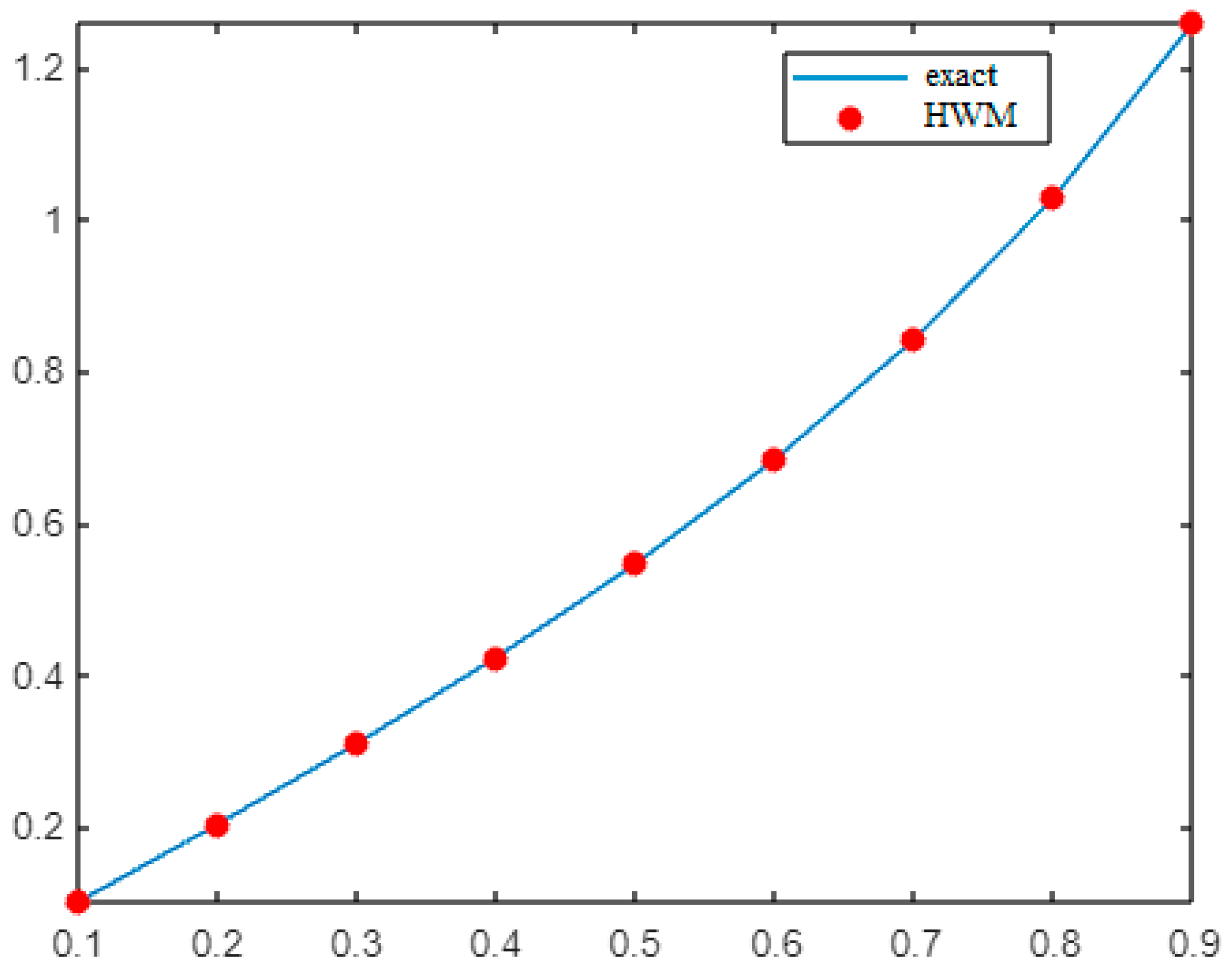
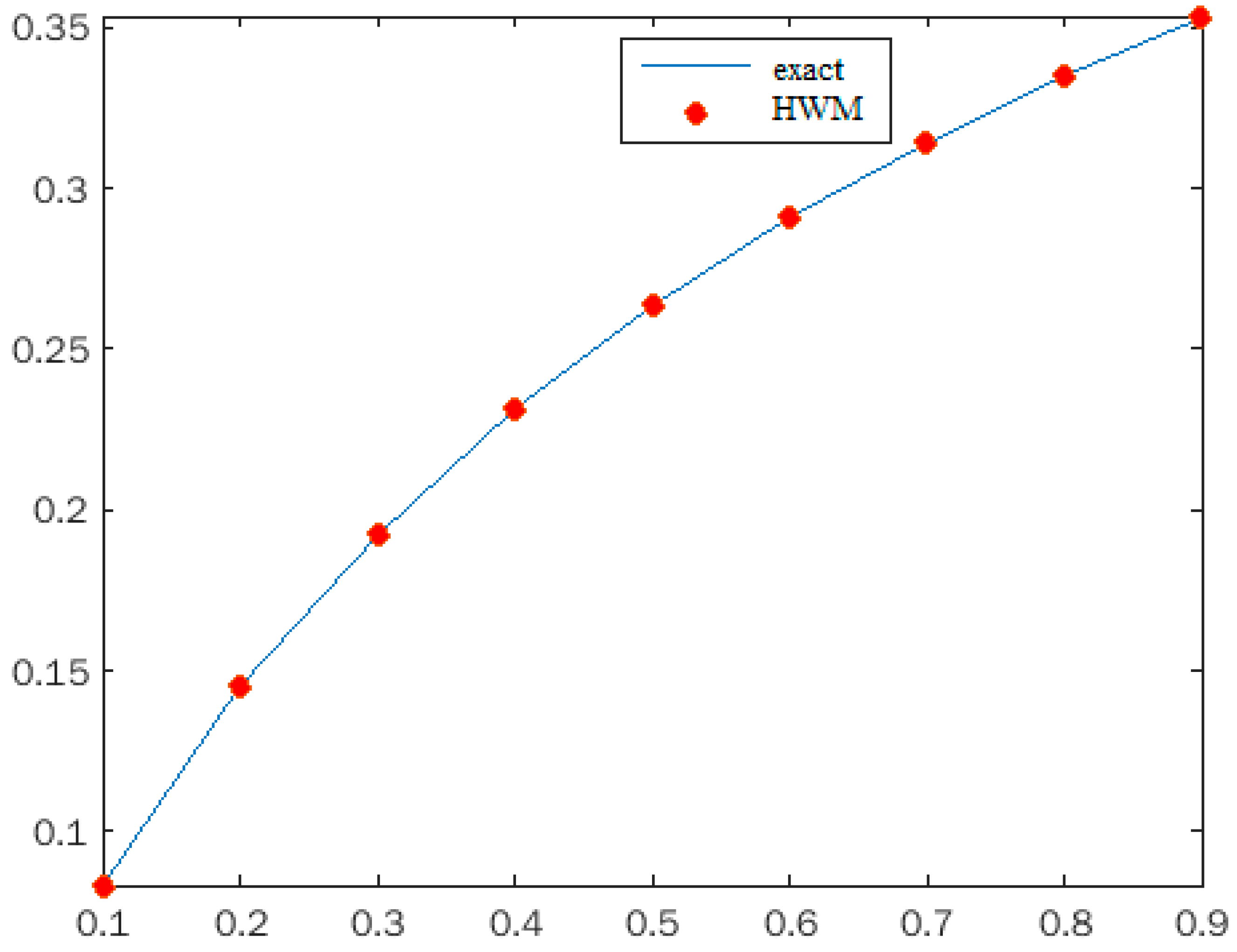
| t | RKM [36] | BPM [37] | IRKHSM [38] | HWOMM [39] | MHPM [34] | |
|---|---|---|---|---|---|---|
| 0.2 | 0.309974 | 0.3073 | 0.3099 | 0.3100 | 0.3095 | 0.3138 |
| 0.4 | 0.481631 | 0.4803 | 0.4816 | 0.4816 | 0.4814 | 0.4929 |
| 0.6 | 0.597783 | 0.5975 | 0.5977 | 0.5978 | 0.5977 | 0.5974 |
| 0.8 | 0.678849 | 0.6796 | 0.6788 | 0.6788 | 0.6788 | 0.6604 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turan Dincel, A.; Tural Polat, S.N.; Sahin, P. Hermite Wavelet Method for Nonlinear Fractional Differential Equations. Fractal Fract. 2023, 7, 346. https://doi.org/10.3390/fractalfract7050346
Turan Dincel A, Tural Polat SN, Sahin P. Hermite Wavelet Method for Nonlinear Fractional Differential Equations. Fractal and Fractional. 2023; 7(5):346. https://doi.org/10.3390/fractalfract7050346
Chicago/Turabian StyleTuran Dincel, Arzu, Sadiye Nergis Tural Polat, and Pelin Sahin. 2023. "Hermite Wavelet Method for Nonlinear Fractional Differential Equations" Fractal and Fractional 7, no. 5: 346. https://doi.org/10.3390/fractalfract7050346
APA StyleTuran Dincel, A., Tural Polat, S. N., & Sahin, P. (2023). Hermite Wavelet Method for Nonlinear Fractional Differential Equations. Fractal and Fractional, 7(5), 346. https://doi.org/10.3390/fractalfract7050346








