On the Bilinear Second Order Differential Realization of an Infinite-Dimensional Dynamical System: An Approach Based on Extensions to M₂-Operators

Abstract

Considering the case of a continual bundle of controlled dynamic processes, the authors have studied the functional-geometric conditions of existence of non-stationary coefficients-operators from the differential realization of this bundle in the class of non-autonomous bilinear second-order differential equations in the separable Hilbert space. The problem under scrutiny belongs to the type of non-stationary coefficient-operator inverse problems for the bilinear evolution equations in the Hilbert space. The solution is constructed on the basis of usage of the functional Relay-Ritz operator. Under this mathematical problem statement, the case has been studied in detail when the operators to be modeled are burdened with the condition, which provides for entire continuity of the integral representation equations of the model of realization. Proposed is the entropy interpretation of the given problem of mathematical modeling of continual bundle dynamic processes in the context of development of the qualitative theory of differential realization of nonlinear state equations of complex infinite-dimensional behavioristic dynamical system.

1. Introduction

A large class of inverse problems of evolution equations is bound up with mathematical modeling of interconnected dynamical systems [1,2,3]; in particular, those possessing a hyperbolic structure [4,5]. In this context, we propose an analytical grounding of solvability of the problem of full, continuous bilinear differential non-autonomous second-order realization for a continual bundle of controlled dynamic processes as a model of the behavioristic system [1]. Noteworthy is the need to construct the qualitative theory of differential realization (QTDR), which was understood long ago. The first (in 1940) pithy step in this direction was undertaken by Kolmogorov [2] in connection with the development of the theory of continuous one-parameter groups of motions.

Firstly, QTDR was elaborated as a direction of system-theoretic analysis of inverse problems for the finite-dimensional dynamic systems [6,7,8,9,10]. Later QTDR was extended up to more abstract statements in Banach infinite-dimensional spaces, whose complete systems of elements [11] (p. 167) represented the basis, what was actively used in the work [12,13,14]; there exists [11] (p. 514) the separable reflexive Banach spaces without the property of approximation (when any compact operator is a uniform limit of the finite rank operators), and, consequently, also without any basis. Furthermore, it was ascertained that serious analytical difficulties were encountered after the transition to the differential realization systems with the order higher than one, when the account of hyperbolic models was needed [15,16,17].

Within the framework of the given context, we consider the aspect of nonlinearity of scrutinized (modeled) equations; in particular, existence of bilinear structures [18] of non-autonomous equations of differential realization. This is the major object of attention in the present paper. Furthermore, we additionally consider the entropy aspect [6] of the theory.

2. QTDR-Terminology, Denotations and the Problem Statement

Let us define a definite terminology and introduce the denotations, which will be used further. From now on $(X, ||\cdot |{|}_X),$ $(Y, ||\cdot |{|}_Y) ,$ $(Z, ||\cdot |{|}_Z)$ are real separable Hilbert spaces (the pre-Hilbert property is given by norms $\left|\right|\cdot |{|}_X,$$\left|\right|\cdot |{|}_Y,$$\left|\right|\cdot |{|}_X$), $U=X\times X\times Y\times Z\times Z\times Z$ is the Cartesian product with the norm $\left|\right|\cdot ,\cdot ,\cdot ,\cdot ,\cdot ,\cdot |{|}_U:={(||\cdot |{|}_X^2+\left|\right|\cdot |{|}_X^2+||\cdot |{|}_Y^2+\left|\right|\cdot |{|}_Z^2+||\cdot |{|}_Z^2+\left|\right|\cdot |{|}_Z^2)}^{1/2}$ (transforming $(U, ||\cdot |{|}_U)$ into Hilbert spaces [11] (p. 162)), $L(Y,X)$ is the Banach space (with the operator norm) of all the linear continuous operators acting from space $Y$ into $X$ (we will introduce $L(\cdot ,\cdot )$ for any two fixed Banach spaces similarly), $\mathcal{L}(X^2,Z)$ are spaces of all the continuous bilinear maps [11] (p. 646) from the Cartesian square $X\times X$ in $Z.$

Let us denote by $T$ a segment of numerical axis $R$ with the Lebesgue measure $\mathsf{\mu }$, by ${\wp }_{\mathsf{\mu }}$—the $\mathsf{\sigma }$ -algebra of all $\mathsf{\mu }$ -measurable subsets from $T$; next, we’ll need $\mathsf{\mu }$ -relations on $T$, so, we’ll introduce (for them) the symbols $\cdot =\cdot , \cdot \ne \cdot , \cdot \ge \cdot , \cdot \le \cdot$ for the cases of equality, inequality and orderings $\mathsf{\mu }$ -almost everywhere in $T$; the record $S\cdot \subseteq \cdot Q$ for $S, Q\in {\wp }_{\mathsf{\mu }}$ means that $\mathsf{\mu }(S\backslash Q)=0$. Moreover, assume that $A{C}^1(T,X)$ is a linear set of all the functions $\mathsf{\phi }:T\to X,$ whose first derivative is an absolutely continuous function on interval $T$ (with respect to the Lebesgue measure $\mathsf{\mu }$). Next, let $(\mathbf{B},||\cdot |{|}_{\mathbf{B}})$ be some Banach space. By ${\mathrm{L}}_p(T,\mathbf{B}), 1\le p\le \infty$ we will denote Lebesgue factor-spaces [19] (p. 52) of all the classes of $\mathsf{\mu }$ -equivalence maps $f:T\to \mathbf{B}$ with norm ${({\displaystyle \underset{T}{\int }{\Vert f(\mathsf{\tau })\Vert }_{\mathbf{B}}^p} \mathsf{\mu }(d\mathsf{\tau }))}^{1/p}<\infty ,$ when $1\le p<\infty ,$ and $\mathrm{ess} {\sup }_T\left|\right|f(t{\left)\right||}_{\mathbf{B}}<\infty$ for $p=\infty .$ Staying within the given context, let us introduce the following auxiliary denotations:

$$\mathrm{II}:=A{C}^1(T,X)\times {\mathrm{L}}_2(T,Y)\times {\mathrm{L}}_2(T,Z)\times {\mathrm{L}}_2(T,Z)\times {\mathrm{L}}_2(T,Z),$$

$${\mathbf{L}}_2:={\mathrm{L}}_2(T,L(X,X))\times {\mathrm{L}}_2(T,L(X,X))\times {\mathrm{L}}_2(T,L(Y,X))\times$$

$$\times {\mathrm{L}}_2(T,L(Z,X))\times {\mathrm{L}}_2(T,L(Z,X))\times {\mathrm{L}}_2(T,L(Z,X));$$

obviously, space ${\mathbf{L}}_2$ (with the topology of product) is an isomorph ${\mathrm{L}}_2(T,L(U,X));$ furthermore, let us agree that any vector from ${\mathbf{L}}_2$ (in the context of the problem of realization) will be called the ${(A_1,A_0,B_0,B_1,B_2,B_3)}_2$ -model.

Henceforth we assume that bilinear maps ${\mathbb{B}}_i\in \mathcal{L}(X^2,Z),$ $i=1, 2, 3$ are fixed, and that

$$N \subset \{ ( x,u,{\mathbb{B}}_1(x,x),{\mathbb{B}}_2(x,dx/dt),{\mathbb{B}}_3(dx/dt,dx/dt) )\in \mathbf{II} \}, \mathrm{Card} N\le \exp {\aleph }_0 ,$$

(1)

is the behavior of the scrutinized dynamic system with $x$ -trajectories, programmed controls $u$ and bilinear relations ${\mathbb{B}}_i,$ $i=1, 2, 3$ ($\exp {\aleph }_0$—continuum, ${\aleph }_0$—aleph- zero); it is obvious that—according to (1)—in the case of a behavioristic $N$ -system, for any dynamic process from $N$ the following relationship is valid

$${\mathbb{B}}_1(x,x), {\mathbb{B}}_2(x,dx/dt), {\mathbb{B}}_3(dx/dt,dx/dt)\in {\mathrm{L}}_2(T,Z).$$

Consider the following QTDR-problem. In the case of a behavioristic $N$ -system (1) it is desirable to find both necessary and sufficient conditions of existence of the ${(A_1,A_0,B_0,B_1,B_2,B_3)}_2$ -model represented by the cortege

$$(A_1,A_0,B_0,B_1,B_2,B_3)\in {\mathbf{L}}_2,$$

for which it is possible to realize a bilinear differential realization (BDR) of the form

$$\begin{gathered} d^{2}x/d{t}^2+A_{1}dx/dt+A_{0}x= \\ =B_{0}u+B_1{\mathbb{B}}_1(x,x)+B_2{\mathbb{B}}_2(x,dx/dt)+B_3{\mathbb{B}}_3(dx/dt,dx/dt) , \end{gathered}$$

(2)

$$\forall (x,u,{\mathbb{B}}_1(x,x),{\mathbb{B}}_2(x,dx/dt),{\mathbb{B}}_3(dx/dt,dx/dt))\in N;$$

on account of Lemma 1 [12], in the construction of the $x$ -solution, we follow [19] (p. 418), i.e., the equality in (2) is considered as an identity in ${\mathrm{L}}_1(T, X)$. This QTDR-statement will later be burdened with the condition of entire continuity (see Definition 3) of an integral form of the non-autonomous BDR-model (2).

3. Reduction of the BDR-Problem to the Problem of $M_2$ -Continuity

At the end of this short paragraph we will show (in Lemma 1) how the mathematical statement of the problem of the BDR-problem may be reformulated in terms of a special division of the theory of extension of linear operators [20] (p. 38) in the functional Banach spaces. We will speak about a “special division” because below we will give a strong mathematical grounding to this operator extension.

Let us redenote (for the purpose of convenience) Hilbert spaces ${\mathrm{L}}_2(T, U)$ with $H_2;$ it is clear that, in accordance with the constructions introduced earlier, the norm in space $H_2$ has the form:

$${\Vert (g,w,v,q,s,h)\Vert }_H:=$$

$$:=({\displaystyle \underset{T}{\int }({\Vert g(\mathsf{\tau })\Vert }_X^2+{\Vert w(\mathsf{\tau })\Vert }_X^2+}{\Vert v(\mathsf{\tau })\Vert }_Y^2+{\Vert q(\mathsf{\tau })\Vert }_Z^2+{\Vert s(\mathsf{\tau })\Vert }_Z^2+{\Vert h(\mathsf{\tau })\Vert }_Z^2) \mathsf{\mu }(d\mathsf{\tau }){)}^{1/2}.$$

Let $L(H_2,X)$ be a space of all linear continuous operators (with the operator norm $\left|\right|\cdot |{|}_{L(H,X)}$) acting from space $H_2$ into space $X.$ Now, for the fixed (somehow) ordered system of operator-functions $(D_1,D_2,D_3,D_4,D_5,D_6)\in {\mathbf{L}}_2$, let us introduce into our consideration the linear operator $\xi \in L(H_2,X),$ which has the following analytical representation

$$\xi (g,w,v,q,s,h):=$$

$$:={\displaystyle \underset{T}{\int }(D_1(\mathsf{\tau })g(\mathsf{\tau })+D_2(\mathsf{\tau })w(\mathsf{\tau })+D_3(\mathsf{\tau })v(\mathsf{\tau })}+D_4(\mathsf{\tau })q(\mathsf{\tau })+D_5(\mathsf{\tau })s(\mathsf{\tau })+D_6(\mathsf{\tau })h(\mathsf{\tau })) \mathsf{\mu }(d\mathsf{\tau }).$$

(3)

Next, space $(X, ||\cdot |{|}_X)$ is locally convex, so (since the conjugate space for $X$ separates the points in $X$), the linear operator $\mathbf{\Gamma }:{\mathbf{L}}_2\to L(H_2,X),$ which—according to formula (3)—realizes the coordination defined as

$$(D_1,D_2,D_3,D_4,D_5,D_6)\mapsto \mathbf{\Gamma }(D_1,D_2,D_3,D_4,D_5,D_6)=\mathsf{\xi } ,$$

is the one-to-one coordination ($\mathrm{Ker} \mathbf{\Gamma }=\{ 0 \} ),$ what allows one to state—with respect to the properties of operator $\mathbf{\Gamma }$—ever more (see Proposition 1 below), under the assumption that the linear manifold of operator-function ${\mathbf{L}}_2$ is allotted with the structure of the topology induced by the norm

$${\Vert (D_1,D_2,D_3,D_4,D_5,D_6)\Vert }_{\mathbf{L}}:=$$

$$:= ({\displaystyle \underset{T}{\int }({\Vert D_1(\mathsf{\tau })\Vert }_{L(X,X)}^2+{\Vert D_2(\mathsf{\tau })\Vert }_{L(X,X)}^2+{\Vert D_3(\mathsf{\tau })\Vert }_{L(Y,X)}^2+{\Vert D_4(\mathsf{\tau })\Vert }_{L(Z,X)}^2+}{\Vert D_5(\mathsf{\tau })\Vert }_{L(Z,X)}^2+{\Vert D_6(\mathsf{\tau })\Vert }_{L(Z,X)}^2) \mathsf{\mu }(d\mathsf{\tau }){)}^{1/2}.$$

Obviously, the pair $({\mathbf{L}}_2, {\Vert \cdot \Vert }_{\mathbf{L}})$ forms the Banach space [20] (p. 81).

There exists another formulation of the fact that $\mathrm{Ker} \mathbf{\Gamma }=\left\{0\right\}$ is rather important to identify it in the capacity of a separate statement (proposition).

Proposition 1.

Operator $\mathbf{\Gamma }$ is a linear homeomorphism.

Now, after the prepared constructions is conducted, we will introduce into consideration one of the operator-theoretic constructions which is most important for us.

Definition 1.

The linear map $M:H_2\to {\mathrm{L}}_1(T,X)$is called the$M_2$-operator, when

$$\exists (D_1,D_2,D_3,D_4,D_5,D_6)\in {\mathbf{L}}_2: M(g,w,v,q,s,h):=$$

$$:=D_{1}g+D_{2}w+D_{3}v+D_{4}q+D_{5}s+D_{6}h , \forall (g,w,v,q,s,h)\in H_2 .$$

Not in the last tern we take interest in the issue of how the class of all the $M_2$-operators is constructed. The general understanding of this issue is represented by the following statement.

Proposition 2.

The class of all $M_2$ -operators belong (how eigen-one) to the Banach space $L(H_2,{\mathrm{L}}_1(T,X)).$

So, there is in-coincidence of the space of bounded operators $L(H_2,{\mathrm{L}}_1(T,X))$ and the class of all $M_2$ -operators.

The theory of extension of linear operators in common Banach spaces has been now developed more completely; so, we will restrict our consideration with reference to well-known (classical) monographs [11,20]. The following definition gives a new functional-analytic direction in this direction of development of the theory of operators:

Definition 2.

Let subset $V\subset H_2$ be fixed. Hence the given linear operator $M^{\#}:\mathrm{Span} V\to {\mathrm{L}}_1(T,X)$ will be called $M_2$ -continuable when $M^{\#}$ admits linear extension to some $M_2$ -operator $M,$ i.e.,

$$\exists (D_1,D_2,D_3,D_4,D_5,D_6)\in {\mathbf{L}}_2: M(g,w,v,q,s,h)=$$

$$=D_{1}g+D_{2}w+D_{3}v+D_{4}q+D_{5}s+D_{6}h , \forall (g,w,v,q,s,h)\in H_2 , M|\mathrm{Span} V=M^{\#} .$$

(Due to Proposition 2, $M_2$ -continuity implies continuous extension of operator $M^{\#}$).

Each pithy mathematical theory has its short list of lemmas, which form the basement of this theory. Within the frames of this context, the basement of the theory of the second-order BDR-realization is formed by the following lemma, which is important for us:

Lemma 1.

BDR-problem (1)–(2) is solvable if and only if operator

$$(g,w,v,q,s,h) \mapsto M^{\#} (g,w,v,q,s,h):=d^{2}w/d{t}^2 ,$$

$$(g,w,v,q,s,h) \in \mathrm{Span} \{ (dw/dt,w,v,q,s,h): (w,v,q,s,h) \in N\}$$

is $M_2$ -continuable.

Before proceeding to solving the issue of BDR-modeling within the frames of the functional-analytical theory of $M_2$ -continuity, let us note that Lemma 1 (in essence) states side-by-side that, while spending more effort on the operational techniques, the same qualitative systems-theoretic results bound up with reduction of the BDR-problem to solving the problem of $M_2$ -continuity may be applied to the bilinear non-autonomous differential evolution equations of higher orders. So, from now on, we do not intend to go deeper into this issue.

4. The Characteristic Indicator of $M_2$ -Continuity

In the previous paragraph we have demonstrated how, when using the structure of linearly functional $M_2$ -operators, it is possible to reduce the BDR-problem to the analytical solution of the problem of $M_2$ -continuity. In this connection, in this section of the paper we continue the study of $M_2$ -operators. We intend to start from the development of the necessary apparatus. In this connection, for the case when $S\in {\wp }_{\mathsf{\mu }}$, let us consider operator $P_{S, \mathrm{L}}:{\mathrm{L}}_1(T,X)\to {\mathrm{L}}_1(T,X)$ [21] (p. 13) assigned by

$$t\in S \Rightarrow P_{S, \mathrm{L}}(y)(t) :=y (t)\in X ,$$

$$t\in T\backslash S \Rightarrow P_{S, \mathrm{L}}(y)(t):=0\in X .$$

Remark 1.

Operator $P_{S, \mathrm{L}}$ is in essence a linear projector $P_{S, \mathrm{L}}{}^2=P_{S, \mathrm{L}} ,$ furthermore, space ${\mathrm{L}}_2(T,X)\subset {\mathrm{L}}_1(T,X)$ is invariant with respect to the actions of projector $P_{S, \mathrm{L}}$. Such an arrangement makes the consideration of a similar linear operator $P_{S, H}:H_2\to H_2,$ which has been constructed according to the functional rule (as a “model specimen”) described above, quite correct.

Below, in two theorems, we will consider (at the level of simple axiomatic schemes) the two forms of the characteristic criterion of $M_2$ -continuability and, simultaneously we will briefly discuss their functional-analytical images (with analysis of their constructive character).

The following structural Theorem 1 and (see below) its algebraic Corollary 1, give essentially universal functional-theoretic calculus on elements of $\mathsf{\sigma }$ -algebra ${\wp }_{\mathsf{\mu }}$ of all $M_2$ -continuable operators; we speak “structural” because in Corollary 1 given is an algebraic criterion of disposition of $M_2$ -continuable operators in space $L(H_2,{\mathrm{L}}_1(T,X)).$

Theorem 1.

Let $E\subset H_2$ be some linear manifold invariant with respect to the projectors $\{P_{S, H}:S\in {\wp }_{\mathsf{\mu }}\}$ and $M^{*}: E\to {\mathrm{L}}_1(T,X)$ be a linear continuous operator. Hence $M^{*}$ is $M_2$ -continuable if and only if for all the subsets $S\in {\wp }_{\mathsf{\mu }}$ and for each $y\in E$ we have

$$M^{*}\circ P_{S, H}(y)=P_{S, \mathrm{L}}\circ M^{*}(y),$$

(4)

what means that for all the subsets $S\in {\wp }_{\mathsf{\mu }}$the following diagram is commutative:

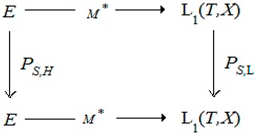On account of Proposition 2, we obtain a new formulation of Definition 1.

Corollary 1.

The linear operator $M:H_2\to {\mathrm{L}}_1(T,X)$ is an $M_2$ -operator if and only if $M\in L(H_2,{\mathrm{L}}_1(T,X))$ and, furthermore, for any $S\in {\wp }_{\mathsf{\mu }}$ the following equality is valid

$$M\circ P_{S, H}=P_{S, \mathrm{L}}\circ M.$$

Unfortunately, if all the elements of $\mathsf{\sigma }$ -algebra ${\wp }_{\mathsf{\mu }}$ are taken into consideration, then constructivity of the characteristic criterion of $M_2$ -continuity does not follow from Theorem 1 and Corollary 1. Below we will try to avoid this shortcoming.

The idea lying at the base of the proposed construction is very simple. Let $V\subset H_2$ and $M^{\#}: \mathrm{Span} V\to {\mathrm{L}}_1(T,X)$ be some linear operator. In order to obtain a compact and efficient (constructive) characteristic criterion of linear-continuous continuity of operator $M^{\#}$ up to some $M_2$ -operator with the aid of Theorem 1, it is necessary (and this can easily be understood) to solve the following analytical problems sequentially:

(a)

Extend the linear hull of $\mathrm{Span} V$ up to some minimal involving the linear manifold $E\subset H_2$ invariant with respect to the family of projectors $\{P_{S, H}:S\in {\wp }_{\mathsf{\mu }}\} ;$

(b)

Construct for the operator $M^{\#}$ its linear extension $M^{*}$ on manifold $E$ (see the previous problem) and demonstrate the fact of continuity of operator $M^{*}: E\to {\mathrm{L}}_1(T,X)$;

(c)

Verify the fact of satisfaction of condition (4) for the linear extension $M^{*}$.

The conditions of solvability of problems (b) and (c) will be demonstrated (and clarified) below by Theorem 2. Meanwhile, the geometric solution of problem (a) is the matter of analysis in the following lemma.

Lemma 2.

Let $V\subset H_2$ and $E=\mathrm{Span} \{P_{S, H}(y): S\in {\wp }_{\mathsf{\mu }} , y\in \mathrm{Span} V\},$ hence

(i) 

$E$ is the smallest linear set in $H_2$, which contains $\mathrm{Span} V$ and is invariant with respect to the family of projectors $\{P_{S, H}: S\in {\wp }_{\mathsf{\mu }}\} ;$

(ii) 

for any $y\in E$ one can find a natural number $k,$ such that for it and for the vector $y$ it is possible to find a family of sets ${\left\{S_i\right\}}_{i=1,\dots ,k}\subset {\wp }_{\mathsf{\mu }}$ and a set vectors ${\left\{y_i\right\}}_{i=1,\dots ,k}\subset \mathrm{Span} V$, such that

$$S_i\cap S_j=\varnothing , i\ne j (i,j=1,\dots ,k)$$

$$y={\displaystyle \sum {}_{i=1,...,k}{P}_{S_i,H}(y_i}).$$

Remark 2.

When considering the geometric expansion of $y={\displaystyle \sum {}_{i=1,...,k}{P}_{S_i,H}(y_i})$, it is possible to assume that conjunction ${\cup }_{i=1,...,k}{S}_i$ exhausts the total interval $T$, because if ${\cup }_{i=1,...,k}{S}_i$ is an eigen-subset in $T$, then, having denoted by $S_{k+1}$ the set $T\backslash {\cup }_{i=1,...,k}{S}_i$ and having accepted that $y_{k+1}=0,$ we obtain the expansion $y={{\displaystyle \sum {}_{i=1,...,k+1}{P}_{S_i,H}(y}}_i) , {\cup }_{i=1,...,k+1}{S}_i=T ;$ i.e., in the case of representation of the vector $y$ with the sum ${\displaystyle \sum {}_{i=1...,k}{P}_{S_i,H}(y_i})$, the finite set of subsets $S_1,\dots ,S_k$ forms a disjunctive decomposition of the time interval $T$.

The Lemma 2 together with Theorem 1 give an opportunity to obtain a rather compact formulation of the characterization of conditions of $M_2$ -continuity.

Theorem 2.

Let $V\subset H_2$ and $M^{\#}: \mathrm{Span} V\to {\mathrm{L}}_1(T,X)$ be some linear operator. Hence $M^{\#}$ is characterized by $M_2$ -continuity if and only if one can find a function $t\mapsto \mathsf{\phi } (t) \cdot \ge \cdot 0$ in ${\mathrm{L}}_2(T,R)$ such that on interval $T$ for all $y\in \mathrm{Span} V$ we have the following $\mathsf{\mu }$ -dependence

$$\left|\right|M^{\#}(y)(t)|{|}_X \cdot \le \cdot \mathsf{\phi }(t) ||y(t)|{|}_U .$$

(5)

Proof. 

(necessary). Obviously, if the linear operator

$$(g,w,v,q,s,h) \mapsto M(g,w,v,q,s,h):=D_1 g+D_2 w+D_3 v+D_4 q+D_5 s+D_6 h$$

is an $M_2$ -operator, which continues $M^{\#}$, then for any vector function

$$y=(g,w,v,q,s,h) \in \mathrm{Span} V$$

the following relations are satisfied on interval $T$:

$$\left|\right|M^{\#}(y)(t)|{|}_X \cdot =\cdot ||M(t)y(t)|{|}_X \cdot \le \cdot \mathsf{\phi }(t) \left|\right|y(t)|{|}_U ,$$

$$t\mapsto \mathsf{\phi }(t)=3^{1/2}( ||D_1(t)|{|}_{L(X,X)}^2|+||D_2(t)|{|}_{L(X,X)}^2+\left|\right|D_3(t)|{|}_{L(Y,X)}^2+$$

$$+ \left|\right|D_4(t)|{|}_{L(Z,X)}^2+||D_5(t)|{|}_{L(Z,X)}^2+\left|\right|D_6(t)|{|}_{L(Z,X)}^2{)}^{1/2} .$$

There is no doubt that the nonnegative function $\mathsf{\phi }(\cdot )$ belongs to class ${\mathrm{L}}_2(T,R)$ (sufficient). Let $E\subset H$ be a linear manifold from the formulation of Lemma 2. Consider the linear operator $M^{*}:E\to {\mathrm{L}}_1(T,X)$, which acts in accordance with the representation

$$M^{*}(y):={\displaystyle \sum {}_{i=1,...,k}{P}_{S_i, \mathrm{L}}}\circ M^{\#}(y_i) ,$$

where the vector functions $y,y_i\in E$ and the subsets $S_i\in {\wp }_{\mathsf{\mu }}$, $i=1,\dots ,k$ are bound (due to Lemma 2 and Remark 2) by the following constructions:

$$y={\displaystyle \sum {}_{i=1,...,k}{P}_{S_i,H}(y_i}) , y_i\in \mathrm{Span} V ,$$

$${\cup }_{i=1,...,k}{S}_i=T, S_i\cap S_j=\varnothing , i\ne j ( i,j=1,\dots ,k) .$$

Finally, it remains to show that the linear operator $M^{*}$ is defined correctly, i.e., that its value is bound up with any vector function $y\in E$ is independent of the representation of $y={\displaystyle \sum {}_{i=1,...,k}{P}_{S_i,H}(y_i})$.

Let $y\in E$ and $y={\displaystyle \sum {}_{i=1,...,k}{P}_{S_i,H}(y_i})={\displaystyle \sum {}_{j=1,...,r}{P}_{S_j,H}(y_j})$, where ${\left\{S_i\right\}}_{i=1,\dots ,k}$ and ${\left\{S_j\right\}}_{j=1,\dots ,r}$ are some fixed disjunctive decompositions of interval $T$, and $y_i,y_j\in \mathrm{Span} V$, $1\le i\le k, 1\le j\le r$. Hence the family of subsets $\{ S_{ij}: S_{ij} =S_i\cap S_j, 1\le i\le k, 1\le j\le r \}$ also forms decomposition of interval $T$. Next, put $y_{ij}:=y_i-y_j$. Since $y(t) \cdot =\cdot y_i(t) \cdot =\cdot y_j(t), t\in T,$ we have $y_{ij}(t) \cdot =\cdot 0$ on every subset $S_{ij}$, and, so, due to condition (5), we obtain

$$\left|\right|M^{\#}(y_{ij})(t)|{|}_X\cdot \le \cdot \mathsf{\phi }(t) ||y_{ij}(t)|{|}_U \cdot =\cdot 0, t\in S_{ij}$$

and, therefore, $M^{\#}(y_{ij})(t)\cdot =\cdot 0, t\in S_{ij}$. Consequently, $M^{\#}(y_i)(t)\cdot =\cdot M^{\#}(y_j)(t), t\in S_{ij}$. In this case, having introduced the denotations $t\mapsto z\prime (t):={\displaystyle \sum {}_{i=1,...,k}{P}_{S_i,\mathrm{L}}\circ M^{\#}(y_i})$ and $t\mapsto z\prime \prime (t):={\displaystyle \sum {}_{j=1,...,r}{P}_{S_j,\mathrm{L}}\circ M^{\#}(y_j})$, for the above functions we obtain a quite obvious chain of equalities

$$z\prime (t)=M^{\#}(y_i)(t) \cdot =\cdot M^{\#}(y_j)(t)=z\prime \prime (t), t\in S_{ij} .$$

Now, taking account of the fact that the system of subsets ${\{ S_{ij}\}}_{1\le i\le k, 1\le j\le r}$ forms a disjunctive decomposition of interval $T$, we obtain a conclusion that the following dependence (correspondence) takes place $z\prime (t)\cdot =\cdot z\prime \prime (t), t\in T$ and, consequently, the linear operator $M^{*}$ has been defined correctly (as a desired extension of operator $M^{\#}$).

Obviously, in order to prove the fact of continuity of $M^{*}$ of the linear map it is sufficient to verify whether relation (5) for the operator $M^{*}$ is valid. In this case, the fact of continuity of operator $M^{*}$ follows from the Cauchy-Bunykovskii integral inequality.

Indeed, let, likewise above, $y={\displaystyle \sum {}_{i=1,...,k}{P}_{S_i,H}(y_i}) , y_i\in \mathrm{Span} V ,$ where ${\left\{S_i\right\}}_{i=1,\dots ,k}$ be the decomposition of interval $T$. Hence from the representation

$$M^{*}(y)={\displaystyle \sum {}_{i=1,...,k}{P}_{S_i, \mathrm{L}}}\circ M^{\#}(y_i)$$

it follows that

$$M^{*}(y)(t)=M^{\#}(y_i)(t) , t\in S_i .$$

So, due to (5), for the function $y_i$ we have

$$\left|\right|M^{*}(y)(t)|{|}_X = ||M^{\#}(y_i)(t)|{|}_X \le \mathsf{\phi }(t) \left|\right|y_i(t)|{|}_U \le \mathsf{\phi }(t) ||y(t)|{|}_U$$

$\mathsf{\mu }$ -almost everywhere in $S_i$. Consequently, this statement is valid $\mathsf{\mu }$ -almost everywhere on interval $T$.

Next, in order to complete the proof, it remains only to confirm the existence of property (4) for the operator $M^{*}$. So, let

$$y\in E, y={\displaystyle \sum {}_{i=1,...,k}{P}_{S_i,H}(y_i}) , y_i\in \mathrm{Span} V ,$$

$$S_i\cap S_j=\varnothing , i\ne j, {\cup }_{i=1,...,k}{S}_i=T, i,j=1,\dots ,k, S\subset T$$

Hence $P_{S,H}(y)={\displaystyle \sum {}_{i=1,...,k}{P}_{S,H}\circ P_{S_i,H}(y_i}) ={\displaystyle \sum {}_{i=1,...,k}{P}_{S\cap S_i,H}(y_i}),$ whence, in accordance with the definition of the construction of operator $M^{*}$ (introduced above), it is possible to summarize:

$$M^{*}\circ P_{S,H}(y)={\displaystyle \sum {}_{i=1,...,k}{P}_{S\cap S_i,\mathrm{L}}\circ M^{\#}(y_i})={\displaystyle \sum {}_{i=1,...,k}{P}_{S,\mathrm{L}}\circ P_{S_i,\mathrm{L}}\circ M^{\#}(y_i})=$$

$$=P_{S,\mathrm{L}}\circ {\displaystyle \sum {}_{i=1,...,k}{P}_{S_i,\mathrm{L}}\circ M^{\#}(y_i})=P_{S,\mathrm{L}}\circ M^{*}(y) .$$

□

Remark 3.

When estimating the perspective of development of the BDR-theory on the whole in the geometric constructions of $M_2$ -continuity, we have to note that the case, when the $N$ -family (1) lies in the uniformly convex Banach space [20] (p. 182), and, furthermore, $\mathrm{Card} N\ge {\aleph }_0$ is analytically more complex (considering the variant of modeling the bilinear structure of the differential model of realization [18]). This qualitative theory contains (in the capacity of a special sub-problem) geometrical constructions of closed decomposable dihedrons [19]. This aspect has not been sufficiently developed in the aspect of analytical grounding of the issue of $M$ -continuity. Furthermore, it is necessary to take account of the fact that—under the geometrical BDR-statement—it is hardly ever productive to make an initial assumption that any closed subspace of the scrutinized Banach space may be complemented, because then this space is an isomorph to some Hilbert space (see Theorem 3 [11] (p. 203)), what finally (NB!) does not extend the functional class of operator coefficients of the inverse problem, which has been briefly discussed above in its QTDR-statement (2).

5. About $M_2$ -Continuity: Existence of a Completely Continuous BDR-Model

It is known that, as far as Banach spaces are concerned, the uniform limit for the sequence of finite rank operators is represented by a compact operator. In this paragraph, in the capacity of extension of the mathematical statement of the problem of differential realization (2) we will consider in detail the case, when the modeled operators are burdened with an additional condition, which provides for obvious continuity of the integral representation of equations of realization models. This is provoked by the fact that there (in the spaces with the basis) any compact operator represents a uniform limit of the finite-rank operators [11] (p. 514), what is especially important in the course of development of numerical procedures bound up with approximation of the realization model.

On the other hand, we will also demonstrate below (in the absence of such analysis in [6]) that, when executing an analytical relationship between the projective geometry and the differential realization of modeled infinite-dimensional second-order dynamic processes, the construction of projectivization of the nonlinear functional Relay-Ritz operator and the functional-geometric analysis of conditions of its continuity may be suitably formulated in terms of the language of compact topological manifolds. Within the given context, the analytical construction of the entropy from [6] (in comparison with the construction proposed below) differs in the aspect that the entropy is computed via projectivization of the Relay-Ritz operator. This allows one to efficiently use the property of compactness of the image of projectivization discussed.

Let $V\subset H_2$. In manifold $\mathrm{Span} V$, the linear operator $M^{\#}: \mathrm{Span} V\to {\mathrm{L}}_1(T,X)$ from Theorem 2 has the corresponding nonlinear Relay-Ritz operator [6,12] constructed according to the following rule:

$$\mathsf{\Psi }(y)(t) := \{ \begin{array}{l}\left|\right|M^{\#}(y)(t)\left|{|}_X\right||y(t)|{|}_U^{-1} , \mathrm{if} y(t)\ne 0\in U,\\ 0\in R , \mathrm{if} y(t)=0\in U .\end{array}$$

Next, in the geometry of the absorbing set we follow [20] (p. 42): set $Q$ in the vector space $L$ is absorbing, when for any $y\in L$ it is possible to find (indicate) a real number $r\in (0,\infty ),$ such that $ry\in Q$; if $L$ is a normalized space, then not only each bounded neighborhood of zero but also its boundary with the zero are absorbing sets. Let us denote by $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p} f(\cdot ) := \{ t\in T: f(t)\ne 0 \}$ the carrier [11] (p. 137) of the real function $f(\cdot )$ measurable on $T$. Such a geometric problem statement allows one to reveal an important refinement of Theorem 2.

Lemma 3.

Let $V\subset H_2$, $M^{\#}: \mathrm{Span} V\to {\mathrm{L}}_1(T,X)$ be a linear operator and $Q$ be some absorbing set in $\mathrm{Span} V$. Hence $M_2$ -continuity of operator $M^{\#}$ is equivalent to the simultaneous satisfaction of the two conditions:

$$\mathrm{supp} \left|\right|M^{\#}(y)(\cdot )|{|}_X \cdot \subseteq \cdot \mathsf{s}\mathsf{u}\mathsf{p}\mathsf{p} ||(y)(\cdot )|{|}_U , \forall y\in Q ,$$

$$\exists \mathsf{\phi }\in {\mathrm{L}}_2(T,R): \mathsf{\Psi }(y)(t) \cdot \le \cdot \mathsf{\phi }(t) , \forall y\in Q .$$

Let us also note another useful BDR-fact.

Lemma 4.

Let $(x,u,{\mathbb{B}}_1(x,x),{\mathbb{B}}_2(x,dx/dt),{\mathbb{B}}_3(dx/dt,dx/dt))\in \mathbf{II}$. Hence

$$\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p} \left|\right|d^{2}x(\cdot )/d{t}^2|{|}_X \cdot \subseteq \cdot$$

$$\cdot \subseteq \cdot \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p} \left|\right|( dx(\cdot )/dt, x(\cdot ), u(\cdot ), {\mathbb{B}}_1(x(\cdot ),x(\cdot )), {\mathbb{B}}_2(x(\cdot ), dx(\cdot )/dt), {\mathbb{B}}_3(dx(\cdot )/dt, dx(\cdot )/dt) )|{|}_U.$$

The proof may be reduced to the compiling of Lemmas 1 and 3 [12].

If we introduce into our consideration the space (vector lattice [11] (p. 363)) of measurable functions $\mathrm{L}(T,R)$ and also ${\le }_{\mathrm{L}}$—quasi-ordering $f_1{\le }_{\mathrm{L}}{f}_2\iff f_1(t) \cdot \le \cdot f_2(t)$ in it with the least lower boundary ${\sup }_{\mathrm{L}}$ for the subsets from $\mathrm{L}(T,R)$, then—on account of item (a) of Theorem 17 [11] (p. 68) and Lemmas 1–4, for the BDR-problem (2)—we obtain the following key analytical result:

Theorem 3.

Let $N$ be a family of processes (1), $Q$ be some absorbing set in

$$\mathrm{Span} \{ (dw/dt,w,v,q,s,h): (w,v,q,s,h)\in N \}$$

and

$$(g,w,v,q,s,h)\mapsto M^{\#}(g,w,v,q,s,h):=d^{2}w/d{t}^2.$$

Hence the BDR-problem

$$\exists (A_1,A_0,B_0,B_1,B_2,B_3)\in {\mathbf{L}}_2:$$

$$d^{2}x/d{t}^2+A_{1}dx/dt+A_{0}x=B_{0}u+B_1{\mathbb{B}}_1(x,x)+B_2{\mathbb{B}}_2(x,dx/dt)+B_3{\mathbb{B}}_3(dx/dt,dx/dt) ,$$

$$\forall (x,u,B_1(x,x),B_2(x,dx/dt),B_3(dx/dt,dx/dt))\in N$$

is solvable if and only if some one of the following two conditions is satisfied

$$\exists \mathsf{\phi }\in {\mathrm{L}}_2(T,R): \mathsf{\Psi }(g,w,v,q,s,h) {\le }_{\mathrm{L}}\mathsf{\phi } , \forall (g,w,v,q,s,h)\in Q ;$$

$$\exists {\sup }_{\mathrm{L}}\mathsf{\Psi }(Q): {\sup }_{\mathrm{L}}\mathsf{\Psi }(Q) \in {\mathrm{L}}_2(T,R) .$$

Remark 4.

According to item (b) of Theorem 17 [11] (p. 68), there exists a contable set

$$Q^{*}\subset Q (1<\mathrm{Card} N< {\aleph }_0\Rightarrow \mathrm{Card} Q=\exp {\aleph }_0)$$

such that if there lies a functional edge ${\sup }_{\mathrm{L}}\mathsf{\Psi }(Q)$ in space $\mathrm{L}(T,R)$, then function $\mathsf{\phi }:={\sup }_{\mathrm{L}}\mathsf{\Psi }(Q)$ is realized by the following sup-construction:

$$t\mapsto \mathsf{\phi }(t)=\sup \{ \mathsf{\Psi }(g,w,v,q,s,h)(t)\in R: (g,w,v,q,s,h)\in Q^{*}\} .$$

Remark 5.

It follows from the structure of Equation (2) that BDR-solvability is realized for the operator-functions $(A_1,A_0,B_0,B_1,B_2,B_3)\in {\mathbf{L}}_2,$ with the accuracy up to the linear manifold

$${\mathbf{L}}^0=\{ (D_1,D_2,D_3,D_4,D_5,D_6)\in {\mathbf{L}}_2: D_{1}g+D_{2}w-D_{3}v-D_{4}q-D_{5}s-D_{6}h =0 ,$$

$$\forall (g,w,v,q,s,h)\in G_N\},$$

where $G_N$ is the Hamel basis (algebraic basis [11] (p. 74)) in

$$\mathrm{Span} \{ (dw/dt,w,v,q,s,h): (w,v,q,s,h)\in N \}$$

furthermore, the case when ${\mathbf{L}}_0=\{ 0\}\subset {\mathbf{L}}_2$ characterizes uniqueness of the BDR-model (2).

In the remaining part of the paper, we intend to address the characteristics of bilinear realizations, which redefine their properties in the aspect of modeling of a posteriori differential equations of systems dynamics.

As far as a system represented by an arbitrary family of processes (1) is concerned, the procedure of constructing equations of its differential realization (2) is rather complex (even in case of a linear model). Meanwhile, the problem becomes quite obvious in one important case (in the context of the problem of approximation [11] (p. 513)); when for the purpose of its bilinear realization (2) its integral $\xi$ -operator (3) is burdened with some additional conditions, which approximate the BDR-problem to the assumption that $\dim X<\infty$ [6,7,8,9,10]. This type of constructing is formalized by the following construction of the ${(A_1,A_0,B_0,B_1,B_2,B_3)}_2$ -model.

Definition 3.

The bilinear differential realization (2) will be called completely continuous if its integral operator (3) is compact.

In the context of Definition 3, we have to note that compact operators (including interval ones) possess a range of attractive analytical properties (see [11,20]) and are rather useful in numerous physics applications. Many problems of classical mathematical physics may be simplified if these are formulated in terms of the language of integral equations. In this connection, it is important to possess an efficient criterion of compactness of the given operator or, better, some general statements about integer classes of such operators.

For the purpose of convenience, the subclass of ${(A_1,A_0,B_0,B_1,B_2,B_3)}_2$ -models corresponding (due to construction (2)) completely to continuous quasi-linear differential realizations will be denoted by ${\mathbf{L}}_2^{\mathrm{com}}$, and, when following Definition 1, a subclass from $L(H_2,L_1(T,X))$ of all $M_2$ -operators is “identified” with the Banach space $({\mathbf{L}}_2, ||\cdot |{|}_{\mathbf{L}})$ of all ${(A_1,A_0,B_0,B_1,B_2,B_3)}_2$ -models; below we use standard denotations $l_r, 1\le r\le \infty$ of Banach spaces for numerical sequences [11] (p. 147).

Proposition 3.

The linear manifold ${\mathbf{L}}_2^{\mathrm{com}}$ is closed in space ${\mathbf{L}}_2$ and represents a (homeomorph) factor-space $l_1$.

Proof. 

Having combined Proposition 1 and Theorem 3 [11] (p. 326), one can come to the conclusion that ${\mathbf{L}}_2^{\mathrm{com}}$ is closed in ${\mathbf{L}}_2$, furthermore (due to separability of spaces $L(X,X)$, $L(Y,X)$, $L(Z,X)$ and Theorem 1.5.18 [22] (p. 150)), the Banach space ${\mathbf{L}}_2^{\mathrm{com}}$ is separable.

Now, let us consider the linear operator $E:l_1\to {\mathbf{L}}_2^{\mathrm{com}}$, while assuming that

$$E:\left\{a_i\right\}\to {\sum }_{i=1,2,\dots } a_i{x}_i, \left\{a_i\right\}\in l_1 ,$$

where $\{x_1,\dots ,x_n,\dots \}\subset {\mathbf{L}}_2^{\mathrm{com}}$ is a countable and everywhere dense set in a unit ball $S_{\mathbf{L}}$ (with its center at zero) from ${\mathbf{L}}_2^{\mathrm{com}}$. Operator $E$ is continuous; compilation of Theorem 5.1 [23] (p. 132), Theorem 3 [11] (p. 260) and the provision

$$( f(x_1) , \dots , f(x_n),\dots )\in l_{\infty } , \forall f\in {\mathbf{L}}_2^{\mathrm{com}}$$

Next, let $S_l$ be a unit ball (with its center at zero) in $l_1$, and since $\{x_1,\dots ,x_n,\dots \}\subset E(S_l)$, the image $E(S_l)$ be dense in ball $S_L$, whence it is possible to conclude that spaces ${\mathbf{L}}_2^{\mathrm{com}}$ and $l_1/\mathrm{Ker} E$ are linearly homomorphous (Lemma 1 [11] (p. 451)). □

Definition 4.

Let $V, W, U$ be some Banach spaces, $D\in L(V, W)$, $J\in L(W,U)$, $G:=\mathrm{Ker} J$ and $\pi :W\to W/G$ be some factor-map. Let us speak that operator $D$ is $J$ -factor-compact, when $J^{*}\circ \pi \circ D=J\circ D$, where $J^{*}:W/G\to U$ “closes” the diagramand, furthermore, the composition $\pi \circ D:V\to W/G$ represents a compact operator.

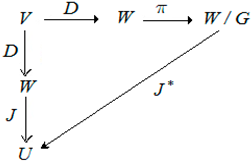Let $J:{\mathrm{L}}_1(T,X)\to X$ be an operator, which realizes the Bochner integral construct [20]; from now on, [⋅] is a closure operation (according to the context, in spaces $H_2, {\mathrm{L}}_1(T,X)/\mathrm{Ker} J,$ or $X$).

Theorem 4.

The following situation is valid for the solvable BDR -problem (1)–(2):

$$(A_1,A_0,B_0,B_1,B_2,B_3)\in {\mathbf{L}}_2^{\mathrm{com}}\iff$$

$$\iff operator (g,w,v,q,s,h)\mapsto M^{\#}(g,w,v,q,s,h):=d^{2}w/d{t}^2,$$

$$(g,w,v,q,h)\in \mathrm{Span} \{(dw/dt,w,v,q,s,h): (w,v,q,s,h)\in N\}$$

continuable up to the $J$ -factor-compact $M_2$ -operator $M:H_2\to {\mathrm{L}}_1(T,X)$.

Proof. 

Let $M$ be a $J$ -factor-compact operator of realization (2). Hence operator (3) is equal to $\xi =J\circ M$ and, therefore, the sufficient conditions represent the fact of item (b) of Theorem 2 [11] (p. 325) and Theorem 1.41 [23] (p. 39). Let us confirm the necessary conditions.

Let in (2)$(A_1,A_0,B_0,B_1,B_2,B_3)\in {\mathbf{L}}_2^{\mathrm{com}}$. Let us take ball $S_r$ of radius $r$ (with the center at zero) in $H_2$, and let $\left\{E_w\right\}$ be some open cover $[\pi \circ M(S_r)]$, where $\pi :{\mathrm{L}}_1(T,X)\to {\mathrm{L}}_1(T,X)/\mathrm{Ker} J$ is a factor-map. The fact that covers $\left\{E_w\right\}$ has a finite sub-cover ${\left\{E_i\right\}}_{i=1,\dots ,n}$ defines, on the one hand, the fact of homeomorphism of $J^{*}:{\mathrm{L}}_1(T,X)/\mathrm{Ker} J\to X$ (Theorem 1.41 [23] (p. 39)) and, on the other hand, the fact that due to (3) $[\xi (S_r)]$ is a compact subset in space $X$, that completes the proof. □

In the process of constructing the differential realization for the family of dynamic processes (1), one, as a rule (see Remark 5 above), has to do not with one system of equations of realization (2), but with a total family of such systems, what provokes to put forward the problems of constructing “optimal realizations” with respect to some formal criteria of “minimization” (in the given case, we do not speak about realizations [4,9] with respect to the criterion of “minimal dimension”). These problem statements assume several formal mathematical interpretations [24], i.e., it is possible to proceed from the problem of “optimal realization” in the structure of the Banach space $\left|\right|\xi |{|}_{L(E,X)}$ with respect to the criterion of norm $\left|\right|\cdot |{|}_{L(H,X)}$, or the space ${\mathbf{L}}_2$ with respect to the criterion of norm $\left|\right|\cdot |{|}_{\mathbf{L}}$. Below we’ll reduce our consideration to the problem bound up with investigation of existence of the realization with the minimal operator norm in space $(L(H_2,X), ||\cdot |{|}_{L(H,X)}).$

Definition 5.

Let us call the differential realization (2) with $M_2$ -operator $M,$ for which $\left|\right|J\circ M|{|}_{L(H,X)}$ = min {$\left|\right|\mathsf{\xi }|{|}_{L(H,X)}: \mathsf{\xi }$ is operator (3) of BDR-model (2)}, the realization optimal with respect to the criterion of the operator norm $\left|\right|\cdot |{|}_{L(H,X)}$.

As known from numerous stories of elaborations of pithy analytical theories, a good definition must be the provision of the theorem. This fact, considered with respect to Definition 5, confirms the following statement.

Theorem 5.

If BDR-model (2) exists, then there exists its $M_2$ -operator $M,$ for which this BDR-model is “$\left|\right|\cdot |{|}_{L(H,X)}$ -optimal” with the operator $\left|\right|\cdot |{|}_{L(H,X)}$ -norm

$$\left|\right|J\circ M|{|}_{L(H,X)}=|\left|\xi \right|{|}_{L(E,X)}, \xi =J\circ M^{*}:E\to X, E\subset H_2 ,$$

where $E$ is a minimal linear manifold, which contains the linear hull

$$\mathcal{L}:=\mathrm{Span} \{ (dw/dt,w,v,q,s,h): (w,v,q,s,h)\in N \}$$

and which is invariant with respect to projectors $\{P_{S, H}: S\in {\wp }_{\mathsf{\mu }}\}$, furthermore, operator $M^{*}\in L(E,X)$ has a narrowing $M^{*}|\mathcal{L}=d^{2}w/d{t}^2,$$(dw/dt,w,v,q,s,h)\in \mathcal{L}$ and possesses property (4).

Proof. 

Note first of all that if there exists a realization (noted in the theorem) then constructions $E$ and $M^{*}$ exist due to Lemma 2 and Theorems 1–3; furthermore, it is obvious that $[E]$ is a Hilbert space in itself. The proof of Theorem 5 will be conducted in the two steps, respectively, for defining the estimate $\left|\right|J\circ M|{|}_{L(H,X)}\le |\left|\xi \right|{|}_{L(E,X)}$ and the estimate $\left|\right|J\circ M|{|}_{L(H,X)}\ge |\left|\xi \right|{|}_{L(E,X)}$.

Defining estimate $\left|\right|J\circ M|{|}_{L(H,X)}\le |\left|\xi \right|{|}_{L(E,X)}$. Consider operators $J\circ M_{+}: [E]\to X$ and $\xi :H_2\to X$, the first one of which is a linear continuous (and unique) continuation $J\circ M^{*}$ on closure $[E]$ with retaining the norms (Theorem 2 [11] (p. 245)), and the second operator is constructed as a linear continuous representation $\xi :=J\circ M_{+}\circ \mathrm{Pr} ,$ where $\mathrm{Pr}$ is a projector in $H_2$ with the kernel $E^{\perp }$ (orthogonal complement of $[E]$; Theorem 5.16 [23] (p. 151)). Obviously, under such a statement, the following case will be realized:

$$\left|\right|\xi |{|}_{L(H,X)}=||J\circ M_{+}\circ \mathrm{Pr}|{|}_{L(H,X)}= \left|\right|\xi |{|}_{L(E,X)} .$$

When turning back to Proposition 1, let us consider the following operator

$$M^{+}:H_2\to {\mathrm{L}}_1(T,X),\hspace{1em}{M}^{+}:={\mathbf{\Gamma }}^{-1}(\mathsf{\xi })=M_{+}\circ \mathrm{Pr}\in L_2 ,$$

in the capacity of the “candidate for the role” of operator $M,$ and, therefore, for the “$\xi$ -model” (3) of the differential realization (2), the estimate with respect to the criterion of the operator norm $\left|\right|\cdot |{|}_{L(H,X)}$, is obviously not larger than $\left|\right|\xi |{|}_{L(E,X)}$.

Defining the estimate $\left|\right|J\circ M|{|}_{L(H,X)}\ge |\left|\xi \right|{|}_{L(E,X)}$. Since $E$ is the minimal linear manifold containing $\mathrm{Span} N$ and invariant with respect to the family of projectors $\{P_{S_i,H}: S\in {\wp }_{\mathsf{\mu }}\}$, the narrowing (on $E$) of any $M_2$ -operator (in particular, also $M^{+}$) corresponding to the differential realization (2), coincides with $M^{*}$, consequently, in case of any realization, the estimate of its “$\xi$ -model” (3) with respect to the criterion of the operator norm $\left|\right|\cdot |{|}_{L(H,X)}$ is not smaller than $\left|\right|\xi |{|}_{L(E,X)}$. This proves the theorem. □

When applying some considerations bound up with modification of the operator $\mathsf{\Psi }$, and using the second characteristic condition from the statement of Theorem 3, it is possible to obtain the result bound up with the “lower $\left|\right|\cdot |{|}_{\mathbf{L}}$ -estimate” for $\left|\right|\cdot |{|}_{L(H,X)}$ -optimal $M_2$ -operator (in particular, $M^{+}$).

Let us proceed to the details. Note, first of all, since the following relations

$$\mathsf{\Psi } (r (g,w,v,q,s,h))=\mathsf{\Psi } (g,w,v,q,s,h), (g,w,v,q,s,h)\in V_N, 0\ne r\in R ,$$

$$V_N:=\{(dw/dt,w,v,q,s,h): (w,v,q,s,h)\in N\} ,$$

hold, let us assume (applying the geometrical techniques [25,26] of projective representations) that

$$\mathsf{\Phi }(\mathsf{\gamma }):=\mathsf{\Psi }[\mathsf{\gamma }] , \mathsf{\gamma }\in P_N (\mathsf{\gamma }\subset \mathrm{Span} V_N) ,$$

where $P_N$ is a real projective space associated with $\mathrm{Span} V_N$; i.e., $P_N$ is a set of orbits of the multiplicative group $R^{*}=R\backslash \left\{0\right\}$ acting upon $\mathrm{Span} V_N\backslash \left\{0\right\}$. As far as the present interpretation is concerned, the topological properties of space $P_N$ are important, $\mathrm{Card} N< {\aleph }_0$ (surely, first of all, its compactness), in particular, if $\dim \mathrm{Span} V_N=3$, then the 2-manifold $P_N$ is constructed like a Möbius bund, to which a round is stuck along its boundary [25] (p. 162). Note, in space $P_N$, $\mathrm{Card} N\le {\aleph }_0$ it is possible to introduce a structure of the CW-complex [25] (p. 140), which is important in case of consideration of the issue of geometric realization $P_N$ [25] (p. 149); furthermore, it simultaneously aids to deepening the theory of vector fields [26]. In the given context, according to Theorem 3 [27], Theorem 2.3 [25] (p. 47) and Theorem 3 [28] (p. 61), under the condition of bijectivity (mutual reciprocity) of operator $\mathsf{\Phi }$, it is possible to compute the fundamental group [25] (p. 46) of the topological space $(\mathsf{\Phi }(P_N),𝒯)$, where $𝒯$ is the topology of convergence with respect to measure $\mathsf{\mu }$ [11] (p. 58).

When using these remarks, one can easily formulate a “projective variant” of Theorem 3 (see Theorem 6), by replacing the construction of the absorbing set $Q$ with a projective space $P_N$, in this case, it is possible to take account of the entropy properties [6] of operator $\mathsf{\Phi }$, while considering the functional of the following form:

$$\mathrm{Entrp} (N):= {({\displaystyle \underset{T}{\int }({\sup }_{\mathrm{L}}\mathsf{\Phi }(P_N)}(\mathsf{\tau }))}^2 \mathsf{\mu } (d\mathsf{\tau }){)}^{1/2}$$

(6)

Without going into obvious details, we have to state that if $N\subset N^{*}$ and $\mathrm{Entrp} (N^{*}) \ne 0$ then $\mathrm{Entrp} (N^{*})\ge \mathrm{Entrp} (N) .$

Theorem 6.

The BDR-problem (1)–(2) is solvable if and only if $\mathrm{Entrp}(N)\ge 0.$ Furthermore, if the map

$$(g,w,v,q,s,h)\mapsto M (g,w,v,q,s,h):=A_{1}g+A_{0}w+B_{0}v+B_{1}q+B_{2}s+B_{3}h$$

represents an $M_2$ -operator of $\left|\right|\cdot |{|}_{L(H,X)}$ -optimal realization (2), then $\left|\right|\cdot |{|}_{\mathbf{L}}$ -norm of operator $M$ has the lowest estimate

$$\left|\right|(A_1,A_0,B_0,B_1,B_2,B_3)|{|}_{\mathbf{L}} \ge \mathrm{Entrp} (N) .$$

Proof. 

According to Theorem 3, ${\sup }_{\mathrm{L}}\mathsf{\Phi }(P_N)\in {\mathrm{L}}_2(T,R)$ and if $(A_1,A_0,$ $B_0,B_1,B_2,B_3)\in {\mathbf{L}}_2$ is an ordered set of the operator functions, which characterizes the $\left|\right|\cdot |{|}_{L(H,X)}$ -optimal $M_2$ -operator of BDR-system (2), then, using the Cauchy−Bunyakovskii inequality, we obtain

$$d^{2}w/d{t}^2=A_{1}g+A_{0}w+B_{0}v+B_{1}q+B_{2}s+B_{3}h , \forall (g,w,v,q,s,h)\in V_N\Rightarrow$$

$$\left|\right|d^{2}w/d{t}^2|{|}_X=|\left|A_1\right|{|}_{L(X,X)}\left|\right|g|{|}_X+|\left|A_0\right|{|}_{L(X,X)}\left|\right|w|{|}_X+|\left|B_0\right|{|}_{L(Y,X)}\left|\right|v|{|}_Y+$$

$$+\left|\right|B_1\left|{|}_{L(Z,X)}\right|\left|q\right|{|}_Z+\left|\right|B_2\left|{|}_{L(Z,X)}\right|\left|s\right|{|}_Z+\left|\right|B_3\left|{|}_{L(Z,X)}\right|\left|h\right|{|}_Z , \forall (g,w,v,q,s,h)\in V_N\Rightarrow$$

$$\Rightarrow \mathsf{\Phi } (g,w,v,q,s,h)(t)\le ( ||A_1(t)|{|}_{L(X,X)}^2+\left|\right|A_0(t)|{|}_{L(X,X)}^2+||B_0(t)|{|}_{L(Y,X)}^2+$$

$$+ \left|\right|B_1(t)|{|}_{L(Z,X)}^2+||B_2(t)|{|}_{L(Z,X)}^2+\left|\right|B_3(t)|{|}_{L(Z,X)}^2{)}^{1/2} , \forall (g,w,v,q,s,h)\in V_N\Rightarrow$$

$$\Rightarrow {( {\displaystyle \underset{T}{\int }({\sup }_{\mathrm{L}}\mathsf{\Phi }(P_N)}(\mathsf{\tau }))}^2 \mathsf{\mu } (d\mathsf{\tau }) {)}^{1/2} \le \left|\right|(A_1,A_0,B_0,B_1,B_2,B_3)|{|}_{\mathbf{L}} .$$

□

In conclusion, consider the two examples illustrating the potential of the aids of computer algebra [29,30] in the bilinear differential modeling described above. Therefore, we intend to partially reject an illusion that the authors have concentrated their efforts exclusively on the ideological (theoretical) aspect the qualitative theory of $M_2$ -continuity (on account of Remark 3).

Example 1.

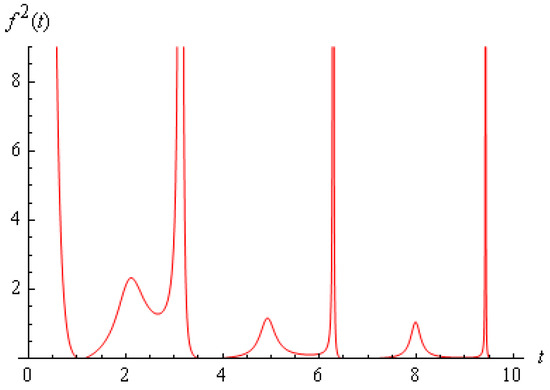
Let $T=[0, 10],$ $Y :=X :=Z ,$ $A_1=0\in L(X,X) , {\mathbb{B}}_1={\mathbb{B}}_3=0\in \mathcal{L}(X^2,X) ,$ ${\mathbb{B}}_2=<\cdot ,\cdot {>}_{X}e ,$ where $<\cdot ,\cdot {>}_X$ is a scalar product in $X, e\in X,$ $\left|\right|e|{|}_X =1$ and

$$t\mapsto x(t)=(t\sin t)e ,t\mapsto u(t)=0\in {\mathrm{L}}_2(T,X).$$

Hence

$$\mathrm{Entrp} \left(N\right)=\mathrm{Entrp} ( \{ (x,u,{\mathbb{B}}_1(x,x),{\mathbb{B}}_2(x,dx/dt),{\mathbb{B}}_3(dx/dt,dx/dt) ) \left\}\right)=\infty$$

i.e., function

$$f:={\sup }_{\mathrm{L}}\mathsf{\Phi }(P_N)=\left|\right|d^{2}x/d{t}^2|{|}_X{(|\left|x\right|{|}_X^2+\left|\right|{\mathbb{B}}_2(x,dx/dt)|{|}_X^2)}^{-1/2}$$

does not belong to class ${\mathrm{L}}_2(T,R)$ (see Figure 1) and, consequently, according to Theorem 6, realization (2) for the uncontrolled process $N$ does not exist.

Figure 1. The entropy $\mathrm{Entrp} (N)$ equal ∞.

$$f^2(t)={(2\cos t-t\sin t)}^2{({( t\sin t)}^2+{(t\sin t)}^2{(\sin t+t\cos t)}^2)}^{-1}$$

Example 2.

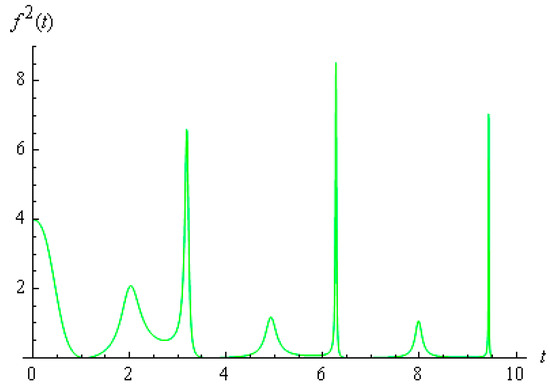
Let us change the problem statement with respect to Example 1, while putting $t\mapsto u(t)=(t{\sin }^{2}t+2^{-1}{t}^2\sin 2t+\cos t)e.$ Hence $\mathrm{Entrp}(N)<\infty$(see Figure 2), i.e.,

$$f:={\sup }_{\mathrm{L}}\mathsf{\Phi }(P_N)=\left|\right|d^{2}x/d t^2|{|}_X{( |\left|x\right|{|}_X^2+\left|\right|{\mathbb{B}}_2(x, d x/d t)|{|}_X^2+|\left|u\right|{|}_Y^2 )}^{-1/2}\in {\mathrm{L}}_2(T,R)$$

and, consequently, realization (2) for the controlled process $N$ exists; it may readily be ascertained that $d^{2}x/d{t}^2+x=2u-2{\mathbb{B}}_2(x,dx/dt).$

Figure 2. The entropy $\mathrm{Entrp} (N)$ is finite.

$$\begin{gathered} f^2(t)={(2\cos t-t\sin t)}^2\times ({( t\sin t)}^2+ \\ +{(t\sin t)}^2{(\sin t+t\cos t)}^2+{( t{\sin }^2 t+2^{-1}{t}^2\sin 2t+\cos t)}^2{)}^{-1} \end{gathered}$$

Examples 1 and 2 illustrate the obvious fact that if the dimension of the behavioristic dynamic system under investigation (modeling) is “rather high” then the automated symbolic analysis of solvability of the problem of its differential realization may be realized only on the methodological ground of contemporary computer algebra (possibly with elaboration of new specialized algorithms). Such direct “contact” of a nonlinear infinite-dimensional theory of differential realization of complex physic phenomena and the methods of computer algebra, is expected to be fruitful both for theoretical physics and for mathematics.

6. Conclusions

As far as the history of natural science is concerned, the problem of “optimization of the adequacy” of mathematical models, which describe the physical processes observed, has always been the central problem (it is sufficient to indicate to Ptolemeus “Almagest” and to Kepler’s laws). Within the frames of the given context, the principal goal of contemporary theoretical natural science presumes an explanation of the given set of the observed physical processes with the aid of some minimal set of postulated mathematical concepts and the quantitative laws expressed via them. The present work has been fulfilled within the framework of exactly this methodological approach, different to the mathematical problems of the bilinear non-autonomous differential second-order realization of infinite-dimensional nonlinear behavioral dynamic systems.

To this end, the present paper has developed a qualitative functional-geometric approach allowing one to see the problems of second-order differential realization bound up with the exogenous behavior of an infinite-dimensional dynamic system (in the system-theoretic problem statement) in a new light, when the modeled operators are burdened with the condition, which provides obvious continuity of the integral representation of equations of the realization model. Furthermore, we would like to understand what corrections have to be introduced into the theory of non-linear functional Relay-Ritz operators [27] in order to reconsider (see in a new light) the provisions of converse problems bound up with bilinear non-autonomous second-order evolution equations and analyze them in greater detail from the viewpoint of projective geometry, entropy analysis and qualitative theory of differential realization.

It so happened that the application aspect of the BDR-problem has remained beyond the frames of the present paper. The solvability of the problem of differential realization itself internally presumes the process of a posteriori constructing models [31,32,33,34], while including also the models for inverse problems of neurodynamics [35,36] on the basis of processing information of contemporary multichannel neural implants [37]. So, it is necessary to note, the material of the present paper may be considered as the basis for the initial (and, possibly, necessary) stage in the study of realization/identification of differential bilinear systems (of orders 2 and higher [7,15]) in the Hilbert space, as a division of the theory of inverse problems of infinite-dimensional nonlinear analysis; in particular, on the basis of development (see Examples 1 and 2 above) of computer algebra methods and aids [29,30]. In this connection, in the case of finite-dimensional systems, we can refer the reader to [38], wherein a constructive procedure of building up bilinear differential realizations has been proposed, which allows us to show how one can model Euler equations in the capacity of some empirical extrapolation of the realization of the observed spatial rotation motions of a rigid body in the aspect of statement of the problem of structural identification of differential equations bound up with dynamics of nonlinear physical processes.

When considering the methodological aspect of the present paper in the context of the entropy issue [6,39], it is worth noting that functional (6) may be interpreted as the entropy characteristic for the behavioristic $N$ -system to be modeled, when the $\left|\right|\cdot |{|}_{\mathbf{L}}$ -estimate of the value of $\mathrm{Entrp} (N)$ for the ${(A_0, A_1, B_0, B_1, B_2, B_3)}_2$ -model of the $\left|\right|\cdot |{|}_{L(H,X)}$ -optimal differential realization of $N$ -system stands out in the capacity of the measure of its “internal disorder”. Therefore, in the case of nonlinear dynamic processes (1), which take place in the scrutinized (BDR-modeled) $N$ -system, entropy (6) either grows or remains constant, when the trajectory bundle $N$ remains unchanged. Due to Theorem 6, within the frames of the given mathematical paradigm, the qualitative BDR-theory may conceptually be constructed on the analytical basis of the following “ad hoc-postulate”: the behavioral $N$ -system (1) possesses BDR-representation (2) if and only if entropy $\mathrm{Entrp} (N)$ is finite.

Without any additional reasoning, which motivates the “ad hoc-postulate” in the context of Remark 3, let us note that the issue bound up with understanding of when the “ad hoc-postulate” makes the corresponding $M_2$ -continuation in the problem statement for the Hilbert space (continuously embedded into the Banach space), while forming an everywhere dense space [21] (p. 175) (and, in this case, some identified operators shall have an analytical representation in the class of strongly positive definite [21] (p. 176) self-conjugated operators), is quite complex and, nevertheless, it is attractive from the system-theoretic viewpoint. The issue of solvability of the problem of differential realization in the class of hyperbolic models [21] (p. 456) is tightly tied up with abovementioned functional-analytical aspect. It surely forms a special (separate) investigation. This direction is seen by us as a quite perspective one, which is bound up with investigations of the QTDR-problems of poly-linear non-autonomous differential evolution equations of higher orders. This is bound up with the application of our ideas to the issues of modeling nonlinear equations of neuro-morphous dynamics [35,36], while giving an excellent example of the interaction between nonlinear functional analysis and mathematical physics. On the whole, the idea of applying abstract methods of the theory of nonlinear differential realization of higher orders (with or without delay) is really useful both as the integrating factor and as the source of new results bound up with the theory of nonlinear mathematical modeling of complex (interconnected) infinite-dimensional dynamic systems. It is possible to hope that development of system-theoretic ideas of QTDR will (i) foster elevation of the level of mathematical culture of physicists, and (ii) stimulate a deeper understanding of important problems and perspectives of physics and a way to develop physics by mathematicians.